Quantum Integral Inequalities in the Setting of Majorization Theory and Applications

Abstract

In recent years, the theory of convex mappings has gained much more attention due to its massive utility in different fields of mathematics. It has been characterized by different approaches. In 1929, G. H. Hardy, J. E. Littlewood, and G. Polya established another characterization of convex mappings involving an ordering relationship defined over ${\mathbb{R}}^{\mathfrak{n}}$ known as majorization theory. Using this theory many inequalities have been obtained in the literature. In this paper, we study Hermite–Hadamard type inequalities using the Jensen–Mercer inequality in the frame of $\underset{\dot{}}{\mathrm{q}}$-calculus and majorized l-tuples. Firstly we derive $\underset{\dot{}}{\mathrm{q}}$-Hermite–Hadamard–Jensen–Mercer (H.H.J.M) type inequalities with the help of Mercer’s inequality and its weighted form. To obtain some new generalized (H.H.J.M)-type inequalities, we prove a generalized quantum identity for $\underset{\dot{}}{\mathrm{q}}$-differentiable mappings. Next, we obtain some estimation-type results; for this purpose, we consider $\underset{\dot{}}{\mathrm{q}}$-identity, fundamental inequalities and the convexity property of mappings. Later on, We offer some applications to special means that demonstrate the importance of our main results. With the help of numerical examples, we also check the validity of our main outcomes. Along with this, we present some graphical analyses of our main results so that readers may easily grasp the results of this paper.

1. Introduction and Preliminaries

A set $\mathcal{C}\subseteq \mathbb{R}$ is said to be convex, if

$$(1-{\varrho }_{\divideontimes }){\tilde{\aleph }}_1+{\varrho }_{\divideontimes }{\tilde{\aleph }}_2\in \mathcal{C},\forall {\tilde{\aleph }}_1,{\tilde{\aleph }}_2\in \mathcal{C},{\varrho }_{\divideontimes }\in [0,1].$$

A mapping $\tilde{\mathfrak{F}}:\mathcal{C}\to \mathbb{R}$ is said to be convex or $\tilde{\mathfrak{F}}\in {\mathcal{C}}_{\mathcal{M}}$, if

$$\tilde{\mathfrak{F}}((1-{\varrho }_{\divideontimes }){\tilde{\aleph }}_1+{\varrho }_{\divideontimes }{\tilde{\aleph }}_2)\le (1-{\varrho }_{\divideontimes })\tilde{\mathfrak{F}}({\tilde{\aleph }}_1)+{\varrho }_{\divideontimes }\tilde{\mathfrak{F}}({\tilde{\aleph }}_2),\forall {\tilde{\aleph }}_1,{\tilde{\aleph }}_2\in \mathcal{C},{\varrho }_{\divideontimes }\in [0,1].$$

These classical concepts of convexity have held a widespread position in the different areas of pure and applied sciences, for example, they play fundamental roles in optimization theory, majorization theory, operations research, and mathematical economics. Convexity has also close a relationship with the idea of symmetry. It is also worth mentioning right here that quite a few big properties of symmetric convex sets can be discovered in the literature. A beneficial factor of viewing this relationship is that we work on one and practice it to the other. For some greater useful information, see [1,2]. Moreover, this principle of convexity additionally has a pivotal role in developing the theory of inequalities. A wide type of inequalities has direct consequences for the purposes of the convexity property of the mappings. One of the most studied effects in the concept of inequalities pertaining to convex mappings is Hermite–Hadamard’s inequality. It reads as:

Let $\tilde{\mathfrak{F}}\in {\mathcal{C}}_{\mathcal{M}}$ on $I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\subseteq \mathbb{R}$, then

$$\tilde{\mathfrak{F}}\left(\frac{{\tilde{\aleph }}_1+{\tilde{\aleph }}_2}{2}\right)\le \frac{1}{{\tilde{\aleph }}_2-{\tilde{\aleph }}_1}\underset{{\tilde{\aleph }}_1}{\overset{{\tilde{\aleph }}_2}{\int }}\tilde{\mathfrak{F}}\left(\mathsf{{\rm Y}}\right)\mathrm{d}\mathsf{{\rm Y}}\le \frac{\tilde{\mathfrak{F}}({\tilde{\aleph }}_1)+\tilde{\mathfrak{F}}({\tilde{\aleph }}_2)}{2}.$$

Another significant result related to the convexity property of the mappings is Jensen’s inequality, which reads as:

Let $0<{\mathsf{{\rm Y}}}_1\le {\mathsf{{\rm Y}}}_2\le {\mathsf{{\rm Y}}}_3\le \dots \le {\mathsf{{\rm Y}}}_{\mathfrak{n}}$, and let $\varpi =({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\mathfrak{n}})$ nonnegative weights such that ${\displaystyle \sum _{\widehat{\varsigma }=0}^{\mathfrak{n}}}\varpi =1$. If $\tilde{\mathfrak{F}}\in {\mathcal{C}}_{\mathcal{M}}$ on $I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\subseteq \mathbb{R}$, then

$$\tilde{\mathfrak{F}}\left(\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{\varpi }_{\widehat{\varsigma }}{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\right)\le \sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{\varpi }_{\widehat{\varsigma }}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\right),$$

where ${\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\in [{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]$, and ${\varpi }_{\widehat{\varsigma }}\in [0,1]$, $(\widehat{\varsigma }=\overline{1,\mathfrak{n}})$. For more detail, see [3].

In Mercer et al. [4] another significant inequality known as Jensen–Mercer inequality was proven.

Let $\tilde{\mathfrak{F}}\in {\mathcal{C}}_{\mathcal{M}}$ on $I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\subseteq \mathbb{R}$, then

$$\tilde{\mathfrak{F}}\left({\tilde{\aleph }}_1+{\tilde{\aleph }}_2-\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{\varpi }_{\widehat{\varsigma }}{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\right)\le \tilde{\mathfrak{F}}\left({\tilde{\aleph }}_1\right)+\tilde{\mathfrak{F}}\left({\tilde{\aleph }}_2\right)-\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{\varpi }_{\widehat{\varsigma }}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\right),$$

(1)

for each ${\mathsf{{\rm Y}}}_{\widehat{\varsigma }}\in [{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]$ and ${\varpi }_{\widehat{\varsigma }}\in [0,1]$, $(\widehat{\varsigma }=\overline{1,\mathfrak{n}})$ with ${\sum }_{\widehat{\varsigma }=1}^{\mathfrak{n}}\varpi =1$.

By using inequality (1), Kian and Moslehian prove the Hermite–Jensen–Mercer inequality in [5]. Recently, several papers have been devoted to the generalization of the Hermite–Jensen–Mercer inequality. For more recent and related results connected with the Jensen–Mercer inequality and the Hermite–Jensen–Mercer inequality, see [6,7,8,9,10].

One of the most investigated and studied generalizations of calculus in the last few decades is known as $\underset{\dot{}}{\mathrm{q}}$-calculus. It is some sort of special case of time scale calculus with domain $\underset{\dot{}}{\mathrm{q}}\in (0,1)$. It has numerous applications in number theory, combinatorics, special mappings, mathematical analysis, etc. It works as a bridge between mathematics and physics. Now, we describe some basics notions of $\underset{\dot{}}{\mathrm{q}}$-calculus that are necessary for further discussion.

Tariboon and Ntouyas have defined the $\underset{\dot{}}{\mathrm{q}}$-derivative as:

Definition 1

([11]). Assume $\tilde{\mathfrak{F}}:J=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\subseteq \mathbb{R}\to \mathbb{R}$ is a continuous mapping and suppose $\mathsf{{\rm Y}}\in J$, then

$$\begin{array}{c}\hfill {}_{{\tilde{\aleph }}_1}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}(\mathsf{{\rm Y}})=\frac{\tilde{\mathfrak{F}}(\mathsf{{\rm Y}})-\tilde{\mathfrak{F}}(\underset{\dot{}}{q}\mathsf{{\rm Y}}+(1-\underset{\dot{}}{q}){\tilde{\aleph }}_1)}{(1-\underset{\dot{}}{q})(\mathsf{{\rm Y}}-{\tilde{\aleph }}_1)},\mathsf{{\rm Y}}\ne {\tilde{\aleph }}_1,0<\underset{\dot{}}{q}<1.\end{array}$$

(2)

We say that $\tilde{\mathfrak{F}}$ is $\underset{\dot{}}{\mathrm{q}}$–differentiable on J provided ${}_{{\tilde{\aleph }}_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\mathsf{{\rm Y}}\right)$ exists for all $\mathsf{{\rm Y}}\in J$. Note that if ${\tilde{\aleph }}_1=0$ in (1), then ${}_0{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}={\mathfrak{D}}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}$, where ${\mathfrak{D}}_{\underset{\dot{}}{\mathrm{q}}}$ is the well-known classical $\underset{\dot{}}{\mathrm{q}}$-derivative of the mapping $\tilde{\mathfrak{F}}\left(\mathsf{{\rm Y}}\right)$ defined by

$$\begin{array}{c}\hfill {\mathfrak{D}}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}(\mathsf{{\rm Y}})=\frac{\tilde{\mathfrak{F}}(\mathsf{{\rm Y}})-\tilde{\mathfrak{F}}(\underset{\dot{}}{\mathrm{q}}\mathsf{{\rm Y}})}{(1-\underset{\dot{}}{\mathrm{q}})\mathsf{{\rm Y}}}.\end{array}$$

Next, we recall the well-known $\underset{\dot{}}{\mathrm{q}}$ number:

$${[\mathfrak{n}]}_{\underset{\dot{}}{\mathrm{q}}}=\frac{1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}}{1-\underset{\dot{}}{\mathrm{q}}}=1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2+\dots +{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}-1},\underset{\dot{}}{\mathrm{q}}\in (0,1).$$

The $\underset{\dot{}}{\mathrm{q}}$-Jackson integral from 0 to ${\tilde{\aleph }}_2$ for $0<\underset{\dot{}}{\mathrm{q}}<1$ is defined as:

$$\begin{array}{c}\hfill {\int }_0^{{\tilde{\aleph }}_2}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right){}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }=(1-\underset{\dot{}}{\mathrm{q}}){\tilde{\aleph }}_2\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left(b{\mathrm{q}}^{\mathfrak{n}}\right),\end{array}$$

(3)

provided the sum converges absolutely. Jackson also gave the $\underset{\dot{}}{\mathrm{q}}$–Jackson integral on a generic interval $[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]$ as:

$$\begin{array}{c}\hfill {\int }_{{\tilde{\aleph }}_1}^{{\tilde{\aleph }}_2}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right)d_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }={\int }_0^{{\tilde{\aleph }}_2}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right)d_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }+{\int }_0^{{\tilde{\aleph }}_1}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right)d_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }.\end{array}$$

We now rewrite the definition of a ${\underset{\dot{}}{\mathrm{q}}}_{{\tilde{\aleph }}_1}$-definite integral.

Definition 2

([11]). Let $\tilde{\mathfrak{F}}:[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ be a continuous mapping. Then, the ${\underset{\dot{}}{q}}_{{\tilde{\aleph }}_1}$-definite integral on $[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]$ is defined as:

$${\int }_{{\tilde{\aleph }}_1}^{{\tilde{\aleph }}_2}\tilde{\mathfrak{F}}{({\varrho }_{\divideontimes })}_{{\tilde{\aleph }}_1}{d}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }=(1-\underset{\dot{}}{q})({\tilde{\aleph }}_2-{\tilde{\aleph }}_1)\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{q}}^{\mathfrak{n}}\tilde{\mathfrak{F}}({\underset{\dot{}}{q}}^{\mathfrak{n}}{\tilde{\aleph }}_2+(1-{\underset{\dot{}}{q}}^{\mathfrak{n}}){\tilde{\aleph }}_1)=({\tilde{\aleph }}_2-{\tilde{\aleph }}_1){\int }_0^1\tilde{\mathfrak{F}}((1-{\varrho }_{\divideontimes }){\tilde{\aleph }}_1+{\varrho }_{\divideontimes }{\tilde{\aleph }}_2)d_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }.$$

The following is the quantum analogue of Hermite–Hadamard’s inequality:

Theorem 1.

Let $\tilde{\mathfrak{F}}:[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ be a convex mapping, then for $0<\underset{\dot{}}{q}<1$, we have

$$\begin{array}{c}\hfill \tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{q}{\tilde{\aleph }}_1+{\tilde{\aleph }}_2}{1+\underset{\dot{}}{q}}\right)\le \frac{1}{{\tilde{\aleph }}_2-{\tilde{\aleph }}_1}{\int }_{{\tilde{\aleph }}_1}^{b}f\left(\mathsf{{\rm Y}}\right){}_{{\tilde{\aleph }}_1}{d}_{\underset{\dot{}}{q}}\mathsf{{\rm Y}}\le \frac{qf\left({\tilde{\aleph }}_1\right)+\tilde{\mathfrak{F}}\left({\tilde{\aleph }}_2\right)}{1+\underset{\dot{}}{q}}.\end{array}$$

(4)

We now present the definition of the ${\underset{\dot{}}{\mathrm{q}}}^{{\tilde{\aleph }}_2}$-definite integral.

Definition 3

([12]). Let $\tilde{\mathfrak{F}}:[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ be a continuous mapping. Then, the ${\underset{\dot{}}{q}}^{{\tilde{\aleph }}_2}$-definite integral on $[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]$ is defined as:

$${\int }_{{\tilde{\aleph }}_1}^{{\tilde{\aleph }}_2}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right){}^{{\tilde{\aleph }}_2}{d}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }=(1-\underset{\dot{}}{q})({\tilde{\aleph }}_2-{\tilde{\aleph }}_1)\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{q}}^{\mathfrak{n}}\tilde{\mathfrak{F}}({\underset{\dot{}}{q}}^{\mathfrak{n}}{\tilde{\aleph }}_1+(1-{\underset{\dot{}}{q}}^{\mathfrak{n}}){\tilde{\aleph }}_2)=({\tilde{\aleph }}_2-{\tilde{\aleph }}_1){\int }_0^1\tilde{\mathfrak{F}}(ta+(1-{\varrho }_{\divideontimes }){\tilde{\aleph }}_2)d_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }.$$

Using Definition 3, one can have the following quantum version of the Hermite–Hadamard’s inequality.

Theorem 2

([13]). Let $\tilde{\mathfrak{F}}:[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ be a convex mapping, then for $0<\underset{\dot{}}{q}<1$, we have

$$\begin{array}{c}\hfill \tilde{\mathfrak{F}}\left(\frac{{\tilde{\aleph }}_1+\underset{\dot{}}{q}{\tilde{\aleph }}_2}{1+\underset{\dot{}}{q}}\right)\le \frac{1}{{\tilde{\aleph }}_2-{\tilde{\aleph }}_1}{\int }_{{\tilde{\aleph }}_1}^{b}f\left(\mathsf{{\rm Y}}\right){}^{{\tilde{\aleph }}_2}{\mathrm{d}}_{\underset{\dot{}}{q}}\mathsf{{\rm Y}}\le \frac{\tilde{\mathfrak{F}}\left({\tilde{\aleph }}_1\right)+qf\left({\tilde{\aleph }}_2\right)}{1+\underset{\dot{}}{q}}.\end{array}$$

(5)

In recent years, we have seen that a variety of different approaches have been used in obtaining new analogues of classical inequalities. For instance, many researchers have used the concepts of quantum calculus. Ref. [14] established some $\underset{\dot{}}{\mathrm{q}}$ variants of the Holder’s, power–mean, and Hermite–Hadamard’s inequalities. After this, Noor et al. [15] derived some $\underset{\dot{}}{\mathrm{q}}$-estimation type results regarding H.H.I. In the following perspective, Alp et al. [13] formulated some $\underset{\dot{}}{\mathrm{q}}$-mid-point H.H type inequalities and provided the correct proof of $\underset{\dot{}}{\mathrm{q}}$-H.H.I. In Ref. [16], the authors obtained some Anderson-like inequalities through h and $\underset{\dot{}}{\mathrm{q}}$ integrals. Ref. [17] Arunrat et al. derived the quantum analogues of the Chebychev inequalities. In ref. [18], Almtairi analysed the $\underset{\dot{}}{\mathrm{q}}$-integral inequalities via $(h,m)$ convexity. In Ref. [19], Kalssom et al. obtained some new generalizations of the Ostrowski-type inequalities via generalized convex mappings.

For some recent studies and more details, see [20,21,22].

Majorization is the characterization of convex mappings the through partial ordered relationship of two l-tuples $u=(u_1,u_2,\dots ,u_l)$ and $\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l)$, if $\theta \prec u$, then, geometrically, it can be viewed as a component of $\mathsf{{\rm Y}}$ that is less spread out then u. Now we recall the majorization theorem due to Hardy Littlewood and Polya [23].

Theorem 3.

Let $u=(u_1,u_2,\dots ,u_l)$ and $\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l)$ be two real l-tuples such that ${\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},u_{{\pi }_{\cdot }}\in I=[a,b]$. Then

$$\begin{array}{c}\hfill \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\end{array}$$

is valid for each continuous convex mapping $\tilde{\mathfrak{F}}:I\to \mathbb{R}$ if and only if $u\prec \mathsf{{\rm Y}}$.

The weighted version of the above theorem is given as:

Theorem 4

([24]). Let $\tilde{\mathfrak{F}}:I\to \mathbb{R}$ be continuous convex mapping and $\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l),u=(u_1,u_2,\dots ,u_l)$ and $p=(p_1,p_2,\dots ,p_l)$ be the three l-tuples such that ${\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},u_{{\pi }_{\cdot }}\in I,p_{{\pi }_{\cdot }}\ge 0,{\pi }_{\cdot }\in \{1,2,3,\dots ,l\}$. If u is a decreasing l-tuple and

$$\begin{array}{c}\hfill \sum _{{\pi }_{\cdot }=1}^k{p}_{{\pi }_{\cdot }}{u}_{[{\pi }_{\cdot }]}\le \sum _{{\pi }_{\cdot }=1}^k{p}_{{\pi }_{\cdot }}{\mathsf{{\rm Y}}}_{[{\pi }_{\cdot }]}k=1,2,3,\dots ,l-1,\end{array}$$

(6)

$$\begin{array}{c}\hfill \sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}{u}_{[{\pi }_{\cdot }]}=\sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}{\mathsf{{\rm Y}}}_{[{\pi }_{\cdot }]},\end{array}$$

then

$$\begin{array}{c}\hfill \sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\le \sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right).\end{array}$$

Theorem 5

([25]). Suppose that $\tilde{\mathfrak{F}}:I\to \mathbb{R}$ is a real valued convex mapping, $\left({\mathsf{{\rm Y}}}_{ij}\right)$ is a $\mathfrak{n}\times m$ real matrix, and $u=(u_1,u_2,\dots ,u_l)$ is a l-tuple such that $u_j,{\mathsf{{\rm Y}}}_{ij}\in I$ for all $\widehat{\varsigma },j,w_{\widehat{\varsigma }}\ge 0$ for $\widehat{\varsigma }=1,2,3,\dots ,\mathfrak{n}$ with ${\sum }_{\widehat{\varsigma }=1}^n{w}_{\widehat{\varsigma }}=1$. If u majorizes every row of ${\mathsf{{\rm Y}}}_{ij}$, then

$$\begin{array}{c}\hfill \tilde{\mathfrak{F}}\left(\sum _{j=1}^l{u}_{{\pi }_{\cdot }}-\sum _{j=1}^{l-1}\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{w}_i{x}_{ij}\right)\le \sum _{j=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\sum _{j=1}^{l-1}\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}{w}_{i}f\left({\mathsf{{\rm Y}}}_{ij}\right).\end{array}$$

Now we provide a weighted version of Theorem 5.

Theorem 6

([26]). Suppose that $\tilde{\mathfrak{F}}:I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ is a real valued convex mapping $\left({\mathsf{{\rm Y}}}_{ij}\right)$ is a $\mathfrak{n}\times m$ real matrix and $u=(u_1,u_2,\dots ,u_l)$ and $p=(p_1,p_2,\dots ,p_l)$ are two l-tuples such that $u_j,{\mathsf{{\rm Y}}}_{ij}\in I$, $p_{\widehat{\varsigma }},w_{\widehat{\varsigma }}\ge 0$ with $p_l\ne 0$ and $\varrho =\frac{1}{p_l}$ for $\widehat{\varsigma }=1,2,3,\dots ,\mathfrak{n}$ with ${\sum }_{\widehat{\varsigma }=1}^n{w}_{\widehat{\varsigma }}=1$. If u majorizes every row of ${\mathsf{{\rm Y}}}_{ij}$ and

$$\begin{array}{c}\hfill \sum _{j=1}^k{p}_j{\mathsf{{\rm Y}}}_{ij}\le \sum _{j=1}^k{p}_j{u}_j;k=1,2,3,\dots ,l-1,\sum _{j=1}^l{p}_j{\mathsf{{\rm Y}}}_{ij}=\sum _{j=1}^l{p}_j{u}_j,\end{array}$$

then

$$\begin{array}{c}\hfill \tilde{\mathfrak{F}}\left(\sum _{j=1}^l\varrho p_j{u}_j-\sum _{j=1}^{l-1}\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}\varrho p_j{w}_i{x}_{ij}\right)\le \sum _{j=1}^l\varrho p_j\tilde{\mathfrak{F}}\left(u_j\right)-\sum _{j=1}^{l-1}\sum _{\widehat{\varsigma }=1}^{\mathfrak{n}}\varrho p_j{w}_{\widehat{\varsigma }}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{ij}\right).\end{array}$$

The theories of majorization and convexity are interlinked with each other and have significant impacts on the theories of inequalities and linear algebra as well. Many researchers have devoted their efforts to generalizing the existing inequalities. Interested readers are referred to [27,28,29,30,31,32].

The main objective of this paper is to derive some new quantum analogues of a generalized Hermite–Hadamard–Jensen–Mercer type of inequalities essentially using $\underset{\dot{}}{\mathrm{q}}$-differentiable convex mappings and majorization theory. We discuss some applications to special means, which demonstrate the significance of our main results. We would like to mention here that, to the best of our knowledge, this is the first study of quantum analogues of certain classical inequalities via the theory of majorization. We hope that the ideas and techniques in this paper will inspire interested readers working in this field.

2. Main Results

In this section, we will discuss our main results.

Theorem 7.

Suppose that $\tilde{\mathfrak{F}}:I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ is real valued convex mapping and $u=(u_1,u_2,\dots ,u_l),\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l),and \Xi =({\Xi }_1,{\Xi }_2,\dots ,{\Xi }_l)$ are three l-tuples $u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }}$ for all ${\pi }_{\cdot }\in \{1,2,3,\dots ,l\}$. If $\mathsf{{\rm Y}}\prec u$ and $\Xi \prec u$, then

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\left[{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }+{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\left[\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{q}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{q}}}\right)+\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{q}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{q}}}\right)\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\sum _{{\pi }_{\cdot }=1}^{l-1}\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right).\hfill \end{array}$$

(7)

Proof. 

Let ${\varrho }_{\divideontimes }\in [0,1]$, then we may write

$$\begin{array}{c}\tilde{\mathfrak{F}}\left({\displaystyle \sum _{{\pi }_{\cdot }=1}^l}{u}_{{\pi }_{\cdot }}-{\displaystyle \sum _{{\pi }_{\cdot }=1}^{l-1}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ =\tilde{\mathfrak{F}}\left({\displaystyle \sum _{{\pi }_{\cdot }=1}^l}{u}_{{\pi }_{\cdot }}-{\displaystyle \sum _{{\pi }_{\cdot }=1}^{l-1}}\left(\frac{{\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }}+{\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{2}\right)\right).\hfill \end{array}$$

(8)

In order to apply Theorem 5 on (8), first we show that u majorizes r and z, where $r=(r_1,r_2,\dots ,r_l),z=(z_1,z_2,\dots ,z_l),r_j={\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }}$ and $z_j={\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}$ for ${\pi }_{\cdot }=\{1,2,3,\dots ,l\}$.

For this, let ${\sum }_{j=1}^k{x}_{[j]}={\beta }_{1k}$ and ${\sum }_{j=1}^k{y}_{[j]}={\beta }_{2k}$ for $k=1,2,\dots ,l-1$. Then we derive

$$\begin{array}{c}\hfill \sum _{j=1}^k{r}_{[j]}={\varrho }_{\divideontimes }\sum _{j=1}^k{x}_{[j]}+(1-{\varrho }_{\divideontimes })\sum _{j=1}^k{y}_{[j]}={\varrho }_{\divideontimes }{\beta }_{1k}+(1-{\varrho }_{\divideontimes }){\beta }_{2k}.\end{array}$$

Since $\mathsf{{\rm Y}}\prec u$ and $\Xi \prec u$, then, from the definition of majorization, we have ${\sum }_{j=1}^k{x}_{[j]}\le {\sum }_{j=1}^k{u}_{[j]}$ and ${\sum }_{j=1}^k{y}_{[j]}\le {\sum }_{j=1}^k{u}_{[j]}$ that is

$$\begin{array}{c}\hfill {\beta }_{1k}\le \sum _{j=1}^k{u}_{[j]}\end{array}$$

(9)

and

$$\begin{array}{c}\hfill {\beta }_{2k}\le \sum _{j=1}^k{u}_{[j]}.\end{array}$$

(10)

Multiplying (9) by ${\varrho }_{\divideontimes }$ and (10) by $(1-{\varrho }_{\divideontimes })$ and then adding the resulting inequalities, we obtain

$$\begin{array}{c}\hfill \sum _{j=1}^k{r}_{[j]}={\varrho }_{\divideontimes }{\beta }_{1k}+(1-{\varrho }_{\divideontimes }){\beta }_{2k}\le \sum _{j=1}^k{u}_{[j]}.\end{array}$$

(11)

However, ${\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}={\sum }_{{\pi }_{\cdot }=1}^l{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}$ and ${\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}={\sum }_{{\pi }_{\cdot }=1}^l{\Xi }_{{\pi }_{\cdot }}$, then by using (11), we have

$$\begin{array}{c}\hfill \sum _{{\pi }_{\cdot }=1}^l{r}_{{\pi }_{\cdot }}=\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}.\end{array}$$

Hence $r\prec u$. Similarly, we can show that $z\prec u$. Then, by using Theorem 5 for $w_1=w_2=\frac{1}{2}$:

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}(\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }})+\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})).\hfill \end{array}$$

(12)

Now, taking $\underset{\dot{}}{\mathrm{q}}$-integration of (12) with respect to ${\varrho }_{\divideontimes }$, we obtain

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}{\int }_0^1\left(\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }})+\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})\right){}_0{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }.\hfill \\ \hfill & =\sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\left[{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v+{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\right],\hfill \end{array}$$

which gives the first inequality in (7). To obtain the second inequality, we use the left sides of Hermite–Hadamard’s inequalities (4) and (5). Thus, we have

$$\begin{array}{c}\hfill -\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\le -\sum _{{\pi }_{\cdot }=1}^{l-1}\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right),\end{array}$$

(13)

and

$$\begin{array}{c}\hfill -\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\le -\sum _{{\pi }_{\cdot }=1}^{l-1}\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right).\end{array}$$

(14)

Summing (13) and (14) and adding ${\sum }_{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)$ in the resulting inequality, we have

$$\begin{array}{cc}\hfill & \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\left[{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v+{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\left[\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)+\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)\right].\hfill \end{array}$$

This gives the second inequality in (7).

To prove our next relation, we use the following expression

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)=\tilde{\mathfrak{F}}\left[\frac{1}{2}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{1+\underset{\dot{}}{\mathrm{q}}}+\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{1+\underset{\dot{}}{\mathrm{q}}}\right)\right]\hfill \end{array}$$

From the convexity of $\tilde{\mathfrak{F}}$, we have

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right)\le \frac{1}{2}\left[\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{1+\underset{\dot{}}{\mathrm{q}}}\right)+\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{1+\underset{\dot{}}{\mathrm{q}}}\right)\right]\hfill \\ -{\displaystyle \sum _{{\pi }_{\cdot }=1}^{l-1}}\frac{1}{2}\left[\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)+\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)\right]\le -{\displaystyle \sum _{{\pi }_{\cdot }=1}^{l-1}}\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right).\hfill \end{array}$$

(15)

Adding ${\sum }_{{\pi }_{\cdot }=1}^l\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)$ to both sides of (15), we obtain the required result. □

Remark 1.

If we choose $l=2$ in Theorem 7, then we have the following inequalities

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(u_1+u_2-\left(\frac{{\mathsf{{\rm Y}}}_1+{\Xi }_1}{2}\right)\right)\hfill \\ \le \tilde{\mathfrak{F}}\left(u_1\right)+\tilde{\mathfrak{F}}\left(u_2\right)-\frac{1}{2\left({\Xi }_1-{\mathsf{{\rm Y}}}_1\right)}\left[{\int }_{{\mathsf{{\rm Y}}}_1}^{{\Xi }_1}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}^{{\Xi }_1}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }+{\int }_{{\mathsf{{\rm Y}}}_1}^{{\Xi }_1}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}_{{\mathsf{{\rm Y}}}_1}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }\right]\hfill \\ \le \tilde{\mathfrak{F}}\left(u_1\right)+\tilde{\mathfrak{F}}\left(u_2\right)-\frac{1}{2}\left[\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_1+\underset{\dot{}}{q}{\Xi }_1}{{[2]}_{\underset{\dot{}}{q}}}\right)+\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{q}{\mathsf{{\rm Y}}}_1+{\Xi }_1}{{[2]}_{\underset{\dot{}}{q}}}\right)\right]\hfill \\ \le \tilde{\mathfrak{F}}\left(u_1\right)+\tilde{\mathfrak{F}}\left(u_2\right)-\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_1+{\Xi }_1}{2}\right),\hfill \end{array}$$

which are proved by Budak and Kara in [22].

Theorem 8.

Suppose that $\tilde{\mathfrak{F}}:I=[{\tilde{\aleph }}_1,{\tilde{\aleph }}_2]\to \mathbb{R}$ is real valued convex mapping and $u=(u_1,u_2,\dots ,u_l),\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l),\Xi =({\Xi }_1,{\Xi }_2,\dots ,{\Xi }_l)$ are three l-tuples $u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }}$ for all ${\pi }_{\cdot }\in \{1,2,3,\dots ,l\}$ with $p_{{\pi }_{\cdot }}\ge 0$, $p_l\ne 0$ and $\varrho =\frac{1}{p_l}$. If Υ and Ξ are decreasing tuples and

$$\begin{array}{cc}\hfill & \sum _{{\pi }_{\cdot }=1}^k{p}_{{\pi }_{\cdot }}{\mathsf{{\rm Y}}}_{is}\le \sum _{{\pi }_{\cdot }=1}^k{p}_s{u}_{{\pi }_{\cdot }};k=1,2,3,\dots ,l-1,\sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}{\mathsf{{\rm Y}}}_{is}=\sum _{{\pi }_{\cdot }=1}^l{p}_s{u}_{{\pi }_{\cdot }},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \sum _{{\pi }_{\cdot }=1}^k{p}_{{\pi }_{\cdot }}{\Xi }_{is}\le \sum _{{\pi }_{\cdot }=1}^k{p}_s{u}_{{\pi }_{\cdot }};k=1,2,3,\dots ,l-1,\sum _{{\pi }_{\cdot }=1}^l{p}_{{\pi }_{\cdot }}{\Xi }_{is}=\sum _{{\pi }_{\cdot }=1}^l{p}_s{u}_{{\pi }_{\cdot }}.\hfill \end{array}$$

Then we have

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}{u}_{{\pi }_{\cdot }}-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{p_s{x}_{{\pi }_{\cdot }}+p_s{y}_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho }{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{p_{{\pi }_{\cdot }}}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\left[{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }+{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left({\varrho }_{\divideontimes }\right)}_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho p_{{\pi }_{\cdot }}}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\left[\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{q}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{q}}}\right)+\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{q}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{q}}}\right)\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}{p}_{s}f\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right).\hfill \end{array}$$

(16)

Proof. 

Let ${\varrho }_{\divideontimes }\in [0,1]$, then we may write

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}{u}_{{\pi }_{\cdot }}-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{p_s{x}_{{\pi }_{\cdot }}+p_s{y}_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ =\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}{u}_{{\pi }_{\cdot }}-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}\left(p_{{\pi }_{\cdot }}\frac{{\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }}+{\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{2}\right)\right).\hfill \end{array}$$

(17)

Let $r=(r_1,r_2,\dots ,r_l),z=(z_1,z_2,\dots ,z_l),r_j={\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }}$ and $z_j={\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}$ for ${\pi }_{\cdot }=\{1,2,3,\dots ,l\}$. By using the similar technique as in Theorem 7, we can show that r and z satisfy the following conditions ${\sum }_{{\pi }_{\cdot }=1}^{l-1}{p}_s{r}_{{\pi }_{\cdot }}\le {\sum }_{{\pi }_{\cdot }=1}^{l-1}{p}_s{u}_{{\pi }_{\cdot }}$, ${\sum }_{{\pi }_{\cdot }=1}^{l-1}{p}_s{z}_{{\pi }_{\cdot }}\le {\sum }_{{\pi }_{\cdot }=1}^{l-1}{p}_s{u}_{{\pi }_{\cdot }}$ for $k=1,2,\dots ,l-1$ and ${\sum }_{{\pi }_{\cdot }=1}^l{p}_s{r}_{{\pi }_{\cdot }}={\sum }_{{\pi }_{\cdot }=1}^l{p}_s{u}_{{\pi }_{\cdot }}$, ${\sum }_{{\pi }_{\cdot }=1}^l{p}_s{z}_{{\pi }_{\cdot }}={\sum }_{{\pi }_{\cdot }=1}^l{p}_s{u}_{{\pi }_{\cdot }}$

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l\varrho p_s{u}_{{\pi }_{\cdot }}-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{p_s{x}_{{\pi }_{\cdot }}+p_s{y}_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{s}f\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho }{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\left(p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }})+p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})\right).\hfill \end{array}$$

(18)

By $\underset{\dot{}}{\mathrm{q}}$-integrating the inequality (18) with respect to ${\varrho }_{\divideontimes }$, we have

$$\begin{array}{c}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l\varrho p_s{u}_{{\pi }_{\cdot }}-\varrho \sum _{{\pi }_{\cdot }=1}^{l-1}\left(\frac{p_s{x}_{{\pi }_{\cdot }}+p_s{y}_{{\pi }_{\cdot }}}{2}\right)\right)\hfill \\ \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho }{2}\sum _{{\pi }_{\cdot }=1}^{l-1}{p}_{{\pi }_{\cdot }}{\int }_0^1\left(\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\Xi }_{{\pi }_{\cdot }})+\tilde{\mathfrak{F}}({\varrho }_{\divideontimes }{\Xi }_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes }){\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})\right){}_0{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ =\sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{1}{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{\varrho }{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{p}_{{\pi }_{\cdot }}\left[{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v+{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\right].\hfill \end{array}$$

This proves the first inequality in (16). From Theorems 1 and 2, we have

$$\begin{array}{c}\hfill -\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\le -\sum _{{\pi }_{\cdot }=1}^{l-1}\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right).\end{array}$$

(19)

and

$$\begin{array}{c}\hfill -\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{1}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\le -\sum _{{\pi }_{\cdot }=1}^{l-1}\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right).\end{array}$$

(20)

From the inequalities (19) and (20), we can write

$$\begin{array}{cc}\hfill \sum _{{\pi }_{\cdot }=1}^l\varrho & p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho }{2}\sum _{{\pi }_{\cdot }=1}^{l-1}\frac{p_{{\pi }_{\cdot }}}{{\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\left[{\int }_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}^{{\Xi }_{\widehat{\varsigma }}}\tilde{\mathfrak{F}}{\left(v\right)}_{{\mathsf{{\rm Y}}}_{\widehat{\varsigma }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v+{\int }_{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}^{{\Xi }_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}{\left(v\right)}^{{\Xi }_{{\pi }_{\cdot }}}{\mathrm{d}}_{\underset{\dot{}}{\mathrm{q}}}v\right]\hfill \\ \hfill & \le \sum _{{\pi }_{\cdot }=1}^l\varrho p_{{\pi }_{\cdot }}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)-\frac{\varrho }{2}\sum _{{\pi }_{\cdot }=1}^{l-1}{p}_{{\pi }_{\cdot }}\left[\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)+\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)\right],\hfill \end{array}$$

which gives the second inequality in (16). The last inequality in (16) is obvious from the fact that

$$\begin{array}{c}\hfill -\frac{1}{2}\left[\tilde{\mathfrak{F}}\left(\frac{\underset{\dot{}}{\mathrm{q}}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)+\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+\underset{\dot{}}{\mathrm{q}}{\Xi }_{{\pi }_{\cdot }}}{{[2]}_{\underset{\dot{}}{\mathrm{q}}}}\right)\right]\le -\tilde{\mathfrak{F}}\left(\frac{{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+{\Xi }_{{\pi }_{\cdot }}}{2}\right).\end{array}$$

(21)

The proof is completed. □

We will now derive a new $\underset{\dot{}}{\mathrm{q}}$-integral identity. This result will serve as an auxiliary result for our coming results.

Lemma 1.

p Let $u=(u_1,u_2,u_3,\dots ,u_l)$, $\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,\dots ,{\mathsf{{\rm Y}}}_l)$ and $\Xi =({\Xi }_1,{\Xi }_2,\dots ,{\Xi }_l$ be the three l-tuples such that $u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }}\in [I]$ for all ${\pi }_{\cdot }\in \{1,2,\dots ,l\},{\varrho }_{\divideontimes }\in [0,1]$ and $\tilde{\mathfrak{F}}:J\to \mathbb{R}$ be a continuous mapping and $0<\underset{\dot{}}{q}<1$. If ${}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}$ is an integrable mapping on J, then

$$\begin{array}{c}\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\hfill \\ =\frac{\underset{\dot{}}{q}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{q}}{\int }_0^1(1-(1+\underset{\dot{}}{q}){\varrho }_{\divideontimes })\hfill \\ \times {}_{\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right){}_0{d}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes },\hfill \end{array}$$

(22)

where

$$\begin{array}{c}\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\hfill \\ \frac{1}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{\int }_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}^{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right){}_{\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{d}_{\underset{\dot{}}{q}}{\varrho }_{\divideontimes }\hfill \\ -\frac{qf\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)+\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)}{1+\underset{\dot{}}{q}}.\hfill \end{array}$$

Proof. 

Considering the right-hand side of (22) and using Definitions 1 and 2, we have

$$\begin{array}{c}\hfill I=\frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{I}_1,\end{array}$$

(23)

where

$$\begin{array}{cc}\hfill & I_1={\int }_0^1(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }){}_{\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right){}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & ={\int }_0^1(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes })\frac{1}{{\varrho }_{\divideontimes }(1-\underset{\dot{}}{\mathrm{q}}){\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\left[\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right.\hfill \\ \hfill & \left.-\tilde{\mathfrak{F}}\left(\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & ={\int }_0^1\frac{1}{{\varrho }_{\divideontimes }(1-\underset{\dot{}}{\mathrm{q}}){\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\left[\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right.\hfill \\ \hfill & \left.-\tilde{\mathfrak{F}}\left(\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & -\frac{(1+\underset{\dot{}}{\mathrm{q}})}{(1-\underset{\dot{}}{\mathrm{q}}){\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{\int }_0^1\left[\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right.\hfill \\ \hfill & \left.-\tilde{\mathfrak{F}}\left(\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes }\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-\underset{\dot{}}{\mathrm{q}}{\varrho }_{\divideontimes })\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & =\frac{1}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\left[\sum _{\mathfrak{n}=0}^{\infty }\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right.\hfill \\ \hfill & \left.-\sum _{\mathfrak{n}=0}^{\infty }\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}+1}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}+1})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]\hfill \\ \hfill & -\frac{1+\underset{\dot{}}{\mathrm{q}}}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\left[\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right.\hfill \\ \hfill & \left.-\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}+1}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}+1})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]\hfill \\ \hfill & =\frac{\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)-\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\hfill \\ \hfill & -\frac{1+\underset{\dot{}}{\mathrm{q}}}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & +\frac{1+\underset{\dot{}}{\mathrm{q}}}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=1}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & =\frac{\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)-\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\hfill \\ \hfill & -\frac{1+\underset{\dot{}}{\mathrm{q}}}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & +\frac{1+\underset{\dot{}}{\mathrm{q}}}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\left[\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)-\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right.\hfill \\ \hfill & \left.+\sum _{\mathfrak{n}=1}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\frac{\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)-\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}-\frac{1+\underset{\dot{}}{\mathrm{q}}}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\hfill \\ \hfill & +\frac{1+\underset{\dot{}}{\mathrm{q}}}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & -\frac{1+\underset{\dot{}}{\mathrm{q}}}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & =-\frac{\underset{\dot{}}{\mathrm{q}}\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)+\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\hfill \\ \hfill & +\frac{(1+\underset{\dot{}}{\mathrm{q}})(1-\underset{\dot{}}{\mathrm{q}})}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\frac{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\tilde{\mathfrak{F}}\left({\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)+(1-{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}})\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)\right)\hfill \\ \hfill & =-\frac{\underset{\dot{}}{\mathrm{q}}\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}\right)+\tilde{\mathfrak{F}}\left({\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)}{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}\hfill \\ \hfill & +\frac{(1+\underset{\dot{}}{\mathrm{q}})}{\underset{\dot{}}{\mathrm{q}}{\left({\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})\right)}^2}{\int }_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}^{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right){}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }.\hfill \end{array}$$

This completes the proof. □

If we take $l=2$, then the above identity gains the following form:

$$\begin{array}{c}\Omega (u_1,u_2,{\mathsf{{\rm Y}}}_1,{\Xi }_1)\hfill \\ =\frac{\underset{\dot{}}{\mathrm{q}}({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{1+\underset{\dot{}}{\mathrm{q}}}{\int }_0^1(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }){}_{\left(u_1+u_2-{\Xi }_1\right)}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)+(1-{\varrho }_{\divideontimes })\left(u_1+u_2-{\Xi }_1\right)\right){}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes },\hfill \end{array}$$

where

$$\begin{array}{c}\Omega (u_1,u_2,{\mathsf{{\rm Y}}}_1,{\Xi }_1)\hfill \\ \frac{1}{({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{\int }_{u_1+u_2-{\Xi }_1}^{u_1+u_2-{\mathsf{{\rm Y}}}_1}\tilde{\mathfrak{F}}\left({\varrho }_{\divideontimes }\right){}_{\left(u_1+u_2-{\Xi }_1\right)}{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }-\frac{\underset{\dot{}}{\mathrm{q}}\tilde{\mathfrak{F}}\left(u_1+u_2-{\Xi }_1\right)+\tilde{\mathfrak{F}}\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)}{1+\underset{\dot{}}{\mathrm{q}}}.\hfill \end{array}$$

Theorem 9.

Let $\tilde{\mathfrak{F}}:J\to \mathbb{R}$ be a continuous mapping. If $\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\right|$ is convex and integrable on J, then

$$\begin{array}{cc}\hfill & \left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|\hfill \\ \hfill & \le \frac{{\underset{\dot{}}{q}}^2{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{{[3]}_{\underset{\dot{}}{q}}{[2]}_{\underset{\dot{}}{q}}^4}\left([2(1+\underset{\dot{}}{q})(1+\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)]\sum _{{\pi }_{\cdot }=1}^l\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|\right.\hfill \\ \hfill & -\left[(1+3{\underset{\dot{}}{q}}^2+2{\underset{\dot{}}{q}}^3)\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|\right.\hfill \\ \hfill & \left.\left.+(1+4\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|\right]\right).\hfill \end{array}$$

Proof. 

By using Lemma 1, we have

$$\begin{array}{cc}\hfill & \left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|\hfill \\ \hfill & =\left|\frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\int }_0^1(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }){}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}\right.\hfill \\ \hfill & \left.D_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right){}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }\left|\right|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}\hfill \\ \hfill & D_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right)|{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }.\hfill \end{array}$$

(24)

Since ${|}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}|$ is convex, using Jensen–Mercer inequality, we obtain

$$\begin{array}{cc}\hfill & \left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|\left(\sum _{{\pi }_{\cdot }=1}^l\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|-\left[{\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|\right.\right.\hfill \\ \hfill & \left.\left.+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|\right]\right){}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & =\frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}\left[\frac{2\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^2}\sum _{{\pi }_{\cdot }=1}^l\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|\right.\hfill \\ \hfill \\ \hfill & -\left(\frac{\underset{\dot{}}{\mathrm{q}}(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}{(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){(1+\underset{\dot{}}{\mathrm{q}})}^3}\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|\right.\hfill \\ \hfill & \left.\left.+\frac{\underset{\dot{}}{\mathrm{q}}(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3)}{(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){(1+\underset{\dot{}}{\mathrm{q}})}^3}\sum _{{\pi }_{\cdot }=1}^{l-1}\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|\right)\right].\hfill \end{array}$$

The proof is completed. □

If we choose $l=2$, then Theorem 9 reduces to the following relation:

$$\begin{array}{cc}\hfill & \left|\Omega (u_1,u_2,{\mathsf{{\rm Y}}}_1,{\Xi }_1)\right|\hfill \\ \hfill & \le \frac{{\underset{\dot{}}{\mathrm{q}}}^2({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{{[3]}_{\underset{\dot{}}{\mathrm{q}}}{[2]}_{\underset{\dot{}}{\mathrm{q}}}^4}\left([2(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)]\left(\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_1\right)\right|\right.\right.\hfill \\ \hfill & \left.+\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_2\right)\right|\right)-\left[(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3)\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_1\right)\right|\right.\hfill \\ \hfill & \left.\left.+(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_1\right)\right|\right]\right).\hfill \end{array}$$

Theorem 10.

Let $\tilde{\mathfrak{F}}:J\to \mathbb{R}$ be a continuous mapping. If ${\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\right|}^r$ is convex and integrable on J, and $r\ge 1$, then

$$\begin{array}{cc}\hfill \left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|& \le \frac{\underset{\dot{}}{q}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{q}}{\left(\frac{2\underset{\dot{}}{q}}{{(1+\underset{\dot{}}{q})}^2}\right)}^{1-\frac{1}{r}}\hfill \\ \hfill & \times \left(\frac{\underset{\dot{}}{q}}{{[3]}_{\underset{\dot{}}{q}}{[2]}_{\underset{\dot{}}{q}}^3}\left(2(1+\underset{\dot{}}{q})(1+\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r\right.\right.\hfill \\ \hfill & -\left[(1+4\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r\right.\hfill \\ \hfill & {\left.\left.\left.+(1+3{\underset{\dot{}}{q}}^2+2{\underset{\dot{}}{q}}^3)\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right]\right)\right)}^{\frac{1}{r}}.\hfill \end{array}$$

Proof. 

Using the power–mean inequality in (24), we obtain

$$\begin{array}{c}{\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }\left|\right|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right)|{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \le {\left({\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right)}^{1-\frac{1}{r}}\hfill \\ \times {\left({\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }\left|\right|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right){|}^r{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right)}^{\frac{1}{r}}.\hfill \end{array}$$

(25)

As $|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}{|}^r$ is convex, using Jensen–Mercer inequality, it follows that

$$\begin{array}{c}{\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }\left|\right|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right){|}^r{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \le \frac{\underset{\dot{}}{\mathrm{q}}}{(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){(1+\underset{\dot{}}{\mathrm{q}})}^3}\left(2(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r\right.\hfill \\ -\left[(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r+(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3)\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right].\hfill \end{array}$$

(26)

Applying the fact that ${\int }_0^1|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }=\frac{2\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^2}$ and substituting (26) into (25), we obtain the desired result. □

If we choose $l=2$, then Theorem 10 yields the following inequality:

$$\begin{array}{cc}\hfill \left|\Omega (u_1,u_2,{\mathsf{{\rm Y}}}_1,{\Xi }_1)\right|& \le \frac{\underset{\dot{}}{\mathrm{q}}({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{1+\underset{\dot{}}{\mathrm{q}}}{\left(\frac{2\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^2}\right)}^{1-\frac{1}{r}}\hfill \\ \hfill & \times \left(\frac{\underset{\dot{}}{\mathrm{q}}}{{[3]}_{\underset{\dot{}}{\mathrm{q}}}{[2]}_{\underset{\dot{}}{\mathrm{q}}}^3}\left(2(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\left({\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_1\right)\right|}^r+{\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_2\right)\right|}^r\right)\right.\right.\hfill \\ \hfill & {\left.-\left[(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_1\right)\right|}^r+(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3){\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_1\right)\right|}^r\right]\right)}^{\frac{1}{r}}.\hfill \end{array}$$

Theorem 11.

Let $\tilde{\mathfrak{F}}:J\to \mathbb{R}$ be a continuous mapping. If ${\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\right|}^r$ is convex and integrable on J, then we have

$$\begin{array}{c}\left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|\hfill \\ \le \frac{\underset{\dot{}}{q}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{q}}{\left(k_1\right)}^{\frac{1}{p}}\left(\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r-\frac{1}{1+\underset{\dot{}}{q}}\left[\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r\right.\right.\hfill \\ {\left.\left.+\underset{\dot{}}{q}\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{q}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right]\right)}^{\frac{1}{r}},\hfill \end{array}$$

(27)

where $r>1$, $\frac{1}{p}+\frac{1}{r}=1$, and

$$\begin{array}{cc}\hfill k_1=& \frac{1-\underset{\dot{}}{q}}{1+\underset{\dot{}}{q}}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{q}}^{\mathfrak{n}}{\left(\frac{1-(1+\underset{\dot{}}{q}){\underset{\dot{}}{q}}^{\mathfrak{n}}}{1+\underset{\dot{}}{q}}\right)}^p+(1-\underset{\dot{}}{q})\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{q}}^{\mathfrak{n}}{((1+\underset{\dot{}}{q}){\underset{\dot{}}{q}}^{\mathfrak{n}}-1)}^p\hfill \\ \hfill & -\frac{1-\underset{\dot{}}{q}}{1+\underset{\dot{}}{q}}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{q}}^{\mathfrak{n}}{\left(\frac{(1+\underset{\dot{}}{q}){\underset{\dot{}}{q}}^{\mathfrak{n}}-1}{1+\underset{\dot{}}{q}}\right)}^p.\hfill \end{array}$$

(28)

Proof. 

By applying Hölder’s inequality in (24) and using the Jensen–Mercer inequality, it follows that

$$\begin{array}{cc}\hfill & \left|\Omega (u_{{\pi }_{\cdot }},{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }},{\Xi }_{{\pi }_{\cdot }})\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\left({\int }_0^1{|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right)}^{\frac{1}{p}}\hfill \\ \hfill & \times {\left({\int }_0^1{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(\sum _{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-({\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }})\right)\right|}^r{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right)}^{\frac{1}{r}}\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\left({\int }_0^1{|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\right)}^{\frac{1}{p}}\left(\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r\right.\hfill \\ \hfill & {\left.-\left[{\varrho }_{\divideontimes }\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r+(1-{\varrho }_{\divideontimes })\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right]\right)}^{\frac{1}{r}}{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & =\frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\left(k_1\right)}^{\frac{1}{p}}\left(\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r-\left[\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r\right.\right.\hfill \\ \hfill & {\left.\left.+\frac{\underset{\dot{}}{\mathrm{q}}}{1+\underset{\dot{}}{\mathrm{q}}}\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right]\right)}^{\frac{1}{r}}\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}{\sum }_{{\pi }_{\cdot }=1}^{l-1}({\Xi }_{{\pi }_{\cdot }}-{\mathsf{{\rm Y}}}_{{\pi }_{\cdot }})}{1+\underset{\dot{}}{\mathrm{q}}}{\left(k_1\right)}^{\frac{1}{p}}\times \left(\sum _{{\pi }_{\cdot }=1}^l{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_{{\pi }_{\cdot }}\right)\right|}^r-\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}\left[\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\mathsf{{\rm Y}}}_{{\pi }_{\cdot }}\right)\right|}^r\right.\right.\hfill \\ \hfill & {\left.\left.+\underset{\dot{}}{\mathrm{q}}\sum _{{\pi }_{\cdot }=1}^{l-1}{\left|{}_{{\sum }_{{\pi }_{\cdot }=1}^l{u}_{{\pi }_{\cdot }}-{\sum }_{{\pi }_{\cdot }=1}^{l-1}{\Xi }_{{\pi }_{\cdot }}}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_{{\pi }_{\cdot }}\right)\right|}^r\right]\right)}^{\frac{1}{r}}.\hfill \end{array}$$

It is easy to check that

$$\begin{array}{cc}\hfill k_1={\int }_0^1{|1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }|}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }& ={\int }_0^{\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}}{(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes })}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }+{\int }_{\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}}^1{((1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }-1)}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & ={\int }_0^{\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}}{(1-(1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes })}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }+{\int }_0^1{((1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }-1)}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & -{\int }_0^{\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}}{((1+\underset{\dot{}}{\mathrm{q}}){\varrho }_{\divideontimes }-1)}^p{}_0{d}_{\underset{\dot{}}{\mathrm{q}}}{\varrho }_{\divideontimes }\hfill \\ \hfill & =\frac{1-\underset{\dot{}}{\mathrm{q}}}{1+\underset{\dot{}}{\mathrm{q}}}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}{\left(\frac{1-(1+\underset{\dot{}}{\mathrm{q}}){\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}}{1+\underset{\dot{}}{\mathrm{q}}}\right)}^p+(1-\underset{\dot{}}{\mathrm{q}})\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}{((1+\underset{\dot{}}{\mathrm{q}}){\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}-1)}^p\hfill \\ \hfill & -\frac{1-\underset{\dot{}}{\mathrm{q}}}{1+\underset{\dot{}}{\mathrm{q}}}\sum _{\mathfrak{n}=0}^{\infty }{\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}{\left(\frac{(1+\underset{\dot{}}{\mathrm{q}}){\underset{\dot{}}{\mathrm{q}}}^{\mathfrak{n}}-1}{1+\underset{\dot{}}{\mathrm{q}}}\right)}^p.\hfill \end{array}$$

This completes the proof. □

If we choose $l=2$, then Theorem 11 reduces to:

$$\begin{array}{cc}\hfill & \left|\Omega (u_1,u_2,{{\rm Y}}_1,{\Xi }_1)\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}({\Xi }_1-{{\rm Y}}_1)}{1+\underset{\dot{}}{\mathrm{q}}}{\left(k_1\right)}^{\frac{1}{p}}\left({\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_1\right)\right|}^r+{\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left(u_2\right)\right|}^r-\frac{1}{1+\underset{\dot{}}{\mathrm{q}}}\left[{\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({{\rm Y}}_1\right)\right|}^r\right.\right.\hfill \\ \hfill & {\left.\left.+\underset{\dot{}}{\mathrm{q}}{\left|{}_{u_1+u_2-{\Xi }_1}{D}_{\underset{\dot{}}{\mathrm{q}}}\tilde{\mathfrak{F}}\left({\Xi }_1\right)\right|}^r\right]\right)}^{\frac{1}{r}}.\hfill \end{array}$$

3. Applications

In this section, we present some applications to special means of arbitrary positive real numbers and give the numerical verification of our main outcomes. Furthermore, we give the graphical analysis of our results. Now, we recall some well-known means of positive real numbers.

For arbitrary real numbers, we consider the following means:

The arithmetic mean: $A({\tilde{\aleph }}_1,{\tilde{\aleph }}_2)=\frac{{\tilde{\aleph }}_1+{\tilde{\aleph }}_2}{2}$.

The generalized $log$-mean: $L_p({\tilde{\aleph }}_1,{\tilde{\aleph }}_2)={\left[\frac{{{\tilde{\aleph }}_2}^{p+1}-{{\tilde{\aleph }}_1}^{p+1}}{(p+1)({\tilde{\aleph }}_2-{\tilde{\aleph }}_1)}\right]}^{\frac{1}{p}}$.

where $p\in \mathbb{R}\setminus \{-1,0\}$, ${\tilde{\aleph }}_1,{\tilde{\aleph }}_2\in \mathbb{R}$, ${\tilde{\aleph }}_1\ne {\tilde{\aleph }}_2$.

Now, we present an application of Theorem 9 to special means.

Proposition 1.

Let $0<\left(u_1+u_2-{\Xi }_1\right)<\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)$, $0<\underset{\dot{}}{q}<1$, then

$$\begin{array}{cc}\hfill & \left|\frac{2A(\underset{\dot{}}{q}{\left(u_1+u_2-{\Xi }_1\right)}^2,{\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)}^2)}{1+\underset{\dot{}}{q}}-\frac{3}{{[3]}_{\underset{\dot{}}{q}}}L{}_2^2\left[u_1+u_2-{\mathsf{{\rm Y}}}_1,u_1+u_2-{\Xi }_1\right]\right|\hfill \\ \hfill & \le \frac{{\underset{\dot{}}{q}}^2({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{{[3]}_{\underset{\dot{}}{q}}{[2]}_{\underset{\dot{}}{q}}^4}\left([2{(1+\underset{\dot{}}{q})}^2(1+\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)]\left(|u_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\varphi }_1)|\right.\right.\hfill \\ \hfill & \left.+|u_2(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\varphi }_1)|\right)-\left[(1+3{\underset{\dot{}}{q}}^2+2{\underset{\dot{}}{q}}^3)|{\mathsf{{\rm Y}}}_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\varphi }_1)|\right.\hfill \\ \hfill & \left.\left.+(1+4\underset{\dot{}}{q}+{\underset{\dot{}}{q}}^2)|{\Xi }_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\varphi }_1)|\right]\right).\hfill \end{array}$$

Proof. 

The proof is obvious from Theorem 9, applied thus, $\tilde{\mathfrak{F}}\left(z\right)=z^2$. □

Example 1.

If we take $\tilde{\mathfrak{F}}\left(z\right)=z^2$ with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,\Xi =2$ and $\underset{\dot{}}{q}=0.5$ in Theorem 9, then we have$0.0952<0.5820$.

Now, we provide a graphical demonstration of Theorem 9 in Figure 1. For this, we consider $\tilde{\mathfrak{F}}\left(\mathsf{{\rm Y}}\right)={\mathsf{{\rm Y}}}^2$ with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,\Xi =2$ and $\underset{\dot{}}{\mathrm{q}}\in (0,1)$ in Theorem 9, then

$$\begin{array}{cc}\hfill & \left|\frac{{\underset{\dot{}}{\mathrm{q}}}^2}{(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}\right|\hfill \\ \hfill & \le \frac{{\underset{\dot{}}{\mathrm{q}}}^2}{{\left[3\right]}_{\underset{\dot{}}{\mathrm{q}}}{\left[2\right]}_{\underset{\dot{}}{\mathrm{q}}}^4}\left[8{(1+\underset{\dot{}}{\mathrm{q}})}^2(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)-2(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3)(1+\underset{\dot{}}{\mathrm{q}})-(1+\underset{\dot{}}{\mathrm{q}})(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\right].\hfill \end{array}$$

Figure 1. This is an image showing the comparison between left and right sides of Theorem 9.

Now, we present an application of Theorem 10 to special means.

Proposition 2.

Let $0<\left(u_1+u_2-{\Xi }_1\right)<\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)$, $0<\underset{\dot{}}{\mathrm{q}}<1$, then

$$\begin{array}{cc}\hfill & \left|\frac{2A(\underset{\dot{}}{\mathrm{q}}{\left(u_1+u_2-{\Xi }_1\right)}^2,{\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)}^2)}{1+\underset{\dot{}}{\mathrm{q}}}-\frac{3}{{[3]}_{\underset{\dot{}}{\mathrm{q}}}}L{}_2^2\left[u_1+u_2-{\mathsf{{\rm Y}}}_1,u_1+u_2-{\Xi }_1\right]\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{\mathrm{q}}({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{1+\underset{\dot{}}{\mathrm{q}}}{\left(\frac{2\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^2}\right)}^r\left(\frac{\underset{\dot{}}{\mathrm{q}}}{(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){(1+\underset{\dot{}}{\mathrm{q}})}^3}\left(2(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)\right.\right.\hfill \\ \hfill & \times {\left|u_1(1+\underset{\dot{}}{\mathrm{q}})+(1-\underset{\dot{}}{\mathrm{q}})(u_1+u_2-{\Xi }_1)\right|}^r+{\left|u_2(1+\underset{\dot{}}{\mathrm{q}})+(1-\underset{\dot{}}{\mathrm{q}})(u_1+u_2-{\Xi }_1)\right|}^r\hfill \\ \hfill & -\left[(1+4\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2){\left||{\mathsf{{\rm Y}}}_1(1+\underset{\dot{}}{\mathrm{q}})+(1-\underset{\dot{}}{\mathrm{q}})(u_1+u_2-{\Xi }_1)\right|}^r\right.\hfill \\ \hfill & {\left.\left.\left.+(1+3{\underset{\dot{}}{\mathrm{q}}}^2+2{\underset{\dot{}}{\mathrm{q}}}^3){\left|{\Xi }_1(1+\underset{\dot{}}{\mathrm{q}})+(1-\underset{\dot{}}{\mathrm{q}})(u_1+u_2-{\Xi }_1)\right|}^r\right]\right)\right)}^{\frac{1}{r}}.\hfill \end{array}$$

Proof. 

The proof is obvious from Theorem 10, applied thus, $\tilde{\mathfrak{F}}\left(z\right)=z^2$. □

Now, we check the validity of Theorem 10 through numerical example.

Example 2.

If we take

$$\tilde{\mathfrak{F}}\left(z\right)=z^2$$

with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,r=2,\Xi =2$ and $\underset{\dot{}}{q}=0.5$ In Theorem 10, then we have$0.0952<0.7559$.

Now, we give graphical demonstration of Theorem 10 in Figure 2. For this, we consider $\tilde{\mathfrak{F}}\left(z\right)=z^2$ with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,r=2,\Xi =2,r=2$, and $\underset{\dot{}}{\mathrm{q}}\in (0,1)$ in Theorem 10, then

$$\begin{array}{cc}\hfill & \left|\frac{{\underset{\dot{}}{\mathrm{q}}}^2}{(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}\right|\hfill \\ \hfill & \le \underset{\dot{}}{\mathrm{q}}{\left(\frac{2\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^2}\right)}^{\frac{1}{2}}{\left(\frac{\underset{\dot{}}{\mathrm{q}}}{{(1+\underset{\dot{}}{\mathrm{q}})}^3(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}\left(20(\underset{\dot{}}{\mathrm{q}}+1)(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)-7{\underset{\dot{}}{\mathrm{q}}}^2-2{\underset{\dot{}}{\mathrm{q}}}^3-4\underset{\dot{}}{\mathrm{q}}-3\right)\right)}^{\frac{1}{2}}.\hfill \end{array}$$

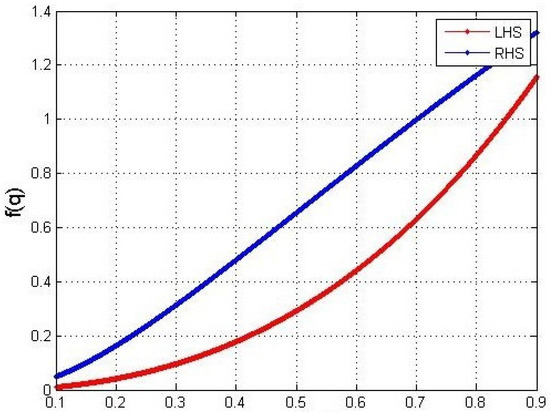
Figure 2. This is an image showing the comparison between left and right sides of Theorem 10.

Next, we present an application of Theorem 11 to special means.

Proposition 3.

Let $0<\left(u_1+u_2-{\Xi }_1\right)<\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)$, $0<\underset{\dot{}}{q}<1$, then

$$\begin{array}{cc}\hfill & \left|\frac{2A(\underset{\dot{}}{q}{\left(u_1+u_2-{\Xi }_1\right)}^2,{\left(u_1+u_2-{\mathsf{{\rm Y}}}_1\right)}^2)}{1+\underset{\dot{}}{q}}-\frac{3}{{[3]}_{\underset{\dot{}}{q}}}L{}_2^2\left[u_1+u_2-{\mathsf{{\rm Y}}}_1,u_1+u_2-{\Xi }_1\right]\right|\hfill \\ \hfill & \le \frac{\underset{\dot{}}{q}({\Xi }_1-{\mathsf{{\rm Y}}}_1)}{1+\underset{\dot{}}{q}}{\left(k_1\right)}^{\frac{1}{p}}\times \left({\left|u_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\Xi }_1)\right|}^r+{\left|u_2(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\Xi }_1)\right|}^r\right.\hfill \\ \hfill & {\left.-\frac{1}{1+\underset{\dot{}}{q}}\left[{\left|{\mathsf{{\rm Y}}}_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\Xi }_1)\right|}^r+\underset{\dot{}}{q}{\left|{\Xi }_1(1+\underset{\dot{}}{q})+(1-\underset{\dot{}}{q})(u_1+u_2-{\Xi }_1)\right|}^r\right]\right)}^{\frac{1}{r}}.\hfill \end{array}$$

Proof. 

The proof is obvious from Theorem 11, applied thus, $\tilde{\mathfrak{F}}\left(z\right)=z^2$. □

In the support of Theorem 11, we discuss a numerical example.

Example 3.

If we take $\tilde{\mathfrak{F}}\left(z\right)=z^2$ with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,r=p=2,\Xi =2$ and $\underset{\dot{}}{q}=0.5$ In Theorem 11, then we have$0.0952<0.6542$.

Now, we give graphical demonstration of Theorem 11 in Figure 3. For this, we consider $\tilde{\mathfrak{F}}\left(\mathsf{{\rm Y}}\right)={\mathsf{{\rm Y}}}^2$ with $u_1=-1,u_2=3,\mathsf{{\rm Y}}=1,r=2,\Xi =2,p=r=2$, and $\underset{\dot{}}{\mathrm{q}}\in (0,1)$ in Theorem 11, then

$$\begin{array}{c}\hfill \left|\frac{{\underset{\dot{}}{\mathrm{q}}}^2}{(1+\underset{\dot{}}{\mathrm{q}})(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}\right|\le \underset{\dot{}}{\mathrm{q}}{\left(\frac{\underset{\dot{}}{\mathrm{q}}}{(1+\underset{\dot{}}{\mathrm{q}}+{\underset{\dot{}}{\mathrm{q}}}^2)}\right)}^{\frac{1}{2}}{\left(10-\frac{1+4\underset{\dot{}}{\mathrm{q}}}{1+\underset{\dot{}}{\mathrm{q}}}\right)}^{\frac{1}{2}}.\end{array}$$

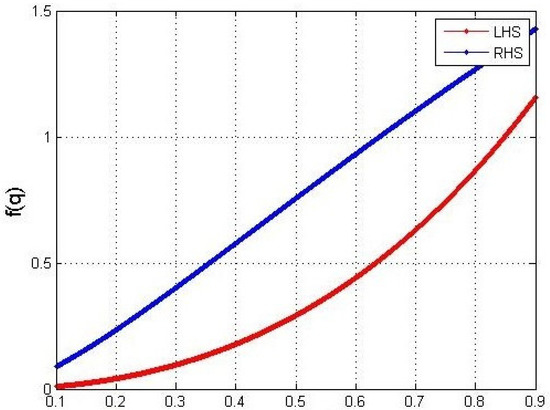
Figure 3. This is an image showing the comparison between left and right sides of Theorem 11.

4. Conclusions

In this article, we analyzed the $\underset{\dot{}}{\mathrm{q}}$-H.H.J.M type inequalities via majorized l-tuples. Moreover, we established some right estimation type results regarding the $\underset{\dot{}}{\mathrm{q}}$-H.H.J.M inequality. In the later sections, we presented some applications to means, numerical examples, and graphical illustrations. In the future, we will extend some other well-known inequalities such as the Simpson–Mercer-type inequalities and the Ostrowski–Mercer-type inequalities through generalized quantum integrals. We expect that the combined study of the theory of majorization and $\underset{\dot{}}{\mathrm{q}}$ calculus will open a new venue for further research in this field.