Construction of General Implicit-Block Method with Three-Points for Solving Seventh-Order Ordinary Differential Equations

Abstract

In order to solve general seventh-order ordinary differential equations (ODEs), this study will develop an implicit block method with three points of the form $y^{\left(7\right)}\left(\xi \right)=f(\xi ,y\left(\xi \right),y^{\prime }\left(\xi \right),y^{″}\left(\xi \right),$$y^{‴}\left(\xi \right),y^{\left(4\right)}\left(\xi \right),y^{\left(5\right)}\left(\xi \right),y^{\left(6\right)}\left(\xi \right))$ directly. The general implicit block method with Hermite interpolation in three points (GIBM3P) has been derived to solve general seventh-order initial value problems (IVPs) using the basic functions of Hermite interpolating polynomials. A block multi-step method is constructed to be suitable with the numerical approximation at three points. However, the construction of the new method has been presented while the numerical results of the implementations are used to prove the efficiency and the accuracy of the proposed method which compared with the RK and RKM numerical methods together to analytical method. We established the characteristics of the proposed method, including order and zero-stability. Applications of various IVP problems are also discussed, and the outcomes are very encouraging for the suggested approach. The proposed GIBM3P method yields more accurate numerical solutions to the test problems than the existing RK method, which are in good agreement with analytical and RKM method solutions.

1. Introduction

Higher order differential equations (ODEs) have a significate role in various fields of applied mathematics and can be used in mathematical models problems that arise in the fields of applied sciences, biology, chemistry, physics, economics and engineering. Partial differential equations (PDEs) or ODEs are tools used to model the mathematical representations of the real problems in applied science and engineering. However, it had been difficult for mathematicians to use their creativity in finding the solutions of various types of DEs, either analytically or numerically. For scientists and engineers to use, there are currently a number of effective classical or modern numerical and analytical methods. The following list includes a review of the literature on various contemporary techniques for solving mathematical models that contain ODEs: for the purpose of solving IVPs, the numerical solutions of special and general sixth-order boundary-value problems (BVPs), with applications to Bénard layer eigenvalue problems, have been studied by researchers in [1], non-polynomial spline was used to solve BVPs by researchers in [2], while a new integrator was created in the research work [3] to solve ODEs of the seventh order. All types of DEs cannot always be solved directly or indirectly by analytical methods. This proposal would require us to research how direct GIBM3P is derived. However, the authors [4,5,6,7,8] have developed linear multistep numerical methods (Lmm) to address this issue, refs [9,10] have developed one-step numerical methods to solve IVPs of ODEs with orders lower than seven. Moreover, for future works, the studying of the authors [11,12,13] for the numerical solutions of a class of fractional order hybrid DEs and using the suggested technique, the oscillation of seventh-order neutral DEs can be modifided.

In this work, a new three-point second-derivative fully implicit block method has been proposed. The Hermite interpolating polynomial is used as the basis function to derive the implicit block method, which incorporates the first derivative of $f({\xi }_i,y_i^{\left(j\right)})$ for $j=0,1,\cdots ,6$ to enhance the accuracy of solutions. The novel contributions of this work are: to study the numerical solutions of seventh-order ODEs, to drive and construct a general implicit block with three-point GIBM3P method for solving ODEs of seventh-order, to use the numerical implementations to prove the efficiency and accuracy of the proposed GIBM3P method compared with the exact and numerical solutions and to apply the constructed method in solving some problems of ODEs of seventh-order comparing with the numerical solutions of RK and RKM methods. The derivatives are incorporated into the formula to produce more precise numerical results. To compare the effectiveness of the new method to numerical and exact solutions, a few numerical examples were evaluated. To obtain the numerical approximation at three points simultaneously, a block formulation is presented. IVPs applications are also discussed, and they produce impressive outcomes for the three-point block method suggested. The proposed GIBM3P method produces numerical results that are more precise than those produced by the current RK and RKM methods for test problems.

2. Preliminary

Definitions that are pertinent to this work are mentioned in this section.

2.1. The General Quasi-Linear Seventh-Order ODEs

The general quasi-linear seventh-order ODEs can be written in the following equation

$$\begin{array}{c}\hfill y^{\left(7\right)}\left(\xi \right)=f(\xi ,y\left(\xi \right),y^{\prime }\left(\xi \right),y^{″}\left(\xi \right),y^{‴}\left(\xi \right),y^{\left(4\right)}\left(\xi \right),y^{\left(5\right)}\left(\xi \right),y^{\left(6\right)}\left(\xi \right));{\xi }_0\le \xi \le {\xi }_1,\end{array}$$

(1)

with the following initial conditions:

$$\begin{array}{c}\hfill y^{\left(j\right)}\left({\xi }_0\right)={\alpha }_j,j=0,1,\cdots ,6.\end{array}$$

(2)

Special Class Quasi-Linear Seventh-Order ODEs

The following form can be used to express the special class of seventh-order quasi-linear ODEs:

$$\begin{array}{c}\hfill y^{\left(7\right)}\left(\xi \right)=\varphi (\xi ,y\left(\xi \right)),{\xi }_0\le \xi \le {\xi }_1,\end{array}$$

(3)

with the initial conditions (ICs) in Equation (2).

Such ODEs are frequently found in many physical and engineering problems. Some scientists and engineers can solve the ODEs in Equation (1) or Equation (3) with ICs (2) using linear multistep methods. Most of them, used to solve higher order ODEs by converting the $n^{th}$-order ODE to equivalent first-order system of ODEs. However, it would be more efficient if ODEs of seventh-order in Equation (1) or Equation (3) with ICs (2) could be solved directly using the GIBM3P method which is more efficient since it has less function evaluations and computational time in implementation. In this paper, we are concerned with the implicit block method for solving seventh-order ODEs. Accordingly, we developed the order conditions for GIBM3P, so that based on the order conditions the GIBM3P method can be derived. By using Hermite polynomials as an approximation, the proposed method has been created.

2.2. RKM Methods for Solving Special Class Quasi-Linear Seventh-Order ODEs

RKM methods with s-stages developed by [3,14] proposed in this subsection for solving special quasi-linear seventh-order ODEs in Equation (3) with ICs (2) take the following form:

$$\begin{array}{ccc}\hfill z_{n+1}& =& z_n+h{z}_n^{\prime }+\frac{h^2}{2!}{z}_n^{″}+\frac{h^3}{3!}{z}_n^{‴}+\frac{h^4}{4!}{z}_n^{\left(4\right)}+\frac{h^5}{5!}{z}_n^{\left(5\right)}+\frac{h^6}{6!}{z}_n^{\left(6\right)}+h^7\sum _{i=1}^s{b}_i{k}_i\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill z_{n+1}^{\prime }& =& z_n^{\prime }+h{z}_n^{″}+\frac{h^2}{2!}{z}_n^{‴}+\frac{h^3}{3!}{z}_n^{\left(4\right)}+\frac{h^4}{4!}{z}_n^{\left(5\right)}+\frac{h^5}{5!}{z}_n^{\left(6\right)}+h^6\sum _{i=1}^s{b}_i^{\prime }{k}_i\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill z_{n+1}^{″}& =& z_n^{″}+h{z}_n^{‴}+\frac{h^2}{2!}{z}_n^{\left(4\right)}+\frac{h^3}{3!}{z}_n^{\left(5\right)}+\frac{h^4}{4!}{z}_n^{\left(6\right)}+h^5\sum _{i=1}^s{b}_i^{″}{k}_i\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill z_{n+1}^{‴}& =& z_n^{‴}+h{z}_n^{\left(4\right)}+\frac{h^2}{2!}{z}_n^{\left(5\right)}+\frac{h^3}{3!}{z}_n^{\left(6\right)}+h^4\sum _{i=1}^s{b}_i^{‴}{k}_i\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(4\right)}& =& z_n^{\left(4\right)}+h{z}_n^{\left(5\right)}+\frac{h^2}{2!}{z}_n^{\left(6\right)}+h^3\sum _{i=1}^s{b}_i^{⁗}{k}_i\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(5\right)}& =& z_n^{\left(5\right)}+h{z}_n^{\left(6\right)}+h^2\sum _{i=1}^s{b}_i^{‴″}{k}_i\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(6\right)}& =& z_n^{\left(6\right)}+h\sum _{i=1}^s{b}_i^{‴‴}{k}_i\hfill \end{array}$$

(10)

where,

$$\begin{array}{cc}{k}_i\hfill & =f(x_n+c_{i}h,y_n+h{c}_i{y}_n^{\prime }+\frac{h^2}{2}{c}_i^2{y}_n^{″}+\frac{h^3}{6}{c}_i^3{y}_n^{‴}+\frac{h^4}{24}{c}_i^4{y}_n^{\left(4\right)}+\frac{h^5}{120}{c}_i^5{y}_n^{\left(5\right)}+\frac{h^6}{720}{c}_i^6{y}_n^{\left(6\right)}\hfill \\ \hfill & +h^7\sum _{j=1}^{i-1}{a}_{ij}{k}_j)\hfill \end{array}$$

(11)

for $i=2,3,\cdots ,s.$ and h is the step-size.

The order conditions of the RKM method for solving special class sixth-order of quasi-linear ODEs have been derived by [10]. The parameters of RKM method’s, in Equations (4)–(11), are $c_i,a_{ij},b_i^{\left(k\right)}$ and are evaluated by resolving the system of algebraic order conditions, for $i,j=1,2,\cdots ,s$ and $k=0,1,2,3,4,5,6$. Table 1 displays Butcher Table for three-stage RKM integrators.

Table 1. Butcher table of RKM method.

0	0
$\frac{3}{5}-\frac{\sqrt{6}}{10}$	$\frac{1}{2}$	0
$\frac{3}{5}+\frac{\sqrt{6}}{10}$	$\frac{1}{2}$	$\frac{1}{2}$	0
	1	0	$-\frac{119}{120}$
	$-\frac{1}{40}-\frac{\sqrt{6}}{360}$	$\frac{1}{60}+\frac{\sqrt{6}}{360}$	0
	$\frac{1}{18}$	$\frac{1}{18}-\frac{\sqrt{6}}{48}$	$\frac{1}{18}+\frac{\sqrt{6}}{48}$
	$\frac{1}{9}$	$\frac{7}{36}-\frac{\sqrt{6}}{48}$	$\frac{7}{18}-\frac{\sqrt{6}}{18}$
	$\frac{1}{9}$	$\frac{7}{36}-\frac{\sqrt{6}}{48}$	$\frac{7}{18}-\frac{\sqrt{6}}{18}$

3. Analysis of Proposed GIBM3P Method for Solving General Quasi-Linear Seventh-Order ODEs

The derived method has been introduced in this section.

3.1. Proposed GIBM3P Method

Using the Hermite interpolating polynomial $P_3\left(\xi \right)$, which is defined in the following equation, the new method is derived.

$$\begin{array}{c}\hfill P_3\left(\xi \right)=\sum _{i=0}^n\sum _{k=0}^{m_{i-1}}{f}_i^{\left(k\right)}{L}_{i,k}\left(\xi \right),\end{array}$$

(12)

where $f_i=f\left({\xi }_i\right),{\xi }_i=a+ih,i=0,1,\cdots$ and $h=\frac{b-a}{n}$, n is a positive integer. $L_{i,k}\left(\xi \right)$ can be defined by

$$L_{i,m_i}\left(\xi \right)={\ell }_{i,m_i}\left(\xi \right),i=0,1,\cdots ,n,$$

$${\ell }_{i,k}\left(\xi \right)=\frac{{(\xi -{\xi }_i)}^k}{k!}\prod _{j=0,j\ne i}^n{\left(\frac{\xi -{\xi }_j}{{\xi }_i-{\xi }_j}\right)}^{m_j},i=0,1,\cdots ,n,k=0,1,\cdots ,m_i.$$

Furthermore, recursively for $k=m_i-2,m_i-3,\cdots ,0.$

$$L_{i,k}\left(\xi \right)={\ell }_{i,k}\left(\xi \right)-\sum _{v=k+1}^{m_i-1}{\ell }_{i,k}^{\left(v\right)}\left({\xi }_i\right)L_{i,v}\left(\xi \right).$$

For the purpose of directly solving the IVPs for the general class in Equation (1) or the special class in Equation (3) with ICs (2), a block method with some derivatives is developed in this paper. The derivation of the proposed method is based on the interpolating of Hermit polynomial denoted by $P_3\left(t\right)$ which interpolates at three points. This Hermit polynomial has the form in Equation (12) where, $f_i=f\left({\xi }_i\right)$ for $j=0,1,\cdots ,6$ and ${\xi }_i=a+ih;$ $i=0,1,2,\cdots ,m$ and $h=\frac{b-a}{m},$ where $L_{ik}\left(\xi \right)$ is the generalized Hermite polynomial for $k=0,1,\cdots ,m_i$ and $i=0,1,\cdots ,m,$ where m is an integer’s positive. We use

$$P_3\left(\xi \right)=f_0{L}_{00}\left(\xi \right)+f_1{L}_{10}\left(\xi \right)+f_2{L}_{20}\left(\xi \right)+f_3{L}_{30}\left(\xi \right)+f_0^{\prime }{L}_{01}\left(\xi \right)+f_1^{\prime }{L}_{11}\left(\xi \right)+f_2^{\prime }{L}_{21}\left(\xi \right)+f_3^{\prime }{L}_{31}\left(\xi \right),$$

where $f^{\prime }=g({\xi }_i,y_i^{\left(j\right)})$ is the derivative of the function f of order one with respect to $\xi$ for $j=0,1,\cdots ,6$ and $i=0,1,2,\cdots ,m.$ The approximation at three points ${\xi }_{m+1},{\xi }_{m+2}$ and ${\xi }_{m+3}$ have computed the approximated solutions, $y_{m+1},y_{m+2}$ and $y_{m+3}$, respectively, where ${\xi }_m=$ starting point and ${\xi }_{m+2}=$ ending point in the block $[{\xi }_m,{\xi }_{m+3}]$ with step-size $3h$. The numerical solution $y_{n+3}$ at the ending point ${\xi }_{m+3}$ should be used as the initial value in the subsequent iteration, see Figure 1 which explains the block method with three points.

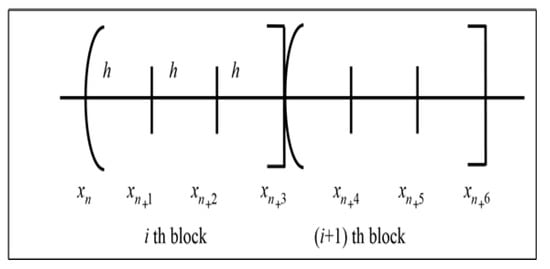
Figure 1. The block method with three points.

Hermite Polynomials

We used Hermite polynomials in this study, which are defined as follows:

$$\begin{array}{ccc}\hfill L_{00}\left(\xi \right)& =& \frac{1}{36}{\xi }^2{(\xi +1)}^2{(\xi +2)}^2(1+\frac{11}{3}(\xi +3))\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill L_{10}\left(\xi \right)& =& \frac{1}{4}{\xi }^2{(\xi +1)}^2{(\xi +3)}^3\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill L_{20}\left(\xi \right)& =& -\frac{1}{4}{\xi }^3{(\xi +2)}^2{(\xi +3)}^2\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill L_{30}\left(\xi \right)& =& \frac{1}{36}{(\xi +1)}^2{(\xi +2)}^2{(\xi +3)}^2(1-\frac{11}{3}\xi )\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill L_{01}\left(\xi \right)& =& \frac{h}{36}{\xi }^2{(\xi +1)}^2{(\xi +2)}^2(\xi +3)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill L_{11}\left(\xi \right)& =& \frac{h}{4}{\xi }^2{(\xi +1)}^2(\xi +2){(\xi +3)}^2\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill L_{21}\left(\xi \right)& =& \frac{h}{4}{\xi }^2(\xi +1){(\xi +2)}^2{(\xi +3)}^2\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill L_{31}\left(\xi \right)& =& \frac{h}{36}\xi {(\xi +1)}^2{(\xi +2)}^2{(\xi +3)}^2\hfill \end{array}$$

(20)

Using the assumption $s=\frac{\xi -{\xi }_{n+3}}{h},$ then, Hermite polynomials can be written in the independent variable $\xi .$

3.2. Derivation of Proposed GIBM3P Method

The three-point fully implicit block method with second derivatives was presented in this section as a solution to general seventh-order ODEs. The domain of definition $[a,b]$ for this proposed method only has three points for each block. The approximated solution $z_{n+1}^{\left(j\right)},$ for $j=0,1,2,3,4,5,6$ at the first point ${\xi }_{n+1}$ of Equation (12) can be obtained by integrating Equation (12) multiple times up to seventh-times with respect to the variable $\xi$, respectively, over the interval $[{\xi }_m,{\xi }_{m+1}]$. The integral formulas can be written as follows:

By integrating Equation (1), we get the following equations:

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(6\right)}& =& z_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi \hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(5\right)}& =& z_n^{\left(5\right)}+h{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi \hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(4\right)}& =& z_n^{\left(4\right)}+h{z}_n^{\left(5\right)}+\frac{h^2}{2!}{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi \hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(3\right)}& =& z_n^{\left(3\right)}+h{z}_n^{\left(4\right)}+\frac{h^2}{2!}{z}_n^{\left(5\right)}+\frac{h^3}{3!}{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi \hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill z_{n+1}^{″}& =& z_n^{″}+h{z}_n^{\left(3\right)}+\frac{h^2}{2!}{z}_n^{\left(4\right)}+\frac{h^3}{3!}{z}_n^{\left(5\right)}+\frac{h^4}{4!}{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi \hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill z_{n+1}^{\prime }& =& z_n^{\prime }+h{z}_n^{″}+\frac{h^2}{2!}{z}_n^{\left(3\right)}+\frac{h^3}{3!}{z}_n^{\left(4\right)}+\frac{h^4}{4!}{z}_n^{\left(5\right)}+\frac{h^5}{5!}{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)\hfill \end{array}$$

(26)

$$z_{n+1}=z_n+h{z}_n^{\prime }+\frac{h^2}{2!}{z}_n^{″}+\frac{h^3}{3!}{z}_n^{\left(3\right)}+\frac{h^4}{4!}{z}_n^{\left(4\right)}+\frac{h^5}{5!}{z}_n^{\left(5\right)}+\frac{h^6}{6!}{z}_n^{\left(6\right)}+{\int }_{{\xi }_n}^{{\xi }_{n+1}}f\left(Z\left(\xi \right)\right)d\xi$$

(27)

where $f\left(Z\left(\xi \right)\right)=f(\xi ,z^{\left(j\right)}\left(\xi \right))$ for $j=0,1,\cdots ,6.$ Let ${\xi }_{n+1}={\xi }_n+h$ and the change of coordinate $s=\frac{\xi -{\xi }_{n+3}}{h},$ $d\xi =hds$ where, f will be replaced by the following interpolating of Hermite polynomial in Equation (12), $\Theta \left(s\right)=f_0{L}_{00}\left(s\right)+f_1{L}_{10}\left(s\right)+f_2{L}_{20}\left(s\right)+f_3{L}_{30}\left(s\right)+g_0{L}_{01}\left(s\right)+g_1{L}_{11}\left(s\right)+g_2{L}_{21}\left(s\right)+g_3{L}_{31}\left(s\right).$ Using the approximate concepts, the following formulas can be obtained:

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(6\right)}& =& z_n^{\left(6\right)}+{\int }_{-3}^{-2}\theta \left(s\right)hds\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(5\right)}& =& z_n^{\left(5\right)}+h{z}_n^{\left(6\right)}-{\int }_{-3}^{-2}h(-2-s)\Theta \left(s\right)hds\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(4\right)}& =& z_n^{\left(4\right)}+h{z}_n^{\left(5\right)}+\frac{h^2}{2!}{z}_n^{\left(6\right)}+{\int }_{-3}^{-2}\frac{{\left(h(-2-s)\right)}^2}{2!}\theta \left(s\right)hds\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill z_{n+1}^{\left(3\right)}& =& z_n^{\left(3\right)}+h{z}_n^{\left(4\right)}+\frac{h^2}{2!}{z}_n^{\left(5\right)}+\frac{h^3}{3!}{z}_n^{\left(6\right)}-{\int }_{-3}^{-2}\frac{{\left(h(-2-s)\right)}^3}{3!}\theta \left(s\right)hds\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill z_{n+1}^{″}& =& z_n^{″}+h{z}_n^{\left(3\right)}+\frac{h^2}{2!}{z}_n^{\left(4\right)}+\frac{h^3}{3!}{z}_n^{\left(5\right)}+\frac{h^4}{4!}{z}_n^{\left(6\right)}+{\int }_{-3}^{-2}\frac{{\left(h(-2-s)\right)}^4}{4!}\theta \left(s\right)hds\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill z_{n+1}^{\prime }& =& z_n^{\prime }+h{z}_n^{″}+\frac{h^2}{2!}{z}_n^{\left(3\right)}+\frac{h^3}{3!}{z}^{\left(4\right)}+\frac{h^4}{4!}{z}_n^{\left(5\right)}+\frac{h^5}{5!}{z}_n^{\left(6\right)}+{\int }_{-3}^{-2}\frac{{\left(h(-2-s)\right)}^5}{5!}\theta \left(s\right)hds\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill z_{n+1}& =& z_n+h{z}_n^{\prime }+\frac{h^2}{2!}{z}_n^{″}+\frac{h^3}{3!}{z}_n^{\left(3\right)}+\frac{h^4}{4!}{z}_n^{\left(4\right)}+\frac{h^5}{5!}{z}_n^{\left(5\right)}+\frac{h^6}{6!}{z}_n^{\left(6\right)}+{\int }_{-3}^{-2}\frac{{\left(h(-2-s)\right)}^6}{6!}\theta \left(s\right)hds\hfill \end{array}$$

(34)

By integration the Equations (28)–(34), we obtained the following new formulas:

$$\begin{array}{c}\hfill z_{n+1}^{(7-i)}={\Delta }_i+h^i(a_{i1}{f}_0+a_{i2}{f}_1+a_{i3}{f}_2+a_{i4}{f}_3)+h^{i+1}(a_{i5}{g}_0+a_{i6}{g}_1+a_{i7}{g}_2+a_{i8}{g}_3).\end{array}$$

(35)

for $i=1,2,\cdots ,7,$ where

$$\begin{array}{ccc}\hfill {\Delta }_i& =& \sum _{j=0}^{i-1}\frac{h^j}{j!}{z}_n^{(7-j)},\hfill \end{array}$$

(36)

and

$$\begin{array}{c}\hfill A=\left(\begin{array}{cccccccc}\frac{6893}{18144}& \frac{313}{672}& \frac{89}{672}& \frac{397}{18144}& \frac{1283}{30240}& \frac{-851}{3360}& \frac{-269}{3360}& \frac{-163}{30240}\\ \\ \frac{19519}{68040}& \frac{1301}{10080}& \frac{181}{2520}& \frac{3329}{272160}& \frac{371}{12960}& \frac{-313}{2520}& \frac{-89}{2016}& \frac{-137}{45360}\\ \\ \frac{62387}{544320}& \frac{89}{3360}& \frac{439}{20160}& \frac{1031}{272160}& \frac{1879}{181440}& \frac{-359}{10080}& \frac{-13}{960}& \frac{-17}{18144}\\ \\ \frac{25883}{816480}& \frac{1457}{332640}& \frac{1579}{332640}& \frac{137}{163296}& \frac{3137}{1197504}& \frac{-89}{11880}& \frac{-283}{95040}& \frac{-311}{1496880}\\ \\ \frac{34673}{5132160}& \frac{325}{532224}& \frac{1091}{1330560}& \frac{10541}{71850240}& \frac{6163}{11975040}& \frac{-3359}{2661120}& \frac{-689}{1330560}& \frac{-871}{23950080}\\ \\ \frac{19607}{16679520}& \frac{73}{988416}& \frac{73}{617760}& \frac{259}{12130560}& \frac{9239}{111196800}& \frac{-7723}{43243200}& \frac{-103}{1372800}& \frac{-589}{111196800}\\ \\ \frac{186629}{1077753600}& \frac{293}{37065600}& \frac{7613}{518918400}& \frac{18719}{7005398400}& \frac{53329}{4670265600}& \frac{-709}{32432400}& \frac{-971}{103783680}& \frac{-1549}{2335132800}\end{array}\right)\end{array}$$

(37)

Evaluating the $P_3\left(x\right)$ at the point $y_{n+2}$ over $[x_{n+1},x_{n+2}]$ obtains a three-point fully implicit method. The second formula, $y_{n+2}$, is obtained by using the same method as for the first formula, $y_{n+1}$

$$\begin{array}{c}\hfill z_{n+2}^{(7-i)}={\Delta }_{7+i}+h^i(b_{i1}{f}_0+b_{i2}{f}_1+b_{i3}{f}_2+b_{i4}{f}_3)+h^{i+1}(b_{i5}{g}_0+b_{i6}{g}_1+b_{i7}{g}_2+b_{i8}{g}_3).\end{array}$$

(38)

for $i=1,2,\cdots ,7,$ where

$$\begin{array}{ccc}\hfill {\Delta }_{7+i}& =& \sum _{j=0}^{i-1}\frac{h^j}{j!}{z}_{n+1}^{(7-j)},\hfill \end{array}$$

(39)

and

$$\begin{array}{c}\hfill B=\left(\begin{array}{cccccccc}\frac{3}{224}& \frac{109}{224}& \frac{109}{224}& \frac{3}{224}& \frac{31}{10080}& \frac{113}{1120}& \frac{-113}{1120}& \frac{-31}{10080}\\ \\ \frac{1921}{272160}& \frac{869}{2520}& \frac{1429}{10080}& \frac{431}{68040}& \frac{73}{45360}& \frac{121}{2016}& \frac{-103}{2520}& \frac{-19}{12960}\\ \\ \frac{569}{272160}& \frac{533}{4032}& \frac{103}{3360}& \frac{941}{544320}& \frac{43}{90720}& \frac{19}{960}& \frac{-103}{10080}& \frac{-73}{181440}\\ \\ \frac{73}{163296}& \frac{11819}{332640}& \frac{1777}{332640}& \frac{283}{816480}& \frac{151}{1496880}& \frac{443}{45040}& \frac{-23}{11880}& \frac{-97}{1197504}\\ \\ \frac{5459}{71850240}& \frac{9869}{1330560}& \frac{2087}{2661120}& \frac{287}{5132160}& \frac{409}{23950080}& \frac{1151}{1330560}& \frac{-799}{2661120}& \frac{-157}{11975040}\\ \\ \frac{131}{12130560}& \frac{157}{123552}& \frac{493}{4942080}& \frac{127}{16679520}& \frac{269}{111196800}& \frac{61}{457600}& \frac{-1717}{43243200}& \frac{-199}{111196800}\\ \\ \frac{9281}{7005398400}& \frac{95987}{518918400}& \frac{2909}{259459200}& \frac{971}{1077753600}& \frac{691}{2335132800}& \frac{1829}{103783680}& \frac{-149}{32432400}& \frac{-991}{4670265600}\end{array}\right)\end{array}$$

(40)

The purpose of evaluating the $P_3\left(x\right)$ at the point $y_{n+3}$ over $[x_{n+2},x_{n+3}]$ is to derive a three-point fully implicit method. By applying the same technique as for the first formula $y_{n+1}$ we have the third formula at $x_{n+3}:$

$$\begin{array}{c}\hfill z_{n+3}^{(7-i)}={\Delta }_{14+i}+h^i(c_{i1}{f}_0+c_{i2}{f}_1+c_{i3}{f}_2+c_{i4}{f}_3)+h^{i+1}(c_{i5}{g}_0+c_{i6}{g}_1+c_{i7}{g}_2+c_{i8}{g}_3).\end{array}$$

(41)

for $i=1,2,\cdots ,7,$ where

$$\begin{array}{ccc}\hfill {\Delta }_{14+i}& =& \sum _{j=0}^{i-1}\frac{h^j}{j!}{z}_{n+2}^{(7-j)},\hfill \end{array}$$

(42)

and

$$\begin{array}{c}\hfill C=\left(\begin{array}{cccccccc}\frac{397}{18144}& \frac{89}{672}& \frac{313}{672}& \frac{6893}{18144}& \frac{163}{30240}& \frac{269}{3360}& \frac{851}{3360}& \frac{-1283}{30240}\\ \\ \frac{1313}{136080}& \frac{611}{10080}& \frac{1697}{5040}& \frac{3617}{38880}& \frac{43}{18144}& \frac{181}{5040}& \frac{1301}{10080}& \frac{-313}{22680}\\ \\ \frac{151}{60480}& \frac{163}{10080}& \frac{2627}{20160}& \frac{107}{6048}& \frac{37}{60480}& \frac{19}{2016}& \frac{767}{20160}& \frac{-89}{30240}\\ \\ \frac{7}{14580}& \frac{1061}{332640}& \frac{1171}{33264}& \frac{2281}{816480}& \frac{703}{5987520}& \frac{61}{33264}& \frac{5477}{665280}& \frac{-37}{74844}\\ \\ \frac{299}{3991680}& \frac{41}{80640}& \frac{467}{63360}& \frac{3029}{7983360}& \frac{73}{3991680}& \frac{769}{2661120}& \frac{173}{120960}& \frac{-557}{7983360}\\ \\ \frac{331}{33359040}& \frac{113}{1647360}& \frac{521}{411840}& \frac{6047}{133436160}& \frac{269}{111196800}& \frac{53}{1372800}& \frac{287}{1372800}& \frac{-3329}{389188800}\\ \\ \frac{5359}{4670265600}& \frac{697}{86486400}& \frac{31891}{172972800}& \frac{11293}{2335132800}& \frac{29}{103783680}& \frac{389}{8646400}& \frac{4579}{172972800}& \frac{-181}{194594400}\end{array}\right)\end{array}$$

(43)

3.3. The Zero-Stability and the Order of the Proposed GIBM3P Method

The zero-stability and the order of the proposed GIBM3P method have been examined in this section.

3.3.1. Order of the GIBM3P Method

The three-point implicit block method’s formulas, which are given in Equations (35), (38) and (41) for $i=1,2,\cdots ,7$, can be expressed in matrix form as follows:

$$\alpha Y_m=h\beta Y_m^{\prime }+h^2\gamma Y_m^{″}+h^3\psi Y_m^{‴}+h^4\delta Y_m^{\left(4\right)}+h^5\phi Y_m^{\left(5\right)}+h^6\lambda Y_m^{\left(6\right)}+h^{7}o{F}_m+h^8\rho G_m$$

where, $\alpha ,\beta ,\gamma ,\psi ,\delta ,\phi ,\lambda ,o$ and $\rho$ are $21\times 21$ matrices. We can define the linear operator as follows

$$\begin{array}{c}\hfill L[Z\left(x\right);h]=\alpha Y_m-h\beta Y_m^{\prime }-h^2\gamma Y_m^{″}-h^3\psi Y_m^{‴}-h^4\delta Y_m^{\left(4\right)}-\phi h^5{F}_m-h^6\lambda -h^{7}o{F}_m-h^8\rho G_m.\end{array}$$

(44)

Expanding Equation (44) using Taylor series at the point x where $Z\left(x\right)$ is an arbitrary differentiable and continuous function.

$$\begin{array}{c}\hfill L[Z\left(x\right);h]=C_{0}Z\left(x\right)+C_{1}h{Z}^{\prime }\left(x\right)+\cdots +C_p{h}^p{Z}^p\left(x\right)+C_{p+1}{h}^{p+1}{Z}^{p+1}\left(x\right)+\cdots \end{array}$$

(45)

The linear operator of the proposed method in Equation (45) has order=p if $C_j=0$ for $j=0,1,\cdots ,p+6$ and $C_{p+7}\ne 0$. Where $C_{p+7}$ is the error constant. In the three-point implicit block method, we have $C_j=0;j=0,1,\cdots ,14.$ Therefore, the order of the three-point block method is eight.

3.3.2. Zero-Stability of the New Method

In this subsection, the zero-stability of the three-point fully implicit block method is studied. The formulas of the new method in Equations (35), (38) and (41) for $i=1,2,\cdots ,7$ are considered as a zero stable in case the roots $r_i=1,2,\cdots ,N$ of the first characteristic polynomial $\rho \left(R\right)=|R{A}^{\left(0\right)}-A^{\left(1\right)}|=0$ are found to satisfy $\mid R\mid \le 1.$

Moreover, in order to determine the matrix form of the first characteristic polynomial of the method, we will employ the following formulas. When the formulas in the Equations (35) and (38) are substituted for $i=1,2,\cdots ,7$, we obtain

$$\begin{array}{cc}\hfill y_{n+2}^{\left(6\right)}& =y_n^{\left(6\right)}+\frac{223h}{567}{f}_n+\frac{20h}{21}{f}_{n+1}+\frac{13h}{21}{f}_{n+2}+\frac{20h}{567}{f}_{n+3}+\frac{43h^2}{945}{g}_n-\frac{16h^2}{105}{g}_{n+1}-\frac{19h^2}{105}{g}_{n+2}\hfill \\ & -\frac{8h^2}{945}{g}_{n+3}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill y_{n+2}^{\left(5\right)}& =2h{y}_n^{\left(6\right)}+y_n^{\left(5\right)}+\frac{5731h^2}{8505}{f}_n+\frac{296h^2}{315}{f}_{n+1}+\frac{109h^2}{315}{f}_{n+2}+\frac{344h^2}{8505}{f}_{n+3}+\frac{206h^3}{2835}{g}_n-\frac{20h^3}{63}{g}_{n+1}\hfill \\ & -\frac{52h^3}{315}{g}_{n+2}-\frac{4h^3}{405}{g}_{n+3}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill y_{n+2}^{\left(4\right)}& =2h^2{y}_n^{\left(6\right)}+2h{y}_n^{\left(5\right)}+y_n^{\left(4\right)}+\frac{5048h^3}{8505}{f}_n+\frac{164h^3}{315}{f}_{n+1}+\frac{4h^3}{21}{f}_{n+2}+\frac{244h^3}{8505}{f}_{n+3}+\frac{172h^4}{2835}{g}_n\hfill \\ & -\frac{4h^4}{15}{g}_{n+1}-\frac{34h^4}{315}{g}_{n+2}-\frac{4h^4}{567}{g}_{n+3}\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill y_{n+2}^{‴}& =\frac{4}{3}{h}^3{y}_n^{\left(6\right)}+2h^2{y}_n^{\left(5\right)}+2h{y}_n^{\left(4\right)}+y_n^{‴}+\frac{1804h^4}{5103}{f}_n+\frac{2168h^4}{10395}{f}_{n+1}+\frac{934h^4}{10395}{f}_{n+2}+\frac{376h^4}{25515}{f}_{n+3}\hfill \\ & +\frac{3224h^5}{93555}{g}_n-\frac{7361909h^5}{53507520}{g}_{n+1}-\frac{16h^5}{297}{g}_{n+2}-\frac{68h^5}{18711}{g}_{n+3}\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill y_{n+2}^{″}& =\frac{2}{3}{h}^4{y}_n^{\left(6\right)}+\frac{4}{3}{h}^3{y}_n^{\left(5\right)}+2h^2{y}_n^{\left(4\right)}+2h{y}_n^{‴}+y_n^{″}+\frac{44761h^5}{280665}{f}_n+\frac{692h^5}{10395}{f}_{n+1}+\frac{361h^5}{10395}{f}_{n+2}\hfill \\ & +\frac{236h^5}{40095}{f}_{n+3}+\frac{1391h^6}{93555}{g}_n-\frac{592h^6}{10395}{g}_{n+1}-\frac{221h^6}{10395}{g}_{n+2}-\frac{136h^6}{93555}{g}_{n+3}\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill y_{n+2}^{\prime }& =\frac{4}{15}{h}^5{y}_n^{\left(6\right)}+\frac{2}{3}{h}^4{y}_n^{\left(5\right)}+\frac{4}{3}{h}^3{y}_n^{\left(4\right)}+2h^2{y}_n^{‴}+2h{y}_n^{″}+y_n^{\prime }+\frac{2749h^6}{47385}{f}_n+\frac{344h^6}{19305}{f}_{n+1}+\frac{43h^6}{3861}{f}_{n+2}\hfill \\ & +\frac{200h^6}{104247}{f}_{n+3}+\frac{4502h^7}{868725}{g}_n-\frac{196h^7}{10725}{g}_{n+1}-\frac{4652h^7}{675675}{g}_{n+2}-\frac{412h^7}{868725}{g}_{n+3}\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill y_{n+2}& =\frac{4}{45}{h}^6{y}_n^{\left(6\right)}+\frac{4}{15}{h}^5{y}_n^{\left(5\right)}+\frac{2}{3}{h}^4{y}_n^{\left(4\right)}+\frac{4}{3}{h}^3{y}_n^{‴}+2h^2{y}_n^{″}+2h{y}_n^{\prime }+y_n+\frac{969008h^7}{54729675}{f}_n+\frac{8368h^7}{2027025}{f}_{n+1}\hfill \\ & +\frac{6152h^7}{2027025}{f}_{n+2}+\frac{2224h^7}{4209975}{f}_{n+3}+\frac{27688h^8}{18243225}{g}_n-\frac{400h^8}{81081}{g}_{n+1}-\frac{3826h^8}{2027025}{g}_{n+2}-\frac{2384h^8}{18243225}{g}_{n+3}\hfill \end{array}$$

(52)

Furthermore, by substituting Equations (46)–(52) into the formulas from the Equation (41) for $i=1,2,\cdots ,7$, we get

$$\begin{array}{cc}\hfill y_{n+3}^{\left(6\right)}& =y_n^{\left(6\right)}+\frac{93h}{224}{f}_n+\frac{243h}{224}{f}_{n+1}+\frac{243h}{224}{f}_{n+2}+\frac{93h}{224}{f}_{n+3}+\frac{57h^2}{1120}{g}_n-\frac{81h^2}{1120}{g}_{n+1}-\frac{81h^2}{1120}{g}_{n+2}\hfill \\ & -\frac{57h^2}{1120}{g}_{n+3}\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill y_{n+3}^{\left(5\right)}& =3h{y}_n^{\left(6\right)}+y_n^{\left(5\right)}+\frac{603h^2}{560}{f}_n+\frac{2187h^2}{1120}{f}_{n+1}+\frac{729h^2}{560}{f}_{n+2}+\frac{27h^2}{160}{f}_{n+3}+\frac{27h^3}{224}{g}_n-\frac{243h^3}{560}{g}_{n+1}\hfill \\ & -\frac{234h^3}{1120}{g}_{n+2}-\frac{9h^3}{280}{g}_{n+3}\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill y_{n+3}^{\left(4\right)}& =\frac{9}{2}{h}^2{y}_n^{\left(6\right)}+3h{y}_n^{\left(5\right)}+y_n^{\left(4\right)}+\frac{657h^3}{448}{f}_n+\frac{2187h^3}{1120}{f}_{n+1}+\frac{2187h^3}{2240}{f}_{n+2}+\frac{117h^3}{1120}{f}_{n+3}+\frac{351h^4}{2240}{g}_n\hfill \\ & -\frac{729h^4}{1120}{g}_{n+1}-\frac{729h^4}{2240}{g}_{n+2}-\frac{27h^4}{1120}{g}_{n+3}\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill y_{n+3}^{‴}& =\frac{9}{2}{h}^3{y}_n^{\left(6\right)}+\frac{9}{2}{h}^2{y}_n^{\left(5\right)}+3h{y}_n^{\left(4\right)}+y_n^{‴}+\frac{27h^4}{20}{f}_n+\frac{16767h^4}{12320}{f}_{n+1}+\frac{729h^4}{1232}{f}_{n+2}+\frac{81h^4}{1120}{f}_{n+3}\hfill \\ & +\frac{3429h^5}{24640}{g}_n-\frac{43938491h^5}{74910528}{g}_{n+1}-\frac{6561h^5}{24640}{g}_{n+2}-\frac{27h^5}{1540}{g}_{n+3}\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill y_{n+3}^{″}& =\frac{27}{8}{h}^4{y}_n^{\left(6\right)}+\frac{9}{2}{h}^3{y}_n^{\left(5\right)}+\frac{9}{2}{h}^2{y}_n^{\left(4\right)}+3h{y}_n^{‴}+y_n^{″}+\frac{46251h^5}{49280}{f}_n+\frac{6561h^5}{8960}{f}_{n+1}+\frac{2187h^5}{7040}{f}_{n+2}\hfill \\ & +\frac{4293h^5}{98560}{f}_{n+3}+\frac{4617h^6}{49280}{g}_n-\frac{579568537h^6}{1498210560}{g}_{n+1}-\frac{729h^6}{4480}{g}_{n+2}-\frac{1053h^6}{98560}{g}_{n+3}\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill y_{n+3}^{\prime }& =\frac{81}{40}{h}^5{y}_n^{\left(6\right)}+\frac{27}{8}{h}^4{y}_n^{\left(5\right)}+\frac{9}{2}{h}^3{y}_n^{\left(4\right)}+\frac{9}{2}{h}^2{y}_n^{‴}+3h{y}_n^{″}+y_n^{\prime }+\frac{24003h^6}{45760}{f}_n+\frac{59049h^6}{183040}{f}_{n+1}\hfill \\ & +\frac{6561h^6}{45760}{f}_{n+2}+\frac{4023h^6}{183040}{f}_{n+3}+\frac{23247h^7}{457600}{g}_n-\frac{705760183h^7}{3477988800}{g}_{n+1}-\frac{37179h^7}{457600}{g}_{n+2}\hfill \\ & -\frac{118669h^7}{21621600}{g}_{n+3}\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill y_{n+3}& =\frac{81}{80}{h}^6{y}_n^{\left(6\right)}+\frac{81}{40}{h}^5{y}_n^{\left(5\right)}+\frac{27}{8}{h}^4{y}_n^{\left(4\right)}+\frac{9}{2}{h}^3{y}_n^{‴}+\frac{9}{2}{h}^2{y}_n^{″}+3h{y}_n^{\prime }+y_n+\frac{1571319h^7}{6406400}{f}_n\hfill \\ & +\frac{387099h^7}{3203200}{f}_{n+1}+\frac{373977h^7}{6406400}{f}_{n+2}+\frac{30213h^7}{3203200}{f}_{n+3}+\frac{5913h^8}{256256}{g}_n-\frac{4992226654501h^8}{56385154425600}{g}_{n+1}\hfill \\ \hfill & -\frac{220887h^8}{6406400}{g}_{n+2}-\frac{1863h^8}{800800}{g}_{n+3}\hfill \end{array}$$

(59)

The Equations (35), (46)–(59) for $i=1,2,\cdots ,7$ have now been substituted in order to determine the matrix and the first characteristic polynomial. The matrices’ general form is $A^{\left(i\right)}$ for $i=0,1$ can be denoted by $A^{\left(1\right)}$ which is a matrix with all of its elements being zero, barring the following situations.

(i,j) ∈ {(1,15), (2,16), (3,17), (4,18), (5,19), (6,20), (7,21), (8,15), (9,16), (10,17), (11,18), (12,19), (13,20), (14,21), (15,15), (16,16), (17,17), (18,18), (19,19), (20,20), (21,21)} are all equal to one, where the Kroneker $A^{\left(0\right)}$ and $A^{\left(1\right)}$ are a 21 × 21 matrices.

Then, $R^{14}{(R-1)}^7=0,$ leads to $R=0$ (14-times) and $R=0$ (7-times). Hence, it can be concluded that the proposed method is zero stable.

4. Numerical Implementations

The seventh-order GIBM3P method is used in this section to solve a collection of seventh-order ODEs. Figure 2 compares the numerical results to show the efficacy of the proposed method. The notations that were used are as follows:

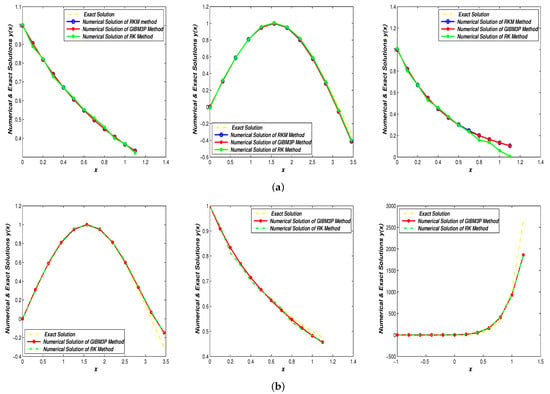
Figure 2. Numerical Solutions Using Proposed GIBM3P Method Versus (a) Classical RK method, RKM method and Analytical Solutions for Examples 1–3. (b) Classical RK method, and Analytical Solutions for Examples 4–6.

• RK Classical Runge–Kutta method.
• RKM Direct Runge–Kutta–Mohammed method.
• GIBM3P Proposed direct implicit block with three points method.

Problems Tested of ODEs

Example 1.

(Linear, non-homogenous ODE)

$$y^{\left(7\right)}\left(t\right)=-2y\left(t\right)+e^{-t},0<t\le b.$$

• Initial conditions, $y^{\left(i\right)}\left(0\right)={(-1)}^i,i=0,1,\cdots ,6.$
• Exact solution: $y\left(t\right)=e^{-t},b=1.$

Example 2.

(Linear, homogenous ODE)

$$y^{\left(7\right)}\left(t\right)=-cos\left(t\right),0<t\le b.$$

• Initial conditions, $y^{(2i+1)}\left(0\right)={(-1)}^i,i=0,1,2;y^{\left(i\right)}\left(0\right)=0;i=0,2,4,6.$
• Exact solution: $y\left(t\right)=sin\left(t\right),b=\pi .$

Example 3.

(Non linear ODE)

$$y^{\left(7\right)}\left(t\right)=y^4\left(t\right)-128y\left(t\right)-e^{-8t},0<t\le b.$$

• Initial conditions, $y\left(0\right)=0;y^{\left(i\right)}\left(0\right)={(-1)}^{i}i!;i=1,\cdots ,6.$
• Exact solution: $y\left(t\right)=e^{-2t},b=1.$

Example 4.

(Homogenous ODE)

$$y^{\left(7\right)}\left(t\right)=y\left(t\right)+y^{\prime }\left(t\right)+y^{″}\left(t\right);,0<t\le b.$$

• Initial conditions, $y^{(2i+1)}\left(0\right)={(-1)}^i,i=0,1,2;y^{\left(2i\right)}\left(0\right)=0,i=0,1,2,3.$
• Exact solution: $y\left(t\right)=sin\left(t\right),b=\pi$

Example 5.

(Nonlinear ODE)

$$y^{\left(7\right)}\left(t\right)=y^6\left(t\right)+y^{\prime }{}^3\left(t\right)-30y^{″}{}^2\left(t\right),0<t\le b.$$

• Initial conditions, $y^{\prime }\left(0\right)={(-1)}^{i}i!,i=0,1,2,\cdots ,6.$
• Exact solution: $y\left(t\right)=\frac{1}{1+t},b=10$

Example 6.

(Homogenous ODE)

$$y^{\left(7\right)}\left(t\right)=y^{\prime }\left(t\right)+y^{″}\left(t\right)+604800{(1+t)}^3+10{(1+t)}^8(10+t),-1<t\le b.$$

• Initial conditions, $y^{\left(i\right)}\left(0\right)=0,i=0,1,\cdots ,6.$
• Exact solution: $y\left(t\right)={(1+t)}^{10},b=1$

5. Discussion and Conclusions

The general implicit block method with three points (GIBM3P) has been developed in this paper using the Hermite approximation method to solve a general class of seventh-order ODEs. The purpose of this article is to develop a direct-implicit block method for the general class of seventh-order ODEs. The proposed method has been numerically compared to direct RKM, existing RK methods, and exact solutions. This comparison leads us to the conclusion that the new method is accurate and effective. Based on the results of the implementations, we can say that the proposed method is more efficient than RK and RKM methods in terms of computation time while also requiring fewer function evaluations.