Verifiable (2, n) Image Secret Sharing Scheme Using Sudoku Matrix

Abstract

As Internet technology continues to profoundly impact our lives, techniques for information protection have become increasingly advanced and become a common discussion topic. With the aim to protect private images, this paper splits a secret image into n individual shares using a Sudoku matrix with authentication features. Later, the shares can be compiled to completely reconstruct the secret image. The shares are meaningful ones in order to avoid detection and suspicion among malicious users. Our proposed matrix is unique because the embedding rate of the secret data is very high, while the visual quality of the shares can be well guaranteed. In addition, the embedded authentication codes can be retrieved to authenticate the integrity of the secret image. Experimental results prove the advantages of our approach in terms of visual quality and authentication ability.

1. Introduction

As Internet technology becomes more sophisticated, users have grown accustomed to backing up digital content, such as text files, photos, and videos, to cloud platforms. These technologies allow users to easily access their photos from anywhere; however, if the platform is not trustworthy, personal privacy can be jeopardized. Image encryption [1,2] is a reliable tool for traditional information security. Files containing sensitive data are usually encrypted prior to uploading. However, traditional encryption methods face shortcomings; for instance, an encrypted image is meaningless and thus easily attracts the attention of hackers, who try to decrypt them through data analysis and data mining. The meaningless content is difficult to manage. In order to facilitate management, image information can be carried under the encrypted image [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], so as to identify the content according to the extracted information later. However, since traditional data are hidden in a single carrier, once the carrier is discovered, the probability of the code being cracked greatly increases. In order to reduce the risk that comes from using a single carrier, Shamir and Blakley [29] proposed a (t, n) threshold secret sharing approach that first decomposes the secret into n parts, which then jointly provide their share to reconstruct the secret, where t is less than or equal to n. It then distributes them to different participants of n. Afterward, participants are greater than $t-1$. However, the shares are still meaningless to users, which arouses the suspicion of malicious attackers. Therefore, secure Internet usage and data privacy have become major issues and given rise to various data-hiding technologies that embed shared content into images.

Chang et al. [30] proposed a reversible secret image sharing system (SIS) using an exploiting modification direction (EMD) matrix. The shared images are embedded into the cover images as stego images. After embedding, the stego image has high visual quality. The shared image can be extracted, and then the secret image can be reconstructed through calculation. To improve the visual quality, Chang et al. [31] proposed an SIS scheme based on the Sudoku matrix and Lagrange polynomial. Later, Yan et al. proposed a reversible image secret sharing scheme [32]. To guarantee the integrity of the shares, the authentication mechanism authenticates which pixels are modified or lost during transmission. In 2018, Liu and Chang [33] proposed applying the authentication mechanism to secret sharing to authenticate whether the shadow images have been tampered with (modified) or not. In 2021, Gao et al. [34] proposed a high-capacity secret sharing scheme with an authentication mechanism. To achieve reversibility, a reversible and verifiable SIS scheme has also been proposed. Gao et al. [35] designed a stick insect matrix to verify the shared image, and embedded the verification code and the secret image into the shared image. However, the shared images generated by these reversible SIS schemes rely on a single cover image, which may increase the possibility that confidential images may be identified through statistical analysis of subtle differences between share images. In order to prevent the discovery of secret images by statistical analysis, Liu et al. [36] and Chang et al. [37] generated shares from different cover images. Nevertheless, these methods cannot construct secret images losslessly.

In this paper, we encode a secret image into n shares using the concept of Sudoku. The schemes [33,34,35,36,38] are not allowed more than three participants. The scheme allows n joint participants, so it is more flexible than the above schemes. To achieve a flexible secret sharing scheme, we encode the shares by using simultaneous algebraic equations, in which the parameters are a hybrid of the secret pixels and the corresponding authentication codes. Later, the shares are embedded into the cover images. The cover images can be different individually. Any two cover images can be combined together to completely restore the secret image. If the pixels in the cover image are missing or have been modified, an authentication mechanism indicates the untrue locations. During the embedding process, the cover image is only slightly modified due to the concept of Sudoku. Therefore, it is difficult to identify the difference between the original cover image and the hidden image, which helps protect the secret image from detection by malicious users. When compared with Gao et al.’s method [34,35], as summarized in Section 4, the proposed approach achieves superior performance in terms of visual quality, hiding capacity, and authentication ability.

The structure of this paper is organized as follows. First, we briefly present the Sudoku matrix in Section 2. Next, we describe our proposed scheme in Section 3, followed by the experimental results and analysis in Section 4. Finally, our conclusions are summarized in Section 5.

2. Sudoku Matrix

This section introduces the concept of the Sudoku matrix M [39], which represents the core of our solution. The size of the Sudoku matrix M is 256 × 256, as shown in Figure 1, calculated using Equation (1), where $n=2$. As can be seen in the Figure 1, each pixel pair, represented by ${\alpha }_1$ and ${\alpha }_2$, can be mapped to a core digit. Based on the core number, there are eight different independent numbers surrounding the core number without any repeated numbers. For example, if ${\alpha }_1=5$ and ${\alpha }_2=2$, as shown in Figure 1, the core digit is 2, the surrounding eight neighboring digits are different from each other, and the range is between 0 and 8, excluding the number 2. By using the Sudoku matrix M, a pixel pair can be moved to a new pixel pair, which is represented by ${\alpha }_1^{\prime }$ and ${\alpha }_2^{\prime }$ according to the hidden number d. For example, if $d=5$, ${\alpha }_1^{\prime }$ and ${\alpha }_2^{\prime }$, obtained through Equation (2), will be 5 and 3, respectively. The maximum distortion of a pixel is 1 in order to maintain good visual quality after secret embedding.

$$\alpha =\sum _{i=1}^n{3}^{i-1}{\alpha }_i\mathrm{mod}{3}^n$$

(1)

$$d=f({\alpha }_1^{\prime },{\alpha }_2^{\prime })={\alpha }_1^{\prime }+3\times {\alpha }_2^{\prime }\mathrm{mod}9$$

(2)

Figure 1. An example of Sudoku matrix M, where $w=2$, ${\alpha }_1=5$ and ${\alpha }_2=2$.

3. Research Methods

In this section, we propose a (t, n)-threshold secret sharing scheme using the Sudoku matrix, where $t\le n$. The secret image can be distributed to n different participants. After this, any t participants together can completely reconstruct the secret image, except in the case where participants whose number of shares minus the result is a multiple of three. An authentication mechanism is also proposed to authenticate the integrity of the proposed scheme. The new proposed Sudoku matrix can markedly improve the embedding capacity of secret data. The proposed approach can be divided into the following parts: (1) the procedure for hiding and extracting secret images, (2) the authentication mechanism, and (3) the reconstruction of the secret image and authentication.

Based on the (t, n)-threshold secret sharing method put forth by Shamir and Blakley in 1979, the matrix that we propose incorporates this concept as a (2, n)-SIS scheme. In our method, there is no limit on the number of shareholders, and each two of the holders can completely retrieve secret data. As the overflow shows in Figure 2a, there can be several cover images to embed secret data, while the same number of shares are produced. Any two of the shares can reconstruct the secret image. For example, as shown in Figure 2b, if n is 29, we select two of the shares, such as the first and the last ones, to reconstruct the secret image.

Figure 2. Schematic diagram of the proposed (2, n)-SIS scheme. (a) Secret sharing process. (b) Recovery process.

If two of the random shares are real, as shown in Figure 3a,b, the secret data can be recovered completely, as in Figure 3c. On the contrary, if any one of the shares is fake, as in Figure 3e, the secret data cannot be retrieved, and the image in the authentication result will appear incomplete, as shown in Figure 3f.

Figure 3. An example of our schematic diagram. (a) Real share 1. (b) Real share 2. (c) Authentication result—fully recovered. (d) Real share 1. (e) Fake share 2. (f) Authentication result—not recovered completely.

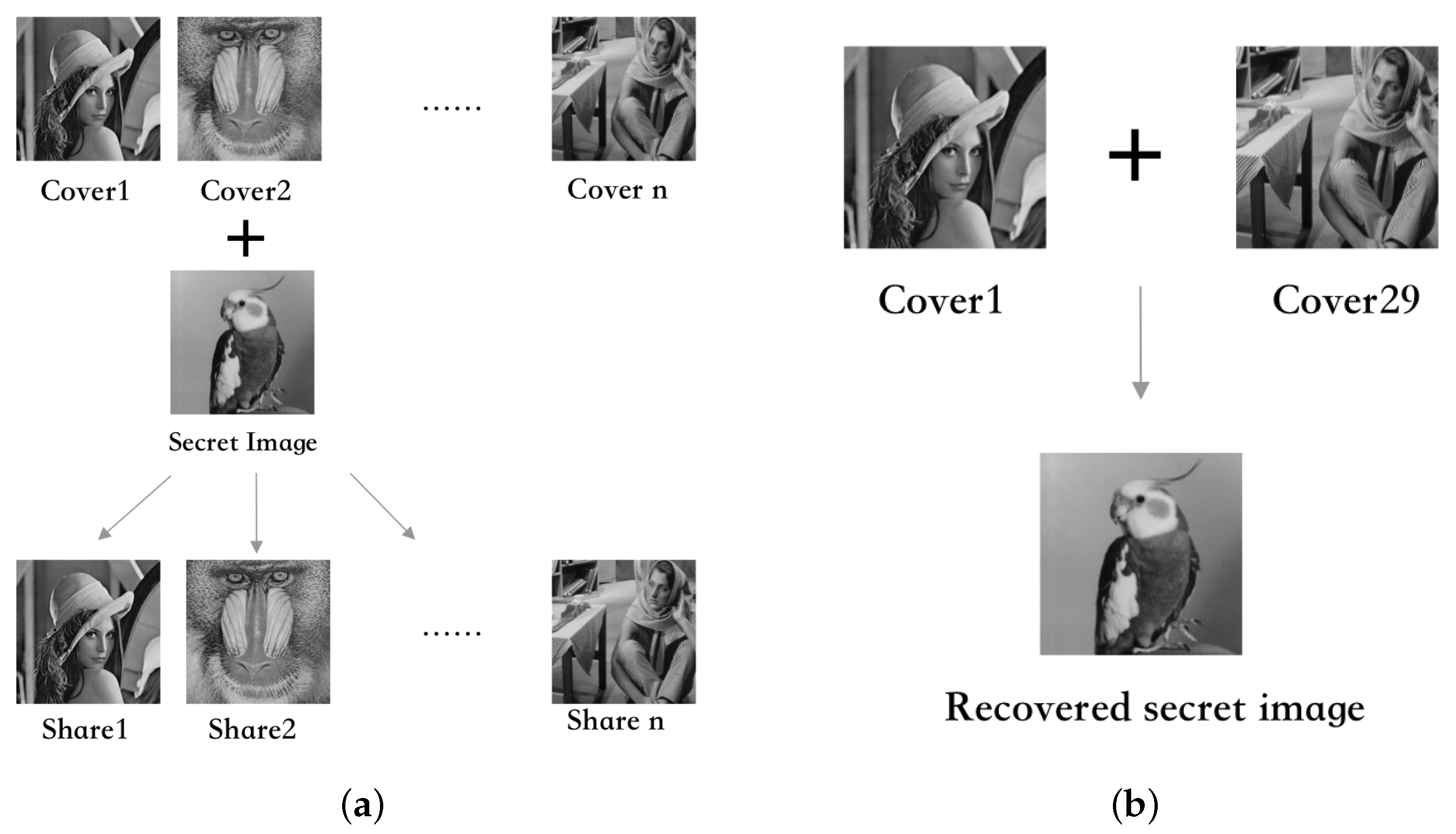
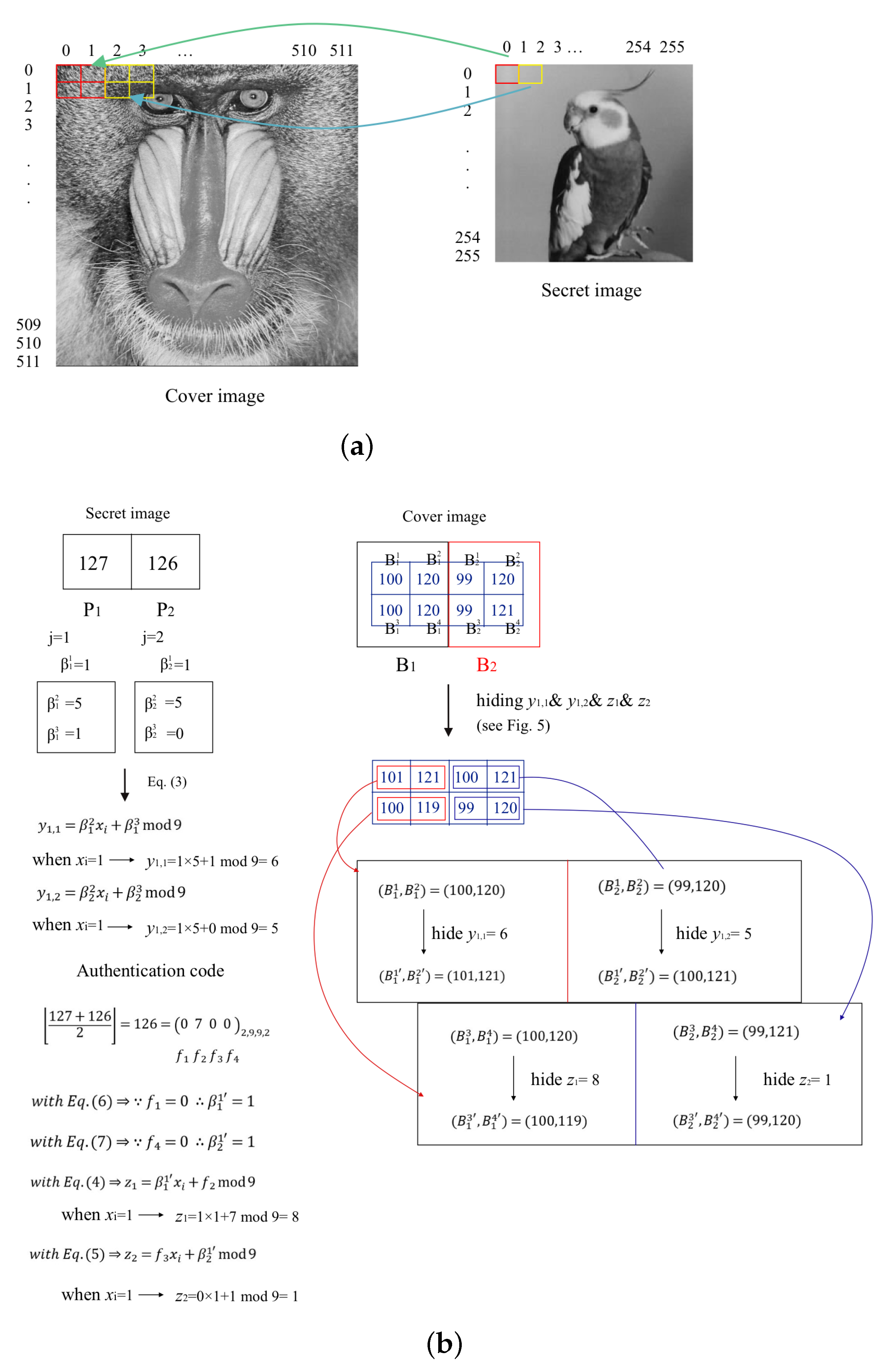
3.1. The Procedure of Hiding Secret Image and Authentication Codes to Cover Images

We adopt Equations (3) and (4), to describe the secret image divided into n shadows and the corresponding authentication codes hidden back into the shadows, respectively. There is a secret image of size $n\times n$ to be hidden, while there can be several cover images of size $2n\times 2n$ depending on the numbers of shareholders participating in hiding the secret data. There are two square pixels of each cover image to hide two pixels of secret data values and the corresponding authentication codes, as shown in Figure 4a. Each square pixel consists of four pixels. The first square pixel, denoted by $B_1$, and the second square pixel, denoted by $B_2$, are used to embed the first pixel, denoted by $p_1$, and the second secret pixel, denoted by $p_2$, of the secret image in different colors, as shown in Figure 4b. Here, for $B_j$ ($j\in \{1,2\}$), the original pixel values of the four pixels, located in the upper-left pixel, the upper-right pixel, the bottom-left pixel, and the bottom-right pixel, are represented as $B_j^1$, $B_j^2$, $B_j^3$, and $B_j^4$, respectively.

Figure 4. Schematic diagram of secret data embedded into a cover image. (a) Schematic diagram. (b) An embedding example.

During the secret sharing procedure, first, the pixel value in the secret image needs to be converted to a base value of 9, denoted by ${\left({\beta }_j^1{\beta }_j^2{\beta }_j^3\right)}_9$, where ${\beta }_j^1$ is in the range of 0 and 3, and ${\beta }_j^2$ and ${\beta }_j^3$ are in the range of 0 and 8, and j are equal to 1 and 2 if the digits are generated by pixels $p_1$ and $p_2$, respectively. Secondly, the ${\beta }_j^2$ and ${\beta }_j^3$ are embedded into the top two pixels ($B_j^1$ and $B_j^2$) of the cover images with Equation (3). Here, the $x_i$ represents the ID number of the cover image.

$$y_{i,j}={\beta }_j^2{x}_i+{\beta }_j^3\mathrm{mod}9$$

(3)

$$z_1={{\beta }_1^1}^{\prime }{x}_i+f_2\mathrm{mod}9$$

(4)

An embedding example is shown in Figure 4b, prior to undergoing the embedding procedure. We suppose that the first pixel value $p_1$ in the pixel pair retrieved by the secret image is 127, for which the ID of the cover image is $x_i=1$, and the converted value is ${\left(151\right)}_9$, indicated as ${\beta }_1^1$, ${\beta }_1^2$, ${\beta }_1^3$, from left to right, respectively. With Equation (3), the $y_i$ is 6 because the equation is generated as $y_{i,1}=5x_i+1$ mod 9 if $x_i=1$. Suppose that the original pixel values of $B_1^1$ and $B_1^2$ are 100 and 120, respectively. To hide the $y_{i,1}$ value, the pixels $B_1^1$ and $B_1^2$ are changed as stego pixels ${B_1^1}^{\prime }$ and ${B_1^2}^{\prime }$, respectively. After embedding $y_{i,1}$ ($y_{i,1}=6$ in the example), the values ${B_1^1}^{\prime }$ and ${B_1^2}^{\prime }$ will be 101 and 121, respectively, as shown in Figure 5. In the same way, the digits ${\beta }_2^2$ and ${\beta }_2^3$ generated by the secret pixel $p_2$ can be hidden as $B_2^1$ and $B_2^2$ to generate the stego pixels ${B_2^1}^{\prime }$ and ${B_2^2}^{\prime }$. For example, if $p_2$ is equal to 126, the values of ${\beta }_2^2$ and ${\beta }_2^3$ are 5 and 0, respectively. After the hiding procedure, the stego pixels ${B_2^1}^{\prime }$ and ${B_2^2}^{\prime }$ are 100 and 121, respectively.

Figure 5. Data embedding example with hidden number 6 changing ${\alpha }_1$ and ${\alpha }_2$ to 101 and 121.

The authentication codes, denoted by $f_1$, $f_2$, $f_3$, and $f_4$, are the average of pixels $p_1$ and $p_2$ and transformed into ${\left(f_1{f}_2{f}_3{f}_4\right)}_{2,9,9,2}$ via a multiple notation system. Later, the digits ${\beta }_1^1$ and ${\beta }_2^1$ are hybridized with the authentication codes for embedding into pixels $B_1^3$, $B_1^4$, $B_2^3$, and $B_2^4$ based on Equations (4) and (5). Here, the values ${{\beta }_1^1}^{\prime }$ and ${{\beta }_2^1}^{\prime }$ are generated according to Equations (6) and (7), respectively.

$$z_2=f_3{x}_i+{{\beta }_1^1}^{\prime }\mathrm{mod}9$$

(5)

$${{\beta }_1^1}^{\prime }=\left\{\begin{array}{cc}{\beta }_1^1\hfill & \mathrm{if}{f}_1=0\hfill \\ {\beta }_1^1+4\hfill & \mathrm{if}{f}_1=1\hfill \end{array}\right.$$

(6)

$${{\beta }_2^1}^{\prime }=\left\{\begin{array}{cc}{\beta }_2^1\hfill & \mathrm{if}{f}_4=0\hfill \\ {\beta }_2^1+4\hfill & \mathrm{if}{f}_4=1\hfill \end{array}\right.$$

(7)

As for embedding the hybrid authentication codes, the pixel pairs ($B_1^3$, $B_1^4$) and ($B_2^3$, $B_2^4$) are used to embed the digits $z_1$ and $z_2$, respectively, using the Sudoku matrix as denoted by (${B_1^3}^{\prime }$, ${B_1^4}^{\prime }$) and (${B_2^3}^{\prime }$, ${B_2^4}^{\prime }$). For example, we assume that the two secret pixels $p_1$ and $p_2$ are 127 and 126. The average value is 126. The generated authentication codes $f_1$, $f_2$, $f_3$, and $f_4$ are 0, 0, 7, and 0, respectively. Since the values of $f_1$ and $f_4$ are all 0 s, the values of ${{\beta }_1^1}^{\prime }$ and ${{\beta }_2^1}^{\prime }$ will be 1 and 1, respectively. The two equations are composed as $z_1=x_i+7$ mod 9 and $z_2=0x_i+1$ mod 9. If $x_i$ equals 1, $z_1$ and $z_2$ are 8 and 1, respectively. After hiding the authentication codes, the stego pixels (${B_1^3}^{\prime }$, ${B_1^4}^{\prime }$) and (${B_2^3}^{\prime }$, ${B_2^4}^{\prime }$) are (100, 119) and (99, 120), respectively.

3.2. The Procedure of Secret Image Reconstruction and Authentication

During secret image reconstruction and authentication extraction, we can retrieve the $y_{i,j}$ value according to the stego pixels ${B_j^1}^{\prime }$ and ${B_j^2}^{\prime }$. Equation (3) can be reconstructed when participant $id$ as $x_i$ is inputted as the participant ID. For example, in the previous example, $y_{i,1}$ can be obtained by mapping the pixels ${B_1^1}^{\prime }$ and ${B_1^2}^{\prime }$ to indicate the digit 6 using a Sudoku matrix. Thus, Equation (3) can be reconstructed as $6={\beta }_1^2+{\beta }_1^3\mathrm{mod}9$. Any two participants can resolve the parameters ${\beta }_1^2$ and ${\beta }_1^3$. Using the same process, the parameters ${\beta }_2^2$ and ${\beta }_2^3$ can be extracted by the stego pixels ${B_2^1}^{\prime }$ and ${B_2^2}^{\prime }$.

The values of $z_1$ and $z_2$ in Equations (4) and (5) can be reconstructed by mapping the stego pixel pairs (${B_1^3}^{\prime }$, ${B_1^4}^{\prime }$) and (${B_2^3}^{\prime }$, ${B_2^4}^{\prime }$). For the previous example, as shown in Figure 6, when inputting the participant $id$$x_i=1$, two equations can be reconstructed as $1={{\beta }_1^1}^{\prime }+f_2$ mod 9 and $8=f_3+{{\beta }_2^1}^{\prime }$ mod 9. With any two participants, the parameters ${{\beta }_1^1}^{\prime }$, $f_2$, $f_3$, and ${{\beta }_2^1}^{\prime }$ can be extracted. The values $f_1$ and $f_4$ can be computed with Equations (8) and (9), respectively.

$$f_1,{\beta }_1^1=\left\{\begin{array}{cc}0,{{\beta }_1^1}^{\prime },\hfill & \mathrm{if}{{\beta }_1^1}^{\prime }<4\hfill \\ 1,{{\beta }_1^1}^{\prime }-4,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(8)

$$f_4,{\beta }_2^1=\left\{\begin{array}{cc}0,{{\beta }_2^1}^{\prime },\hfill & \mathrm{if}{{\beta }_2^1}^{\prime }<4\hfill \\ 1,{{\beta }_2^1}^{\prime }-4,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(9)

Figure 6. Example of secret pixel reconstruction and authentication code extraction, where the same shape is used for the same parameters in the analytical equation.

After this, the secret pixels $p_1$ and $p_2$ can be reconstructed with Equation (10). Moreover, the average pixel, denoted by $avg$, can be obtained via Equation (11). The reconstructed pixels $p_1$ and $p_2$ can be computed as an average value, denoted by $av{g}^{\prime }$. The pixel is judged as authentic if the value $av{g}^{\prime }$ is equal to $avg$; otherwise, it is labeled inauthentic.

$$p_j={\beta }_j^1\times 9^2+{\beta }_j^2\times 9+{\beta }_j^3.$$

(10)

$$avg=f_1\times (2\times 9^2)+f_2\times (2\times 9)+f_3\times 2+f_4.$$

(11)

4. Experimental Results

In the experiment, two secret images of size 256 × 256 pixels, as shown in Figure 7a,b, and four cover images of size 512 × 512 pixels, as shown in Figure 7c–f, were used. During the retrieval and authentication procedure, if the cover images were real, without evidence of tampering, we could reconstruct the full secret images completely, as shown in Figure 8a,b. To measure the visual quality of the cover images and reconstructed secret image, PSNR (peak signal-to-noise ratio) was used with Equation (12), where MSE (mean-squared error) was calculated with Equation (13), in which $I(i,j)$ and $K(i,j)$ were the values of the original pixel and that of the stego pixel located at location (i,j), and m and n were the size (height and width) of the image. Generally, the higher the PSNR value is, the better the visual quality will be. Furthermore, we evaluated the visual quality between the cover image and the shared image using the structural similarity (SSIM) of Equation (14), where ${\mu }_x$ and ${\mu }_y$ are the averages of x and y; ${\sigma }_x$ and ${\sigma }_y$ are the standard deviation values of x and y; and values $c_1$ and $c_2$ are two constant values, which are set to 1 s. If the SSIM value equals 1, it means that the two images are identical without any distortion. Visual quality comparisons of the shadow images shown in Table 1 demonstrate high visual quality. It is difficult to recognize the differences between cover images and share images.

$$\mathit{PSNR}=10{log}_{10}\frac{{255}^2}{\mathit{MSE}}$$

(12)

$$\mathit{MSE}=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n{[I(i,j)-K(i,j)]}^2$$

(13)

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)({\sigma }_{x}y+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}$$

(14)

Figure 7. Secret images and cover images. (a) Secret image “Bird”. (b) Secret image “Jet(F16)”. (c) Cover image “Lena”. (d) Cover image “Baboon”. (e) Cover image “Pepper”. (f) Cover image “Zelda”.

Figure 8. Reconstructed secret images. (a) Recovered image “Bird” (PSNR = ∞). (b) Recovered image “Jet(F16)” (PSNR = ∞).

Table 1. Visual quality of shadow images when embedding different secret images.

Secret Images	Lena		Baboon		Pepper		Zelda
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Bird	49.88	0.993	49.88	0.998	49.88	0.993	49.89	0.990
Jet(F16)	49.88	0.994	49.89	0.998	49.88	0.993	49.88	0.990

We also compared several additional features listed in Table 2, which shows that our proposed scheme achieved high performance and met all requirements.

Table 2. Comparison to other methods.

Features	Gao et al.’s Scheme [35]	Li et al.’s Scheme [38]	Liu et al.’s Scheme [33]	Liu et al.’s Scheme [36]	Gao et al.’s Scheme [34]	Proposed Scheme
Meaningful shares	Yes	Yes	Yes	Yes	Yes	Yes
Reversibility	Yes	Yes	Yes	-	-	Yes
Different cover images	-	-	-	Yes	Yes	Yes
(k,n)-SIS	(2,2)-SIS	(3,3)-SIS	(2,2)-SIS	(2,2)-SIS	(2,3)-SIS	(2, n)-SIS
Fault tolerance	Yes	-	-	-	Yes	Yes
Average PSNR	32.96	49.07	48.72	41.71	40.41	49.88
Embedding capacity (bits)	786,432	624,215	524,288	785,525	1,310,720	786,432

There were three fake logos, as shown in Figure 9a–c, which were replaced with the content of stego images. If a stego image had been modified (tampered with), as shown in Figure 9d (128 × 128 in size), the secret image could not be completely reconstructed, as shown in Figure 9f. Figure 9g demonstrates the authentication results; the modified region is shown in black, while the unmodified area is in white. The accuracy rate of detecting an inauthentic region was depicted by BER (Bit Error Rate) using Equation (15). The BER of Figure 9g was 99.50% on average. The BER value was much higher for our approach than for [work] as shown in Table 3, in which the first column shows the detection results for Gao et al.’s method, where the two shadow images join in the authentication procedure, and the second column shows the results that incorporate three shadow images.

$$BER=\frac{\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{truly}\mathrm{detected}\mathrm{pixels}}{\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{fake}\mathrm{pixels}}\times 100\%.$$

(15)

Figure 9. An authentication example. (a) Special image (fake logo). (b) Standard image (fake logo). (c) Uniform noise (fake logo). (d) Image with tampering (fake cover). (e) Image without tampering (real cover). (f) Reconstructed secret image. (g) Detected inauthentic region (painted in black).

Table 3. BER values compared to Gao et al.’s approach.

Tampered Image	Gao et al.’s Scheme [34]		Proposed Scheme
Special image	0.684	0.942	0.997
Standard image	0.084	0.834	0.995
Uniform noise	0.097	0.836	0.995

5. Conclusions

This paper proposes a verifiable image secret sharing method that can divide a secret image into several shares, and then embed the shares containing authentication codes into cover images as stego images. Later, the secret image can be completely reconstructed, and the authentication codes can be extracted via any two stego images. Experiments show that the hiding capacity of the proposed method exceeds that of other approaches for both smooth and complex types of images. Moreover, the visual quality of the stego images in our approach is superior to that found in the experiments, while the BER values are much higher than those achieved.