Gaussian States: Evaluation of the Covariance Matrix from the Implementation with Primitive Component

Abstract

Quantum Gaussian states play a fundamental role in quantum communications and in quantum information. This paper deals with the implementation of multimode, and particularly of two-mode Gaussian unitaries and Gaussian states with primitive components (phase shifters, single-mode real squeezers, displacements, and beam splitters). The architecture thus obtained allows one to obtain an insight into the physical meaning of each variable involved. Moreover, following the implementation architecture, it is possible to formulate an easy algebra (radical free) for the main operations and transformations of Gaussian states.

1. Introduction

In recent years, quantum systems based on continuous variables have attracted great attention for the development of quantum information transmission and processing [1,2,3]. A large amount of theoretical work has been dedicated to multimode quantum states and transformations, with the prominence of Gaussian states and Gaussian transformations which can be more easily implemented and manipulated. In particular, the multimode case is attracting a lot of interest, since it may exhibit entanglement, which is a key resource for several quantum protocols and applications, such as teleportation, computing, and cryptography.

An efficient approach dealing with Gaussian unitaries and Gaussian states is based on the decomposition of the so-called fundamental Gaussian unitaries (FGUs), which are given by displacement, rotation, and squeezing, as shown in Figure 1.

Figure 1. Decomposition of a Gaussian unitary in terms of fundamental Gaussian unitaries.

Combination of these three FGUs allows for the implementation of the whole class of multimode Gaussian unitaries and the generation of the whole class of multimode Gaussian states, arriving at explicit closed-form results [4]. Another important approach is obtained resorting to the Bloch–Messiah reduction [1,5] in which the multimode squeezer is decomposed into the parallel of local and real single-mode squeezers, as shown in Figure 2.

Figure 2. Decomposition of a Gaussian unitary obtained by the Bloch–Messiah reduction.

There are several tools to efficiently describe Gaussian unitaries/states. For Gaussian unitaries, the main tools are given by Bogoliubov and symplectic transformations; in the N-mode, the former are specified by two complex matrices of order N, while the latter are specified by a $2N\times 2N$ real matrix. For Gaussian states, the main tool is given by the covariance matrix, a $2N\times 2N$ symmetric matrix with real elements (the mean vector is often neglected in the analysis).

A key role is played by the specification of the variables involved, which determine the degree of freedom of Gaussian unitary/states. For the decomposition of Figure 1, the variables are: the rotation matrix $\mathbf{\varphi }$, the squeeze matrix $\mathbf{z}$, and the displacement vector $\mathbf{\alpha }$; this is the usual specification for a unitary matrix, which we call for convenience the algebraic specification. For the decomposition of Figure 2, the variables are: two rotation matrices, $\mathbf{\varphi }$ and $\mathbf{\gamma }$, a real diagonal squeeze matrix ${\mathbf{r}}_D$, and the displacement vector $\mathbf{\alpha }$ which we call structural or physical specification. Since a Gaussian state is obtained by processing a multimode thermal state through a Gaussian unitary, in order to characterize a Gaussian state, we have to add the N single mode thermal states in the specification.

However, with the algebraic specification, the first step is the evaluation of the polar decomposition of the squeeze matrix $\mathbf{z}$. The formula contains radicals of radicals, which “propagate” on all the subsequent elaborations, leading to cumbersome formulas. This is completely avoided if we start from the structural specification.

The target of the paper is the implementation of Gaussian unitaries/states developing the cascade of Figure 2 with primitive components, starting from the structural specification and using the technique of Bloch–Messiah reduction. The primitive components are rotations, squeezers, displacements in the single mode, and beam splitters [6]. The architecture thus obtained allows one to obtain an insight into the physical meaning of each component involved. Moreover, following the implementation architecture, it is possible to formulate an (radical–free) easy algebra for the main operations and transformations of Gaussian states.

This paper is organized as follows. In Section 2, we formulate the Gaussian unitaries and their decompositions in FUGs, according to the Bloch–Messiah (BM) reduction. In Section 3, we formulate Gaussian states according to Williamson’s theorem. Section 4 deals with the implementation of Gaussian unitaries with primitive components, where the squeeze matrix is decomposed according to the Takagi factorization [7]. The implementation could be considered for multimode [6], but for simplicity, it is carried out for the two-mode one. Continuing with the two-mode, from the architecture with primitive components in Section 5, we evaluate the symplectic transformations and in Section 6, the covariance matrix. As we will realize, all the results are simple and radical free (for comparison, the same evaluation is carried out in Appendix A using the algebraic approach). In the final part of the paper, we focus our attention on the covariance matrix, in which the two-mode depends on 10 real variables. Examples of application are outlined by fixing the variables to specific values. Furthermore, in Section 8, we consider the so-called standard form of the covariance, which only depends on four real variables (symplectic invariants) and contains all the relevant information on the Gaussian state, particularly the entanglement property. We outline a simple method for the evaluation of the symplectic invariants of arbitrary Gaussian states in the two mode.

2. Gaussian Unitaries

2.1. Gaussian Unitary in Terms of Fundamental Unitaries (FGUs)

We remind that a quantum transformation is Gaussian when it transforms Gaussian states into Gaussian states. When the Gaussian transformation is defined by a unitary map, it is called Gaussian unitary.

It is known [2] that Gaussian unitaries can be expressed in the form $\mathbf{U}=exp(-i\mathbf{H}/2)$, where the Hamiltonian $\mathbf{H}$ is a second-order polynomial in the bosonic operators $a_i$ and $a_i^{*}$ or in the field operators $q_i,p_i$. When these unitaries are applied to the annihilators $\mathbf{a}={[a_1,\dots ,a_N]}^{\mathrm{T}}$, we obtain a Bogoliubov transformation, and, in terms of field operators, a symplectic transformation. For the purpose of describing Gaussian unitaries, the two types of transformations are equivalent.

Any Gaussian unitary can be expressed by FGUs. The fundamental unitaries are defined in terms of the column vectors ${\mathbf{a}}_{*}$ and $\mathbf{a}$ of size N, collecting the bosonic operators $a_m^{*}$ and $a_m$, as:

• N-mode displacement operator

  $$D\left(\mathbf{\alpha }\right):={\mathrm{e}}^{{\mathbf{\alpha }}^{\mathrm{T}}{\mathbf{a}}_{*}-{\mathbf{\alpha }}^{*}\mathbf{a}},\mathbf{\alpha }={[{\mathbf{\alpha }}_1,\dots ,a_n]}^{\mathrm{T}}\in {\mathbb{C}}^N$$

  (1)

  where $\mathbf{\alpha }$ is called the displacement vector.
• N-mode rotation operator

  $$R\left(\mathbf{\varphi }\right):={\mathrm{e}}^{i{\mathbf{a}}^{*}\mathbf{\varphi }\mathbf{a}},\mathbf{\varphi }N\times N\mathrm{Hermitian}\mathrm{matrix}$$

  (2)

  where $\mathbf{\varphi }$ is called the rotation matrix.
• N-mode squeeze operator

  $$S\left(\mathbf{z}\right):={\mathrm{e}}^{\frac{1}{2}\left[({\mathbf{a}}^{*}\mathbf{z}{\mathbf{a}}_{*}-{\mathbf{a}}^{\mathrm{T}}{\mathbf{z}}^{*}a)\right]},\mathbf{z}N\times N\mathrm{symmetric}\mathrm{matrix}$$

  (3)

where $\mathbf{z}$ is called the squeeze matrix. The polar decomposition applied to $\mathbf{z}$ gives $\mathbf{z}=\mathbf{r}{e}^{i\theta }$ where $\mathbf{r}$ is positive semidefinite and $\theta$ is Hermitian symmetric. The matrix $\mathbf{r}$ is uniquely determined by $\mathbf{z}$ as $\mathbf{r}=\sqrt{\mathbf{z}\times \mathbf{z}}$. If $\mathbf{r}$ is positive definite, the phase matrix $\theta$ associated with the squeeze operator is determined as $e^{i\theta }={\mathbf{r}}^{-1}\mathbf{z}$. Then [4],

Theorem 1.

The most general Gaussian unitary is obtained by the cascade of the three fundamental Gaussian unitaries $D\left(\mathbf{\alpha }\right)$, $S\left(\mathbf{z}\right)$, and $R\left(\mathbf{\varphi }\right)$, where the order is arbitrary, that is, $S\left(\mathbf{z}\right)D\left(\mathbf{\alpha }\right)R\left(\mathbf{\varphi }\right)$, $R\left(\mathbf{\varphi }\right)D\left(\mathbf{\alpha }\right)S\left(\mathbf{z}\right)$, etc.

One can pass from one cascade to any other one using the so-called switching rules, which provide a slight change in the parameters [4]. In the following, without loss of generality, we refer to the cascade

$$U_g=D\left(\mathbf{\alpha }\right)S\left(\mathbf{z}\right)R\left(\mathbf{\varphi }\right)$$

(4)

which is illustrated in Figure 1.

2.2. Gaussian Unitaries Decomposed according to the Block–Messiah Reduction

The Block–Messiah reduction [1,5] was reconsidered in [7] in terms of the Takagi factorization [8].

Theorem 2.

The most general Gaussian unitary can be decomposed into the cascade of a rotation operator $R\left(\mathbf{\psi }\right)$, a local squeeze operator $S\left({\mathbf{r}}_D\right)$ with a real diagonal matrix ${\mathbf{r}}_D$, another rotation operator $R\left(\mathbf{\gamma }\right)$, and finally a displacement operator $D\left(\mathbf{\alpha }\right)$.

The theorem, illustrated in Figure 2, is essentially based on the Takagi factorization [8] of the squeeze matrix

$$\mathbf{z}={\mathbf{U}}_z{\mathbf{r}}_D{\mathbf{U}}_z^{\mathrm{T}}=e^{i\mathbf{\beta }}{\mathbf{r}}_D{e}^{-i\mathbf{\beta }}$$

(5)

which leads to the decomposition of the squeeze operator as $S\left(\mathbf{z}\right)=R\left(\mathbf{\beta }\right)S\left({\mathbf{r}}_D\right)R(-\mathbf{\beta })$. Then, the general unitary given by (4), becomes

$${\mathbf{U}}_g=D\left(\mathbf{\alpha }\right)R\left(\mathbf{\beta }\right)\mathbf{S}\left({\mathbf{r}}_D\right)R\left(\mathbf{\psi }\right)$$

(6)

where $R\left(\mathbf{\psi }\right)=R(-\mathbf{\beta })R\left(\mathbf{\varphi }\right)$ (with $\mathbf{\psi }$ uniquely determined by $e^{i\mathbf{\psi }}=e^{-\mathbf{\beta }}{e}^{i\mathbf{\varphi }}$). From (6), one can easily obtain the original form (4), in particular the squeeze matrix

$$\mathbf{z}=e^{i\mathbf{\gamma }}{\mathbf{r}}_D{e}^{i{\mathbf{\gamma }}^{\mathrm{T}}}$$

(7)

Starting from other cascades in the application of Theorem 1, the Bloch–Messiah reduction leads to other architectures, but all are equivalent in representing the most general Gaussian unitary.

Specification and Degree of Freedom

Theorem 1 states that the specification of any N-mode Gaussian unitary is given by the matrices $\mathbf{\alpha },\mathbf{z},\mathbf{\varphi }$. Considering their symmetry, the associated degrees of freedom are

$$2N^2+3N\mathrm{real}\mathrm{variables}$$

(8)

As a verification, from Theorem 2 and the BM architecture of Figure 2, for the two-mode, one finds that the number of degrees of freedom is given by 14, which is to be expected, due to the equivalence between the two architectures.

3. Gaussian States

Gaussian states can be obtained from a Gaussian unitary driven by thermal states; in particular, pure Gaussian states are obtained when the thermal states degenerate into vacuum states. To formalize this statement, it is convenient to recall that a Gaussian state is completely described by the covariance matrix and the mean vector. In particular, the covariance matrix can always be written in the form (Williamson’s theorem)

$$\mathbf{V}=\mathbf{S}{\mathbf{V}}^{\oplus }{\mathbf{S}}^{\mathrm{T}}$$

(9)

where S is an N-mode symplectic matrix and

$${\mathbf{V}}^{\oplus }=\mathrm{diag}[{\nu }_1,{\nu }_1,\cdots ,{\nu }_N,{\nu }_N]$$

(10)

corresponds to a tensor product of N thermal states with an average number of thermal photons

$${\mathcal{N}}_k=\frac{{\nu }_k-1}{2},k=1,2,\dots ,N$$

(11)

The quantities $\left\{{\nu }_k\right\}$ are called the symplectic eigenvalues of the CM $\mathbf{V}$ and the operation performed by the matrix $\mathbf{S}$ is said to be the symplectic diagonalization of $\mathbf{V}$.

With reference to the previous decompositions of the Gaussian unitaries shown in Figure 1 and Figure 2, we find that, when the input is driven by N thermal states, at the output, we obtain the most general N-mode Gaussian state.

Note that a decomposition into unitaries of the Lie group $Sp(2N,\mathbb{R})$ has also been used in [9,10] for the dynamical symmetry group describing the vibronic transitions in polyatomic molecules.

3.1. Specification and Degree of Freedom

To the specification of the Gaussian unitary, one has to add the specification of the input thermal noise, given by N real variables, as in (9). On the other hand, we have a reduction of the degrees of freedom because a rotation operator is irrelevant for the input thermal noise, such as the rotation $R\left(\mathbf{\varphi }\right)$ of Figure 1, or the rotation $R\left(\mathbf{\psi }\right)$ of Figure 2. Then, the degree of freedom of an N-mode Gaussian state results in

$$2N^2+3N+N-N^2=N^2+4N\mathrm{real}\mathrm{variables}$$

(12)

3.2. Gaussian States in the Two-Mode

Since we focus on two-mode Gaussian states, we review in detail their specification, which is given by the complex matrices (see Figure 1)

$$\mathbf{\alpha }=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right],\mathbf{\varphi }=\left[\begin{array}{cc}{\varphi }_{11}& {\varphi }_{1,2}\\ {\varphi }_{12}^{*}& {\varphi }_{22}\end{array}\right],\mathbf{z}=\left[\begin{array}{cc}{z}_{11}& z_{12}\\ z_{12}& z_{22}\end{array}\right].$$

(13)

and two thermal noises ${\mathcal{N}}_1,{\mathcal{N}}_2$.

From (8), a two-mode Gaussian unitary has 14 real variables as degrees of freedom, while from (12), a two-mode Gaussian state has 12 real variables degrees of freedom.

We want to evaluate the quantities involved in the two-mode in terms of the parameters given by (13).

4. Implementation with Primitive Components

The implementation of Gaussian unitaries and the generation of Gaussian states with primitive components could be carried out in the general N-mode [6], but hereafter, it will be developed in great detail in the two mode.

4.1. Primitive Components

They are: (1) single-mode displacement; (2) single-mode rotation operators, briefly shifters; (3) single-mode real squeezers; and (4) beam splitters (BSs). Figure 3 shows the graphical symbols we use for these components.

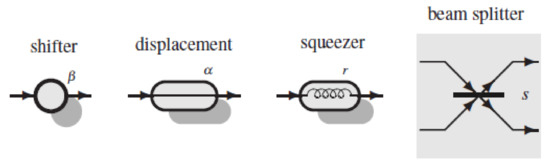
Figure 3. Graphical representation of the primitive components.

A shifter is specified by a phase $\beta \in [0,2\pi )$, which leads to the $1\times 1$ exponential matrix $e^{i\beta }$. A single-mode squeezing operator is specified by the squeeze factor $r\in \mathbb{R}$. A free-phase BS is defined by a two-mode rotation operator corresponding to the phase matrix with antidiagonal entries

$${\mathbf{\varphi }}_{\mathrm{bs}}=\left[\begin{array}{cc}0& -i\varphi \\ i\varphi & 0\end{array}\right]\to R\left({\mathbf{\varphi }}_{\mathrm{bs}}\right):={\mathrm{e}}^{\varphi (a_1^{*}{a}_2-a_2{a}_1^{*})}.$$

(14)

where $\varphi$ describe the reflectivity ($s:=sin\varphi$) and the transmittance ($c:=cos\varphi$) of the BS. An equivalent specification is given by the rotation matrix

$${\mathbf{U}}_{\mathrm{bs}}:={\mathrm{e}}^{i\mathbf{\varphi }}=exp\left[\begin{array}{cc}0& \varphi \\ -\varphi & 0\end{array}\right]=\left[\begin{array}{cc}cos\varphi & sin\varphi \\ -sin\varphi & cos\varphi \end{array}\right]=\left[\begin{array}{cc}c& s\\ -s& c\end{array}\right].$$

(15)

4.2. Implementation in the Two Mode

The target is the implementation in the two-mode of the architecture of Figure 2 with primitive components. The squeezer is already decomposed into primitive components. The implementation of the two-mode displacement operator $D\left(\mathbf{\alpha }\right)$ is trivial, since it is given by two parallel single-mode displacement operators $D\left({\alpha }_1\right)$ and $D\left({\alpha }_2\right)$. For the rotation operators, we have (for the proof, see the appendixes of [6]).

Proposition 1.

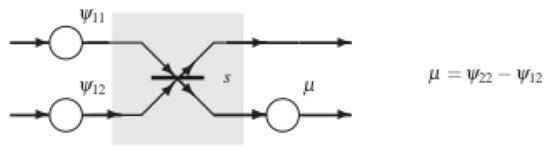
An arbitrary two-mode rotation operator defined by the unitary matrix $\mathbf{U}=e^{i\mathbf{\psi }}:=\left[{\rho }_{hk}{e}^{i{\mathbf{\gamma }}_{hk}}\right]$ can be implemented by the cascade of (1) two phase shifters with phases ${\psi }_{11}$ and ${\psi }_{12}$, (2) a BS with reflectivity $s={\rho }_{12}$, and (3) a phase shifter with phase $\mu ={\psi }_{22}-{\psi }_{12}$, as illustrated as in Figure 4. (The scheme of Figure 4 is sometimes called beam splitter with phase [11,12].)

Figure 4. The beam splitter with phase.

The matrix $\mathbf{U}=e^{i\psi }$ can be written as

$$\mathbf{U}=e^{i\psi }=\left[\begin{array}{cc}c{\mathrm{e}}^{i{\psi }_{11}}& s{\mathrm{e}}^{i{\psi }_{12}}\\ -s{\mathrm{e}}^{i({\psi }_{11}+\mu )}& c{\mathrm{e}}^{i({\psi }_{12}+\mu )}\end{array}\right]\mathrm{with}\mu ={\psi }_{22}-{\psi }_{11}$$

(16)

and also

$$\mathbf{U}=\left[\begin{array}{cc}1& 0\\ 0& e^{i\mu }\end{array}\right]\left[\begin{array}{cc}c& s\\ -s& c\end{array}\right]\left[\begin{array}{cc}{\mathrm{e}}^{i{\psi }_{11}}& 0\\ 0& {\mathrm{e}}^{i{\psi }_{12}}\end{array}\right]$$

(17)

The interpretation of the above factorization proves the proposition.

We are now ready to draw the Gaussian unitary of Theorem 1 with primitive components (see Figure 5). Note that this architecture can be used to specify the whole class of two-mode Gaussian unitaries. It is given by six shifters, two BSs, two real squeezers, and two displacements, corresponding to 14 real variables, in agreement with (8).

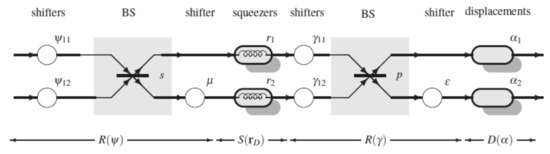
Figure 5. Implementation with primitive components of the most general two-mode Gaussian unitary, according to the Bloch–Messiah reduction and the Takagi factorization of the squeeze matrix.

The second target is the generation of two-mode Gaussian states. They are obtained when the architecture of Figure 5 is driven by two thermal noises (Figure 6). Now, the shifters ${\gamma }_{11}$ and ${\gamma }_{12}$ are removed because they are irrelevant when driven by thermal states. Furthermore, the final displacements were removed because they do not give a contribution to the covariance matrix $\mathbf{V}$ (whose evaluation is the main target of the paper).

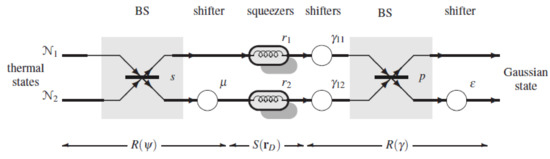
Figure 6. Generation with primitive components of a general two-mode Gaussian state, starting from two thermal states ${\mathcal{N}}_1$ and ${\mathcal{N}}_2$. The two initial rotations ${\psi }_{11}$ and ${\psi }_{12}$ and the final displacements ${\alpha }_1$, ${\alpha }_2$ are not introduced because they do not influence the covariance matrix.

4.3. Strategy for the Evaluation

The above architectures (Figure 5 and Figure 6) represent the key basis of our theory, which has the goal to understand the action of each primitive component as well as obtain simple and meaningful formulas for the main descriptions of Gaussian unitaries/states, in particular to be “radical free”. This possibility relies ultimately on the Bloch–Messiah reduction.

In the next sections, following the architectures, we will evaluate the symplectic matrix and the covariance matrix. This is called for convenience the structural approach or physical approach, in competition with the algebraic approach more often considered in the literature (in special cases, e.g., with EPR states, the algebraic approach turns out to be easy, but not in the general case).

Here, we develop only the first step of the algebraic approach to see how the complication is originated. From the algebraic specification given by (13), to proceed, one has to obtain the polar decomposition of the squeeze matrix $\mathbf{z}$ and the singular values (SVs) of $\mathbf{z}$, which are given by

$${\sigma }_{1,2}=\frac{1}{\sqrt{2}}\sqrt{{\left|z_{11}\right|}^2+{\left|z_{22}\right|}^2+2{\left|z_{12}\right|}^2\mp P}$$

(18)

where

$$P=\sqrt{4{\left|z_{11}{z}_{12}^{*}+z_{12}{z}_{22}^{*}\right|}^2+{\left({\left|z_{11}\right|}^2-{\left|z_{22}\right|}^2\right)}^2}$$

(19)

To proceed, we have to distinguish between the cases of distinct and coincident SVs because the matrix functions have different formulas. This is a further complication. The details of the algebraic approach are given in Appendix A.

Example 1.

We consider squeezing with matrix

$$\mathbf{z}=\left[\begin{array}{cc}-\frac{5}{8}{r}_0& \frac{3}{8}\sqrt{3}{e}^{iϵ}{r}_0\\ \frac{3}{8}\sqrt{3}{e}^{iϵ}{r}_0& \frac{1}{8}{e}^{2iϵ}{r}_0\end{array}\right]$$

(20)

In the algebraic approach, the squeeze matrix is one of the data and the first step requires the evaluation of the polar decomposition $\mathbf{z}=\mathbf{r}{e}^{i\theta }$, which results in

$$\mathbf{r}=\left[\begin{array}{cc}\frac{7r_0}{8}& -\frac{1}{8}\sqrt{3}{e}^{-iϵ}{r}_0\\ -\frac{1}{8}\sqrt{3}{e}^{iϵ}{r}_0& \frac{5r_0}{8}\end{array}\right],e^{i\theta }=\left[\begin{array}{cc}-\frac{1}{2}& \frac{1}{2}\sqrt{3}{e}^{iϵ}\\ \frac{1}{2}\sqrt{3}{e}^{iϵ}& \frac{1}{2}{e}^{2iϵ}\end{array}\right]$$

(21)

Additionally, the SVs of $\mathbf{z}$ must be evaluated. They result in ${\sigma }_1=r_0/\sqrt{2}$ and ${\sigma }_2=\sqrt{2}{r}_0$.

With the structural approach, the squeeze matrix (20) is obtained with the data: $r_1=r_0,r_2=r_0/2,{\gamma }_{11}=\pi /2,{\gamma }_{12}=0$ and balanced BSs, so that the free variables are only $r_0$ and ϵ. However, neither the polar decomposition nor the SVs are needed to proceed.

5. Evaluation of Symplectic Matrices

The Symplectic Matrix (SM)

Here, we consider the real interlaced SM $\mathbf{S}$, where the phase-space variables are arranged in the form $\mathbf{X}:={[q_1,p_1,q_2,p_2]}^{\mathrm{T}}$. A symplectic transformation is of the form

$$\mathbf{X}\to \mathbf{S}\mathbf{X}+\mathbf{d}$$

(22)

where $\mathbf{S}$ is a $4\times 4$ real matrix and $\mathbf{d}\in {\mathbb{R}}^4$. The commutation relations require the condition

$$\mathbf{S}\Omega {\mathbf{S}}^{\mathrm{T}}=\Omega \mathrm{with}\Omega =\underset{i=1}{\overset{2}{⨁}}\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$$

(23)

A matrix $\mathbf{S}$ is called symplectic if it verifies this condition. Following the architecture of Figure 5, we find

$$\mathbf{S}={\mathbf{S}}_{\mathrm{rot}}\left(\mathbf{\gamma }\right){\mathbf{S}}_{\mathrm{sq}}\left({\mathbf{r}}_D\right){\mathbf{S}}_{\mathrm{rot}}\left(\mathbf{\psi }\right)$$

(24)

where we can use the general formulas

$${\mathbf{S}}_{\mathrm{rot}}\left(\mathbf{\varphi }\right)=\mathbf{\Pi }\left[\begin{array}{cc}cos\mathbf{\varphi }& -sin\mathbf{\varphi }\\ sin\mathbf{\varphi }& cos\mathbf{\varphi }\end{array}\right]{\mathbf{\Pi }}^{\mathrm{T}}$$

(25)

$${\mathbf{S}}_{\mathrm{sq}}\left(\mathbf{r}{\mathrm{e}}^{i\theta }\right)=\mathbf{\Pi }\left[\begin{array}{cc}cosh\mathbf{r}+sinh\mathbf{r}cos\mathbf{\theta }& sinh\mathbf{r}sin\mathbf{\theta }\\ sinh\mathbf{r}sin\mathbf{\theta }& cosh\mathbf{r}-sinh\mathbf{r}cos\mathbf{\theta }\end{array}\right]{\mathbf{\Pi }}^{\mathrm{T}}$$

(26)

with $\mathbf{\Pi }$ the permutation matrix

$$\mathbf{\Pi }=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

For the central squeezer, considering that it is real and diagonal, we find that

$$\left[\begin{array}{cc}cosh\mathbf{r}+sinh\mathbf{r}& 0\\ 0& cosh\mathbf{r}-sinh\mathbf{r}\end{array}\right]=\left[\begin{array}{cc}{e}^{\mathbf{r}}& 0\\ 0& e^{-\mathbf{r}}\end{array}\right]$$

where $e^{\mathbf{r}}=\mathrm{diag}\left[e^{r_1},e^{r_2}\right]$. Then,

$${\mathbf{S}}_{\mathrm{sq}}=\mathbf{\Pi }\left[\begin{array}{cc}{e}^r& 0\\ 0& e^{-r}\end{array}\right]{\mathbf{\Pi }}^{\mathrm{T}}=\begin{array}{cc}{e}^r& 0\\ 0& e^{-r}\end{array}=\left[\begin{array}{cccc}{e}^{r_1}& 0& 0& 0\\ 0& e^{-r_1}& 0& 0\\ 0& 0& e^{r_2}& 0\\ 0& 0& 0& e^{-r_2}\end{array}\right]$$

This completes the evaluation of the global symplectic matrices.

We developed the structural approach for the description of Gaussian unitaries based on the primitive-components architecture of Figure 5. Clearly all the formulas are “radical free”.

6. Evaluation of the Covariance Matrix (CM)

This is an important topic considered by several authors, e.g., [13,14,15,16,17]. In particular, [15] uses a similar approach to characterize Gaussian states, based on Williamson’s theorem and Bloch-Messiah decomposition, describing the symplectic transformations that correspond to the fundamental operators of squeezing, rotation and beam splitters. However, the final results are only provided for the single-mode and a couple of specific examples of two-mode states. In [13], the integration within an ordered product (IWOP) is used to express the covariance matrix of N-mode in terms of the squeeze matrix. Note, however, that the hyperbolic tangent of the squeeze matrix must be evaluated. The final derivation is obtained in two specific examples for the two-mode case. Ref. [14] derives the elements of the covariance matrix of a two-mode Gaussian state, with a generalized squeezing, by using the technique of integration within an ordered product (IWOP). The objective is to characterize the entanglement and non-locality properties of the corresponding state.

Here, we explicitly evaluate the CV $\mathbf{V}$ in the two-mode following the structural approach, where $\mathbf{V}$ is evaluated from the interlaced SM by adding the information on thermal noise (see (9))

$$\mathbf{V}=\mathbf{S}{V}^{\oplus }{\mathbf{S}}^{\mathrm{T}},{\mathbf{V}}^{\oplus }=\mathrm{diag}[{\nu }_1,{\nu }_1,{\nu }_2,{\nu }_2]$$

(27)

For the explicit evaluation of the trigonometric matrices in the two-mode appearing in the SM $\mathbf{S}$, we use Proposition 1 and (16), with $\mu ={\psi }_{22}-{\psi }_{12}$, starting from the exponential

$$e^{i\mathbf{\psi }}=\left[\begin{array}{cc}c{\mathrm{e}}^{i{\psi }_{11}}& s{\mathrm{e}}^{i{\psi }_{12}}\\ -s{\mathrm{e}}^{i({\psi }_{11}+\mu )}& c{\mathrm{e}}^{i({\psi }_{12}+\mu )}\end{array}\right]$$

Then

$$\begin{gathered} {\displaystyle \phantom{(}cos\left(\mathbf{\psi }\right)=\left[\begin{array}{cc}ccos\left({\psi }_{11}\right)& scos\left({\psi }_{12}\right)\\ -scos({\psi }_{11}+\mu )& ccos({\psi }_{12}+\mu )\end{array}\right] \\ sin\left(\mathbf{\psi }\right)=\left[\begin{array}{cc}csin\left({\psi }_{11}\right)& ssin\left({\psi }_{12}\right)\\ -ssin({\psi }_{11}+\mu )& csin({\psi }_{12}+\mu )\end{array}\right]} \end{gathered}$$

(28)

Analogously

$$\begin{gathered} {\displaystyle \phantom{(}cos\left(\mathbf{\gamma }\right)=\left[\begin{array}{cc}qcos\left({\gamma }_{11}\right)& pcos\left({\gamma }_{12}\right)\\ -pcos({\gamma }_{11}+ϵ)& qcos({\gamma }_{12}+ϵ)\end{array}\right] \\ sin\left(\mathbf{\gamma }\right)=\left[\begin{array}{cc}qsin\left({\gamma }_{11}\right)& psin\left({\gamma }_{12}\right)\\ -psin({\gamma }_{11}+ϵ)& qsin({\gamma }_{12}+ϵ)\end{array}\right]} \end{gathered}$$

(29)

where p is the reflectivity of the second BS and $q=\sqrt{1-p^2}$.

In order to characterize the CM, it is more convenient to express the result partitioned into $2\times 2$ blocks. Letting

$$\mathbf{S}=\left[\begin{array}{cc}{\mathbf{S}}_{11}& {\mathbf{S}}_{12}\\ {\mathbf{S}}_{21}& {\mathbf{S}}_{22}\end{array}\right]$$

we obtain:

$$\mathbf{V}=\left[\begin{array}{cc}\mathbf{A}& \mathbf{C}\\ {\mathbf{C}}^{\mathrm{T}}& \mathbf{B}\end{array}\right]$$

(30)

where

$$\begin{gathered} {\displaystyle \phantom{(}\mathbf{A}={\nu }_1{\mathbf{S}}_{11}{\mathbf{S}}_{11}^{\mathrm{T}}+{\nu }_2{\mathbf{S}}_{12}{\mathbf{S}}_{12}^{\mathrm{T}} \\ \mathbf{B}={\nu }_1{\mathbf{S}}_{21}{\mathbf{S}}_{21}^{\mathrm{T}}+{\nu }_2{\mathbf{S}}_{22}{\mathbf{S}}_{22}^{\mathrm{T}} \\ \mathbf{C}={\nu }_1{\mathbf{S}}_{11}{\mathbf{S}}_{21}^{\mathrm{T}}+{\nu }_2{\mathbf{S}}_{12}{\mathbf{S}}_{22}^{\mathrm{T}}} \end{gathered}$$

(31)

Considering that the CM refers to Gaussian states, as remarked above in Figure 6, the dependence is on the 10 real parameters ${\nu }_1,{\nu }_2,s,\mu ,r_1,r_2,{\gamma }_{11},{\gamma }_{12},p,ϵ$, notwithstanding that the ${\mathbf{S}}_{ij}$ also depend on the phases ${\psi }_{11},{\psi }_{12}$.

A Gaussian state then depends on 10 real $+2$ complex parameters, namely ${\nu }_1$, ${\nu }_2$, s, $\mu$, $r_1$, $r_2$, ${\gamma }_{11}$, ${\gamma }_{12}$, p, $ϵ$, ${\alpha }_1$, ${\alpha }_2$.

6.1. Standard Form of the Covariance Matrix

We remind that, for any two-mode Gaussian states, there exists a local symplectic operation ${\mathbf{S}}_l$ that brings the covariance matrix to the standard form, Simon2000, [18]

$${\mathbf{S}}_l^{\mathrm{T}}\mathbf{V}{\mathbf{S}}_l={\mathbf{V}}_{sf}=\left[\begin{array}{cccc}a& 0& c_{+}& 0\\ 0& a& 0& c_{-}\\ c_{+}& 0& b& 0\\ 0& c_{-}& 0& b\end{array}\right]$$

(32)

where the correlation terms $a,b,c_{+}$ and $c_{-}$ are obtained from the ordinary CM $\mathbf{V}$ by the four local symplectic invariants

$$\det \mathbf{V}=(ab-c_{+}^2+)(ab-c_{-}^2),\det \mathbf{A}=a^2,\det \mathbf{B}=b^2,\det \mathbf{C}=c_{+}{c}_{-}$$

(33)

The importance of the standard form and of the symplectic invariants lies on the fact that they concentrate all the relevant information on the two-mode Gaussian states, particularly that concerning the entanglement [19]. This means that the essential degree of freedom is reduced to 4 real variables, instead of the 10 variables listed above.

Evaluation of “invariants” $(\mathbf{a},\mathbf{b},{\mathbf{c}}_{\pm }$) from the ordinary CM $\mathbf{V}$. The invariants can be obtained from the blocks of the ordinary (nonstandard) covariance matrix (see (30)).

Proposition 2.

From the blocks of the ordinary covariance matrix $\mathbf{V}$, evaluate the quantities

$$\Delta V:=\det \mathbf{V},\Delta C:=\det \mathbf{C},R=\sqrt{{\left(a^2{b}^2-\Delta V+\Delta C^2\right)}^2-4a^2{b}^2\Delta C^2}$$

(34)

Then, the invariants result in: $a=\sqrt{\det \mathbf{A}}$, $b=\sqrt{\det \mathbf{B}}$, and

$$c_{+}=\mp \frac{\sqrt{\mp R+a^2{b}^2-\Delta V+\Delta C^2}}{\sqrt{2ab}},c_{-}=\mp \frac{\sqrt{2ab}\Delta C}{\sqrt{\mp R+a^2{b}^2-\Delta V+\Delta C^2}}$$

(35)

The proof is in Appendix B.

We give a numerical example. With the data

$$\begin{gathered} {\displaystyle \phantom{(}{\nu }_1=3.2,{\nu }_2=1.6,\mu =0.999,{\mathbf{\gamma }}_{11}=0.9,{\mathbf{\gamma }}_{12}=0.66,ϵ=0.7, \\ {r}_1=0.66,r_2=0.18,p=0.3,q=0.953939,s=c=0.707} \end{gathered}$$

$$\mathbf{A}=\left[\begin{array}{cc}3.523& 3.538\\ 3.538& 4.829\end{array}\right], \mathbf{B}=\left[\begin{array}{cc}1.821& 0.160\\ 0.160& 4.565\end{array}\right], \mathbf{C}=\left[\begin{array}{cc}0.682& -1.835\\ 0.695& -1.860\end{array}\right]$$

Then

$$\det \mathbf{A}=4.49884,\det \mathbf{B}=8.28805,\det \mathbf{C}=0.00655408,\det \mathbf{V}=26.2144$$

$$a=2.12105,b=2.8789$$

The four solutions are

$$c_{+}\to -1.34656,c_{-}\to -0.00486726,c_{+}\to -0.00486726,c_{-}\to -1.34656$$

$$c_{+}\to 0.00486726,c_{-}\to 1.34656,c_{+}\to 1.34656,c_{-}\to 0.00486726$$

6.2. Physical Analysis of the Global Architectures

The architectures of Figure 5 and Figure 6 allow us to obtain a physical insight into the dependence of the global performance, as stated by the symplectic matrix and by the covariance matrix, from each primitive component. In the limit, we can remove a single component from the architecture to see the effect on the ordinary covariance matrix $\mathbf{V}$. In a forthcoming paper [20], we will show that a quantum state, having as ordinary covariance just the standard covariance matrix ${\mathbf{V}}_{sf}$, can be obtained by removing all the shifters. This shows that the shifters have less relevance with respect to the other primitive components.

7. Examples

By choosing the 14 parameters listed above, one can evaluate the description of all Gaussian unitaries in the two-mode. Analogously, by choosing the 10 parameters of Figure 6, one can evaluate the description of all two-mode Gaussian states. Here, we outline a few cases of Gaussian states focusing the attention on the covariance matrix.

Case 1: All-zero phases

A first case is considered with all zero phases, with parameters as in Table 1.

Table 1. Parameters of the architecture in Case 1. In red the free variables.

thermal states	${\nu }_1$	${\nu }_2$
phases	$\mu =0$	${\gamma }_{11}=0$	${\gamma }_{12}=0$	$ϵ=0$
squeezers	$r_1$	$r_2$
beam splitters	p	q	s	c

The squeeze matrix results in

$$\mathbf{z}=\left[\begin{array}{cc}{r}_2{p}^2+q^2{r}_1& pq{r}_2-pq{r}_1\\ pq{r}_2-pq{r}_1& r_1{p}^2+q^2{r}_2\end{array}\right]$$

The blocks which constitute the covariance matrix $\mathbf{V}$ are given by

$$\mathbf{A}=\left[\begin{array}{cc}{\nu }_1{\left(cq{e}^{r_1}-ps{e}^{r_2}\right)}^2+{\left(cp{e}^{r_2}+qs{e}^{r_1}\right)}^2{\nu }_2& 0\\ 0& {\nu }_1{\left(cq{e}^{-r_1}-ps{e}^{-r_2}\right)}^2+{\left(cp{e}^{-r_2}+qs{e}^{-r_1}\right)}^2{\nu }_2\end{array}\right]$$

$$\mathbf{B}=\left[\begin{array}{cc}{\nu }_2{\left(cq{e}^{r_2}-ps{e}^{r_1}\right)}^2+{\left(cp{e}^{r_1}+qs{e}^{r_2}\right)}^2{\nu }_1& 0\\ 0& {\nu }_2{\left(cq{e}^{-r_2}-ps{e}^{-r_1}\right)}^2+{\left(cp{e}^{-r_1}+qs{e}^{-r_2}\right)}^2{\nu }_1\end{array}\right]$$

$$\mathbf{C}=\left[\begin{array}{cc}{c}_1& 0\\ 0& c_2\end{array}\right]$$

where

$$\begin{gathered} {\displaystyle \phantom{(}{c}_1=\left(c{e}^{r_2}q-e^{r_1}ps\right)\left(c{e}^{r_2}p+e^{r_1}qs\right){\nu }_2-\left(c{e}^{r_1}q-e^{r_2}ps\right)\left(c{e}^{r_1}p+e^{r_2}qs\right){\nu }_1 \\ {c}_2=c{e}^{-r_1-r_2}(p^2-q^2)s({\nu }_1-{\nu }_2)+e^{-2r_2}pq\left({\nu }_2{c}^2+s^2{\nu }_1\right)-e^{-2r_1}pq\left({\nu }_1{c}^2+s^2{\nu }_2\right)} \end{gathered}$$

Case 2: All–zero phases, $r_1=r_2=r_0$, and the second BS balanced

We consider another case, with all zero phases, the same squeezing on each mode and balanced BS, as in Table 2.

Table 2. Parameters of the architecture in Case 2. In red the free variables.

thermal states	${\nu }_1$	${\nu }_2$
phases	$\mu =0$	${\gamma }_{11}=0$	${\gamma }_{12}=0$	$ϵ=0$
squeezers	$r_1=r_0$	$r_2=r_0$
beam splitters	$p=1/\sqrt{2}$	$q=1/\sqrt{2}$	s	c

The squeeze matrix results in

$$\mathbf{z}=\left[\begin{array}{cc}{r}_0& 0\\ 0& r_0\end{array}\right]$$

The blocks of the covariance matrix $\mathbf{V}$ are given by

$$\mathbf{A}=\left[\begin{array}{cc}\frac{1}{2}{e}^{2r_0}\left({\nu }_1{(c-s)}^2+{(c+s)}^2{\nu }_2\right)& 0\\ 0& \frac{1}{2}{e}^{-2r_0}\left({\nu }_1{(c-s)}^2+{(c+s)}^2{\nu }_2\right)\end{array}\right]$$

$$\mathbf{B}=\left[\begin{array}{cc}\frac{1}{2}{e}^{2r_0}\left({\nu }_2{(c-s)}^2+{(c+s)}^2{\nu }_1\right)& 0\\ 0& \frac{1}{2}{e}^{-2r_0}\left({\nu }_2{(c-s)}^2+{(c+s)}^2{\nu }_1\right)\end{array}\right]$$

$$\mathbf{C}=\left[\begin{array}{cc}-\frac{1}{2}{e}^{2r_0}(c-s)(c+s)({\nu }_1-{\nu }_2)& 0\\ 0& -\frac{1}{2}{e}^{-2r_0}(c-s)(c+s)({\nu }_1-{\nu }_2)\end{array}\right]$$

Case 3: EPR state with noise

The EPR unitary is a squeeze with the following matrix

$$\mathbf{z}=\left[\begin{array}{cc}0& e^{i\theta }{r}_0\\ e^{i\theta }{r}_0& 0\end{array}\right]$$

To obtain this unitary, the primitive-component architecture must have the following data $r_1=r_2=r_0$, balanced BSs $p=q=s=c=\frac{1}{\sqrt{2}}$ and the phases indicated in Table 3.

Table 3. Parameters of the architecture in Case 3. In red the free variables.

states	${\nu }_1$	${\nu }_2$
phases	$\mu =\pi /2$	${\gamma }_{11}=-\pi /4$	${\gamma }_{12}=\pi /4$	$ϵ=-\pi /2$
squeezers	$r_1=r_0$	$r_2=r_0$
beam splitters	$s=1/\sqrt{2}$	$c=1/\sqrt{2}$	$p=1/\sqrt{2}$	$q=1/\sqrt{2}$

The blocks of the covariance matrix $\mathbf{V}$ result in

$$\begin{gathered} {\displaystyle \phantom{(}\mathbf{A}=\left[\begin{array}{cc}{\nu }_1{cosh}^2\left(r_0\right)+{\nu }_2{sinh}^2\left(r_0\right)& 0\\ 0& {\nu }_1{cosh}^2\left(r_0\right)+{\nu }_2{sinh}^2\left(r_0\right)\end{array}\right] \\ \mathbf{B}=\left[\begin{array}{cc}{\nu }_2{cosh}^2\left(r_0\right)+{\nu }_1{sinh}^2\left(r_0\right)& 0\\ 0& {\nu }_2{cosh}^2\left(r_0\right)+{\nu }_1{sinh}^2\left(r_0\right)\end{array}\right] \\ \mathbf{C}=\left[\begin{array}{cc}cos\left(\theta \right)cosh\left(r_0\right)({\nu }_1+{\nu }_2)sinh\left(r_0\right)& cosh\left(r_0\right)({\nu }_1+{\nu }_2)sin\left(\theta \right)sinh\left(r_0\right)\\ cosh\left(r_0\right)({\nu }_1+{\nu }_2)sin\left(\theta \right)sinh\left(r_0\right)& -cos\left(\theta \right)cosh\left(r_0\right)({\nu }_1+{\nu }_2)sinh\left(r_0\right)\end{array}\right]} \end{gathered}$$

In particular, for $\theta =0$, the block $\mathbf{C}$ results in

$$\mathbf{C}=\left[\begin{array}{cc}cosh\left(r_0\right)({\nu }_1+{\nu }_2)sinh\left(r_0\right)& 0\\ 0& -cosh\left(r_0\right)({\nu }_1+{\nu }_2)sinh\left(r_0\right)\end{array}\right]$$

in agreement with the result indicated in [19].

8. Separability and Entanglement

The separability and the entanglement properties of any two-mode Gaussian state can be handled from both the ordinary CM $\mathbf{V}$ and the standard CM ${\mathbf{V}}_{sf}$. Now, a Gaussian state is separable if its standard CM is diagonal. Hence, from (32), the separability condition is

$$c_{+}=0,c_{-}=0$$

(36)

When the standard CM is evaluated from the ordinary CM using Proposition 2, Equation (35) is not useful because it leads to degeneracy. Instead of (33), namely $\det \mathbf{V}=(ab-c_{+}^2+)(ab-c_{-}^2)$ and $\det \mathbf{C}=c_{+}{c}_{-}$, one finds the conditions on the symplectic invariants

$$\det {\mathbf{V}}_{sf}=a^2{b}^2,\det \mathbf{C}=0$$

On the other hand, the separability based on the ordinary CM is that $\mathbf{V}$ must be diagonal. Then, from (30) and (31), the conditions read

$$\mathbf{A},\mathbf{B}\mathrm{diagonal},\mathbf{C}=0$$

Recalling that ${\nu }_1\ge 1,{\nu }_2\ge 1$, from (31), we find the conditions

$$\begin{gathered} {\displaystyle \phantom{(}{\mathbf{S}}_{11}{\mathbf{S}}_{11}^{\mathrm{T}},{\mathbf{S}}_{12}{\mathbf{S}}_{12}^{\mathrm{T}},{\mathbf{S}}_{21}{\mathbf{S}}_{21}^{\mathrm{T}},{\mathbf{S}}_{22}{\mathbf{S}}_{22}^{\mathrm{T}}\mathrm{diagonal} \\ {\mathbf{S}}_{11}{\mathbf{S}}_{21}^{\mathrm{T}}=0,{\mathbf{S}}_{12}{\mathbf{S}}_{22}^{\mathrm{T}}=0} \end{gathered}$$

(37)

9. Conclusions

For the description of Gaussian unitaries/states, we considered the algebraic and structural approaches. We remark that the class of noisy Gaussian states generated by the algebraic specification and by the structural specification coincide, since both approaches generate the whole class of noisy Gaussian states. In other words, one can choose the first class as well as the second class as the definition of noisy Gaussian states. In terms of performance, both the methods and also alternative solutions proposed in [13,14,15] achieve the same covariance matrix, since no approximations are introduced, but at different costs, in terms of complexity and often only in some particular cases. In particular, in [15], the solution is provided only for a couple of specific examples. In [13], the covariance matrix is obtained considering only a squeezed state, not a general one, by means of integration within an ordered product (IWOP), starting from the knowledge of the correlation operator. Note also that the hyperbolic tangent of the squeeze matrix must be evaluated. Furthermore, in [14], only the squeezing is considered, again with the same complexity of IWOP, and the objective is to characterize the entanglement of the corresponding state.

The main target of the paper is to show the advantages of the structural approach in the description of the most generic Gaussian states, namely:

• The structural approach is completely radical free compared to the algebraic approach and requires several matrix operations leading to results that contain the radicals of radicals. Note that the key to avoiding radicals is the following: the quantities which exhibit radicals in the algebraic approach become independent variables (data) in the structural approach.
• The structural approach is completely general, while the algebraic approach exhibits several degeneracies (mainly coincident eigenvalues) concerning some very important cases (see EPR states). These cases should be treated separately with ad hoc procedures. Such a distinction is not required in the structural approach.
• In the structural approach, all the variables have a precise physical meaning, related to the corresponding components of the architecture, i.e., squeezers, beam splitters, phase shifters, and one can choose the specific variables to achieve the desired properties of the covariance matrix, for example, the entanglement.

Finally, we note that the theory, here developed in detail for the two-mode, could be extended to higher modes, of course with the penalty of complication at the increase in the order. We developed the three–mode (not reported here) with the structural approach and without difficulty, resulting, however, in long formulas (which were radical free). With the algebraic approach, the three mode results to be very complicated, mainly for the large number of particular cases to be treated separately.

Appendix A.1. Polar Decomposition of the Squeeze Matrix z

This requires the evaluation of the SVs of z. With the form (13), the SVs are

$${\sigma }_{1,2}=\frac{1}{\sqrt{2}}\sqrt{{\left|z_{11}\right|}^2+{\left|z_{22}\right|}^2+2{\left|z_{12}\right|}^2\mp P}$$

(A1)

where

$$P=\sqrt{4{\left|z_{11}{z}_{12}^{*}+z_{12}{z}_{22}^{*}\right|}^2+{\left({\left|z_{11}\right|}^2-{\left|z_{22}\right|}^2\right)}^2}$$

(A2)

We have to distinguish between the cases of distinct and coincident SVs because the matrix functions have different formulas. From (18), the conditions of coincident eigenvalues are $|z_{11}|=|z_{22}|$ and $z_{11}{z}_{12}^{*}+z_{12}{z}_{22}^{*}=0$. We suppose that the matrix z is not diagonal (because the diagonal case is trivial with matrix functions). Hence, with $z_{12}\ne 0$, the condition of coincident SVs becomes $z_{22}=-z_{11}^{*}{z}_{12}/z_{12}^{*}$.

The polar decomposition $\mathbf{r}{\mathrm{e}}^{i\mathbf{\theta }}$ is obtained considering that $\mathbf{z}$ is complex symmetric, $\mathbf{r}$ is Hermitian PSD with eigenvalues equal to the SVs of $\mathbf{z}$, and ${\mathrm{e}}^{i\mathbf{\theta }}$ is unitary. Then, with distinct SVs, one finds

$$\mathbf{r}=\frac{1}{{\sigma }_1+{\sigma }_2}\left[\begin{array}{cc}{\left|z_{11}\right|}^2+{\left|z_{12}\right|}^2+{\sigma }_1{\sigma }_2& z_{11}{z}_{12}^{*}+z_{12}{z}_{22}^{*}\\ z_{12}{z}_{11}^{*}+z_{22}{z}_{12}^{*}& {\left|z_{12}\right|}^2+{\left|z_{22}\right|}^2+{\sigma }_1{\sigma }_2\end{array}\right]$$

(A3)

$${\mathrm{e}}^{i\theta }=\left[\begin{array}{cc}\frac{a_{11}\left(-{\left|a_{11}\right|}^2-2{\left|a_{12}\right|}^2+J\right)-a_{12}^2{a}_{22}^{*}}{{\sigma }_1{\sigma }_2({\sigma }_1+{\sigma }_2)}& \frac{(J-M)a_{12}-a_{11}{a}_{22}{a}_{12}^{*}}{{\sigma }_1{\sigma }_2({\sigma }_1+{\sigma }_2)}\\ \frac{(J-M)a_{12}-a_{11}{a}_{22}{a}_{12}^{*}}{{\sigma }_1{\sigma }_2({\sigma }_1+{\sigma }_2)}& \frac{a_{22}\left(-2{\left|a_{12}\right|}^2-{\left|a_{22}\right|}^2+J\right)-a_{12}^2{a}_{11}^{*}}{{\sigma }_1{\sigma }_2({\sigma }_1+{\sigma }_2)}\end{array}\right]$$

(A4)

where

$$J={\sigma }_1^2+{\sigma }_2{\sigma }_1+{\sigma }_2^2,M={\left|z_{11}\right|}^2+{\left|z_{12}\right|}^2+{\left|z_{22}\right|}^2$$

(A5)

With coincident SVs and the nondiagonal $\mathbf{z}$, the PD reads

$$\mathbf{r}=\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_1\end{array}\right],{\mathrm{e}}^{i\mathbf{\theta }}=\left[\begin{array}{cc}\frac{z_{11}}{{\sigma }_1}& \frac{z_{12}}{{\sigma }_1}\\ \frac{z_{12}}{{\sigma }_1}& -\frac{z_{12}{z}_{11}^{*}}{z_{12}^{*}{\sigma }_1}\end{array}\right]$$

(A6)

where the SV is given by ${\sigma }_1=\sqrt{{\left|z_{11}\right|}^2+{\left|z_{12}\right|}^2}$.

Appendix A.2. Evaluation of the Matrices cosh(r) and sinh(r)

Considering that the eigenvalues of $\mathbf{r}$ are the singular values of z, that is, ${\sigma }_1$, ${\sigma }_2$, and using the expression of $\mathbf{r}$ given by (A3), with distinct SVs, one obtains

$$G\left(\mathbf{r}\right)=\left[\begin{array}{cc}\frac{G\left({\sigma }_2\right)\left(-{\left|a_{11}\right|}^2-{\left|a_{12}\right|}^2+{\sigma }_1^2\right)+G\left({\sigma }_1\right)\left({\left|a_{11}\right|}^2+{\left|a_{12}\right|}^2-{\sigma }_2^2\right)}{{\sigma }_1^2-{\sigma }_2^2}& \frac{\left(a_{11}{a}_{12}^{*}+a_{12}{a}_{22}^{*}\right)(G\left({\sigma }_1\right)-G\left({\sigma }_2\right))}{{\sigma }_1^2-{\sigma }_2^2}\\ \frac{\left(a_{12}{a}_{11}^{*}+a_{22}{a}_{12}^{*}\right)(G\left({\sigma }_1\right)-G\left({\sigma }_2\right))}{{\sigma }_1^2-{\sigma }_2^2}& \frac{G\left({\sigma }_2\right)\left(-{\left|a_{12}\right|}^2-{\left|a_{22}\right|}^2+{\sigma }_1^2\right)+G\left({\sigma }_1\right)\left({\left|a_{12}\right|}^2+{\left|a_{22}\right|}^2-{\sigma }_2^2\right)}{{\sigma }_1^2-{\sigma }_2^2}\end{array}\right]$$

(A7)

Hence, with $G\left(x\right)=cosh\left(x\right)$ and $G\left(x\right)=sinh\left(x\right)$, we can obtain the desired matrix functions. With coincident eigenvalues, one obtains

$$cosh\left(\mathbf{r}\right)=cosh\left({\sigma }_1\right){\mathbf{I}}_2,sinh\left(\mathbf{r}\right)=sinh\left({\sigma }_1\right){\mathbf{I}}_2.$$

(A8)

Appendix A.3. Evaluation of the Phase Matrix ϕ

We first evaluate the eigenvalues of $\mathbf{\varphi }$, which are given by

$${\mu }_{1,2}=\frac{1}{2}\left[\mp \sqrt{4{\left|{\varphi }_{12}\right|}^2+{({\varphi }_{11}-{\varphi }_{22})}^2}+{\varphi }_{11}+{\varphi }_{22}\right].$$

(A9)

Assuming distinct eigenvalues, we find

$${\mathrm{e}}^{i\mathbf{\varphi }}=\frac{1}{{\psi }_{11}-{\psi }_{21}}\left[\begin{array}{cc}{\mathrm{e}}^{i{\psi }_{21}}({\psi }_{11}-{\varphi }_{11})+{\mathrm{e}}^{i{\psi }_{11}}({\varphi }_{11}-{\psi }_{21})& \left[{\mathrm{e}}^{i{\psi }_{11}}-{\mathrm{e}}^{i{\psi }_{21}}\right]{\varphi }_{12}\\ \left[{\mathrm{e}}^{i{\psi }_{11}}-{\mathrm{e}}^{i{\psi }_{21}}\right]{\varphi }_{12}^{*}& {\mathrm{e}}^{i{\psi }_{21}}({\psi }_{11}-{\varphi }_{22})+{\mathrm{e}}^{i{\psi }_{11}({\varphi }_{22}-{\psi }_{21})}\end{array}\right]$$

(A10)

The eigenvalues (A9) become coincident when ${\varphi }_{11}={\varphi }_{22}$ and ${\varphi }_{12}=0$. Then, $\mathbf{\varphi }={\varphi }_{11}{\mathbf{I}}_2$ and the rotation matrix becomes

$${\mathrm{e}}^{i\mathbf{\varphi }}={\mathrm{e}}^{i{\varphi }_{11}}{\mathbf{I}}_2$$

(A11)

Appendix A.4. Evaluation of Matrices cosϕ and sinϕ

We can start from (A10) and use the identities

$$cos\varphi =\frac{1}{2}(e^{i\varphi }+e^{-i\varphi }),sin\varphi =\frac{1}{2i}(e^{i\varphi }-e^{-i\varphi })$$

(A12)

From (18), the conditions of coincident eigenvalues are $|z_{11}|=|z_{22}|$ and $z_{11}{z}_{12}^{*}+z_{12}{z}_{22}^{*}=0$. We suppose that the matrix z is not diagonal (because the diagonal case is trivial with matrix functions). Hence, with $z_{12}\ne 0$, the condition of coincident SVs becomes $z_{22}=-z_{11}^{*}{z}_{12}/z_{12}^{*}$.