Abstract
In a foregoing paper, the author reported evidence that the multi-spin-axis magnetic structure proposed in 1964 by van Laar is realized in antiferromagnetic CoO. Within the nonadiabatic Heisenberg model, this tetragonal body-centered structure is generated by atomic-like electrons in a special magnetic band of CoO, a mechanism that may emerge only because the nonadiabatic Heisenberg model goes beyond the adiabatic approximation. The present paper compares the band structures of the transition-metal monoxides NiO, CoO, FeO, and MnO, and shows that only CoO possesses a magnetic band which may produce the tetragonal magnetic structure proposed by van Laar. The magnetic bands of the other monoxides, NiO, FeO, and MnO, are clearly related to the monoclinic base-centered magnetic structure experimentally observed in these materials.
1. Introduction
The transition-metal monoxides NiO, CoO, FeO, and MnO are antiferromagnetic below the respective Néel temperatures and insulators in both the paramagnetic and the magnetic state. In the paramagnetic state, all of them have fcc symmetry (with the space group ). While the magnetic structures of the three oxides NiO, FeO, and MnO are clearly monoclinic [1,2,3,4], the structure of antiferromagnetic CoO cannot easily be understood [5,6].
However, it is generally accepted that in CoO the transition to the antiferromagnetic state is accompanied by a marked tetragonal deformation (there is a 1.2% contraction along the c axis in the magnetically ordered state [3]) together with a small monoclinic deformation [7] of the crystal. On the basis of this experimental observation, van Laar proposed in 1964 that CoO possesses a noncollinear multi-spin-axis magnetic structure with tetragonal symmetry [5]. His model is clearly confirmed by the nonadiabatic Heisenberg model (NHM) [8] going beyond the adiabatic approximation. Within the NHM, there is evidence that a magnetic super band related to the magnetic group (in Equation (1)) produces the tetragonal magnetic structure proposed by van Laar [9]. The adjective “super” shall express that the magnetic band allows the crystal to be a Mott insulator. In a system invariant under time inversion, the tetragonal magnetic structure is stabilized by the experimentally observed marked tetragonal distortion of the crystal. This distortion produces in turn the “monoclinic-like” deformation of the array of the oxygen atoms.
In short, in [9] I reported evidence that the tetragonal distortion of antiferromagnetic CoO can only be understood when the magnetic structure is tetragonal. However, I did not compare the band structures of NiO, CoO, FeO, and MnO in order to understand why only CoO, but not the three other monoxides NiO, FeO, and MnO, possess a tetragonal magnetic structure invariant under the magnetic group . The present paper is intended to change this. First, in Section 2, the paramagnetic band structures of NiO, CoO, FeO, and MnO are considered as they are given in former papers. Then, in Section 3, the magnetic bands of these monoxides are determined or transferred from previous papers.
2. Paramagnetic CoO, NiO, FeO, and MnO
Figure 1 shows the conventional band structure of paramagnetic fcc CoO as it was determined in [9]. The bold lines highlight the “insulating” band
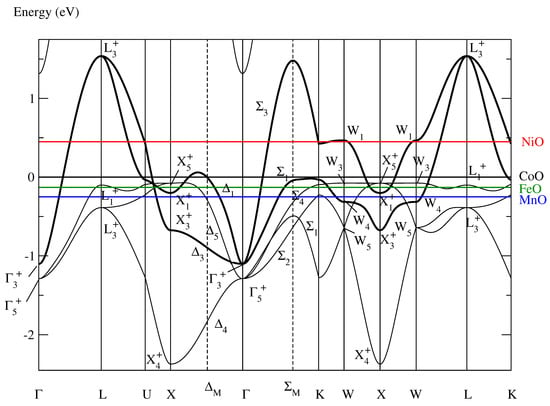
Figure 1.
Conventional band structure of paramagnetic fcc CoO as determined in [9] serving in this section as approximation of the band structures of paramagnetic fcc NiO, FeO, and MnO when the Fermi energies are adjusted. The colored horizontal lines denote the different Fermi energies, and the insulating band of CoO is highlighted by the bold lines. The symmetry labels are defined in Table A1 of [10].
- being roughly half-filled,
- comprising all the Bloch electrons at the Fermi level, and
- defining Bloch functions which can be unitarily transformed into Wannier functions that
- –
- are adapted to the fcc structure,
- –
- possess the two-dimensional symmetry,
- –
- are optimally localized, and
- –
- are situated on the Co atoms.
The NHM provides evidence that this insulating band produces the Mott insulation in paramagnetic CoO [9]. The NHM always starts from “conventional” band structure calculations, i.e., from pure one-electron band structure calculations not taking into account any correlation effect. Correlation effects enter into the theory when we leave the adiabatic approximation as specified by the three postulates of the NHM [8].
The band structure in Figure 1 approximates the paramagnetic band structures of NiO, FeO, and MnO when the Fermi energies are adjusted. In comparison with the other transition-metal monoxides NiO, FeO, and MnO, paramagnetic CoO possesses a nearly ideal insulating band (highlighted in Figure 1 by the bold lines):
- An insulating band defining Wannier functions with the two-dimensional symmetry exists neither in paramagnetic FeO nor in MnO because in these materials the Bloch states with , , , and symmetry lie above the Fermi energy. Thus, in FeO and in MnO more than two branches cross the Fermi level and, consequently, the optimally localized and symmetry-adapted Wannier functions have a five-dimensional symmetry [11] because we demand that the band comprises all the Bloch electrons at the Fermi level.
- NiO possesses an insulating band with optimally localized Wannier functions of the two-dimensional symmetry [10]. However, the Fermi energy in NiO is moved upward by roughly 0.5 eV (Figure 1). As a consequence, the highlighted band is in NiO not so precisely half-filled than in CoO.
This observation leads to the presumption that the nearly ideal insulating band in the paramagnetic band structure of CoO is responsible for the special magnetic structure proposed to exist in CoO, namely the noncollinear multi-spin-axis magnetic structure with tetragonal symmetry. In the following Section 3, we show that this supposition is corroborated by the NHM.
3. Magnetic Bands
In this section, we consider the magnetic bands of the transition-metal monoxides CoO, MnO, FeO, and NiO.
3.1. CoO
The magnetic band of CoO was exhaustively examined in [9]. The Bloch functions of the insulating fcc band of CoO in Figure 1 can be unitarily transformed into Wannier functions symmetry-adapted to the magnetic group
where K and I denote the time-inversion operator and the inversion, respectively. The unitary subgroup of the type III Shubnikov group bears the international number 110. defines a magnetic super band that evidently produces the tetragonal noncollinear multi-spin-axis magnetic structure, the small monoclinic-like deformation of the array of the oxygen atoms, and the Mott insulation in antiferromagnetic CoO [9].
Just as in NiO, the Bloch functions of the insulating fcc band of CoO could also be unitarily transformed into Wannier functions symmetry-adapted to the monoclinic magnetic group
given in Equation (12) of [10], where the unitary subgroup of the type III Shubnikov group now bears the international number 9. denotes the rotation through defined in Figure 1.3 of [12] (and indicated in Figure 2 of [10]). defines a magnetic super band that would produce the monoclinic base-centered magnetic structure, the small rhombohedral-like deformation of the array of the oxygen atoms and the Mott insulation as observed in NiO, FeO, and MnO.
The experimental observation [5,6,7] of the tetragonal distortion of CoO in the antiferromagnetic state together with the small monoclinic-like deformation suggests that the magnetic super band in CoO is related to , but not to [9].
3.2. MnO
In Section 6.2 of [11], we identified a band of six branches in the monoclinic base-centered Brillouin zone as the magnetic band of MnO related to the magnetic group (2) and, consequently, producing the monoclinic base-centered antiferromagnetic structure. This band represents three sets of Wannier functions each containing two symmetry-adapted Wannier functions situated either at the two Mn or the two O atoms [11]. Moreover, this band is a magnetic super band because it involves all the Bloch states at the Fermi level, and, consequently, allows antiferromagnetic MnO to be a Mott insulator.
In this section, we hypothetically assume that MnO has the same magnetic structure as CoO. Thus, we assume that antiferromagnetic MnO
- possesses eight Mn atoms and eight O atoms in the unit cell and
- is invariant under the magnetic group in Equation (1).
When folding the band of paramagnetic fcc MnO (in Figure 2 of [11]) into the Brillouin zone for the body-centered tetragonal Bravais lattice of , we receive the band structure depicted in Figure 2. It shows only the bands on the line with its endpoints and Z (as defined in Figure 3.10b of [12]). It should be noted that the line and its two endpoints and Z have the same symmetry. This rather unusual circumstance in the theory of Brillouin zones leads to a strong coupling between the Bloch functions at and Z.
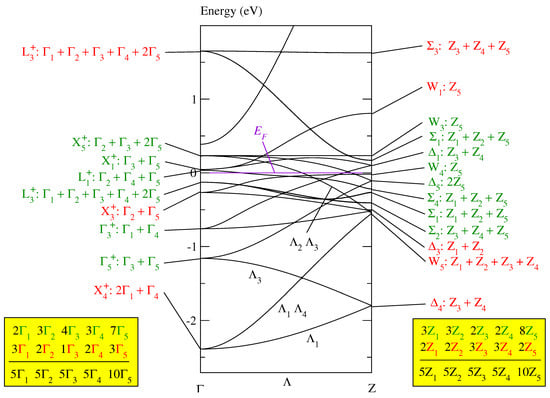
Figure 2.
The conventional band structure of paramagnetic MnO in Figure 2 of [11] folded into the Brillouin zone for the tetragonal body-centered lattice as given in Figure 3.10b of [12]. The bands are calculated by the FHI-aims program [13,14]. The symmetry labels are defined in Table A2 of [9] and the compatibility relations between the line and its endpoints and Z are given in Table A6b of [9].
In the tetragonal Brillouin zone, the fcc band consists of branches. In Figure 2, the symmetry of the Bloch functions is given, first, at the equivalent point in the fcc Brillouin zone and then, after the colon, in the tetragonal body-centered Brillouin zone. The equivalence of the symmetry points is specified in Table A5 of [9]. The representations and of the body-centered tetragonal space group are defined in Table A2 of [9]. Each of the eight representations , , , , , , , and occurs exactly five times and each of the two representations and exactly ten times in the band, as indicated by the third line in the boxes in Figure 2. Thus, the Bloch functions of this band can be unitarily transformed into five sets of optimally localized Wannier functions symmetry-adapted to , where each set contains eight Wannier functions, see Table A4 of [9]. These eight Wannier functions may be constructed in such a way that they are situated either at the eight Mn or the eight O atoms, as detailed in Section 5.2 of [9].
This band of 40 branches cannot be the magnetic band of MnO because it is significantly broader than the monoclinic magnetic band of MnO depicted in Figure 3 of [11], unless it would be possible to construct even within the Brillouin zone for a sufficiently narrow magnetic band consisting only of a part of the 40 branches. We show that this is not the case.
Each Bloch function in the paramagnetic fcc band structure of MnO (given in Figure 2 of [11]) is, on the one hand, equivalent to Bloch functions in the monoclinic band structure depicted in Figure 3 of [11] and, on the other hand, to Bloch functions in the tetragonal band structure shown in Figure 2. In this way, a relation is defined: Bloch functions in the monoclinic Brillouin zone are related to Bloch functions in the tetragonal Brillouin zone if they are equivalent to the same Bloch functions in the paramagnetic fcc Brillouin zone. The Bloch functions highlighted in green in Figure 2 are related to the Bloch functions of the monoclinic magnetic band of MnO given in Figure 3 of [11]; the remaining Bloch functions are highlighted in red. The relationship is defined by Table A5 of [10] and Table A5 of [9].
The magnetic super band in the monoclinic band structure of MnO (Figure 3 of [11]) consists of six branches. Thus, in the monoclinic system, we need sets of Wannier functions (containing 2 Wannier functions each) to completely represent the Bloch functions at the Fermi energy. Hence, in the tetragonal system we also need at least three sets of Wannier functions which now contain eight Wannier functions each. That means that we need a magnetic band consisting of branches at least to represent a Mott insulator.
The Bloch functions highlighted in green do not form three times the magnetic band in Table A4 of [9] since the Bloch functions with , , and symmetry occur only two times among the green functions, as indicated in the two boxes at the bottom of Figure 2. Thus, we cannot define in the tetragonal Brillouin zone a magnetic super band as narrow as the magnetic super band of MnO in the monoclinic Brillouin zone.
We could try to solve this problem by adding, for instance, the four red Bloch functions with : symmetry, or, at least, the two Bloch functions with symmetry, to the green functions. However, this would considerably broaden the magnetic band because the Bloch function with symmetry is connected via the states on the line with one of the states of the energetically lowest states labeled by : (see Table A6b of [9]).
In conclusion, any magnetic super band of MnO adapted to the tetragonal symmetry of would be markedly broader than the magnetic super band of MnO related to the monoclinic base-centered group in Equation (2). Consequently, the antiferromagnetic structure in MnO is not tetragonal but monoclinic.
3.3. FeO
Just as in MnO, the Wannier functions in fcc paramagnetic FeO also have a five-dimensional symmetry (Section 2). Hence, in FeO the antiferromagnetic structure is also not tetragonal but monoclinic.
3.4. NiO
Figure 3 shows the conventional band structure of fcc paramagnetic NiO. Two bands are highlighted:
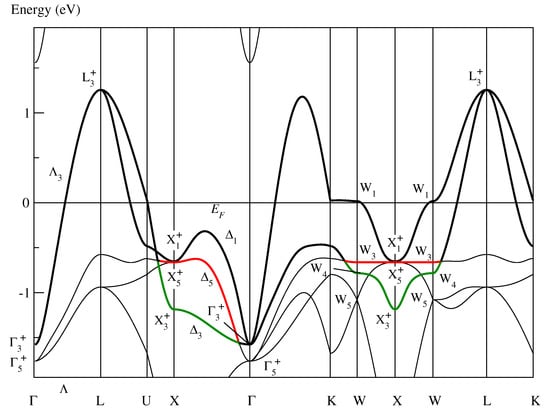
Figure 3.
Conventional band structure of paramagnetic fcc NiO as determined in [10] showing “band red” and “band green” defined in the text. As in Figure 1, the symmetry labels are defined in Table A1 of [10].
- Band red:
- Defined by the bold lines in black and in red.
- Band green:
- Defined by the bold lines in black and in green.
Band green is the active band of CoO and already considered in Section 3.1. In the band structure of NiO, band green is no longer half-filled and, thus, band red becomes the roughly half-filled active band in NiO. In the monoclinic base-centered system, band red forms a magnetic super band related to (2) that is evidently responsible for the monoclinic base-centered magnetic structure and the Mott insulation in NiO [10].
When band red is folded into the Brillouin zone for , the tetragonal body-centered Bravais lattice, it does not form a closed band that is a precondition for the existence of optimally localized and symmetry-adapted Wannier functions [15]. For instance, a part of the Bloch functions on the line in the fcc system lies on the line in the tetragonal system and keeps its symmetry of the point group (while the line completely loses its symmetry in the monoclinic system). Thus, the Bloch functions (Figure 3) are even in the tetragonal subgroup not connected with the state but with the state. Consequently, band red is not closed and, hence, does not form a magnetic band producing the tetragonal magnetic structure in NiO.
4. Discussion
The paper applies the nonadiabatic Heisenberg model (NHM) to the conventional band structures of the transition-metal monoxides NiO, CoO, FeO, and MnO. All these materials possess a narrow, roughly half-filled magnetic super band related to the monoclinic base-centered magnetic group in Equation (2). In addition, CoO (and only CoO) possesses a narrow, roughly half-filled magnetic super band related to the tetragonal magnetic group in Equation (1). Indeed, the other transition-metal monoxides also have such a band related to in their band structures, but these bands are either too broad (FeO and MnO) or not as exactly half-filled as in CoO (NiO).
Consequently, the magnetic super bands in NiO, FeO, and MnO are clearly related to and produce the monoclinic base-centered magnetic structure experimentally observed in these monoxides, together with the Mott insulation and the (small) rhombohedral-like deformation of the array of the oxygen atoms. On the other hand, the magnetic super band in CoO is related to and produces the tetragonal noncollinear multi-spin-axis magnetic structure as predicted by van Laar [5] together with the Mott insulation, the experimentally proven tetragonal deformation of the crystal, and the small monoclinic-like distortion of the array of the oxygen atoms [9]. These experimental findings demonstrate that the electronic system in CoO prefers the magnetic structure with the higher symmetry, i.e., the tetragonal magnetic structure is energetically (a little) more favorable than the monoclinic.
The results on magnetism presented by the NHM do not contradict the generally accepted concept of exchange or super exchange interactions responsible for any magnetic order. In a magnetic band related to a magnetic group M, the electron system activates an exchange mechanism producing a magnetic structure invariant under M in order to gain the nonadiabatic condensation energy defined in Equation (2.20) of [8]. Such an activation of a specific exchange mechanism is achieved by a modification of the localized orbitals in the nonadiabatic system, where atomic-like electrons no longer move on rigid localized orbitals, see the detailed discussion in [16].
Funding
This publication was supported by the Open Access Publishing Fund of the University of Stuttgart.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I am much indebted to Guido Schmitz for his continuing support of my work.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NHM | Nonadiabatic Heisenberg model |
| I | Inversion |
| K | Antiunitary operator of time inversion |
References
- Rooksby, H. A note on the structure of nickel oxide at subnormal and elevated temperatures. Acta Crystallogr. 1948, 1, 226. [Google Scholar] [CrossRef]
- Shull, C.G.; Strauser, W.A.; Wollan, E.O. Neutron Diffraction by Paramagnetic and Antiferromagnetic Substances. Phys. Rev. 1951, 83, 333–345. [Google Scholar] [CrossRef]
- Roth, W.L. Magnetic Structures of MnO, FeO, CoO, and NiO. Phys. Rev. 1958, 110, 1333–1341. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Joshua, S.J. The space group corepresentations of antiferromagnetic NiO. Math. Proc. Camb. Philos. Soc. 1969, 66, 493–504. [Google Scholar] [CrossRef]
- van Laar, B. Multi-Spin-Axis Structure for CoO. Phys. Rev. 1965, 138, A584–A587. [Google Scholar] [CrossRef]
- Timm, L.; Tucker, M.G.; Keen, D.A.; Thygesen, P.M.M.; Saines, P.J.; Goodwin, A.L. Exploration of antiferromagnetic CoO and NiO using reverse Monte Carlo total neutron scattering refinements. Phys. Scr. 2016, 91, 114004. [Google Scholar] [CrossRef] [Green Version]
- Jauch, W.; Reehuis, M.; Bleif, H.J.; Kubanek, F.; Pattison, P. Crystallographic symmetry and magnetic structure of CoO. Phys. Rev. B 2001, 64, 052102. [Google Scholar] [CrossRef]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B 2001, 63, 144403. [Google Scholar] [CrossRef] [Green Version]
- Krüger, E. Magnetic Structure of CoO. Symmetry 2021, 13, 1513. [Google Scholar] [CrossRef]
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Insulating Ground State of NiO. Symmetry 2019, 12, 56. [Google Scholar] [CrossRef] [Green Version]
- Krüger, E. Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO. Symmetry 2020, 12, 1913. [Google Scholar] [CrossRef]
- Bradley, C.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef] [Green Version]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient O(N)O(N) integration for all-electron electronic structure calculation using numeric basis functions. Comput. Phys. Commun. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Krüger, E.; Strunk, H.P. Group Theory of Wannier Functions Providing the Basis for a Deeper Understanding of Magnetism and Superconductivity. Symmetry 2015, 7, 561–598. [Google Scholar] [CrossRef] [Green Version]
- Krüger, E. Energy band with Wannier functions of ferromagnetic symmetry as the cause of ferromagnetism in iron. Phys. Rev. B 1999, 59, 13795–13805. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).