An Iterative Algorithm for the Generalized Reflexive Solution Group of a System of Quaternion Matrix Equations

Abstract

In the present paper, an iterative algorithm is proposed for solving the generalized $(P,Q)$-reflexive solution group of a system of quaternion matrix equations ${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s,s=1,2,\dots ,N$. A generalized $(P,Q)$-reflexive solution group, as well as the least Frobenius norm generalized $(P,Q)$-reflexive solution group, can be derived by choosing appropriate initial matrices, respectively. Moreover, the optimal approximate generalized $(P,Q)$-reflexive solution group to a given matrix group can be derived by computing the least Frobenius norm generalized $(P,Q)$-reflexive solution group of a reestablished system of matrix equations. Finally, some numerical examples are given to illustrate the effectiveness of the algorithm.

1. Introduction

Throughout, ${\mathbb{R}}^{m\times n}$ and ${\mathbb{H}}^{m\times n}$ denote the set of all $m\times n$ real matrices and the set of all $m\times n$ matrices over the quaternion algebra $\mathbb{H}=\{a_1+a_{2}i+a_{3}j+a_{4}k$ |$i^2=j^2=k^2=ijk=-1$, $a_1,a_2,a_3,a_4\in \mathbb{R}\}$, respectively. The identity matrix and zero matrix are denoted by I and O, respectively. A matrix with all elements equal to one is denoted by E. The real part, the trace, the transpose, the conjugate transpose, the column space, the $mn\times 1$ vector formed by the vertical concatenation of the respective columns of a matrix $A\in {\mathbb{H}}^{m\times n}$ are denoted by $Re(A),$ $tr(A),$ $A^T,$ $A^H,$ $R(A),$ $vec(A),$ respectively. For $A=A_1+A_{2}i+A_{3}j+A_{4}k\in {\mathbb{H}}^{m\times n}and\eta \in \{i,j,k\}$, the $\eta$-conjugate of $A,$ is denoted by $\tilde{A},$ i.e.,

$$\begin{array}{cc}\hfill \tilde{A}& =A_1+A_{2}i-A_{3}j-A_{4}k,\mathrm{for}\eta =i,\hfill \\ \hfill \tilde{A}& =A_1-A_{2}i+A_{3}j-A_{4}k,\mathrm{for}\eta =j,\hfill \\ \hfill \tilde{A}& =A_1-A_{2}i-A_{3}j+A_{4}k,\mathrm{for}\eta =k.\hfill \end{array}$$

The Frobenius norm of A is denoted by $∥A∥.$ The Kronecker matrix product and Hadmard matrix product of the matrices A and B are denoted by $A\otimes B$ and $A\odot B,$ respectively. A is called generalized reflexive (generalized anti-reflexive) if there are two generalized reflection matrices P and Q, i.e., $P=P^H=P^{-1}$ and $Q=$ $Q^H=Q^{-1},$ such that $A=PAQ$ ($A=-PAQ$). The generalized reflexive matrices have been widely used in engineering and scientific computations [1,2,3]. Throughout, ${\mathbb{H}}_r^{m\times n}(P,Q)$ (${\mathbb{H}}_a^{m\times n}(P,Q)$) stands for the set of $m\times n$ generalized reflexive (generalized anti-reflexive) quaternion matrices with respect to the generalized reflection matrix pair $(P,Q).$

Recently, researchers have paid much attention to the necessary and sufficient conditions for the existence of solutions as well as the general solutions to several quaternion matrix equations, which can be found in [4,5,6,7,8,9,10]. Based on the definition of the column-row determinant of quaternion matrix, Cramer’s rules for the solutions of several quaternion matrix equations are also derived in [11,12,13,14,15,16,17,18]. Moreover, the $\eta$(-skew)-Hermitian solutions of some quaternion matrix equations are considered in [19,20,21,22]. Obviously, the conjugate matrix is a special case of the $\eta$-conjugate matrix; therefore, it is interesting to study the $\eta$-conjugate solution to some quaternion matrix equations, (see, e.g., [23,24,25,26]).

The iterative method is a very effective method for solving matrix equations. Dehghan and Shirilord [27] propose an approximation algorithm for the generalized Lyapunov matrix equations $AX+X{A}^T+{\displaystyle \sum _{j=1}^M}{N}_{j}X{N}_j^T=C$. Hajarian and Chronopoulos [28] propose the GCDs method for solving the coupled Sylvester matrix equations $A_{1}X{B}_1+C_{1}Y{D}_1=E_1,A_{2}X{B}_2+C_{2}Y{D}_2=E_2$ over partially bisymmetric matrices X and Y with a prescribed submatrix constraint. Wang and Zhang [29] propose an iterative algorithm for solving the minimum-norm pure imaginary solution of the quaternionic least squares problem. Zhang and Wang [30] propose the preconditioned BiCG and BiCR algorithms based on tensor form for the Sylvester tensor equation ${\chi }_{{\times }_1}{A}_1+{\chi }_{{\times }_2}{A}_2+\cdots +{\chi }_{{\times }_m}{A}_m=\mathcal{B}$. Yan and Ma [31] give an iterative algorithm for the Hamiltonian solution of the generalized coupled Sylvester-conjugate matrix equations. Song and Wang [32] propose a modified CGLS iterative algorithm for solving the symmetric least squares solution of generalized Sylvester-conjugate matrix equation ${\displaystyle \sum _{i=1}^p}{A}_{i}X{B}_i+{\displaystyle \sum _{j=1}^t}{C}_j\overline{X}{D}_j=E$. Wu, Zhang and Sun [33] establish an iterative algorithm to solve the discrete Lyapunov matrix equation $AX{A}^T-X=-Q.$ By making use of structure of real representation matrices, some preconditioned LSQR algorithms for quaternionic least squares problems are proposed in [34,35,36]. By extending the CGLS method, iterative algorithms for the $\eta$-(anti)-Hermitian solutions of quaternionic least squares problems are proposed in [37,38,39].

As far as we know, the generalized $(P,Q)$-reflexive solution group of the system of quaternion matrix equations

$${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s,s=1,2,\dots N$$

(1)

has not been considered so far. Motivated by the work mentioned above, in this paper, we mainly consider an iterative algorithm for the following two problems:

Problem 1.

For given matrices $A_{ls},$ $C_{ls}\in {\mathbb{H}}^{p\times m},$ $B_{ls},$ $D_{ls}\in {\mathbb{H}}^{n\times q},$ $F_s\in {\mathbb{H}}^{p\times q},$ $l=1,2,\dots ,M,$ $s=1,2,\dots ,N,$ and the generalized reflection matrices $P\in {\mathbb{H}}^{m\times m},$ $Q\in {\mathbb{H}}^{n\times n}$, find the matrix group $X_l\in {\mathbb{H}}_r^{m\times n}(P,Q),l=1,2,\dots ,M,$ such that

$$\stackrel{M}{\sum _{l=1}}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s,s=1,2,\dots N.$$

Problem 2.

If Problem 1 is consistent, and $Z_1$ denotes its solution set. For a given matrix group $X_{0l}\in {\mathbb{H}}^{m\times n},l=1,2,\dots ,M,$ find $\left(X_1^{*},X_2^{*},\cdots ,X_M^{*}\right)\in Z_1,$ such that

$$\stackrel{M}{\sum _{l=1}}{∥X_l^{*}-X_{0l}∥}^2=\underset{Z_1}{min}\stackrel{M}{\sum _{l=1}}{∥X_l-X_{0l}∥}^2.$$

2. Preliminaries

Throughout this paper, $\left({\mathbb{H}}^{m\times n},⟨·,·⟩\right)$ denotes the inner product space deduced by inner product

$$⟨A,B⟩=Re[tr(B^{H}A)],A,B\in {\mathbb{H}}^{m\times n}.$$

(2)

Note that $\sqrt{⟨A,A⟩}=\sqrt{Re[tr(A^{H}A)]}=\sqrt{tr(A^{H}A)}=∥A∥,$ then the induced matrix norm by (2) is exactly the Frobenius norm. Let $E_{st}$ denote the $m\times n$ matrix whose $(s,t)$ entry is 1, and the other elements are zeros. For the inner product space $\left({\mathbb{H}}^{m\times n},⟨·,·⟩\right),$ it is easy to verify that $E_{st}$, $E_{st}i$, $E_{st}j,$ $E_{st}k,$ $s=1,2,\dots ,m,$ $t=1,2,\dots ,n,$ is an orthonormal basis, which is saying that the dimension of $\left({\mathbb{H}}^{m\times n},⟨·,·⟩\right)$ is 4 mn.

Lemma 1.

Let $P\in {\mathbb{H}}^{m\times m}$ and $Q\in {\mathbb{H}}^{n\times n}$ be two generalized reflection matrices. If $A\in {\mathbb{H}}_r^{m\times n}(P,Q),$ $B\in {\mathbb{H}}_a^{m\times n}(P,Q),$ then we have $⟨A,B⟩=0.$

Proof. 

From $⟨A,B⟩=Re[tr(B^{H}A)]=-Re[tr({\left(PBQ\right)}^{H}PAQ)]=-Re[tr(Q^H{B}^H{P}^{H}PAQ)]=-Re[tr(Q{B}^{H}AQ)]=-Re[tr(B^{H}A)]=-⟨A,B⟩,$ Lemma 1 holds. □

For an quaternion matrix $A=A_1+A_{2}i+A_{3}j+A_{4}k\in {\mathbb{H}}^{m\times n},$ a real representation of A, can be defined as

$$\varphi (A)=\left[\begin{array}{cccc}{A}_1& -A_2& -A_3& -A_4\\ A_2& A_1& -A_4& A_3\\ A_3& A_4& A_1& -A_2\\ A_4& -A_3& A_2& A_1\end{array}\right]\in {\mathbb{R}}^{4m\times 4n}.$$

(3)

From [40], $\varphi (·)$ satisfies the following properties:

• $A=B\iff \varphi (A)=\varphi (B);$
• $\varphi (A+B)=\varphi (A)+\varphi (B),\varphi (AB)=\varphi (A)\varphi (B),\varphi (kA)=k\varphi (A),k\in \mathbb{R};$
• $\varphi (A^H)={\varphi }^T(A);$
• $\varphi (A)=T_m^{-1}\varphi (A)T_n=R_m^{-1}\varphi (A)R_n=S_m^{-1}\varphi (A)S_n,$ where

  $$R_t=\left[\begin{array}{cc}O& -I_{2t}\\ I_{2t}& O\end{array}\right],S_t=\left[\begin{array}{cccc}O& O& O& -I_t\\ O& O& I_t& O\\ O& -I_t& O& O\\ I_t& O& O& O\end{array}\right],T_t=\left[\begin{array}{cccc}O& -I_t& O& O\\ I_t& O& O& O\\ O& O& O& I_t\\ O& O& -I_t& O\end{array}\right],t=m,n.$$
  Through a simple verification, we derive that $\varphi (·)$ also satisfies the following two properties which is useful for some deductions in this paper:
• $∥\varphi (A)∥=2∥A∥;$
• $\varphi (\tilde{A})=-\varphi (A)+2\varphi (A)\odot W_{\eta },\eta \in \left\{i,j,k\right\},$ where

  $$W_i=\left[\begin{array}{cccc}E& E& O& O\\ E& E& O& O\\ O& O& E& E\\ O& O& E& E\end{array}\right],W_j=\left[\begin{array}{cccc}E& O& E& O\\ O& E& O& E\\ E& O& E& O\\ O& E& O& E\end{array}\right],W_k=\left[\begin{array}{cccc}E& O& O& E\\ O& E& E& O\\ O& E& E& O\\ E& O& O& E\end{array}\right].$$

  (4)

3. The Solution of Problem 1

In this section, an algorithm is proposed to solve Problem 1 and its convergence is also proved.

Lemma 2.

Assume $\{R_s(i)\}$ and $\{P_l(i)\},$ $s=1,2,\dots ,N,l=1,2,\dots ,M,i=1,2,\dots$, are generated by Algorithm 1, then

$Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(j)R_s(i))]=0$ and $Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(j)P_l(i))]=0$ for $i,j=1,2,\dots ,i\ne j.$

Proof. 

See Appendix A.    □

Lemma 3.

Assume Problem 1 is consistent and $(X_1,X_2,\cdots ,X_M)\in Z_1$, then, $\{R_s(i)\}$, $\{P_l(i)\}$ and $\{X_l(i)\},$ $s=1,2,\dots ,N,$ $l=1,2,\dots ,M,$ $i=1,2,\dots$, generated by Algorithm 1 satisfy

$$Re\{tr[\stackrel{M}{\sum _{l=1}}{(X_l-X_l(i))}^H{P}_l(i)]\}=\stackrel{N}{\sum _{s=1}}{∥R_s(i)∥}^2,i=1,2,\dots .$$

(5)

Proof. 

See Appendix A.    □

Algorithm 1: Iterative algorithm for Problem 1.

1. Input $X_l(1)\in {\mathbb{H}}_r^{m\times n}(P,Q),$ $l=1,2,\dots ,M;$ 2. Calculate $$\begin{array}{cc}\hfill R_s(1)& =F_s-{\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l(1)B_{ls}+C_{ls}\widetilde{X_l(1)}{D}_{ls}),s=1,2,\dots N;\hfill \\ \hfill P_l(1)& =\frac{1}{2}[\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}Q)],\hfill \\ \hfill l& =1,2,\dots ,M;\hfill \\ \hfill k& :=1;\hfill \end{array}$$ 3. If $\left[\begin{array}{c}{R}_1(k)\\ R_2(k)\\ ⋮\\ R_N(k)\end{array}\right]=O$, or $\left[\begin{array}{c}{R}_1(k)\\ R_2(k)\\ ⋮\\ R_N(k)\end{array}\right]\ne O$ and $\left[\begin{array}{c}{P}_1(k)\\ P_2(k)\\ ⋮\\ P_M(k)\end{array}\right]=O,$ stop; else $k:=k+1;$ 4. Calculate $$\begin{array}{cc}\hfill X_l(k)& =X_l(k-1)+\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(k-1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(k-1)∥}^2}{P}_l(k-1),l=1,2,\dots ,M;\hfill \\ \hfill R_s(k)& =R_s(k-1)-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(k-1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(k-1)∥}^2}{\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(k-1)B_{ls}+C_{ls}\widetilde{P_l(k-1)}{D}_{ls}),s=1,2,\dots N;\hfill \\ \hfill P_l(k)& =\frac{1}{2}{\displaystyle \sum _{s=1}^N}(A_{ls}^H{R}_s(k)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(k)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(k)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(k)}\widetilde{D_{ls}^H}Q)\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(k)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(k-1)∥}^2}{P}_l(k-1),l=1,2,\dots ,M;\hfill \end{array}$$ 5. Go to Step 3.

If it appears that $\left[\begin{array}{c}{R}_1(i)\\ R_2(i)\\ ⋮\\ R_N(i)\end{array}\right]\ne O$ and $\left[\begin{array}{c}{P}_1(i)\\ P_2(i)\\ ⋮\\ P_M(i)\end{array}\right]=O,$ then we can derive Problem 1 is inconsistent from Lemma 3, and the Algorithm 1 will stop in Step 3.

Theorem 1.

If Problem 1 is consistent, a solution group can be obtained from Algorithm 1 in no more than 4Npq steps for any $X_l(1)\in {\mathbb{H}}_r^{m\times n}(P,Q)$, $l=1,2,\dots ,M,$ without considering roundoff errors.

Proof. 

From Lemma 3, we have if $\left[\begin{array}{c}{R}_1(i)\\ R_2(i)\\ ⋮\\ R_N(i)\end{array}\right]\ne O,i=1,2,\dots ,4Npq,$ then $\left[\begin{array}{c}{P}_1(i)\\ P_2(i)\\ ⋮\\ P_M(i)\end{array}\right]\ne O,i=1,2,\dots ,4Npq.$ Hence $\left[\begin{array}{c}{R}_1(4Npq+1)\\ R_2(4Npq+1)\\ ⋮\\ R_N(4Npq+1)\end{array}\right]$ and $\left[\begin{array}{c}{P}_1(4Npq+1)\\ P_2(4Npq+1)\\ ⋮\\ P_M(4Npq+1)\end{array}\right]$ can be computed.

From Lemma 2, we have

$$⟨\left[\begin{array}{c}{R}_1(i)\\ R_2(i)\\ ⋮\\ R_N(i)\end{array}\right],\left[\begin{array}{c}{R}_1(j)\\ R_2(j)\\ ⋮\\ R_N(j)\end{array}\right]⟩=Re[tr(\stackrel{N}{\sum _{s=1}}{R}_s^H(j)R_s(i))]=0\mathrm{for}i,j=1,2,\dots ,4Npq,i\ne j.$$

(6)

Then $\left[\begin{array}{c}{R}_1(1)\\ R_2(1)\\ ⋮\\ R_N(1)\end{array}\right],\left[\begin{array}{c}{R}_1(2)\\ R_2(2)\\ ⋮\\ R_N(2)\end{array}\right],\dots ,\left[\begin{array}{c}{R}_1(4Npq)\\ R_2(4Npq)\\ ⋮\\ R_N(4Npq)\end{array}\right]$ is a basis of $({\mathbb{H}}^{Np\times q},⟨·,·⟩).$

Also by Lemma 2, we have

$$⟨\left[\begin{array}{c}{R}_1(i)\\ R_2(i)\\ ⋮\\ R_N(i)\end{array}\right],\left[\begin{array}{c}{R}_1(4Npq+1)\\ R_2(4Npq+1)\\ ⋮\\ R_N(4Npq+1)\end{array}\right]⟩=0\mathrm{for}i=1,2,\dots ,4Npq.$$

(7)

Since $({\mathbb{H}}^{Np\times q},⟨·,·⟩)$ is $4Npq$-dimensional, it follows that $\left[\begin{array}{c}{R}_1(4Npq+1)\\ R_2(4Npq+1)\\ ⋮\\ R_N(4Npq+1)\end{array}\right]=O,$ which implies that $X_l(4Npq+1),$ $l=1,2,\dots ,M,$ is a solution group of Problem 1. □

4. The Solution of Problem 2

In this section, we first prove that Algorithm 1 will produce the least Frobenius norm generalized $(P,Q)$-reflexive solution group of (1) by inputing a group of appropriate initial matrices. Then, we solve Problem 2 by computing the least Frobenius norm generalized $(P,Q)$-reflexive solution group of a reestablished system of matrix equations.

Lemma 4

([41]). Assume that the linear system of equations $My=b$ has a solution $y_0\in R(M^T)$, then $y_0$ is the least Frobenius norm solution of the system of linear equations.

Lemma 5.

Problem 1 is consistent if and only if the system of quaternion matrix equations

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s,\\ {\displaystyle \sum _{l=1}^M}(A_{ls}P{X}_{l}Q{B}_{ls}+C_{ls}\tilde{P}\tilde{X}\widetilde{{}_{l}Q}{D}_{ls})=F_s,s=1,2,\dots ,N\end{array}\right.$$

(8)

is consistent. Moreover, if the solution set of (8) is denoted by $Z_2$ , then, $Z_1\subseteq Z_2$ holds.

Proof. 

Assume $X_l,$ $l=1,2,\dots ,M,$ is a solution group of Problem 1. By ${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s,,s=1,2,\dots ,N,$ and $P{X}_{l}Q=X_l,$ $l=1,2,\dots ,M,$ we can obtain ${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s$ and ${\displaystyle \sum _{l=1}^M}(A_{ls}P{X}_{l}Q{B}_{ls}+C_{ls}\tilde{P}\tilde{X}\widetilde{{}_{l}Q}{D}_{ls})=F_s,s=1,2,\dots ,N,$ which implies that $X_l,$ $l=1,2,\dots ,M,$ is a solution group of quaternion matrix Equation (8), and $Z_1\subseteq Z_2$.

Conversely, suppose (8) is consistent. Let $X_l,$ $l=1,2,\dots ,M,$ be a solution group of (8). Set $X_{la}=\frac{X_l+P{X}_{l}Q}{2},$ $l=1,2,\dots ,M.$ It is obvious that $X_{la}\in$ ${\mathbb{H}}_r^{m\times n}(P,Q),$ $l=1,2,\dots ,M$. Now we can write

$$\begin{array}{cc}\hfill {\displaystyle \sum _{l=1}^M}(A_{ls}{X}_{la}{B}_{ls}+C_{ls}\widetilde{X_{la}}{D}_{ls})& =\frac{1}{2}{\displaystyle \sum _{l=1}^M}[A_{ls}(X_l+P{X}_{l}Q)B_{ls}+C_{ls}(\widetilde{X_l}+\tilde{P}\widetilde{X_l}\tilde{Q})D_{ls}]\hfill \\ \hfill & =\frac{1}{2}{\displaystyle \sum _{l=1}^M}[A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls}+A_{ls}P{X}_{l}Q{B}_{ls}+C_{ls}\tilde{P}\widetilde{X_l}\tilde{Q}{D}_{ls}]\hfill \\ \hfill & =\frac{1}{2}[F_s+F_s]\hfill \\ \hfill & =F_s.\hfill \end{array}$$

Hence $X_{la},$ $l=1,2,\dots ,M$ is a solution group of Problem 1. □

Lemma 6.

The system (8) is consistent if and only if the system of real matrix equations

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[\varphi (A_{ls}){\left[X_{ijl}\right]}_{4\times 4}\varphi (B_{ls})-\varphi (C_{ls}){\left[X_{ijl}\right]}_{4\times 4}\varphi (D_{ls})\\ +2\varphi (C_{ls})\left({\left[X_{ijl}\right]}_{4\times 4}\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),s=1,2,\dots N\end{array}\right.$$

(9)

is consistent, where $X_{ijl}\in {\mathbb{H}}^{m\times n},$ $i,$ $j=1,$ $2,$ $3,$ 4, $l=1,2,\dots ,M,$ are submatrices of the unknown matrices. Moreover, let the solution set of (9) is denoted by $Z_3,$ we have $\varphi (Z_2)\subseteq Z_3.$

Proof. 

See Appendix A. □

Lemma 7.

The system (9) is equivalent to

$$\left[\begin{array}{cccc}{U}_{11}& U_{12}& \dots & U_{1M}\\ V_{11}& V_{12}& \dots & V_{1M}\\ ⋮& ⋮& \dots & ⋮\\ U_{N1}& U_{N2}& \dots & U_{NM}\\ V_{N1}& V_{N2}& \dots & V_{NM}\end{array}\right]\left[\begin{array}{c}vec({\left[X_{ij1}\right]}_{4\times 4})\\ vec({\left[X_{ij2}\right]}_{4\times 4})\\ ⋮\\ vec({\left[X_{ijM}\right]}_{4\times 4})\end{array}\right]=\left[\begin{array}{c}vec(\varphi (F_1))\\ vec(\varphi (F_1))\\ ⋮\\ vec(\varphi (F_N))\\ vec(\varphi (F_N))\end{array}\right].$$

(10)

where

$$\begin{array}{cc}\hfill U_{sl}& ={\varphi }^T(B_{ls})\otimes \varphi (A_{ls})-{\varphi }^T(D_{ls})\otimes \varphi (C_{ls})+2({\varphi }^T(D_{ls})\otimes \varphi (C_{ls}))diag(vec(W_{\eta })),\hfill \\ \hfill V_{sl}& ={\varphi }^T(B_{ls})\varphi (Q)\otimes \varphi (A_{ls})\varphi (P)-{\varphi }^T(D_{ls})\varphi (Q)\otimes \varphi (C_{ls})\varphi (P)\hfill \\ \hfill & +2({\varphi }^T(D_{ls})\otimes \varphi (C_{ls}))diag(vec(W_{\eta }))(\varphi (Q)\otimes \varphi (P)),\hfill \\ \hfill s& =1,2,\dots ,N,l=1,2,\dots ,M.\hfill \end{array}$$

Lemma 7 can be easily demonstrated by the operating properties of $vec(·),$ ⊗ and ⊙.

Theorem 2.

Assume Problem 1 is consistent, $({\mathring{X}}_1,{\mathring{X}}_2,\cdots ,{\mathring{X}}_M)\in Z_1$ , and ${\mathring{X}}_l$ can be expressed as

$${\mathring{X}}_l=\stackrel{N}{\sum _{s=1}}(A_{ls}^H{G}_s{B}_{ls}^H+\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}+P{A}_{ls}^H{G}_s{B}_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}Q),G_s\in {\mathbb{H}}^{p\times q},s=1,2,\dots N,l=1,2,\dots ,M,$$

then, ${\mathring{X}}_l,$ $l=1,2,\dots ,M,$ is the least Frobenius norm solution group of Problem 1.

Proof. 

From the operational properties of $\varphi$, we derive

$$\begin{array}{cc}\hfill & vec(\varphi ({\mathring{X}}_l))\hfill \\ \hfill & =vec\{\stackrel{N}{\sum _{s=1}}[{\varphi }^T(A_{ls})\varphi (G_s){\varphi }^T(B_{ls})-{\varphi }^T(C_{ls})\varphi (G_s){\varphi }^T(D_{ls})\hfill \\ \hfill & +2({\varphi }^T(C_{ls})\varphi (G_s){\varphi }^T(D_{ls}))\odot W_{\eta }+\varphi (P){\varphi }^T(A_{ls})\varphi (G_s){\varphi }^T(B_{ls})\varphi (Q)\hfill \\ \hfill & -\varphi (P){\varphi }^T(C_{ls})\varphi (G_s){\varphi }^T(D_{ls})\varphi (Q)+2\varphi (P)(({\varphi }^T(C_{ls})\varphi (G_s){\varphi }^T(D_{ls}))\odot W_{\eta })\varphi (Q)]\}\hfill \\ \hfill & =\stackrel{N}{\sum _{s=1}}\{[\varphi (B_{ls})\otimes {\varphi }^T(A_{ls})-\varphi (D_{ls})\otimes {\varphi }^T(C_{ls})+2diag(vec(W_{\eta }))(\varphi (D_{ls})\otimes {\varphi }^T(C_{ls})]vec(\varphi (G_s))\hfill \\ \hfill & +[\varphi (Q)\varphi (B_{ls})\otimes \varphi (P){\varphi }^T(A_{ls})-\varphi (Q)\varphi (D_{ls})\otimes \varphi (P){\varphi }^T(C_{ls})\hfill \\ \hfill & +2(\varphi (Q)\otimes \varphi (P))diag(vec(W_{\eta }))(\varphi (D_{ls})\otimes {\varphi }^T(C_{ls}))]vec(\varphi (G_s))\}\hfill \\ \hfill & =\left[\begin{array}{ccccc}{U}_{1l}^T& V_{1l}^T& \dots & U_{Nl}^T& V_{Nl}^T\end{array}\right]\left[\begin{array}{c}vec(\varphi (G_1))\\ vec(\varphi (G_1))\\ ⋮\\ vec(\varphi (G_N))\\ vec(\varphi (G_N))\end{array}\right],l=1,2,\dots ,M.\hfill \end{array}$$

So, we get

$$\begin{array}{cc}\hfill \left[\begin{array}{c}vec(\varphi ({\mathring{X}}_1))\\ vec(\varphi ({\mathring{X}}_2))\\ ⋮\\ vec(\varphi ({\mathring{X}}_M))\end{array}\right]& =\left[\begin{array}{ccccc}{U}_{11}^T& V_{11}^T& \dots & U_{N1}^T& V_{N1}^T\\ U_{12}^T& V_{12}^T& \dots & U_{N2}^T& V_{N2}^T\\ ⋮& ⋮& \dots & ⋮& ⋮\\ U_{1M}^T& V_{1M}^T& \dots & U_{NM}^T& V_{NM}^T\end{array}\right]\left[\begin{array}{c}vec(\varphi (G_1))\\ vec(\varphi (G_1))\\ ⋮\\ vec(\varphi (G_N))\\ vec(\varphi (G_N))\end{array}\right]\hfill \\ \hfill & \in R{\left[\begin{array}{cccc}{U}_{11}& U_{12}& \dots & U_{1M}\\ V_{11}& V_{12}& \dots & V_{1M}\\ ⋮& ⋮& \dots & ⋮\\ U_{N1}& U_{N2}& \dots & U_{NM}\\ V_{N1}& V_{N2}& \dots & V_{NM}\end{array}\right]}^T.\hfill \end{array}$$

By Lemma 4, $\left[\begin{array}{c}vec(\varphi ({\mathring{X}}_1))\\ vec(\varphi ({\mathring{X}}_2))\\ ⋮\\ vec(\varphi ({\mathring{X}}_M))\end{array}\right]$ is the least Frobenius norm solution of (10).

It follows from Lemmas 5–7 that ${\mathring{X}}_l,$ $l=1,2,\dots ,M,$ is the least Frobenius norm solution group of Problem 1. □

It is obvious that if we set the initial iteration matrices in Algorithm 1 as

$$\begin{array}{cc}\hfill X_l(1)& =\stackrel{N}{\sum _{s=1}}(A_{ls}^H{G}_s{B}_{ls}^H+\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}+P{A}_{ls}^H{G}_s{B}_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}Q),\hfill \\ \hfill G_s& \in {\mathbb{H}}^{p\times q},s=1,2,\dots ,N,l=1,2,\dots ,M.\hfill \end{array}$$

(11)

then all the generated $X_l(k)$ have the form

$$\begin{array}{cc}\hfill X_l(k)& =\stackrel{N}{\sum _{s=1}}(A_{ls}^H{G}_{sk}{B}_{ls}^H+\widetilde{C_{ls}^H}\widetilde{G_{sk}}\widetilde{D_{ls}^H}+P{A}_{ls}^H{G}_{sk}{B}_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{G_{sk}}\widetilde{D_{ls}^H}Q),\hfill \\ \hfill G_{sk}& \in {\mathbb{H}}^{p\times q},s=1,2,\dots ,N,l=1,2,\dots ,M.\hfill \end{array}$$

(12)

Considering Theorem 2, we obtain Theorem 3.

Theorem 3.

Suppose that Problem 1 is consistent. Set the initial iteration matrices in Algorithm 1 as

$$X_l(1)=\stackrel{N}{\sum _{s=1}}(A_{ls}^H{G}_s{B}_{ls}^H+\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}+P{A}_{ls}^H{G}_s{B}_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}Q),l=1,2,\dots ,M,$$

(13)

where $G_s,$ $s=1,2,\dots ,N,$ are freely selected in ${\mathbb{H}}^{p\times q}$, then the solution group generated by Algorithm 1 is the least Frobenius norm solution group of Problem 1.

For a matrix group $X_{0l}\in {\mathbb{H}}^{m\times n},l=1,2,\dots ,M,$ and $(X_1,X_2,\cdots ,X_M)\in Z_1,$ it is easy to verify that $X_l-\frac{X_{0l}+P{X}_{0l}Q}{2}\in {\mathbb{H}}_r^{m\times n}(P,Q)$ and $\frac{X_{0l}-P{X}_{0l}Q}{2}\in {\mathbb{H}}_a^{m\times n}(P,Q)$ $,l=1,2,\dots ,M.$ By Lemma 1, we get

$$\begin{array}{cc}\hfill {∥X_l-X_{0l}∥}^2& ={∥X_l-\frac{X_{0l}+P{X}_{0l}Q}{2}-\frac{X_{0l}-P{X}_{0l}Q}{2}∥}^2\hfill \\ \hfill & ={∥X_l-\frac{X_{0l}+P{X}_{0l}Q}{2}∥}^2+{∥\frac{X_{0l}-P{X}_{0l}Q}{2}∥}^2,l=1,2,\dots ,M.\hfill \end{array}$$

(14)

Hence, Problem 2 is equivalent to finding $(X_1^{*},X_2^{*},\cdots ,X_M^{*})\in Z_1,$ such that ${\displaystyle \sum _{l=1}^M}{∥X_l^{*}-\frac{X_{0l}+P{X}_{0l}Q}{2}∥}^2={\displaystyle \underset{Z_1}{min}}{\displaystyle \sum _{l=1}^M}{∥X_l-\frac{X_{0l}+P{X}_{0l}Q}{2}∥}^2.$ Let $X_l^{\prime }=X_l-\frac{X_{0l}+P{X}_{0l}Q}{2},l=1,2,\dots ,M,$ $F_s^{\prime }=F_s-{\displaystyle \sum _{l=1}^M}(A_{ls}\frac{X_{0l}+P{X}_{0l}Q}{2}{B}_{ls}+C_{ls}\frac{\widetilde{X_{0l}}+\tilde{P}\widetilde{X_{0l}}\tilde{Q}}{2}{D}_{ls}),s=1,2,\dots N,$ we have

$${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s\iff {\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l^{\prime }{B}_{ls}+C_{ls}{\widetilde{X^{\prime }}}_l{D}_{ls})=F_s^{\prime },s=1,2,\dots N.$$

(15)

Therefore, Problem 2 is equivalent to finding the least Frobenius norm generalized $(P,Q)$-reflexive solution group $X_l^{\#},$ $l=1,2,\dots ,M,$ of the system of quaternion matrix equations

$${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}{\tilde{X}}_l{D}_{ls})=F_s^{\prime },s=1,2,\dots N,$$

(16)

By setting the initial iteration matrices $X_l(1)={\displaystyle \sum _{s=1}^N}(A_{ls}^H{G}_s{B}_{ls}^H+\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}+P{A}_{ls}^H{G}_s{B}_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{G_s}\widetilde{D_{ls}^H}Q),$ $l=1,2,\dots ,M,$ where $G_s,$ $s=1,2,\dots ,N,$ are freely selected in ${\mathbb{H}}^{p\times q},$ the least Frobenius norm generalized $(P,Q)$-reflexive solution group $X_l^{\#},$ $l=1,2,\dots ,M,$ of (16) can be derived from Algorithm 1. Then, the solution group of Problem 2, $X_l^{*},$ $l=1,2,\dots ,M,$ can be expressed as

$$X_l^{*}=X_l^{\#}+\frac{X_{0l}+P{X}_{0l}Q}{2},l=1,2,\dots ,M.$$

(17)

5. Examples

In this section, we give three examples to illustrate the efficiency of the theoretical results.

Example 1.

Consider the system of quaternion matrix equations with k-conjugate

$$\left\{\begin{array}{c}{A}_{11}{X}_1{B}_{11}+C_{11}\widetilde{X_1}{D}_{11}+A_{21}{X}_2{B}_{21}+C_{21}{\tilde{X}}_2{D}_{21}=F_1,\\ A_{12}{X}_1{B}_{12}+C_{12}\widetilde{X_1}{D}_{12}+A_{22}{X}_2{B}_{22}+C_{22}{\tilde{X}}_2{D}_{22}=F_2,\end{array}\right.$$

(18)

where

$$A_{11}=\left[\begin{array}{ccc}-5+23i+5j+6k& 13+9j& 4+4i+12j+3k\\ 7-i+2j+k& 2-i-j& 3+3i+3j-7k\end{array}\right],$$

$$A_{21}=\left[\begin{array}{ccc}6+i+j& 16-4i+k& -5-9i+7j\\ 3-5i-4j+k& 7+2j+k& 21-i+6j+8k\end{array}\right],$$

$$A_{12}=\left[\begin{array}{ccc}5i+j+3k& 1-i& 3+3i-11k\\ -2-5i+j+k& -7+j& -i+5k\end{array}\right],$$

$$A_{22}=\left[\begin{array}{ccc}3-6i-j& i+4j+k& 1+i+9j+k\\ 10-j+7k& -1+8i+j+k& 2+3i+6j-8k\end{array}\right],$$

$$B_{11}=\left[\begin{array}{cc}-2+3i+2j+k& 8i+3j\\ 5+5i-9j-17k& -4+6j+k\\ 3+21i-j-8k& 11+i+4j+4k\\ 3+4i+j+k& -7j+4k\end{array}\right],B_{21}=\left[\begin{array}{cc}6+2i+7j+k& 19+i+3j-14k\\ 2-i+3j+k& 1+7i+2k\\ 3+7i+8j+3k& -2-4i-3j+k\\ 6+i+j+6k& 3+16i+2j\end{array}\right],$$

$$B_{12}=\left[\begin{array}{cc}10+2i+2j& -1+i+12j+k\\ 3-i+5j-k& 6+7i+11k\\ 3i-j-8k& 2+2i+4j+4k\\ 1+i+j+k& 2i-2j+4k\end{array}\right],B_{22}=\left[\begin{array}{cc}7-5i+3j+k& 8+i+2j+5k\\ i+2k& 2-4i+3j+k\\ 3+12i+j+3k& -1-i+4j+4k\\ 18+i+9k& 2+7j+9k\end{array}\right],$$

$$C_{11}=\left[\begin{array}{ccc}8+2j+k& 6+2i+j-2k& 7+3j+5k\\ 3+3i+j+2k& -3+i+2j+k& -7-5i-5j+3k\end{array}\right],$$

$$C_{21}=\left[\begin{array}{ccc}6+3i& i+3j+13k& i+10j+2k\\ 1+6i+2j+3k& -2+7i-7j+2k& 4-16i+3j+2k\end{array}\right],$$

$$C_{12}=\left[\begin{array}{ccc}5+6i+j+12k& 1+3i+2j+3k& 2i+j+4k\\ 2+5i+4j+2k& 2+5i+4j-11k& 1+2i+9j\end{array}\right],$$

$$C_{22}=\left[\begin{array}{ccc}6+2i+21k& 2+2i+13j+k& 1+18i+j+12k\\ 8+2i+j+3k& 8-5i-7j& 2+i+2j+k\end{array}\right],$$

$$D_{11}=\left[\begin{array}{cc}12+5i+4j+k& 1+3i+3j+4k\\ 1+i-3j+3k& -2-2i-4j+7k\\ 4+i& 5+2i+4j+k\\ 3-i+9j-2k& 2+i+18j+5k\end{array}\right],D_{21}=\left[\begin{array}{cc}7+i+2j& 2+6i+6j+3k\\ 4+i+8j& 2-18j+2k\\ 4+4i+8j+8k& -8+4i+7j-4k\\ -11-i+23j+k& 1+i+j-7k\end{array}\right],$$

$$D_{12}=\left[\begin{array}{cc}1+i+5j+k& 6i+7j+4k\\ i-3j+6k& 2-4j+8k\\ 2-16i-5j+k& -8-2i+4j\\ 1-4i+2j+2k& 1+i-j+8k\end{array}\right],D_{22}=\left[\begin{array}{cc}3+13i+6j-k& 3+i+k\\ -4-i+j+10k& 1+3j+2k\\ 14+i-8j+k& -2+4i+2j+2k\\ -1+5i+15j+k& 1+2i-2j+k\end{array}\right],$$

$$F_1=\left[\begin{array}{cc}5+6i+8j& 5-9i+5k\\ -2-5i+4j+k& 1+4i+j+4k\end{array}\right],F_2=\left[\begin{array}{cc}1+4i+3k& -7i-4j+8k\\ 4+2i+4j+k& 7+2i+j-5k\end{array}\right].$$

We aim to find the generalized $(P,Q)$-reflexive solution group of (18), where

$$P=\left[\begin{array}{ccc}0.28& 0& 0.96k\\ 0& 1& 0\\ -0.96k& 0& -0.28\end{array}\right]andQ=\left[\begin{array}{cccc}-0.28& 0& -0.96k& 0\\ 0& 0.28& 0& -0.96j\\ 0.96k& 0& 0.28& 0\\ 0& 0.96j& 0& -0.28\end{array}\right]$$

are generalized reflection matrices.

For the initial matrices

$X_1(1)=X_2(1)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0.64& 0& -0.48j\\ 0& 0& 0& 0\end{array}\right]\in {\mathbb{H}}_r^{3\times 4}(P,Q),$ we obtain a solution group from Algorithm 1 after 45 steps,

$$\begin{array}{cc}\hfill X_1(45)& =\hfill \\ \hfill & \left[\begin{array}{cc}-0.007314+0.1105i-0.04929j-0.02714k& -0.03311+0.08033i+0.08465j+0.0722k\\ -0.05654+0.04319i-0.02891j-0.03486k& 0.2752+0.03737i+0.04132j+0.124k\\ -0.005407+0.1617i+0.03015j+0.02663k& 0.06176+0.1024i+0.01517j-0.04204k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}-0.02124-0.133i+0.03432j+0.03089k& 0.1024+0.06176i-0.04204j+0.01517k\\ -0.04648+0.03855i+0.05758j+0.07538k& 0.03099+0.09297i-0.2064j-0.02803k\\ 0.007314+0.1105i-0.04929j+0.02714k& -0.08918+0.05764i-0.03618j-0.02493k\end{array}\right],\hfill \\ \hfill X_2(45)& =\hfill \\ \hfill & \left[\begin{array}{cc}0.02452-0.03385i+0.03673j+0.07426k& -0.008699-0.03658i+0.003438j-0.04804k\\ 0.1021+0.02011i+0.0947j+0.02373k& 0.2776-0.07761i+0.05927j-0.02094k\\ -0.03775+0.002827i-0.04744j+0.01797k& -0.06408-0.01196i-0.01857j+0.06529k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}0.005565-0.02426i+0.0277j+0.003668k& -0.01196-0.06408i+0.06529j-0.01857k\\ 0.03164-0.1263i+0.02682j-0.1362k& 0.04446-0.0157i-0.2082j+0.05821k\\ -0.02452-0.03385i+0.03673j-0.07426k& 0.04741-0.02939i+0.01066j-0.01041k\end{array}\right],\hfill \end{array}$$

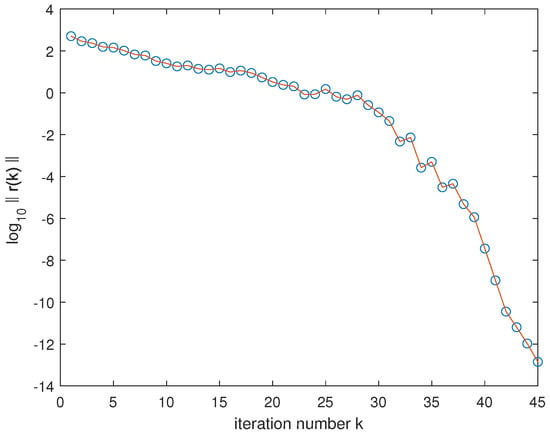
with $∥R_1(45)∥=1.0116\times {10}^{-13},$ $∥R_2(45)∥=9.8130\times {10}^{-14}.$ Figure 1 displays the convergence curve for $r(k)=\sqrt{{∥R_1(k)∥}^2+{∥R_2(k)∥}^2},k=1,2,\cdots ,45.$

Figure 1. The lagarithm of residual Frobenius norm from Example 1.

Example 2.

In this example, we aim to find the optimal approximation generalized $(P,Q)$-reflexive solution group of the system (18) to the given matrix group

$$X_{01}=\left[\begin{array}{cccc}j& j& j& j\\ j& j& j& j\\ j& j& j& j\end{array}\right],X_{02}=\left[\begin{array}{cccc}k& k& k& k\\ k& k& k& k\\ k& k& k& k\end{array}\right].$$

Let $F_1^{\prime }=F_1-A_{11}\frac{X_{01}+P{X}_{01}Q}{2}{B}_{11}-A_{21}\frac{X_{02}+P{X}_{02}Q}{2}{B}_{21}-C_{11}\frac{\widetilde{X_{01}}+\tilde{P}\widetilde{X_{01}}\tilde{Q}}{2}{D}_{11}-C_{21}\frac{\widetilde{X_{02}}+\tilde{P}\widetilde{X_{02}}\tilde{Q}}{2}{D}_{21}$ and $F_2^{\prime }=F_2-A_{12}\frac{X_{01}+P{X}_{01}Q}{2}{B}_{12}-A_{22}\frac{X_{02}+P{X}_{02}Q}{2}{B}_{22}-C_{12}\frac{\widetilde{X_{01}}+\tilde{P}\widetilde{X_{01}}\tilde{Q}}{2}{D}_{12}-C_{22}\frac{\widetilde{X_{02}}+\tilde{P}\widetilde{X_{02}}\tilde{Q}}{2}{D}_{22}.$ We apply Algorithm 1 to the system of quaternion matrix equations

$$\left\{\begin{array}{c}{A}_{11}{X}_1{B}_{11}+C_{11}\widetilde{X_1}{D}_{11}+A_{21}{X}_2{B}_{21}+C_{21}{\tilde{X}}_2{D}_{21}=F_1^{\prime },\\ A_{12}{X}_1{B}_{12}+C_{12}\widetilde{X_1}{D}_{12}+A_{22}{X}_2{B}_{22}+C_{22}{\tilde{X}}_2{D}_{22}=F_2^{\prime },\end{array}\right.$$

(19)

by setting the initial matrics $X_1(1)=X_2(1)=O$ (select $G_s=O\in {\mathbb{H}}^{p\times q}$ in (13)). Then we obtain the least Frobenius norm generalized $(P,Q)$-reflexive solution group of (19) after 45 steps,

$$\begin{array}{cc}\hfill X_1(45)& =\hfill \\ \hfill & \left[\begin{array}{cc}-0.3703-0.07156i-0.7633j+2.087k& 0.4008+0.438i-0.6514j+0.5596k\\ 0.3821-0.4035i-0.1425j-0.04042k& -0.00817+0.5893i-0.208j-0.1589k\\ -1.72+1.093i+0.3474j-0.3005k& -0.2348+0.1604i+0.3145j-0.3037k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}-0.5024-0.6474i-0.3891j-0.08448k& 0.1604-0.2348i-0.3037j+0.3145k\\ -0.05389+0.19i-0.538j-0.5094k& -0.156-0.1191i+0.006128j-0.442k\\ 0.3703-0.07156i-0.7633j-2.087k& -0.6215-0.2237i-0.6965j+0.7449k\end{array}\right],\hfill \\ \hfill X_2(45)& =\hfill \\ \hfill & \left[\begin{array}{cc}-0.04958+0.1932i+0.3075j+0.4997k& 0.1341-0.08018i+0.497j+0.503k\\ -0.4916-0.1075i-0.008578j-0.8279k& -0.6366-0.2836i+0.0215j-0.8362k\\ -0.01431-0.4552i-0.4937j-0.9693k& -0.3595+0.1997i-0.2429j+0.05877k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}0.2772+0.2758i+0.6064j-0.9404k& 0.1997-0.3595i+0.05877j-0.2429k\\ -1.104+0.01144i-0.1433j+0.6555k& 0.01612-0.6271i+0.4774j+0.2127k\\ 0.04958+0.1932i+0.3075j-0.4997k& 0.2219-0.1684i-0.7127j-0.3805k\end{array}\right],\hfill \end{array}$$

with $∥R_1(45)∥=3.4750\times {10}^{-13},$ $∥R_2(45)∥=2.5177\times {10}^{-13}.$ Figure 2 displays the convergence curve for $r(k)=\sqrt{{∥R_1(k)∥}^2+{∥R_2(k)∥}^2},k=1,2,\cdots ,45.$

Figure 2. The lagarithm of residual Frobenius norm from Example 2.

Therefore, the optimal approximation generalized $(P,Q)$-reflexive solution group to the matrix group $X_{01},$ $X_{02}$ is

$$\begin{array}{cc}\hfill & X_1(45)+\frac{X_{01}+P{X}_{01}Q}{2}\hfill \\ \hfill & =\left[\begin{array}{cc}-0.3703+0.1972i+0.1583j+2.087k& 0.2664+0.3036i-0.1122j+0.09879k\\ 0.3821+0.07649i+0.2175j-0.04042k& -0.4882+0.5893i+0.432j-0.1589k\\ -1.72+0.8238i+0.4258j-0.3005k& -0.1004+0.2948i+0.7753j+0.1571k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}-0.5024-0.9162i-0.3107j-0.08448k& 0.2948-0.1004i+0.1571j+0.7753k\\ -0.05389-0.29i+0.102j-0.5094k& 0.324-0.1191i+0.3661j-0.442k\\ 0.3703+0.1972i+0.1583j-2.087k& -0.7559-0.3581i-0.1573j+0.2841k\end{array}\right],\hfill \\ \hfill & X_2(45)+\frac{X_{02}+P{X}_{02}Q}{2}\hfill \\ \hfill & =\left[\begin{array}{cc}-0.04958+0.1932i+0.3075j+0.4997k& -0.0003182-0.2146i+0.03618j+1.042k\\ -0.9716-0.1075i-0.008578j-0.4679k& -0.6366-0.7636i+0.0215j-0.1962k\\ -0.01431-0.4552i-0.4937j+0.03068k& -0.2251+0.3341i+0.2179j+0.5196k\end{array}\right.\hfill \\ \hfill & \left.\begin{array}{cc}0.2772+0.2758i+0.6064j+0.05961k& 0.3341-0.2251i+0.5196j+0.2179k\\ -0.6238+0.01144i-0.1433j+1.295k& 0.01612-0.1471i+0.4774j+0.5727k\\ 0.04958+0.1932i+0.3075j-0.4997k& 0.0875-0.3028i-1.174j+0.1587k\end{array}\right].\hfill \end{array}$$

Example 3.

In this example, we solve the $(P,Q)$-reflexive solution group of the system (18) with large scale matrices, where

$$\begin{array}{cc}\hfill A_{11},A_{21},A_{12},A_{22},C_{11},C_{21},C_{12},C_{22}& \in {\mathbb{H}}^{100\times 300};\hfill \\ \hfill B_{11},B_{21},B_{12},B_{22},D_{11},D_{21},D_{12},D_{22}& \in {\mathbb{H}}^{400\times 100};F_1,F_2\in {\mathbb{H}}^{100\times 100}\hfill \end{array}$$

are random selected with real numbers of elements no more than 100, and

$$P=\left[\begin{array}{cc}-I_{100}& O\\ O& I_{200}\end{array}\right],Q=\left[\begin{array}{cc}{I}_{200}& O\\ O& -I_{200}\end{array}\right]$$

are generalized reflection matrices.

For the initial matrices $X_1(1)=X_2(1)=O\in {\mathbb{H}}_r^{300\times 400}(P,Q),$ we obtain a solution group after 858 steps, with $∥R_1(858)∥=5.1821\times {10}^{-13},$ $∥R_2(858)∥=5.3129\times {10}^{-13}$. Figure 3 displays the convergence curve for $r(k)=\sqrt{{∥R_1(k)∥}^2+{∥R_2(k)∥}^2},k=1,2,\cdots 858.$ The results show that Algorithm 1 is quite efficient.

Figure 3. The lagarithm of residual Frobenius norm from Example 3.

6. Conclusions

In this paper, we have proposed an iterative algorithm for solving the generalized $(P,Q)$-reflexive solution group of the system of quaternion matrix equations ${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s$, $s=1,2,\dots ,N$. We proved that the proposed algorithm can automatically determine the solvability of the problem, and the algorithm will generate a solution group in finite iteration steps, when the problem is solvable. We also have proved that the least Frobenius norm generalized $(P,Q)$-reflexive solution group of the system ${\displaystyle \sum _{l=1}^M}(A_{ls}{X}_l{B}_{ls}+C_{ls}\widetilde{X_l}{D}_{ls})=F_s$ can be obtained from the algorithm, by choosing a group of appropriate initial matrices. After that, we solved the optimal approximately generalized $(P,Q)$-reflexive solution group of the system. Finally, the proposed numerical examples illustrated the effectiveness of the algorithm.

Appendix A.1. The Proof of Lemma 2

Note that $Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(j)R_s(i))]=Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(i)R_s(j))]$ and $Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(j)P_l(i))]=Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(i)P_l(j))],$ we only need to prove $Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(j)R_s(i))]=0$ and $Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(j)P_l(i))]=0$ for $1\le i<j.$

We will use mathematical induction to show that

$$Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(i+1)R_s(i))]=0\mathrm{and}Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(i+1)P_l(i))]=0fori=1,2,\dots .$$

(A1)

When $i=1,$ we have

$$\begin{array}{cc}\hfill & Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(2)R_s(1))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{s=1}^N}{(R_s(1)-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}{\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(1)B_{ls}+C_{ls}\widetilde{P_l(1)}{D}_{ls}))}^H{R}_s(1)]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}(P_l^H(1)A_{ls}^H{R}_s(1)B_{ls}^H+{\widetilde{P_l(1)}}^H{C}_{ls}^H{R}_s(1)D_{ls}^H)]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}{P}_l^H(1)(A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}(P_l^H(1)\hfill \\ \hfill & {\displaystyle \sum _{s=1}^N}\frac{A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}Q}{2})]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}{\displaystyle \sum _{s=1}^N}{∥P_l(1)∥}^2\hfill \\ \hfill & =0.\hfill \end{array}$$

(A2)

$$\begin{array}{cc}\hfill & Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(2)P_l(1))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}(\frac{1}{2}({\displaystyle \sum _{s=1}^N}(A_{ls}^H{R}_s(2)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(2)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(2)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(2)}\widetilde{D_{ls}^H}Q)\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{P}_l{(1))}^H{P}_l(1)]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2+Re\{tr[{\displaystyle \sum _{l=1}^M}(P_l^H(1)\hfill \\ \hfill & {\displaystyle \sum _{s=1}^N}\frac{A_{ls}^H{R}_s(2)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(2)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(2)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(2)}\widetilde{D_{ls}^H}Q}{2})]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2+Re\{tr[{\displaystyle \sum _{l=1}^M}{\displaystyle \sum _{s=1}^N}{P}_l^H(1)(A_{ls}^H{R}_s(2)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(2)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2+Re\{tr[{\displaystyle \sum _{s=1}^N}(R_s^H(2)\stackrel{M}{\sum _{l=1}}(A_{ls}{P}_l(1)B_{ls}+C_{ls}\widetilde{P_l(1)}{D}_{ls}))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2+\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(2)(R_s(1)-R_s(2))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2-\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}{\displaystyle \sum _{s=1}^N}{∥R_s(2)∥}^2\hfill \\ \hfill & =0.\hfill \end{array}$$

(A3)

Assume conclusion (A1) holds for $1\le i\le t-1,$ then

$$\begin{array}{cc}\hfill & Re[tr(\stackrel{N}{\sum _{s=1}}{R}_s^H(t+1)R_s(t))]\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}{(R_s(t)-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}\stackrel{M}{\sum _{l=1}}(A_{ls}{P}_l(t)B_{ls}+C_{ls}\widetilde{P_l(t)}{D}_{ls}))}^H{R}_s(t)]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}{P}_l^H(t)(A_{ls}^H{R}_s(t)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}(P_l^H(t)\hfill \\ \hfill & {\displaystyle \sum _{s=1}^N}\frac{A_{ls}^H{R}_s(t)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(t)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(t)}\widetilde{D_{ls}^H}Q}{2})]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(t)(P_l(t)-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t-1)∥}^2}{P}_l(t-1))]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2\hfill \\ \hfill & =0\hfill \end{array}$$

(A4)

In addition, it can also be obtained that

$$\begin{array}{cc}\hfill & Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(t+1)P_l(t))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}(\frac{1}{2}\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(t+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H}\hfill \\ \hfill & +P{A}_{ls}^H{R}_s(t+1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H}Q)+\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{P}_l{(t))}^H{P}_l(t)]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2\hfill \\ \hfill & +Re\{tr[{\displaystyle \sum _{l=1}^M}\stackrel{N}{\sum _{s=1}}{P}_l^H(t)(A_{ls}^H{R}_s(t+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2\hfill \\ \hfill & +Re\{tr[\stackrel{N}{\sum _{s=1}}{\displaystyle \sum _{l=1}^M}{R}_s^H(t+1)A_{ls}{P}_l(t)B_{ls}+\widetilde{P_l^H(t)}{C}_{ls}^H{R}_s(t+1)D_{ls}^H]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2\hfill \\ \hfill & +Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(t+1)({\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(t)B_{ls}+C_{ls}\widetilde{P_l(t)}{D}_s))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2\hfill \\ \hfill & +\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(t+1)(R_s(t)-R_s(t+1))]\}\hfill \\ \hfill & =0.\hfill \end{array}$$

(A5)

Conclusion (A1) holds by mathematical induction principle.

Assume that $Re[tr({\displaystyle \sum _{s=1}^N}{R}_s^H(i+r)R_s(i))]=0$ and $Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(i+r)P_l(i))]=0$ for $i\ge 1$ and $r\ge 1.$ We next show that

$$Re[tr(\stackrel{N}{\sum _{s=1}}{R}_s^H(i+r+1)R_s(i))]=0\mathrm{and}Re[tr(\stackrel{M}{\sum _{l=1}}{P}_l^H(i+r+1)P_l(i))]=0.$$

(A6)

It follows from Algorithm 1 that

$$\begin{array}{cc}\hfill & Re[tr(\stackrel{N}{\sum _{s=1}}{R}_s^H(i+r+1)R_s(i))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{s=1}^N}(R_s(i+r)\hfill \\ \hfill & -\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2}{\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(i+r)B_{ls}+C_{ls}\widetilde{P_l(i+r)}{D}_{ls}){)}^H{R}_s(i)]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}(R_s^H(i+r)R_s(i)]\}\hfill \\ \hfill & -\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}(P_l^H(i+r)\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(i)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(i)}\widetilde{D_{ls}^H}))]\}\hfill \\ \hfill & =-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}(P_l^H(i+r)\hfill \\ \hfill & {\displaystyle \sum _{s=1}^N}\frac{A_{ls}^H{R}_s(i)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(i)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(i)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(i)}\widetilde{D_{ls}^H}Q}{2})]\}\hfill \\ \hfill & =-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(i+r)(P_l(i)-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(i-1)∥}^2}{P}_l(i-1))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2{\displaystyle \sum _{s=1}^N}{∥R_s(i-1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(i+r)P_l(i-1)]\}\hfill \end{array}$$

(A7)

and

$$\begin{array}{cc}\hfill & Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(i+r+1)P_l(i))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}(\frac{1}{2}\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(i+r+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(i+r+1)}\widetilde{D_{ls}^H}\hfill \\ \hfill & +P{A}_{ls}^H{R}_s(i+r+1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(i+r+1)}\widetilde{D_{ls}^H}Q)\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2}{P}_l{(i+r))}^H{P}_l(i)]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}\stackrel{N}{\sum _{s=1}}{(A_{ls}^H{R}_s(i+r+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(i+r+1)}\widetilde{D_{ls}^H})}^H{P}_l(i)]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}(R_s^H(i+r+1){\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(i)B_{ls}+C_{ls}\widetilde{P_l(i)}{D}_{ls}))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(i)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(i+r+1)(R_s(i)-R_s(i+1))]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(i)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(i+r+1)R_s(i)]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(i)∥}^2{\displaystyle \sum _{s=1}^N}{∥R_s(i+r)∥}^2{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(i)∥}^2{\displaystyle \sum _{l=1}^M}{∥P_l(i+r)∥}^2{\displaystyle \sum _{s=1}^N}{∥R_s(i-1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(i+r)P_l(i-1)]\}.\hfill \end{array}$$

(A8)

From (A7) and (A8), we get

$$Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(i+r+1)R_s(i)]\}=\dots =\alpha Re\{tr[\stackrel{M}{\sum _{l=1}}{P}_l^H(r+2)P_l(1)]\};$$

(A9)

$$Re\{tr[\stackrel{M}{\sum _{l=1}}{P}_l^H(i+r+1)P_l(i)]\}=\dots =\beta Re\{tr[\stackrel{M}{\sum _{l=1}}{P}_l^H(r+2)P_l(1)]\}.$$

(A10)

From Algorithm 1, we have

$$\begin{array}{cc}\hfill & Re[tr(\stackrel{N}{\sum _{s=1}}{R}_s^H(r+2)R_s(1))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{s=1}^N}(R_s(r+1)\hfill \\ \hfill & -\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(r+1)∥}^2}{\displaystyle \sum _{l=1}^M}(A_{ls}{P}_l(r+1)B_{ls}+C_{ls}\widetilde{P_l(r+1)}{D}_{ls}){)}^H{R}_s(1)]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(r+1)R_s(1)]\}\hfill \\ \hfill & -\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)(A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(r+1)R_s(1)]\}-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)\hfill \\ \hfill & \frac{A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}Q}{2}]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(r+1)R_s(1)]\}-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)P_l(1)]\}\hfill \\ \hfill & =0.\hfill \end{array}$$

(A11)

From Algorithm 1 and (A11) ,we can write

$$\begin{array}{cc}\hfill & Re[tr({\displaystyle \sum _{l=1}^M}{P}_l^H(r+2)P_l(1))]\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}(\frac{1}{2}\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(r+2)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(r+2)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(r+2)B_{ls}^{H}Q\hfill \\ \hfill & +P\widetilde{C_{ls}^H}\widetilde{R_s(r+2)}\widetilde{D_{ls}^H}Q)+\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}{P}_l{(r+1))}^H{P}_l(1)]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}\stackrel{N}{\sum _{s=1}}{(A_{ls}^H{R}_s(r+2)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(r+2)}\widetilde{D_{ls}^H})}^H{P}_l(1)]\}\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)P_l(1)]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(r+2)({\displaystyle \sum _{l=1}^M}{A}_{ls}{P}_l(1)B_{ls}+C_{ls}\widetilde{P_l(1)}{D}_{ls})]\}\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)P_l(1)]\}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{l=1}^M}{∥P_l(1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2}Re\{tr[{\displaystyle \sum _{s=1}^N}{R}_s^H(r+2)(R_s(1)-R_s(2))]\}\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(r+2)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(r+1)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{P}_l^H(r+1)P_l(1)]\}\hfill \\ \hfill & =0.\hfill \end{array}$$

(A12)

It follows from (A9), (A10), (A12) that (A6) holds.

Lemma 2 holds by mathematical induction principle.

Appendix A.2. The Proof of Lemma 3

When $i=1,$ we have

$$\begin{array}{cc}\hfill & Re\{tr[{\displaystyle \sum _{l=1}^M}{(X_l-X_l(1))}^H{P}_l(1)]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}({(X_l-X_l(1))}^H\hfill \\ \hfill \stackrel{N}{\sum _{s=1}}& \frac{A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}+P{A}_{ls}^H{R}_s(1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}Q}{2})]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}({(X_l-X_l(1))}^H{\displaystyle \sum _{s=1}^N}(A_{ls}^H{R}_s(1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(1)}\widetilde{D_{ls}^H}))]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}(R_s^H(1){\displaystyle \sum _{l=1}^M}(A_{ls}(X_l-X_l(1))B_{ls}+C_{ls}(\widetilde{X_l}-\widetilde{X_l(1)})D_{ls}))]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(1)R_s(1)]\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(1)∥}^2.\hfill \end{array}$$

(A13)

Assume (5) holds for $i=t$, that is

$$Re\{tr[\stackrel{M}{\sum _{l=1}}{(X_l-X_l(t))}^H{P}_l(t)]\}=\stackrel{N}{\sum _{s=1}}{∥R_s(t)∥}^2.$$

(A14)

Then, when $i=t+1$

$$\begin{array}{cc}\hfill & Re\{tr{\displaystyle \sum _{l=1}^M}[{(X_l-X_l(t+1))}^H{P}_l(t+1)]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}{(X_l-X_l(t+1))}^H(\frac{1}{2}\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(t+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H}\hfill \\ \hfill & +P{A}_{ls}^H{R}_s(t+1)B_{ls}^{H}Q+P\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H}Q)+\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{P}_l(t))]\}\hfill \\ \hfill & =Re\{tr[{\displaystyle \sum _{l=1}^M}{(X_l-X_l(t+1))}^H\stackrel{N}{\sum _{s=1}}(A_{ls}^H{R}_s(t+1)B_{ls}^H+\widetilde{C_{ls}^H}\widetilde{R_s(t+1)}\widetilde{D_{ls}^H})]\}\hfill \\ \hfill & +\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}Re\{tr[{\displaystyle \sum _{l=1}^M}{(X_l-X_l(t+1))}^H{P}_l(t)]\}\hfill \\ \hfill & =Re\{tr[\stackrel{N}{\sum _{s=1}}{R}_s^H(t+1)({\displaystyle \sum _{l=1}^M}(A_{ls}(X_l-X_l(t+1))B_{ls}+C_{ls}(\widetilde{X_l}-\widetilde{X_l(t+1)})D_{ls}))]\}+\hfill \\ \hfill & \frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}\{Re\{tr[\stackrel{M}{\sum _{l=1}}{(X_l-X_l(t))}^H{P}_l(t)]\}-Re\{tr[\stackrel{M}{\sum _{l=1}}{(X_l(t+1)-X_l(t))}^H{P}_l(t)]\}\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2+\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2}{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}\{\stackrel{N}{\sum _{s=1}}{∥R_s(t)∥}^2-\frac{{\displaystyle \sum _{s=1}^N}{∥R_s(t)∥}^2}{{\displaystyle \sum _{l=1}^M}{∥P_l(t)∥}^2}Re\{tr[\stackrel{M}{\sum _{l=1}}{P}_l^H(t)P_l(t)]\}\}\hfill \\ \hfill & ={\displaystyle \sum _{s=1}^N}{∥R_s(t+1)∥}^2.\hfill \end{array}$$

(A15)

So, Lemma 3 is proved by mathematical induction principle.

Appendix A.3. The Proof of Lemma 6

Suppose that (8) has a solution group $X_l,$ $l=1,2,\dots ,M.$ Applying properties $1,2$ and 6 of $\varphi (·)$ to (8) yields

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (X_l)\varphi (B_{ls})-\varphi (C_{ls})\varphi (X_l)\varphi (D_{ls})+2\varphi (C_{ls})\left(\varphi (X_l)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P)\varphi (X_l)\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P)\varphi (X_l)\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P)\varphi (X_l)\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),s=1,2,\dots ,N,\end{array}\right.$$

which implies that $\varphi (X_l),$ $l=1,2,\dots ,M,$ is a solution group of (9) and $\varphi (Z_2)\subseteq Z_3$.

Conversely, suppose that matrix group ${\left[X_{ijl}\right]}_{4\times 4},$ $l=1,2,\dots ,M,$ is a solution group of (9). That is

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[\varphi (A_{ls}){\left[X_{ijl}\right]}_{4\times 4}\varphi (B_{ls})-\varphi (C_{ls}){\left[X_{ijl}\right]}_{4\times 4}\varphi (D_{ls})\\ +2\varphi (C_{ls})\left({\left[X_{ijl}\right]}_{4\times 4}\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),s=1,2,\dots ,N.\end{array}\right.$$

By property 4 of $\varphi (·)$, we have

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[T_p^{-1}\varphi (A_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (B_{ls})T_q-T_p^{-1}\varphi (C_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (D_{ls})T_q\\ +2T_p^{-1}\varphi (C_{ls})T_m\left({\left[X_{ijl}\right]}_{4\times 4}\odot W_{\eta }\right)T_n^{-1}\varphi (D_{ls})T_q]=T_p^{-1}\varphi (F_s)T_q,\\ {\displaystyle \sum _{l=1}^M}[T_p^{-1}\varphi (A_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (B_{ls})T_q-T_p^{-1}\varphi (C_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (D_{ls})T_q\\ +2T_p^{-1}\varphi (C_{ls})T_m\left(\left(\varphi (P){\left[X_{ijl}\right]}_{4\times 4}\varphi (Q)\right)\odot W_{\eta }\right)T_n^{-1}\varphi (D_{ls})T_q]=T_p^{-1}\varphi (F_s)T_q,s=1,2,\dots ,N,\end{array}\right.$$

which is equal to

$$\left\{\begin{array}{c}\begin{array}{c}{\displaystyle \sum _{l=1}^M}[T_p^{-1}\varphi (A_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (B_{ls})T_q-T_p^{-1}\varphi (C_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (D_{ls})T_q\\ +2T_p^{-1}\varphi (C_{ls})\left(T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})T_q]=T_p^{-1}\varphi (F_s)T_q,\end{array}\\ \begin{array}{c}{\displaystyle \sum _{l=1}^M}[T_p^{-1}\varphi (A_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (B_{ls})T_q-T_p^{-1}\varphi (C_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (D_{ls})T_q\\ +2T_p^{-1}\varphi (C_{ls})\left(\left(\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})T_q]=T_p^{-1}\varphi (F_s)T_q,s=1,2,\dots ,N.\end{array}\end{array}\right.$$

Similarly, we get

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[R_p^{-1}\varphi (A_{ls})R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (B_{ls})R_q-R_p^{-1}\varphi (C_{ls})R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (D_{ls})R_q\\ +2R_p^{-1}\varphi (C_{ls})\left(R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})R_q]=R_p^{-1}\varphi (F_s)R_q,\\ {\displaystyle \sum _{l=1}^M}[S_p^{-1}\varphi (A_{ls})S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (B_{ls})S_q-S_p^{-1}\varphi (C_{ls})S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (D_{ls})S_q\\ +2S_p^{-1}\varphi (C_{ls})\left(S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})S_q]=S_p^{-1}\varphi (F_s)S_q,\\ {\displaystyle \sum _{l=1}^M}[R_p^{-1}\varphi (A_{ls})\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\varphi (B_{ls})R_q-R_p^{-1}\varphi (C_{ls})\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\varphi (D_{ls})R_q\\ +2R_p^{-1}\varphi (C_{ls})\left(\left(\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})R_q]=R_p^{-1}\varphi (F_s)R_q,\\ {\displaystyle \sum _{l=1}^M}[S_p^{-1}\varphi (A_{ls})\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\varphi (B_{ls})S_q-S_p^{-1}\varphi (C_{ls})\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\varphi (D_{ls})S_q\\ +2S_p^{-1}\varphi (C_{ls})\left(\left(\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})S_q]=S_p^{-1}\varphi (F_s)S_q,s=1,2,\dots ,N.\end{array}\right.$$

Hence,

$$\left\{\begin{array}{c}{\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (B_{ls})-\varphi (C_{ls})T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (B_{ls})-\varphi (C_{ls})R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (B_{ls})-\varphi (C_{ls})S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P)T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P)R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),\\ {\displaystyle \sum _{l=1}^M}[\varphi (A_{ls})\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\varphi (B_{ls})-\varphi (C_{ls})\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\varphi (D_{ls})\\ +2\varphi (C_{ls})\left(\left(\varphi (P)S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\varphi (Q)\right)\odot W_{\eta }\right)\varphi (D_{ls})]=\varphi (F_s),s=1,2,\dots ,N,\end{array}\right.$$

which implies that matrix groups

$$\begin{array}{cc}\hfill T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1},l& =1,2,\dots ,M,\hfill \\ \hfill R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1},l& =1,2,\dots ,M,\hfill \\ \hfill S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1},l& =1,2,\dots ,M,\hfill \end{array}$$

are also solutions of (9). Thus,

$$\frac{1}{4}({\left[X_{ijl}\right]}_{4\times 4}+T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}+R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}+S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}),l=1,2,\dots ,M,$$

is a solution group of (9), where

$$\begin{array}{cc}{\left[X_{ijl}\right]}_{4\times 4}+T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}+R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}+S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}\hfill & ={\left[\widehat{X_{ijl}}\right]}_{4\times 4},\hfill \\ \hfill i,j& =1,2,3,4,l=1,2,\dots ,M,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \widehat{X_{11l}}& =X_{11l}+X_{22l}+X_{33l}+X_{44l},\widehat{X_{12l}}=X_{12l}-X_{21l}+X_{34l}-X_{43l},\hfill \\ \hfill \widehat{X_{13l}}& =X_{13l}-X_{24l}-X_{31l}+X_{42l},\widehat{X_{14l}}=X_{14l}+X_{23l}-X_{32l}-X_{41l},\hfill \\ \hfill \widehat{X_{21l}}& =-X_{12l}+X_{21l}-X_{34l}+X_{43l},\widehat{X_{22l}}=X_{11l}+X_{22l}+X_{33l}+X_{44l},\hfill \\ \hfill \widehat{X_{23l}}& =X_{14l}+X_{23l}-X_{32l}-X_{41l},\widehat{X_{24l}}=-X_{13l}+X_{24l}+X_{31l}-X_{42l},\hfill \\ \hfill \widehat{X_{31l}}& =-X_{13l}+X_{24l}+X_{31l}-X_{42l},\widehat{X_{32l}}=-X_{14l}-X_{23l}+X_{32l}+X_{41l},\hfill \\ \hfill \widehat{X_{33l}}& =X_{11l}+X_{22l}+X_{33l}+X_{44l},\widehat{X_{34l}}=X_{12l}-X_{21l}+X_{34l}-X_{43l},\hfill \\ \hfill \widehat{X_{41l}}& =-X_{14l}-X_{23l}+X_{32l}+X_{41l},\widehat{X_{42l}}=X_{13l}-X_{24l}-X_{31l}+X_{42l},\hfill \\ \hfill \widehat{X_{43l}}& =-X_{12l}+X_{21l}-X_{34l}+X_{43l},\widehat{X_{44l}}=X_{11l}+X_{22l}+X_{33l}+X_{44l},l=1,2,\dots ,M.\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill {\widehat{X}}_l& =\frac{1}{4}(X_{11l}+X_{22l}+X_{33l}+X_{44l})+\frac{1}{4}(-X_{12l}+X_{21l}-X_{34l}+X_{43l})i\hfill \\ \hfill & +\frac{1}{4}(-X_{13l}+X_{24l}+X_{31l}-X_{42l})j+\frac{1}{4}(-X_{14l}-X_{23l}+X_{32l}+X_{41l})k,l=1,2,\dots ,M.\hfill \end{array}$$

We can verify that

$$\varphi ({\widehat{X}}_l)=\frac{1}{4}({\left[X_{ijl}\right]}_{4\times 4}+T_m{\left[X_{ijl}\right]}_{4\times 4}{T}_n^{-1}+R_m{\left[X_{ijl}\right]}_{4\times 4}{R}_n^{-1}+S_m{\left[X_{ijl}\right]}_{4\times 4}{S}_n^{-1}),l=1,2,\dots ,M.$$

Therefore, ${\widehat{X}}_l,$ $l=1,2,\dots ,M,$ is a solution group of (8) by property 1 of $\varphi (·)$.