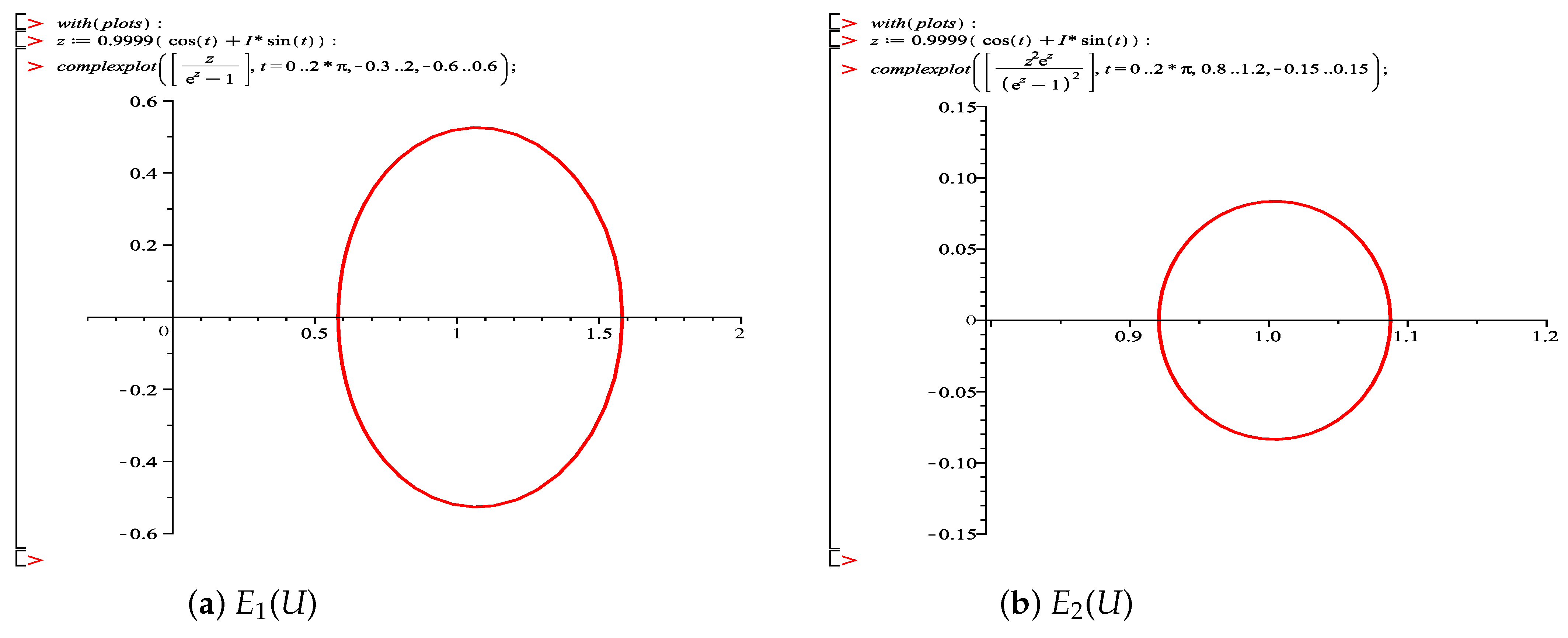Application of Einstein Function on Bi-Univalent Functions Defined on the Unit Disc

Abstract

Motivated by q-calculus, we define a new family of $\Sigma$, which is the family of bi-univalent analytic functions in the open unit disc U that is related to the Einstein function $E\left(z\right)$. We establish estimates for the first two Taylor–Maclaurin coefficients $|a_2|$, $|a_3|$, and the Fekete–Szegö inequality $\left|a_3-\mu a_2^2\right|$ for the functions that belong to these families.

1. Introduction and Basic Concepts

Let $\mathcal{A}$ denote the family of functions f normalized by

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,$$

(1)

which are analytic and univalent in the open unit disc $U=\{z:|z|<1\}$ and satisfy the usual normalization condition $f\left(0\right)=f^{\prime }\left(0\right)-1=0$. In addition, an important class of functions will be called $\mathcal{P}$. $\mathcal{P}$ is the family of analytic univalent functions $\varphi$ with positive real part mapping U onto domains symmetric with respect to the real axis and starlike with respect to $\varphi \left(0\right)=1$ such that ${\varphi }^{\prime }\left(0\right)>0$. In 1994, Ma and Minda [1] introduced the following subset of functions:

$${\mathcal{S}}^{*}\left(\varphi \right)=\left\{f\in \mathcal{A}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \varphi \left(z\right),\varphi \in \mathcal{P},z\in U\right\},$$

where the symbol “≺” refers to the subordination given in Definition 1 below. Ma and Minda [1] investigated certain useful problems, including distortion, growth and covering theorems.

Now, taking some particular functions instead of $\varphi$ in ${\mathcal{S}}^{*}\left(\varphi \right)$, we achieve many sub-families of the collection $\mathcal{A}$ which have different geometric interpretations, as for example:

(i)

If $\varphi \left(z\right)=\frac{1+Az}{1+Bz}$ with $-1\le B<A\le 1$, then ${\mathcal{S}}^{*}[A,B]:={\mathcal{S}}^{*}\left(\frac{1+Az}{1+Bz}\right)$ is the set of Janowski starlike functions; see [2]. Some interesting problems such as convolution properties, coefficient inequalities, sufficient conditions, subordinate results and integral preserving were discussed recently in [3,4,5,6,7] for some of the generalized families associated with circular domains;

(ii)

The class ${\mathcal{S}}_L^{*}:={\mathcal{S}}^{*}\left(\sqrt{1+z}\right)$ was introduced by Sokól and Stankiewicz [8], consisting of functions $f\in \mathcal{A}$ such that $z{f}^{\prime }\left(z\right)/f\left(z\right)$ lies in the region bounded by the right-half of the lemniscate of Bernoulli given by $\left|w^2-1\right|<1$;

(iii)

When we take $\varphi \left(z\right)=e^z$, then we have ${\mathcal{S}}_e^{*}:={\mathcal{S}}^{*}\left(e^z\right)$ [9];

(iv)

The family ${\mathcal{S}}_R^{*}:={\mathcal{S}}^{*}\left(1+\frac{z}{k}\frac{k+z}{k-z}\right)$, $k=\sqrt{2}+1$, the rational function is studied in [10];

(v)

For ${\mathcal{S}}_{sin}^{*}:={\mathcal{S}}^{*}\left(1+sinz\right)$, the class ${\mathcal{S}}_{sin}^{*}$ is introduced in [11];

(vi)

By setting $\varphi \left(z\right)=1+\frac{4}{3}z+\frac{2}{3}{z}^2$, the family ${\mathcal{S}}^{*}\left(\varphi \right)$ reduces to $S_{car}$ introduced by Sharma and his coauthors [12], consisting of functions $f\in \mathcal{A}$ such that $z{f}^{\prime }\left(z\right)/f\left(z\right)$ lies in the region bounded by the cardioid given by ${(9x^2+9y^2-18x+5)}^2-16(9x^2+9y^2-6x+1)=0$, for more subclasses see [13,14,15,16,17].

In mathematics, Einstein function is a name occasionally used for one of the functions (see [18,19]): $E_1\left(z\right):={\displaystyle \frac{z}{e^z-1}},$$E_2\left(z\right):={\displaystyle \frac{z^2{e}^z}{{\left(e^z-1\right)}^2}},$$E_3\left(z\right):=log\left(1-e^{-z}\right),$ $E_4\left(z\right):={\displaystyle \frac{z}{e^z-1}}-log\left(1-e^{-z}\right)$.

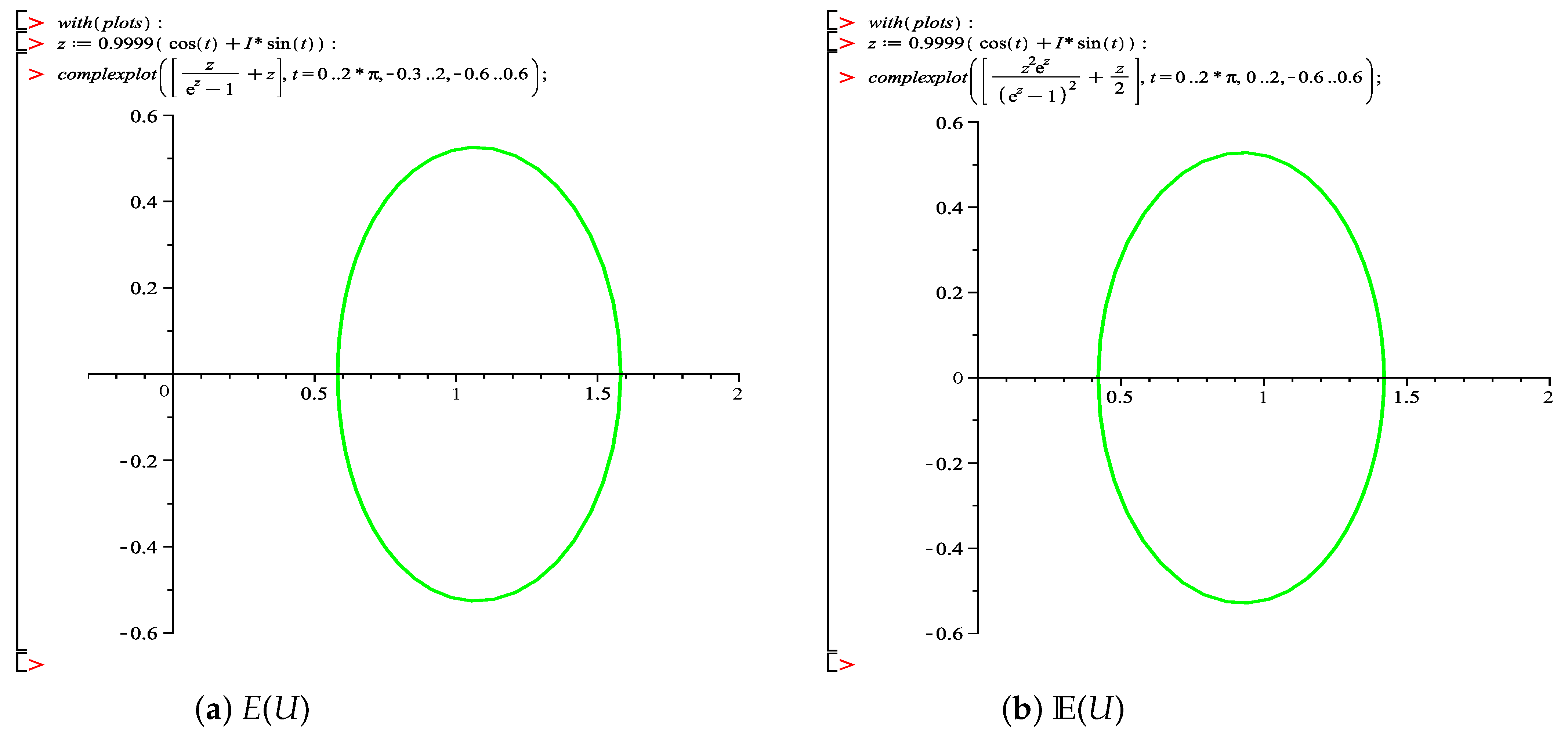
It is easily noticed that both $E_1$ and $E_2$ have these nice properties (see Figure 1); the image domain of $E_{1,2}$ ($E_{1,2}$ are convex functions with $Re\left(E_{1,2}\left(z\right)\right)>0$∀$z\in U$) is symmetric along the real axis and starlike about $E_{1,2}\left(0\right)=1$. Unfortunately, $E_{1,2}^{\prime }\left(0\right)\ngtr 0$, thus, we shall define the new functions $E\left(z\right):=E_1\left(z\right)+z$ and $\mathbb{E}\left(z\right):=E_2\left(z\right)+\frac{1}{2}z$. Now, we can say that $E,\mathbb{E}\in \mathcal{P}$ (see Figure 2).

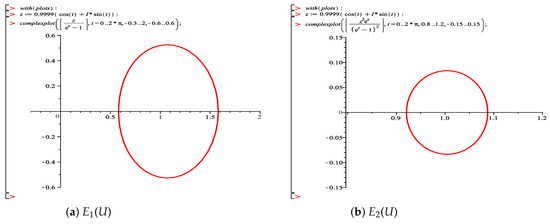
Figure 1. The images of unit disc U of the Einstein functions $E_1$ and $E_2$.

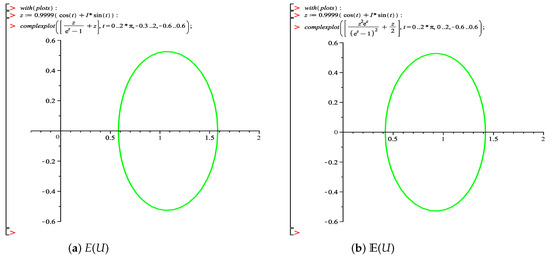
Figure 2. The images of unit disc U of the modified Einstein functions E and $\mathbb{E}$.

The series representations are given as follows:

$$E\left(z\right)=1+z+\sum _{n=1}^{\infty }{\displaystyle \frac{B_n}{n!}}{z}^n,$$

(2)

and

$$\mathbb{E}\left(z\right)=1+{\displaystyle \frac{1}{2}}z+\sum _{n=1}^{\infty }{\displaystyle \frac{(1-n)B_n}{n!}}{z}^n,$$

(3)

where $B_n$ is the nth Bernoulli number; it is known that the Bernoulli numbers $B_n$ can be defined by the contour integral (see [20])

$$B_n=\frac{n!}{2\pi i}\oint {\displaystyle \frac{z}{e^z-1}}\frac{dz}{z^{n+1}},$$

(4)

where the contour encloses the origin, has radius less than $2\pi i$, and is traversed in a counterclockwise direction; the first few members are

$$B_0=1,B_1=-\frac{1}{2},B_2=\frac{1}{6},B_4=-\frac{1}{30},B_6=\frac{1}{42},\dots$$

and

$$B_{2n+1}=0\forall n\in \mathbb{N}.$$

Here, in this paper, we will deal with the first function E, the function $\mathbb{E}$ is left as open problem.

Let $\mathcal{S}$ be the subfamily of $\mathcal{A}$ consisting of all functions of the form (1) which are univalent in U.

It is well known, by using the Koebe one-quarter theorem [21], that every univalent function $f\in \mathcal{S}$ containing a disc of radius $\frac{1}{4}$ has an inverse function $f^{-1}$, which is defined by

$$f^{-1}\left(f\left(z\right)\right)=z,(z\in \mathcal{U}),$$

and

$$f\left(f^{-1}\left(\omega \right)\right)=\omega \left(\omega \in ▵=\left\{\omega \in \mathbb{C}:\left|\omega \right|<\frac{1}{4}\right\}\right).$$

A function $f\in \mathcal{S}$ is said to be bi-univalent in U if both f and $f^{-1}$ are univalent in U. Let $\Sigma$ denote the subfamily of $\mathcal{S}$, consisting of all bi-univalent functions defined on the unit disc U. Since $f\in \Sigma$ has the Maclaurin series expansion given by (1), a simple calculation shows that its inverse $g=f^{-1}$ has the series expansion

$$g\left(\omega \right)=f^{-1}\left(\omega \right)=w-a_2{w}^2+(2a_2^2-a_3)w^3-\dots .$$

(5)

Examples of functions in the class $\Sigma$ are

$$\frac{z}{1-z},-log\left(1-z\right)\mathrm{and}\frac{1}{2}log\left(\frac{1+z}{1-z}\right)$$

and so on. However, the familiar Koebe function is not a member of $\Sigma$. Other common examples of functions in $\mathcal{S}$, such as

$$z-\frac{z^2}{2}\mathrm{and}\frac{z}{1-z^2},$$

are also not members of $\Sigma$.

Now, we recall some notations about the q-difference operator which is used in investigating our main families. In view of Annaby and Mansour [22], the q-difference operator is defined by

$${\partial }_{q}f\left(z\right)=\left\{\begin{array}{ccc}\frac{f\left(qz\right)-f\left(z\right)}{z(q-1)}\hfill & ,& z\ne 0;\\ \\ f^{{}^{\prime }}\left(0\right)\hfill & ,& z=0;\end{array}\right.$$

and

$${\partial }_q^{0}f\left(z\right)=f\left(z\right),{\partial }_q^{1}f\left(z\right)={\partial }_{q}f\left(z\right)\mathrm{and}{\partial }_q^{m}f\left(z\right)={\partial }_q\left({\partial }_q^{m-1}f\left(z\right)\right)(m\in \mathbb{N}).$$

Thus, for the function $f\in \mathcal{A}$ defined by (1), we have

$${\partial }_{q}f\left(z\right)=1+\sum _{n=2}^{\infty }{\left[n\right]}_q{a}_n{z}^{n-1}(z\ne 0),$$

(6)

where

$${\left[\nu \right]}_q=\frac{q^{\nu }-1}{q-1}={\displaystyle \sum _{j=0}^{\nu -1}}{q}^j,\nu \in \mathbb{N}.$$

We note that ${lim}_{q\to 1^{-}}{\left[n\right]}_q=n$ and ${lim}_{q\to 1^{-}}{\partial }_{q}f\left(z\right)=f^{\prime }\left(z\right)$.

Definition 1

([23,24]). An analytic function f is said to be subordinate to another analytic function g, written as $f\left(z\right)\prec g\left(z\right)(z\in U)$, if there exists a Schwarz function ω, which is analytic in U with $\omega \left(0\right)=0$ and $\left|\omega \right(z\left)\right|<1(z\in U)$, such that $f\left(z\right)=g\left(w\right(z\left)\right)$. In particular, if the function g is univalent in U, then we have the following equivalence:

$$f\left(z\right)\prec g\left(z\right)\iff f\left(0\right)=g\left(0\right)\mathrm{and}f\left(U\right)\subset g\left(U\right).$$

The aim of this article is to introduce new subfamilies of analytic bi-univalent functions subordinate to the Einstein function $E\left(z\right)$. Furthermore, we deduce some estimations to $|a_2|$, $|a_3|$ and also the Fekete–Szegö inequalities for the functions that belong to these subfamilies.

Definition 2.

Consider $0\le \delta \le 1$, $0\le \lambda \le 1$ and $q\in (0,1)$. The function $f\in \Sigma$ is said to be in ${\mathcal{M}}_{\Sigma }(\delta ,\lambda ;E)$ if it satisfies

$$(1-\delta ){\left(\frac{z}{f\left(z\right)}\right)}^{1-\lambda }{\partial }_{q}f\left(z\right)+\delta \frac{{\partial }_q\left(z{\partial }_{q}f\left(z\right)\right)}{{\partial }_{q}f\left(z\right)}\prec E\left(z\right),$$

(7)

and

$$(1-\delta ){\left(\frac{\omega }{g\left(\omega \right)}\right)}^{1-\lambda }{\partial }_{q}g\left(\omega \right)+\delta \frac{{\partial }_q\left(\omega {\partial }_{q}g\left(\omega \right)\right)}{{\partial }_{q}g\left(\omega \right)}\prec E\left(\omega \right),$$

(8)

where $g=f^{-1}$ is given by (5) and $z,\omega \in U$.

Definition 3.

Consider $0\le \alpha \le 1$, $0\le \beta \le 1$ and $q\in (0,1)$. The function $f\in \mathcal{A}$ is said to be in ${\mathcal{N}}_{\Sigma }(\alpha ,\beta ;E)$ if it satisfies

$$(1-\alpha )\frac{f\left(z\right)}{z}+\alpha {\partial }_{q}f\left(z\right)+\beta z{\partial }_q^{2}f\left(z\right)\prec E\left(z\right),$$

(9)

and

$$(1-\alpha )\frac{g\left(\omega \right)}{\omega }+\alpha {\partial }_{q}g\left(\omega \right)+\beta \omega {\partial }_q^{2}g\left(\omega \right)\prec E\left(\omega \right),$$

(10)

where $g=f^{-1}$ is given by (5) and $z,\omega \in U$.

Lemma 1

([25,26]). Let $\alpha ,\beta \in \mathbb{R}$ and $p_1,p_2\in \mathbb{C}$. If $|p_1|,|p_2|<\zeta$, then

$$\left|(\alpha +\beta )p_1+(\alpha -\beta )p_2\right|\le \left\{\begin{array}{ccc}2\left|\alpha \right|\zeta ,& & \left|\alpha \right|\ge \left|\beta \right|,\\ 2\left|\beta \right|\zeta ,& & \left|\alpha \right|\le \left|\beta \right|.\end{array}\right.$$

Lemma 2

([21]). Suppose that $\chi \left(z\right)$ is analytic in the unit open disc U with $\chi \left(0\right)=0$, $\left|\chi \right(z\left)\right|<1$, and that

$$\chi \left(z\right)={\rho }_{1}z+\sum _{n=2}^{\infty }{\rho }_n{z}^{n}forallz\in U.$$

(11)

Then,

$$|{\rho }_1|\le 1,\mathrm{and}|{\rho }_n|\le 1-|{\rho }_1{|}^2\left(n\in \mathbb{N}\backslash \left\{1\right\}\right).$$

(12)

2. Main Results

Unless otherwise mentioned, we assume in the reminder of this article that $0\le \delta \le 1$, $0\le \lambda \le 1$, $0\le \alpha \le 1$, $0\le \beta \le 1$, $q\in (0,1)$, and also $z,\omega \in U$.

Theorem 1.

Let $f\in {\mathcal{M}}_{\Sigma }(\delta ,\lambda ;E)$, then

$$\begin{array}{ccc}\hfill |a_2|& \le & \frac{1}{\sqrt{\left|K_2+K_4-\frac{2}{3}{K}_1^2\right|+4K_1^2}},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill |a_3|& \le & \frac{|K_2|+|K_4|}{2K_3\left|K_2+K_4\right|},\hfill \end{array}$$

(14)

where

$$\left.\begin{array}{c}{K}_1=(1-\delta )({\left[2\right]}_q+\lambda -1)+\delta {\left[2\right]}_q({\left[2\right]}_q-1),\\ K_2=(1-\delta )(\lambda -1)({\left[2\right]}_q+\frac{\lambda }{2}-1)-\delta {\left[2\right]}_q({\left[2\right]}_q-1),\\ K_3=(1-\delta )({\left[3\right]}_q+\lambda -1)+\delta {\left[3\right]}_q({\left[3\right]}_q-1),\\ K_4=(1-\delta )(\lambda -1)({\left[2\right]}_q+\frac{\lambda }{2}+1)-\delta {\left[2\right]}_q^2({\left[2\right]}_q-1)+2(1-\delta ){\left[3\right]}_q+2\delta {\left[3\right]}_q({\left[3\right]}_q-1).\end{array}\right\}$$

(15)

Proof. 

Let f and g be in ${\mathcal{M}}_{\Sigma }(\delta ,\lambda ;E)$, then, it satisfies the conditions (7) and (8). However, according to subordination principle Definition 1 and Lemma 2, there exist two Schwarz functions $u\left(z\right)$ and $v\left(\omega \right)$ of the form

$$u\left(z\right)=\sum _{n=1}^{\infty }{c}_n{z}^n,\mathrm{and}v\left(\omega \right)=\sum _{n=1}^{\infty }{d}_n{\omega }^n,$$

such that

$$(1-\delta ){\left(\frac{z}{f\left(z\right)}\right)}^{1-\lambda }{\partial }_{q}f\left(z\right)+\delta \frac{{\partial }_q\left(z{\partial }_{q}f\left(z\right)\right)}{{\partial }_{q}f\left(z\right)}=E\left(u\left(z\right)\right),$$

(16)

and

$$(1-\delta ){\left(\frac{\omega }{g\left(\omega \right)}\right)}^{1-\lambda }{\partial }_{q}g\left(\omega \right)+\delta \frac{{\partial }_q\left(\omega {\partial }_{q}g\left(\omega \right)\right)}{{\partial }_{q}g\left(\omega \right)}=E\left(v\left(\omega \right)\right).$$

(17)

After some simple calculations, we deduce

$$\begin{array}{ccc}\hfill E\left(u\right(z\left)\right)& =& \frac{u\left(z\right)e^u\left(z\right)}{e^{u\left(z\right)}-1}\hfill \\ \hfill & =& 1+\frac{u\left(z\right)}{2}+\frac{{\left(u\left(z\right)\right)}^2}{12}-\frac{{\left(u\left(z\right)\right)}^4}{720}+\cdots \hfill \\ & =& 1+\frac{c_1}{2}z+\frac{1}{2}\left(c_2+\frac{c_1^2}{6}\right)z^2+\cdots ,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill E\left(v\right(\omega \left)\right)& =& \frac{v\left(\omega \right)e^v\left(\omega \right)}{e^{v\left(\omega \right)}-1}\hfill \\ \hfill & =& 1+\frac{v\left(\omega \right)}{2}+\frac{{\left(v\left(\omega \right)\right)}^2}{12}-\frac{{\left(v\left(\omega \right)\right)}^4}{720}+\cdots \hfill \\ & =& 1+\frac{d_1}{2}\omega +\frac{1}{2}\left(d_2+\frac{d_1^2}{6}\right){\omega }^2+\cdots .\hfill \end{array}$$

(19)

Moreover,

$$(1-\delta ){\left(\frac{z}{f\left(z\right)}\right)}^{1-\lambda }{\partial }_{q}f\left(z\right)+\delta \frac{{\partial }_q\left(z{\partial }_{q}f\left(z\right)\right)}{{\partial }_{q}f\left(z\right)}=1+K_1{a}_{2}z+\left(K_3{a}_3+K_2{a}_2^2\right)z^2+\cdots$$

(20)

$$(1-\delta ){\left(\frac{\omega }{g\left(\omega \right)}\right)}^{1-\lambda }{\partial }_{q}g\left(\omega \right)+\delta \frac{{\partial }_q\left(\omega {\partial }_{q}g\left(\omega \right)\right)}{{\partial }_{q}g\left(\omega \right)}=1-K_1{a}_2\omega +\left(K_4{a}_2^2-K_3{a}_3\right){\omega }^2+\cdots ,$$

(21)

where $K_j:j=1,2,3,4$ are stated in (15).

By substituting from (20), (21), (18) and (19) into (16) and (17), and by comparing the coefficients on both sides, we obtain

$$K_1{a}_2=\frac{c_1}{2},$$

(22)

$$K_3{a}_3+K_2{a}_2^2=\frac{1}{2}\left(c_2+\frac{c_1^2}{6}\right),$$

(23)

$$-K_1{a}_2=\frac{d_1}{2},$$

(24)

$$-K_3{a}_3+K_4{a}_2^2=\frac{1}{2}\left(d_2+\frac{d_1^2}{6}\right).$$

(25)

As a direct result of Equations (22) and (23), we get

$$c_1=-d_1,$$

(26)

and also,

$$c_1^2+d_1^2=8K_1^2{a}_2^2.$$

(27)

By adding (23) to (25) and then using (27), we obtain

$$\left(K_2+K_4-\frac{2}{3}{K}_1^2\right)a_2^2=\frac{1}{2}\left(c_2+d_2\right).$$

(28)

Equations (26) and (28) together with using Lemma 2 imply that

$$\left|K_2+K_4-\frac{2}{3}{K}_1^2\right||a_2{|}^2\le 1-{\left|c_1\right|}^2.$$

(29)

However, from Equation (22), we can deduce

$$|c_1{|}^2=4K_1^2{\left|a_2\right|}^2.$$

(30)

By using (30) into (29), we obtain

$$|a_2|\le \frac{1}{\sqrt{\left|K_2+K_4-\frac{2}{3}{K}_1^2\right|+4K_1^2}}.$$

(31)

Further, from (23) and (25) and also using (26), we get

$$K_3\left(K_2+K_4\right)a_3=\frac{1}{2}\left(c_2{K}_4-K_2{d}_2+\frac{c_1^2}{6}(K_4-K_2)\right).$$

(32)

Thus, by virtue of Lemma 2, we find

$$K_3\left|K_2+K_4\right|\left|a_3\right|\le \frac{1}{2}\left(|K_2|+|K_4|+|c_1{|}^2\left(\frac{|K_4-K_2|}{6}-|K_2|-|K_4|\right)\right).$$

(33)

On the other hand, from the properties of the modulus, the term $\frac{|K_4-K_2|}{6}-|K_2|-|K_4|\le 0$. Then, we conclude

$$|a_3|\le \frac{|K_2|+|K_4|}{2K_3\left|K_2+K_4\right|}.$$

(34)

Thus, the proof is completed. □

Theorem 2.

Let $f\in {\mathcal{N}}_{\Sigma }(\alpha ,\beta ;E)$, then

$$\begin{array}{ccc}\hfill |a_2|& \le & \frac{1}{\sqrt{2\left|\mathsf{{\rm Y}}(\alpha ,\beta ;q)\right|+4{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2}},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill |a_3|& \le & \left\{\begin{array}{ccc}\frac{1}{2\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)},& & \frac{2{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2}{1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q}\ge 1,\\ & & \\ \frac{\mathsf{{\rm Y}}(\alpha ,\beta ;q)+1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q}{2\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)\left(\mathsf{{\rm Y}}(\alpha ,\beta ;q)+2{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2\right)},& & \frac{2{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2}{1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q}\le 1,\end{array}\right.\hfill \end{array}$$

(36)

where

$$\mathsf{{\rm Y}}(\alpha ,\beta ;q)=1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q-\frac{1}{3}{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2.$$

(37)

Proof. 

Suppose f and g are in ${\mathcal{N}}_{\Sigma }(\alpha ,\beta ;E)$, then they satisfy the conditions (7) and (8). According to subordination principle Definition 1 and Lemma 2, there exist two Schwarz functions $u\left(z\right)\mathrm{and}v\left(\omega \right)$ of the form

$$u\left(z\right)=\sum _{n=1}^{\infty }{c}_n{z}^n,\mathrm{and}v\left(\omega \right)=\sum _{n=1}^{\infty }{d}_n{\omega }^n,$$

such that

$$(1-\alpha )\frac{f\left(z\right)}{z}+\alpha {\partial }_{q}f\left(z\right)+\beta z{\partial }_q^{2}f\left(z\right)=E\left(u\left(z\right)\right),$$

(38)

and

$$(1-\alpha )\frac{g\left(\omega \right)}{\omega }+\alpha {\partial }_{q}g\left(\omega \right)+\beta \omega {\partial }_q^{2}g\left(\omega \right)=E\left(v\left(\omega \right)\right).$$

(39)

With some simple calculations, we get

$$(1-\alpha )\frac{f\left(z\right)}{z}+\alpha {\partial }_{q}f\left(z\right)+\beta z{\partial }_q^{2}f\left(z\right)=1+\sum _{n=2}^{\infty }\left(1+\alpha \left({\left[n\right]}_q-1\right)+\beta {[n-1]}_q{\left[n\right]}_q\right)a_n{z}^n$$

(40)

and

$$(1-\alpha )\frac{g\left(\omega \right)}{\omega }+\alpha {\partial }_{q}g\left(\omega \right)+\beta \omega {\partial }_q^{2}g\left(\omega \right)=1-\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)a_2\omega +\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)a_2{\omega }^2+\cdots .$$

(41)

By substituting from (18), (19), (40) and (41) into (38) and (39) as well as by comparing the coefficients on both sides, we conclude

$$\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)a_2=\frac{c_1}{2},$$

(42)

$$\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)a_3=\frac{1}{2}\left(c_2+\frac{c_1^2}{6}\right),$$

(43)

$$-\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)a_2=\frac{d_1}{2},$$

(44)

and

$$\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)(2a_2^2-a_3)=\frac{1}{2}\left(d_2+\frac{d_1^2}{6}\right).$$

(45)

From (42) and (44), we obtain

$$c_1=-d_1,$$

(46)

and also,

$$c_1^2+d_1^2=8{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2{a}_2^2.$$

(47)

By adding (43) to (45) with using (47), we get

$$2\mathsf{{\rm Y}}(\alpha ,\beta ;q)a_2^2=\frac{1}{2}(c_2+d_2).$$

(48)

In view of Lemma 2, Equation (48) together with (46) imply that

$$2\left|\mathsf{{\rm Y}}(\alpha ,\beta ;q)\right||a_2{|}^2\le 1-{\left|c_1\right|}^2.$$

(49)

On the other hand, from Equation (42), we can write

$$|c_1{|}^2=4{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2{\left|a_2\right|}^2.$$

(50)

By using (50) in (49), we get

$$|a_2|\le \frac{1}{\sqrt{2\left|\mathsf{{\rm Y}}(\alpha ,\beta ;q)\right|+4{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2}},$$

(51)

where $\mathsf{{\rm Y}}(\alpha ,\beta ;q)$ is defined in (37).

Further, by subtracting (45) from (43) and using (46), we have

$$a_3=a_2^2+\frac{c_2-d_2}{4\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)}.$$

(52)

In view of Lemma 2, Equation (52) together with (50) imply that

$$|a_3|\le \left(1-\frac{2{\left(1+\alpha \left({\left[2\right]}_q-1\right)+\beta {\left[2\right]}_q\right)}^2}{1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q}\right){\left|a_2\right|}^2+\frac{1}{2\left(1+\alpha \left({\left[3\right]}_q-1\right)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)}.$$

(53)

By the virtue of (51), we can get the desired result. Thus, we completed the proof. □

Theorem 3.

Suppose $f\in {\mathcal{M}}_{\Sigma }(\delta ,\lambda ;E)$ and $\mu \in \mathbb{R}$, then

$$|a_3-\mu a_2^2|\le \frac{1}{2K_3}\left\{\begin{array}{ccc}\left|\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)\right|,& & \left|\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)\right|\ge 1,\\ 1,& & \left|\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)\right|\le 1,\end{array}\right.$$

(54)

where

$$\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)=\frac{K_4-K_2-2\mu K_3}{K_2+K_4-\frac{2}{3}{K}_1^2},$$

(55)

and $K_1,K_2,K_3$, and $K_4$ are given by (15).

Proof. 

To investigate the desired result, subtract (25) from (23) by using (26), we get

$$a_3=\frac{K_4-k-2}{2K_3}{a}_2^2+\frac{\left(c_2-d_2\right)}{4K_3}.$$

(56)

Thus,

$$a_3-\mu a_2^2=\left(\frac{K_4-K_2-2\mu K_3}{2K_3}\right)a_2^2+\frac{\left(c_2-d_2\right)}{4K_3}.$$

(57)

As a result of subsequent computations performed by using (28), we obtain

$$\left|a_3-\mu a_2^2\right|\le \frac{1}{4K_3}\left|\left(\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)+1\right)c_2+\left(\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)-1\right)d_2\right|,$$

(58)

where $\mathsf{\Phi }(\mu ,\delta ,\lambda ;q)$ is given by (55).

However, in view of Kanas et al. [27] and (12), we can obtain

$$\left|c_2\right|\le 1-|c_1{|}^2\le 1\mathrm{and}\mathrm{also}\left|d_2\right|\le 1-{\left|d_1\right|}^2\le 1.$$

(59)

Now, applying Lemma 1 to (58), we can obtain the desired result directly. Thus, we completed the proof. □

Theorem 4.

Let us consider $f\in {\mathcal{N}}_{\Sigma }(\alpha ,\beta ;E)$ and $\mu \in \mathbb{R}$, then

$$|a_3-\mu a_2^2|\le \left\{\begin{array}{ccc}\left|\frac{1-\mu }{2\mathsf{{\rm Y}}(\alpha ,\beta ;q)}\right|,& & \left|\frac{1-\mu }{\mathsf{{\rm Y}}(\alpha ,\beta ;q)}\right|\ge \frac{1}{1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q},\\ \frac{1}{2\left(1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)},& & \left|\frac{1-\mu }{\mathsf{{\rm Y}}(\alpha ,\beta ;q)}\right|\le \frac{1}{1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q},\end{array}\right.$$

(60)

where $\mathsf{{\rm Y}}(\alpha ,\beta ;q)$ is defined by (37).

Proof. 

In order to investigate the desired result (60), subtract (45) from (43) taking in consideration (46), we conclude

$$a_3-\mu a_2^2=(1-\mu )a_2^2+\frac{c_2-d_2}{4\left(1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)}.$$

(61)

By virtue of (48), we can get that

$$\begin{array}{ccc}\hfill a_3-\mu a_2^2& =& c_2\left(\frac{1-\mu }{4\mathsf{{\rm Y}}(\alpha ,\beta ;q)}+\frac{1}{4\left(1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)}\right)\hfill \\ & & +d_2\left(\frac{1-\mu }{4\mathsf{{\rm Y}}(\alpha ,\beta ;q)}-\frac{1}{4\left(1+\alpha ({\left[3\right]}_q-1)+\beta {\left[2\right]}_q{\left[3\right]}_q\right)}\right).\hfill \end{array}$$

(62)

By applying Lemma 1 to (62) and using (59), we obtain the required result which completes the proof. □