Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation

Abstract

Quantum cryptography is a well-stated field within quantum applications where quantum information is used to set secure communications, authentication, and secret keys. Now used in quantum devices with those purposes, particularly Quantum Key Distribution (QKD), which proposes a secret key between two parties free of effective eavesdropping, at least at a higher level than classical cryptography. The best-known quantum protocol to securely share a secret key is the BB84 one. Other protocols have been proposed as adaptations of it. Most of them are based on the quantum indeterminacy for non-orthogonal quantum states. Their security is commonly based on the large length of the key. In the current work, a BB84-like procedure for QKD based on double quantum teleportation allows the sharing of the key statement using several parties. Thus, the quantum bits of information are assembled among three parties via entanglement, instead of travelling through a unique quantum channel as in the traditional protocol. Asymmetry in the double teleportation plus post-measurement retains the secrecy in the process. Despite requiring more complex control and resources, the procedure dramatically reduces the probability of success for an eavesdropper under individual attacks, because of the ignorance of the processing times in the procedure. Quantum Bit Error Rate remains in the acceptable threshold and it becomes configurable. The article depicts the double quantum teleportation procedure, the associated control to introduce the QKD scheme, the analysis of individual attacks performed by an eavesdropper, and a brief comparison with other protocols.

1. Introduction

With the development of quantum applications, particularly quantum cryptography [1], new cryptosystems intended to be unconditionally secure are being developed. Such cryptosystems are commonly composed of a sender and a receiver assuming to share an Encryption and a Decryption key [2]. Then, a message can be encrypted and transmitted from the sender’s end to the receiver’s end. Along the way, an eavesdropper can try to steal the key intended to be transmitted between them. For instance, experimental implementations are led using imperfect photon detectors, thus allowing the loss of some photons [3] and allowing an intruder to tamper these imperfect devices to obtain advantages against the security of the protocol [4,5]. Due to this feasibility, it is necessary to strengthen the security in all cryptosystems.

With this purpose, new research aiming to obtain better unbreakable ways of key distribution between two parties has been conducted. Such development has boosted technology implementing Quantum Key Distribution (QKD). There, two entities (sender and receiver) can communicate securely to set codification keys. The peculiarity of quantum cryptography is the use of fundamental aspects of quantum mechanics such as the uncertainty principle [6], entanglement [7], and the quantum measurement theory [8] to provide a set of constraints on the communication channel to make it safer [9]. The generation of this quantum key can be distributed through many protocols developed for this purpose [10]. Some existing QKD protocols include BB84 [11], B92 [12], SARG04 [13], and E91 [14].

In this sense, quantum cryptography has become a leading development for the secure transmission of data [15]. After the last-mentioned QKD protocols, quantum cryptography has been refining its methods and complexity to keep off quantum hacking as a counterpart [16]. Thus, post-quantum cryptography pursues cryptography algorithms being secure against cryptanalytic attacks performed by quantum computers [17]. Otherwise, QKD can be made unconditionally secure over arbitrarily long distances against attacks by an eavesdropper [18]. Thus, quantum cryptography is requiring more complex procedures including quantum processing to enhance security.

In another trend, for the development of communications, quantum teleportation has played a central role in communication enhancements. Various approaches seeking experimental implementations of such algorithms soon emerged [19,20]. Since then, the great importance of the development of quantum teleportation has boosted applications in quantum communication to a large extent. Some of them include the creation of quantum networks [21], cryptography applications regarding quantum computing systems [22], settlement of photonic quantum computing [23], and particularly teleportation-based quantum cryptography protocols [24] as complementary scaffolding procedures improving its efficiency and security.

Improvements in the quality of teleportation involve new approaches. Some of them for long-distance quantum teleportation with the use of a fiber-delayed Bell state measurement (BSM) [25] and others using optical fiber to avoid using large-aperture optics and other complex techniques [26,27]. Teleportation is being combined with quantum strategies as a causal order [28] to remove some underlying noisy effects. Recently, an analysis for a double teleportation process for the same input state has been presented in [29,30]. In such a scenario, one main party (Alice) has prepared the input state and then shared two entangled resources with another two parties (here called Bob${}_0$ and Bob${}_1$) keeping one qubit of each pair. A central resource, in principle accessible for the three parties, works as a control to decide who of the Bob’s will receive the teleported state. With such a scheme, cryptography protocols can be performed to set secure authentication methods [30].

This work presents a BB84-like shared protocol exploiting double teleportation to generate controlled correlated information to set a quantum key between two final parties. Despite BB84 being one of the first quantum cryptography protocols, it has remained as a heraldic one. Nowadays, variations of such protocol are still proposed to improve some of its features, thus remaining valid in the contemporary literature. While the traditional BB84 protocol employs a single quantum channel to transmit the key in the form of two-level states first settled on an unknown basis for the receiver, in the current proposal, non-local features of double teleportation combined with asymmetric post-processing allow us to assemble this key during it. It reduces the action time for an eavesdropper by reducing his rate of success while the key has still not been assembled. Some outstanding outcomes in this procedure are:

• A notable rate of success for the coincident basis scenario between the sender and the receiver closer to the ideal case in the original BB84 protocol;
• A dramatic reduction of success for an eavesdropper under individual attacks for the undetected scenario during a reconciliation step;
• A practical reduced time of action for an eavesdropper due to the non-local properties of the key assembling and the absence of a physical quantum channel;
• A configurable setup to adjust some quantitative working features in the procedure as the eavesdropper success ratio or the Quantum Bit Error Rate (QBER).

The structure of the article is as follows. The second section introduces the protocol in the contemporary scenario of quantum cryptography. The third section develops the main lines to perform the double teleportation and the necessary post-processing for the task, together with some remarks about its non-locality features. Then, the control of such asymmetric post-processing to distribute quantum keys between those two parties is presented in the fourth section, setting the scenario for QKD. The fifth section first discusses the contemporary validity of the BB84 protocol in the literature; then, it properly analyses the QKD protocol departing from the previous development, as well as the inclusion of an eavesdropper in the process presented to quantify the vulnerability under individual attacks in terms of its success and detection. The sixth section includes brief discussions about benchmarking for the procedure, possible effects related to decoherence, and fidelity. Conclusions are settled in the last section.

2. Introductory Remarks for Contemporary Post-Quantum Cryptography

Quantum cryptography is the science that pretends to exploit any quantum mechanical feature to perform cryptography tasks, which means methods of encryption naturally using the properties of quantum mechanics to secure and transmit data without hacking. The economy in quantum cryptography has been pursued through the main original developments despite the contemporary technology at the time those works were published. Possibly, QKD is the most important contribution to quantum cryptography by promoting the fusion of classical and quantum approaches, setting a natural incubator in which to develop the field.

The first quantum protocol for QKD was the BB84 one [11] based on quantum conjugate variables. Such protocol states a procedure to state a key in the form of a chain of zeroes and ones without a direct transmission from the sender to the receiver. Instead, the key is codified through a series of quantum resources randomly prepared by the sender on one from two orthogonal agreed bases. Then, they are stochastically found by the receiver through random measurements on such bases. In the end, the bases used are shared by both parts to conserve the identical outcomes when the bases meet. Such a procedure allows us to detect eavesdropping when it intermediately alters the coincident bases and outcomes through a different basis measurement.

Thus, QKD protocols, as that mentioned before, first used quantum correlations to set a quantum key between two parties (another one similar is the B92 [12]). Soon, other protocols appeared exploiting the statistical nature of quantum systems involved, as in the SARG04 [13]. While alternative protocols such as the E91 [14] used entanglement pairs more than just the quantum nature of states in terms of orthogonal basis in a symmetrical treatment of information to construct the key together. Moreover, Quantum Key Agreement (QKA) protocols [31] introduced a shared decision generation for the key.

When quantum computers are introduced to break quantum codes of such developments, the scenario was moved to secure protocols including quantum computer-based attacks. It has raised the post-quantum cryptography terrain to set secure protocols against quantum computer attacks. Despite this, the roadmap is unclear because some of the most current classical symmetric cryptographic protocols are still considered to be relatively secure against quantum computer attacks [32], thus it is believed that classical approaches in theoretical cryptography could be combined with quantum cryptography trends [33].

The current development introduces some elements exploiting quantum processing together with extreme features of quantum information as double teleportation, non-local operations performed via entanglement, and controlled measurements by quantum machines. Some features of the protocol also combine QKA approaches. Thus, they allocate the current proposal in the terrain of post-quantum cryptography (or quantum-safe cryptography) to set a QKD procedure reducing the eavesdropper success.

Other technology concerns should be considered because of the growing complexity of the post-quantum protocols including more complex processing and finer theoretical cryptography considerations. Such aspects are similar to those premises considered in quantum processing: quality and reliability on state generation processes, development of coherent quantum gates to preserve their supposed quantum nature, and faithfully quantum measurement. Those aspects are remarked through the development.

3. Double Teleportation as Superposition and Parallel Post-Processing

Multiple teleportation exploits the quantum linearity to extend the traditional teleportation procedure to perform virtual transference of states and processing. In the end, global states could be recovered for concrete tasks. Quantum states obtained by multiple teleportation exhibit interesting non-local properties [29] and they could be used with cryptography purposes [30]. In this section, we will describe the process only for double teleportation (DT) with additional post-processing (PP). Then, in Section 4, we deal with the control problem (TC) to share and transfer concrete quantum states to be used for QKD purposes (QKD) in Section 5. To ease the reading, we first account in Table 1 for the key symbols (states, operators, and related key quantities) through the entire development.

Table 1. States, Gates, and Parameters involved in the analysis through each step (DT, PP, TC, QKD) of the whole QKD protocol.

Symbol	Process	Description
$|{\psi }_0⟩$	DT	Original qubit state to be teleported
$|{\psi }_C⟩$	DT	Control state to manage the final receiver in double teleportation
$p_i$	DT	Superposition probabilities for each receiver in double teleportation
$|{\beta }_{ij}⟩$	DT	Entangled resources for teleportation in the for of Bell states
$C_U,H_0$	DT	Controlled $C^{a}NO{T}_b$ and Hadamard gates to manage the double teleportation
$|\psi ⟩,|{\psi }^{\prime }⟩$	DT	Initial state and pre-measurement state during the double teleportation process
$|{\psi }_{pm}⟩,|{\psi }_{teleported}⟩$	DT	Post-measurement and corrected states at the end of double teleportation process
${\mathcal{U}}_{i_k}$	PP	Local processing operators on the qubit k in possession of party i
${\omega }_i$	PP	Parametric continuous characterization of each local processing
$C_{\mathcal{U}}$	PP	Controlled operation to apply local processing ${\mathcal{U}}_{i_k}$ on each receiver
$|{\psi }_0^i⟩$	PP	Output state from the each local processing on $|{\psi }^{\prime }⟩$
$|{\psi }_{proc}⟩,|{\psi }_{final}⟩$	PP	Local processing operators on the qubit k in possession of party i
${\beta }_i,{\varphi }_m$	TC	Parameters for the basis measurement of the control state
$P_i$	TC	Success probability for each outcome of the control measurement
$K,m,j$	QKD	Key parameters in the QKD process
P	QKD	Absolute rate of the success eavesdropper without reconciliation
$P_E$	QKD	Relative rate of the success eavesdropper with reconciliation
$P_{QBE{R}_{abs}},P_{QBE{R}_{rel}}$	QKD	Absolute and relative QBER

3.1. Double Teleportation Process as Superposition

Figure 1a synthetically depicts the process followed for double teleportation immersed in the context of QKD. In the current section, we develop the double teleportation process as it was originally presented [29]. As it was stated, one party (Alice) generates secretly an arbitrary state $|{\psi }_0⟩$ (known or unknown) to then potentially transmit it in superposition by teleportation to other two parties (Bob${}_0$ and Bob${}_1$). The presence of an eavesdropper (Eve) acting on Bob${}_1$ is possible, so it is shown in Figure 1a,b, but her action will be considered and depicted at the end. In this case, instead of the traditional algorithm, the process intends to virtually teleport such state to those two simultaneous receivers, Bob${}_0$ and Bob${}_1$ [29].

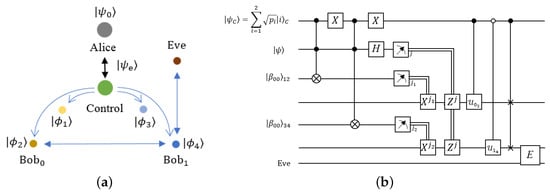
Figure 1. (a) Three main parties performing double controlled teleportation with a central control accessible for all of them; a possible eavesdropper is present; (b) Quantum circuit representing the main elements of the double teleportation process.

The process begins with the main qubit $|{\psi }_0⟩$ to be teleported in possession of Alice, where $|{\psi }_0⟩={\alpha }_0|0⟩+{\alpha }_1|1⟩$. In this work, the Bell states will be written: $|{\beta }_{ij}⟩=\frac{1}{\sqrt{2}}(|0j⟩+{(-1)}^i|1j\oplus 1⟩)$. Then, a pair of Bell entangled resources $|{\beta }_{00}{⟩}_{12},{|{\beta }_{00}⟩}_{34}$ are prepared to be shared with each one of both receivers to implement the teleportation process (subscripts state the numbering of the resources). In the process, a control state is required to rule the quantum transmission on a concrete receiver $|{\psi }_C⟩={\sum }_{i=0}^1\sqrt{p_i}{|i⟩}_C$, with: ${\sum }_{i=0}^1{p}_i=1$. Thus, if control is settled in the state ${|0⟩}_C$ then $|{\psi }_0⟩$ is teleported to Bob${}_0$, otherwise to Bob${}_1$ if the control is ${|1⟩}_C$. Then, the global initial state being considered becomes:

$$|\psi ⟩=|{\psi }_0⟩\otimes |{\psi }_C⟩\otimes |{\beta }_{00}{⟩}_{12}\otimes {|{\beta }_{00}⟩}_{34}$$

(1)

Then, the following controlled gate is applied: $C_U={|0⟩}_C⟨0|\otimes C^{0}NO{T}_1+{|1⟩}_C⟨1|\otimes C^{0}NO{T}_3$, which is clearly unitary [29]. In fact, this gate is basically a pair of Toffoli gates each one followed by another:

$$\begin{array}{ccc}\hfill C_U& =& {\mathrm{Toff}}_{C,0,3}·{\mathbf{X}}_C·{\mathrm{Toff}}_{C,0,1}·{\mathbf{X}}_C\hfill \\ & =& {(|0⟩}_C⟨0|\otimes {\mathbf{1}}_3+{|1⟩}_C⟨1|\otimes C^{0}NO{T}_3)·{(|0⟩}_C⟨0|\otimes C^{0}NO{T}_1+{|1⟩}_C⟨1|\otimes {\mathbf{1}}_1)\hfill \end{array}$$

(2)

Then, remarking that $C^{a}NO{T}_b={|0⟩}_a⟨0|\otimes {\mathbf{1}}_b+{|1⟩}_a⟨1|\otimes {\mathbf{X}}_b$ (there, X is the NOT gate), and considering that ${\mathbf{X}}_a|{\beta }_{00}{⟩}_{ab}={|{\beta }_{01}⟩}_{ab}$, the double teleportation process follows by applying a Hadamard gate on the qubit to be teleported, $|{\psi }^{\prime }⟩=H_0·C_U|\psi ⟩$:

$$\begin{array}{ccc}\hfill |{\psi }^{\prime }⟩& =& \sqrt{p_0}{|0⟩}_C\left[{\alpha }_0{|+⟩}_0|{\beta }_{00}{⟩}_{12}+{\alpha }_1{|-⟩}_0{|{\beta }_{01}⟩}_{12}\right]{|{\beta }_{00}⟩}_{34}\hfill \\ & & +\sqrt{p_1}{|1⟩}_C{|{\beta }_{00}⟩}_{12}\left[{\alpha }_0{|+⟩}_0|{\beta }_{00}{⟩}_{34}+{\alpha }_1{|-⟩}_0{|{\beta }_{01}⟩}_{34}\right]\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& =& \frac{{|0⟩}_0}{2}(\sqrt{p_0}{|0⟩}_C\left({|0⟩}_1{\mathbf{1}}_2+{|1⟩}_1{\mathbf{X}}_2\right)|{\psi }_0{⟩}_2{|{\beta }_{00}⟩}_{34}\hfill \\ & & +\sqrt{p_1}{|1⟩}_C\left({|0⟩}_3{\mathbf{1}}_4+{|1⟩}_3{\mathbf{X}}_4\right)|{\psi }_0{⟩}_4{|{\beta }_{00}⟩}_{12})\hfill \\ & & +\frac{{|1⟩}_0}{2}(\sqrt{p_0}{|0⟩}_C\left({|0⟩}_1{\mathbf{Z}}_2+{|1⟩}_1{\mathbf{X}}_2{\mathbf{Z}}_2\right)|{\psi }_0{⟩}_2{|{\beta }_{00}⟩}_{34}\hfill \\ & & +\sqrt{p_1}{|1⟩}_C\left({|0⟩}_3{\mathbf{Z}}_4+{|1⟩}_3{\mathbf{X}}_4{\mathbf{Z}}_4\right)|{\psi }_0{⟩}_4{|{\beta }_{00}⟩}_{12})\hfill \end{array}$$

(4)

dropping the tensor products for the sake of simplicity, remarking that $H|0⟩=|+⟩$ and $H|1⟩=|-⟩$, and expanding some Bell states to express it in terms of $|{\psi }_0⟩$ [29]. Clearly, those steps state an extension of the traditional teleportation algorithm [34] for qubits. Finally, performing measurements on the original qubit to teleportate, as well as the qubits 1 and 3 (being part of the entangled resources) with respective outcomes $s_0,s_1$ and $s_3$, we get the un-normalized post-measurement state:

$$\begin{array}{c}\hfill |{\psi }_{pm}⟩=\frac{|s_0{⟩}_0|s_1{⟩}_1{|s_3⟩}_3}{2\sqrt{2}}\otimes \left(\sqrt{p_0}{|0⟩}_C|s_3{⟩}_4{\mathbf{X}}_2^{s_1}{\mathbf{Z}}_2^{s_0}|{\psi }_0{⟩}_2+\sqrt{p_1}{|1⟩}_C|s_1{⟩}_2{\mathbf{X}}_4^{s_3}{\mathbf{Z}}_4^{s_0}{|{\psi }_0⟩}_4\right)\end{array}$$

(5)

where if the exponent on an operator is zero, it implies that such operator is omitted. It is easy to notice that each one of the eight possible measurement outcomes occur with probability of $\frac{1}{8}$. Thus, normalizing and finally, as a function of the outcomes, applying the generic correction ${\mathbf{Z}}_2^{s_0}{\mathbf{X}}_2^{s_1}{\mathbf{Z}}_4^{s_0}{\mathbf{X}}_4^{s_3}$ ($\mathbf{X},\mathbf{Y},\mathbf{Z}$ are the Pauli operators), we obtain [29]:

$$\begin{array}{c}\hfill |{\psi }_{teleported}⟩=\sqrt{p_0}{|0⟩}_C|{\psi }_0{⟩}_2{|0⟩}_4+\sqrt{p_1}{|1⟩}_C{|0⟩}_2{|{\psi }_0⟩}_4\end{array}$$

(6)

where we dropped the states for the qubits 1 and 3, as well as the original qubit for the sake of simplicity. This state represents the virtual teleportation to both Bob’s. Figure 1b shows the quantum circuit of the process depicted, based on the traditional teleportation algorithm [34]. Black dots in the controlled operations are traditional controls $C^a{G}_b$, while white dots corresponds to negative controls: ${\mathbf{X}}_a·C^a{G}_b·{\mathbf{X}}_a$. The action of Eve is just indicative, we deal with the eavesdropping intervention below. In the next subsection, we will perform certain post-processing to introduce the necessary tasks to set QKD.

3.2. Post-Processing Following to Double Teleportation

In the last expression, each outcome still can be managed by the control state to perform different processing on each virtual teleported qubit. Applying the operator (see Figure 1b on the right in the form of a pair of controlled gates):

$$\begin{array}{ccc}\hfill C_{\mathcal{U}}& =& {(|0⟩}_C⟨0|\otimes {\mathcal{U}}_{0_2}+{|1⟩}_C⟨1|\otimes {\mathbf{1}}_2)·{(|0⟩}_C⟨0|\otimes {\mathbf{1}}_4+{|1⟩}_C⟨1|\otimes {\mathcal{U}}_{1_4})\hfill \\ & =& {|0⟩}_C⟨0|\otimes {\mathcal{U}}_{0_2}\otimes {\mathbf{1}}_4+{|1⟩}_C⟨1|\otimes {\mathbf{1}}_2\otimes {\mathcal{U}}_{1_4}\hfill \end{array}$$

(7)

Such asymmetric post-processing following to the double teleportation will set the successful secrecy for the QKD procedure. Thus, by defining $|{\psi }_0^{i-1}{⟩}_{2i}={\alpha }_0^i{|0⟩}_{2i}+{\alpha }_1^i{|1⟩}_{2i}$ (with $i=1,2$) as the output of each processing ${\mathcal{U}}_{{(i-1)}_{2i}}$, then we will get:

$$\begin{array}{ccc}\hfill |{\psi }_{proc}⟩=C_{\mathcal{U}}|{\psi }_{teleported}⟩& =& \sqrt{p_0}{|0⟩}_C\otimes {\mathcal{U}}_{0_2}|{\psi }_0{⟩}_2\otimes {|0⟩}_4+\sqrt{p_1}{|1⟩}_C\otimes {|0⟩}_2\otimes {\mathcal{U}}_{1_4}{|{\psi }_0⟩}_4\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& \sqrt{p_0}{|0⟩}_C\otimes |{\psi }_0^0{⟩}_2\otimes {|0⟩}_4+\sqrt{p_1}{|1⟩}_C\otimes {|0⟩}_2\otimes {|{\psi }_0^1⟩}_4\hfill \end{array}$$

(9)

As a useful possibility for further applications, we consider the final transference of the state from Bob${}_0$ to Bob${}_1$ by applying a controlled $SWAP$ to send the processed output state on the qubit 4: ${C_{SWAP}}_{2,4}={|0⟩}_C⟨0|\otimes SWA{P}_{2,4}+{|1⟩}_C⟨1|\otimes {\mathbf{1}}_{\mathbf{2}}\otimes {\mathbf{1}}_{\mathbf{4}}$ (see Figure 1b on the right).

Note operations $C_{\mathcal{U}}$ and ${C_{SWAP}}_{2,4}$ are few practical because qubits $C,2$ are far away from qubit 4. We show them in such last synthetic forms, but they can be equivalently achieved using additional entangled resources between Alice/Bob${}_0$ and Bob${}_1$. The details about the equivalence of such processes are given in the Appendix A and Appendix B. There, related techniques required are delayed measurements [35] and quantum controlled measurements [36,37]. In any case, it gives the following state settled on the qubit 4 in possession of Bob${}_1$:

$$\begin{array}{c}\hfill {|0⟩}_2\otimes |{\psi }_{final}⟩\equiv {C_{SWAP}}_{2,4}|{\psi }_{proc}{⟩=|0⟩}_2\otimes {(\sqrt{p_0}|0⟩}_C\otimes |{\psi }_0^0{⟩}_4+\sqrt{p_1}{|1⟩}_C\otimes |{\psi }_0^1{⟩}_4)\end{array}$$

(10)

disregarding the separable qubit 2. In addition, Alice will decide to measure the control state on an eligible orthogonal basis ${\{|b_0⟩}_C,|b_1{⟩}_C\}$ given by ${|0⟩}_C={\beta }_0|b_0{⟩}_C+e^{i{\varphi }_m}{\beta }_1|b_1{⟩}_C{,|1⟩}_C=e^{-i{\varphi }_m}{\beta }_1|b_0{⟩}_C-{\beta }_0{|b_1⟩}_C$, with ${\varphi }_m,{\beta }_0,{\beta }_1\in \mathbf{R},{\beta }_0^2+{\beta }_1^2=1$. It means, $|{\psi }_{final}⟩$ can be written as:

$$\begin{array}{c}\hfill |{\psi }_{final}⟩=\sqrt{p_0}{({\beta }_0|b_0⟩}_C+e^{i{\varphi }_m}{\beta }_1|b_1{⟩}_C)\otimes |{\psi }_0^0{⟩}_4+\sqrt{p_1}{(e^{-i{\varphi }_m}{\beta }_1|b_0⟩}_C-{\beta }_0|b_1{⟩}_C)\otimes |{\psi }_0^1{⟩}_4\end{array}$$

(11)

to ease the identification of the measurement outcomes in such basis. In the following, we will commonly drop the labels C for the control and 4 for the qubit 4, which now become clear from the development.

3.3. Entanglement and Non-Locality Activation

The double teleportation plus post-processing process depicted at this point has been previously analysed in terms of generation of non-local properties [29]. In fact, after of the measurement of the control state on the basis $\{|b_0⟩,|b_1⟩\}$, a wide type of entangled states could be generated if each Bob introduces additional local resources. Using the concurrence as entanglement measurement, it was shown that they can range from separable states to maximally entangled ones. In addition, the Clauser-Horne-Shimony-Holt (CHSH) inequality has been used to demonstrate the non-locality activation through the involved quantity $S(|\psi ⟩,\theta )\equiv |E(S^A,S^B)+E(S^A,S^{B^{\prime }})+E(S^{A^{\prime }},S^B)-E(S^{A^{\prime }},S^{B^{\prime }})|$ (there, $E(S^1,S^2)$ is the correlation between the measurements $S^1,S^2$). This quantity reaches the Tsirelson’s bound in the process, indicating the non-locality activation. Such analysis dealt with the measurement basis settled by the operators $\{S^A=\mathbf{X},S^{A^{\prime }}=\mathbf{Z}\}$ and $\{S^B=cos\theta \mathbf{X}+sin\theta \mathbf{Z},S^{B^{\prime }}=-sin\theta \mathbf{X}+cos\theta \mathbf{Z}\}$ to get the correlations on a setup testing of the CHSH inequality. It means that the state transference depicted strongly undergoes through a non-local process generating non-locality correlations. Such non-local transference has been also demonstrated between a couple of semiconductor microcavities connected by optical fiber for solid-state physics [38,39] using geometric quantum discord and concurrence as main non-locality quantifiers. Despite the process presented in that article proposing entanglement to generate quantum states at distance, those works set a certain kind of alternative technology to share or generate quantum states in a second party using non-classical light.

3.4. Concrete Post-Processing and Information Transference via Post-Measurement

We will consider the asymmetric post-processing performed by Bob${}_0$ and Bob${}_1$ as:

$${\mathcal{U}}_{i_{2i+2}}=cos{\omega }_i\mathbf{1}+isin{\omega }_i\mathbf{Y},i=0,1$$

(12)

characterized by the parameter ${\omega }_i$. Thus, asymmetry is introduced by the differentiated parameter ${\omega }_i$ in each post-processing, together with the different value for the strength of the teleportation, $p_i$ and the control measurement. By expressing $|{\psi }_0⟩=cos\frac{\theta }{2}|0⟩+e^{i\varphi }sin\frac{\theta }{2}|1⟩$ in its Bloch representation, in such scenario, the probabilities to get the measurement outcome of $|b_0⟩$ or $|b_1⟩$ becomes [30]:

$$\begin{array}{ccc}\hfill P_0& =& {\beta }_0^2{p}_0+{\beta }_1^2{p}_1+2{\beta }_0{\beta }_1\sqrt{p_0{p}_1}cos{\varphi }_m(cos{\mathsf{\Delta }}^{-}\omega -tan{\varphi }_{m}sin{\mathsf{\Delta }}^{-}\omega sin\theta sin\varphi )\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill P_1& =& {\beta }_1^2{p}_0+{\beta }_0^2{p}_1-2{\beta }_0{\beta }_1\sqrt{p_0{p}_1}cos{\varphi }_m(cos{\mathsf{\Delta }}^{-}\omega -tan{\varphi }_{m}sin{\mathsf{\Delta }}^{-}\omega sin\theta sin\varphi )\hfill \end{array}$$

(14)

where ${\mathsf{\Delta }}^{\pm }\omega \equiv {\omega }_0\pm {\omega }_1$. Because $P_0+P_1=1$, for such reason if ${\omega }_0={\omega }_1$, then the probability to get $|{\psi }_0^0⟩=|{\psi }_0^1⟩$ is one in any case. As we will see, we can use the previous process to generate and distribute quantum keys, if Alice works together with Bob${}_0$ as a central computer performing part of the processing, while Bob${}_1$ is an associated user.

4. Transference of Programmed Quantum States Using Double Teleportation

In the current section, we deal with the control problem for the transference to Bob${}_1$ of a programmed state prepared by Alice/Bob${}_0$. The post-processing in (12) is stated to introduce a public and classical authentication fingerprint ${\omega }_1$. Then, we will assume this fingerprint could be known as an extreme case by an eavesdropper to emphasize the quantum features of the procedure. Without such authentication, the remaining state exchange will not work [30]. In addition, as we will note in the procedure to be presented, an advantage is that the state being transferred does not exist until it becomes assembled by the collaboration of the involved parts.

4.1. Generation of Quantum States as a Collaboration among Three Parties

Following the discussion in the last section, by inserting explicitly the action of (12) on $|{\psi }_0⟩$:

$$\begin{array}{c}\hfill |{\psi }_0^j⟩=cos{\omega }_j(cos\frac{\theta }{2}|0⟩+e^{i\varphi }sin\frac{\theta }{2}|1⟩)+sin{\omega }_j(e^{i\varphi }sin\frac{\theta }{2}|0⟩-cos\frac{\theta }{2}|1⟩)\end{array}$$

(15)

with $j=0,1$. We note that if $e^{i\varphi }\in \mathbf{R}$, it means such parameter takes one of the two possible values ${\varphi }_p=0,\pi$ or $e^{i{\varphi }_p}={(-1)}^p,p=0,1$. In such case, the last expression naturally states an orthogonal basis defined by the couple of vectors:

$$\begin{array}{ccc}\hfill {|0⟩}_{\theta ,p}& =& cos\frac{\theta }{2}|0⟩+{(-1)}^{p}sin\frac{\theta }{2}|1⟩\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {|1⟩}_{\theta ,p}& =& {(-1)}^{p}sin\frac{\theta }{2}|0⟩-cos\frac{\theta }{2}|1⟩\hfill \end{array}$$

(17)

they could be selected through the initial election of $|{\psi }_0⟩$ on the Bloch sphere meridian containing the states $|0⟩,|1⟩$ and $|+⟩,|-⟩$. It still leaves sufficient room to choose a quasi arbitrary state. Integrating those expressions in (11), we get:

$$\begin{array}{ccc}\hfill |{\psi }_{final}⟩& =& e^{-i{\varphi }_m}|b_0⟩[(\sqrt{p_0}{\beta }_{0}cos{\omega }_0{e}^{i{\varphi }_m}-\sqrt{p_1}{\beta }_{1}cos{\omega }_1){|0⟩}_{\theta ,p}\hfill \\ & & +(\sqrt{p_0}{\beta }_{0}sin{\omega }_0{e}^{i{\varphi }_m}-\sqrt{p_1}{\beta }_{1}sin{\omega }_1){|1⟩}_{\theta ,p}]\hfill \\ & & +|b_1⟩[(\sqrt{p_0}{\beta }_{1}cos{\omega }_0{e}^{i{\varphi }_m}+\sqrt{p_1}{\beta }_{0}cos{\omega }_1){|0⟩}_{\theta ,p}\hfill \\ & & +(\sqrt{p_0}{\beta }_{1}sin{\omega }_0{e}^{i{\varphi }_m}+\sqrt{p_1}{\beta }_{0}sin{\omega }_1){|1⟩}_{\theta ,p}]\hfill \end{array}$$

(18)

For further applications, we will require certain coefficients of each pair ${|0⟩}_{\theta ,p},{|1⟩}_{\theta ,p}$ in the previous expression become zero. It is only possible if $e^{i{\varphi }_m}\in \mathbf{R}$, meaning that ${\varphi }_m=0,\pi$. Then, $e^{i{\varphi }_m}={(-1)}^m,m=0,1$. In such case, the probabilities (13) and (14) for the measurements on the control state are:

$$\begin{array}{ccc}\hfill P_0& =& {\beta }_0^2{p}_0+{\beta }_1^2{p}_1+2{\beta }_0{\beta }_1\sqrt{p_0{p}_1}{(-1)}^{m}cos{\mathsf{\Delta }}^{-}\omega \hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill P_1& =& {\beta }_1^2{p}_0+{\beta }_0^2{p}_1-2{\beta }_0{\beta }_1\sqrt{p_0{p}_1}{(-1)}^{m}cos{\mathsf{\Delta }}^{-}\omega \hfill \end{array}$$

(20)

4.2. General Notation for the Control of Post-Selection Problem

In the current subsection, we are interested in the post-selection by Alice/Bob${}_1$ of certain states as well as in the control and Bob${}_1$ systems. With that purpose, we develop a general notation to solve the problem. First, by defining:

$$\begin{array}{c}\hfill f_k(\omega )=\left\{\begin{array}{cc}cos\omega ,\hfill & k=0\hfill \\ sin\omega ,\hfill & k=1\hfill \end{array}\right.\end{array}$$

(21)

then, clearly $|{\psi }_0^j⟩={\sum }_{k=0}^1{f}_k({\omega }_j){|k⟩}_{\theta ,p}$. In those terms, $|{\psi }_{final}⟩$ reads:

$$\begin{array}{ccc}\hfill |{\psi }_{final}⟩& =& \sum _{j=0,1}{(-1)}^{mj}|b_j⟩\sum _{k=0,1}{|k⟩}_{\theta ,p}(\sqrt{p_0}{\beta }_{0\oplus j}{f}_k({\omega }_0)-{(-1)}^{j+m}\sqrt{p_1}{\beta }_{1\oplus j}{f}_k({\omega }_1))\hfill \end{array}$$

(22)

If then Alice/Bob${}_0$ pretends to control the post-selection of $|b_j⟩$ and ${|k\oplus 1⟩}_{\theta ,p}$, two conditions should be imposed. The first one is:

$$\begin{array}{c}\hfill \sqrt{p_0}{\beta }_{0\oplus j}{f}_k({\omega }_0)={(-1)}^{j+m}\sqrt{p_1}{\beta }_{1\oplus j}{f}_k({\omega }_1)\end{array}$$

(23)

which post-selects one of ${|k\oplus 1⟩}_{\theta ,p},k=0,1$ for certain j. It could be solved by demanding:

$$\begin{array}{c}\hfill 0<K\equiv \frac{\sqrt{p_1}{\beta }_{1\oplus j}}{\sqrt{p_0}{\beta }_{0\oplus j}},K\in {\mathbf{R}}^{+}\end{array}$$

(24)

Such a condition states a possible asymmetric treatment ($K\ne 1$) to introduce the secrecy of the QKD procedure [29]. Such condition states an asymmetric treatment to introduce the secrecy of the QKD procedure because the transmitted state to Bob${}_1$ remains uncertain. It immediately implies the fulfilling of:

$$\begin{array}{c}\hfill f_k({\omega }_0)={(-1)}^{j+m}K{f}_k({\omega }_1)\end{array}$$

(25)

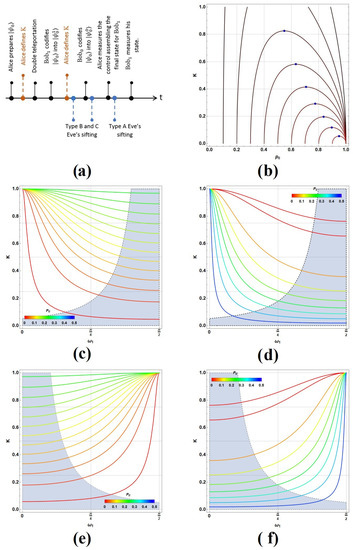
Equation (25) states the way to select ${\omega }_0$ when ${\omega }_1$ is first settled choosing certain value for K stating certain secret asymmetry in the election (together with $j,m$, all those parameters under the control of Alice/Bob${}_0$). Figure 2a,b show such process for $k=0$ and $k=1$ respectively (remembering that the selected state for Bob${}_1$ is $k\oplus 1$). If the restriction ${\omega }_1\in [0,\frac{\pi }{2}]$ is settled (such condition it is not completely necessary but it eases some further expressions), upon the selection of $K>0,j+m=0$, then ${\omega }_0$ could be selected as it is indicated by the green circles in both figures ($K>1$ or $K<1$); otherwise, if $K>0,j+m=1$, ${\omega }_0$ could be selected as in the red circles ($K>1$ or $K<1$). There, we restrict ${\omega }_0\in [0,\pi ]$ for $k=0$ and ${\omega }_0\in [-\frac{\pi }{2},\frac{\pi }{2}]$ for $k=1$. Note in any case that $f_{k\oplus 1}({\omega }_0)>0$ will fulfill. Consequently, the election of K stated by (24) relates $p_0$ with ${\beta }_0$. Those relations are shown in Figure 2c,d for $k=0$ and $k=1$ respectively. Each red curve corresponds to certain K value being selected. While $K>0$, the darkest red curves show the lowest values for $K\approx 0$, and the lightest ones the largest values for $K\to \infty$.

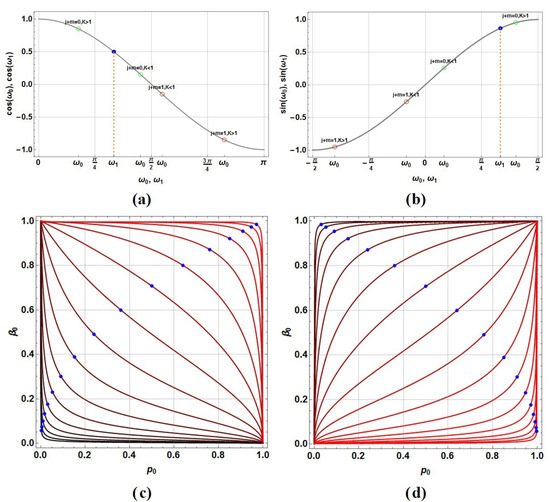
Figure 2. (a,b) Plots exhibiting the process of selection of ${\omega }_0$ departing from the selection of ${\omega }_1$ through the condition (25) for each case $k=0$ (left) or $k=1$ (right). (c,d) Possible values for the combination of $p_0, {\beta }_0$ upon the prior selection of K (each red curve) for each case $k=0$ (left) or $k=1$ (right); blue dots show the values of $p_0=\frac{1}{1+K}$ maximizing $P_j$.

The second condition is obtained by substituting the first condition in the probability of success (13) or (14) for $|b_j⟩$:

$$\begin{array}{ccc}\hfill P_j& =& p_0{\beta }_{0\oplus j}^2+p_1{\beta }_{1\oplus j}^2-2\sqrt{p_0{p}_1}{\beta }_0{\beta }_1{(-1)}^{j+m}cos{\mathsf{\Delta }}_{\omega }^{-}\hfill \\ & =& p_0{\beta }_{0\oplus j}^2(1+K^2-2K{(-1)}^{j+m}cos{\mathsf{\Delta }}_{\omega }^{-})\hfill \end{array}$$

(26)

by choosing a high value for $P_j$ (ideally $P_j=1$). By defining $c_{\omega }^{-}={(-1)}^{j+m}cos{\mathsf{\Delta }}_{\omega }^{-}$, we note that $P_j$ depends from $p_0,{\beta }_0$, and $c_{\omega }^{-}$ in general, as Figure 3 shows. Figure 3a,b show the contours on which $P_j$ become constant in agreement with the color scale on the right (for $j=0,1$ on the left and right respectively). Below, Figure 3c,d show the three dimensional version of Figure 2c,d with their K values shown in black in their top. In addition, each contour was additionally coloured in agreement with their $P_j$ value in each point of the space (from the reddest for $P_j\approx 0$ to the bluest for $P_j\approx 1$, also in agreement with the color bar besides and with the previous plots). In fact, the solutions are first found by selecting K and then intersecting each lower plot with its corresponding upper plot (for the same j value). Despite, $c_{\omega }^{-}$ is not an independent parameter as the last intersection shows.

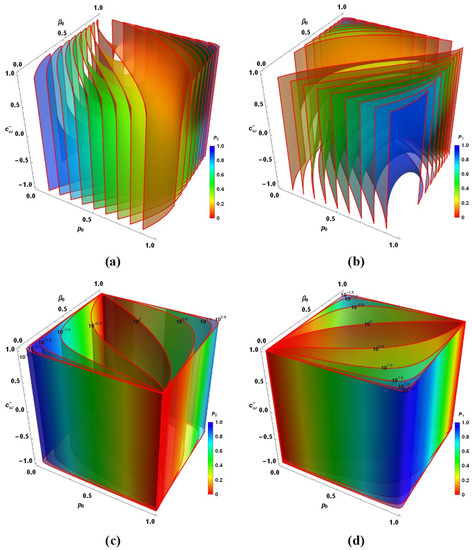
Figure 3. (a,b) Contour plots of $P_j$ for $j=0,1$ respectively as function of $p_0,{\beta }_0$, and $c_{\omega }^{-}$. (c,d) Three-dimensional version of plots in Figure 2c,d, now including $c_{\omega }^{-}$ and coloured from red ($P_j=0$) to blue ($P_j=1$) in agreement with $P_j$ values through them for $j=0,1$ respectively.

4.3. Control Prescriptions for the Quantum State Transference

In fact, we can analyse $c_{\omega }^{-}$ in terms of $k,{\omega }_1$ and K (using the fact $f_{k\oplus 1}({\omega }_0)>0$ with ${\omega }_1\in [0,\frac{\pi }{2}]$):

$$\begin{array}{c}\hfill \frac{c_{\omega }^{-}}{{(-1)}^{j+m}}=cos{\mathsf{\Delta }}_{\omega }^{-}=cos({\omega }_0-{\omega }_1)=f_k^2({\omega }_1){(-1)}^{j+m}K+f_{k\oplus 1}({\omega }_1)\sqrt{1-K^2{f}_k^2({\omega }_1)}\end{array}$$

(27)

Thus, when each upper contour intersects to their lower partner, it generates the affordable solutions. Such solutions are shown in the Figure 4 but in the variables to be selected, ${\omega }_1,K,j,k,m$ (remembering that the selected state for Bob${}_1$ is $k\oplus 1$): (a) $k=0,j+m=0$, (b) $k=0,j+m=1$, (c) $k=1,j+m=0$, and (d) $k=1,j+m=1$ (in fact, $j\oplus m=0,1$, but we will maintain just those simpler expressions in the following). Curves in each plot show some affordable solutions (black region) for each $c_{\omega }^{-}$ value in color from red ($c_{\omega }^{-}=-1$) to blue ($c_{\omega }^{-}=1$). We have plotted the region only in the more convenient interval for ${\omega }_1\in [0,\frac{\pi }{2}]$ being congruent with the previous remark. $K>0$ values are not restricted in their strength, but clearly $K>1$ reduces the possible solutions.

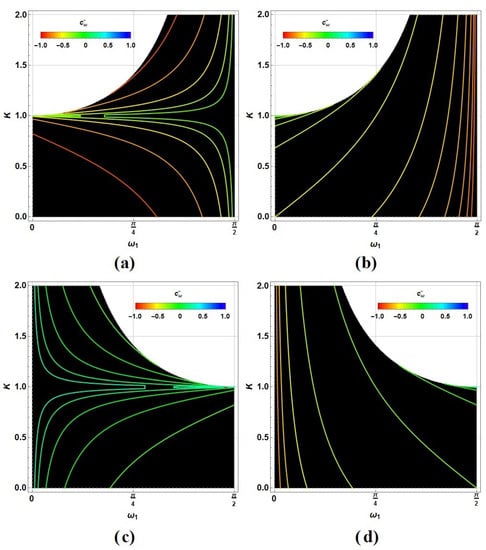
Figure 4. Solutions for $c_{\omega }^{-}$ as function of ${\omega }_1$ and K in color (reddest for $c_{\omega }^{-}\approx -1$ and bluest for $c_{\omega }^{-}\approx 1$) for (a) $k=0, j+m=0$, (b) $k=0, j+m=1$, (c) $k=1, j+m=0$, and (d) $k=1, j+m=1$.

Solving (24) for ${\beta }_{0\oplus j}^2$ and introducing the overall restrictions in (26), we get the following expression for $P_j$:

$$\begin{array}{c}\hfill P_j=\frac{p_0(1-p_0)}{1-p_0(1-K^2)}\left[1+K^2-2K(f_k^2({\omega }_1)K-{(-1)}^{j+m}{f}_{k\oplus 1}({\omega }_1)\sqrt{1-K^2{f}_k^2({\omega }_1)}\right]\end{array}$$

(28)

The coefficient there, $C_0(p_0,K)\equiv \frac{p_0(1-p_0)}{1-p_0(1-K^2)}$, depends only on $p_0$ and K. An easy analysis shows that such coefficient reaches its maximum for $p_{0_{max}}=\frac{1}{1+K}$ becoming $C_{0_{max}}=\frac{1}{{(1+K)}^2}$. Such optimal values are also shown for each K-curve in Figure 2c,d with blue dots. Because it is zero in their edges $p_0=0,1$, then the values of such coefficient are folded in the intervals $p_0\in [0,p_{0_{max}}]$ and $p_0\in [p_{0_{max}},1]$.

Figure 5 depicts $P_j$ for (a) $k=0,j+m=0$, (b) $k=0,j+m=1$, (d) $k=1,j+m=0$, and (e) $k=1,j+m=1$ (remembering that the selected state transmitted to Bob${}_1$ is $k\oplus 1$). They are three-dimensional regions (transparent clear gray regions) under the main maximal surface plotted in dark gray, which corresponds to the two folded points generated vertically by $p_0\in [0,1]$ (shown by the arrows in the Figure 5a,b,d,e). Figure 5c,f show the comparison between the corresponding maximum values in each case, (c) $k=0$ and (f) $k=1$ respectively, remarking the advantage for $j+m=1$ (green) against $j+m=0$ (red), thus it is better to choose m with a different parity of the selected j. In such cases, ${\omega }_1$ could be selected almost openly, to then select those K values reaching $P_j$ at least near from 1, thus controlling better the stochastic selection of $|b_j⟩$. Note in the figures, that the regions have been maintained in ${\omega }_1\in [0,\frac{\pi }{2}]$ as it was initially recommended in the procedure. In addition, we have not extended the interval for K further than $K=1$, because plot regions there become restricted to narrower non-rectangular regions as it was shown in the Figure 4, becoming unpractical because of the restricted combinations of ${\omega }_1$ and K values able to be selected. Still, in the practice, $K>1$ also provides valuable solutions.

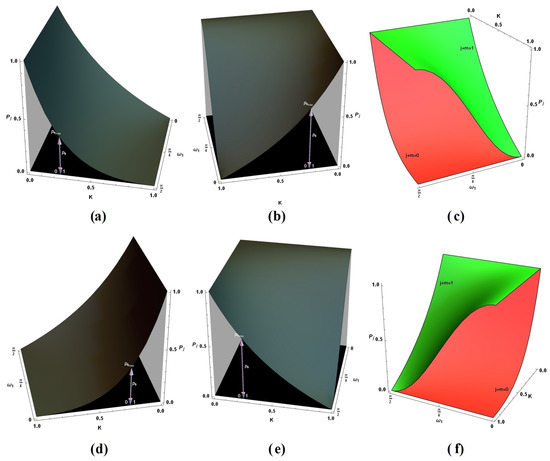
Figure 5. Plots for $P_j$ in (28) as function of ${\omega }_1$ and K for the cases (a) $k=0, j+m=0$, (b) $k=0, j+m=1$, (c) $k=1, j+m=0$, and (d) $k=1, j+m=1$. Comparisons for the cases (e) $k=0$, and (f) $k=1$ exhibiting the advantage for $j+m=1$ to reach higher values for $P_j$.

Another important remark should be stated—Despite the election of $p_{0_{max}}$ is quite recommendable to maximize $P_j$. It implies that Alice should decide to prepare the control state determining K from the beginning. Instead, the election of K independently of $p_0$ opens the opportunity to not fix the form of the states until the application of ${\mathcal{U}}_{0_2}$ when ${\omega }_0$ should be settled (at least around a certain neighborhood of $p_{0_{max}}$ to reach the higher values of $P_j$, still keeping the efficiency of the process).

5. A QKD Protocol Based on a Shared Collaboration among Three Parties

Despite many cryptography developments for QKD having emerged since 1984 after the BB84 protocol, most of them to a large extent are based on it. By proposing modifications or alternative approaches, they have improved the security or efficiency, together to prevent more sophisticated kinds of attack, particularly those possibly coming from a quantum computer. Thus, some of them have received names by their authors, as it occurs in the area. Thus, BB84 based protocols are completely valid nowadays. Among the BB84-like protocols for QKD, we can find the six-state protocol [40] which, rather than using two or four states as in the BB84, uses six states on three bases X, Y and Z, thus causing the eavesdropper to produce a higher rate of error. For the case of the SARG04 protocol [13], it shares the first step of photon transmission with BB84, but then, for the second step, Alice does not directly announce her bases, but a pair of non-orthogonal states instead, one of which is being used to encode her bit. Another protocol, the BBM92 [41] coincides with BB84 in the fact that if Alice possesses the source, then her measurement (which is led on a random basis) would prepare the state to be sent to Bob in one of the four possible states of those used in the BB84, and there is no way of knowing whether Alice first measured part of a Bell state or she prepared a qubit state using a random number generator. In [42], a simplified three-state BB84 protocol was presented. In this case, Alice sends three possible states to Bob, but he performs a simplified measurement with a basis-independent detection efficiency condition, thus limiting an eavesdropper to control the efficiency of detection, depending on Bob’s basis choice. Another approach, based on the BB84, is the protocol presented in [43], where both, sender and receiver, select a random basis for modulation, encode on basis of random bits. Thus, both send the qubits over a quantum channel to each other. Then, both decode on basis of their random bits. Finally, both exchange their random basis and correct the positions of common bits. This process allows both, sender and receiver, to get two keys and a final key can be generated by combining them. Another protocol is presented in [44], which is identical to the BB84 protocol for the entire quantum mechanism, but the difference is that such protocol uses private reconciliation from a random seed and asymmetric cryptography for the classic procedures. In another trend, Quantum Key Agreement (QKA) protocols (those whereby two or more parties agree upon a key over insecure communication channels based on their exchanged messages) which are based on the BB84 protocol [45], but the outcome of the protocol is going to be influenced by both parties. Therefore, no one can determine the shared key alone and the protocol has 50% qubit efficiency after the random sampling discussion and it provides unconditional security.

In our current proposal, several parties meet to generate the quantum key but via teleportation, entanglement, and collaboration, thus reducing the rate of success for an individual eavesdropper. At this point in our development, we have shown the prescriptions to solve the control problem of post-selecting the states in the Alice/Bob${}_0$ and Bob${}_1$ subsystems. In such sense, Alice/Bob${}_0$ pretends, after Bob${}_1$ applies the transformation characterized by an agreed ${\omega }_1$, to control the system configuration in possession of Bob${}_1$ (the control and the Bob${}_1$ subsystem inclusively) to secretly reach one of the states $|b_j⟩$ in the control and to set one of the orthogonal states ${|0⟩}_{\theta ,p},{|1⟩}_{\theta ,p}$ (note that this knowledge keeps unknown for him). In the following subsection, we will exploit this procedure to state the QKD scheme.

5.1. QKD Protocol Description Based on a Shared Generation

In this section, we will describe how to afford a QKD scheme with the previous procedure based on double teleportation. The process is partially based on the BB84 protocol [11], but there, any sensitive information is transmitted through a quantum channel directly. Instead, it is generated by post-measurement. BB84 protocol is based on the transmission of a series of unknown states by the receiver, to then compare the outcomes between two bases independently selected. Still, they should be communicated directly through a quantum channel, nevertheless, it is relatively secure. Other protocols, as the E91 [14], exploit the entangled properties of certain states to transmit no-communicated correlations to set the key. Similarly, as the BB84, the B92 protocol [12] uses the comparison between two non-orthogonal bases to shade part of the information to a possible eavesdropper, while previously agreed correlations allow us to set the key. Nevertheless, BB92 protocol still lets an eavesdropper gain more information [46] as compared with other protocols.

Thus, in this subsection, we use the previous procedure to set an improved BB84-like QKD protocol. First, Alice supported by Bob${}_0$ (which could be assumed to be part of the same system) sets the double teleportation algorithm to virtually transmit a state just known by her. It is previously configured to be generated as one element of two different bases selected at a time by Alice, $B_A$. It is reached by selecting $\theta =0,\frac{\pi }{2}$ and $\varphi =0$ (it implies $p=0$), setting after the basis $H=\{|0⟩,|1⟩\}$ or $D=\{|-⟩,|+⟩\}$. $K,p_0$ should be selected at this point to define the control state (if the strategy is to increase the probability of success $P_j$ in the stochastic step to choose the correct control state $|b_j⟩$, otherwise it could be delayed after the processing of Bob${}_1$).

Thus, through a public key statement dictating which ${\omega }_1$ is applied by Bob${}_1$ in a concrete time (see Figure 6a exhibiting a step pseudo-random function to generate ${\omega }_1$ for instance), Alice can improve the election of the basis and the outcome for the QKD protocol. At the same time, she has settled, in advance, the future state in possession of Bob${}_1$ upon the selection of the parameter ${\omega }_0$ depending on K (then also ${\beta }_0$, related with the further measurement on the control, by using the maximal prescription $p_{0_{max}}$). In fact, in the process, K could be selected randomly but always secretly by a classical procedure.

Figure 6. (a) Timely generation of ${\omega }_1$ agreed between Alice and Bob${}_1$ through a classical public channel, (b) $SWAP$ gates used by Eve to stole and reinsert the state of Bob${}_1$, (c,d) alternating $CNOT$ gates to infer the Bob${}_1$ state by Eve.

Then, through the controlled processing ${\mathcal{U}}_{0_2}$ and ${\mathcal{U}}_{1_4}$ by Bob${}_0$ and Bob${}_1$ respectively, we get the state (18), which is ready to begin the QKD protocol, still without transmitting any sensible information. Finally, all is decided by the control measurement performed by Alice. It is reached by settling an apparatus of measurement in agreement with the ${\beta }_0$ value (which indeed was already decided upon the selection of ${\omega }_1$ and K), and the selection of $j,m$ in agreement with $j+m=1$ to get the maximum $P_j$ (if that is the strategy being followed). Note that $0.5P_j$ represents the efficiency in the generation of a useful key, compared with $0.5$ for the traditional BB84 protocol. Despite possibly lower, additional advantages against eavesdropping are present as it will be discussed below. Thus, when the control measurement stochastically fits with the selection of j, Alice has successfully transferred a qubit in one specific state from the respective set expanding the Hilbert space on the basis selected by Alice. Then, Bob${}_1$ should measure his state by selecting one of the two agreed basis, $B_B\in \{H,D\}$. Thus, if Bob${}_1$ selects the same basis H or D to measure his state (characterized by $\alpha$ instead $\theta$ in (16) or (17)), the outcome is already known previously by Alice, thus sharing secretly a common element of the key. It only happens if the control measurement fits with j and if both bases coincide ($\theta =\alpha$), precisely as the BB84 protocol works.

At this point, still they can infer the key until Alice publishes her basis ($\theta$ or $B_A$) also as Bob${}_1$ ($\alpha$ or $B_B$). Still, Alice also should skip the failed control measurements (they are expected to be a minimum as she is closer to $P_j=1$) but still communicate it to Bob${}_1$ as a failed outcome. Table 2 shows an illustrative sequence of such procedure until the information sharing, thus getting the useful key using QKD based on double teleportation. It skips the technical details dealt with in the previous subsection.

Table 2. Example of a series of shared information bits to set the quantum secret key.

Setup		Selection			Measurement				Sharing		Decision
Alice		Alice			Alice	Bob${}_1$			Alice	Bob${}_1$	Alice/Bob${}_1$
$\theta$	$B_A$	j	m	${|k\oplus 1⟩}_{\theta ,p}$	$|b_j⟩$	$\alpha$	$B_B$	${|k\oplus 1⟩}_{\alpha ,p}$	$B_A$	$B_B$	A/R	key
0	H	0	1	${|0⟩}_{0,0}$	$|b_0⟩$	0	H	${|0⟩}_{0,0}$	H	H	✓	0
$\frac{\pi }{2}$	D	1	0	${|0⟩}_{\frac{\pi }{2},0}$	$|b_0⟩$	$\frac{\pi }{2}$	D	${|0⟩}_{\frac{\pi }{2},0}$	×	D	✗	-
0	H	1	0	${|0⟩}_{0,0}$	$|b_1⟩$	$\frac{\pi }{2}$	D	${|0⟩}_{\frac{\pi }{2},0}$	H	D	✗	-
$\frac{\pi }{2}$	D	1	0	${|1⟩}_{\frac{\pi }{2},0}$	$|b_1⟩$	$\frac{\pi }{2}$	D	${|1⟩}_{\frac{\pi }{2},0}$	D	D	✓	1
$\frac{\pi }{2}$	D	1	0	${|1⟩}_{\frac{\pi }{2},0}$	$|b_0⟩$	0	H	${|0⟩}_{0,0}$	×	H	✗	-
0	H	0	1	${|1⟩}_{0,0}$	$|b_0⟩$	0	H	${|1⟩}_{0,0}$	H	H	✓	1
$\frac{\pi }{2}$	D	0	1	${|0⟩}_{\frac{\pi }{2},0}$	$|b_0⟩$	$\frac{\pi }{2}$	D	${|0⟩}_{0,0}$	D	D	✓	0
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮

The first two columns state the $\theta$ value selected by Alice, thus implying the basis $B_A$ selected, H or D, used to state the final transferred state. Third to fifth columns state the elections of Alice: $j,m$, and the ${|k\otimes 1⟩}_{\theta ,p}$ selected to be delivered to Bob${}_1$. The following four columns state the related information regarding the measurement outcomes: $|b_j⟩$ performed by Alice on the control; $\alpha$ or $B_B$ the measurement basis selection of Bob${}_1$, as well as the corresponding outcome ${|k\oplus 1⟩}_{\alpha ,p}$. The tenth and eleventh columns exhibit information sharing through a public channel. Note that Alice should report the failed events marked there with ×. Two last columns show the understood decisions of usefulness, acceptation, or rejection (A/R), of each event with ✓ (success) or ✗ (fail), as well as the useful bit keys: $0110...$. Note that the key just arises with their non-communicated outcomes when the registers of bases coincide and the Alice measurement on the control succeeds her predictions.

As in the BB84 protocol, the key still should pass an error correction reconciliation by sharing and comparing part of the key to detect transmission errors, otherwise the presence of an eavesdropper through the quantification of the QBER. Another relevant characteristic of this procedure is that Alice can switch the BB84 four-state protocol into a six-state protocol [40,47] adapting the post-processing (12) and selecting $\theta ,\varphi$ conveniently.

5.2. Action and Impact of a Possible Eavesdropper under an Individual Attack

QKD schemes are subject to security attacks. In the analysis of quantum security, several types of attacks are normally considered. There, in the most simple level, individual attacks include quantum interactions with a single quantum channel carrying the information to be read as a single register under measurement (in this case the qubit of Bob${}_1$). Other types of attacks consider collective attacks [48,49], where measurements are not individual, instead, they are allowed to be performed coherently together. Otherwise, coherent attacks [48,50] allow us to apply unitary transformations to the whole set of measurements in addition. While collective and coherent attacks are out of the scope of this work, in this subsection, we analyse a type of individual attack showing a certain advantage on the traditional BB84 protocol.

For the sifting of the Bob${}_1$ state, Eve achieves it using an alternative pair of $SWAP$ gates exchanging the states between Bob${}_1$ and Eve to thus steal and return it. In such a case, an intermediate measurement of the stolen state by Eve is then returned to Bob${}_1$ before his measurement (see Figure 6b). The initial state in possession of Eve could be non-meaningful.

Otherwise, an alternative $C^{a}NO{T}_b$ gate arrangement could be performed upon the election of the measurement basis (see Figure 6c,d). In this case, Eve first bets by the basis on which Alice has prepared the state. If she supposes the basis is H, then she should arrange the procedure presented in Figure 6c, just stating a $C^{a}NO{T}_b$ gate between her qubit in the state ${|0⟩}_E$ and controlled by the Bob${}_1$ state; instead, if she bets for the basis D, she should implement the circuit in Figure 6d using complementary H gates to translate the Bob${}_1$ states to the previous situation, but still returning him his original one. It is immediate to demonstrate that any of those circuits effectively copy the Bob${}_1$ state if Eve hits the correct basis in which Alice has prepared the final state for Bob${}_1$:

$$\begin{array}{ccc}\hfill {|i⟩}_{{\mathrm{Bob}}_1}\in \{|0⟩,|1⟩\}& ⟶& C^{{\mathrm{Bob}}_1}NO{T}_{\mathrm{Eve}}·{|i⟩}_{{\mathrm{Bob}}_1}\otimes {|0⟩}_{\mathrm{Eve}}={|i⟩}_{{\mathrm{Bob}}_1}\otimes {|i⟩}_{\mathrm{Eve}}\hfill \\ \hfill {|i⟩}_{{\mathrm{Bob}}_1}\in \{|+⟩,|-⟩\}& ⟶& H_{\mathrm{Eve}}{H}_{{\mathrm{Bob}}_1}{C}^{{\mathrm{Bob}}_1}NO{T}_{\mathrm{Eve}}{H}_{{\mathrm{Bob}}_1}·{|i⟩}_{{\mathrm{Bob}}_1}\otimes {|0⟩}_{\mathrm{Eve}}={|i⟩}_{{\mathrm{Bob}}_1}\otimes {|i⟩}_{\mathrm{Eve}}\hfill \end{array}$$

(29)

Otherwise, if Eve fails in the basis selection, then her outcomes are non-meaningful so they do not change the overall probabilistic distribution in the BB84 protocol with Eve using the $SWAP$ gate as before, thus giving the same outcomes previously discussed.

As it is well-known for the BB84 protocol, for the individual attacks on the qubits coming from Alice, Eve will have success in the $50\%$ ($\frac{1}{4}/\frac{1}{2}=\frac{1}{2}$ in Table 3) of the useful key where she passes unnoticed. Table 3 classifies the possible cases. There, probability P is absolute concerning the entire cases, so it should be divided by $1/2$ to get the conditional probability for the useful cases. Class 1 in the first row corresponds to the previous situation where the three bases selected meet. In this case, Eve becomes unnoticed and in possession of a valuable key bit. Class 4 corresponds to the cases conducting to the non-useful key because Alice and Bob${}_1$ do not meet in their basis if Eve does or not. Thus, only Classes 1 to 3 correspond with a possible useful key.

Table 3. Classification of basis selection and outcomes considering the presence of an eavesdropper for the traditional BB84 protocol.

Basis Selection and Outcomes Classes	Alice		Eve		Bob${}_1$		P
	Basis	Out	Basis	Out	Basis	Out
1: Basis selections completely meets	$B_A$	$o_{\alpha }$	$B_A$	$o_{\alpha }$	$B_A$	$o_{\alpha }$	$\frac{1}{4}$
2: Eve basis fails but Bob${}_1$ output not	$B_A$	$o_{\alpha }$	$B_{E\ne A}$	$o_{ϵ}$	$B_A$	$o_{\alpha }$	$\frac{1}{8}$
3: Bob${}_1$ basis meets but output fails	$B_A$	$o_{\alpha }$	$B_{E\ne A}$	$o_{ϵ}$	$B_A$	$o_{\beta \ne \alpha }$	$\frac{1}{8}$
4: Bob${}_1$ basis and output fail	$B_A$	$o_{\alpha }$	$B_E$	$o_{ϵ}$	$B_{B\ne A}$	$o_{\beta }$	$\frac{1}{2}$

If Alice and Bob${}_1$ spend some part of the key, they could detect the Eve presence [11] by comparing their outcomes in a reconciliation procedure. Considering just the useful key (or part of it), $25\%$ ($\frac{1}{8}/\frac{1}{2}=\frac{1}{4}$ in Table 3) of it corresponds to the QBER in the protocol (Class 3). QBER is due to the presence of an eavesdropper, or otherwise to the presence of noisy communication in the quantum channel. Finally, Class 2 corresponds to the cases where the presence of Eve is undetectable for Alice and Bob${}_1$. Despite this, Eve has no certainty if their key is correct because her basis does not meet with that of them (assuming she has access to that information published in a public channel). In the following, we will assume that such a class is not successful for Eve.

For the scheme presented here, the situation runs identical if such attack is performed just before Bob${}_1$ measures his state, but after to be assembled by Alice/Bob${}_0$. In any case, this intervention assumes the possibility to steal the system and then be reintegrated ready for the Bob${}_1$ measurement (otherwise gaining complete access to it, still being classically unnoticed, but no quantumly). In any case, it requires non-trivial interventions on the Bob${}_1$ state as it was shown in the circuits in Figure 6b,c. Despite their technical complexity, note those procedures should be performed during the state transmission in the BB84 protocol, but in the current procedure, they should be performed after Alice measures their control state. Despite, if Eve pretends to perform the sifting of the Bob${}_1$ state under the current protocol, then the probability of Class 1 ($P_E$ in the following) and the only successful for Eve, changes dramatically. Then, we perform our analysis around this quantity and upon such assumptions.

Figure 7a exhibits the eavesdropper temporal action through the events in the protocol. Instead of remaining the quantum channel opened all time as in the BB84 original eavesdropping, in our case, Eve needs to sift the Bob${}_1$ state during the entire process consisting of the stages shown in black. There, the action performed by Alice to define K (orange) determines the beginning of the assembling of the transmitted state to Bob${}_1$. Such selection could be made since the beginning when she prepares the control state (particularly if she wants to maximize $C_0(p_0,K)$ by selecting ($p_0=p_{0_{max}}$), or otherwise just before Bob${}_0$ should perform his processing ${\mathcal{U}}_{0_2}$ if milder $P_j$ values are allowed. Thus, Eve can perform several types of individual attacks during such a period. Type A, after Alice’s control measurement, has been already discussed as equivalent to the traditional individual attack in the BB84 protocol. Despite this, such a possibility is not meaningful here because the information is not properly travelling through a quantum channel. Anyway, Bob${}_1$ should avoid this possibility by using this resource rapidly after the assembling. In addition, if Eve has not to control the time assembling of the transmitted state, she can perform her attack just before Alice’s control measurement (type C) or still before the ${\mathcal{U}}_{0_2}$ codification by Bob${}_0$ (type B). Both attacks conduct to the same Eve’s success probability outcome as it is seen in the Appendix C. Note this procedure is not equivalent to the BB84 one, so the success probability changes, despite it still requires the exchange methods depicted in Figure 6.

Figure 7. (a) Eavesdropping temporal action through the protocol; (b) contour lines of $C_0(p_0,K)$ as function of $p_0$ and K with their maximal values as blue dots; and contour lines for the conditional probability for the Eve success, $P_E$, as function of ${\omega }_1$ and K in color for (c) $k=0,\theta =0$; (d) $k=0,\theta =\frac{\pi }{2}$; (e) $k=1,\theta =0$; and (f) $k=1,\theta =\frac{\pi }{2}$. $P_j\ge 0.9$ corresponds to the gray region.

In addition, the difference does not depend on the open selection of $C_0(p_0,K)$ (becoming better choosing $C_{0_{max}}$ to maximize $P_j$) as will be seen. For both cases (Type B and C), $P_E$ is given by (see Appendix C):

$$\begin{array}{ccc}\hfill P_E& =& \frac{P}{P_j}=\frac{C_0(p_0,K)}{P_j}{(f_{k\oplus 1}(\frac{\theta }{2})\sqrt{1-K^2{f}_k^2({\omega }_1)}-K{f}_{k\oplus 1}({\omega }_1))}^2\hfill \end{array}$$

(30)

then, an attempt to maximize $P_j$ (the rate for the successful key) directly should raise the value of P, but not $P_E$. Figure 7b shows such dependence through contour lines. As function of $p_0$, K could be selected almost openly, despite only one value maximizes the value of $C_0(p_0,K)$ with $p_0$ fixed (blue dots in Figure 7b). The color of each point on the curves reflects the $C_0(p_0,K)$ value (darkest for the lowest values and brightest for the highest ones). Blue dots mark the value where the maximum of $C_0(p_0,K)$ is reached for a given $p_0$ or K. Nevertheless, many other values of K could still keep $P_j$ in a higher value to maintain the performance of the key generation, but still to conveniently reduce $P_E$. In Figure 7c–f, the involved regions marked in gray with $P_j\ge 0.9$ (just for the $j+m=1$ cases), remark certain criteria for the random election of K. In any case, the meaningful quantity to evaluate the performance of Eve is the conditional probability $P_E$ which is independent of $C_0(p_0,K)$. It just accounts for the useful key cases when Alice reaches correctly her selection $|b_j⟩$, as similarly the conditional probabilities for the Table 3 were calculated concerning the useful key outcomes. It is plotted as a function of ${\omega }_1$ and K, and coloured in agreement with the color bar inside. Cases correspond to (c) $k=0,\theta =0$; (d) $k=0,\theta =\frac{\pi }{2}$; (e) $k=1,\theta =0$; and (f) $k=1,\theta =\frac{\pi }{2}$ (remembering that the selected state for Bob${}_1$ is $k\oplus 1$). In any case, clearly, the strategy lets a notable lowering for the probabilities for the success of Eve to great extent. The reason is now evident, P has a wide distribution in the region where $P_j$ is high, then it still lets the selection of low values for P. The last behavior is due to the election of basis by Eve before Alice did, thus modifying the global state and lowering the success notably in most cases. In fact, performing a numerical analysis based on a Monte Carlo simulation about the average value of $P_E$ inside the gray region for the random selection of ${\omega }_1$ and K defined by the threshold of $P_j\ge 0.9$, we get: ${\overline{P}}_{E_H}=0.076$ for $\theta =0$ and ${\overline{P}}_{E_D}=0.173$ for $\theta =\frac{\pi }{2}$. It clearly shows a notable advantage against individual attacks of Types B and C. Such outcomes could increase only if Eve has strict control over the knowledge about the period when Alice already has performed her control measurement and only if Bob${}_1$ maintains such resource without use.

5.3. Considerations for Complexity and Number of Resources in the Procedure

Secure communications remain safe against attacks, particularly by those performed by quantum computers. They require effective and strong protocols of QKD. In any case, even when the use of a minimum of resources has been mainly pursued in the original contributions to those protocols, extreme security only requires a sizable, but a finite number of resources and signals.

The BB84 protocol is the earliest QKD protocol [11]. It has inspired a variety of other similar slender protocols as the B92 protocol [12] but reducing the communication efficiency and the practicability. Still, the six-state protocol is a more secure extension of the BB84 protocol, despite raising the upper limit of the QBER. Otherwise, limited to the current single-photon source technology, it is not possible to obtain ideal single photons, instead of using multi-photon sources [13] as in the decoy-state [51], the most widely implemented QKD scheme. Such protocols anyway introduce higher complexity compared to the more theoretical QKD protocols being proposed. As well, single-photon QKD systems commonly include polarization and phase encoding, thus introducing a higher number of resources to the theoretical ideal approaches.

Thus, the BB84 protocol uses the fewest resources to produce each bit of the key, a single ideal qubit properly prepared on a certain basis and two signals, one travelling through a single quantum channel and a classical one to share the basis used by both main parties, after the receiver measures the incoming qubit. Compared with the procedure being presented, the current protocol uses five qubits partially entangled by pairs. This number, as it was seen, increases to nine qubits for feasible implementations: two for performing the $C^C{\mathcal{U}}_{1_4}$ and two more for performing the $C_{SWA{P}_{24}}$ among the faraway qubits $2,4$. In addition, two more classical signals should be added in each case (see Appendix A and Appendix B). A more elaborated infrastructure is expected in terms of quantum gates and entanglement control. Despite this, the asymmetric processing combined with the shared assembling via teleportation allow for a strategy to lower the eavesdropping rate of success to a great extent. In any case, the number of resources grows linearly concerning the key block length.

More complex proposals have been considered in real scenarios to avoid environmental factors lowering the efficiency of quantum cryptography [52]. Other complex deployments currently consider more specialized quantum and optical resources in QKD protocols [53]. Thus, entangled resources and shared multipartite schemes as in the current proposal should be considered to set more secure procedures, particularly in the small block length regime [54]. Complexity is not equivalent to impossibility, until now, first approaches to QKD have arisen in parallel with our technological scope. Nevertheless, while more control is reached on quantum systems, more new audacious proposals are being tried combining full quantum resources to reach more outstanding outcomes.

Considering the outcomes for the success of Eve, ${\overline{P}}_{E_H}=0.073$ for $\theta =0$ (basis H) and ${\overline{P}}_{E_D}=0.164$ for $\theta =\frac{\pi }{2}$ (basis D), we note she has a higher probability to guess outcomes in the last basis. The last outcomes are not the complete picture because still Alice should decide which $\theta$ will use (basis) and also the pair $j,k$ to impose the adequate prescriptions. Thus, the global average success probability for Eve in a key of length $N=n_H+n_D$ (when Alice decides to use $n_H$ times the basis H and $n_D$ times the basis D) is:

$$\begin{array}{ccc}\hfill {\overline{P}}_{E_{Total}}& =& {(\frac{n_H}{N}{\overline{P}}_{E_H}+\frac{n_D}{N}{\overline{P}}_{E_D})}^N={({\overline{P}}_{E_H}+f_D({\overline{P}}_{E_D}-{\overline{P}}_{E_H}))}^N\hfill \end{array}$$

(31)

where $f_D\equiv \frac{n_D}{N}$. Such formula goes into the continuous dominion for large N, but for small N is discrete. Figure 8 shows in color ${\overline{P}}_{E_{Total}}$ in agreement with the color bar inside on the left.

Figure 8. ${\overline{P}}_{E_{Total}}$ values for keys of small block length as function of $f_D$ (Alice’s proportion for choosing D) and their length N. Values are coloured as c in ${\overline{P}}_{E_{Total}}={10}^{-c}$. Red dashed line corresponds to the typical case $f_D=0.5$ when Alice selects randomly the basis.

Note such bar refers to the exponent c for ${\overline{P}}_{E_{Total}}={10}^{-c}$. Then, blue corresponds to lowest ${\overline{P}}_{E_{Total}}$ values and red for the highest ones. A horizontal dashed black line shows the typical case where both cases are equally selected. As it could be expected, the case $f\to 0$ gives the lower advantage for Eve. Despite this, such an election is not the best because Eve could change her strategy by learning from the public sharing of basis. Thus, if as an extreme fact Eve knows Alice always selects the basis H, then the new conditional probability will become one because we add the sure knowledge of the basis by Eve, thus getting a sure outcome. If $f_D=0.5$, it does not add new knowledge, thus the values of ${\overline{P}}_{E_{Total}}$ become as those on the dashed red line in Figure 8. In any case, the probability ${\overline{P}}_{E_{Total}}$ never exceeds $0.013$ for $N\ge 2$. As a reference, we are included the coloured bar at the bottom (using the same color pattern) which refers to the success probability for Eve using the BB84 protocol: $0.5^N$. It shows an outstanding advantage for the current procedure.

6. Some Final Considerations about Benchmarking, Decoherence Effects, and Fidelity

Through the history of QKD developments since the BB84 protocol, many other approaches and different aspects in the key distribution have been tried. Of course, one of the main aspects is the security against eavesdropping, but others aspects sometimes go in different directions, for instance, the economy in the quantum resources or the robustness against quantum computer attacks. In the last case, the reduction of quantum resources in terms of not only efficiency but a feasible operation is important. Clearly, in the procedure being developed here, the economy has not been the focus, instead of the security, particularly based on the distributed tasks to set the key.

6.1. QBER and a Brief Comparison with Other Similar QKD Protocols

Thus, comparison between protocols is usually complicated because there are lots of elements to be performed. Moreover, some developments put more attention on certain variables to highlight the goodness of their approaches. In this subsection, we account for a review of similar BB84-like protocols in terms of some relative indicators for security. Despite the current development, the $P_E$ is the outstanding feature because it measures the effective use of the sifting for Eve (when she gets the correct outcome without detection), the most common comparative reference is the QBER. Thus, we show in the Appendix D, that the conditional QBER (relative to the useful outcomes when the basis of Alice and Bob${}_1$) becomes:

$$\begin{array}{c}\hfill P_{QBE{R}_{rel}}=\frac{C_0(p_0,K)}{P_j}{K}^2\sum _{k^{\prime }=0}^1{\left[f_k({\omega }_1)f_{k^{\prime }}(\frac{{\theta }^{\prime }}{2})-{(-1)}^{k^{\prime }(k+k^{\prime })}{f}_k({\omega }_1+\frac{\mathsf{\Delta }\theta }{2})f_{k\oplus k^{\prime }}(\frac{\mathsf{\Delta }\theta }{2})\right]}^2\end{array}$$

(32)

Again, note the coefficient $C_0(p_0,K)$ is non-meaningful due $P_j$, but instead, $P_{QBE{R}_{rel}}$ is proportional to $K^2$. In addition, note that ${\theta }^{\prime }\ne \theta$, then ${\theta }^{\prime }=\frac{\pi }{2}-\theta ,\mathsf{\Delta }\theta =\frac{\pi }{2}-2\theta$. Figure 9 shows the contour plots for $P_{QBE{R}_{rel}}$ as function of $\omega$ and K corresponding to (a) $k=0,\theta =0$; (b) $k=0,\theta =\frac{\pi }{2}$; (c) $k=1,\theta =0$; and (d) $k=1,\theta =\frac{\pi }{2}$ remarking the region with $P_j>0.9$. Each contour value of $P_{QBE{R}_{rel}}$ was coloured in agreement with the color bar besides.

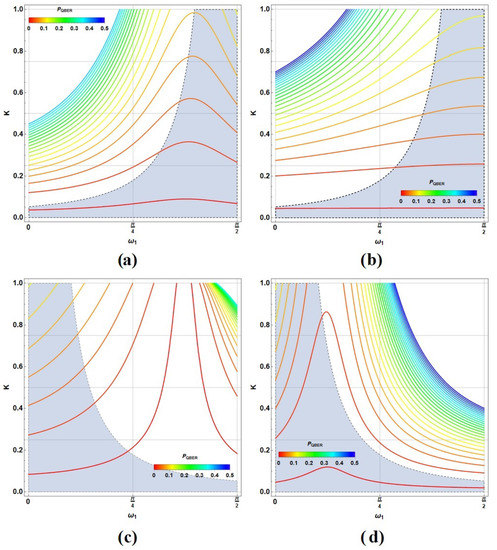
Figure 9. Contour lines for the conditional QBER, $P_{QBE{R}_{rel}}$, as function of ${\omega }_1$ and K in color for (a) $k=0,\theta =0$; (b) $k=0,\theta =\frac{\pi }{2}$; (c) $k=1,\theta =0$; and (d) $k=1,\theta =\frac{\pi }{2}$. $P_j\ge 0.9$ corresponds to the gray region.

Inside the region shown with $P_j\ge 0.9$ and $0\le K\le 1$, the QBER drops in average around (a) $0.03$, (b) $0.04$, (c) $0.03$, and (d) $0.02$ relative to each figure. Despite, alternative elections with larger K and $P_j$ values (as instance $0.8\le K\le 20$ and $P_j>0.95$) raises those values to (a) $0.09$, (b) $0.12$, (c) $0.11$, and (d) $0.07$ respectively, near of the threshold for the QBER in the BB84 protocol [55], and under the security bound of $0.25$ [56]. This fact is interesting because the method is configurable by selecting the region where $P_E$ and $P_{QBE{R}_{rel}}$ are both satisfactory. Thus, if QBER is the main goal (the detection of eavesdropper more than its failure), then, regions with larger K values could be more practical. Still, some considerations should be analysed due to decoherence effects that could increase the QBER [57], thus reaching the security bound. It will be discussed in the next subsection.

As it was stated in Section 5, the trend of BB84-like protocols has continued by proposing new approaches mainly based on this protocol. Thus, the BBM92 protocol [12] reports for individual attacks a theoretical QBER of $\frac{1}{4}$ and a success probability of eavesdropping of $\frac{1}{4}$ as the BB84 one. The SSP98 protocol [40] has reported theoretical QBER values of $\frac{2}{3}$ and success probability of $\frac{1}{3}$. Nevertheless, practical implementations report QBER’s of $0.110$ and $0.126\%$ [58] for BB84 and SSP98 respectively. The SARG04 protocol [13] has reported QBER from $0.968\%$ and $0.271\%$ for single-photon and double photon pulses respectively. In newer protocols based on BB84 as MKP16 protocol [43] the QBER range from $0.56$ until $0.25$ depending on the initial number of qubits generated. Thus, the development of QKD protocols is not uniformly developed going first on the proposal, the QBER or success probability analysis, the attack type to be considered in the analysis. Each one could have different complexity, requiring further developments for its analysis through those several approaches highlighting their goodness. For the current procedure, the QBER is on the range of the BB84 protocols, despite, it exhibits outstanding properties in terms of the reduced Eve success probability, his possible configuration, and the existence of quantum correlations during the quantum key generation.

6.2. Fidelity and Possible Decoherence Effects Due to the Environment

Technical implementations for security protocols involving quantum processing, as the current one, will depend strongly on the physical system where it pretends to be implemented. Quantum decoherence due to the interaction with the environment differently affects setups settled on photonic systems than matter systems. While photonic implementations are recommended whenever quantum information should not be stored. Despite quantum processing is commonly settled on gates models, all of them finally involve or reduce to physical interactions ruled by a Hamiltonian. For matter, the preferred approach to analyse such decoherence are the quantum open systems equations as Linblad or Redfield ones [59]. A simpler but none-less useful approach is the modelling of decoherence through non-Hermitian Hamiltonians [60]. Still, both approaches can become complex if a large number of gates are involved.

Thus, quantum decoherence is the main challenge to reach scalability and reliability. In addition, it is known that decoherence effects (dephasing, amplitude, and depolarizing) increase harmfully the QBER to undesired effects near from the security bound [57]. A precise quantification about the fidelity of such systems is complex because it depends on the type and size of the gate and its architecture; also, on the number and kind of the quantum states involved, particularly those involving entanglement. For these reasons, together with the development of quantum information and its processing, this problem has been tackled through practical considerations for different implementations on matter and for the most typical gates [61]. While for photonic implementations decoherence becomes mild, it is not true for matter systems. Thus, gates as $NOT$, Hadamard, $C^{a}NO{T}_b$, Toffoli, and so forth, all of them involved in the current procedure, have been recently analysed for Nuclear Magnetic Resonance (NMR) using the Lindblad equation to give certain guidelines to quantum circuit designers about the decoherence for the most typical gates, thus reporting their fidelity behavior [62]. Such analysis shows as expected, that the decoherence process and the further loss of fidelity depend on the input state and the type of decoherence. By analyzing amplitude and phase damping as the most representative examples of noise, several aspects arise in the analysis: (a) deeper circuits (circuits with more gates) of course exhibit lower fidelity, (b) multiqubit gates do not necessarily show lower fidelity than single qubit ones, and (c) shorter time-scales to reach each gate still maintain fidelities near to one. For Noisy Intermediate Scale Quantum (NISQ) technologies, global coherence times are in the range of 50–100 $\mathsf{\mu }$s. Dealing with fidelities routinely implemented above $0.99$ for single qubits gates, but also many two qubits gates. While, individual operation times are in the order of nanoseconds, so large circuits can be addressed during the entire coherence times [63]. Thus, circuits containing tens of gates are currently able to be implemented. Table 4 accounts for the gates and their barely type arranged by process (DT for double teleportation and PP for post-processing) and the number of qubits involved. More than half are single qubits gates, showing that the implementation on matter-based technologies is in order.

Table 4. Depth and number of each type of gate involved through the different steps of the whole QKD protocol (DT and PP).

Process & Qubits	1			2			3	Total
	X	Z	Hadamard	${\mathit{C}}^{\mathit{a}}{\mathit{NOT}}_{\mathit{b}}$	${\mathit{SWAP}}_{\mathit{ab}}$	${\mathit{C}}^{\mathit{a}}{\mathcal{U}}_{{\mathit{i}}_{\mathit{j}}}$	Toffoli
DT	4	2	1	0	0	0	2	9
PP	4	1	1	1	1	10	1	19

6.3. Quantum Processing in QKD Developments and Post-Quantum Cryptography

The protocol proposed has implemented quantum processing to a great extent compared with the most traditional procedures. Because quantum cryptography promises unconditional security in data communication because it is currently pretended to be deployed for military and commercial applications, it should be secure. Despite QKD is being widely adopted, it still faces several important challenges regarding the rates for secret key settlement, communication distance and decoherence, deployment sizes, the effective cost in terms of quantum resources, maintenance, and security [64]. As it was stated through the development, quantum coherence is preferable mandatory to reach all the basic features provided by Quantum mechanics.

Quantum computers are believed to solve (at least via problem translation) any exponential problem in principle solvable by a classical computer but not in a finite time. Then, due to classical cryptography protocols are commonly breakable in an exponential time, they are susceptible to failure under such scenarios. Then, with the advent of quantum computers, the necessity to develop secure QKD protocols under their possible attacks is mandatory. Post-quantum cryptography (sometimes also referred as quantum-safe cryptography) deals with cryptographic algorithms thought to be secure against cryptanalytic attacks performed by an ideal quantum computer in terms of coherence, prompt quantum resources, and speed-up [32].

While in conventional symmetric cryptography algorithms, the security in communication is solely related to the secrecy of the encryption key, other QKD protocols currently studied, exploit an asymmetry in their implementation, thus stating the state-of-the-art in their practical implementations [64]. In the post-quantum cryptography terrain, despite currently experimental quantum computers still lacking processing power to break any contemporary cryptographic algorithm, people working in the frontier of theoretical cryptography are preparing impressive protocols to prepare for a time when quantum computers become a real threat. It requires implementing mathematics, physics, and technology to a great extent.

Cryptography systems are commonly grouped in several cryptographic classes [17]. Despite linear, our procedure could be adapted to be asymmetrically non-linear in (24); together, authentication introduced by ${\omega }_i$ parameters could be specialized to introduce a Courtois, Finiasz and Sendrier Signature scheme [65], thus being able to fall in the Multivariate-quadratic-equations and the Code-based schemes. It suggests a fusion between the classical cryptography schemes with trends based on Quantum mechanics features.

7. Conclusions

The BB84 protocol is the most representative protocol in quantum cryptography. The protocol uses a single quantum channel to transfer quantum encoding states. Despite an outstanding security performance, it still allows the possibility to steal the key by interfering with the mentioned quantum channel under individual attacks by an eavesdropper. Since its development, many other BB84-like protocols have been developed, many of them called by specific names despite their clear similitude to the BB84 one. There is not a unique line of development, instead, they commonly attend to some improvements in the protocol such as economy, security, and so forth.

In the present work, a protocol for the settlement of QKD using double teleportation and quantum processing together has been proposed. The procedure generates an entangled multipartite system among three parties plus a control system. The involved entanglement, together with local control, still allows us to manipulate the global quantum state on different parts to those exerting it. The process involved in the double teleportation plus post-processing has been shown to have non-locality activation, thus stating quantum correlations. Thus, an asymmetric post-processing scheme is proposed to generate and assemble a quantum state on a selected basis (defined by the state to teleport) on one of those parts. Then, it is shaped under the proper control, finally setting the QKD protocol.

7.1. Summarizing and Featuring the Protocol

The QKD procedure presented is intended to generate sensitive secret information to transmit it to a second party but is still assembled by post-measurement during the process, instead of like previous QKD protocols, such as the BB84, where any sensible information is transmitted by a quantum channel directly, being affordable for eavesdroppers at all times. Thus, the protocol presented also considers the action of a possible eavesdropper performing an individual attack under time uncertainty. In fact, with the correct prescriptions, Alice can guarantee with the desired success threshold on her post-measurement, a faithful reproduction of the BB84 protocol. Nevertheless, the control complexity is increased, together with implementations of double teleportation and quantum processing, the success for the eavesdropper becomes notably reduced if the attack is performed before the assembling. QBER remains in the typical range and it could be configurable on the election region of the parameters. Thus, while the eavesdropper has in the BB84 protocol a theoretical $50\%$ chance of success on the useful key, in the present protocol, the probability of success drops down to as low as between $7\%$ and $17\%$, thus improving the security.

Due to the processing complexity involved, aspects regarding the decoherence demand attention. There is not a unique procedure to quantify the loss of fidelity for a trend of gates, mainly because it depends on their architecture, specific physical realization and, inclusively, on the input states being considered. Despite this, for technologies other than light (which reaches large decoherence times), such as NISQ ones, currently there is a good fidelity performance of around $0.9$ for the range of tens of gates. Then, despite the reports stating an increase of QBER due to decoherence, it still could be controlled by reducing the operation times of the gates as in the NISQ technologies.

7.2. Future and Additional Research

Additional research of course should be extended to probe the effectiveness extent against collective and coherent eavesdropping attacks for this protocol using asymptotic formulas or numerical analytic approaches [66]. We have limited our analysis to individual attacks, assuming Eve only has access to public communication and the end of quantum edge of Bob${}_1$ before the assembling of the key. However, for collective attacks, where Eve brings each quantum signal and hears all public communication between Alice and Bob [18], more decisive probes are needed.

Together, extensions for the current approach in the six-states protocol direction [40,47] should be tried with more general and complex processing to that established in (12), instead with the full form for two-quibit rotations: ${\mathcal{U}}_k=e^{i{\omega }_k{\overrightarrow{n}}_k·\overrightarrow{\sigma }}$, with $\overrightarrow{\sigma }=(\mathbf{X},\mathbf{Y},\mathbf{Z})$, thus introducing additional parameters for the basis selection. In that trend, deeper elements regarding the classical authentication ${\omega }_k$ and the mathematical relation stated by the parameter K could be oriented to well-stated methods in classical cryptography.

An optimality analysis should be performed to reach adequate prescriptions fixing affordable values for the QBER and the eavesdropper rate of success in terms of the configurable selection of the parameters on the region settled by the Figure 7 and Figure 9.