Eventual Positivity of a Class of Double Star-like Sign Patterns

Abstract

Identifying and classifying the potentially eventually positive sign patterns and the potentially eventually exponentially positive sign patterns of orders greater than 3 have been raised as two open problems since 2010. In this article, we investigate the potential eventual positivity of the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$ whose underlying graph $G\left({\mathfrak{S}}_{(n,m,1)}\right)$ is obtained from the underlying graph $G\left({\mathcal{S}}_{(n,m)}\right)$ of the $(n+m)$-by-$(n+m)$ double star sign patterns ${\mathcal{S}}_{(n,m)}$ by adding an additional vertex adjacent to the two center vertices and removing the edge between the center vertices. We firstly establish some necessary conditions for a double star-like sign pattern to be potentially eventually positive, and then identify all the minimal potentially eventually positive double star-like sign patterns. Secondly, we classify all the potentially eventually positive sign patterns in the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$. Finally, as an application of our results about the potentially eventually positive double star-like sign patterns, we identify all the minimal potentially eventually exponentially positive sign patterns and characterize all the potentially eventually exponentially positive sign patterns in the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$.

1. Introduction

The study of combinatorial and qualitative information, which is only related to the signs of its entries and independent of the magnitudes of its entries of a real matrix, has attracted great attention. A sign pattern is a matrix $\mathcal{A}=\left({\alpha }_{ij}\right)$ whose entries belong to the set $\{+,-,0\}$. A real matrix $A=\left(a_{ij}\right)$ with the sign of $a_{ij}$ being the same as ${\alpha }_{ij}$ for all i and j is called a realization of $\mathcal{A}$. The set of all realizations of sign pattern $\mathcal{A}$ is denoted by $Q\left(\mathcal{A}\right)$, and is called the qualitative class of $\mathcal{A}$; see [1] for example. An n-by-n sign pattern $\mathcal{B}=\left({\beta }_{ij}\right)$ is a subpattern of $\mathcal{A}=\left({\alpha }_{ij}\right)$ if ${\beta }_{ij}={\alpha }_{ij}$ whenever ${\beta }_{ij}\ne 0$. If $\mathcal{B}$ is a subpattern of $\mathcal{A}$ and $\mathcal{B}\ne \mathcal{A}$, then $\mathcal{B}$ is a proper subpattern of $\mathcal{A}$. If $\mathcal{B}$ is a subpattern of $\mathcal{A}$, then $\mathcal{A}$ is said to be a superpattern of $\mathcal{B}$. A sign pattern $\mathcal{A}$ is reducible if there is a permutation matrix $\mathcal{P}$ such that

$${\mathcal{P}}^T\mathcal{A}\mathcal{P}=\left(\begin{array}{cc}{\mathcal{A}}_{11}& 0\\ {\mathcal{A}}_{21}& {\mathcal{A}}_{22}\end{array}\right),$$

where ${\mathcal{A}}_{11}$ and ${\mathcal{A}}_{22}$ are square matrices of order at least one. A sign pattern is irreducible if it is not reducible; see [2,3] for more details.

An n-by-n real matrix A is said to be eventually positive if there exists a positive integer $k_0$, such that $A^k>0$ for all $k\ge k_0$; see [4,5] for example. Eventually positive matrices have been widely applied into the system of linear differential equations $\dot{x}\left(t\right)=Ax\left(t\right)$ ($A\in {\mathbb{R}}^{n\times n}$, $x_0=x\left(0\right)\in {\mathbb{R}}^n$, $t\ge 0$) whose solutions become positive at finite time and remain positive for all time thereafter; see, for example, [6]. An n-by-n sign pattern $\mathcal{A}$ is said to be potentially eventually positive (PEP) if there exists some eventually positive matrices in the qualitative class of $\mathcal{A}$. PEP sign patterns are studied first by Berman et al. [7], in which some sufficient conditions and some necessary conditions for an arbitrary sign pattern to be PEP are established, and all the PEP sign patterns of small orders (≤3) are classified. However, the identification and classification of PEP sign patterns of orders greater than 3 have not been solved since 2010. To classify the PEP sign patterns, [8] introduced the minimal potentially eventually positive sign pattern. Recall that an n-by-n sign pattern $\mathcal{A}$ is said to be a minimal potentially eventually positive sign pattern (MPEP), if $\mathcal{A}$ is PEP and everyproper subpattern of $\mathcal{A}$ is not PEP.

An n-by-n sign pattern $\mathcal{A}$ is said to be potentially eventually exponentially positive (PEEP), if there exists some $A\in Q\left(\mathcal{A}\right)$ such that A is eventually exponentially positive. PEEP sign patterns were studied first in [9], where some sufficient or necessary conditions for PEEP sign patterns were established. However, as stated in [9], there are many open problems about the PEEP sign patterns. For example, identifying and classifying the PEEP sign patterns of orders greater than 3 were posed as open problems. To classify the PEEP sign patterns, the MPEEP sign patterns were introduced naturally in [10]. Recall that an n-by-n sign pattern $\mathcal{A}$ is said to be a minimal potentially eventually exponentially positive sign pattern (MPEEP), if $\mathcal{A}$ is PEEP and every proper subpattern of $\mathcal{A}$ is not PEEP.

In the last few years, there has been an increasing interest in potentially eventual positivity of sign patterns, see [11,12,13,14,15]. Notably, the PEP sign patterns and PEEP sign patterns with some special graph structures have been identified and classified, such as the star sign patterns, the double star sign patterns, the Broom sign patterns, etc. However, there is no literature that studies the potential eventual (exponential) positivity of sign patterns obtained by some graph operations from the known PEP (PEEP) sign patterns.

In this article, we investigate the potential eventual positivity of the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$ whose underlying graph $G\left({\mathfrak{S}}_{(n,m,1)}\right)$ is obtained from the underlying graph $G\left({\mathcal{S}}_{(n,m)}\right)$ of the $(n+m)$-by-$(n+m)$ double star sign patterns ${\mathcal{S}}_{(n,m)}$ by adding an additional vertex adjacent to the two center vertices, and removing the edge between these center vertices. We first establish some necessary conditions for a double star-like sign pattern to be PEP, and then identify all the MPEP sign patterns in the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$, and consequently we classify all the PEP sign patterns in the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$. As an application of our results, we identify all the MPEEP sign patterns and classify all the PEEP sign patterns in the class of double star-like patterns ${\mathfrak{S}}_{(n,m,1)}$.

2. Eventual Positivity of the Double Star-like Sign Patterns ${\mathfrak{S}}_{(\mathbf{n},\mathbf{m},\mathbf{1})}$

We begin this section by introducing some necessary graph theoretical concepts which can be found in [2,4], and the references therein. A square sign pattern $\mathcal{A}=\left({\alpha }_{ij}\right)$ is combinatorially symmetric if ${\alpha }_{ij}\ne 0$ whenever ${\alpha }_{ji}\ne 0$. Let $G\left(\mathcal{A}\right)$ be the graph of order n with vertices $1,2,\dots ,n$ and an edge $\{i,j\}$ joining vertices i and j if and only if $i\ne j$ and ${\alpha }_{ij}\ne 0$. We call $G\left(\mathcal{A}\right)$ the graph of the sign pattern $\mathcal{A}$. A combinatorially symmetric sign pattern matrix $\mathcal{A}$ is called a double star (respectively, star, Broom) sign pattern if $G\left(\mathcal{A}\right)$ is a double star (respectively, star, Broom) graph. A sign pattern $\mathcal{A}=\left({\alpha }_{ij}\right)$ has signed digraph $\mathsf{\Gamma }\left(\mathcal{A}\right)$ with vertex set $\{1,2,\cdots ,n\}$ and a positive (respectively, negative) arc from i to j if and only if ${\alpha }_{ij}$ is positive (respectively, negative). A (directed) simple cycle of length k is a sequence of k arcs $(i_1,i_2),(i_2,i_3),\cdots ,(i_k,i_1)$ such that the vertices $i_1,\cdots ,i_k$ are distinct. Recall that a digraph D is primitive if it is strongly connected and the greatest common divisor of the lengths of its simple cycles is 1. It is well known that a digraph D is primitive if and only if there exists a natural number k such that for all vertices i and j, there is a walk of length k from vertex i to vertex j. A nonnegative sign pattern $\mathcal{A}$ is primitive if its signed digraph $\mathsf{\Gamma }\left(\mathcal{A}\right)$ is primitive; see, e.g., [7] for more details.

For a sign pattern $\mathcal{A}=\left({\alpha }_{ij}\right)$, the positive part of $\mathcal{A}$ is defined to be ${\mathcal{A}}^{+}=\left({\alpha }_{ij}^{+}\right)$, where ${\alpha }_{ij}^{+}=+$ if ${\alpha }_{ij}=+$, and ${\alpha }_{ij}^{+}=0$ otherwise. The negative part of $\mathcal{A}$ (denoted by ${\mathcal{A}}^{-}$) is defined similarly. In [7], it is observed that if the sign pattern ${\mathcal{A}}^{+}$ is primitive, then $\mathcal{A}$ is PEP. Furthermore, it is shown that if an n-by-n sign pattern $\mathcal{A}$ is PEP, then every superpattern of $\mathcal{A}$ is PEP. Following [9], let ${\mathcal{A}}_{D(+)}$ (respectively, ${\mathcal{A}}_{D\left(0\right)}$ and ${\mathcal{A}}_{D(-)}$) be the sign pattern obtained from sign pattern $\mathcal{A}$ by changing all diagonal entries to + (respectively, 0 and −), for the readers’ conveniences. Note that $\widehat{\mathcal{A}}$ is used for ${\mathcal{A}}_{D(+)}$ in [7], where it is shown that $\widehat{\mathcal{A}}$ is PEP, if $\mathcal{A}$ is PEP. For an n-by-n sign pattern to be PEP, the following two results from [7] are very necessary.

Lemma 1

([7]). If an n-by-n sign pattern $\mathcal{A}$ is PEP, then there is an eventually positive matrix $A\in Q\left(\mathcal{A}\right)$ such that

(1) $\rho \left(A\right)=1$, where $\rho \left(A\right)$ is the spectral radius of A.

(2) $A\mathbf{1}=\mathbf{1}$, where $\mathbf{1}$ is the $n\times 1$ all ones vector.

(3) If $n\ge 2$, the sum of all the off-diagonal entries of A is positive.

To proceed, we denote a sign pattern consisting entirely of positive (respectively, negative) entries by $[+]$ (respectively, $[-]$), and let ${[+]}_i$ be a square block sign pattern of order i consisting entirely of positive entries. For block sign patterns, we have the following Lemma 2, which is shown in [7].

Lemma 2

([7]). Let $\mathcal{A}$ be the checkerboard block sign pattern

$$\left(\begin{array}{cccc}[+]& [-]& [+]& \cdots \\ [-]& [+]& [-]& \cdots \\ [+]& [-]& [+]& \cdots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right)$$

with square diagonal blocks. Then

(1) 

−𝒜 is not PEP;

(2) 

if 𝒜 has a negative entry, then 𝒜 is not PEP.

Now we turn to the double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$. As shown in Figure 1, the graph $G\left({\mathfrak{S}}_{(n,m,1)}\right)$ consists of two stars $S_n$ and $S_m$, together with one additional vertex adjacent to the center vertices of $S_n$ and $S_m$.

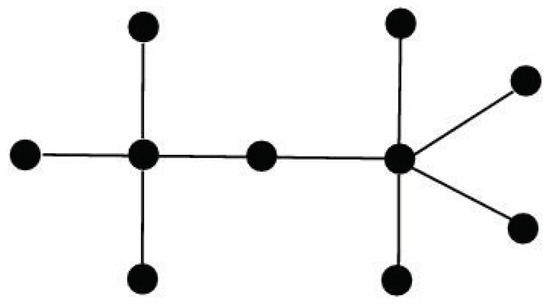
Figure 1. The graph $G\left({\mathfrak{S}}_{(4,5,1)}\right)$ of sign pattern ${\mathfrak{S}}_{(4,5,1)}$.

Note that ${\mathfrak{S}}_{(n,m,1)}$ is a double star sign pattern for $n=1$ or $m=1$, and is a broom sign pattern for $n=2$ or $m=2$. The PEP double star sign patterns have been investigated in [8], and the PEP broom sign patterns have been investigated in [15]. Throughout the paper, we assume that $n\ge 3$ and $m\ge 3$. Clearly, a sign pattern $\mathcal{A}$ is PEP if and only if ${\mathcal{A}}^T$ or ${\mathcal{P}}^T\mathcal{A}\mathcal{P}$ is PEP, for any permutation sign pattern $\mathcal{P}$. Without loss of generality, let the $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ be of the following form

$$\left(\begin{array}{ccccccccc}?& \ast & & & & \ast & & & \\ \ast & ?& \ast & \cdots & \ast & & & & \\ & \ast & ?& & & & & & \\ & ⋮& & \ddots & & & & & \\ & \ast & & & ?& & & & \\ \ast & & & & & ?& \ast & \cdots & \ast \\ & & & & & \ast & ?& & \\ & & & & & ⋮& & \ddots & \\ & & & & & \ast & & & ?\end{array}\right),(\ast )$$

where ? denotes an entry from $\{+,-,0\}$, ∗ denotes a nonzero entry, and the unspecified entries are all zeros.

Now we turn to establish the first necessary condition for the $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ to be PEP.

Theorem 1.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a double star-like sign pattern of order $n+m+1$ of the form $(\ast )$. If ${\mathfrak{S}}_{(n,m,1)}$ is PEP, then ${\mathfrak{S}}_{(n,m,1)}$ is symmetric.

Proof. 

Since ${\mathfrak{S}}_{(n,m,1)}$ is PEP, by Lemma 1 there is an eventually positive matrix $A=\left(a_{i,j}\right)\in Q\left({\mathfrak{S}}_{(n,m,1)}\right)$ such that $\rho \left(A\right)=1$ and $A\mathbf{1}=\mathbf{1}$, where $\mathbf{1}$ is the $n\times 1$ all ones vector. Let $w={(w_1,w_2,\dots ,w_{n+m+1})}^T$ be a positive left eigenvector corresponding to $\rho \left(A\right)$. Then by $w^{T}A=w^T$, which ensures that for all $k=3,4,\dots ,m+1$,

$$w_{n+2}{a}_{n+2,n+k}+w_{n+k}(1-a_{n+k,n+2})=w_{n+k},$$

(1)

$$w_1{a}_{1,n+2}+w_{n+2}(1-a_{n+2,1}-\sum _{k=3}^{m+1}{a}_{n+2,n+k})+\sum _{k=3}^{m+1}{w}_{n+k}{a}_{n+k,n+2}=w_{n+2},$$

(2)

and for $i=3,4,\dots ,n+1$,

$$w_2{a}_{2,i}+w_i(1-a_{i,2})=w_2,$$

(3)

$$w_1{a}_{1,2}+w_2(1-a_{2,1}-\sum _{i=3}^{n+1}{a}_{2,i})+\sum _{i=3}^{n+1}{w}_i{a}_{i,2}=w_2.$$

(4)

By Equality (1), we deduce that

$$w_{n+2}{a}_{n+2,n+k}=w_{n+k}{a}_{n+k,n+2}.$$

(5)

Then $\frac{a_{n+2,n+k}}{a_{n+k,n+2}}=\frac{w_{n+k}}{w_{n+2}}>0$ and

$$\sum _{k=3}^{m+1}{w}_{n+2}{a}_{n+2,n+k}=\sum _{k=3}^{m+1}{w}_{n+k}{a}_{n+k,n+2}.$$

(6)

It follows that ${\alpha }_{n+2,n+k}={\alpha }_{n+k,n+2}$ for all $k=3,4,\dots ,m+1$. By adding Equality (6) to Equality (2), we obtain

$$w_1{a}_{1,n+2}=w_{n+2}{a}_{n+2,1}.$$

(7)

Thus $\frac{a_{1,n+2}}{a_{n+2,1}}=\frac{w_{n+2}}{w_1}>0$. It follows that ${\alpha }_{1,n+2}={\alpha }_{n+2,1}$. By Equality (3), we obtain that,

$$w_2{a}_{2,i}=w_i{a}_{i,2}$$

(8)

which shows that ${\alpha }_{2,i}={\alpha }_{i,2}$ for $i=3,4,\dots ,n+1$, and

$$\sum _{i=3}^{n+1}{w}_2{a}_{2,i}=\sum _{i=3}^{n+1}{w}_i{a}_{i,2}.$$

(9)

By adding Equality (9) to Equality (4), we obtain

$$w_1{a}_{1,2}=w_2{a}_{2,1}.$$

(10)

It follows that ${\alpha }_{2,1}={\alpha }_{1,2}$. Therefore ${\mathfrak{S}}_{(n,m,1)}$ is symmetric. □

Next, we proceed to establish more necessary conditions for an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ to be PEP.

Lemma 3.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a symmetric double star-like sign pattern of order $n+m+1$ of the form $(\ast )$ with ${\alpha }_{1,2}={\alpha }_{2,1}=+$ and ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$. If there is some $i\in \{3,4,\dots ,n+1\}$ with ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ with ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Proof. 

Let s be the number of indices i such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$ and $i\in \{3,4,\dots ,n+1\}$. Let t be the number of indices j such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$ and $j\in \{n+3,n+4,\dots ,n+m+1\}$. To complete the proof, the following three cases need to be considered respectively.

Case 1.$s>0$ and $t=0$.

Up to equivalence,

$${\mathfrak{S}}_{(n,m,1)}=\left(\begin{array}{cccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& {\mathfrak{S}}_{1,3}& \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& & \\ {\left({\mathfrak{S}}_{1,3}\right)}^T& & {\mathfrak{S}}_{3,3}& {\mathfrak{S}}_{3,4}\\ & & {\left({\mathfrak{S}}_{3,4}\right)}^T& {\mathfrak{S}}_{4,4}\end{array}\right),$$

where ${\mathfrak{S}}_{1,1}=\left(\begin{array}{cc}?& +\\ +& ?\end{array}\right)$, ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order s, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(n-s)$, ${\mathfrak{S}}_{4,4}=diag(?,\dots ,?)$ of order $(m-1)$, the 2-by-s matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(n-s)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{cccc}0& \cdots & 0& +\\ +& \cdots & +& 0\end{array}\right)$, and the $(n-s)$-by-$(m-1)$ matrix ${\mathfrak{S}}_{3,4}=\left(\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\\ +& \cdots & +\end{array}\right)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{ccc}{[+]}_2& [-]& [+]\\ [-]& {[+]}_s& [-]\\ [+]& [-]& {[+]}_{n+m-s-1}\end{array}\right)$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 2.$t>0$ and $s=0$.

Similarly, by permutation similarity, let ${\mathfrak{S}}_{(n,m,1)}$ be of the form in Case 1 with ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order t, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(m-t)$, ${\mathfrak{S}}_{4,4}=diag(?,\dots ,?)$ of order $(n-1)$, the 2-by-m matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(m-t)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{cccc}0& \cdots & 0& +\\ +& \cdots & +& 0\end{array}\right)$, and the $(m-t)$-by-$(n-1)$ matrix ${\mathfrak{S}}_{3,4}=\left(\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\\ +& \cdots & +\end{array}\right)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{ccc}{[+]}_2& [-]& [+]\\ [-]& {[+]}_t& [-]\\ [+]& [-]& {[+]}_{n+m-t-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Hence, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 3.$s>0$ and $t>0$.

Up to equivalence,

$${\mathfrak{S}}_{(n,m,1)}=\left(\begin{array}{ccccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& {\mathfrak{S}}_{1,3}& & \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& & & \\ {\left({\mathfrak{S}}_{1,3}\right)}^T& & {\mathfrak{S}}_{3,3}& {\mathfrak{S}}_{3,4}& {\mathfrak{S}}_{3,5}\\ & & {\left({\mathfrak{S}}_{3,4}\right)}^T& {\mathfrak{S}}_{4,4}& \\ & & {\left({\mathfrak{S}}_{3,5}\right)}^T& & {\mathfrak{S}}_{5,5}\end{array}\right),$$

where ${\mathfrak{S}}_{1,1}=\left(\begin{array}{cc}?& +\\ +& ?\end{array}\right)$, ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order s, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(n-s)$, ${\mathfrak{S}}_{4,4}=diag(?,\dots ,?)$ of order t, ${\mathfrak{S}}_{5,5}=diag(?,\dots ,?)$ of order $(m-t-1)$, the 2-by-s matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(n-s)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{cccc}0& \cdots & 0& +\\ +& \cdots & +& 0\end{array}\right)$, the $(n-s)$-by-t matrix ${\mathfrak{S}}_{3,4}=\left(\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, and the $(n-s)$-by-$(m-t-1)$ matrix ${\mathfrak{S}}_{3,5}=\left(\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\\ +& \cdots & +\end{array}\right).$ Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{ccccc}{[+]}_2& [-]& [+]& [-]& [+]\\ [-]& {[+]}_s& [-]& [+]& [-]\\ [+]& [-]& {[+]}_{n-s}& [-]& [+]\\ [-]& [+]& [-]& {[+]}_t& [-]\\ [+]& [-]& [+]& [-]& {[+]}_{m-t-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP. □

Lemma 4.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a symmetric double star-like sign pattern of order $n+m+1$ of the form $(\ast )$ with ${\alpha }_{1,2}={\alpha }_{2,1}=+$ and ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=-$. If there is some $i\in \{3,4,\dots ,n+1\}$ with ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ with ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Proof. 

Let s be the number of indices i such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$ and $i\in \{3,4,\dots ,n+1\}$. Let t be the number of indices j such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$ and $j\in \{n+3,n+4,\dots ,n+m+1\}$. To complete the proof, it suffices to consider the following three cases.

Case 1.$s>0$ and $t=0$.

Up to equivalence, let

$${\mathfrak{S}}_{(n,m,1)}=\left(\begin{array}{ccccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& {\mathfrak{S}}_{1,3}& {\mathfrak{S}}_{1,4}& \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& & & \\ {\left({\mathfrak{S}}_{1,3}\right)}^T& & {\mathfrak{S}}_{3,3}& & \\ {\left({\mathfrak{S}}_{1,4}\right)}^T& & & {\mathfrak{S}}_{4,4}& {\mathfrak{S}}_{4,5}\\ & & & {\left({\mathfrak{S}}_{4,5}\right)}^T& {\mathfrak{S}}_{5,5}\end{array}\right),$$

where ${\mathfrak{S}}_{1,1}=\left(\begin{array}{cc}?& +\\ +& ?\end{array}\right)$, ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order s, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(n-s-1)$, ${\mathfrak{S}}_{4,4}=diag(?)$, ${\mathfrak{S}}_{5,5}=diag(?,\dots ,?)$ of order $(m-1)$, the 2-by-s matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(n-s-1)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{ccc}0& \cdots & 0\\ +& \cdots & +\end{array}\right)$, the 2-by-1 matrix ${\mathfrak{S}}_{1,4}={(-,0)}^T$, and the 1-by-$(m-1)$ matrix ${\mathfrak{S}}_{4,5}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccc}{[+]}_2& [-]& [+]& [-]\\ [-]& {[+]}_s& [-]& [+]\\ [+]& [-]& {[+]}_{n-s-1}& [-]\\ [-]& [+]& [-]& {[+]}_m\end{array}\right)$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 2.$t>0$ and $s=0$.

By permutation similarity, let ${\mathfrak{S}}_{(n,m,1)}$ be of the form in Case 1 with a minor modification: ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order t, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(m-t-1)$, ${\mathfrak{S}}_{5,5}=diag(?,\dots ,?)$ of order $(n-1)$, the 2-by-t matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(m-t-1)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{ccc}0& \cdots & 0\\ +& \cdots & +\end{array}\right)$, and the 1-by-$(n-1)$ matrix ${\mathfrak{S}}_{4,5}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccc}{[+]}_2& [-]& [+]& [-]\\ [-]& {[+]}_t& [-]& [+]\\ [+]& [-]& {[+]}_{m-t-1}& [-]\\ [-]& [+]& [-]& {[+]}_n\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 3.$s>0$ and $t>0$.

Up to equivalence,

$${\mathfrak{S}}_{(n,m,1)}=\left(\begin{array}{cccccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& {\mathfrak{S}}_{1,3}& {\mathfrak{S}}_{1,4}& & \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& & & & \\ {\left({\mathfrak{S}}_{1,3}\right)}^T& & {\mathfrak{S}}_{3,3}& & & \\ {\left({\mathfrak{S}}_{1,4}\right)}^T& & & {\mathfrak{S}}_{4,4}& {\mathfrak{S}}_{4,5}& {\mathfrak{S}}_{4,6}\\ & & & {\left({\mathfrak{S}}_{4,5}\right)}^T& {\mathfrak{S}}_{5,5}& \\ & & & {\left({\mathfrak{S}}_{4,6}\right)}^T& & {\mathfrak{S}}_{6,6}\end{array}\right),$$

where ${\mathfrak{S}}_{1,1}=\left(\begin{array}{cc}?& +\\ +& ?\end{array}\right)$, ${\mathfrak{S}}_{2,2}=diag(?,\dots ,?)$ of order s, ${\mathfrak{S}}_{3,3}=diag(?,\dots ,?)$ of order $(n-s-1)$, ${\mathfrak{S}}_{4,4}=diag(?)$, ${\mathfrak{S}}_{5,5}=diag(?,\dots ,?)$ of order t, ${\mathfrak{S}}_{6,6}=diag(?,\dots ,?)$ of order $(m-t-1)$, the 2-by-s matrix ${\mathfrak{S}}_{1,2}=\left(\begin{array}{ccc}0& \cdots & 0\\ -& \cdots & -\end{array}\right)$, the 2-by-$(n-s-1)$ matrix ${\mathfrak{S}}_{1,3}=\left(\begin{array}{ccc}0& \cdots & 0\\ +& \cdots & +\end{array}\right)$, the 2-by-1 matrix ${\mathfrak{S}}_{1,4}={(-,0)}^T$, the 1-by-t matrix ${\mathfrak{S}}_{4,5}=(-,\cdots ,-)$, and the 1-by-$(m-t-1)$ matrix ${\mathfrak{S}}_{4,6}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccccc}{[+]}_2& [-]& [+]& [-]& [+]& [-]\\ [-]& {[+]}_s& [-]& [+]& [-]& [+]\\ [+]& [-]& {[+]}_{n-s-1}& [-]& [+]& [-]\\ [-]& [+]& [-]& {[+]}_1& [-]& [+]\\ [+]& [-]& [+]& [-]& {[+]}_t& [-]\\ [-]& [+]& [-]& [+]& [-]& {[+]}_{m-t-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP. □

Lemma 5.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a symmetric double star-like sign pattern of order $n+m+1$ of the form $(\ast )$ with ${\alpha }_{1,2}={\alpha }_{2,1}=-$ and ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$. If there is some $i\in \{3,4,\dots ,n+1\}$ with ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ with ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Proof. 

By permutation similarity, the proof is similar to that of Lemma 4. □

Lemma 6.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a symmetric double star-like sign pattern of order $n+m+1$ of the form $(\ast )$ with ${\alpha }_{1,2}={\alpha }_{2,1}=-$ and ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=-$. If there is some $i\in \{3,4,\dots ,n+1\}$ such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Proof. 

Let s be the number of indices i such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$ and $i\in \{3,4,\dots ,n+1\}$. Let t be the number of indices j such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$ and $j\in \{n+3,n+4,\dots ,n+m+1\}$. To complete the proof, the following three cases need to be considered respectively.

Case 1.$s>0$ and $t=0$.

Up to equivalence, assume

$${\mathfrak{S}}_{(n,m,1)}=\left(\begin{array}{ccccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& 0& {\mathfrak{S}}_{1,4}& \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& {\mathfrak{S}}_{2,3}& {\mathfrak{S}}_{2,4}& \\ 0& {\left({\mathfrak{S}}_{2,3}\right)}^T& {\mathfrak{S}}_{3,3}& & \\ {\left({\mathfrak{S}}_{1,4}\right)}^T& {\left({\mathfrak{S}}_{2,4}\right)}^T& & {\mathfrak{S}}_{4,4}& {\mathfrak{S}}_{4,5}\\ & & & {\left({\mathfrak{S}}_{4,5}\right)}^T& {\mathfrak{S}}_{5,5}\end{array},\right)$$

where ${\mathfrak{S}}_{1,1}={\mathfrak{S}}_{2,2}=(?)$, ${\mathfrak{S}}_{3,3}=diag(?,\cdots ,?)$ of order s, ${\mathfrak{S}}_{4,4}=diag(?,\cdots ,?)$ of order $(n-s)$, ${\mathfrak{S}}_{5,5}=diag(?,\cdots ,?)$ of order $(m-1)$, ${\mathfrak{S}}_{1,2}=(-)$, the 1-by-$(n-s)$ matrix ${\mathfrak{S}}_{1,4}=(0,\cdots ,0,-)$, the 1-by-s matrix ${\mathfrak{S}}_{2,3}=(-,\cdots ,-)$, the 1-by-$(n-s+1)$ matrix ${\mathfrak{S}}_{2,4}=(+,\cdots ,+,0)$, and the 1-by-$(t-1)$ matrix ${\mathfrak{S}}_{4,5}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccc}{[+]}_1& [-]& [+]& [-]\\ [-]& {[+]}_1& [-]& [+]\\ [+]& [-]& {[+]}_s& [-]\\ [-]& [+]& [-]& {[+]}_{n+m-s-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 2.$t>0$ and $s=0$.

Up to equivalence, by permutation similarity, let ${\mathfrak{S}}_{(n,m,1)}$ be of the form in Case 1, where ${\mathfrak{S}}_{1,1}={\mathfrak{S}}_{2,2}=(?)$, ${\mathfrak{S}}_{3,3}=diag(?,\cdots ,?)$ of order t, ${\mathfrak{S}}_{4,4}=diag(?,\cdots ,?)$ of order $(m-t)$, ${\mathfrak{S}}_{5,5}=diag(?,\cdots ,?)$ of order $(n-1)$, ${\mathfrak{S}}_{1,2}=(-)$, the 1-by-$(m-t)$ matrix ${\mathfrak{S}}_{1,4}=(0,\cdots ,0,-)$, the 1-by-t matrix ${\mathfrak{S}}_{2,3}=(-,\cdots ,-)$, the 1-by-$(m-t)$ matrix ${\mathfrak{S}}_{2,4}=(+,\cdots ,+,0)$, and the 1-by-$(n-1)$ matrix ${\mathfrak{S}}_{4,5}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccc}{[+]}_1& [-]& [+]& [-]\\ [-]& {[+]}_1& [-]& [+]\\ [+]& [-]& {[+]}_t& [-]\\ [-]& [+]& [-]& {[+]}_{n+m-t-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP.

Case 3.$s>0$ and $t>0$.

Up to equivalence,

$${\mathfrak{S}}_{n,m,1}=\left(\begin{array}{cccccc}{\mathfrak{S}}_{1,1}& {\mathfrak{S}}_{1,2}& 0& {\mathfrak{S}}_{1,4}& & \\ {\left({\mathfrak{S}}_{1,2}\right)}^T& {\mathfrak{S}}_{2,2}& {\mathfrak{S}}_{2,3}& {\mathfrak{S}}_{2,4}& & \\ 0& {\left({\mathfrak{S}}_{2,3}\right)}^T& {\mathfrak{S}}_{3,3}& & & \\ {\left({\mathfrak{S}}_{1,4}\right)}^T& {\left({\mathfrak{S}}_{2,4}\right)}^T& & {\mathfrak{S}}_{4,4}& {\mathfrak{S}}_{4,5}& {\mathfrak{S}}_{4,6}\\ & & & {\left({\mathfrak{S}}_{4,5}\right)}^T& {\mathfrak{S}}_{5,5}& \\ & & & {\left({\mathfrak{S}}_{4,6}\right)}^T& & {\mathfrak{S}}_{6,6}\end{array},\right)$$

where ${\mathfrak{S}}_{1,1}={\mathfrak{S}}_{2,2}=(?)$, ${\mathfrak{S}}_{3,3}=diag(?,\cdots ,?)$ of order s, ${\mathfrak{S}}_{4,4}=diag(?,\cdots ,?)$ of order $(n-s)$, ${\mathfrak{S}}_{5,5}=diag(?,\cdots ,?)$ of order t, ${\mathfrak{S}}_{6,6}=diag(?,\cdots ,?)$ of order $(m-t-1)$, ${\mathfrak{S}}_{1,2}=(-)$, the 1-by-$(n-s)$ matrix ${\mathfrak{S}}_{1,4}=(0,\cdots ,0,-)$, the 1-by-s matrix ${\mathfrak{S}}_{2,3}=(-,\cdots ,-)$, the 1-by-$(n-s)$ matrix ${\mathfrak{S}}_{2,4}=(+,\cdots ,+,0)$, the 1-by-t matrix ${\mathfrak{S}}_{4,5}=(-,\cdots ,-)$, and the 1-by-$(m-t-1)$ matrix ${\mathfrak{S}}_{4,6}=(+,\cdots ,+)$. Let $\widetilde{{\mathfrak{S}}_{D(+)}}$ be a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ of the form

$$\left(\begin{array}{cccccc}{[+]}_1& [-]& [+]& [-]& [+]& [-]\\ [-]& {[+]}_1& [-]& [+]& [-]& [+]\\ [+]& [-]& {[+]}_s& [-]& [+]& [-]\\ [-]& [+]& [-]& {[+]}_{n-s}& [-]& [+]\\ [+]& [-]& [+]& [-]& {[+]}_t& [-]& \\ [-]& [+]& [-]& [+]& [-]& {[+]}_{m-t-1}\end{array}\right).$$

By Lemma 2, $\widetilde{{\mathfrak{S}}_{D(+)}}$ is not PEP. Thus, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is not PEP. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is not PEP. □

Proposition 1.

The double star-like sign pattern

$${\mathcal{S}}_1=\left(\begin{array}{ccccccccc}?& +& & & & -& & & \\ +& ?& +& \cdots & +& & & & \\ & +& ?& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & ?& & & & \\ -& & & & & ?& +& \cdots & +\\ & & & & & +& ?& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & ?\end{array}\right),$$

is not PEP.

Proof. 

Assume that ${\mathcal{S}}_1$ is PEP. Then ${\left({\mathcal{S}}_1\right)}_{D(+)}$ and all its superpattern are also PEP. Let

$$\widetilde{{\mathcal{S}}_1}=\left(\begin{array}{cc}{[+]}_{n+1}& [-]\\ [-]& {[+]}_m\end{array}\right).$$

Then $\widetilde{{\mathcal{S}}_1}$ is a superpattern of ${\left({\mathcal{S}}_1\right)}_{D(+)}$ and is PEP. However, $\widetilde{{\mathcal{S}}_1}$ is a checkerboard block sign pattern and is not PEP by Lemma 2; a contradiction. □

Proposition 2.

The double star-like sign pattern

$${\mathcal{S}}_2=\left(\begin{array}{ccccccccc}?& -& & & & -& & & \\ -& ?& +& \cdots & +& & & & \\ & +& ?& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & ?& & & & \\ -& & & & & ?& +& \cdots & +\\ & & & & & +& ?& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & ?\end{array}\right),$$

is not PEP.

Proof. 

Assume that ${\mathcal{S}}_2$ is PEP. Then ${\left({\mathcal{S}}_2\right)}_{D(+)}$ and all its superpattern are also PEP. Let

$$\widetilde{{\mathcal{S}}_2}=\left(\begin{array}{cc}{[+]}_1& [-]\\ [-]& {[+]}_{n+m}\end{array}\right).$$

Then $\widetilde{{\mathcal{S}}_2}$ is a superpattern of ${\left({\mathcal{S}}_2\right)}_{D(+)}$ and is PEP. However, $\widetilde{{\mathcal{S}}_2}$ is a checkerboard block sign pattern and is not PEP by Lemma 2; a contradiction. □

Proposition 3.

The double star-like sign pattern

$${\mathcal{S}}_3=\left(\begin{array}{ccccccccc}?& -& & & & +& & & \\ -& ?& +& \cdots & +& & & & \\ & +& ?& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & ?& & & & \\ +& & & & & ?& +& \cdots & +\\ & & & & & +& ?& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & ?\end{array}\right),$$

is not PEP.

Proof. 

Assume that ${\mathcal{S}}_3$ is PEP. Then ${\left({\mathcal{S}}_3\right)}_{D(+)}$ and all its superpattern are also PEP. Let

$$\widetilde{{\mathcal{S}}_3}=\left(\begin{array}{ccc}{[+]}_1& [-]& [+]\\ [-]& {[+]}_n& [-]\\ [+]& [-]& {[+]}_m\end{array}\right).$$

Then $\widetilde{{\mathcal{S}}_3}$ is a superpattern of ${\left({\mathcal{S}}_3\right)}_{D(+)}$ and is PEP. However, $\widetilde{{\mathcal{S}}_3}$ is a checkerboard block sign pattern and is not PEP by Lemma 2; a contradiction. □

For every n-by-n ($n\ge 2$) sign pattern, there is an eventually positive matrix realization with the sum of all nonzero off-diagonal entries being positive. However, for the $(n+m+1)$-by-$(n+m+1)$ PEP double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$ of the form $(\ast )$, the conclusion can be strengthened.

Theorem 2.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. If ${\mathfrak{S}}_{(n,m,1)}$ is PEP, then ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$.

Proof. 

Recall that every double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ that is PEP must be symmetric by Theorem 1. Suppose that ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=-$. If there is some $i\in \{3,4,\dots ,n+1\}$ such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP by Lemma 4. Thus ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$, and ${\mathfrak{S}}_{(n,m,1)}={\mathcal{S}}_1$. However, by Proposition 1 ${\mathcal{S}}_1$ is not PEP; a contradiction.

Suppose that ${\alpha }_{1,2}={\alpha }_{2,1}=-$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$. If there exists some $i\in \{3,4,\dots ,n+1\}$ such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP by Lemma 5. Thus ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$, and ${\mathfrak{S}}_{(n,m,1)}={\mathcal{S}}_3$. However, by Proposition 3 ${\mathcal{S}}_3$ is not PEP; a contradiction.

Suppose that ${\alpha }_{1,2}={\alpha }_{2,1}=-$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=-$. If there exists some $i\in \{3,4,\dots ,n+1\}$ such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP by Lemma 6. Thus ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$, and ${\mathfrak{S}}_{(n,m,1)}={\mathcal{S}}_2$. However, by Proposition 2, ${\mathcal{S}}_2$ is not PEP; a contradiction.

Consequently, ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$. If there exists some $i\in \{3,4,\dots ,n+1\}$ such that ${\alpha }_{2,i}={\alpha }_{i,2}=-$, or some $j\in \{n+3,n+4,\dots ,n+m+1\}$ such that ${\alpha }_{n+2,j}={\alpha }_{j,n+2}=-$, then ${\mathfrak{S}}_{(n,m,1)}$ is not PEP by Lemma 3. If follows that ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$. □

Lemma 7.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. If ${\mathfrak{S}}_{(n,m,1)}$ is PEP, then there is some $i\in \{1,2,\dots ,n+m+1\}$ such that ${\alpha }_{i,i}=+$.

Proof. 

Suppose that there is no $i\in \{1,2,\dots ,n+m+1\}$ such that ${\alpha }_{i,i}=+$. Since ${\mathfrak{S}}_{(n,m,1)}$ is PEP, ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(-)}$ is PEP. By Theorem 2, ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$. Let

$$\widetilde{{\mathfrak{S}}_{D(-)}}=\left(\begin{array}{ccccc}{[-]}_1& [+]& [-]& [+]& [-]\\ [+]& {[-]}_1& [+]& [-]& [+]\\ [-]& [+]& {[-]}_{n-1}& [+]& [-]\\ [+]& [-]& [+]& {[-]}_1& [+]& \\ [-]& [+]& [-]& [+]& {[-]}_{m-1}\end{array}\right).$$

Then $\widetilde{{\mathfrak{S}}_{D(-)}}$ is a proper superpattern of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(-)}$ and is PEP. However, $\widetilde{{\mathfrak{S}}_{D(-)}}$ is a checkerboard block sign pattern and is not PEP by Lemma 2; a contradiction. It follows that there exist some $i\in \{1,2,\dots ,n+m+1\}$ such that ${\alpha }_{i,i}=+$. □

Now we proceed to characterize the PEP double star-like sign patterns of the form $(\ast )$.

Theorem 3.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. Then ${\mathfrak{S}}_{(n,m,1)}$ is PEP if and only if ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$, and there is some $i\in \{1,2,\dots ,n+m+1\}$ such that ${\alpha }_{i,i}=+$.

Proof. 

The necessity follows from Theorem 2 and Lemma 7. The sufficiency follows from the fact that the positive part of ${\mathfrak{S}}_{(n,m,1)}$ is primitive. □

Next we turn to identifying all the MPEP double star-like sign pattern of the form $(\ast )$. To state clearly, let ${\mathfrak{S}}_{(n,m,1)}^{\left(i\right)}=\left({\alpha }_{i,j}\right)$ be the $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$ such that all nonzero off-diagonal entries are +, ${\alpha }_{i,i}=+$ and ${\alpha }_{j,j}=0$ for all $j\ne i$. For example,

$${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}=\left(\begin{array}{ccccccccc}+& +& & & & +& & & \\ +& 0& +& \cdots & +& & & & \\ & +& 0& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & 0& +& \cdots & +\\ & & & & & +& 0& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right),$$

$${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}=\left(\begin{array}{ccccccccc}0& +& & & & +& & & \\ +& +& +& \cdots & +& & & & \\ & +& 0& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & 0& +& \cdots & +\\ & & & & & +& 0& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right),$$

$${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}=\left(\begin{array}{ccccccccc}0& +& & & & +& & & \\ +& 0& +& \cdots & +& & & & \\ & +& +& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & 0& +& \cdots & +\\ & & & & & +& 0& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right),$$

$${\mathfrak{S}}_{(n,m,1)}^{(n+2)}=\left(\begin{array}{ccccccccc}0& +& & & & +& & & \\ +& 0& +& \cdots & +& & & & \\ & +& 0& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & +& +& \cdots & +\\ & & & & & +& 0& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right)$$

and

$${\mathfrak{S}}_{(n,m,1)}^{(n+3)}=\left(\begin{array}{ccccccccc}0& +& & & & +& & & \\ +& 0& +& \cdots & +& & & & \\ & +& 0& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & 0& +& \cdots & +\\ & & & & & +& +& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right).$$

Note that double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(4\right)}$, …, ${\mathfrak{S}}_{(n,m,1)}^{(n+1)}$ are equivalent to each other. Similarly, double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+4)}$, …, ${\mathfrak{S}}_{(n,m,1)}^{(n+m+1)}$ are equivalent to each other, especially if $n=m$, then ${\mathfrak{S}}_{(n,m,1)}^{\left(i\right)}$ is equivalent to ${\mathfrak{S}}_{(n,m,1)}^{(n+i)}$ for all $i=2,3,\dots ,n+1$.

Proposition 4.

The sign patterns${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$ are MPEP.

Proof. 

${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$ is PEP for its positive part is primitive. If some nonzero off-diagonal entries of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$ are changed to be 0, then the corresponding sign pattern is not irreducible and thus is not PEP. If the only one positive diagonal entry is changed to be 0, then the corresponding sign pattern is not PEP by Lemma 7. It follows that ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$ is MPEP. By a similar discussion, we can show that ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$, and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$ are MPEP. □

Theorem 4.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. If $n\ne m$, then ${\mathfrak{S}}_{(n,m,1)}$ is MPEP if and only if ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. If $n=m$, then ${\mathfrak{S}}_{(n,m,1)}$ is MPEP if and only if ${\mathfrak{S}}_{n,m,1}$ is equivalent to one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$ and ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$.

Proof. 

It suffices to show the first case. The sufficiency follows from Proposition 4. For the necessity, since ${\mathfrak{S}}_{(n,m,1)}$ is MPEP, by Theorem 2, ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$. There is some $i\in \{1,2,\dots ,n+m+1\}$ such that ${\alpha }_{i,i}=+$ by Lemma 7. If ${\mathfrak{S}}_{(n,m,1)}$ has at least two nonzero diagonal entries, then ${\mathfrak{S}}_{(n,m,1)}$ is a proper superpattern of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ or ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$, up to equivalence. Since ${\mathfrak{S}}_{(n,m,1)}$ is MPEP, one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$ is not PEP, contradicting Proposition 4. Consequently, ${\mathfrak{S}}_{(n,m,1)}$ has exactly one positive diagonal entry. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. □

Note that Theorem 4 indicates that for the class of $(n+m+1)$-by-$(n+m+1)$ double star-like sign patterns of the form $(\ast )$, if $n\ne m$, then there are exactly five MPEP sign patterns, and if $n=m$, then there are exactly three MPEP sign patterns, up to equivalence. Thus, we identify all the MPEP sign patterns in the class of double star-like sign patterns of the form $(\ast )$. Next, it is time to classify all the PEP double star-like sign patterns of the form $(\ast )$.

Theorem 5.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. If $n\ne m$, then ${\mathfrak{S}}_{(n,m,1)}$ is PEP if and only if ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to a superpattern of one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. If $n=m$, then ${\mathfrak{S}}_{(n,m,1)}$ is PEP if and only if ${\mathfrak{S}}_{n,m,1}$ is equivalent to a superpattern of one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$ and ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$.

Proof. 

It is enough to show the case $n\ne m$. The sufficiency is clear. For the necessity, if ${\mathfrak{S}}_{(n,m,1)}$ is MPEP, then ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$ by Theorem 4. If ${\mathfrak{S}}_{(n,m,1)}$ is PEP but not MPEP, then ${\mathfrak{S}}_{(n,m,1)}$ must be a proper superpattern of one MPEP double star-like sign pattern. By Theorem 4, there are exactly five MPEP sign patterns in the class of $(n+m+1)$-by-$(n+m+1)$ double star-like sign patterns of the form $(\ast )$, up to equivalence. It follows that ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to a superpattern of one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. □

It is known from [16] that if every matrix realization of an arbitrary n-by-n sign pattern $\mathcal{A}$ is eventually positive, the $\mathcal{A}$ is said to require the eventual positivity. Clearly, if the sign pattern $\mathcal{A}$ requires the eventual positivity, then $\mathcal{A}$ is PEP. In general, the converse does not hold. However, for the double star-like sign pattern of the form $(\ast )$ with exactly one nonzero diagonal entry, the answer is positive.

Proposition 5.

Let ${\mathfrak{S}}_{(n,m,1)}$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$ with exactly one nonzero diagonal entry. Then the following statements are equivalent:

(1) ${\mathfrak{S}}_{(n,m,1)}$ is MPEP;

(2) ${\mathfrak{S}}_{(n,m,1)}$ is nonnegative and primitive;

(3) ${\mathfrak{S}}_{(n,m,1)}$ requires eventual positivity.

Proof. 

$\left(1\right)⟹\left(2\right)$ follows from Theorem 4. $\left(2\right)⟹\left(3\right)$ follows from Theorem 2.3 in [16]. If ${\mathfrak{S}}_{(n,m,1)}$ requires eventual positivity, then ${\mathfrak{S}}_{(n,m,1)}$ is PEP. By Theorem 5, ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to a superpattern of one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. For ${\mathfrak{S}}_{(n,m,1)}$ has exactly one nonzero diagonal entry, ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to one of ${\mathfrak{S}}_{(n,m,1)}^{\left(1\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(2\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{\left(3\right)}$, ${\mathfrak{S}}_{(n,m,1)}^{(n+2)}$ and ${\mathfrak{S}}_{(n,m,1)}^{(n+3)}$. Consequently, $\left(3\right)⟹\left(1\right)$ follows from Proposition 4. □

3. Eventual Exponential Positivity of the Double Star-like Sign Patterns ${\mathfrak{S}}_{(n,m,1)}$

In this section, we investigate the eventual exponential positivity of the double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$ of the form $(\ast )$. First, we cite a necessary condition for an n-by-n sign pattern to be PEEP shown in [9].

Lemma 8

([9]). If an n-by-n sign pattern $\mathcal{A}$ is PEEP, then ${\mathcal{A}}_{D(+)}$ is PEP.

The following proposition provides a necessary condition for a double star-like sign pattern of the form $(\ast )$ to be PEEP.

Proposition 6.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. If ${\mathfrak{S}}_{(n,m,1)}$ is PEEP, then ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$.

Proof. 

Suppose that the double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ is PEEP. Then ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ is PEP by Lemma 8. By Theorem 2, all nonzero off-diagonal entries of ${\left({\mathfrak{S}}_{(n,m,1)}\right)}_{D(+)}$ must be +. □

Now we turn to identifying all MPEEP double star-like sign patterns.

Proposition 7.

The double star-like sign pattern

$${\mathfrak{S}}_{(n,m,1)}^o=\left(\begin{array}{ccccccccc}0& +& & & & +& & & \\ +& 0& +& \cdots & +& & & & \\ & +& 0& & & & & & \\ & ⋮& & \ddots & & & & & \\ & +& & & 0& & & & \\ +& & & & & 0& +& \cdots & +\\ & & & & & +& 0& & \\ & & & & & ⋮& & \ddots & \\ & & & & & +& & & 0\end{array}\right)$$

is MPEEP.

Proof. 

The double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}^o$ is PEEP for its positive part ${\left({\mathfrak{S}}_{(n,m,1)}^o\right)}^{+}$ is irreducible. It is clear that each proper subpattern of ${\mathfrak{S}}_{(n,m,1)}^o$ is not irreducible and thus is not PEEP. It follows that ${\mathfrak{S}}_{(n,m,1)}^o$ is MPEEP. □

Now we identify all the MPEP sign patterns in class of double star-like sign patterns of the form $(\ast )$.

Theorem 6.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. Then ${\mathfrak{S}}_{(n,m,1)}$ is MPEEP if and only if ${\mathfrak{S}}_{(n,m,1)}={\mathfrak{S}}_{(n,m,1)}^o$, up to equivalence.

Proof. 

Proposition 7 implies the sufficiency. For the necessity, assume that the $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ is MPEEP. Then ${\mathfrak{S}}_{(n,m,1)}$ is PEEP, and by Proposition 6, ${\alpha }_{1,2}={\alpha }_{2,1}=+$, ${\alpha }_{1,n+2}={\alpha }_{n+2,1}=+$, ${\alpha }_{2,k}={\alpha }_{k,2}=+$ for all $k=3,4,\dots ,n+1$, and ${\alpha }_{n+2,k}={\alpha }_{k,n+2}=+$ for all $k=n+3,n+4,\dots ,n+m+1$. Suppose that some diagonal entries of ${\mathfrak{S}}_{(n,m,1)}$ are nonzero. Then ${\mathfrak{S}}_{(n,m,1)}$ is a proper superpattern of ${\mathfrak{S}}_{(n,m,1)}^o$. Since ${\mathfrak{S}}_{(n,m,1)}$ is MPEEP, ${\mathfrak{S}}_{(n,m,1)}^o$ is not PEEP. However, ${\mathfrak{S}}_{(n,m,1)}^o$ is MPEEP by Proposition 7. It is a contradiction. Consequently, all the diagonal entries of ${\mathfrak{S}}_{(n,m,1)}$ must be 0. It follows that ${\mathfrak{S}}_{(n,m,1)}={\mathfrak{S}}_{(n,m,1)}^o$, up to equivalence. □

Theorem 6 indicates that there is exactly one MPEEP sign pattern for the class of double star-like sign patterns of the form $(\ast )$, up to equivalence. Now we turn to classify all the $(n+m+1)$-by-$(n+m+1)$ double star-like sign patterns that are PEEP.

Proposition 8.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be an $(n+m+1)$-by-$(n+m+1)$ double star-like sign pattern of the form $(\ast )$. Then ${\mathfrak{S}}_{(n,m,1)}$ is PEEP if and only if ${\mathfrak{S}}_{(n,m,1)}$ is equivalent to one of superpatterns of ${\mathfrak{S}}_{(n,m,1)}^o$.

Proof. 

The sufficiency is clear. For the necessity, if ${\mathfrak{S}}_{(n,m,1)}$ is MPEEP, then the conclusion follows from Theorem 6. If ${\mathfrak{S}}_{(n,m,1)}$ is PEEP, but not MPEEP, then ${\mathfrak{S}}_{(n,m,1)}$ must be a proper superpattern of the exactly one MPEEP double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}^o$ by Theorem 6, up to equivalence. □

It is known from [16] that if every matrix realization of sign pattern $\mathcal{A}$ is eventually exponentially positive, then $\mathcal{A}$ is said to require the eventual exponential positivity. Clearly, if a sign pattern $\mathcal{A}$ requires eventual exponential positivity, then $\mathcal{A}$ is also PEEP. Furthermore, the converse does not hold generally. However, for the double star-like sign patterns of the form $(\ast )$, the converse holds. The following theorem, which follows readily from Proposition 8 and Theorem 2.9 in [16], establishes the characterizations of the PEEP double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$.

Theorem 7.

Let ${\mathfrak{S}}_{(n,m,1)}=\left({\alpha }_{i,j}\right)$ be a double star-like sign pattern of order $n+m+1$ of the form $(\ast )$. Then the following statements are equivalent:

(1) ${\mathfrak{S}}_{(n,m,1)}$ is PEEP;

(2) All arcs of the simple 2-cycles $(v_i,v_j)$, $(v_j,v_i)$ of the signed digraph $\mathsf{\Gamma }\left({\mathfrak{S}}_{(n,m,1)}\right)$ are positive;

(3) All nonzero off-diagonal entries of ${\mathfrak{S}}_{(n,m,1)}$ are +;

(4) ${\mathfrak{S}}_{(n,m,1)}$ requires eventual exponential positivity;

(5) ${\mathfrak{S}}_{(n,m,1)}$ requires eventual positivity.

Note that it is shown in [17] that the n-by-n sign pattern requires the eventual exponential positivity, then every cycle in its signed digraph of length 2 or more is arc-positive.

4. Discussion and Conclusions

For the class of double star-like sign patterns ${\mathfrak{S}}_{(n,m,1)}$ of order $n+m+1$ of the form $(\ast )$, we have identified the minimal PEP sign patterns and the minimal PEEP sign patterns, and consequently classified their PEP sign patterns and PEEP sign patterns. Our results indicate that the double star-like sign pattern ${\mathfrak{S}}_{(n,m,1)}$ is MPEEP if and only if the star sign patterns $S_n$ and $S_m$ are MPEEP, and the arcs $(v_1,v_{n+2})$ and $(v_{n+2},v_1)$ are positive. However, it is not true for the general sign patterns. It is interesting to ask how we can extend the previous result to some extent.