Reduced-Kernel Weighted Extreme Learning Machine Using Universum Data in Feature Space (RKWELM-UFS) to Handle Binary Class Imbalanced Dataset Classification

Abstract

Class imbalance is a phenomenon of asymmetry that degrades the performance of traditional classification algorithms such as the Support Vector Machine (SVM) and Extreme Learning Machine (ELM). Various modifications of SVM and ELM have been proposed to handle the class imbalance problem, which focus on different aspects to resolve the class imbalance. The Universum Support Vector Machine (USVM) incorporates the prior information in the classification model by adding Universum data to the training data to handle the class imbalance problem. Various other modifications of SVM have been proposed which use Universum data in the classification model generation. Moreover, the existing ELM-based classification models intended to handle class imbalance do not consider the prior information about the data distribution for training. An ELM-based classification model creates two symmetry planes, one for each class. The Universum-based ELM classification model tries to create a third plane between the two symmetric planes using Universum data. This paper proposes a novel hybrid framework called Reduced-Kernel Weighted Extreme Learning Machine Using Universum Data in Feature Space (RKWELM-UFS) to handle the classification of binary class-imbalanced problems. The proposed RKWELM-UFS combines the Universum learning method with a Reduced-Kernelized Weighted Extreme Learning Machine (RKWELM) for the first time to inherit the advantages of both techniques. To generate efficient Universum samples in the feature space, this work uses the kernel trick. The performance of the proposed method is evaluated using 44 benchmark binary class-imbalanced datasets. The proposed method is compared with 10 state-of-the-art classifiers using AUC and G-mean. The statistical t-test and Wilcoxon signed-rank test are used to quantify the performance enhancement of the proposed RKWELM-UFS compared to other evaluated classifiers.

1. Introduction

The performance of a classification problem is affected by various data complexity measures such as class imbalance, class overlapping, length of the decision boundary, small disjuncts of classes, etc. In the classification domain, most of the real-world problems are class imbalanced. Examples of such problems are cancer detection [1,2], fault detection [3], intrusion detection system [4], software test optimization [5], speech quality assessment [6], pressure prediction [7], etc. In a problem when the number of samples in one class outnumbers the numbers of samples in some other class, it is considered as a class imbalanced/asymmetric problem. The class with a greater number of instances is the majority class and the class with fewer instances is the minority class. In real-world problems, usually, the minority class instances have more importance than the majority class.

Traditional classifiers such as the support vector machine (SVM), Naive Bayes, decision tree, and extreme learning machine (ELM) are biased towards the correct classification of majority class data. Various approaches have been proposed to handle such class-imbalanced classification problems, which can be classified as data sampling, algorithmic and hybrid methods [8].

In classification, the idea of using additional data along with the original training data has been used widely for better training of the model. The virtual example method, oversampling method, noise injection method, and Universum data creation method are some examples that use additional data. The oversampling method generates additional data in the majority class to balance the data distribution in the classes. In the virtual example and noise injection methods, labeled synthetic data are created that may not come from the same distribution as the original data. Universum data creation methods allow the classifier to encode prior knowledge by representing meaningful concepts in the same domain as the problem at hand as stated in [9]. In Universum learning-based classification models, the Universum data are added to the training data to enhance performance. Universum data are data that do not belong to any of the target classes. The two main factors which affect the performance of Universum data are the number of Universum data created and the method used for the creation of Universum data. Different methods have been used for the creation of Universum; among those, the two most common methods widely used are the use of examples from other classes and random averaging [9].

Several methods have been proposed that use Universum data in the training of SVM based classifiers to handle the class imbalance problem, such as the Universum Support Vector Machine (USVM) [9], Twin support vector machine with Universum data (TUSVM) [10], and Cost-Sensitive Universum-SVM (CS-USVM) [11]. A Universum support vector machine-based model for EEG signal classification has been proposed in [12]. A nonparallel support vector machine for a classification problem with Universum learning has been proposed in [13]. An improved non-parallel Universum support vector machine and its safe sample screening rules are proposed in [14]. Tencer et al. [15] used Universum data with other classifiers such as fuzzy models to demonstrate its usefulness in combination with fuzzy models. Recently, a Multiple Universum Empirical Kernel Learning (MUEKL) [16] classifier has been proposed to handle class imbalance by combining the Universum learning with Multiple Empirical Kernel Learning (MEKL).

Extreme Learning Machine (ELM) [17] is a single hidden-layer feed-forward neural network designed for regression and classification with fast speed and better generalization performance, but it cannot handle the classification of class-imbalanced problems effectively. Various ELM based models have been proposed to handle the classification of class imbalance problems, such as Weighted Extreme Learning Machine (WELM) [18], Class-Specific Cost Regulation Extreme Learning Machine (CCR-ELM) [19], Class-Specific Kernelized Extreme Learning Machine (CSKELM) [20], Reduced-Kernelized Weighted Extreme Learning Machine (RKWELM) [21], UnderBagging-based Kernelized Weighted Extreme Learning Machine (UBKWELM) [22], and UnderBagging-based Reduced-Kernelized Weighted Extreme Learning Machine (UBRKWELM) [21]. The proposed work is motivated by the idea that none of the existing ELM-based models for classification encode prior knowledge in the training model using Universum data.

This work proposes a novel hybrid classification model called Reduced-Kernel Weighted Extreme Learning Machine using Universum data in Feature Space (RKWELM-UFS) which incorporates the Universum data in the RKWELM model. The contributions of the proposed approach are listed below.

• This work is the first attempt that utilized the Universum data in a Reduced-Kernelized Weighted Extreme Learning Machine (RKWELM)-based classification model to handle the class imbalance problem.
• The Weighted Kernelized Synthetic Minority Oversampling Technique (WKSMOTE) [23] is an oversampling-based classification method in which the synthetic samples are created in the feature space of the Support Vector Machine (SVM). Inspired by WKSMOTE, the proposed work creates the Universum samples in the feature space.
• The proposed method uses the kernel trick to create the Universum samples in the feature space between randomly selected instances of the majority and minority classes.
• In a classification problem, the samples located near the decision boundary contribute more to better training. The creation of Universum samples in feature space ensures that the Universum samples lie near the decision boundary.

The rest of the paper is structured as follows. In the related work section, Universum learning, class imbalance learning, ELM classifier, and its variants are discussed in detail. The proposed work section provides a detailed explanation of the proposed RKWELM-UFS classifier. The experimental setup and result analysis section provide the specification of the dataset used in the experiments, parameter settings of the proposed algorithm, the evaluation metrics used for performance evaluation, and the experimental results obtained in form of various tables and figures. The last section provides the concluding remarks and future research directions.

2. Related Work

The following section provides the literature related to Universum learning, class imbalance learning, and some of the existing ELM-based models to handle class imbalance learning.

2.1. Universum Learning

The idea of using Universum data is close to the idea of using the prior knowledge in Bayesian classifiers [9]. However, there is a conceptual difference between the two approaches, i.e., the prior knowledge is knowledge about decision rules used in Bayesian inference, while the Universum is knowledge about the admissible collection of examples. Similarly to the Bayesian prior probability, the Universum data encode prior information.

It has been observed by various researchers [9,15,24] that the effect of Universum is dependent on the quality of Universum samples created. A safe sample screening rule for Universum support vector machines, in which the non-contributed data can be identified and safely eliminated before the training process, can obtain the same solution as solving the original problem is proposed in [25]. An improved version of the non-parallel Universum support vector machine and its safe sample screening rule is proposed in [14]. It is suggested in [24] that not all the Universum samples are helpful for effective classification, so they proposed selecting the informative Universum samples for semi-supervised learning, which is a method used to identify informative samples among the Universum samples. An empirical study on the Universum support vector machine (USVM), which describes some practical conditions for evaluating the effectiveness of random averaging for the creation of Universum data, is performed in [26].

2.2. Class Imbalance Learning

The classification performance of traditional classifiers degrades when there is an imbalance in the ratio of the majority and minority class data. Different approaches have been used in classification to deal with the problem of class imbalance. Table 1 provides the categorization of the proposed methods and other methods used in this work for comparison. Table 1 also provides the strategy and basic ideas used in the respective methods. The broad categories of these approaches are discussed in the following subsections.

Table 1. Categorization and comparison of the proposed method and other methods in comparison used to handle classification of class imbalance problems.

Category	Strategy	Method	Basic Idea of the Method
Algorithmic	Cost Sensitive	WELM	This method minimizes the weighted least-square error to handle the class imbalance.
		CCR-KELM	This method assigns a class-specific regularization parameter to handle class imbalance.
		RKELM	This method uses a reduced number of centroids in kernels function to handle class imbalance
Data-level	Under-sampling	Random-Under-sampling	This method uses random under-sampling to balance the imbalanced training data.
	Oversampling	SMOTE	This method creates artificial minority class samples to balance the imbalanced training data.
		CSMOTE	This method generates some artificial samples whose dimension is equal to 5 times the number of minority samples.
	Universum	USVM	This method creates Universum data to sift the separating hyper plane of the SVM classifier
		MUEKL	This method combines Multiple Empirical Kernel Learning with the Universum learning.
Hybrid	Data-level combined with Ensemble	RUS-Boost	This method combines RUS with boosting.
		UBKELM	This method uses random under-sampling with KELM-based ensemble.
		UBRKELM	This method uses random under-sampling with RKELM-based ensemble.
	Cost-sensitive combined with Ensemble	BWELM	This method combines boosting with WELM.
	Data-level combined with cost sensitive	RKWELM-UFS (the proposed method)	The proposed method creates a Universum sample in the feature space and uses RKWELM as the classification algorithm.

2.2.1. Data Level Approach

The data-level methods are based on balancing the ratio of data to convert an imbalanced classification problem into a balanced classification problem. These methods can be seen as data pre-processing methods because they try to handle the class imbalance present in the data before the classification model generation. The data-level approaches can be broadly categorized as under-sampling, oversampling and, hybrid sampling methods.

The under-sampling methods remove some of the data (i.e., the majority samples) to decrease the imbalance ratio of a training dataset. These methods may suffer from data loss, as some of the important samples may be removed. The efficiency of an under-sampling method lies in its ability to select the right samples which can be removed from the dataset. The under-sampling methods reduce the time complexity of a given class-imbalanced classification problem. A combined weighted multi-objective optimizer for instance reduction in a two-class imbalanced data problem is proposed in [27]. Clustering-Based Under-Sampling (CBUS) [28] uses clustering of majority class data for the under-sampling. Fast Clustering-Based Under-Sampling (FCBUS) [29] is a modified version of CBUS which clusters the minority class data for under-sampling to reduce the time complexity of CBUS.

The oversampling method adds some additional data (in the minority class) to decrease the imbalance ratio of the training dataset. The additional samples are obtained by creating synthetic minority class samples or replicating the existing minority class samples. These methods can lead to over-fitting problems in model generation. The oversampling methods increase the time complexity of a given class imbalance classification problem. The synthetic minority oversampling technique (SMOTE) [30] is a popular oversampling method, widely used to handle class imbalance, in which synthetic minority samples are created. Several variants of SMOTE have been proposed to further enhance the performance of class imbalance dataset classification, such as Borderline SMOTE, Borderline SMOTE1, Borderline SMOTE2, Safe- Level-SMOTE, MSMOTE [31], and CSMOTE [32]. The hybrid sampling methods such as SCUT [16] try to reduce the class imbalance by using both oversampling and under-sampling.

2.2.2. Algorithmic Approach

There are some approaches in which the classification algorithm is able to handle class imbalance problems, such as cost-sensitive and one-class learning approaches. The cost-sensitive methods assign a different cost to the misclassification of different classes. In an imbalance problem, generally, the misclassification cost of minority class samples is higher than the misclassification cost of majority class samples. The efficiency of any cost-sensitive method lies in the selection of misclassification costs for different classes. Multiple Random Empirical Kernel Learning (MREKL) [33] is a cost-sensitive classification model which emphasizes the importance of samples located in overlapping regions of positive and negative classes and ignores the effects of noisy samples to achieve better performance in class imbalance problems. Weighted Extreme Learning Machine (WELM) [18] is a weighted version of Extreme Learning Machine (ELM) [17] that minimizes the weighted error by incorporating a weight matrix in the optimization problem of ELM. Class-Specific Extreme Learning Machine (CSELM) [34] is a variant of WELM which replaces the weight matrix with two constant weight values for each class. Class-Specific Kernel Extreme Learning Machine (CSKELM) [20] is the modification of CSELM which uses the Gaussian kernel function to map the input data to feature space. Class-Specific Cost-Regulation Extreme Learning Machine (CCR-KELM) [19] is the variant of KELM which uses different regularization perimeters for the classes.

The one-class learning approach is also called single-class learning. In these methods, the classifier learns only one class as the target class. In this approach generally, the minority class is considered as the target class. Multi-Kernel Support Vector Data Description with boundary information proposes a novel method called MKL-SVDD [35] by introducing Multi- Kernel Learning (MKL) into the traditional Support Vector Data Description (SVDD) based on the boundary information to form one-class learning.

2.2.3. Hybrid Approach

In a hybrid approach, multiple classification approaches are combined to handle a class imbalance problem. Some hybrid techniques combine ensemble techniques with data sampling methods such as over-sampling or under-sampling to handle class imbalance problems. RUSBoost [36] is a hybrid technique that combines random under-sampling with boosting to create an ensemble of classifiers. UBKELM [22] and UBRKELM [21] are two hybrid classification models that combine underbagging with KELM and RKELM respectively. BPSO-AdaBoost-KNN [37] is a method that implements BPSO as the feature selection algorithm and then designs an AdaBoost-KNN classifier to convert the traditional weak classifier into a strong classifier. UBoost: Boosting with the Universum [38] is a technique that combined the Universum sample creation with a boosting framework. An Adaptive-Boosting (AdaBoost) algorithm [39] uses multiple iterations to learn multiple classifiers in a serial manner to generate a single strong learner.

Some hybrid techniques combine cost-sensitive approaches with ensemble techniques such as Ensemble of Weighted Extreme Learning Machine (EWELM) [40] and Boosting Weighted Extreme Learning machine (BWELM) [41]. In EWELM, the weight of each component classifier in the ensemble is optimized by using a differential evolution algorithm. BWELM is a modified AdaBoost framework that combines multiple Weighted ELM-based classifiers in a boosting manner. The main idea of BWELM is to find the better weights in each base classifier.

2.3. Extreme Learning Machine (ELM) and Its Variants to Handle Class Imbalance Learning

ELM [17,42] is a generalized single hidden-layer feed-forward neural network, which provides good generalization performance and disposes of the iterative time-consuming training process. It uses the Moore–Penrose pseudoinverse for computing the weights between the hidden and the output layer which make it fast. For a given classification dataset with N training samples ${\left\{\left(x_i,t_i\right)\right\}}_{i=1}^N$, where $x_i={\left[x_{i1},x_{i2,\dots \dots ., } x_{in}\right]}^Tϵ R^n$ is the input feature vector and $t_i={\left[t_{i1},t_{i2,\dots \dots ., } t_{im}\right]}^Tϵ R^m$ is the output label vector. Here, the vector/matrix transpose is denoted by superscript T. During the training time, these weights are randomly generated and are not changed further. The hidden neurons bias matrix is denoted by $b=b_1{\left[,b_{2 },..b_j,.. b_L\right]}^Tϵ R^L$, where $b_j$ is the bias of the jth hidden neuron. In ELM, for a given training/testing sample, i.e., $x_i$, the hidden layer output $h\left(x_i\right)$ is calculated as follows:

$$h\left(x_i\right)=G\left(a{x}_i+b\right)$$

(1)

Here, $G\left(.\right)$ is the activation function of the hidden neurons. In ELM, for a binary classification problem, the decision function, i.e., $f\left(x_i\right)$ for a sample $x_i$is given as:

$$f\left(x_i\right)=sign\left(h\left(x_i\right)\beta \right)$$

(2)

where $\beta$ is the output weight matrix. The hidden layer output matrix H can be written as follows:

$$H={\left[\begin{array}{cccc}{h}_1\left(x_1\right)& h_2\left(x_1\right)& .& h_L\left(x_1\right)\\ h_1\left(x_2\right)& h_2\left(x_2\right)& .& h_L\left(x_2\right)\\ .& .& .& .\\ h_1\left(x_N\right)& h_2\left(x_N\right)& .& h_L\left(x_N\right)\end{array}\right]}_{N\times L}$$

(3)

ELM minimizes the training error and the norm of the output weights as:

$$Minimize:\Vert H\beta -T{\Vert }^2 and \Vert \beta \Vert$$

(4)

In the original implementation of ELM [17], the minimal norm least-square method instead of the standard optimization method was used to find β.

$$\beta =H^{+}T$$

(5)

where $H^{+}$ is the Moore–Penrose generalized inverse of matrix H. In [17,42] the orthogonal projection method is used to calculate $H^{+}$, which can be used in two cases.

When $H^{T}H$is nonsingular then,

$$H^{+}={\left(H^{T}H\right)}^{-1}{H}^T$$

When $H^{T}H$ is singular then

$$H^{+}=H^T{\left(H{H}^T\right)}^{-1}$$

In ELM the constrained optimization-based problem for classification with multiple output nodes was formulated as follows:

$$Minimize=\frac{1}{2}\Vert \beta {\Vert }^2+C\frac{1}{2}{\displaystyle \sum }_{i=1}^N\Vert {\xi }_i{\Vert }^2$$

(6)

Subjected to: $h\left(x_i\right)\beta =t_i^T-{\xi }_i^T, i=1,\dots , N$

The output layer weights $\beta$ can be obtained using two solutions

Case 1. Where the Number of Training Samples is Not Huge:

$$\beta =H^T{\left(\frac{I}{C}+H{H}^T\right)}^{-1}T$$

(7)

Case 2. Where the Number of Training Samples is Huge:

$$\beta ={\left(\frac{I}{C}+H^{T}H\right)}^{-1}{H}^{T}H$$

(8)

2.3.1. Weighted Extreme Learning Machine (WELM)

Conventional ELM does not account for good generalization performance while dealing with the class-imbalance learning problems. Weighted Extreme Learning Machine (WELM) [18] is a cost-sensitive version of ELM which was proposed for handling the class-imbalanced learning problem effectively. In cost-sensitive learning methods, the different cost is assigned to the misclassification of different class samples. In WELM, two generalized weighting schemes were proposed. These generalized weighting schemes assign weights to the training samples as per their class distribution. In WELM [18], the following optimization problem is formulated:

$$Minimize=\frac{1}{2}\Vert \beta {\Vert }^2+\frac{1}{2}CW{\displaystyle \sum }_{i=1}^N\Vert {\xi }_i{\Vert }^2$$

(9)

Subjected to: $h\left(x_i\right)\beta =t_i^T-{\xi }_i^T, i=1,\dots , N$

Here, C is the regularization parameter and $W=diag\left(W_{ii}\right)$ is a $N\times N$diagonal matrix whose diagonal elements are the weights assigned to the training samples. The two weighting schemes proposed by WELM are:

Weighting scheme W1:

$$W_{ii}=\frac{1}{q_k}$$

(10)

Here, $k=t_i$and $q_k$ is the total number of samples belonging to kth class.

Weighting scheme W2:

$$W_{ii}=\left\{\begin{array}{c}\frac{0.618}{qk} if (q_k>q_{avg})\\ \frac{1}{qk} if (q_k<=q_{avg})\end{array}\right.$$

(11)

Here, $q_{avg}$ represents the average number of samples for all classes. Weight $W_{ii}$ is assigned to the ith samples. Samples belonging to the minority class will be assigned weights equal to$1/q_i$, in both the weighting schemes. The second weighting scheme assigns a lesser weight to the majority class samples compared to the first weighting scheme. The two variants of WELM are sigmoid node-based WELM and Gaussian kernel-based WELM, which are described as follows.

• Sigmoid node-based Weighted Extreme Learning Machine

The Sigmoid node-based WELM uses random input weights and Sigmoid activation function i.e., G(.), to find the hidden layer output matrix H given in Equation (3). The solution of the optimization problem of WELM as given in [18] is reproduced below:

$$\beta =\left\{\begin{array}{c}{H}^T{\left(\frac{I}{C}+WH{H}^T\right)}^{-1}WT if (N>L)\\ {\left(\frac{I}{C}+H^{T}WH\right)}^{-1}{H}^{T}WH if (N>L)\end{array}\right.$$

(12)

The two solutions are given for two cases. The first solution is given for the case when the number of training samples is smaller than the number of selected hidden layer neurons. The second solution is given for the case where the number of selected hidden layer neurons is smaller than the number of training samples.

• Gaussian kernel-based Weighted Extreme Learning Machine (KWELM)

In KELM [42], the kernel matrix of the hidden layer is represented as follows:

$$\mathsf{\Omega }={\left[\begin{array}{cccc}K\left(x_1, x_1\right)& K\left(x_1, x_2\right)& .& K\left(x_1, x_N\right)\\ K\left(x_2, x_1\right)& K\left(x_2, x_2\right)& .& K\left(x_2, x_N\right)\\ .& .& .& .\\ K\left(x_N, x_1\right)& K\left(x_N, x_2\right)& .& K\left(x_N, x_N\right)\end{array}\right]}_{N\times N}$$

(13)

The Gaussian kernel-based WELM maps the input data to the feature space as follows:

$$K\left(x_i, x_j\right)=exp\left(\frac{-\Vert x_i-x_j{\Vert }^2}{{\sigma }^2}\right)$$

(14)

Here, $\sigma$ represents the kernel width parameter, $x_i$ represents the ith sample and $x_j$ represents the jth centroid; $\left(i, j\in 1, 2, \dots N\right). K\left(x_i, x_j\right)$ represents the distance of the jth centroid $x_j$to the ith input sample$x_i$. The number of Gaussian kernel functions i.e., the centroids used in [32] was equal to the number of training samples. On applying Mercer’s condition, the kernel matrix of KELM [42] can be represented as given below:

$${\mathsf{\Omega }}_{KELM}=H{H}^T:{\mathsf{\Omega }}_{KEL{M}_{i,j}}=h\left(x_i\right).h\left(x_j\right)=K\left(x_{i, }{x}_{j }\right)$$

(15)

The output of KWELM is determined in [18] which is represented as follow:

$$f\left(x\right)=sign{\left[\begin{array}{c}K\left(x,x_1\right)\\ .\\ .\\ K\left(x,x_N\right)\end{array}\right]}^T{\left(\frac{I}{C}+W{\mathsf{\Omega }}_{KELM}\right)}^{-1}WT$$

(16)

Compared to the Sigmoid node-based WELM, KWELM has better classification performance, as stated in [18].

2.3.2. Reduced Kernel Weighted Extreme Learning Machine (RKWELM)

Reduced-Kernel Extreme Learning Machine (RKELM) [43] is a fast and accurate kernel-based supervised algorithm for classification. Unlike Support Vector Machine (SVM) or Least-Square SVM (LS-SVM), which identify the support vectors or weight vectors iteratively, the RKELM randomly selects a subset of the available data samples as centroids or mapping samples. The weighted version of RKELM i.e., Reduced-Kernel Weighted Extreme Learning Machine (RKWELM) is proposed in [21] for class imbalance learning. In RKWELM, a reduced number of kernels are selected, which act as the centroids. The number of Gaussian kernel functions used in RKWELM is denoted as $\tilde{N}$ where $\tilde{N}\subset N$. The kernel matrix of the hidden layer can be reproduced as given by the following equation.

$${\mathsf{\Omega }}_{RKELM}={\left[\begin{array}{cccc}K\left(x_1, x_1\right)& K\left(x_1, x_2\right)& .& K\left(x_1, x_N\right)\\ K\left(x_2, x_1\right)& K\left(x_2, x_2\right)& .& K\left(x_2, x_N\right)\\ .& .& .& .\\ K\left(x_N, x_1\right)& K\left(x_N, x_2\right)& .& K\left(x_N, x_{\tilde{N}}\right)\end{array}\right]}_{N\times \tilde{N}}$$

(17)

Here, $x_{i }$represents the ith sample and $x_{j }$represents the jth centroid $\left(i\in 1, 2, \dots N\right)$ and $\left(j\in 1, 2, \dots N\right)$. In the case when $\left(N==\tilde{N}\right),$ the output of RKWELM can be given by the following equation.

The final output of RKWELM, as given in [43], is computed as:

$$f\left(x\right)=sign{\left[\begin{array}{c}K\left(x,x_1\right)\\ .\\ K\left(x,x_{\tilde{N}}\right)\end{array}\right]}^T{\left(\frac{I}{C}+{\mathsf{\Omega }}_{RKELM}^{T}W{\mathsf{\Omega }}_{RKELM}\right)}^{-1}{\mathsf{\Omega }}_{RKELM}^{T}WT$$

(18)

2.3.3. UnderBagging-Based Kernel Extreme Learning Machine (UBKELM)

UnderBagging-Based Kernel Extreme Learning Machine (UBKELM) [22] is an ensemble of KELM. UBKELM creates several balanced training subsets by random under-sampling of the majority class samples. K is the number of balanced subsets that are created by selecting M number of majority samples and all the minority samples in each subset, where M is the number of minority samples in the training dataset and K is the ceiling value of the imbalance ratio of the training dataset. In the subset creation, the majority samples are selected using the random under-sampling method. There are two variants of UBKELM, i.e., UnderBagging-Based Kernel Extreme Learning Machine-Max Voting (UBKELM-MV) and UnderBagging-Based Kernel Extreme Learning Machine-Soft Voting (UBKELM-SV) in which the ultimate outcome of the ensemble is computed by majority voting and soft voting respectively.

2.3.4. UnderBagging-Based Reduced-Kernelized Weighted Extreme Learning Machine

UnderBagging-based Reduced-Kernelized Weighted Extreme Learning Machine (UBRKELM) [21] is an ensemble of Reduced Kernelized Weighted Extreme Learning Machine (RKWELM). The UBRKELM creates several balanced training subsets and learns multiple classification models with these balanced training subsets using RKWELM as the classification algorithm. K is the number of balanced subsets that are created by selecting M number of majority samples and all the minority samples in each subset, where M is the number of minority samples in the training dataset and K is the ceiling value of the imbalance ratio of the training dataset. In UBRKELM the reduced number of kernel functions is used as centroids to learn an RKELM model. Two variants of UBRKWELM are proposed, UBRKWELM-MV and UBRKWELM-SV, in which the final outcome of the ensemble is computed by majority voting and soft voting respectively.

3. Proposed Method

This work proposes a novel Reduced-Kernel Weighted Extreme Learning Machine using Universum data in Feature Space (RKWELM-UFS) to handle the class imbalance classification problem. In the proposed work, the Universum data along with the original training data is provided to the classifier for training purposes, to improve its learning capability. The proposed method creates Universum samples in the feature space because the mapping of input data from the input space to the feature space is not conformal.

The following subsections describe the process of creation of the Universum samples in the input space, the process of creation of the Universum samples in the feature space, the proposed RKWELM-UFS classifier, and the computational complexity of the proposed RKWELM-UFS classification model. Algorithm 1 provides the pseudo-code of the proposed RKWELM-UFS.

3.1. Generation of Universum Samples in the Input Space

To generate a Universum sample $x_u$ between a majority sample $x_m$ and a minority sample $x_n$, the following equation can be used:

$$x_u=x_m+\delta \left(x_n-x_m\right)$$

(19)

where δ represents a random number in the uniform distribution U [0, 1].

3.2. Generation of Universum Samples in the Feature Space

To generate a Universum sample in the feature space between a majority sample $x_m$ and a minority sample $x_n$ the following equation can be utilized:

$$\varphi \left(x^{mn}\right)=\varphi \left(x_m\right)+{\delta }^{mn}\left(\varphi \left(x_n\right)-\varphi \left(x_m\right)\right)$$

(20)

where, $\varphi \left(.\right)$ is the feature transformation function which is generally unknown and ${\delta }^{mn}$ is a random number between [0, 1]. The proposed work uses ${\delta }^{mn}$ = 0.5. Similarly to SVM, LS-SVM, and PSVM, the transformation function $\varphi \left(.\right)$ need not be known to users; instead, its kernel function $K(x_m, x_n)$ can be deployed. If a feature mapping $\varphi \left(.\right)$ is unknown to users, one can apply Mercer’s conditions on ELM to define a kernel matrix for KELM [17] as follows:

$${\mathsf{\Omega }}_{KELM}=H{H}^T:{\mathsf{\Omega }}_{KEL{M}_{m,n}}=K\left(x_m, x_n\right)=\varphi {\left(x_m\right)}^T.\varphi \left(x_n\right)$$

(21)

In the proposed work, we have to calculate the kernel function $K\left(x_i, x_j^{mn}\right)$, where $x_i$ represents the original target training sample and $x_j^{mn}$is the Universum sample. According to [23] without computing$\varphi \left(x_i\right)$ and $(x_j^{mn})$, we can obtain the corresponding kernel $K\left(x_i,x_j^{mn}\right)$ using the following equation:

$$\begin{gathered} K\left(x_j^{mn}, x_i\right)=\varphi {\left(x_i\right)}^T \varphi \left(x_j^{mn}\right)=\varphi {\left(x_i\right)}^T(\varphi \left(x_m\right)+{\delta }^{mn}\left(\varphi \left(x_n\right)-\left(\varphi \left(x_m\right)\right)\right)= \\ \varphi {\left(x_i\right)}^T(\varphi \left(x_m\right)+{\delta }^{mn}\varphi {\left(x_i\right)}^T\varphi \left(x_n\right)-{\delta }^{mn}\varphi {\left(x_i\right)}^T\varphi \left(x_m\right)=K\left(x_i, x_m\right)+ \\ {\delta }^{mn}K\left(x_i, x_n\right)+{\delta }^{mn}K\left(x_i, x_m\right)K\left(x_j^{mn}, x_i\right)=\left(1-{\delta }^{mn}\right)K\left(x_i, x_m\right)+{\delta }^{mn}K\left(x_i, x_n\right) \end{gathered}$$

(22)

3.3. Proposed Reduced-Kernel Weighted Extreme Learning Machine Using Universum Samples in Feature Space (RKWELM-UFS)

Training of an ELM [42] based classifier requires the computation of the output layer weight matrix β. The proposed RKWELM-UFS uses the same equation as RKWELM [21] to obtain the output layer weight matrix β which is reproduced below:

$$\beta ={\left(\frac{I}{C}+{\mathsf{\Omega }}_{RKELM-UFS}^T W{\mathsf{\Omega }}_{RKELM-UFS}\right)}^{-1}{\mathsf{\Omega }}_{RKELM-UFS}^T WT$$

(23)

where, W is the diagonal weight matrix, which gives different weights to the majority class, the minority class, and the Universum instances using Equation (10), T is the target vector in which the class label for Universum samples is set to 0 (given the class label of majority and minority class are +1 and −1 respectively), and ${\mathsf{\Omega }}_{RKELM-UFS}$ is the kernel matrix of the proposed RKWELM-UFS.

In the proposed work, the Universum instances are added to the training process along with the original training instances. The reason behind computing β in the same manner as RKWELM is that the proposed RKWELM-UFS computes the kernel matrix ${\mathsf{\Omega }}_{RKELM-UFS}$ by deploying the original training instances excluding the Universum instances as centroids. The value of ${\mathsf{\Omega }}_{RKELM-UFS}$ is obtained by augmentation of the two matrices ${\mathsf{\Omega }}_{RKELM }and$ ${\mathsf{\Omega }}_{UFS }$. The following subsections describe the computation of ${\mathsf{\Omega }}_{RKELM }$, ${\mathsf{\Omega }}_{UFS }$ and ${\mathsf{\Omega }}_{RKELM-UFS}$.

3.3.1. Computation of ${\mathsf{\Omega }}_{\mathrm{KELM} }$

The proposed work computes the kernel matrix for the N number of original training instances termed as ${\mathsf{\Omega }}_{KELM }$ in the same manner as it was computed in the KELM [42], which is represented as:

$${\mathsf{\Omega }}_{KELM}={\left[\begin{array}{cccc}K\left(x_1, x_1\right)& K\left(x_1, x_2\right)& .& K\left(x_1, x_N\right)\\ K\left(x_2, x_1\right)& K\left(x_2, x_2\right)& .& K\left(x_2, x_N\right)\\ .& .& .& .\\ K\left(x_N, x_1\right)& K\left(x_N, x_2\right)& .& K\left(x_N, x_N\right)\end{array}\right]}_{N\times N}$$

(24)

3.3.2. Computation of ${\mathsf{\Omega }}_{\mathrm{UFS} }$

Equation (20) can be used to create a Universum sample $\varphi \left(x_{mn}\right)$ between two original training samples $\varphi \left(x_m\right)$ and $\varphi \left(x_n\right)$ in feature space. As we have discussed the transformation function $\varphi \left(.\right)$ is unknown to the user, so the computation of $\varphi \left(x_{mn}\right)$ is not possible here. For convenience, we will refer to the Universum sample $\varphi \left(x_{mn}\right)$ as $\varphi \left(u_i\right)$. In the proposed work without computing $\varphi \left(u_i\right)$, we can directly compute the corresponding kernel $K\left(u_i,x_j\right)$. $K(u_i,x_j$) is calculated using Equation (22). In the proposed algorithm, only the original training samples are used as centroids, so the matrix ${\mathsf{\Omega }}_{UFS}$ for p number of Universum samples and N number of original training samples can be represented as:

$${\mathsf{\Omega }}_{UFS}={\left[\begin{array}{cccc}K\left(u_1, x_1\right)& K\left(u_1, x_2\right)& .& K\left(u_1, x_N\right)\\ K\left(u_2, x_1\right)& K\left(u_2, x_2\right)& .& K\left(u_2, x_N\right)\\ .& .& .& .\\ K\left(u_p, x_1\right)& K\left(u_p, x_2\right)& .& K\left(u_p, x_N\right)\end{array}\right]}_{p\times N}$$

(25)

3.3.3. Computation of ${\mathsf{\Omega }}_{\mathrm{RKELM}-\mathrm{UFS}}$

The addition of Universum samples in the training process requires that the original kernel matrix i.e., ${\mathsf{\Omega }}_{RKELM}$ be augmented to include the matrix ${\mathsf{\Omega }}_{UFS}$. The final hidden layer output kernel matrix of the proposed RKWELM-UFS is obtained by augmentation of the two matrices ${\mathsf{\Omega }}_{KELM}$ and ${\mathsf{\Omega }}_{UFS}$ which is denoted as ${\mathsf{\Omega }}_{RKELM-UFS}$.

$${\mathsf{\Omega }}_{RKELM-UFS}={\left[\begin{array}{cccc}K\left(x_1, x_1\right)& K\left(x_1, x_2\right)& .& K\left(x_1, x_N\right)\\ K\left(x_2, x_1\right)& K\left(x_2, x_2\right)& .& K\left(x_2, x_N\right)\\ .& .& .& .\\ .& .& .& .\\ K\left(x_{\mathrm{N}}, x_1\right)& K\left(x_{\mathrm{N}}, x_2\right)& .& K\left(x_{\mathrm{N}}, x_N\right)\\ K\left(u_1, x_1\right)& K\left(u_1, x_2\right)& .& K\left(u_1, x_N\right)\\ K\left(u_2, x_1\right)& K\left(u_2, x_2\right)& .& K\left(u_2, x_N\right)\\ .& .& .& .\\ .& .& .& .\\ K\left(u_p, x_1\right)& K\left(u_p, x_2\right)& .& K\left(u_p, x_N\right)\end{array}\right]}_{\left(\right(N+P)\times N)}$$

(26)

The output of RKWELM-UFS can be obtained using Equation (18) used in RKWELM, which is reproduced below:

$$f\left(x\right)=sign{\left[\begin{array}{c}K\left(x_t,x_1\right)\\ .\\ K\left(x_t,x_i\right)\\ .\\ .\\ K\left(x_t,x_N\right)\end{array}\right]}^T{\left(\frac{I}{C}+{\mathsf{\Omega }}_{RKELM-UFS}^T W{\mathsf{\Omega }}_{RKELM-UFS}\right)}^{-1}{ \mathsf{\Omega }}_{RKELM-UFS}^T WT$$

(27)

Here $x_t$ represents the test instance and $x_{i }$represent the training instance for i = 1, 2, …, N.

Algorithm 1 Pseudocode of the proposed RKWELM-UFS

INPUT: Training Dataset $X{\left(x_i,t_i\right)}_{i=1}^N$

Number of Universum samples to be generated: p

OUTPUT:

1: Calculate the kernel matrix ${\mathsf{\Omega }}_{KELM} ϵ \left(N\times N\right)$ as shown in Equation (24) for the N number of original training instances using Equation (21).

2: Calculate the kernel matrix ${\mathsf{\Omega }}_{UFS} ϵ \left(p\times N\right)$ as shown in Equation (25) for the N number of training instances and p number of Universum instances as follows.

for j = 1 to p

Randomly select one majority instance $x_m$

Randomly select one minority instance $x_n$

for i = 1 to N

calculate $K\left(x_j^{mn}, x_i\right)$ using Equation (22)

End

End

3: Augment the matrix ${\mathsf{\Omega }}_{KELM}$ with the matrix ${\mathsf{\Omega }}_{UFS}$ to obtain the reduced kernel matrix using Universum samples ${\mathsf{\Omega }}_{RKELM-UFS}$ shown in Equation (26).

4: To obtain the output weight matrix β use the Equation (23).

5: To determine the class label of an instance x use the Equation (27).

3.4. Computational Complexity

For training of the ELM-based classification algorithm, it is necessary to obtain the output layer weight matrix i.e., $\beta$. For the proposed RKWELM-UFS $\beta$ is obtained using Equation (23) which is reproduced below:

$$\beta ={\left(\frac{I}{C}+{\mathsf{\Omega }}_{RKELM-UFS}^T W{\mathsf{\Omega }}_{RKELM-UFS}\right)}^{-1}\ast {\mathsf{\Omega }}_{RKELM-UFS}^T WT$$

(28)

Here, ${\mathsf{\Omega }}_{RKELM-UFS}$ is a matrix of size $\left(N+p\right)\times N$, where N is the number of training instances and p is the number of Universum samples. The weight matrix, i.e., W, is of size $\left(N+p\right)\times \left(N+p\right)$ and the target matrix i.e., T is of size $\left(N+p\right)\times \left(c\right)$ where c is the number of target class labels; here, the number of target class labels is 2 because we are using the binary classification problems. To compute ${\mathsf{\Omega }}_{RKELM-UFS}$ first we need to compute the ${\mathsf{\Omega }}_{RKELM}$ and ${\mathsf{\Omega }}_{UFS}$. In the following steps the computational complexity of computing $\beta$ is identified step by step:

• The computational complexity of calculating ${\mathsf{\Omega }}_{RKELM}$ i.e., the kernel matrix shown in Equation (24) is $O\left(n{N}^2\right)$, where n is the number of features of training data in input space.
• The computational complexity of calculating matrix ${\mathsf{\Omega }}_{UFS}$ shown in Equation (25) is $O\left(p\right)$.
• The computational complexity of the output weights $\beta$ can be calculated as

  3.1

  Matrix multiplications: $({\mathsf{\Omega }}_{RKELM-UFS}^T W{\mathsf{\Omega }}_{RKELM-UFS})$

  Computational complexity: $O\left(2N{\left(N+p\right)}^2\right)$

  3.2

  Computational complexity of computing the inverse of N × N matrix computed in Step 3.1 is $O\left(N^3\right)$

  3.3

  Computational complexity of matrix multiplications $\left({\mathsf{\Omega }}^{T}WT\right)$ is

  $O\left(N^2\left(N+p\right)+Nc\left(N+p\right)\right)$

  3.4

  Computational complexity of matrix multiplication of 2 matrices obtained in Step 3.1 and Step 3.3 is $O\left(N^{2}c\right)$

The final computational complexity of calculating β is $O\left(2N{\left(N+p\right)}^2+N^3+N^2\left(N+p\right)+N^{2}n+N^{2}c+Nc\left(N+p\right)+p\right)$. The computational complexity can be simplified to $O\left(N^3\right)$ because the value of c is 2, the value of n is smaller than N, and the maximum value of p can be N.

4. Experimental Setup and Result Analysis

This section provides the experiments performed to evaluate the proposed work, which includes the specification of the datasets used for experimentation, the parameter settings of the proposed algorithm, the evaluation metrics used for performance comparison, and the results obtained through experiments and performance comparison with the state-of-the-art classifiers.

4.1. Dataset Specifications

The proposed work uses 44 binary class-imbalanced datasets for performing the experiments. These datasets are downloaded from the KEEL dataset repository [44,45] in 5-fold cross-validation format. Table 2 provides the specification of these datasets. In Table 2, # Attributes denote the number of features, # Instances denotes the number of instances and, IR denotes the class imbalance ratio in the presented datasets. The class imbalance ratio (IR) for the binary class dataset can be defined as follows:

$$IR=\frac{number of instances in majority class}{number of instances in minority class}$$

(29)

Table 2. Specification of 44 benchmark datasets from KEEL dataset repository.

Dataset Name	# Attributes	IR (%)	# Instances	Dataset Name	# Attributes	IR (%)	# Instances
abalone9-18	8	16.70	731	glass6	9	6.43	214
ecoli-01	7	0.54	220	haberman	3	2.81	306
ecoli-013726	7	43.80	281	iris0	4	2.00	150
ecoli-01235	7	9.26	244	new-thyroid1	5	5.14	215
ecoli-01465	6	13.00	280	new-thyroid2	5	5.14	215
ecoli-01472356	7	10.65	336	page-blocks134	10	16.14	472
ecoli-014756	6	12.25	332	pima	8	1.87	768
ecoli-015	6	11.00	240	segment0	19	6.02	2308
ecoli-02345	7	9.06	202	shuttle-c0c4	9	13.78	1829
ecoli-026735	7	9.53	224	Shuttle-c2c4	9	24.75	129
ecoli-0345	7	9.00	200	Vehicle0	18	3.25	846
ecoli-03465	7	9.25	205	Vehicle1	18	2.91	846
ecoli-034756	7	9.25	257	Vehicle2	18	2.89	846
ecoli-0465	6	9.13	203	Vehicle3	18	3.00	846
ecoli-06735	7	9.41	222	vowel0	13	9.97	988
ecoli-0675	6	10.00	220	wisconsin	9	1.86	683
ecoli1	7	3.39	336	yeast05679vs4	8	10.00	528
Ecoli2	7	5.54	336	yeast1289vs7	8	31.00	947
glass016vs2	9	10.00	192	yeast1458vs7	8	28.00	693
glass0123vs456	9	4.00	214	yeast1vs7	7	15.00	459
glass1	9	1.85	214	yeast1vs8	8	24.00	482
glass4	9	16.00	214	yeast3	8	8.13	1484

The datasets used for the experiments are normalized using min-max normalization in the range [1, −1] using the following equation:

$$x^{\prime }=\left(\frac{x-mi{n}_n}{ma{x}_n-mi{n}_n}\right) \ast 2-1$$

(30)

Here, the original feature value of nth feature is denoted by x, minimum value of nth feature is denoted by min_n and the maximum value of nth feature is denoted by max_n.

4.2. Evaluation Matrix

The confusion matrix, also called the error matrix, can be employed to evaluate the performance of a classification model. It allows the visualization of the performance of an algorithm. In a confusion matrix TP denotes True Positive, TN denotes True Negative, FP denotes False Positive, and FN denotes False Negative.

Accuracy is not a suitable measure to evaluate the performance of a classifier when dealing with a class-imbalanced problem. The other performance matrices used for the performance evaluation in such problems are G-mean and AUC (area under the ROC curve). The AUC defines the measure of the entire area under the ROC curve in two dimensions. The ROC known as receiver operating characteristic curve is a graph that shows the performance of the model by plotting $T{P}_{rate}$ and $T{N}_{rate}$ on the graph.

$$\begin{gathered} G_{mean}=\sqrt{T{P}_{rate}\ast T{N}_{rate}} \\ AUC=\frac{1+T{P}_{rate }-T{N}_{rate}}{2} \end{gathered}$$

Here,

$$T{P}_{rate}=\frac{TP}{TP+FN} and T{N}_{rate}=\frac{TN}{TN+FP}$$

4.3. Parameter Settings

The proposed RKWELM-UFS creates Universum samples between randomly selected pairs of majority and minority samples. Because of the randomness, this work presents the mean (denoted as tstR or TestResult) and standard deviation (denoted as std) of the test G-mean and test AUC obtained for 10 trials. The proposed RKWELM-UFS has two parameters, namely the regularization parameter C and the Kernel width parameter σ (denoted as KP). The optimal values of these parameters are obtained using grid search, by varying them on the range $\left\{2^{-18},2^{-16},\dots ,2^{48}, 2^{50}\right\} and \left\{2^{-18},2^{-16},\dots ,2^{18}, 2^{20}\right\}$respectively.

4.4. Experimental Results and Performance Comparison

The proposed RKWELM-UFS is compared with three sets of algorithms used to handle class imbalance learning. The first set contains the existing approaches which use Universum samples in the classification model generation to handle class-imbalanced problems such as MUEKL [16] and USVM [9]. The second set of approaches consists of the single classifiers such as KELM [46], WKELM [18], CCR-KELM [19], and WKSMOTE [23] which are used to handle class-imbalanced problems. The third set contains the popular ensemble classifiers such as RUSBoost [36], BWELM [41], UBRKELMMV [21], UBRKELM-SV [21], UBKELM-MV [22], and UBKELM-SV [22].

The statistical t-test and Wilcoxon signed-rank test are used to evaluate the performance of the proposed RKWELM-UFS and other methods in consideration. In the t-test result, the value of H (null hypothesis) is 1 if the test rejects the null hypothesis at the 5% significance level, and 0 otherwise.

In the Wilcoxon signed-rank test result, the value of H (null hypothesis) is 1 if the test rejects the null hypothesis that there is no difference between the grade medians at the 5% significance level. In the statistical tests, the p-value indicates the level of significant difference between the compared algorithms; the lower the p-value, the higher the significant difference between the compared algorithms. This work uses AUC and G-mean as the measures of the performance evaluation. The AUC results of classifiers MUEKL and USVM shown in Table 3 are obtained from the work MUEKL [16].

Table 3. Performance comparison of the proposed RKWELM-UFS with other existing Universum-based classifiers in terms of average AUC (std, KP, and C denote the standard deviation, Kernel width parameter, and regularization parameter, respectively.

Dataset	MUEKL Test Result% ± std.	USVM Test Result% ± std.	(KP, C)	RKWELM-UFS Test Result% ± std.
abalone9-18	75.06 ± 12.53	69.92 ± 12.75	(26, 226)	94.97 ± 0.52
ecoli-01	98.67 ± 1.83	97.29 ± 2.5	(22, 28)	98.67 ± 0.00
ecoli-01235	90.68 ± 17.67	85.27 ± 14.45	(2−2, 2−18)	92.68 ± 0.00
ecoli013726	85.00 ± 22.36	92.88 ± 1.63	(24, 2−2)	95.99 ± 0.00
ecoli-01465	90.00 ± 13.69	89.62 ± 11.34	(210, 250)	94.34 ± 1.56
ecoli01472356	88.00 ± 7.28	86.73 ± 9.4	(22, 26)	93.95 ± 0.11
ecoli-014756	91.51 ± 4.76	88.13 ± 4.05	(212, 242)	94.93 ± 0.04
ecoli-015	91.59 ± 10.77	88.41 ± 9.62	(28, 234)	95.91 ± 0.04
ecoli-02345	93.89 ± 7.89	88.93 ± 10.36	(28, 234)	94.53 ± 0.08
ecoli-026735	86.51 ± 11.9	78.82 ± 12.03	(22, 24)	90.22 ± 0.09
ecoli-0345	92.22 ± 11.73	91.11 ± 11.65	(28, 240)	91.59 ± 3.29
ecoli-03465	91.96 ± 6.76	88.24 ± 7.94	(210, 244)	97.15 ± 0.07
ecoli-034756	94.49 ± 5.20	88.40 ± 11.89	(210, 240)	95.55 ± 0.00
ecoli-0465	92.23 ± 10.97	89.19 ± 11.15	(26, 234)	94.70 ± 0.06
ecoli-06735	89.50 ± 16.97	86.00 ± 16.62	(2−2, 20)	92.68 ± 0.06
ecoli-0675	91.75 ± 7.05	87.50 ± 7.55	(26, 240)	91.59 ± 0.21
ecoli1	90.48 ± 6.29	87.16 ± 5.03	(22, 211)	93.62 ± 0.29
ecoli2	94.31 ± 4.47	88.78 ± 5.23	(20, 28)	95.35 ± 0.04
glass1	79.66 ± 7.41	67.64 ± 4.64	(2−4, 24)	81.67 ± 0.25
glass6	93.06 ± 7.08	90.63 ± 6.33	(26, 210)	93.41 ± 0.21
haberman	64.27 ± 4.35	62.84 ± 4.56	(28, 242)	68.17 ± 0.73
new-thyroid1	100.00 ± 0.00	96.03 ± 3.7	(2−4, 224)	100.00 ± 0.00
new-thyroid2	100.00 ± 0.00	94.37 ± 4.49	(28, 242)	99.98 ± 0.04
page-blocks134	84.21 ± 19.45	71.49 ± 16.64	(20, 212)	100.00 ± 0.00
pima	73.03 ± 3.11	70.16 ± 5.63	(20, 24)	79.62 ± 0.05
Segment0	99.22 ± 0.90	89.02 ± 3.74	(2−4, 22)	99.93 ± 0.00
shuttle-c0c4	100.00 ± 0.00	99.77 ± 0.27	(22, 2−8)	100.00 ± 0.00
shuttle-c2c4	100.00 ± 0.00	100.00 ± 0.00	(24, 218)	100.00 ± 0.00
vehicle0	99.18 ± 0.66	81.28 ± 6.51	(24, 234)	99.88 ± 0.13
vehicle1	77.43 ± 4.15	62.37 ± 5.14	(26, 232)	90.26 ± 0.45
vehicle2	99.15 ± 0.68	83.59 ± 1.52	(22, 228)	99.73 ± 0.00
vehicle3	76.47 ± 4.81	65.08 ± 3.32	(28, 240)	89.88 ± 0.25
vowel0	100.00 ± 0.00	93.61 ± 3.63	(2−10, 2−18)	100.00 ± 0.00
wisconsin	97.99 ± 0.61	97.09 ± 1.77	(212, 242)	99.08 ± 0.09
yeast3	87.72 ± 2.18	89.60 ± 2.12	(210, 238)	95.09 ± 0.12
Average	90.26 ± 6.73	85.34 ± 6.83		94.15 ± 0.25

4.4.1. Performance Analysis in Terms of AUC

Table 3, Table 4 and Table 5 provide the performance of the proposed RKWELM-UFS and other classification models in terms of AUC. The reported test AUC of the proposed RKWELM-UFS given in Table 3, Table 4 and Table 5 is the averaged test AUC obtained in 10 trials, using 5-fold cross-validation in each trial. Table 3 provides the performance of the proposed RKWELM-UFS and the existing Universum-based classifiers MUEKL and USVM on 35 datasets in terms of average AUC, where the RKWELM outperforms the other classifiers on 32 datasets. Table 4 provides the performance of the proposed RKWELM-UFS and the existing single classifiers like KELM, WKELM, CCR-KELM, and WKSMOTE on 21 datasets in terms of average AUC, where the RKWELM outperforms the other classifiers on 14 datasets. Table 5 provides the performance of the proposed RKWELM-UFS and the existing ensemble of classifiers such as RUSBoost, BWELM, UBRKELM-MV, UBRKELMSV, UBKELM-MV, UBKELM-SV on 21 datasets in terms of average AUC, where the RKWELM outperforms the other classifiers on 10 datasets.

Table 4. Performance comparison of the proposed RKWELM-UFS with existing single classifiers in terms of average AUC (std., KP, and C denotes the standard deviation, Kernel width parameter, and regularization parameter, respectively.

Dataset	KELM Test Result%	WKELM Test Result%	CCR-KELM Test Result%	WKSMOTE Test Result%	(KP, C)	RKWELM-UFS Test Result% ± std.
abalone9vs18	83.81	95.24	83.81	90.91	(26, 226)	94.97 ± 0.52
ecoli01vs5	89.50	92.39	89.50	96.22	(28, 234)	95.91 ± 0.04
glass0123vs456	93.84	97.03	93.84	98.86	(2−2, 24)	97.66 ± 0.54
glass016vs2	81.36	84.11	81.36	83.52	(216, 240)	88.25 ± 0.16
glass4	88.08	93.37	88.00	94.86	(28, 236)	93.34 ± 0.07
haberman	63.91	67.81	63.91	67.34	(28, 242)	68.17 ± 0.73
iris0	100.00	100.00	100.00	100.00	(2−10, 2−18)	100.00 ± 0.00
newthyroid1	99.60	100.00	99.60	99.71	(2−4, 224)	100.00 ± 0.00
newthyroid2	99.60	100.00	99.60	99.92	(28, 242)	99.98 ± 0.04
pageblock13vs4	98.00	100.00	98.00	99.96	(20, 212)	100.00 ± 0.00
pima	74.14	78.30	74.14	79.18	(20, 24)	79.62 ± 0.05
segment0	97.89	98.07	99.80	99.91	(2−4, 22)	99.93 ± 0.00
shuttleC0vsC4	100.00	100.00	100.00	100.00	(22, 2−8)	100.00 ± 0.00
shuttleC2vsC4	100.00	100.00	100.00	100.00	(24, 218)	100.00 ± 0.00
vowel0	100.00	100.00	100.00	57.38	(2−10, 2−18)	100.00 ± 0.00
wisconsin	98.15	98.75	98.15	98.8	(212, 242)	99.08 ± 0.09
yeast05679vs4	74.54	85.72	74.54	78.8	(2−2, 26)	85.63 ± 0.37
yeast1289vs7	65.45	78.73	65.45	77.51	(26, 228)	79.96 ± 0.66
yeast1458vs7	61.76	70.63	61.76	74.91	(26, 218)	71.49 ± 0.41
yeast1vs7	72.15	81.00	72.15	82.89	(24, 216)	83.67 ± 0.10
yeast2vs8	79.39	83.55	79.39	85.55	(2−2, 248)	85.56 ± 0.00
Average	86.72	90.70	86.81	88.87		91.58 ± 0.18

Table 5. Performance Comparison of the proposed RKWELM-UFS with existing ensemble of classifiers in terms of average AUC (std, KP, and C denote the standard deviation, Kernel width parameter, and regularization parameter, respectively).

Dataset	RUSBoost TstR ± std.	BWELM TstR	UBRKELM MV TstR ± std.	UBRKELM SV TstR ± std.	UBKELM MV TstR ± std.	UBKELM SV TstR ± std.	(KP, C)	RKWELM UFS TstR ± std.
abalone9vs18	93.67 ± 0.87	94.13	96.74 ± 1.21	96.84 ± 0.68	96.79 ± 0.55	96.55 ± 0.50	(26, 226)	94.97 ± 0.52
ecoli01vs5	93.94 ± 2.37	93.94	97.53 ± 0.30	97.00 ± 0.09	94.90 ± 2.34	94.13 ± 2.25	(28, 234)	95.91 ± 0.04
glass0123vs456	97.48 ± 0.72	96.57	97.61 ± 0.97	97.40 ± 0.34	97.36 ± 0.80	97.35 ± 0.00	(2−2, 24)	97.66 ± 0.54
glass016vs2	59.25 ± 4.34	85.43	87.10 ± 1.39	87.00 ± 1.40	86.07 ± 0.46	86.74 ± 1.58	(216, 240)	88.25 ± 0.16
glass4	96.18 ± 2.78	96.37	97.51 ± 2.49	97.51 ± 1.91	97.38 ± 0.19	97.83 ± 0.00	(28, 236)	93.34 ± 0.07
haberman	70.38 ± 4.29	68.22	68.50 ± 0.15	68.36 ± 0.22	69.25 ± 0.97	69.32 ± 1.46	(28, 242)	68.17 ± 0.73
iris0	54.85 ± 5.12	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.0 ± 0.0	(2−10, 2−18)	100.0 ± 0.0
newthyroid1	99.70 ± 0.51	100.00	100.00 ± 0.00	100.00 ± 1.11	100.00 ± 0.00	100.00 ± 0.00	(2−4, 224)	100.00 ± 0.00
newthyroid2	99.60 ± 0.21	100.00	100.00 ± 0.00	99.98 ± 0.52	100.00 ± 0.00	100.00 ± 0.00	(28, 242)	99.98 ± 0.04
pageblock13vs4	99.86 ± 0.2	98.00	99.97 ± 1.90	99.91 ± 0.13	100.00 ± 0.00	99.68 ± 0.28	(20, 212)	100.00 ± 0.00
pima	79.91 ± 0.93	79.10	80.03 ± 1.14	80.78 ± 0.48	79.87 ± 0.42	80.55 ± 0.48	(20, 24)	79.62 ± 0.05
segment0	100.0 ± 0.0	99.89	99.95 ± 0.00	99.91 ± 0.13	99.84 ± 0.00	99.64 ± 5.80	(2−4, 22)	99.93 ± 0.00
shuttleC0vsC4	80.00 ± 6.67	99.20	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(22, 2−8)	100.00 ± 0.00
shuttleC2vsC4	81.91 ± 7.10	99.20	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(24, 218)	100.00 ± 0.00
vowel0	100.00 ± 0.00	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.0 ± 0.0	(2−10, 2−18)	100.0 ± 0.00
wisconsin	98.37 ± 0.31	98.15	99.05 ± 0.00	98.98 ± 0.14	98.72 ± 0.15	99.08 ± 0.14	(212, 242)	99.08 ± 0.09
yeast05679vs4	87.97 ± 1.02	84.08	86.09 ± 0.30	86.25 ± 1.28	85.86 ± 0.84	88.75 ± 1.07	(2−2, 26)	85.63 ± 0.37
yeast1289vs7	74.91 ± 1.81	78.44	80.59 ± 0.84	80.60 ± 0.53	80.52 ± 0.08	80.59 ± 0.07	(26, 228)	79.96 ± 0.66
yeast1458vs7	65.94 ± 2.14	70.72	72.77 ± 0.00	72.77 ± 1.08	72.98 ± 2.11	73.08 ± 1.37	(26, 218)	71.49 ± 0.41
yeast1vs7	86.53 ± 2.05	82.89	82.90 ± 1.17	82.41 ± 0.76	84.06 ± 1.29	86.09 ± 0.58	(24, 216)	83.67 ± 0.10
yeast2vs8	79.92 ± 2.45	84.42	84.32 ± 2.14	84.62 ± 1.29	84.08 ± 0.12	84.35 ± 0.00	(2−2, 248)	85.56 ± 0.00
Average	85.73 ± 2.19	90.89	91.94 ± 0.67	91.92 ± 0.58	91.79 ± 0.49	92.08 ± 0.74		91.58 ± 0.18

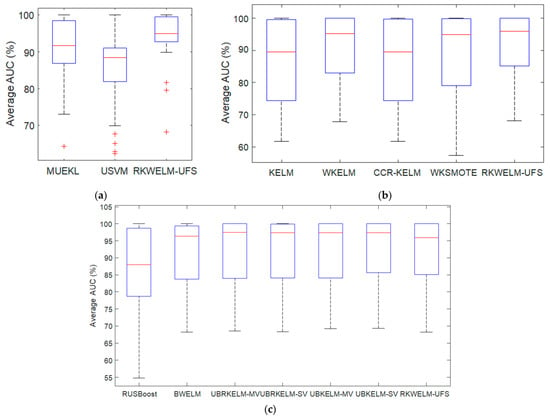
Figure 1a–c shows the boxplot diagram for the AUC results of the classifiers on various datasets shown in Table 3, Table 4 and Table 5 respectively. The boxplot creates a visual representation of the data to visualize the performance. It can be seen in Figure 1a,b that the proposed method RKWELM-UFS has the highest median value and smallest inter-quantile range, which shows that the RKWELM-UFS is performing better than MUEKL, USVM, KELM, WKELM, CCR-KELM, and WKSMOTE. It can be seen in Figure 1c that RKWELM-UFS is performing better than RUSBoost. Table 6 provides the t-test results and Table 7 provides the Wilcoxon Signed-rank test results on the AUC of various algorithms provided in Table 3, Table 4 and Table 5 for comparison. The results provided in Table 6 and Table 7 suggest that the proposed RKWELM-UFS performs significantly better than MUEKL, USVM, KELM, WKELM, CCR-KELM, RUSBoost, and BWELM, and its performance is approximately similar to that of WKSMOTE, UBRKELM-MV, UBRKELM-SV, UBKELMMV, and UBKELM-SV in terms of AUC.

Figure 1. Boxplot diagrams; each box visually represents the performance in terms of average AUC of algorithms labeled on X axis. (a) Boxplot for results of Table 3. (b) Boxplot for results given in Table 4. (c) Boxplot for results given in Table 5.

Table 6. T-test results for performance comparison in terms of AUC between the methods given in Table 3, Table 4 and Table 5.

Methods Compared	Stats	p	H (0.05)
MUEKL vs. RKWELM-UFS	[−5.610820138186867; −2.152174147527417]	6.32 × 10−5	1
USVM vs. RKWELM-UFS	[−11.440221923933274; −6.167915218923865]	8.34 × 10−8	1
KELM vs. RKWELM-UFS	[−6.93534639982032; −2.78405360017968]	8.98 × 10−5	1
WKELM vs. RKWELM-UFS	[−1.46246304953657; −0.301698855225338]	4.81 × 10−3	1
CCR-KELM vs. RKWELM-UFS	[−6.88366104582675; −2.66145323988753]	1.33 × 10−4	1
WKSMOTE vs. RKWELM-UFS	[−6.99623994510679; 1.56922089748774]	2.01 × 10−1	0
RUSBoost vs. RKWELM-UFS	[−11.4335320049264; −0.266820376026017]	0.040906	1
BWELM vs. RKWELM-UFS	[−1.21328125091469; −0.165166368132924]	0.012527	1
UBRKELM-MV vs. RKWELM-UFS	[−0.169420432040612; 0.87763947965966]	0.17363	0
UBRKELM-SV vs. RKWELM-UFS	[−0.196630485917308; 0.872468581155405]	0.20219	0
UBKELM-MV vs. RKWELM-UFS	[−0.352563193428057; 0.776972717237582]	0.44236	0
UBKELM-SV vs. RKWELM-UFS	[−0.184407389564474; 1.18500738956447]	0.14312	0

Table 7. Wilcoxon Signed-rank test results for performance comparison in terms of AUC between the methods given in Table 3, Table 4 and Table 5.

Methods Compared	Zval	Signedrank	p-Value	H (0.05)
MUEKL vs. RKWELM-UFS	−4.62478463	12.00	3.75 × 10−6	1
USVM vs. RKWELM-UFS	−5.086213249	0.00	3.65 × 10−7	1
KELM vs. RKWELM-UFS	−3.621365173	0	2.93 × 10−4	1
WKELM vs. RKWELM-UFS	0	10	2.62 × 10−3	1
CCR-KELM vs. RKWELM-UFS	−3.621365173	0	2.93 × 10−4	1
WKSMOTE vs. RKWELM-UFS	−1.763789403	45	7.78 × 10−2	0
RUSBoost vs. RKWELM-UFS	−2.015964161	51	0.043803724	1
BWELM vs. RKWELM-UFS	−2.765775456	22	0.005678762	1
UBRKELM-MV vs. RKWELM-UFS	1.189301687	91	0.234320972	0
UBRKELM-SV vs. RKWELM-UFS	0.930757842	86	0.351978842	0
UBKELM-MV vs. RKWELM-UFS	0	73	0.488708496	0
UBKELM-SV vs. RKWELM-UFS	1.241010456	92	0.214601886	0

4.4.2. Performance Analysis in Terms of G-mean

Table 8 and Table 9 provide the performance of the proposed RKWELM-UFS and other classification models in terms of the G-mean. The reported test G-mean of the proposed RKWELM-UFS given in Table 8 and Table 9 is the averaged test g-mean obtained in 10 trials, using 5-fold cross-validation in each trial. Table 8 provides the performance of the proposed RKWELM-UFS and the existing single classifiers such as KELM, WKELM, CCR-KELM, and WKSMOTE on 21 datasets in terms of average G-mean, where the RKWELM outperforms the other classifiers on 16 datasets. Table 9 provides the performance of the proposed RKWELM-UFS and the existing ensemble of classifiers such as RUSBoost, BWELM, UBRKELM-MV, UBRKELMSV, UBKELM-MV, and UBKELM-SV on 21 datasets in terms of average Gmean, where the RKWELM outperforms the other classifiers on seven datasets.

Table 8. Performance Comparison of the proposed RKWELM-UFS with existing single classifiers in terms of average G-mean (std., KP, and C denote the standard deviation, Kernel width parameter, and regularization parameter, respectively).

Dataset	KELM Test Result%	WKELM Test Result%	CCR-KELM Test Result%	WKSMOTE Test Result%	(KP, C)	RKWELM-UFS TestResult% ± std.
abalone9vs18	72.71	89.76	76.56	91.94	(26, 226)	92.23 ± 0.57
ecoli01vs5	88.36	91.34	88.36	88.00	(210, 242)	93.01 ± 0.11
glass0123vs456	93.26	95.41	93.26	94.19	(2−2, 24)	96.06 ± 0.55
glass016vs2	63.20	83.59	81.36	79.00	(216, 240)	84.46 ± 0.50
glass4	85.93	91.17	87.22	89.00	(28, 236)	91.49 ± 0.14
haberman	57.23	66.26	59.71	65.21	(24, 212)	66.02 ± 0.57
iris0	100.00	100.00	100.00	100.00	(2−10, 2−18)	100.00 ± 0.00
newthyroid1	99.16	99.72	99.16	88.69	(2−2, 212)	99.44 ± 0.00
newthyroid2	99.44	99.72	99.44	90.72	(2−6, 2−18)	99.44 ± 0.00
pageblock13vs4	97.89	98.07	97.84	97.38	(20, 216)	100.00 ± 0.00
pima	71.16	75.58	73.61	74.00	(20, 24)	75.60 ± 0.19
segment0	97.89	98.07	99.57	100.00	(2−8, 2−18)	99.54 ± 0.00
shuttleC0vsC4	100.00	100.00	100.00	100.00	(22, 2−8)	100.00 ± 0.00
shuttleC2vsC4	94.14	100.00	100.00	100.00	(24, 218)	100.00 ± 0.00
vowel0	100.00	100.00	100.00	100.00	(2−10, 2−18)	100.00 ± 0.00
wisconsin	97.22	97.70	97.18	96.33	(212, 242)	97.89 ± 0.07
yeast05679vs4	68.68	82.21	82.24	81.00	(2−2, 26)	81.03 ± 0.47
yeast1289vs7	60.97	71.41	59.28	69.83	(2−2, 20)	73.35 ± 0.05
yeast1458vs7	59.89	69.32	66.24	67.00	(2−4, 26)	67.54 ± 0.09
yeast1vs7	64.48	77.72	68.32	76.00	(22, 22)	77.77 ± 0.15
yeast2vs8	77.24	77.89	78.91	80.00	(20, 226)	81.36 ± 1.42
Average	83.28	88.81	86.11	87.06		89.74 ± 0.17

Table 9. Performance Comparison of the proposed RKWELM-UFS with existing ensemble of classifiers in terms of average G-mean (std., KP, and C denote the standard deviation, Kernel width parameter, and regularization parameter, respectively).

Dataset	RUSBoost TstR ± std.	BWELM TstR	UBRKELM MV TstR ± std.	UBRKELM SV TstR ± std.	UBKELM MV TstR ± std.	UBKELM SV TstR ± std.	(KP, C)	RKWELM UFS TstR ± std.
abalone9vs18	86.40 ± 1.33	90.12	92.28 ± 0.00	92.30 ± 0.00	91.53 ± 0.96	91.07 ± 3.45	(26, 226)	92.23 ± 0.57
ecoli01vs5	88.92 ± 1.55	89.36	93.53 ± 0.00	93.09 ± 0.09	93.63 ± 0.43	94.02 ± 1.07	(210, 242)	93.01 ± 0.11
glass0123vs456	93.74 ± 0.84	94.21	95.67 ± 0.68	95.91 ± 0.51	95.24 ± 0.90	95.45 ± 0.25	(2−2, 24)	96.06 ± 0.55
glass016vs2	52.46 ± 3.04	84.21	84.26 ± 0.50	84.42 ± 0.35	84.48 ± 0.43	83.89 ± 1.29	(216, 240)	84.46 ± 0.50
glass4	87.31 ± 2.82	90.30	91.69 ± 2.10	91.57 ± 2.86	92.91 ± 2.82	92.86 ± 3.30	(28, 236)	91.49 ± 0.14
haberman	53.36 ± 7.21	65.14	66.34 ± 0.13	70.20 ± 4.23	66.70 ± 0.88	66.49 ± 1.50	(24, 212)	66.02 ± 0.57
iris0	19.85 ± 10.38	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(2−10, 2−18)	100.0 ± 0.0
newthyroid1	98.05 ± 0.95	100.00	99.55 ± 0.20	99.61 ± 0.14	99.29 ± 0.49	99.47 ± 0.13	(2−2, 212)	99.44 ± 0.00
newthyroid2	96.94 ± 0.91	99.72	99.44 ± 0.13	99.44 ± 0.13	99.13 ± 0.00	99.30 ± 0.08	(2−6, 2−18)	99.44 ± 0.00
pageblock13vs4	97.96 ± 1.21	99.89	99.41 ± 0.12	99.91 ± 0.13	100.00 ± 0.00	100.00 ± 0.00	(20, 216)	100.00 ± 0.00
pima	70.34 ± 1.45	75.48	76.11 ± 0.21	76.22 ± 0.22	75.76 ± 0.31	75.84 ± 0.34	(20, 24)	75.60 ± 0.19
segment0	99.99 ± 0.00	99.89	99.80 ± 0.13	99.68 ± 0.28	99.63 ± 1.10	99.64 ± 5.80	(2−8, 2−18)	99.54 ± 0.00
shuttleC0vsC4	60.00 ± 13.33	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(22, 2−8)	100.00 ± 0.00
shuttleC2vsC4	68.50 ± 15.89	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(24, 218)	100.00 ± 0.00
vowel0	100.00 ± 0	100.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	(2−10, 2−18)	100.00 ± 0.00
wisconsin	95.46 ± 0.77	97.18	97.81 ± 0.00	97.81 ± 0.00	97.72 ± 0.20	97.79 ± 0.18	(212, 242)	97.89 ± 0.07
yeast05679vs4	77.55 ± 1.63	80.96	81.82 ± 1.98	82.62 ± 0.09	82.24 ± 0.33	83.45 ± 2.29	(2−2, 26)	81.03 ± 0.47
yeast1289vs7	67.83 ± 2.96	72.67	75.54 ± 0.84	75.27 ± 0.12	74.28 ± 1.05	74.73 ± 1.72	(2−2, 20)	73.35 ± 0.05
yeast1458vs7	59.59 ± 3.43	69.87	69.54 ± 1.48	69.54 ± 1.74	71.24 ± 1.69	70.15 ± 1.31	(2−4, 26)	67.54 ± 0.09
yeast1vs7	73.49 ± 1.79	77.72	78.90 ± 7.44	78.41 ± 0.76	77.73 ± 0.00	77.90 ± 1.54	(22, 22)	77.77 ± 0.15
yeast2vs8	72.16 ± 1.83	78.35	80.77 ± 2.42	80.10 ± 0.22	80.05 ± 2.44	81.69 ± 1.51	(20, 226)	81.36 ± 1.42
Average	77.39 ± 3.59	89.34	90.08 ± 0.80	90.30 ± 0.58	90.08 ± 0.58	90.10 ± 1.21		89.74 ± 0.17

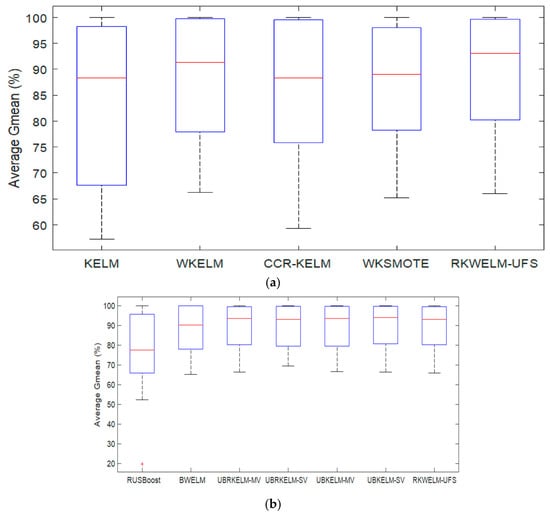
Figure 2a,b shows the boxplot diagram for the G-mean results of the classifiers on various datasets shown in Table 8 and Table 9, respectively. It can be seen in Figure 2a that the proposed RKWELM-UFS has the highest median value and smallest inter-quantile range, which shows that the RKWELM-UFS is performing better than KELM, WKELM, CCR-KELM, and WKSMOTE in terms of the G-mean. It can be seen in Figure 2b that RKWELM-UFS is performing better than RUSBoost and BWELM in terms of the G-mean. Table 10 provides the t-test results and Table 11 provides the Wilcoxon signed-rank test results on the G-mean of various algorithms provided in Table 8 and Table 9 for comparison. The results provided in Table 10 and Table 11 suggest that the proposed RKWELM-UFS performs significantly better than KELM, CCR-KELM, WKSMOTE, and RUSBoost, and performs approximately similarly to WKELM, BWELM, UBRKELM-MV, UBRKELM-SV, UBKELM-MV, UBKELM-SV in terms of the G-mean.

Figure 2. Boxplot diagrams; each box visually represents the performance in terms of average G-mean of algorithms labelled on X axis. (a) Boxplot for G-mean results given in Table 8. (b) Boxplot for G-mean results given in Table 9.

Table 10. T-test results for performance comparison in terms of G-mean between the methods given in Table 8 and Table 9.

Methods Compared	Stats	p	H (0.05)
KELM vs. RKWELM-UFS	[−8.97586793133104; −3.15547492581182]	3.12 × 10−4	1
WKELM vs. RKWELM-UFS	[−1.10027216529072; 0.0251197843383338]	6.01 × 10−2	0
CCR-KELM vs. RKWELM-UFS	[−5.34275272694909; −1.13049489209853]	4.44 × 10−3	1
WKSMOTE vs. RKWELM-UFS	[−3.63784233634963; −0.927786235078946]	2.18 × 10−3	1
RUSBoost vs. RKWELM-UFS	[−20.961933935114; −3.45036130298126]	0.0086978	1
BWELM vs. RKWELM-UFS	[−1.12033850136527; 0.0575670727938417]	7.45 × 10−2	0
UBRKELM-MV vs. RKWELM-UFS	[−0.0326448040855254; 0.626063851704572]	0.074868	0
UBRKELM-SV vs. RKWELM-UFS	[−0.0440133837744108; 0.984099098060123]	0.070939	0
UBKELM-MV vs. RKWELM-UFS	[−0.207557995239237; 0.715262757143997]	0.26467	0
UBKELM-SV vs. RKWELM-UFS	[−0.0647504586179029; 0.780074268141712]	0.092621	0

Table 11. Wilcoxon signed-rank test results for performance comparison in terms of G-mean between the methods given in Table 8 and Table 9.

Methods Compared	Zval	Signed Rank	p-Value	H (0.05)
KELM vs. RKWELM-UFS	−3.723555406	0	1.96 × 10−4	1
WKELM vs. RKWELM-UFS	−1.822772421	38	6.83 × 10−2	0
CCR-KELM vs. RKWELM-UFS	−3.289998425	7	1.00 × 10−3	1
WKSMOTE vs. RKWELM-UFS	−3.479350852	3	5.03 × 10−4	1
RUSBoost vs. RKWELM-UFS	−3.882597643	1	1.03 × 10−4	1
BWELM vs. RKWELM-UFS	−1.917193327	36	5.52 × 10−2	0
UBRKELM-MV vs. RKWELM-UFS	1.585826579	110	0.112778655	0
UBRKELM-SV vs. RKWELM-UFS	1.917193327	117	0.055213376	0
UBKELM-MV vs. RKWELM-UFS	0.723922766	82	0.469113152	0
UBKELM-SV vs. RKWELM-UFS	1.525663664	97.5	0.127093648	0

5. Conclusions and Future Work

The use of additional data for training along with the original training data has been employed in many approaches. The Universum data are used to add prior knowledge about the distribution of data in the classification model. Various ELM-based classification models have been suggested to handle the class imbalance problem, but none of these models use prior knowledge. The proposed RKWELM-UFS is the first attempt that employs Universum data to enhance the performance of the RKWELM classifier. This work generates the Universum samples in the feature space using the kernel trick. The reason behind the creation of the Universum instances in the feature space is that the mapping of input data to the feature space is not conformal. The proposed work is evaluated on 44 benchmark datasets with an imbalance ratio between 0:45 to 43:80 and a number of instances between 129 to 2308. The proposed method is compared with 10 state-of-the-art methods used for class-imbalanced dataset classification. G-mean and AUC are used as metrics to evaluate the performance of the proposed method. The paper also incorporates statistical tests to verify the significant performance difference between the proposed and compared methods.

In Universum data-based learning, it has been observed that the efficiency of such classifiers depends on the quality and volume of Universum data created. The methodology of choosing or creating the appropriate Universum samples should be the subject of further research. In the proposed work, the Universum samples are created between randomly selected pairs of majority and minority class samples. In the future, some strategic concepts can be used to select the majority and minority samples instead of random selection. In the future, Universum data can be incorporated in other ELM-based classification models to enhance their learning capability on class imbalance problems. The future work also includes the development of a multi-class variant of the proposed RKWELM-UFS.