Predication and Photon Statistics of a Three-Level System in the Photon Added Negative Binomial Distribution

Abstract

Statistical and artificial neural network models are applied to forecast the quantum scheme of a three-level atomic system (3LAS) and field, initially following a photon added negative binomial distribution (PANBD). The Mandel parameter is used to detect the photon statistics of a radiation field. Explicit forms of the PANBD are given. The prediction of the Mandel parameter, atomic probability of the 3LAS in the upper state, and von Neumann entropy are obtained using time series and artificial neural network methods. The influence of probability success photons and the number of added photons to the NBD are examined. The total density matrix is used to compute and analyze the time evolution of the initial photonic negative binomial probability distribution that governs the 3LAS–field photon entanglement behavior. It is shown that the statistical quantities are strongly affected by probability success photons and the number of added photons to the NBD. Also, the prediction of quantum entropy is achieved by the time series and neural network.

1. Introduction

Nonclassical states of the radiation fields, including number states, coherent states, and phase states, are significant in quantum optics and literature [1]. The statistical features of the radiation field in the Binomial Distribution (BD) and Negative Binomial Distribution (NBD) were examined by Barnett [2]. It is shown that the two types of field states share parallel features if the roles of the creation and annihilation operators are interchanged. Also, the photon number distribution of the field in the NBD has been introduced. It is shown that these states demonstrate a powerful squeezing impact and follow the super-Poissonian statistics [3,4]. The NBD was found along much the same lines as even, odd, superposition, entangled and deformed states, and special cases of nonlinear coherent states [5]. For instance, the statistical estimation of the even and odd BD was explored (e.g., [6]). Furthermore, the quantum superposition version of these states was represented in [7]. Another generalization was introduced as q-deformed BD [8]. The non-classical features and algebraic arrangements of the even and odd Wigner NBD were investigated [9]. Other interesting non-classical states caused by the excitations of quantum states underwent examination. Originally, Agarwal and Tara [10] developed these states in the form of the Photon Added Coherent State (PACS), which depicts a remarkable non-classical property, including sub-Poissonian photon statistics and squeezing in a radiation field. The photon-added quantum states, e.g., even and odd coherent states, excited squeezed states, as well as excited thermal states, were examined [11,12,13,14].

The excited quantum state of light resulting from adding a number of photons to the optical field photon distributions play a central role in quantum statistics and quantum information processing. In the framework of probability theory, the authors of [15,16] explored the non-classical states engendered by excitations on particular quantum states. These states exhibit remarkable non-classical features, including sub-Poissonian photon statistics and squeezing in the quadrature of the radiation field. The literature contains many excited quantum states such as even and odd excited coherent states [17], Even and odd nonlinear negative binomial states [9,18], photon-subtracted squeezed thermal states [19], and excited thermal states [20]. To determine the observable information about a parameter, the quantum Fisher information is used to define the statistical features of two qubits in two modes of a Gaussian distribution [21].

The photon addition and subtraction perform different tasks in quantum optics and information processing. In this regard, a new kind of photon-added entangled coherent states (PA-ECSs) [22], and by performing repeatedly a f-deformed photon-addition operation has been introduced [23], as well as a new entangled quantum states which were studied by applying local coherent superposition in the cases of photon subtraction and addition to each mode of an even entangled coherent state [24]. It is shown that the improving of entanglement and fidelity depend on the even or odd order of coherent superposition. Furthermore, the influence of two-qubit entangled states on the Dissipative entanglement swapping in the presence of detuning and Kerr medium has been investigated [25]. The obtained results clarified that the main conditions of creating a long-living atom-atom maximally entangled state in the presence of Kerr effect and dissipation.

The outcomes of measuring some physical quantities led to understanding the behavior of many different physical systems [26,27]. In addition, the expansion of quantum information technology gave more information and increased awareness of the nonlocal correlation phenomena. These phenomena performed an important task in quantum estimation and quantum metrology [26,27]. The entanglement or the nonlocal correlation can be the core of several implementations of quantum technologies [28,29,30]. Also, entanglement performs optimal tasks in quantum algorithms and quantum image processing.

The Auto Regressive Integrated Moving Average (ARIMA) can typically attract linear forms within a time series competently. Various papers were conducting on evaluating the relationships between variables or using ARIMA forecasts as a benchmark against which to examine other models’ effectiveness [31]. Along with the evolution of machine-learning algorithms for identifying phases of matter, utilizing artificial neural networks has developed to characterize quantum states and resolve related quantum many-body issues [32]. Also, the mathematical modeling and statistical analysis of results have different applications in quantum and fluid mechanics [33,34,35,36].

In this article, the statistical data analysis is investigated for the dynamics of a generalized model depending on the interaction between a 3LAS and a field initially prepared in the NBD and PANBD. Its structure is in the following form. The related statistical model based on time series and artificial neural network is presented in Section 2. Section 3 investigates the dynamics of the radiation field in NBD and PANBD. The main quantities related to the field’s statistical and nonlocal features, including photon statistics via the evolution of Mandel parameter, atomic population probability, and nonlocal correlation between 3LAS and radiation field measured by the von Neumann entropy are investigated in Section 4. The last section contains the conclusion.

2. The Related Statistical Model

A determined task is establishing the appropriate time series models. A time series with single (scalar) observations recorded sequentially over equal time increments is known as “univariate time series”. Forecasting is envisaging the values for the series of phenomena under study [37]. The time series is a prerequisite of envisaging time series with ARIMA model and should be stationary, or, at least, trend stationary [38]. A stationary series is one that has no trend and the various values around the mean demonstrate a constant amplitude [39,40]. Although ARIMA expects a stationary stochastic process as input, very few datasets are natively in such a format. Thus, the use of differencing “stationarise” is in the model identification stage. The ARIMA model has 3 key parameters (p, d, q) that are non-negative integers: p denotes the order (the number of time lags) of the autoregressive model, d denotes the degree of differentiating (the times in which the data had past values subtracted when choosing a random walk), and q represents the order of the moving-average model. The values for $p, d$ and $q$ are determined using calculations and subsequent analyses. Establishing an appropriate ARIMA model by calculating these parameters is commonly known as the Box–Jenkins method.

The integration of the $p$ autoregressive and $q$ moving average terms gives rise to the formula [41]

$$\widehat{y}=c+{ϵ}_t+{{\displaystyle \sum }}_{i=1}^p{\varnothing }_i{y}_t+{{\displaystyle \sum }}_{i=1}^q{\theta }_i{ϵ}_{t-1}$$

(1)

where $c$ represents a constant variable, error terms $ϵ$ are usually thought of as being independent, uniformly distributed random variables, $\widehat{y}$ are previous observed values of the time-series, and ${\varnothing }_i$ and ${\theta }_i$ are the coefficients determined as part of the process.

Multi-Layer Perceptrons (MLP) Model

The definition of an artificial neural network is a computational system that consists of a set of highly interconnected processing elements called neurons that process information in response to external stimuli. By using mathematical equations, an artificial neuron simulates the signal integration and threshold firing behavior of biological neurons. Like their biological counterparts, artificial neurons are connected by connections that define the flow of information between them. An excitatory or inhibitory stimulus can be transmitted from one element to another via synapses. If a neuron that receives excitatory input is more likely to transmit excitatory signals to the other neurons it is connected to. The opposite would be the case for inhibitory input.

The inputs established using one processing element (depicted in Figure 1) are representable as an input vector $A=\left(x_1,x_2,\dots .,x_n\right),$ in which ai denotes the signal from the ith input. A weight relates to each connected pair of neurons. Therefore, weights related to the jth neuron are representable as a weight vector of the form $W=\left(w_1,w_2,\dots .,w_m\right)$, where $w_m$ denotes the weight related to the connection of the processing element ai to the processing element $x_n$. A threshold value is contained in a neuron to regulate its action potential. The weights related to the neuron’s inputs define the action potential of a neuron (Equation (1)), whereas a threshold modifies a neuron’s response to a certain stimulus restricting such response to a pre-defined range of values. Equation (2) determines the output y of a neuron as an activation function $\phi$ of the weighted sum of n + 1 inputs. These n + 1 agree with the n incoming signals. The threshold, as an extra input, is combined into the equation.

$$y=\phi \left({\displaystyle \sum }_{i=1}^n{x}_i{w}_i \right),$$

(2)

$$\phi \left(x\right)=\left\{\begin{array}{c}1 \mathrm{i}\mathrm{f} \phi \left({\displaystyle \sum _{i=0}^n}{x}_i{w}_i\right)>0 \\ 0 \mathrm{i}\mathrm{f} \phi \left({\displaystyle \sum _{i=0}^n}{x}_i{w}_i\right)<0\end{array} \right.$$

(3)

$$\phi \left(x\right)=\frac{e^x}{e^x + 1 },$$

(4)

$$\phi \left(x\right)=\frac{e^{2x} - 1}{e^{2x} + 1 }$$

(5)

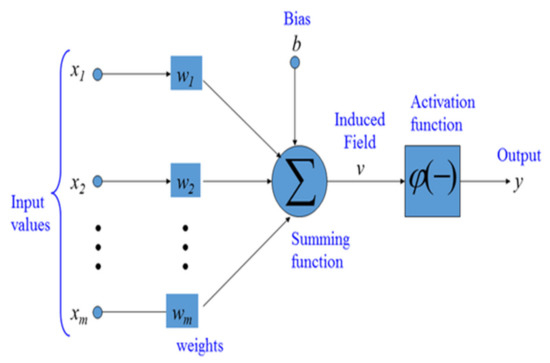
Figure 1. The inputs established using one single processing element.

In this study, the commonly used accuracy metrics to judge forecasts are applied [37]:

➢

Mean Absolute Percentage Error (MAPE)

➢

Symmetric Mean Absolute Percentage Error (SMAPE)

➢

Mean Absolute Scaled Error (MASE)

3. Dynamics of Radiation Field in the PANBD

In this section, we argue that the photons are initially arranged separately with a NBD and PANBD by the experimental set-up presented in [42,43], respectively, then brought to the cavity through a tiny aperture. The initial state of the photonic field takes the form of

$${\rho }_{RF}\left(0\right)=|p;M⟩⟨p;M|,$$

(6)

where

$${|p; M⟩}_{\mathrm{NBS}}={\displaystyle \sum }_{n=0}^{\infty }\sqrt{B_n\left(p,M\right)}|n⟩$$

(7)

with

$$B_n\left(p;M\right)=\left(\begin{array}{c}M+n-1\\ n\end{array}\right)p^n{\left(1-p\right)}^M, n=0,1,\dots \dots$$

(8)

where $M$ denotes the fixed positive integer, $p$ represents the probability of success fulfilling $0<p<1$. The states (7) are labeled NBD because their photon distribution $⟨n|p;M⟩=B_n\left(p;M\right)$ is the NBD.

As a probability distribution satisfies ${\displaystyle \sum }_{n=0}^{\infty }{B}_n\left(p,M\right)=1$. For the case of $p\to 0$, $B_n\left(p,M\right)\to {\delta }_{n0}$ the NBD go to the vacuum state. For the case of $p\to 0$ and $M\to \infty$ with fixed finite $pM={⟨n⟩}^2$, the NBD goes to the Poisson distribution, and $B_n\left(p,M\right)$ will be the coherent state $B_n\left(p,M\right)\to \frac{e^{-{⟨n⟩}^2}{⟨n⟩}^n}{n!}$. Therefore, the NBD degenerates to the ordinary coherent states. The PANBD via some photons added to the field $k$ is obtained by $|p;M,k{⟩}_{\mathrm{PANBS}}={\widehat{\mathrm{b}}}^{†}{}^k|p;M{⟩}_{\mathrm{NBS}}$ where is the creation operator.

An extension of the 3LAS has $\Xi$ -type, coupled to a mode field described by the Hamiltonian, is considered as

$$\begin{gathered} {\widehat{H}}_I={\alpha }_1\left(\widehat{\mathrm{b}}|u⟩⟨m|+{\hat{\mathrm{b}}}^{†}|m⟩⟨u|\right) \\ +{\alpha }_2\left(\hat{\mathrm{b}}|m⟩⟨l|+{\hat{\mathrm{b}}}^{†}|l⟩⟨m|\right), \end{gathered}$$

(9)

In Equation (9), the 3LAS consists of two transitions of one photon, between the upper level $|u⟩$ and the middle level $|\mathit{m}⟩$. The operators $\widehat{\mathit{b}}$ and ${\widehat{\mathit{b}}}^{+}$, respectively, denoting the annihilation and creation operators of the field, ${\mathit{\alpha }}_{\mathbf{1}}$ and ${\mathit{\alpha }}_{\mathbf{2}}$ are the field-atom coupling constants and assumed to be an equal ${\mathit{\alpha }}_{\mathbf{2}}={\mathit{\alpha }}_{\mathbf{1}}=$ $\mathit{\alpha }$. The transition between the lower atomic level $|\mathit{l}⟩$ and the middle atomic level $|\mathit{m}⟩$ is also achieved by one photon. Finally, the transition between levels $|\mathit{u}⟩$ and $|\mathit{l}⟩$ is dipole forbidden.

The wave function is then obtained by solution of the Schrodinger equation

$$i\frac{d}{dt}|\psi \left(\mathrm{t}\right)⟩={\widehat{\mathit{H}}}_I|\psi \left(\mathrm{t}\right)⟩,\hspace{1em}\hspace{1em}\hspace{1em}\mathit{\hslash }=1.$$

(10)

The bipartite system wave function at $t=0$ takes the form of

$$|{\psi }_{3\mathrm{LAS}-F}\left(\mathbf{0}\right)⟩=|{\psi }_{3\mathrm{LAS}}\left(\mathbf{0}\right)⟩\otimes |{\psi }_F\left(\mathbf{0}\right)=|u⟩\otimes |p;M,k⟩$$

(11)

The final 3LAS-field state at any time takes the following form

$$|{\psi }_{3\mathrm{LAS}-F}\left(\mathit{t}\right)⟩={\displaystyle \sum }_{\mathit{n}=\mathbf{0}}^{\infty }{\mathit{y}}_{\mathbf{1}}\left(\mathit{n},\mathit{t}\right) |\mathit{n},\mathit{u}⟩+{\mathit{y}}_{\mathit{2}}\left(\mathit{n},\mathit{t}\right) |\mathit{n}+\mathbf{1},\mathit{m}⟩+{\mathit{y}}_{\mathbf{3}}\left(\mathit{n},\mathit{t}\right) |\mathit{n}+\mathbf{2},\mathit{l}⟩$$

(12)

Under the Hamiltonian (9) and substituting in the Schrödinger Equation (10) we have three coupled ordinary differential equations are obtained as

$$\begin{gathered} \mathit{i}\frac{\mathit{d}{\mathit{y}}_{\mathbf{1}}\left(\mathit{n},\mathit{t}\right)}{\mathit{d}\mathit{t}}={\mathbf{\alpha }}_{\mathbf{1}}\mathit{f}\sqrt{\mathit{n}}{\mathit{y}}_{\mathbf{2}}\left(\mathit{n}\mathbf{-}\mathbf{2},\mathit{t}\right), \\ \mathit{i}\frac{\mathit{d}{\mathit{y}}_{\mathbf{2}}\left(\mathit{n},\mathit{t}\right)}{\mathit{d}\mathit{t}}={\mathbf{\alpha }}_{\mathbf{1}}\sqrt{\mathit{n}\mathbf{+}\mathbf{2}}{\mathit{y}}_{\mathbf{1}}\left(\mathit{n}+\mathbf{2},\mathit{t}\right) \\ +{\mathbf{\alpha }}_{\mathbf{2}}\mathit{f}\left(\mathit{n}+\mathbf{1}\right)\sqrt{\mathit{n}+\mathbf{1}}{\mathit{y}}_{\mathbf{3}}\left(\mathit{n}-\mathbf{2},\mathit{t}\right), \\ \mathit{i}\frac{\mathit{d}{\mathit{y}}_{\mathbf{3}}\left(\mathit{n},\mathit{t}\right)}{\mathit{d}\mathit{t}}={\mathbf{\alpha }}_{\mathbf{2}}\sqrt{\mathit{n}+\mathbf{2}}{\mathit{y}}_{\mathbf{2}}\left(\mathit{n}+\mathbf{2},\mathit{t}\right). \end{gathered}$$

(13)

The reduced density operator ${\mathbf{\rho }}_{3\mathrm{LAS}}\left(\mathit{t}\right)$ maybe written as

$${\mathbf{\rho }}_{3\mathrm{LAS}}\left(\mathit{t}\right)=\mathbf{T}{\mathbf{r}}_{\mathbf{F}}\{|{\psi }_{3\mathrm{LAS}-F}\left(\mathit{t}\right){\psi }_{3\mathrm{LAS}-F}\left(\mathit{t}\right)|\}=\left[\begin{array}{ccc}{\mathbf{\rho }}_{\mathbf{11}}& {\mathbf{\rho }}_{\mathbf{12}}& {\mathbf{\rho }}_{\mathbf{13}}\\ {\mathbf{\rho }}_{\mathbf{21}}& {\mathbf{\rho }}_{\mathbf{22}}& {\mathbf{\rho }}_{\mathbf{23}}\\ {\mathbf{\rho }}_{\mathbf{31}}& {\mathbf{\rho }}_{\mathbf{32}}& {\mathbf{\rho }}_{\mathbf{33}}\end{array}\right]$$

(14)

where the diagonal elements of the reduced density matrix ${\mathbf{\rho }}_{3\mathrm{LAS}}\left(\mathit{t}\right)$ define the atomic occupation’s probabilities on the levels $\mathit{l}$, $\mathit{m}$, and $\mathit{u}$. The density matrix elements (14) evaluate the other quantities related to the dynamical performance of the entanglement degree, and photon statistics of the field can be investigated [44].

4. Statistical Quantities and Quantifiers of Quantum Information

The photon statistics of the field based on developing the Mandel parameter are discussed. The von Neumann entropy defines the way of generating quantum entanglement between the 3LAS and the field initially in the PANBD. The paper explores the probability of success photon parameter of the NBD and number of photon addition to the field based on the NBD on the photon statistics of the field and nonlocal correlation between the 3LAS and field besides to its effect on the time evolution of the probability of finding the 3LAS in its upper condition.

4.1. Photon Statistics and Mandel Parameter

The Mandel parameter (MP) is adopted for measuring the non-classicality of arbitrary quantum conditions. Mandel [45,46] made an earlier attempt to highlight the non-classicality of a quantum condition. These studies investigated the field and presented the parameter of measuring the photon number statistics’ deviation from the Poisson distribution and the coherent states’ features and defined as

$${\mathit{Q}}_{\mathit{M}}=\frac{\mathrm{Tr}{\left({\hat{\mathrm{b}}}^{†}\hat{\mathrm{b}}\right)}^2-{\left\{\mathrm{Tr}\left({\hat{\mathrm{b}}}^{†}\hat{\mathrm{b}}\right)\right\}}^2}{\mathrm{Tr}\left({\hat{\mathrm{b}}}^{†}\hat{\mathrm{b}}\right)}-1,$$

(15)

where $\mathrm{Tr}\left({\hat{\mathrm{b}}}^{†}\hat{\mathrm{b}}\right)=⟨\psi \left(\mathrm{t}\right){|\hat{\mathrm{b}}}^{†}\hat{\mathrm{b}}|\psi \left(\mathrm{t}\right)⟩$.

The Mandel parameter indicates the field photon statistics that are thought to follow sub-Poissonian statistics ($Q_M<0$), determining the non-classical example. Therefore, binomial states follow either sub-Poissonian statistics or super-Poissonian ($Q_M>0$). To conclude, the field distribution becomes Poissonian when $Q_M=0$ and defines the semi-classical states.

At this point, the dynamical behavior of the field photon statistics is discussed when the field interacts with a 3LAS from the NBD and PANBD with two values of the probability of success $p$. As the field in the NBD with the probability of success $p=1/4$, the MP depicts all the cases of the field distribution as sub-Poissonian ($Q_M<0)$ at the first stage of the interaction time. As time goes on, the field distribution changes between Poissonian ($Q_M=0)$ and supper-Poissonian ($Q_M>0)$ (see Figure 2a). Figure 2b–d show that the distribution of the field is completely sub-Poissonian at the interaction when the field is in PANBD and with increasing the value of the probability of success $p=0.75$. Thus, the MP is strongly affected by the number of photons added to the NBD and with the probability of success $p,$ as confirmed by the results of the prediction of artificial neural networks.

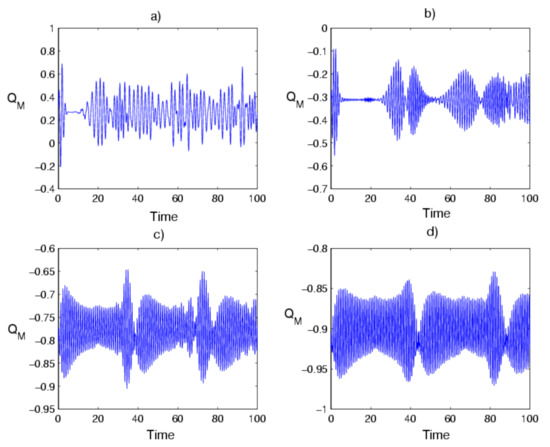
Figure 2. The time evolution of the Mandel parameter $Q_M$ of 3LAS interacting with the field of radiation follow the NBD $(k=0$) in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The NBD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

As seen in Figure 3a, where a neural network has one input neuron (Time), one output neuron (The Mandel parameter), and one hidden layer consisting of two hidden neurons, while Figure 3b has three hidden neurons. To each of the synapses, a weight is attached indicating the effect of the corresponding neuron, and all data pass the neural network as signals, Synaptic Weight > 0 (Normal line) and Synaptic Weight < 0 (Bold line).

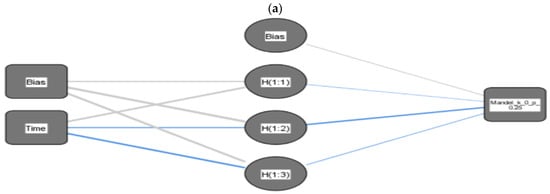
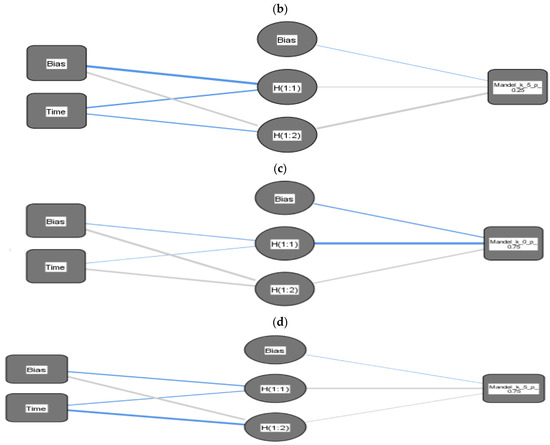
Figure 3. The prediction of the Mandel parameter $Q_M$ using an artificial neural network where the field follows the NBD $(k=0$) in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The NBD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

4.2. The Atomic Upper State Probability

The present section shows discovering the revival and collapse periods of the atomic upper state probability ${\mathit{\rho }}_{\mathbf{11}}$ as a function of the time. The revival and collapse of the qubit entanglement associate with the revival and collapse of the atomic population probability of the system [47,48,49]. The section also illustrates the effect of the added photons to the NBD of the field state on revival and collapse periods.

Figure 4 presents the dynamical behavior of the atomic probability of exciting the 3LAS in its upper state within the interaction time. As observed, the appearance of the revival and collapse phenomena is connected with the initial field distribution and the success parameter, where the collapse appears in the case of NBD at the first stage and increases by adding five photons to the BD (see Figure 4b). Increasing the value of the success parameter leads to the rising of oscillations with no collapse at all. Also, the new complected form of the oscillations found in Figure 4c,d is related to the statistical properties of the field that correspond to the field, which is more sub-Poissonian.

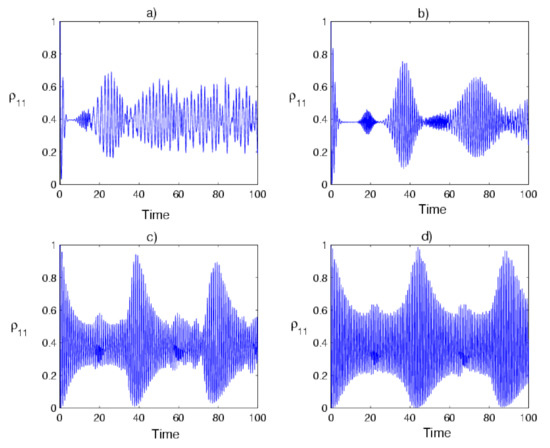
Figure 4. The time evolution of the atomic probability ${\rho }_{11}$ of a 3LAS interacting with the field of radiation follows the NBD $(k=0$) in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

As seen in Figure 5 and Figure 6, one neural network with input neurons (Time), an output neuron (the atomic probability ${\rho }_{11}$) and a hidden layer comprising three unseen neurons. However, Figure 6b has two unseen neurons. A weight is attached to each synapse to show how the conforming neuron is affected. The data go through the neural network in the form of signals, Synaptic Weight > 0 (Normal line), and Synaptic Weight < 0 (Bold line).

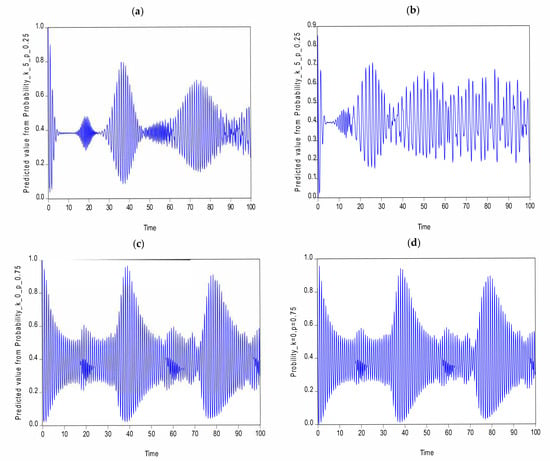
Figure 5. The prediction of the atomic probability ${\rho }_{11}$ using TS with ARIMA (0, 1, 2) of a 3LAS interacting with the field of radiation follows the NBD $(k=0$) in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

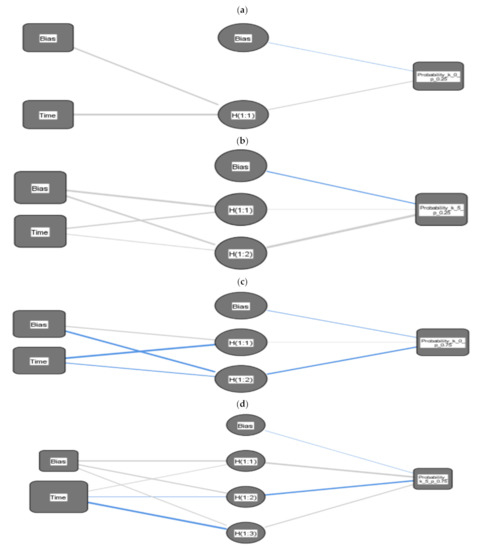
Figure 6. The prediction of the atomic probability ${\rho }_{11}$ using ANN of a 3LAS interacting with the field of radiation follows the NBD $\left(k=0\right)$ in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

4.3. Quantum Entropy and Degree of Entanglement

The results concerning the evolution of the 3LAS (field) quantum entropy are presented and compared with the Mandel parameter of the proposed 3LAS and field. The quantum entropy of the 3LAS (field) basis is defined as

$$S_{3LA\left[F\right]}=-\mathrm{T}{\mathrm{r}}_{3LA\left[F\right]}\left\{{\rho }_{3LA\left[F\right]}\ln \left[{\rho }_{3LAA\left[F\right]}\right]\right\},$$

(16)

where ${\rho }_{3LA\left[F\right]}$ represents the subsystem’s density operator in the form of

$${\mathit{\rho }}_{3\mathrm{L}\mathrm{A}\left[\mathrm{F}\right]}=\mathbf{T}{\mathbf{r}}_{\mathrm{F}\left[3\mathrm{L}\mathrm{A}\right]}\left[{\widehat{\mathit{\rho }}}_{\mathrm{A}\mathrm{F}}\right]$$

(17)

Concerning the 3LAS-field state, the entanglement’s amount takes the form of [50]

$${\mathit{S}}_F={\mathit{S}}_{3\mathrm{L}\mathrm{A}}=-{\displaystyle \sum }_{j=1}^3{\mathit{\varpi }}_j\mathit{ln}{\mathit{\varpi }}_j,$$

(18)

where ${\mathit{\varpi }}_j$ denotes the density matrix’s eigenvalues (14), fulfilling the equation of the third order

$${\mathit{\varpi }}^{\mathit{3}}-{\mathit{\varpi }}^{\mathit{2}}+{\mathit{X}}_{\mathbf{1}}\varpi +{\mathit{X}}_{\mathbf{2}}=\mathbf{0},$$

(19)

where

$$\begin{gathered} {\mathit{X}}_{\mathbf{1}}={\mathit{\rho }}_{\mathbf{33}}{\mathit{\rho }}_{\mathbf{22}}+{\mathit{\rho }}_{\mathbf{22}}{\mathit{\rho }}_{\mathbf{11}}+{\mathit{\rho }}_{\mathbf{11}}{\mathit{\rho }}_{\mathbf{33}}-\left|{\mathit{\rho }}_{\mathbf{12}}{|}^{\mathbf{2}}-\right|{\mathit{\rho }}_{\mathbf{23}}{|}^{\mathbf{2}}-|{\mathit{\rho }}_{\mathbf{31}}{|}^{\mathbf{2}}, \\ {\mathit{X}}_{\mathbf{2}}=-{\mathit{\rho }}_{\mathbf{33}}{\mathit{\rho }}_{\mathbf{22}}{\mathit{\rho }}_{\mathbf{11}}-{\mathit{\rho }}_{\mathbf{12}}{\mathit{\rho }}_{\mathbf{23}}{\mathit{\rho }}_{\mathbf{31}}-{\mathit{\rho }}_{\mathbf{13}}{\mathit{\rho }}_{\mathbf{21}}{\mathit{\rho }}_{\mathbf{32}}+{\mathit{\rho }}_{\mathbf{11}}\left|{\mathit{\rho }}_{\mathbf{23}}{|}^2+{\mathit{\rho }}_{\mathbf{22}}\right|{\mathit{\rho }}_{\mathbf{13}}{|}^{\mathbf{2}}+{\mathit{\rho }}_{\mathbf{33}}|{\mathit{\rho }}_{\mathbf{12}}{|}^{\mathbf{2}} . \end{gathered}$$

(20)

It is assumed that equation (14) has three real diverse roots introduced by

$${\mathit{\varpi }}_j=\frac{\mathbf{1}}{\mathbf{3}}+\frac{\mathbf{2}}{\mathbf{3}}cos({\mathit{\phi }}_j)\sqrt{\mathbf{1}-\mathbf{3}{\mathit{X}}_{\mathbf{1}}}$$

where

$$\mathbf{3}{\mathit{\phi }}_j={\mathbf{cos}}^{-\mathbf{1}}\left(\frac{-\mathbf{9}{\mathit{X}}_{\mathbf{1}}-\mathbf{27}{\mathit{X}}_2+\mathbf{2}}{\mathbf{2}\sqrt{{(\mathbf{1}-\mathbf{3}{\mathit{X}}_{\mathbf{1}})}^{\mathbf{3}}}}\right)+\left(\mathit{j}-\mathbf{1}\right)\frac{\mathbf{2}\mathit{\pi }}{\mathbf{3}}, \mathrm{with} \mathit{j}=\mathbf{1},\mathbf{2},\mathbf{3}.$$

(21)

In Figure 7, the entanglement concerning the 3LAS and the field via the von Neumann entropy $S_{3\mathrm{LA}}$ was studied for the field initially in the NBD through a single-photon transition case, which will reduce the values of the success probability $p=0.25$ in Figure 7a,b. The entropy quantifier function $S_{3\mathrm{LAS}}=0$ means that the system has a separable state. As time goes on, the function $S_{3\mathrm{LAS}}$ increases and achieves the maximum value of entanglement. The entropy is more regular and periodic within the time by adding five photons to the NBD (see Figure 7b). As noticed from Figure 7c,d, the structure of the von Neumann changes and becomes more complicated where the minimum value appears. Hence, the 3LAS-PANBD entanglement decreased by increasing the success probability.

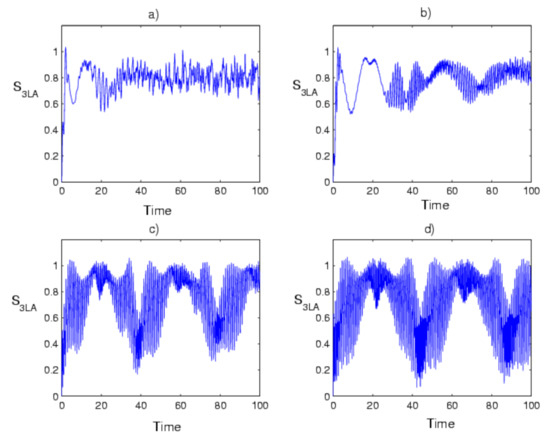
Figure 7. Time evolution of the entropy function $S_{3\mathrm{L}\mathrm{A}}$ of a 3LAS interaction with the field of radiation following the NBD $(k=0$) in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

The prediction of the von Neumann entropy value of the proposed system using time series ARIMA (2, 1, 8) is presented in Figure 8. We use an artificial neural network with one input neuron (Time), an output neuron (Entropy), and a hidden layer comprising three hidden neurons. Figure 9b has five hidden neurons, and Figure 9c has nine hidden ones. A weight is devoted to each synapse, indicating the conforming neuron’s impact. Additionally, all data go through the neural network in the form of signals, Synaptic Weight > 0 (Normal line), and Synaptic Weight < 0 (Bold line) (see Figure 9).

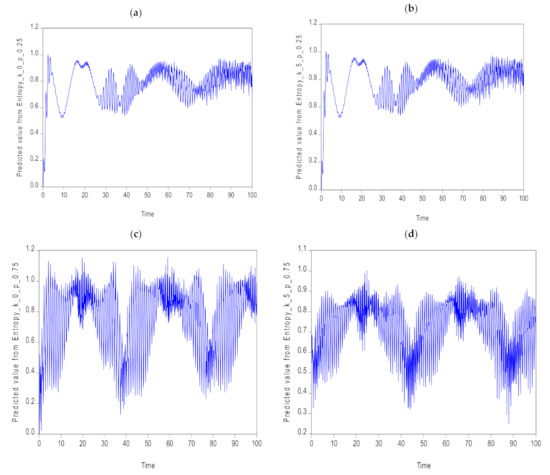
Figure 8. The prediction of the entropy value using TS ARIMA (2, 1, 8) of a 3LAS interacting with the field of radiation follows the NBD $\left(k=0\right)$ in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

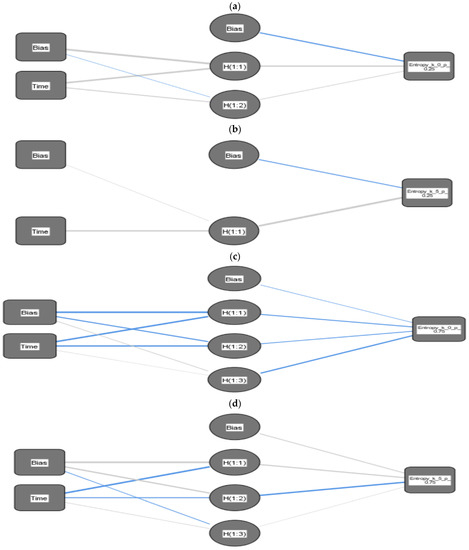
Figure 9. The prediction of the entropy value using ANN of a 3LAS interacting with the field of radiation follows the NBD $\left(k=0\right)$ in (a,c) and PANBD via five-photon addition ($k=5$) in (b,d). The BD probability of success is $p=0.25$ in (a,b) and $p=0.75$ in (c,d).

5. Conclusions

The present paper utilized the time series model and investigated applying the neural network problem of envisaging a significant issue’s statistical quantities. The MLP networks and the Box–Jenkins model were built and showed the highest findings of normalizing the input, in which the AM is less (see Table 1). The statistical analysis and prediction of the Mandel parameter and quantum entropy were considered to detect the 3LAS–field’s nonlocal correlation or entanglement. The time evolution of the quantum entropy of the atomic basis and its relation to the 3LAS–field entanglement was investigated. Also, the link between quantum entropy within the field basis and photon statistics examined by developing the Mandel parameter underwent examination. The preliminary field models were the negative binomial and excited negative binomial distributions. Therefore, the quantum entropy was effective in the entanglement quantifier calculations and helped understand the structure of the quantum states. Moreover, the statistical features of the field calculated by the field quantum entropy related to the nonlocal features between the field and 3LAS measured by the atomic quantum entropy. The suggested statistical quantities proved to be sensitive to the number of photons addition to the field and negative binomial distribution parameters.

Table 1. Show the performance of the forecasting models.

The Models	MLP			Time Series Model
Accuracy Measurement (AM)	SMAPE	MASE	MAPE	SMAPE	MASE	MAPE
$\mathrm{Probability} k=0, p=0.25$	0.272673	0.106000	0.275690	0.181352	0.074612	0.101629
$\mathrm{Probability} k=5, p=0.25$	0.269640	0.106048	0.266703	0.303286	0.123703	0.313733
$\mathrm{Probability} k=0, p=0.75$	0.272166	0.106337	0.271658	0.358737	0.152961	0.436352
$\mathrm{Probability} k=5, p=0.75$	0.268924	0.106493	0.262484	0.336588	0.138450	0.395716
$\mathrm{Mandel} k=0, p=0.25$	0.383728	0.139320	2.150776	0.136885	0.064584	0.219269
$\mathrm{Mandel} k=5, p=0.25$	0.094810	0.055219	1.579632	0.385134	0.139075	1.579632
$\mathrm{Mandel} k=0, p=0.75$	0.323735	0.129914	0.339708	0.094810	0.013144	0.055219
$\mathrm{Mandel} k=5, p=0.75$	0.323735	0.129914	0.339708	0.392462	0.148357	0.430555
$\mathrm{Entropy} k=0, p=0.25$	0.239194	0.088341	3.135094	0.239194	0.088341	13.135094
$\mathrm{Entropy} k=5, p=0.25$	0.222427	0.089129	13.135094	0.242729	0.089129	13.141410
$\mathrm{Entropy} k=0, p=0.75$	0.251210	0.090017	13.155419	0.251210	0.090017	13.155419
$\mathrm{Entropy} k=5, p=0.75$	0.266287	0.093399	13.185244	0.266287	0.093399	13.185244