A Secure Interoperability Management Scheme for Cross-Blockchain Transactions

Abstract

Blockchain technology has recently attracted tremendous interest due to its potential to revolutionize the industry by achieving decentralization while increasing the number of data sources, transparency, reliability, auditability, and trustworthiness. However, one of the major barriers to the widespread adoption of blockchain applications is the lack of mutual consensus and management across blockchains. Cross-blockchain consensus refers to one blockchain network reaching a consensus with another blockchain network to provide the ability to interact and share data. In this paper, we propose a secure management scheme with symmetric cross-blockchain communication and certificateless signature primitives, in which two heterogeneous blockchains are linked by a relay chain to simultaneously deliver cross-blockchain transaction security, achieve compatibility among various blockchains, and ensure the consistency of data exchanged, in practice. Additionally, our evaluation and security analysis shows the practicability and security of our proposed management scheme and demonstrates that a common test platform based on Ethereum can achieve acceptable computation costs.

1. Introduction

The blockchain, which originated from Bitcoin, was first proposed by Satoshi Nakamoto in 2008 [1]. It is a comprehensive innovation employing multiple technologies such as cryptography, consensus mechanisms, distributed databases, and peer-to-peer networks. Possessing the characteristics of decentralization, anonymity, immutability, traceability, and transparency, blockchain has gained much attention in the fields of finance [1], data provenance [2], healthcare [3], supply chain management [4], and e-government [5], among others. Most current blockchain projects are based on various application scenarios and design concepts and involve adopting different technical architectures to develop heterogeneous blockchains. These blockchain projects are like isolated islands that are disconnected from each other and unable to exchange and synchronize assets and data. With the widespread application of blockchain technology in many different areas, the need for integration between scenarios is increasing, and the demand for cross-chain transactions is also receiving more attention.

In recent years, many interoperability technologies linked to heterogeneous blockchains have been studied extensively, in light of their practical importance in numerous fields. These studies concentrate on indirect integration of cross-chain values and data transmission to avoid direct integration of all data on cross-chain transactions. This brings about the super-positioning of ledger data and a surge in data-carrying and computing. These interoperability technologies enable homogeneous or heterogeneous blockchains to transfer assets or data. Nevertheless, to provide mutual trust guarantees, a third-party organization is usually required to act as an intermediary in the indirect integration of cross-chain networks. In addition, if there is no intermediary agency, data transfers will be restricted, lowering the value of the data. Intermediary costs and transaction risks are incurred even when using intermediary agencies. Alternatively, in the absence of adequate cross-chain transaction protection mechanisms, most cross-chain schemes are vulnerable to malicious Internet-based attacks, i.e., man-in-the-middle (MITM) attacks, replay attacks, denial of service (DoS) attacks, and counterfeiting [6]. Moreover, current cross-chain techniques have room for improvement, especially in terms of standards and interoperability. In particular, widely recognized standards for cross-chain transactions are still lacking, which impedes the development of system interoperability. Due to the current situation, we are motivated to propose a secure and privacy-aware interoperability management scheme for cross-blockchain transactions that is capable of protecting sensitive user data, such as personal and private information, proprietary information, and related passwords, as well as sensitive and valuable corporate or organizational data, from being tampered with or disclosed when transacting and transmitting it through a cross-chain platform. Additionally, the proposed scheme must satisfy the following security requirements:

• Data confidentiality is critical for cross-chain transactions with asset transfers involving all parties, including private/consortium chains and users of cross-chain transactions and blockchain service providers (or platforms). Since the data associated with cross-chain transactions are sensitive and can reveal much about the people and organizations holding the data, privacy is extremely important.
• Data integrity is also critical for cross-chain transactions and asset transfers. We must ensure that confidential information cannot be secretly altered or deleted by intruders during cross-chain transactions.
• Non-repudiation of cross-chain transactions is also indispensable. Cross-chain transactions must be non-repudiable and traceable. If transactions are undeniable, when there is a dispute about cross-chain transactions, neither the involved parties nor the relay agencies can deny that data were transmitted and received. This makes it easier to resolve disputes and is useful for auditing purposes.
• During cross-chain entity communication for transactions, a malicious adversary can deceive the entities in a variety of ways by sending counterfeit and modified connections or messages. First, a malicious adversary may launch impersonation attacks and man-in-the-middle (MITM) attacks, accompanied by fake messages, to deceive legal entities and make them believe that the adversaries are also legal transaction entities, i.e., legal blockchains. Therefore, legal entities will not question an adversary’s “legitimate but malicious” behaviors, allowing the latter to steal sensitive user data. Second, an attacker may listen in on, or even interrupt legally transmitted cross-chain transaction information, obtain the network status and confidential information of others, and reuse this information between sessions to deceive a legitimate entity. Since the communication is legally issued by a legitimate entity, its authenticity will be confirmed if no further replay behavior checks are performed. Third, a denial of service (DoS) attack could cause the cross-blockchain transaction process to be disrupted. In most cases, the attacker will send legal signals to the communicating entity, thus exhausting the victim’s computing power and capacity. Thus, the service availability of cross-chain transactions cannot be guaranteed. Based on the above contingencies, it is critical to include a verification mechanism in a secure blockchain interoperability scheme to ensure the validity of interacting organizations. On the other hand, a secure blockchain interoperability scheme for the cross-chain transactions or data transfer must ensure immunity to man-in-the-middle (MITM) attacks, replay attacks, denial of service (DoS) attacks, and counterfeiting.

Based on the above discussion, we would like to propose a secure interoperability management scheme for cross-blockchain transactions, in which two heterogeneous blockchains are connected through a relay chain. The following contributions are provided through this study:

• First, our proposed scheme is based on the Elliptic Curve Discrete Logarithm Problem (ECDLP) and the Certificateless Signature Scheme to provide the security of cross-blockchain transactions, realizes the compatibility between various blockchains, and ensures the consistency, confidentiality, and integrity of data exchange in practice. The traceable digital signature ensures non-repudiation of transactions and greatly reduces the possibility of MITM attacks, replay attacks, DoS attacks, and counterfeiting.
• Second, we extensively surveyed and studied the major cross-blockchain approaches and related consensus mechanisms across blockchains. In addition, we have demonstrated the robustness and efficiency of our proposed secure interoperability management scheme through the formal security analysis and performance evaluation and vulnerability discussion of web3 used in our implementation. These results demonstrate the feasibility of our proposed management scheme and show our contribution to the development of research for cross-blockchain transactions.

The rest of this paper is organized as follows. Section 2 introduces the state-of-the-art of blockchain interoperability solutions and discusses recent related work. Section 3 presents a definition of an elliptic curve and reviews the characteristics of a Certificateless Signature Scheme (CLS). We next present our proposed interoperability management scheme based on relays in Section 4. Then, in Section 5, we present a security analysis and performance evaluation of the proposed scheme as a practical check and discuss the security issues associated with the adoption of web3 in our implementation. Finally, we give conclusions and summarize our future work in Section 6.

2. Related Work

In 2016, Buterin [7] defined three major interoperability solutions, i.e., notary schemes, sidechain and relay schemes, and hash time-lock contracts and distributed private key control, in one of the earliest and most well-known works on blockchain interoperability. Table 1 shows the comparison of our scheme with the existing cross-blockchain mechanisms. The detailed discussions are below.

Table 1. Comparison among existing cross-blockchain consensus mechanisms.

Approaches	Decentralization	Trustworthy	Cross-Blockchain Consensus
XCLAIM [6]	Yes	Yes	Consensus verification depends on the consensus mechanism that supports the use of the blockchain, and the relay chain can adjust the verification method according to the consensus used by different participants.
Interledger [8]	No	No	Not the cross-blockchain consensus mechanism, but a technical protocol for cross-chain value transfer. When all participants reach a consensus on funds through intermediaries, they can trade.
BTC Relay [9]	Yes	Yes	The consensus of Bitcoin is required for block header transfer.
Cosmos [10]	Yes	Yes	A certain number of signatures are required for the transfer of block headers. Safety issues due to the lack of guarantees surrounding atomic behavior.
Polkadot [11]	Yes	Yes	Parachains use the shared consensus technique to share the relay chain consensus.
Lightning Network [12]	Yes	Yes	Not the cross-blockchain consensus mechanism, but a 2-layer payment protocol that works on the blockchain (primarily for Bitcoin).
Egger et al. [13]	Yes	Yes	Not the cross-blockchain consensus mechanism, but they propose a protocol for atomic multi-channel updates (AMCU), and simplified collateral compatible with Bitcoin (and other cryptocurrencies with reduced scripting capabilities).
Jin et al. [14]	-	-	Not the cross-blockchain consensus mechanism, but they reinterpret the consensus protocol in the context of cross-blockchain interaction as a verification protocol.
Li et al. [15]	Yes	Yes	Consensus is based on multi-signatures signed by transaction operators, and the system will only confirm cross-chain programs if the number of valid signatures exceeds a preset threshold ratio.
Pang [16]	Yes	Yes	A new consensus protocol, Multi-tokens Proof of Stake (MPoS), for blockchain interoperability architecture, which can reinforce the token network effects in cross-chain ecosystems and grow the user base of parachains exponentially.
Wu et al. [17]	Yes	Yes	A message-oriented verification consensus, and a common framework for cross-blockchain communication based on a cyclical committee rotation mechanism to support the exchange of information for various transactions across multiple heterogeneous blockchain systems.
Qiao et al. [18]	Yes	Yes	The consensus as a threshold digital signature process with multiple privileged subgroups.
Wang and Nixon [19]	Yes	Yes	The proposed InterTrust scheme has an atomic cross-chain communication protocol, a threshold signature scheme, and a trusted hardware design, and thus can provide consistency, verifiability, and trusted services in the target blockchain systems.
Li et al. [20]	Yes	Yes	The proposed PolyBridge scheme is based on a PolyChain architecture and a web application implementation, enabling communications among existing blockchain platforms with various consensus models and atomicity.
Zhang and Ge [21]	No	No	The proposed scheme adopts various cryptographic techniques, i.e., SM2, SM3, SM4, SM9, and ZUC, verified by China to satisfy the security functionalities such as encryption, decryption, signature, and verification of cross-chain transactions.
Cao and Song [22]	Yes	Yes	An implementation is presented with several techniques, such as atomic swaps, Schnorr protocol, and smart contract, to guarantee distributed asynchronous transactions among blockchain networks with appropriate system efficiency, throughput, and scalability.
Sober et al. [23]	Yes	Yes	The proposed scheme integrates the voting-based signatures into blockchain interoperability to support that communicating nodes can generate a distributed private key to execute an off-chain aggregation mechanism, and further achieve interoperability among various blockchains.
Our Proposed Scheme	Yes	Yes	A secure interoperability management scheme that can be interpreted as the new consensus of cross-blockchain transactions relies on digital signatures with certificateless signature primitives to ensure the security and traceability of cross-blockchain transactions.

The notary schemes are those in which a trustworthy set of entities function as intermediaries to allow atomic contact and information exchange between multiple blockchains. Interledger [8] is a representative solution that offers trustworthy Escrow (third-party depository) and notary services. A connector, which is also a top encryption custody system, can be anyone who has two or more digital asset accounts. This method is simple and easy to understand, but it also has the disadvantage of requiring a trustworthy third-party intermediary, which results in an excessive concentration of power in the third-party intermediary.

Sidechains and relay schemes are another way to conduct transactions. These are multi-centralized approaches to solving the trust problem. The sidechain was first proposed for the testing and development of new Bitcoin features. In contrast to the main chain, the sidechain can verify and parse block and ledger data on the main chain. The BTC Relay [9] is the first Ethereum-based sidechain that enables users to verify Bitcoin transactions using smart contracts. As a source blockchain, it uses a Proof of Work (PoW) consensus algorithm that can be verified on the destination blockchain. In other words, Ethereum smart contracts can be used to verify the PoW algorithm used by Bitcoin. However, verifying Ethereum’s time and memory, the hard Ethash PoW algorithm programmatically requires excessive memory and is difficult to perform in smart contract languages. In 2019, Zamyatin et al. proposed XCLAIM [6] to build trustless cross-chain trading protocols. This method sends transaction inclusion proofs from Bitcoin to Ethereum using the BTC Relay protocol. The protocol is based on an underlying cross-chain consensus, allowing atomic value transfers from Bitcoin to Ethereum. It also makes use of an off-chain entity called ‘Vault and Issuing Smart Contract’ (iSC) to make transfers easier. Furthermore, the representative of relay-based blockchain interoperability is Cosmos [10]. Cosmos is a decentralized network of parallel blockchains powered by the Tendermint consensus algorithm. In Cosmos architecture, there are two roles: Hub and Zone. A Hub is a type of relay chain that is used to process asset transactions across multiple chains. A Zone is a parachain with two major characteristics: Fast Finality and Sovereignty, which means that the cross-chain does not directly support PoW and other blockchains based on probability-determined models. Each Zone will have a set of validators that can determine who has the power to generate a block. The other protocol is Polkadot [11]. It is a heterogeneous multi-chain network consisting of relay chains, parachains, and bridges, with four participants: validators, nominators, collators, and phisher men. Relay chains are the core of Polkadot, providing a unified consensus and security guarantee for the entire system, while the parachains share the security guarantee from the relay chain. Bridges allow transactions to be routed to non-Polkadot blockchain systems, such as Bitcoin, Ethereum, and so on. These blockchains have their own consensus algorithms and can be connected to Polkadot for cross-chain transactions via various bridges. The parachain blocks are approved by groups of validators, who then publish them to the parachain and seal the parachain block header to the relay chain. Validators are designated to parachains at random and the allocation is changed regularly. Furthermore, the verifiers adopt the Proof of Stake (PoS) consensus algorithm to achieve shared consensus across all parachains. Collators collect transactions from the parachains, create blocks, and provide zero-knowledge, non-interactive proofs that the transactions change the validator’s state. Nominators give funds to validators they believe will carry out the PoS consensus. Phisher men monitor the parachain and present the verifier with proof of fraud. Cross-parachain transactions are the same as typical external account transactions. A transaction on a parachain will cause a collator on that chain to place a message in the outbound queue.

A third approach is the use of hash time-lock contracts, which are primarily used to ensure that any transfer between two nodes can be completed through a payment channel mediated by a smart contract. A hash-lock was first used by the Bitcoin Lightning Network [12]. Cross-chain asset exchange supports a certain number of both blockchain A’s and blockchain B’s assets for atomic exchange. The implementation of a hash-lock is very clever. The asset receiver is forced to confirm the payment within a specified timeframe and generate a receipt certificate for the remitter, using the hash-lock and time-lock, or the asset will be returned to the remitter. However, there are practical constraints. This approach is interactive and relies on assumptions about synchronization. Therefore, a long waiting time is often generated during the transmission process. As Egger et al. [13] point out, hash time-lock contracts are favorable in the case of partial renewal, which may result in coin losses.

In this study, we focus on the consensus and management scheme of cross-blockchain transactions. Hence, we present the state-of-the-art of cross-blockchain consensus. In 2018, Jin et al. [14] considered the requirement that the consensus protocol should try to maintain the correctness of the blockchain system state. This is because the state and underlying protocol in the heterogeneous blockchain system are completely different. When conducting cross-chain transactions, the consensus protocol should be reinterpreted as a verification protocol. The consensus protocol is used to ensure the integrity and data source of the transmitted data when performing cross-blockchain interactions. The following year, Li et al. [15] achieved a consensus among multiple chains by designing multiple roles in the proposed cross-blockchain system. When the system detects that a node proposes a cross-blockchain transaction, the trading operator in the system who is responsible for cross-blockchain transaction records will take over this demand and deliver the demand to the trading group for verification and pass the signature threshold set by the system. If it is passed, the transaction record will be sent back to the two nodes, where the transaction is conducted and recorded in the relay chain. After the transaction is completed, the transaction fee in the process will be attributed to the trading operator who signed the transaction. The node can upload the transaction record to the relay chain to extract cross-blockchain transaction information and value, and the record is provided to the nodes participating in the transaction for post-transaction record query and transaction verification. Next, in 2020, Pang [16] proposed an interoperability architecture for the novel cross-blockchain consensus algorithm, i.e., Multi-tokens Proof of Stake. This architecture provides a value exchange mechanism in the relay chain. Different blockchains calculate the weights in the heterogeneous blockchains and the real-time price of the native tokens in each sub-chain so that nodes can use the native tokens in the blockchain to mortgage and strive to become validators of cross-chain transactions. This architecture can effectively solve the Balkanization of the blockchain. Through the token network effect, the blockchain that joins the cross-chain network can attract more users. The study emphasizes the analytical model compared to the single-token PoS and ensures the superior security of the given model. Later, Wu et al. [17] presented a new generic framework for cross-blockchain communication based on a regular committee rotation mechanism for transaction data exchange across multiple heterogeneous blockchain systems. They also designed a message-oriented verification consensus, which can securely and efficiently verify and integrate the information collected from the ledgers on the relay chain and connect the heterogeneous blockchain through the committee to have stronger trust than the notary method. In addition, it regularly reorganizes the committee and replaces downed nodes first to ensure the reliability of the system, to reduce the impact of downed nodes on time. In another work, Qiao et al. [18] proposed a cross-chain consensus mechanism based on threshold digital signatures in the context of a medical consortium chain, hoping to ensure the consistency of cross-chain transaction results and simultaneously confirm the cross-blockchain transaction through the consensus mechanism. They assumed that there is a list of verification nodes in a consortium chain, and the verification nodes among them will perform consensus verification. If a node is verified, it will use the signature method to express its vote. Finally, after passing the threshold, a key pair will be formed. The deployed transaction is signed, and a new block is simultaneously generated. Their cross-blockchain consensus protocol combines multiple verification node lists from the consortium chain systems of disparate environments into a verification node group, and the node group performs cross-blockchain consensus verification. When transactions are transmitted between heterogeneous blockchains, the same transaction will be continuously signed by the public and private key pairs obtained in the path through the consensus verification between different blockchains. Then, the signature of the target chain will be verified. Finally, the secret-sharing method and the Diffie–Hellman algorithm will be recalculated to form a new public/private key pair. The transaction will require a final signature for the source chain to ensure that the transaction is indeed completed. The cross-blockchain consensus method can ensure the trustworthiness of the passing node and the passing path through the signature verification of the passing node and guarantee the traceability of cross-blockchain transaction data.

Recently, Wang and Nixon [19] proposed an interoperable scheme for arbitrary blockchain architectures, called InterTrust, to support interoperability and trustworthiness. An atomic cross-chain communication protocol is presented to integrate existing blockchain systems. In addition, InterTrust is embedded with two mechanisms, i.e., a threshold signature scheme and a trusted hardware design, in which the threshold signature scheme can guarantee consistency and verifiability in the target blockchain systems, and the trusted hardware is able to provide trusted services among distinct blockchain systems, respectively. Moreover, Li et al. [20] demonstrated a cross-chain bridge, called PolyBridge, for heterogeneous blockchains to interoperate with existing cryptocurrencies. The proposed PolyBridge is based on an underlying PolyChain and a pair of relays to confirm the consistency of cross-chain transactions and form consensus among relevant parties. It enables an interface to existing blockchain platforms with various consensus models and atomicity. PolyBridge is realized through a web application implementation which can support cross-chain requests with over 200 types of cryptocurrencies on 18 blockchains. Next, Zhang and Ge [21] presented an identity authentication for heterogeneous alliance blockchain networks. The proposed scheme adopts various cryptographic techniques, i.e., SM2, SM3, SM4, SM9, and ZUC, verified by China to satisfy the security functionalities such as encryption, decryption, signature, and verification of cross-chain transactions. Meanwhile, to ensure transaction consistency among different blockchains, Cao and Song [22] introduced a cross-chain protocol and further implemented a platform enabled by the proposed cross-chain protocol, atomic swaps, Schnorr protocol, and smart contract. Then, the authors demonstrated some experimental results, showing that the implemented cross-chain platform can guarantee distributed asynchronous transactions among blockchain networks with appropriate system efficiency, throughput, and scalability. Finally, Sober et al. [23] investigated the possibility of integrating the voting-based signatures into blockchain interoperability. The proposed method supports that communicating nodes can generate a distributed private key to execute an off-chain aggregation mechanism to collectively respond to requests, and further achieve interoperability among various blockchains.

3. Preliminaries

An elliptic curve, $E$, over a prime finite field, $E_p$, is denoted using the notation $E/E_p$. It is defined by an equation $y^2=x^3+ax+b$, where $a, b\in F_p$ are constants such that $\mathrm{\Delta }=4a^3+27b^2 \ne 0$. The set $E/E_p$ consists of all points $P_i=\left(x_i,y_i\right)$ on $E$, and a special point $O$, called the point at infinity, which forms a cyclic group, $G$, under the operation of point addition, $R=P+Q$, which is defined according to a chord-and-tangent rule. Additionally, $t·P=P+P+\cdots +P$ (t times) is regarded as scalar multiplication, and $P$ is a generator of a cyclic group $G$ of order $n$. The inverse operation is described as follows. Let $E$ be an elliptic curve over a prime finite field, $E_p$, and let a group, $G$, be elliptic curve points of prime order n. Given a generator $P$ of $G$ and a point $x·P$, the Elliptic Curve Discrete Logarithm Problem (ECDLP) is computationally infeasible to derive $x$, where $x\in Z_n^{*}$.

A generic construction of a Certificateless Signature Scheme (CLS) comprises six algorithms, i.e., Setup, PartialPrivateKeyExtract, SetSecretValue, SetPublicKey, Sign, and Verify [24]. Their specific phases are as follows:

• Setup: This phase is executed by a trusted third party (TTP), such as a Trusted System Authority (TSA) or a trusted Key Generation Center (KGC). A TTP produces the master private key $s$, using a random number as the security parameter $k$, and then uses the master private key $s$ to generate the master public key, $P{K}_{KGC}$. Lastly, it transmits the master public key and a list of public system parameters, $params$, to all system users.
• PartialPrivateKeyExtract: TTP takes the user i’s identity, $I{D}_i$, the master secret key $s$, and $params$ as input, and outputs a partial secret key, $D_i$, for the user i.
• SetSecretValue: The user i inputs the user i’s partial private key, $D_i$, the system parameter params, and randomly selects a value $x_i\in Z_n^{*}$ as his/her secret. Later, the user i generates a complete private key, $S{K}_i$, which only the user knows.
• SetPublicKey: In this phase, the user i outputs his/her public key, $P{K}_i$, using $params$ and the secret value $x_i$ of the user.
• Sign: This phase takes the message, m, master public key, $P{K}_{KGC}$, the user i’s private key, $S{K}_i$, his/her identity, $I{D}_i$, and $params$ as input, and outputs a signature ${\sigma }_{i }=\left(R_i,T_i,{\tau }_i\right)$ on m.
• Verify: This phase takes the master public key, $P{K}_{KGC}$, the user i’s partial private key, $D_i$, $params$, the message, m, and the signature ${\sigma }_i=\left(R_i,T_i,{\tau }_i\right)$ as inputs, and returns 1 for a valid output; otherwise, it returns 0.

The design of our proposed scheme is based on the integration of ECDLP and CLS, and then we applied our proposed scheme for cross-chain transaction scenarios. Next, in Section 4, we will introduce the operation processes of our proposed scheme. Before that, Table 2 presents the notations used in our proposed scheme.

Table 2. Notations used in our proposed scheme.

Notation	Description
$A, B$	blockchains
$RC$	relay chain
$A_i$, $B_j$	member of blockchain $A$ or $B$
$Tra{n}_{A_i{B}_j}$	A transaction, $Tra{n}_{A_i{B}_j}$, involved with $A_i$ and $B_j$
$P_{A_i{B}_j}$	A producer, $P_{A_i{B}_j}$, who is responsible for generating a block corresponding to $Tra{n}_{A_i{B}_j}$ inside $RC$.
$k$	A security parameter based on the ECDLP
$H$	A secure hash function $H:{\left\{0,1\right\}}^{*}\times G\to Z_q^{*}$
$s_{A_i}$, $s_{B_j}$	Private keys $s_{A_i}, s_{B_j}, x_{A_i{B}_j}\in Z_n^{*}$
$P{K}_{A_i}$, $P{K}_{B_j}$, $P{K}_{A_i{B}_j}$	Public keys $P{K}_{A_i}=s_{A_i}·P, P{K}_{B_j}=s_{B_j}·P$, $P{K}_{A_i{B}_j}=x_{A_i{B}_j}·P$
$I{D}_{A_i{B}_j}$	The public identity, $I{D}_{A_i{B}_j}$, of $P_{A_i{B}_j}$
$r_{A_i}$, $r_{B_j}$, $t_{A_i{B}_j}$	Random numbers $r_{A_i}, r_{B_j}, t_{A_i{B}_j}\in Z_n^{*}$
$Sig{n}_{last}$	The signature contained in the last valid block generated in a legitimate manner and adopted by the relay chain.
${\sigma }_{A_i{B}_j}$	The signature of $Tra{n}_{A_i{B}_j}$

4. The Proposed Scheme

We considered the common scenarios for cross-chain transactions, such as e-Healthcare, finance, e-government, and cross-industry supply chains, to achieve cross-blockchain consensus in such scenarios. Here, we present the detailed processes of our proposed interoperability management scheme, which can achieve cross-blockchain consensus by linking two private/consortium/public blockchains, i.e., $A$ and $B$, with a relay chain, i.e., $RC$. The relay chain, $RC$, is based on the Delegated Proof of Stake (DPoS) consensus protocol, regardless of the heterogeneity of consensus protocols that blockchains $A$ and $B$ adopt. In the proposed scheme, each member, $A_i$, of blockchain $A$ will be matched with a member, $B_j$, of blockchain $B$. In addition, there will be a producer, $P_{A_i{B}_j}$, who is responsible for generating a block corresponding to the transactions, $Tra{n}_{A_i{B}_j}$, involved with $A_i$ and $B_j$ inside the relay chain, $RC$. Figure 1 depicts the initial stage of a cross-blockchain transaction. Furthermore, the security of the proposed interoperability management scheme is provided by the hardness of the ECDLP. The details of the phases are presented below.

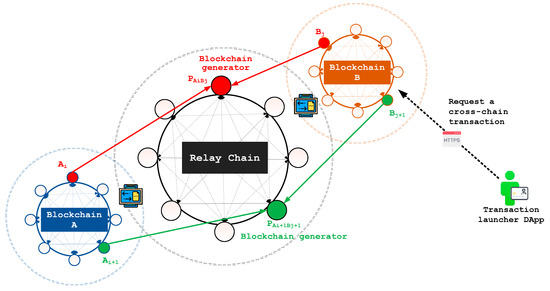
Figure 1. The initial stage of a cross-blockchain transaction.

• Setup (Figure 2):
  

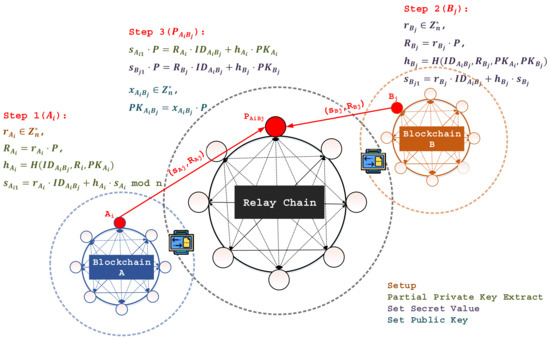  Figure 2. The Setup, Partial Private Key Extract, Set Secret Value, and Set Public Key phases.
  • Once the transaction launcher asks for a cross-blockchain transaction, blockchain $B$ sends a transaction request to blockchain $A$. When blockchain $A$ receives a transaction request from the relay chain, it selects a security parameter, $k$, based on the ECDLP, generates a group, $G$, of elliptic curve points of prime order $n$, and determines a generator, $P$, of $G$.
  • Then, blockchain $A$ chooses a secure hash function $H:{\left\{0,1\right\}}^{*}\times G\to Z_q^{*}$ [25], and securely shares $\left\{G, P,H\right\}$ with all members of $A$.
  • After that, member $A_i$ chooses a private key, $s_{A_i}\in Z_n^{*}$, and calculates a public key, $P{K}_{A_i}=s_{A_i}·P$. Finally, $A_i$ publishes $params=\left\{G, P,P{K}_{A_i},H\right\}$ and keeps $s_{A_i}$ securely.

• Partial Private Key Extract (Figure 2):
  • Given $params$, $s_{A_i}$, and the public identity, $I{D}_{A_i{B}_j}$, of the producer, $P_{A_i{B}_j}$,$A_i$ generates a random number, $r_{A_i}\in Z_n^{*}$, and calculates $R_{A_i }= r_{A_i}·P$, $h_{A_i}=H\left(I{D}_{A_i{B}_j}, R_{A_i},P{K}_{A_i}\right)$, and $s_{A_{i1}}=r_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·s_{A_i}$ mod n.
  • Then, $A_i$ returns a partial private key $\left(s_{A_{i1}},R_{A_i}\right)$ to the producer, $P_{A_i{B}_j}$, who checks the validity of $\left(s_{A_{i1}},R_{A_i}\right)$ on the basis of whether the two computed values, i.e., $s_{A_{i1}}·P$ and $R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}$, are equal or not, where $I{D}_{A_i{B}_j}, R_i$ and $P{K}_{A_i}$ are publicly known, and $h_{A_i}=H\left(I{D}_{A_i{B}_j}, R_i,P{K}_{A_i}\right)$ is computed.

$$s_{A_{i1}}·P=\left(r_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·s_{A_i}\right)·P=r_{A_i}·I{D}_{A_i{B}_j}·P+h_{A_i}·s_{A_i}·P=R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}$$

• Set Secret Value (Figure 2):
  • After the producer, $P_{A_i{B}_j}$, confirms the validity of $\left(s_{A_{i1}},R_{A_i}\right)$, the producer, $P_{A_i{B}_j}$, sends $params=\left\{G, P,P{K}_{A_i},H\right\}$ to member $B_j$ of blockchain $B$.
  • $B_j$ immediately chooses a private key, $s_{B_j}\in Z_n^{*},$ and calculates a public key, $P{K}_{B_{j }}=s_{B_j}·P$.
  • Next, $B_j$ generates a random number, $r_{B_j}\in Z_n^{*}$, and calculates $R_{B_j}=r_{B_j}·P$, $h_{B_j}=H\left(I{D}_{A_i{B}_j}, R_{B_j},P{K}_{A_i},P{K}_{B_j}\right)$, and $s_{B_{j1}}=r_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·s_{B_j}$ mod n.
  • Then, $B_j$ outputs a partial private key $\left(s_{B_{j1}},R_{B_j}\right)$ to the producer, $P_{A_i{B}_j}$. Once $\left(s_{B_{j1}},R_{B_j}\right)$ is received, $P_{A_i{B}_j}$ checks the validity of the $\left(s_{B_{j1}},R_{B_j}\right)$ values with the equation $s_{B_{j1}}·P=R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j}$. If the equation holds, the producer, $P_{A_i{B}_j}$, updates the public $params=\left\{G, P,H,P{K}_{A_i},P{K}_{B_j}\right\}$.

$$\begin{array}{ll}{s}_{B_{j1}}·P& =\left(r_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·s_{B_j}\right)·P=r_{B_j}·I{D}_{A_i{B}_j}·P+h_{B_j}·s_{B_j}·P \\ & =R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j}\end{array}$$

• Set Public Key (Figure 2):
  The producer, $P_{A_i{B}_j}$, picks a random number, $x_{A_i{B}_j}\in Z_n^{*}$, as its secret value. Given $params$ and $x_{A_i{B}_j}$, the producer, $P_{A_i{B}_j}$, computes $P{K}_{A_i{B}_j}=x_{A_i{B}_j}·P$ as its public key.
• Sign (Figure 3):
  

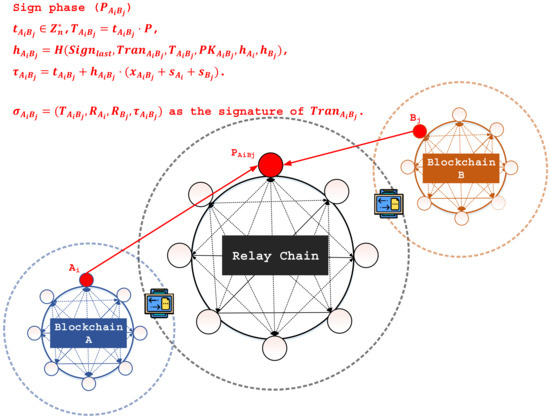  Figure 3. The Sign phase.
  Given $params$, $x_{A_i{B}_j}$, and a transaction, $Tra{n}_{A_i{B}_j}$, involved with members $A_i$ and $B_j$, the producer, $P_{A_i{B}_j}$, generates a signature for $Tra{n}_{A_i{B}_j}$ via the following computations:
  • Choose a random number, $t_{A_i{B}_j}\in Z_n^{*}$.
  • Compute $T_{A_i{B}_j}=t_{A_i{B}_j}·P$, $h_{A_i{B}_j }=H\left(Sig{n}_{last},Tra{n}_{A_i{B}_j},T_{A_i{B}_j}, P{K}_{A_i{B}_j},h_{A_i},h_{B_j}\right)$, and ${\tau }_{A_i{B}_j}=t_{A_i{B}_j}+h_{A_i{B}_j}·(x_{A_i{B}_j}+s_{A_{i1}}+s_{B_{j1}})$ mod n. Note that $Sig{n}_{last}$ is the signature contained in the last valid block generated in a legitimate manner and adopted by the relay chain.
  • Output ${\sigma }_{A_i{B}_j}=\left(T_{A_i{B}_j},R_{A_i},R_{B_j},{\tau }_{A_i{B}_j}\right)$ as the signature of the transaction, $Tra{n}_{A_i{B}_j}$.
• Verify (Figure 4):
  

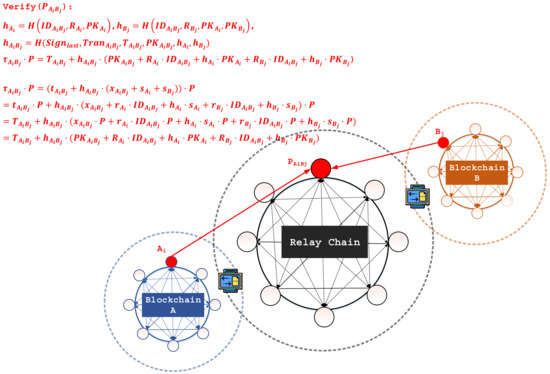  Figure 4. The Verify phase.
  Given $params=\left\{G, P,H,P{K}_{A_i},P{K}_{B_j}\right\}$, $I{D}_{A_i{B}_j}$, $P{K}_{A_i{B}_j}$, $Tra{n}_{A_i{B}_j}$, and ${\sigma }_{A_i{B}_j}=\left(T_{A_i{B}_j},R_{A_i},R_{B_j},{\tau }_{A_i{B}_j}\right)$, the verifier examines the validity of ${\sigma }_{A_i{B}_j}$ via the following computations:
  • Compute $h_{A_i}=H\left(I{D}_{A_i{B}_j}, R_{A_i},P{K}_{A_i}\right)$, $h_{B_j}=H\left(I{D}_{A_i{B}_j}, R_{B_j},P{K}_{A_i},P{K}_{B_j}\right)$, and $h_{A_i{B}_j}=H\left(Sig{n}_{last},Tra{n}_{A_i{B}_j},T_{A_i{B}_j}, P{K}_{A_i{B}_j},h_{A_i},h_{B_j}\right)$, where $P{K}_{A_i{B}_j}$ and $Sig{n}_{last}$ can be obtained by inquiry through the relay chain.
  • Determine if ${\tau }_{A_i{B}_j}·P=T_{A_i{B}_j}+h_{A_i{B}_j}·(P{K}_{A_i{B}_j}+R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}+R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j}$ hold. The correctness of the signature, ${\sigma }_{A_i{B}_j}=\left(T_{A_i{B}_j},R_{A_i},R_{B_j},{\tau }_{A_i{B}_j}\right)$, is presented as follows:

    $$\begin{array}{c}{\tau }_{A_i{B}_j}·P=(t_{A_i{B}_j}+h_{A_i{B}_j}·(x_{A_i{B}_j}+s_{A_{i1}}+s_{B_{j1}}))·P\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ =t_{A_i{B}_j}·P+h_{A_i{B}_j}·(x_{A_i{B}_j}+r_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·s_{A_{i1}}+r_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·s_{B_{j1}})·P\hfill \\ =T_{A_i{B}_j}+h_{A_i{B}_j}·(x_{A_i{B}_j}·P+r_{A_i}·I{D}_{A_i{B}_j}·P+h_{A_i}·s_{A_{i1}}·P+r_{B_j}·I{D}_{A_i{B}_j}·P+h_{B_j}·s_{B_{j1}}·P)\hfill \\ =T_{A_i{B}_j}+h_{A_i{B}_j}·(P{K}_{A_i{B}_j}+R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}+R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j})\hfill \end{array}$$

Upon completion, the DApp of the transaction launcher receives a notification about the status (success/failure) of the cross-blockchain transaction. After that, the DApp creates a status notification and displays a screen indicating success (or failure) for the cross-chain transaction for the end user.

5. Performance and Security Analysis

5.1. Performance Evaluation of the Proposed Interoperability Management Scheme for Cross-Chain Transactions

To investigate the practicability of our scheme, we implemented a prototype cross-blockchain system to verify the practical potential of our proposed interoperability management scheme and calculate the corresponding time cost. Table 3 shows the environment of our implementation, in which the VM resources simulate the cross-blockchain transaction.

Table 3. Implementation Environment.

Item	Description
VM Resources	Intel i9-10900 Processor, ADATA 32 GB 2633 MHz DDR4 RAM, ADATA 500 GB M.2 SSD
Software Platform	Windows 10 64-Bit, Ethereum, Go 1.8.9, Solidity 4.2.26, Remix IDE, Web3.js 1.5.0, Oracle Java 11, Eclipse 3.8 with Open JDK, Geth 1.10.2 with puppet, Bouncy Castle library [18] for Java

Figure 5 illustrates the network structure of our scheme, which is operated on the Ethereum platform. To pursue the best security and explore the possibility of combining our proposed scheme with next-generation cryptography, we adopted SHA-3 (with a 256-bit output sequence) as a secure one-way hash function [16]. We adopted the crypto-modules with the Bouncy Castle Crypto Library for Java [26] to implement ECC-based scalar multiplication operations (with a 384-bit prime n), and the SHA-3 hash function takes a random-length binary sequence (96-bit) as input, and outputs a 256-bit sequence. The implementation is programmed with Open JDK and Eclipse 3.8, and the smart contract uses Solidity and Remix. The application binary interface (ABI) and source code (Bytecode) files generated after compilation by Remix are converted into Java code by Web3j CLI. We used Java with Web3j CLI to listen to the state of each blockchain. All evaluations are built on Ethereum, and we established three blockchains that exploit different consensus protocols, to simulate cross-blockchain transactions. The number of nodes in each blockchain was set to 3, and the internal consensus protocols executed within a single blockchain, i.e., private chain $A$ and private chain $B$, are Proof of Work (PoW) and Proof of Authority (PoA), respectively. Moreover, the relay chain, $RC$, is based on the DPOS consensus protocol, and the nodes of the relay chain, $RC$, are deployed by Docker. Note that the above construction of the blockchain is realized with Geth and puppet, and we set web3j to sleep for 0.5 s after each call instead of the default 15 s.

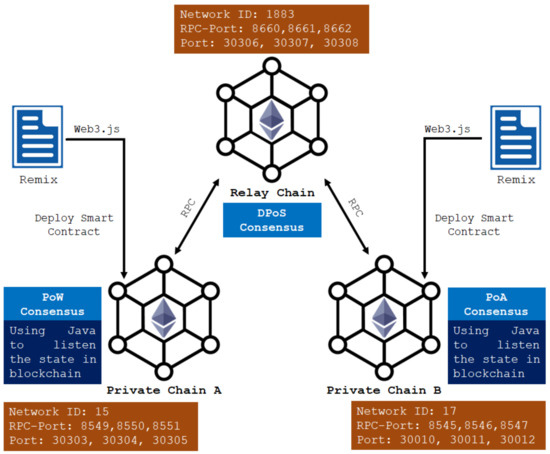
Figure 5. The network structure of the implementation of our proposed scheme.

We implemented our scheme as shown in Figure 6, and Table 4 shows the cost of calculating core security components and uploading parameters to the smart contract required for our proposed scheme, which takes 625.824 ms to perform 4 random number generation operations, 6 SHA-3 operations, and 21 ECC-based scalar multiplication operations. Moreover, the performance was measured by the following metrics: P1 to P5. For each of the metrics, we conducted the evaluation ten times to determine the average time cost. Table 5 shows the results.

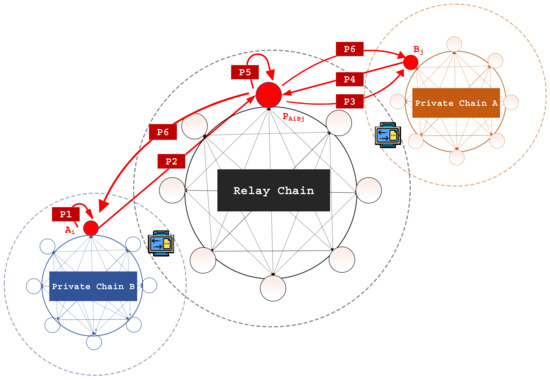
Figure 6. The implementation of the performance evaluation of our proposed scheme.

Table 4. Computation cost of core security components and smart contract uploading for our proposed scheme.

Phase	Process	ms	Percentage
P1	Generate$s_{A_i}$,$I{D}_{A_i{B}_j}$	1.317	0.21%
	Upload$s_{A_i}$and$I{D}_{A_i{B}_j}$to the SC *	6.001	0.96%
Computation Time of P1		7.318	1.17%
P2	Generate$r_{A_i}$	1.263	0.2%
	Compute$P{K}_{A_i}$,$s_{A_{i1}}$, and$R_{A_i}$	44.583	7.12%
	Compute$s_{A_{i1}}·P$	56.099	8.97%
	Compute$R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}$	43.01	6.87%
	Upload$P{K}_{A_i}$,$s_{A_{i1}}$, and$R_{A_i}$to the SC *	6	0.96%
Computation Time of P2		150.955	24.12%
P3	Generate$r_{B_j}$and$s_{B_j}$	3.006	0.48%
	Compute$P{K}_{B_j}$,$s_{B_{j1}}$, and$R_{B_j}$	44.584	7.12%
	Compute$s_{B_{j1}}·P$	56.589	9.04%
	Compute$R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j}$	42.039	6.72%
	Upload$P{K}_{B_j}$,$s_{B_{j1}}$, and$R_{B_j}$to the SC *	6	0.96%
Computation Time of P3		152.218	24.32%
P4	Generate$x_{A_i{B}_j}$	1.263	0.2%
	Compute$P{K}_{A_i{B}_j}$	14.845	2.37%
	Upload$P{K}_{A_i{B}_j}$to the SC *	5.977	0.96%
Computation Time of P4		22.085	3.53%
P5	Generate$t_{A_i{B}_j}$	1.265	0.2%
	Compute$T_{A_i{B}_j}$,$h_{A_i{B}_j}$, and${\tau }_{A_i{B}_j}$	16.615	2.66%
	Upload$T_{A_i{B}_j}$,$h_{A_i{B}_j}$, and${\tau }_{A_i{B}_j}$to the SC *	6.001	0.96%
Computation Time of P5		23.881	3.82%
P6	Compute$h_{A_i}$	0.315	0.05%
	Compute$h_{B_j}$	0.329	0.05%
	Compute$h_{A_i{B}_j}$	0.343	0.06%
	Compute${\tau }_{A_i{B}_j}·P$	102.668	16.41%
	Compute$T_{A_i{B}_j}+h_{A_i{B}_j}·(P{K}_{A_i{B}_j}+R_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·P{K}_{A_i}+R_{B_j}·I{D}_{A_i{B}_j}+h_{B_j}·P{K}_{B_j}$	159.711	25.52%
	Upload$h_{A_i}$,$h_{B_j}$, and$h_{A_i{B}_j}$to the SC *	6.001	0.96%
Computation Time of P6		269.367	43.04%
Total Computation Time		625.824	100%

* SC: Smart contract.

Table 5. Time cost for our proposed scheme.

Phase	Mining Cost/per	Computation Cost/per
P1	10.601 s	7.318 ms
P2	10.592 s	150.955 ms
P3	10.441 s	152.218 ms
P4	20.32 s	22.085 ms
P5	10.446 s	23.881 ms
P6	24.811 s	269.367 ms
Total Cost	87.211 s	625.824 ms

• Phase P1 models the private chain $A$ choosing a security parameter $k$ in the initial stage of the blockchain. Then, it exploits the elliptic curve discrete logarithm problem (ECDLP) to generate a secure hash function, $H$, with the SHA3-256 algorithm, and securely shares it with all members of A via a smart contract. The above processes are referred to as phase P1. According to our implementation, it requires 10.601 s for the mining procedure, and the computation cost of core security components and smart contract uploading was 7.318 ms.
• Phase P2 models the following processes. First, the producer sends its ID to the private chain $A$. Private chain $A$ then uses the elliptic curve Diffie–Hellman (ECDH) algorithm to generate a shared key, $K_A$, with the producer’s ID and the private chain $A$’s private key. Next, by deploying a smart contract on chain $A$, a transaction,$Tran(K_A)$, is generated, and $K_A$ is sent to the producer with the transaction. The above processes are represented as phase P2. Based on our implementation, we obtained an average mining time of 10.592 s, and the computation cost of core security components and smart contract uploading was 150.955 ms for P2.
• In phase P3, the producer validates $K_A$, and sends a success (or failure) acknowledgment to chain $A$. Then, the producer transmits the smart contract, which stores chain $A$’s public key and secure hash function, H, to private chain $B$. In this phase, we achieved an average mining cost of 10.441 s, and the computation cost of core security components and smart contract uploading was 152.218 ms for P3.
• For phase P4, private chain $B$ exploits the ECDH algorithm to generate a shared key, $K_B$, using the producer’s ID and its private key. After that, by deploying a smart contract on chain $B$, a transaction, $Tran(K_B)$, is generated, and $K_B$ is sent to the producer with the transaction. On average, a mining time of 20.32 s is required, and the computation cost of core security components and smart contract uploading was 22.085 ms for P4.
• For phase P5, the producer validates $K_B$, and sends a success (or failure) acknowledgment to chain $B$. Then, the producer issues a digital signature on the transaction. Note that the digital signature scheme is the Elliptic Curve Digital Signature Algorithm (ECDSA). In our implementation, an average mining time of 10.446 s was required, and the computation cost of core security components and smart contract uploading was 23.881 ms for P5.
• Phase P6 represents the producer’s return of the signature of the cross-chain transaction to the two private chains, whereupon the private chain’s verification of the signature occurs. The experimental results show that the computation time of core security components from sending the signature to uploading the smart contract to the two private chains required 269.367 ms, and a mining time of 20.32 s was required, on average.

From Table 5, we know that the most expensive part is the mining procedure, which takes 87.211 s, and this process is generally required for cross-blockchain transactions. To reduce the cost of the mining procedure, we discovered that submitting multiple transactions in batches reduces the average time cost. In our experiments, we set each transaction to complete the actions that must be performed in this stage before the end of each stage, and then checked whether each blockchain has completed internal consensus and proceeded to the next stage, instead of confirming the internal consensus state on a transaction-by-transaction basis. Meanwhile, we conducted ten experiments. Figure 7 and Figure 8 depict the computational cost and mining cost when increasing from 1 to 100, respectively. From Figure 7, we can observe that as the number of transactions increased, the average computation time remained around 625 ms, indicating that the increase in the number of transactions does not affect the average computation time per transaction. Figure 8 clearly shows that when the number of transactions increased to 10, the average mining time dropped significantly to 59.827 s. Subsequently, as the number of transactions increased, the average mining time also steadily decreased. Therefore, batch-submitting multiple transactions is very efficient for our proposed scheme.

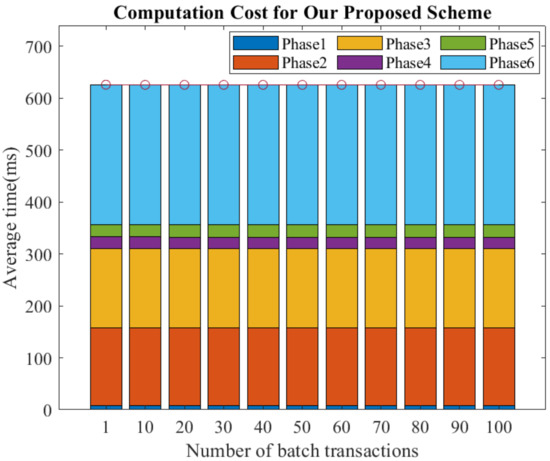
Figure 7. The computation cost with batch transactions for our proposed scheme.

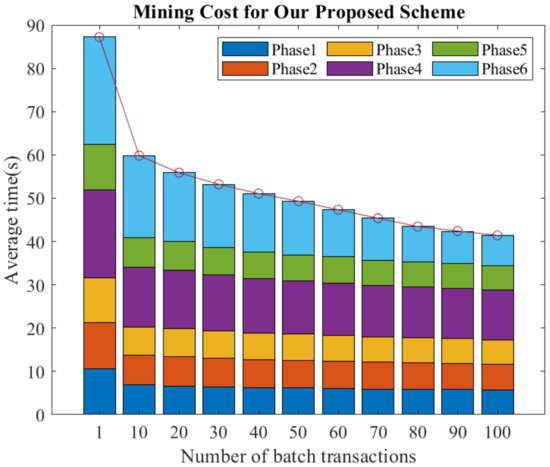
Figure 8. The mining cost with batch transactions for our proposed scheme.

5.2. Security Analysis

In this section, we present the security analysis of the proposed scheme under the assumptions of the following adversary model. That is, an adversary, Ad, may break the robustness of the proposed scheme through the following oracles:

• $\left({\mathrm{O}}_1\right)\mathrm{InitEntity}():$ This oracle allows Ad to launch a session, $k$, of the process of our proposed scheme and get back a session identifier $kid$.
• $\left({\mathrm{O}}_2\right)\mathrm{Send}\left(N_k, k, m\right):$ This oracle allows Ad to send a message, $m$, to any given node, $N_k$, and get back $N_k\prime \mathrm{s}$ response from session $k$.
• $\left({\mathrm{O}}_3\right)\mathrm{Eavesdrop}\left(N_{i\_k}, N_{j\_k}, k, m\right):$ This oracle models a passive attack by allowing Ad to eavesdrop and gain reading access to the message, $m$, exchanged between $N_{i\_k}$ and $N_{j\_k}$ in session $k$.
• $\left({\mathrm{O}}_4\right)\mathrm{Int}ercept\left(N_{i\_k}, N_{j\_k}, k, m\right):$ This oracle models an active attack by allowing Ad to interrupt and modify the message, $m$, exchanged between $N_{i\_k}$ and $N_{j\_k}$ in session $k$.

Definition: Let $E$ be the event that an adversary, Ad, can correctly generate a counterfeit but valid signature during any given session, $k$. In that case, an adversary,$Ad\left(ϵ, t, n_1, n_2, n_3, n_4\right),$ generates a counterfeit but valid signature if the probability that $E$ occurs, i.e., $Pr\left[E\right]$, is at least $ϵ$, and the run time of Ad is at most $t$, where $ϵ$ is non-negligible and $t$ is a polynomial time that depends on the execution time of oracles ${\mathrm{O}}_1, {\mathrm{O}}_2$, ${\mathrm{O}}_3$, and ${\mathrm{O}}_4$. In brief, our proposed scheme provides $\left(ϵ, t, n_1, n_2, n_3, n_4\right)$-robustness against a counterfeit signature attack if there exists no adversary, $Ad\left(ϵ, t, n_1, n_2, n_3, n_4\right)$, generating a counterfeit but valid signature against our proposed scheme.

Claim 1: The proposed scheme provides $\left(ϵ, t, 1, n_2, n_3, n_4\right)$-robustness against a counterfeit signature attack where $n_2, n_3, \mathrm{and} n_4$ are arbitrary numbers.

Oracle ${\mathrm{O}}_1$ can be launched easily as an adversary, Ad, can register with the service provider of our proposed scheme. Once the oracle ${\mathrm{O}}_1$ is performed, oracles ${\mathrm{O}}_2$, ${\mathrm{O}}_3$, and ${\mathrm{O}}_4$ can be launched with little effort by an adversary under the assumption that the communication channel is public. After that, with oracle queries ${\mathrm{O}}_2$ and ${\mathrm{O}}_3$, an Ad may eavesdrop on the communication among nodes of blockchains and the relay chain to obtain transmitted messages as many times as it wants. However, the proposed scheme achieves transmission confidentiality via the HTTPS protocol. Sensitive data engaged with cross-chain transactions are protected and, thus, an Ad cannot obtain the secret parameters from the secure channel. In addition, Ad may utilize ${\mathrm{O}}_4$ to interrupt and modify the messages obtained via ${\mathrm{O}}_2$ and ${\mathrm{O}}_3$. Nevertheless, the proposed scheme utilizes certificateless signature primitives to provide the tamper-resistant characteristic for transmitted cross-chain transactions. Furthermore, non-repudiation of these transactions can be guaranteed through the adoption of the certificateless signature, as well. Accordingly, an Ad cannot break the robustness of our proposed scheme.

Claim 2: The proposed scheme can provide resistance against replay attack and man-in-the-middle attack, and the security requirements, i.e., non-repudiation and data integrity, for cross-chain transactions.

In our proposed scheme, all transmitted messages such as $\left(s_{A_{i1}},R_{A_i}\right)$, $\left(s_{B_{j1}},R_{B_j}\right),$ and ${\sigma }_{A_i{B}_j}$ are involved with random numbers $r_{A_i}, r_{B_j}$ and $t_{A_i{B}_j}$. All these random numbers are one-time valid and accordingly, our proposed scheme can resist the replay attack. Moreover, based on equations, i.e., $s_{A_{i1} }=r_{A_i}·I{D}_{A_i{B}_j}+h_{A_i}·s_{A_i}$ and $R_{A_i}=r_{A_i}·P$, we can clearly see that the $s_{A_{i1}}$ and $R_{A_i}$ are well-protected through $s_{A_i}$ and $r_{A_i}$ with ECDLP. Therefore, attackers between all the communicating entities cannot impersonate other legitimate entities with a fake but valid message $(s_{A_{i1}}$,$R_{A_i})$. The same situation is applied to the message $\left(s_{B_{j1}},R_{B_j}\right)$. Then, based on the equation ${\sigma }_{A_i{B}_j}=\left(T_{A_i{B}_j},R_{A_i},R_{B_j},{\tau }_{A_i{B}_j}\right)$, it is believed that ${\sigma }_{A_i{B}_j}$ is secure via the random number $t_{A_i{B}_j}$ and ECDLP. Hence, it is extremely hard to counterfeit a fake but valid signature of the transaction, $Tra{n}_{A_i{B}_j}$, under the computational hardness of ECDLP. In brief, our proposed scheme can resist a man-in-the-middle attack. Next, it is clear that our proposed scheme is naturally embedded with the non-repudiation and data integrity characteristics. This is because the ECDLP and CLS are integrated to construct our proposed scheme. Based on the verification of $\left(s_{A_{i1}},R_{A_i}\right)$, $\left(s_{B_{j1}},R_{B_j}\right)$, and ${\sigma }_{A_i{B}_j}$, any possibility of violating the non-repudiation and data integrity will be detected immediately.

5.3. Discussion on Security Issues with the Adoption of Web3 in Our Implementation

In our implementation, we adopted web3, a JavaScript API that connects to the Generic JSON RPC specification. According to [27], it is vulnerable to insecure credential storage. The current implementation of web3.js may lead to wallet decryption in some cases. When the wallet is saved and encrypted into local storage, the private key is required to load the wallet. However, this private key is available through LocalStorage and can be read in clear text on a web page after loading into the wallet. Attackers could abuse this implementation via client-side attacks, primarily cross-site scripting (XSS), and could lead to the theft of the consumer’s wallet private key. Against XSS attacks, one should avoid storing wallet addresses in plain text and use their hashed versions instead. In this case, we think that the simplest mitigation is for the website program to include a security header such as “X-Frame-Options” to eliminate the html script “iframe” which can lead to clickjacking and tricking users into obtaining wallet addresses.

ReactJS is another mitigation, as it appears to be resistant to most XSS attacks due to the way it generates DOM nodes and the string values it can automatically escape through user input. Its disadvantage is that data passed to props are not automatically escaped until rendered to the React DOM, and many properties available in ReactJS still allow XSS attacks, including, but not limited to:

<img src={}/> and <a href="{}"/>.

Thus, classic cross-site scripting attacks that use URLs containing malicious scripts, such as:

<a href="javascript:alert(123)">Button</a>

can still work in ReactJS, as shown in:

ReactDOM.render(<a href=“JavaScript:

alert(1)">Button</a>,document.getElementById(‘root’));

When the button is clicked, the script embedded in the href property is executed.

Therefore, we recommend another mitigation, which is to load/decrypt the wallet only when the private or public key is needed. When you do not need to access the key itself, simply save the load from locally to access the address using the following command:

let wallet = JSON.parse(localStorage[“web3.js_wallet”])

The level of security is much higher by doing so and decrypting only when we needed to access the keystore, rather than simply loading the wallet and attaching it to the global object for later use. Furthermore, we suggest that web3 developers can consider a complete redesign of the XOR mask that incorporates a user-created PIN or password to provide an additional layer of security in the future version of web3. Another issue with regular-expression denial of service (ReDoS) is that the WebSocket (ws) package allows a specially crafted header value to be used to significantly reduce the server speed. However, to resolve it, developers using the ws package only need to upgrade to version 7.4.6, 6.2.2, 5.2.3, or later, so it is not discussed here.

6. Conclusions

In this paper, we presented a secure interoperability management scheme with a certificateless cryptographic primitive for cross-blockchain transactions. Unlike most existing cross-chain transaction methods, we redefined the consensus method as a verification method, and used it to ensure the integrity and data provenance of the transferred data when performing cross-blockchain interactions. The scheme relies on cross-blockchain consensus with relays to improve the compatibility between heterogeneous blockchains. To test the proposed method in a real-world context, we implemented our scheme on VM resources, with all blockchains based on a private blockchain network with Ethereum. Moreover, the relay chain, which was deployed by Docker, was based on Delegated Proof of Stake (DPoS), regardless of the heterogeneity of consensus protocols that blockchains adopted, and the number of nodes in each blockchain was set as 3. Furthermore, the evaluation demonstrated that the total time of a cross-blockchain transaction was 87.837 s. Our proposed scheme delivers compatibility among heterogeneous blockchains and guarantees the consistency of transaction data exchanged. It also achieves better security for cross-blockchain transactions. In brief, according to our evaluation results, we showed that our management scheme is secure and practical for common cross-blockchain transactions. In the future, we can also further study how to reduce the return time of performing the consensus verification to make cross-blockchain transactions more versatile. Moreover, it is worthy to investigate the scalability of our proposed scheme with existing public blockchain solutions.