Qualitative Behavior of an Exponential Symmetric Difference Equation System
Abstract
1. Introduction
2. Preliminaries
- (i)
- is revealed as stable if ∀, ∃ provided that initials , , implies ∀.
- (ii)
- , if not stable, is designated unstable.
- (iii)
- If ∃ provided that as and , then is designated an asymptotically stable.
- (iv)
- If as , then is designated as a global attractor.
- (v)
- If is a global attractor and stable, then it is said to be a global asymptotic attractor.
3. Boundedness and Persistence
4. Uniqueness and Existence
5. Global and Local Stability
6. Convergence Rate
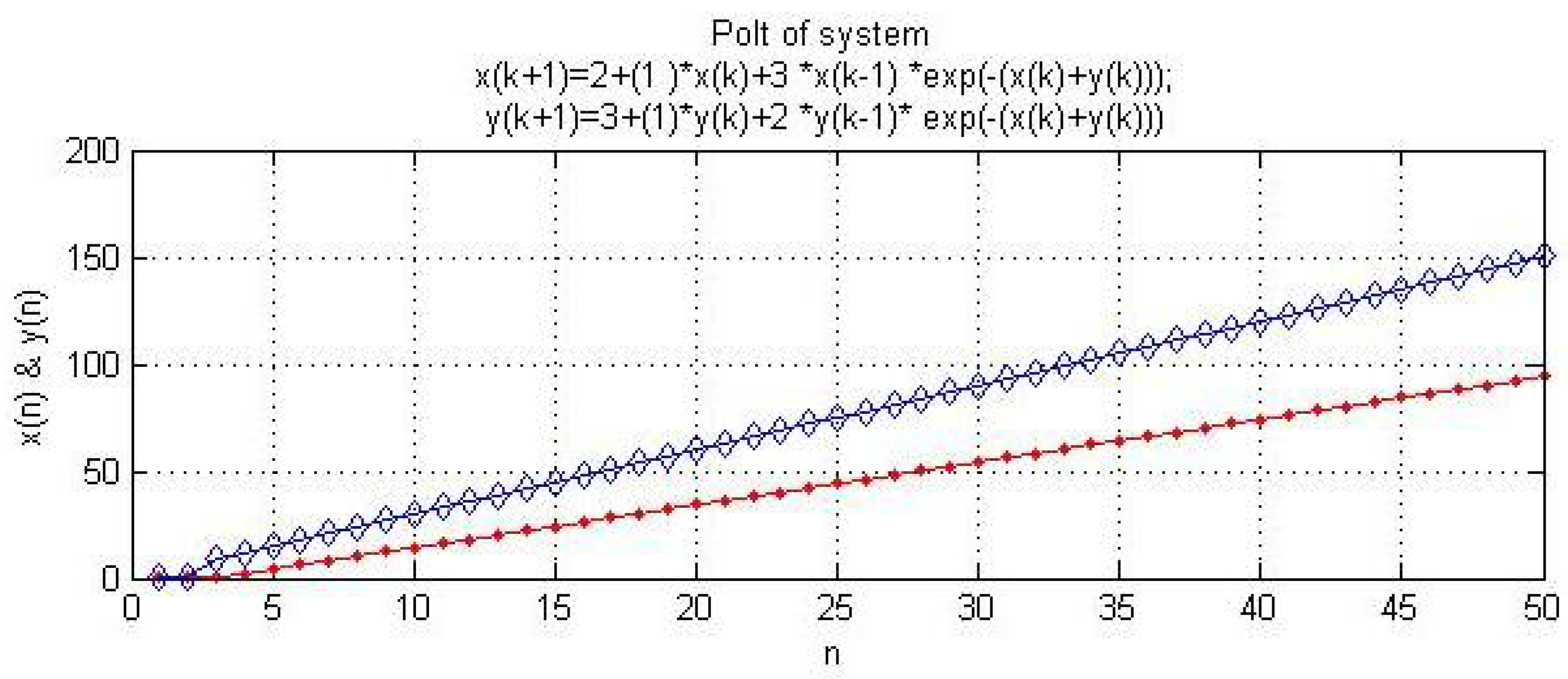
7. Unbounded Solution’s Existence
- (i)
- (ii)
- (iii)
- (iv)
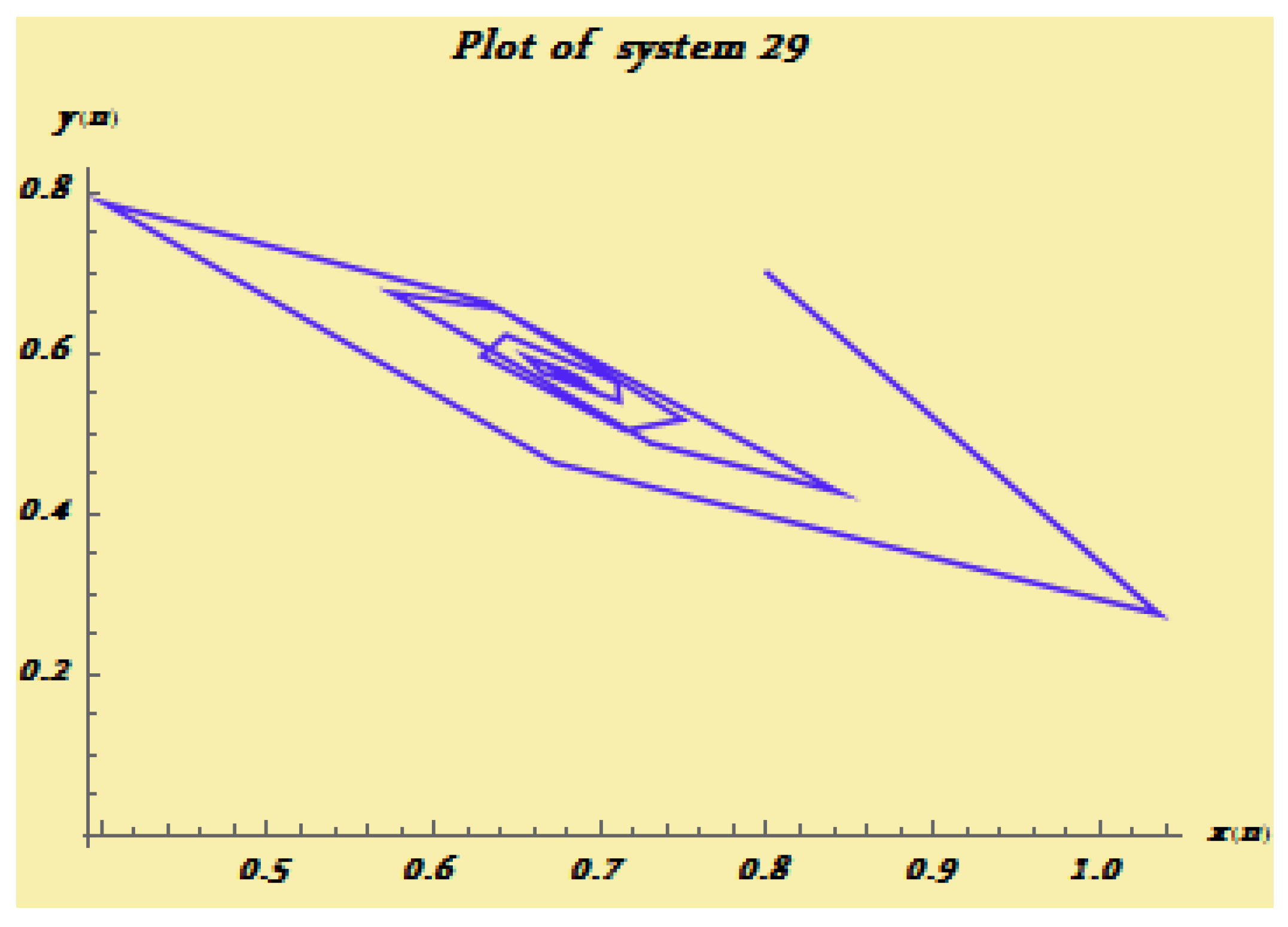
8. Numerical Examples
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agarwal, R.P. Difference Equations and Inequalities, 2nd ed.; Revised and Expended; Marcel Dekker: New York, NY, USA, 2000; p. 980. [Google Scholar]
- Camouzis, E.; Ladas, G. Dynamics of Third-Order Rational Difference Equations: With Open Problems and Conjectures; Chapman and Hall/HRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Çinar, C.; Simsek, D.; Yalçinkaya, İ. On the recursive sequence . Int. J. Contem. Math. Sci. 2006, 1, 475–480. [Google Scholar]
- Din, Q.; Ibrahim, T.F.; Khan, K.A. Behavior of a competitive system of second-order difference equations. Sci. World J. 2014, 2014, 283982. [Google Scholar] [CrossRef] [PubMed]
- Elsayed, E.M. On the solutions and periodic nature of some systems of difference equations. Int. J. Biomath. 2014, 7, 1450067. [Google Scholar] [CrossRef]
- Grove, E.A.; Ladas, G. Periodicities in Nonlinear Difference Equations; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Hamza, A.E.; Khalaf-Allah, R. Global behavior of a higher order difference equation. J. Math. Stat. 2007, 3, 17–20. [Google Scholar] [CrossRef][Green Version]
- Kalabuŝić, S.; Kulenović, M.R.S.; Pilav, E. Global dynamics of a competitive system of rational difference equations in the plane. Adv. Differ. Eq. 2009, 2009, 132802. [Google Scholar] [CrossRef][Green Version]
- Kuleovic, M.; Nurkanovic, Z. The rate of convergence of the solution of a three-dimensional linear fractional system of difference equations. Zb. Rad. PMF 2005, 2, 1–6. [Google Scholar]
- Khan, A.Q. Global dynamics of two systems of exponential difference equations by Lyapunov function. Ad. Diff. Eq. 2014, 1, 297. [Google Scholar] [CrossRef]
- Ozturk, I.; Bozkurt, F.; Ozen, S. On the difference equation . Appl. Math. Comput. 2006, 181, 1387–1393. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Psarros, N.; Papaschinopoulos, G.; Papadopoulos, K.B. Long-term behavior of positive solutions of an exponentially self-regulating system of difference equations. Int. J. Biomath. 2017, 10, 1750045. [Google Scholar] [CrossRef]
- Pituk, M. More on Poincare’s and Perron’s theorems for difference equations. J. Diff. Eq. Appl. 2002, 8, 201–216. [Google Scholar] [CrossRef]
- El-Moneam, M.A.; Ibrahim, T.F.; Alamoudy, S.O. Stability of A Fractional Difference Equation of high order. J. Nonlinear Sci. Appl. 2019, 12, 65–74. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.; Liu, J. Dynamics of a system of rational third order difference equation. Adv. Diff. Eq. 2012, 2012, 136. [Google Scholar] [CrossRef]
- El-Metwally, E.; Grove, E.A.; Ladas, G.; Levins, R.; Radin, M. On the difference equation . Nonlinear Anal. 2001, 47, 4623–4634. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Schinas, C.J. On the dynamics of two exponential type systems of difference equations. Comput. Math. Appl. 2012, 64, 2326–2334. [Google Scholar] [CrossRef]
- Ibrahim, T.F. Generalized Partial ToDD’s Difference Equation in n-dimensional space. J. Comput. Anal. Appl. 2019, 26, 910–926. [Google Scholar]
- Ibrahim, T.F. Bifurcation and Periodically Semicycles for Fractional Difference Equation of fifth order. J. Nonlinear Sci. Appl. 2018, 11, 375–382. [Google Scholar] [CrossRef]
- Ibrahim, T.F.; El-Moneam, M.A. Global stability of a higher-order difference equation. Iran. J. Sci. Technol. Trans. Sci. 2017, 41, 51–58. [Google Scholar] [CrossRef]
- Ibrahim, T.F. Closed Form Expressions of some systems of Nonlinear Partial Difference Equations. J. Comput. Anal. Appl. 2017, 23, 433–445. [Google Scholar]
- Ibrahim, T.F. Behavior of Two and Three-Dimensional Systems of Difference Equations in Modelling Competitive Populations. Dyn. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 2017, 24, 395–418. [Google Scholar]
- Ibrahim, T.F. Closed Form Expression of Tractable Semi-Max-type Two-Dimensional system of Difference equations with variable coefficients. J. Egypt. Math. Soc. 2016, 24, 538–544. [Google Scholar] [CrossRef]
- Ibrahim, T.F. Behavior of Some Higher Order Nonlinear Rational Partial Difference Equations. J. Egypt. Math. Soc. 2016, 24, 532–537. [Google Scholar] [CrossRef]
- Ibrahim, T.F. Solving a class of three-order max-type difference equations. Dyn. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 2014, 21, 333–342. [Google Scholar]
- Ibrahim, T.F.; Touafek, N. Max-type system of difference equations with positive two-periodic sequences. Math. Methods Appl. Sci. 2014, 37, 2562–2569. [Google Scholar] [CrossRef]
- Ibrahim, T.F. Periodicity and Global Attractivity of Difference Equation of Higher Order. J. Comput. Anal. Appl. 2014, 16, 552–564. [Google Scholar]
- Ibrahim, T.F.; Zhang, Q. Stability of an anti-competitive system of rational difference equations. Arch. Des Sci. 2013, 66, 44–58. [Google Scholar]
- Ibrahim, T.F. Asymptotic behavior of a difference equation model in exponential form. Appear Math. Methods Appl. Sci. 2022, 45, 10736–10748. [Google Scholar] [CrossRef]
- Khan, A.Q.; Qureshi, M.N. Stability analysis of a discrete biological model. Int. J. Biomath. 2016, 9, 1650021. [Google Scholar] [CrossRef]
- Elaydi, S. An introduction to Difference Equations. In Undergraduate Texts in Mathematics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Sedaghat, H. Nonlinear Difference Equations: Theory with Applications to Social Science Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, T.F.; Refaei, S.; Khaliq, A.; El-Moneam, M.A.; Younis, B.A.; Osman, W.M.; Al-Sinan, B.R. Qualitative Behavior of an Exponential Symmetric Difference Equation System. Symmetry 2022, 14, 2474. https://doi.org/10.3390/sym14122474
Ibrahim TF, Refaei S, Khaliq A, El-Moneam MA, Younis BA, Osman WM, Al-Sinan BR. Qualitative Behavior of an Exponential Symmetric Difference Equation System. Symmetry. 2022; 14(12):2474. https://doi.org/10.3390/sym14122474
Chicago/Turabian StyleIbrahim, Tarek F., Somayah Refaei, Abdul Khaliq, Mohamed Abd El-Moneam, Bakri A. Younis, Waleed M. Osman, and Bushra R. Al-Sinan. 2022. "Qualitative Behavior of an Exponential Symmetric Difference Equation System" Symmetry 14, no. 12: 2474. https://doi.org/10.3390/sym14122474
APA StyleIbrahim, T. F., Refaei, S., Khaliq, A., El-Moneam, M. A., Younis, B. A., Osman, W. M., & Al-Sinan, B. R. (2022). Qualitative Behavior of an Exponential Symmetric Difference Equation System. Symmetry, 14(12), 2474. https://doi.org/10.3390/sym14122474




