The Reappearance of Poetic Beauty in Chaos

Abstract

Different forms of attractors, or basins of attraction, in chaotic systems often bring people the enjoyment of beauty. This attraction is reminiscent of ancient Chinese poetry and introduces people to a poetic and magical world, bringing them a sense of wonder and enlightenment. In this work, some cases of the beauty of chaos, including forms of symmetry, asymmetry, conditional symmetry, and extension, are demonstrated. The chaos theory of science and engineering and the art of literature are innovatively combined and integrated here. The unique charm of chaotic attractors is revealed and endowed to the artistic realm of ancient Chinese poetry, helping people to understand the poetic beauty of the chaotic world. Through bold association and imagination, chaotic attractors are endowed with fresh vitality, thus showing people a world of artistic space that is full of fantasy.

1. Introduction

Nature is full of wonderful things, such as storms, thunder, lightning, and thousands of weather phenomena. Everything runs according to its laws, and it shows various colors in the different seasons. Human beings, who are the soul of all things, have explored the mysteries of the universe. In nature, chaos is everywhere, such as the white clouds floating in the sky, flowing water, the smoke from farmers’ chimneys, etc. The chaotic beauty of nature has aroused many literary tourists’ poetic feelings, which have always been sung in literary works, as shown in Figure 1.

Figure 1. “Lonely smoke straight in the desert, the long river of the yen down” by poet Wei Wang (Tang Dynasty).

In the vast desert, wisps of smoke rise slowly. The poem “Lonely smoke straight in the desert, and the long river of the yen down”, which was written in the year of 737 by Wei Wang, who was a poet of the Tang Dynasty, is clearly voiced in Figure 1.

The chaotic attractors are various and changeable. Furthermore, the colorful attractors trigger the readers’ rich and diverse associations, and the poetic kingdom arises spontaneously. The beauty of chaotic attractors is studied in the next four sections. The elegant fractal structure of the attractor [1,2,3], or the associated basins, agree with the beauty of the poems and the songs in traditional Chinese culture. The artistic conception in the poem perfectly connects with the beauty of chaos. The unique structure of the chaotic systems that have been selected with elegant attractors in this report reflect the connection between science and art and bring the great convenience for understanding the technology of chaos-based engineering [4,5,6]. Furthermore, it is proven that, from the view of chaos production [7,8,9], the evolution of chaos compared with poems does bring a wonderful and deep impression for engineers and encourages them to make use of chaos more proactively.

2. Formal Beauty in Chaos

Chaotic attractors are colorful and morphotropic, such as the curling smoke from kitchen chimneys [10,11] shown in Figure 2.

$$\{\begin{array}{l}\dot{x}=y+yz\\ \dot{y}=-xz+yz\\ \dot{z}=-az-xy+b\end{array}$$

(1)

$$\{\begin{array}{l}\dot{x}=y^2-0.4z^2\\ \dot{y}=-z^2-1.75y+3\\ \dot{z}=yz+(\left|x\right|-3)\end{array}$$

(2)

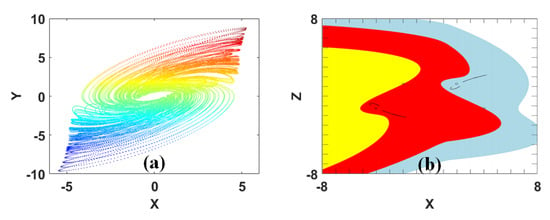
Figure 2. Typical smoke-like dynamical behavior: (a) x-y plane, when a = 0.6, b = 3, IC (initial conditions) = (1, −1, 1) in System (1), (b) basins of attraction in System (2) for coexisting reflection symmetric attractors in the y = −1.5.

Anshi Wang’s “West Taiyi Palace Building” (a poet of the Northern Song Dynasty in the year of 1068) states the following: “The smoke of the evening cooks is lonely, and I don’t know whose family the fish net is.” This poem writes that there is a fisherman’s house with a wisp of cooking smoke, similar to a chaotic attractor, rising like a dream. There is also a pair of fishing nets, which are sunbathed next to the house, beautiful and poetic.

Some attractors are similar to the free white goose [12,13], as shown in Figure 3.

$$\{\begin{array}{l}\dot{x}=(y+z)\mathrm{sgn}(z)\\ \dot{y}=-x\mathrm{sgn}(z)\\ \dot{z}=(a{x}^2+yz)\mathrm{sgn}(z)\end{array}$$

(3)

$$\{\begin{array}{l}\dot{x}=1-ayz\\ \dot{y}=z^2-z\\ \dot{z}=2\sin (x)-bz\end{array}$$

(4)

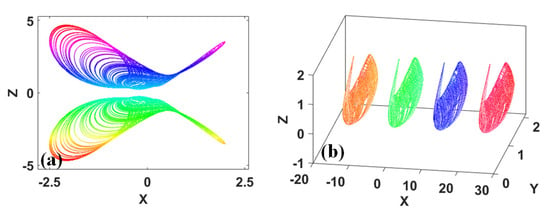
Figure 3. Typical coexisting goose-like attractors: (a) x-z plane, where a = 3 in System (3) and upside: IC = (0, −0.23, 1), underside: IC = (0, 0.23, −1), (b) when a = 3.55 and b = 0.5 in System (4), the initial conditions from left to right are respectively set to: IC = (−5, 0, −1), IC = (−2, 0, −1), IC = (−1, 0, −1), and IC = (2, 0, −1).

This is reminiscent of the Tang Dynasty poet Binwang Luo’s “Song of Goose”, which was composed in the year of 633 when he was seven years old. The poem is written as follows: “Goose! Goose! goose! Facing the blue sky, a group of geese is singing with bent necks. White feathers, floating on the green water. The red soles of the feet, stirring the clear water waves among them, Goose! Goose! Goose!”. This poem depicts the beautiful sound of the white goose and compares the lines and the colors of the goose with those of the sky, the white feathers, the green water, its red feet, and the clear water waves. Meanwhile, the words “sing”, “float”, and “stir” also depict the dynamic beauty of the goose by perfectly combining hearing and vision, static and dynamic, and sound and color; therefore, the sound and the shape of the goose are written intelligently.

3. Beauty of Symmetry

Many ancient Chinese poems also show symmetrical beauty as the chaotic attractors [14,15,16,17,18]. For example, Zongyuan Liu’s “River Snow”, which was written in the Tang Dynasty in 807, is written as follows: “Thousands of mountains without a bird, thousands of paths without a footprint.” The two sentences are symmetrical, with the same number of words, and the words in the sentence have the same method of speech and structure. “Thousands of mountains” and “Thousands of paths” are both of a partial structure. Here, the words “bird” and “footprint” are both nouns. “Flying off” and “disappearing” are both descriptions of the absence of any trace, therefore, the birds and the human beings cannot be seen. These two sentences mean that birds cannot be seen in thousands of mountains and ridges, and people cannot see the footprints of pedestrians. This is an example of a description of symmetry in poem. It is likely that there are many symmetrical attractors in dynamical systems, which brings us great feelings of the beauty of symmetry.

Some chaotic attractors look like symmetrical butterflies [19,20], fish, conch, and so on. For example, the chaotic attractor is similar to a butterfly dancing in the flowers in Systems (5) and (6), as plotted in Figure 4.

$$\{\begin{array}{l}\dot{x}=a(y-x)\\ \dot{y}=cx-y-xz\\ \dot{z}=xy-bz\end{array}$$

(5)

$$\{\begin{array}{l}\dot{x}=\mathrm{sgn}(x)(c-(b\left|y\right|-1)(\left|z\right|-e))\\ \dot{y}=a{(\left|z\right|-e)}^2-y(\left|z\right|-e)\\ \dot{z}=\mathrm{sgn}(z)(\left|x\right|-d)\end{array}$$

(6)

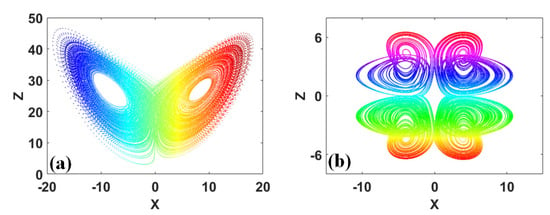
Figure 4. Typical butterfly-like attractors: (a) x−z plane, when a = 10, b = 8/3, and c = 28, IC = (1, 1, 1) in System (5), (b) x−z plane, when a = 0.6, b = 1, c = 1, d = 4, and e = 2, IC = (1, 1, 1) in System (6).

Butterflies fly as soon as they emerge, and they die within a few days. At the moment of breaking the cocoon, the butterfly must wait for its wings to dry and harden, otherwise, it is impossible for them to fly, and during this process it is easy for them to become the prey of natural enemies. Butterflies are covered with colorful wings; however, this beautiful romance is short and eternal. As described in “Inscription on the Falling Flower Butterfly”, which was written by poet Gongen Miao (1756–1841) during the Qing Dynasty, “Butterflies also cherish the beautiful spring, looking for fallen flowers along the stream.” The poem describes butterflies that cherish the beautiful spring and dance along the stream in search of falling flowers. The intention of the butterfly and the falling flower in the poem is to create a butterfly that intentionally becomes drunk for the flower, and the tears of the residual flower splash into the water; the falling flowers intentionally follow the flowing water and the flowing water has no intention for the falling flowers.

The chaotic attractors of conditional symmetry or symmetry are similar to moving symmetrical fish, as shown in Figure 5 [21,22].

$$\{\begin{array}{l}\dot{x}=y^2-a{z}^2\\ \dot{y}=-z^2-by+c\\ \dot{z}=yz+d\sin (x)\end{array}$$

(7)

$$\{\begin{array}{l}\dot{x}=\mathrm{sgn}(x)({(\left|y\right|-d_3)}^2-a)\\ \dot{y}=b\mathrm{sgn}(y)(\left|z\right|-d_4)\\ \dot{z}=\mathrm{sgn}(z)(-(\left|y\right|-d_3)-(\left|z\right|-d_4)+(\left|x\right|-d_1))\end{array}$$

(8)

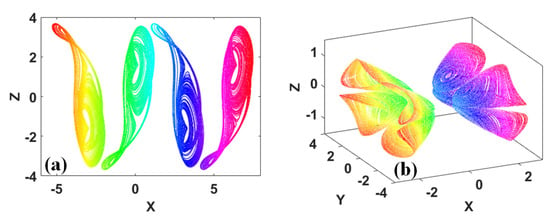
Figure 5. Typical coexisting fish-like attractors of Systems (7) and (8): (a) x−z plane, when a = 0.4, b = 1.75, c = 3, and d = 6.2 in System (7), the initial conditions from left to right are, respectively, set to: IC = (1 − π, −1, 1), IC = (1, −1, 1), IC = (1 + π, −1, 1), and IC = (1 + 2π, −1, 1), (b) when a = 1.22, b = 8.48, d₁ = 2, d₃ = 2.2, and d₄ = 0.45 in System (8), left side: IC = (−1.5, 3.2, 0.95) and right side: IC = (1.5, 3.2, 0.95).

This picture is easily reminiscent of the following line: “The egret in front of Xisai Mountain is flying freely, and in the river, the fat mandarin fish is swimming happily, and the peach blossoms floating in the water are so bright and full.” from “Fishing Songs”, which was written in the year of 823 by Zhihe Zhang, who was a famous poet in the Tang Dynasty. The meaning of this poem is that, in front of Cisse Mountain, many egrets fly freely. In the river, you can see a fat mandarin fish swimming happily, and the peach blossoms that are floating in the water are bright and full.

In addition, some of the chaotic attractors are similar to symmetrical and beautiful conchs, which are reminiscent of the verses of Zhongyan Fan (989–1052) “Treat Guanghua Li the second poem” of the Song Dynasty, as follows: “The poet boiled tea and drank wine, and had a good time with the guests. Gusts didn’t enjoy themselves until late at night, and moved to autumn moonlight to continue drinking”. In the poem, the images of the utensils for cooking, the tea, the conch, the wine, and so on illuminate the beautiful and happy time of the guests’ tea contests and drinking wine during the banquet, and the “milky white” and “wave red” represent the beautiful color of the tea and the wine. The wine was fragrant with the tea, and the guests were full of pleasure, therefore, they went out into the moonlight to continue to feast and have fun. The typical conch-like attractors are shown in Figure 6 [23,24].

$$\{\begin{array}{l}{x}_{n+1}=a{x}_n(1-y_n^2)\\ y_{n+1}=x_n,\end{array}$$

(9)

$$\{\begin{array}{l}\dot{x}=-ax+xy\\ \dot{y}=z^2-x^2\\ \dot{z}=y^2-byz\end{array}$$

(10)

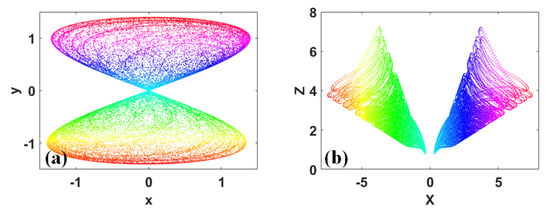
Figure 6. Typical conch-like attractors: (a) when a = 1.99 and IC = (0.1, 0.1) in map (9), (b) coexisting phase orbits of System (10) on x-z plane, where a = 1.2 and b = 1.2, left side: IC = (−2, 0, 3), right side: IC = (2, 0, 3).

The aesthetic value of coexisting hidden attractors [25,26,27] can also be found. Some chaotic attractors look like two symmetrical fans. The typical coexisting fan-like attractors are plotted in Figure 7.

$$\{\begin{array}{l}\dot{x}=y\\ \dot{y}=-x-yz\\ \dot{z}=\left|x\right|+xy-1.4\end{array}$$

(11)

$$\{\begin{array}{l}\dot{x}=-\frac{45}{17}x-yz+10\\ \dot{y}=-10y+xz-w\\ \dot{z}=-3.6z+xy\\ \dot{u}=-0.001x\end{array}$$

(12)

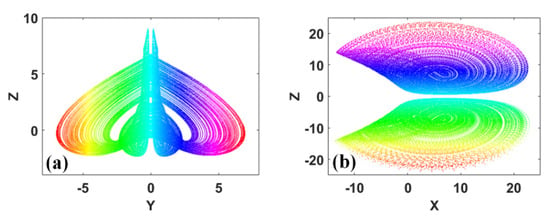
Figure 7. Typical fan-like attractors: (a) coexisting attractors of System (11) on y-z plane, where right side: IC = (0, 0.1, 0) and left side: IC = (0, –0.1, 0), (b) coexisting orbits of System (12) on x-z plane, where upside: IC = (1, 1, 1, 1) and downside: IC = (–1, –1, –1, 1).

The coexisting attractors can make us recall the poem of “Reminiscent of Autumn Evening”, which was written by Mu Du (813–852) in the Tang Dynasty. The poem is written as follows: “Silver candle and autumn light painted a cold screen, and a small fan fluttered the fireflies. The night in day order is as cool as water, sitting and watching the Altair and Vega.” This poem describes a lonely maid in waiting, who looks up at Altair and Vega on both sides of the Tianhe River on Tanabata night, longing for incomparable love in her heart. Sometimes, she gently beats away the fireflies that are flying in the air with a fan in order to relieve the loneliness in her heart, which reflects the unfortunate fate of court women and shows the depressed mood of a woman who is lonely without friends. The coexisting attractors that have been shown above are similar to the fans representing the mood of a lonely woman.

4. Asymmetrical Beauty in Chaos

Some attractors, such as straw hats and fisherman hats, are not axisymmetric, but are also very beautiful and lovely, as exhibited in Figure 8 [24,28].

$$\{\begin{array}{l}\dot{x}=ayz-y^2\\ \dot{y}=z-by-z^2\\ \dot{z}=x\end{array}$$

(13)

$$\{\begin{array}{l}\dot{x}=y+y^2-ayz\\ \dot{y}=-z^2+byz\\ \dot{z}=xy\end{array}$$

(14)

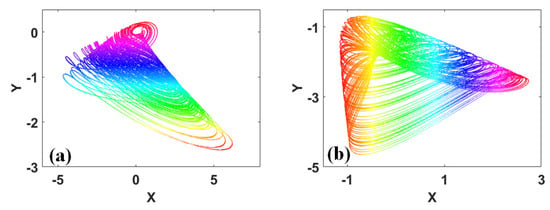
Figure 8. Typical asymmetrical attractors: (a) x-y plane, when a = 6 and b = 1 under IC = (1, 1, 0) in System (13), (b) x-y plane, when a = 0.9 and b = 1 under IC = (0.8, −2, 0) in System (14).

This picture cannot help but remind people of the poem that is titled “The Painting of Fishing Alone in the Autumn River”, which was written by Shizhen Wang (1634–1711) in the Qing Dynasty, as follows: “Wearing a hat and a hemp fiber, sitting in a boat, with a fishing line ten feet long and a fishing hook one inch long; Sing a fishing song loudly, drink a bottle of wine and go fishing alone on the river this autumn”. The poem describes a man who was dressed as a fisherman, fishing on the river in autumn. He was wearing a hemp fiber and a fisherman’s hat, sitting in a small boat, holding a fishing rod, singing a fishing song, and drinking a bottle of wine while he was fishing. The ease of fishing is vividly depicted here. We can appreciate the autumn scenery and the colors of a river, how carefree and unrestrained it is, and we can enjoy the beauty of nature. However, fishing alone on a river during the autumn also reveals some desolation and loneliness in the process of being free and unfettered.

5. Extending Beauty

Some attractors continue to extend, similar to continuous steep mountain peaks [29,30], as shown in Figure 9.

$$\{\begin{array}{l}\dot{x}=-y-z\\ \dot{y}=x+ay\\ \dot{z}=b+z(x-c)\end{array}$$

(15)

$$\{\begin{array}{l}\dot{x}=-y-yz\\ \dot{y}=x+ay\\ \dot{z}=b+z(x^2-c)\end{array}$$

(16)

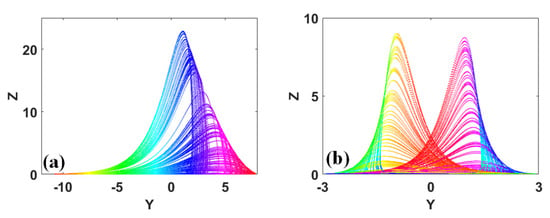
Figure 9. Typical extending attractors: (a) y-z plane, when a = b = 0.2 and c = 5.7 under IC = (−9, 0, 0) in System (15), (b) y-z plane, when a = 0.2, b = 0.2, and c = 6.5 under IC = (1, 0, 1) in System (16).

This picture reminds people of Shi Su’s “Write on the wall of Xilin Temple”, which was written in the Northern Song Dynasty in the year of 1084. The poem is written as follows: “From the front and side, the mountains of Lushan Mountain are rolling and the peaks stand tall. From distance, near, high and low places, Lushan Mountain presents various appearances. The reason why I can’t recognize the true face of Lushan Mountain is that I am in Lushan Mountain”. This poem is about the feeling that is experienced after visiting the Lushan Mountain. It describes the mountains and the valleys of the Lushan Mountain, which includes the ups and downs of the peaks, and their variety. The visitors are in different positions, and they experience different scenery. Because one is in the middle of the Lushan Mountain, their vision is limited by the peaks of the mountain. What one visitor sees is only the peaks, the ridges, and the valleys of the Lushan Mountain, which are only partial and are bound to be one-sided. It enlightens people to know the philosophy of dealing with others, in that because people are in different positions and have different starting points, their understanding of objective things is inevitably one-sided. In order to know the truth and the whole picture of things, we must go beyond the narrow scope and cast aside subjective stereotypes.

6. Conclusions

Chaotic attractors and basins have abundant evolvement, even within a simple equation. The beauty of phase portrait, symmetry, asymmetry, conditional symmetry, and extension is common in chaotic systems. As a result, splendid and novel attractors, or basins of attraction, easily remind people of curious phenomena, animals, plants, or objects in nature. In addition, it also easily reminds people of many popular poems from ancient China, which bring people wonderful feelings and enlightenment.