A Modified Wei-Hua-He Digital Signature Scheme Based on Factoring and Discrete Logarithm

Abstract

A symmetric cipher such as AES in cryptography is much faster than an asymmetric cipher but digital signatures often use asymmetric key ciphers because they provides the sender’s identity and data integrity. In this paper, a modified-He digital signature scheme is proposed using a one-way hash function. The proposed scheme, unlike the He signature technique, employs Euclid’s Division Lemma with large prime moduli p. Its security is built on large integer factoring, discrete logarithms and expanded root problems. The time complexity of the proposed scheme is $\mathcal{O}\left(lo{g}^{3}p\right)$. The proposed modified-He scheme is efficient, as evidenced by the analytical results with key lengths greater than 512 bits.

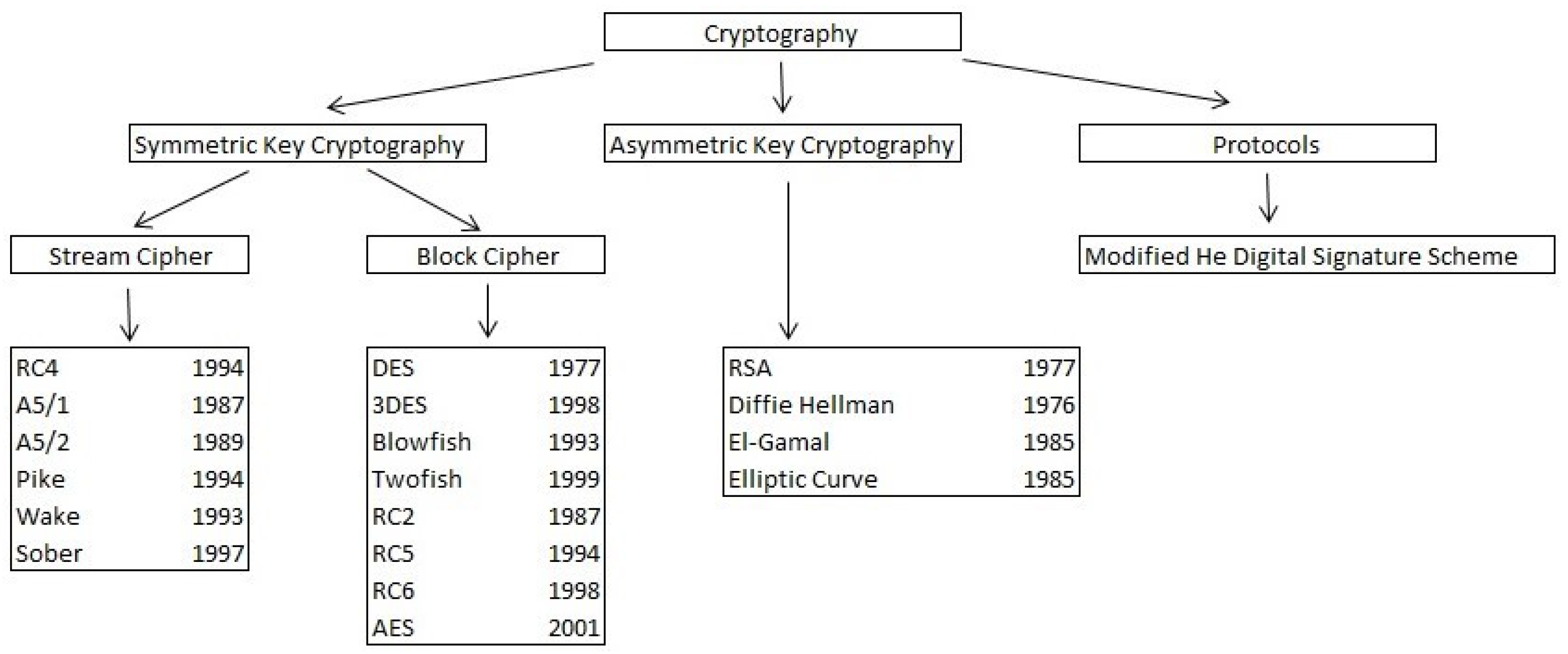
1. Introduction

The purpose of cryptography is to design and analyze protocols that prohibit third parties or the general public from reading private communications. The three prevalent categories of cryptography are symmetric cryptography, asymmetric cryptography and protocols. In this paper, a modified-He digital signature scheme is proposed using a one-way hash function. The paper focuses mainly on asymmetric key ciphers because they satisfy most of the security service requirements. The cryptography classification is shown in Figure 1. No further algorithmic requirements are required for design of protocols as symmetric and asymmetric cryptosystems are sufficient. In general, a stream cipher is faster than a block cipher. A5/2 is a stream cipher that replaces A5/1, voice used to protect the privacy of voice calls in the GSM cellular telephone protocol.

In 1976, Whitfield Diffie and Martin Hellman were the first to explain the concept of a digital signature scheme. In 1977, RSA developed the first asymmetric key family-based digital signature scheme. Its security was based on factoring a large composite integer. In 1985, Elgamal proposed an alternative digital signature scheme, which was based on the discrete logarithm problem. In 1994, Harn presented a new digital signature scheme to improve digital signature security. One must break both the RSA and the Elgamal scheme simultaneously to break the Harn signature scheme. In 1995, Lee showed that if hackers solve the DL problem, they will be able to forge signatures with a high probability.

The suggested bit lengths of the private key and public key algorithms for the security levels are shown in

Table 1. Public-key and private-key algorithm bit lengths.

Cryptosystems	Cipher	Security Level (bit)
		256
Asymmetric key cryptosystem	RSA	15,360 bit
	DH, DSA, Elgamal	15,360 bit
	ECDH, ECDSA	512 bit
Symmetric key cryptosystem	AES, 3DES	256 bit

. RSA and discrete-logarithm techniques need longer keys. The key length of an elliptic curve scheme is considerably shorter, but it is still twice as long as the key length of a symmetric cipher with the same cryptographic strength [1].

The authors of the papers [2,3,4,5,6,7,8,9] presented a digital signature scheme based on IFP and DLP. In 2007, Yu-Fang Chung et al. [10] suggested a technique depending on the difficulty of solving the ECDLP. In 2011, Pin-Chang Su [11] introduced the enhanced short signature method, which is based on knapsack and Gap Diffie–Hellman (GDH) groups and whose security is strongly connected to the discrete logarithm assumption. The authors of the papers [12,13,14] outlined a new digital signature scheme based on two difficult problems. In 2018, the authors of the papers [15,16,17] developed and presented new digital signature techniques based on the IFP and DLRP over $Z_n$. In 2020, Xuan et al. [18] proposed a new digital signature scheme based on the difficulty of solving expanded root problems over $Z_p$. In 2021–2022, the authors of the papers [19,20,21] presented a digital signature over HMAC entangled chains, the hidden logarithm problem and visually meaningful image encryption algorithm.

The purpose of this study is to get beyond the He-digital signature method’s limitations. The He digital signature scheme is based on the group $Z_{(4p_1{q}_1+1)}$, where $p_1$ and $q_1$ are safe prime numbers [8]. Because $p-1=4p_1{q}_1$ has two larger prime factors, $p_1$ and $q_1$, factoring $p-1$ is extremely difficult in practice. As n increases, the likelihood of the prime $p_n$ being a safe prime decreases dramatically. Furthermore, finding an element $g\in Z_p$ such that $\left|g\right|=R$, where $R=p_1{q}_1$ and the primes of the form $p=4p_1{q}_1+1$ are difficult. As a result, a modified-He digital signature scheme using a one-way hash function is proposed to increase efficiency. The proposed scheme comes under the category of asymmetric key digital signature.

2. Motivation and Outline of the Paper

The digital signature is now the most important part of cryptography because it is used so often. Digital signatures can be used to sign contracts legally, update software in a safer way and make online transactions safe by using digital certificates. It provides integrity, message authentication and nonrepudiation. This paper is organized as follows: Section 3 details the mathematical background: FACT, DLP and expanded root problems; Section 4 presents the proposed algorithm; Section 5 provides a concrete example of the proposed scheme; Section 6 depicts the situation of security attacks; and the last section concludes the contribution of the paper.

3. Security Model

3.1. Factoring Large Integer

Consider the expression  

$$x_1{x}_2=a{y}_1{y}_2+b.$$

(1)

where the variable $x_1$, $x_2$, $y_1$ and $y_2$ are all unknown. Factoring the solution $x_1{x}_2$ into $x_1$, $x_2$ and $y_1{y}_2$ into $y_1$, $y_2$ is extremely difficult for large integers. Equation (1) is known as another form of Euclid’s Division Lemma [22].

3.2. Discrete Logarithm Problem

It is difficult to find the unique exponent x ($0\le x\le (p-1)$) of g for given integers $y,g\in Z_p$, i.e.,)

$$y\cong g^x\left(modp\right).$$

(2)

where g is a primitive root and p is a prime number.

3.3. Expanded Root Problem

The following problem is known as a discrete logarithm since a is a constant, b and x are variables [23]

$$x=a^{b}modp.$$

The above problem is called an expanded root problem [18], if both a and b are variables.

4. Proposed a Modified-He Digital Signature Scheme

4.1. Modified-He Digital Signature Scheme

Figure 2 demonstrates that Alice signed her message m using her private key x and Alice’s signature $(r_1,r_2,s,k)$ along with the message m is sent through an insecure channel. Later, this signature is validated by Bob.

4.1.1. Public Parameter

Alice randomly chooses the prime p and she chooses another element $g\in Z_p$ such that $gcd(g,p)=1$. Then, the public parameter is the pair $(p,g)$. The three main parts of the digital signature are key generation, signature generation and signature verification, which are as follows.

4.1.2. Key Generation

Alice randomly chooses two distinct primes, $q_1$ and $q_2$ ($q_1<q_2<p$); she computes

$$x={(q_1+q_2)}^{q_1{q}_2}modp$$

(3)

and

$$y=g^{{\left(q_{1}x\right)}^2}modp.$$

(4)

Then, Alice’s private key is x and the public key is y. The key generation algorithm can be described on Algorithm 1 as:

Algorithm 1 Key Generation Algorithm

Require:  (p, g) Ensure:  $(p,q_1,q_2,x,y)$ 1: generate p 2: select g: $g\in Z_p$ 3: generate $q_1$, $q_2$: $q_1<q_2<p$ 4: $x\leftarrow {(q_1+q_2)}^{q_1{q}_2}\mathrm{m}\mathrm{o}\mathrm{d}p$ 5: $y\leftarrow g^{{\left(q_{1}x\right)}^2}\mathrm{m}\mathrm{o}\mathrm{d}p$ 6: return $(q_1,q_2,x,y)$

Wherein:

-

p, g: Global parameters.

-

x: Alice’s Private key.

-

y: Alice’s Public key.

4.1.3. Signature Generation

To sign a message, m, the following steps are taken:

Alice chooses the random integers $n,t\in Z_P$ for each message m and she computes

$$r_1=g^{nt}modp$$

(5)

and

$$r_2=g^{{\left(nt\right)}^2}modp.$$

(6)

Then, Alice finds positive integer s and k values satisfying

$$q_{1}x=h\left(m\right)nts+k.$$

(7)

where hashing the message m is denoted by $h\left(m\right)$. Alice chooses different n and t values, if either $s=0$ or $k=0$. Alice sends the quadruple $(r_1,r_2,s,k)$ associated with m to the Bob. So, the signature algorithm is described in Algorithm 2 as:

Algorithm 2 Signature Generation Algorithm

Require:  $(p,g,q_1,x)$ Ensure:  $(r_1,r_2,s,k,m)$ 1: select n, t $\in Z_p$ 2: $r_1\leftarrow g^{nt}\mathrm{m}\mathrm{o}\mathrm{d}p$ 3: $r_2\leftarrow g^{{\left(nt\right)}^2}\mathrm{m}\mathrm{o}\mathrm{d}p$ 4: choose the message m 5: $q_{1}x\leftarrow h\left(m\right)nts+k$ 6: if (s == 0) or (k == 0) then 7:     go to 1 8: end if 9: return $(r_1,r_2,s,k,m)$

Wherein:

-

m: The message must be signed.

-

$(r_1,r_2,s,k)$: Alice’s signature on m.

4.1.4. Signature Verification

Alice verifies $r_1,r_2\in [1,p-1]$. Then, she computes

$$y^{\prime }\cong r_1^{2h\left(m\right)sk}{r}_2^{{\left(h\left(m\right)s\right)}^2}{g}^{k^2}modp$$

(8)

By checking the equality of y and $y^{\prime }$, Bob can validate the validity of the signature.

The signature verification algorithm can be described in Algorithm 3 as:

Algorithm 3 Signature Verification Algorithm

Require:  $p,g,r_1,r_2,s,k,m$ Ensure:  $True/False$ 1: $y^{\prime }\leftarrow r_1^{2h\left(m\right)sk}{r}_2^{{\left(h\left(m\right)s\right)}^2}{g}^{k^2}\mathrm{m}\mathrm{o}\mathrm{d}p$ 2: if ($y==y^{\prime }$) then 3:     return $True$ 4: else 5:     return $False$ 6: end if

If Alice adheres to the guidelines outlined above, the signature is always accepted by Bob. Taking squares on Equation (7) and exponentiating the generator g with the resultant over modulo p proves that $y=y^{\prime }$.

The time complexity for modular multiplication is $\mathcal{O}\left({log}^{2}p\right)$, modular exponentiation is $\mathcal{O}\left({log}^{3}p\right)$. In addition, finding $H\left(m\right)$ and k require $\mathcal{O}\left({log}^{3}p\right)$ [23]. Therefore the time complexity of the proposed scheme for key generation, signature generation and signature verification is $\mathcal{O}\left({log}^{3}p\right)$.

5. Concrete Example

5.1. Case No.1

For a length greater than 512 bits, choose the positive integer values $q_1$, $q_2$, p, x and g.

-

Key Generation:

$q_1$ value:

2420486813318595494805271112659432590495064415097071947578388354952602668412058

55659505138654859300727460454797773666986729182991603814770235090895215821733113

72610467900279664561595681832113078528139

$q_2$ value:

4617372583291384712143640062021204393676109921851738590563914376765677713803946

98799915239171541117812406778705516832492655921658465074485024434115325388634881

66829223210826165970651547223649717795467

p value:

9760931680847287045440530210204909063192640016500706477933143065532097667650962

82378572720912985645950160085179394695951416047723311167446701459687872262367248

39270110107504464205570942192609743912751

x value:

9692704345950699260416031111357144055354191987761545225287532706046357785368360

12332017828151337498266627600294980305848047030175485493391021932459591307403361

43062341792496995862986391669440371955440

g value:

6001310042347550337639961765134798951604590905052286996190622619992059507517166

08939637937878930120129688405542840182523567695574377242201167067875678136576135

54342599141372868197388513025892460290169

y value:

8535742705442694219922758684650481304434355569158881113149175859182000360759108

77965350544642764993689838000946347087871008851877971179943102770766380127138257

90478365924942604617693838464217803924069

-

Signature Generation:

n value:

6606054386291357364822658203234928691403561908506902958678631526085068054203034

649360833665962190203

t value:

8053063664829756788647635899905504492016188419011410808052242481159600935020471

507742315216319919049

$r_1$ value:

7006721042764329416622213899302779854965775269797846974404842250031729465874048

65559262052854004454710120160764491585735612429869210457734558118246897598446896

82710067019646496820350622771577003668315

$r_2$ value:

6328641363981448804495135653267291704860226173165833704390639006389709116678057

07907574742385263642260107645513855361159128859962530276301865496115179354573685

17603605898077282586571429762806196993171

$h\left(m\right)$ value:

4362334494999478712775223492146009226763303825372585916187531903065240668375193

030266442109201908173

s value:

1010940152238788936235489305203763121952981082723639705154480301629307466362041

8259531567409456774642

k value:

8988107920153833822039340601523819535892912627596752483423202482955251766375351

72652236143784599782840228491223323548789813015203405124770207070756926532028072

05629702940580761107577790339645950841917584875586333453715730999863979292629122

054004168288828032880046018817432607968266238388909227544658

-

Signature Verification:

$r_1$ value:

7006721042764329416622213899302779854965775269797846974404842250031729465874048

65559262052854004454710120160764491585735612429869210457734558118246897598446896

82710067019646496820350622771577003668315

$r_2$ value:

6328641363981448804495135653267291704860226173165833704390639006389709116678057

07907574742385263642260107645513855361159128859962530276301865496115179354573685

17603605898077282586571429762806196993171

$h\left(m\right)$ value:

4362334494999478712775223492146009226763303825372585916187531903065240668375193

030266442109201908173

s value:

1010940152238788936235489305203763121952981082723639705154480301629307466362041

8259531567409456774642

k value:

8988107920153833822039340601523819535892912627596752483423202482955251766375351

72652236143784599782840228491223323548789813015203405124770207070756926532028072

05629702940580761107577790339645950841917584875586333453715730999863979292629122

054004168288828032880046018817432607968266238388909227544658

y value:

8535742705442694219922758684650481304434355569158881113149175859182000360759108

77965350544642764993689838000946347087871008851877971179943102770766380127138257

90478365924942604617693838464217803924069

$y^{\prime }$ value:

8535742705442694219922758684650481304434355569158881113149175859182000360759108

77965350544642764993689838000946347087871008851877971179943102770766380127138257

90478365924942604617693838464217803924069

In this scenario, Bob accepts Alice’s signature (Because Alice’s public key y = Bob’s computed public key y’).

5.2. Case No.2—The Digital Signature s Is a Forgery

-

Key Generation:

$q_1$ value:

2420486813318595494805271112659432590495064415097071947578388354952602668412058

55659505138654859300727460454797773666986729182991603814770235090895215821733113

72610467900279664561595681832113078528139

$q_2$ value:

4617372583291384712143640062021204393676109921851738590563914376765677713803946

98799915239171541117812406778705516832492655921658465074485024434115325388634881

66829223210826165970651547223649717795467

p value:

9760931680847287045440530210204909063192640016500706477933143065532097667650962

82378572720912985645950160085179394695951416047723311167446701459687872262367248

39270110107504464205570942192609743912751

x value:

9692704345950699260416031111357144055354191987761545225287532706046357785368360

12332017828151337498266627600294980305848047030175485493391021932459591307403361

43062341792496995862986391669440371955440

g value:

6001310042347550337639961765134798951604590905052286996190622619992059507517166

08939637937878930120129688405542840182523567695574377242201167067875678136576135

54342599141372868197388513025892460290169

y value:

8535742705442694219922758684650481304434355569158881113149175859182000360759108

77965350544642764993689838000946347087871008851877971179943102770766380127138257

90478365924942604617693838464217803924069

-

Signature Generation:

n value:

6606054386291357364822658203234928691403561908506902958678631526085068054203034

649360833665962190203

t value:

8053063664829756788647635899905504492016188419011410808052242481159600935020471

507742315216319919049

$r_1$ value:

7006721042764329416622213899302779854965775269797846974404842250031729465874048

65559262052854004454710120160764491585735612429869210457734558118246897598446896

82710067019646496820350622771577003668315

$r_2$ value:

6328641363981448804495135653267291704860226173165833704390639006389709116678057

07907574742385263642260107645513855361159128859962530276301865496115179354573685

17603605898077282586571429762806196993171

$h\left(m\right)$ value:

4362334494999478712775223492146009226763303825372585916187531903065240668375193

030266442109201908173

s value:

1010940152238788936235489305203763121952981082723639705154480301629307466362041

8259531567409456774642

k value:

8988107920153833822039340601523819535892912627596752483423202482955251766375351

72652236143784599782840228491223323548789813015203405124770207070756926532028072

056297029405807611075777903396459508419175848755863334537157309998639792926291220

54004168288828032880046018817432607968266238388909227544658

-

Signature Verification:

$r_1$ value:

7006721042764329416622213899302779854965775269797846974404842250031729465874048

65559262052854004454710120160764491585735612429869210457734558118246897598446896

82710067019646496820350622771577003668315

$r_2$ value:

6328641363981448804495135653267291704860226173165833704390639006389709116678057

07907574742385263642260107645513855361159128859962530276301865496115179354573685

17603605898077282586571429762806196993171

$h\left(m\right)$ value:

4362334494999478712775223492146009226763303825372585916187531903065240668375193

030266442109201908173

s value:

4521308241444014122898680809477187136593433501725012770600777497339439501606330

425756001185558080619

k value:

8988107920153833822039340601523819535892912627596752483423202482955251766375351

72652236143784599782840228491223323548789813015203405124770207070756926532028072

056297029405807611075777903396459508419175848755863334537157309998639792926291220

54004168288828032880046018817432607968266238388909227544658

y value:

8535742705442694219922758684650481304434355569158881113149175859182000360759108

77965350544642764993689838000946347087871008851877971179943102770766380127138257

90478365924942604617693838464217803924069

$y^{\prime }$ value:

9480540477028311916918423793403684938900932985285694043732920251435267867511238

49980243933726059009825976798077779373747254148325146243299965626426118226559631

13671746537255685709398262399855215280623.

The signature s has been changed in this instance and the result is a denial of the signature and message authentication. As a result ($y\ne y^{\prime }$), Bob rejects the forged signature.

6. Security Attacks

6.1. Public Key Attack

Assume an enemy tries to launch an assault by exposing the private key deriving it from the public key. First, the enemy has to solve the discrete logarithm problem from (4) to acquire ${\left(q_{1}x\right)}^2$. Then, the enemy has to solve the FAC problem to obtain x from ${\left(q_{1}x\right)}^2$.

6.2. Valid Signature Attack

In case an enemy tries to launch an assault by exposing the private key from a valid signature ($r_1,r_2,s,k$) for the known message m. To obtain x from (7), first, the enemy must be aware of $q_1$, n and t. Nonetheless, given y, g and $r_1$ or $r_2$, obtaining $nt$ from (5) or (6) is likewise subject to the FAC and DL assumptions.

6.3. Forging a Valid Signature Attack

In case an enemy tries to launch an assault by faking a legitimate signature $(r_1,r_2,s,k)$ with a certain message m without being aware of any acceptable signatures or Alice’s private key. With the message m in mind, if the enemy tries to solve a four-variable $r_1$, $r_2$, s and k satisfying (8). Then, three variables are set to fixed integers before determining the answer to the last variable from (8). Given y, g, m, $r_1$, s, k or given y, g, m, $r_2$, s, k, finding $r_1$ or $r_2$ in order to satisfy (8) is according to FAC and the DL assumptions.

6.4. Known Message Attack

Suppose the enemy has access to the signatures $(r_1,r_2,s_1,k_1)$, $(r_1,r_2,s_2,k_2)$, …, $(r_1,r_2,s_z,k_z)$ for a set of messages $m_1$, $m_2$, …, $m_z$. Then, the enemy tries to find the $nt$ value from the following formula to make a forgery:

$$nt=\frac{1}{z-1}\frac{(z-1)k_z-{\sum }_{i=1}^{z-1}{k}_i}{{\sum }_{i=1}^{z-1}{A}_i-A_z},$$

(9)

where $A_i=h\left(m_i\right)s_i$, but finding x to satisfy (7) is according to FAC.

6.5. Total Break

Since (3) is an expanded root problem, finding the private key x is impossible.

6.6. Existential Unforgeability under Chosen Message Attack

Suppose the information $(m_1,s_1,k_1)$ and $(m_2,s_2,k_2)$ are known to the enemy. With these details, there must be at least one $(m^{\prime },s^{\prime },k^{\prime })$ that meets the (8) condition. The above strategy only works if the $nt$ value is the same for both $m_1$ and $m_2$ messages. Alice chooses different n and t values for each message m. As a result, $(m^{\prime },s^{\prime },k^{\prime })$ does not satisfy the requirement of (8).

7. Conclusions

Finding the primes of the form $p=4p_1{q}_1+1$, where $p_1$ and $q_1$ are safe prime numbers, is challenging in the Wei-Hua-He signature scheme. So, the He digital signature scheme is inappropriate for large prime numbers. The contribution of the paper is to get rid of the flaws in the He digital signature scheme. As a result, a modified-He digital signature scheme is proposed based on a one-way hash function with a big prime modulus p. The time complexity of the algorithm is $\mathcal{O}\left(lo{g}^{3}p\right)$. The proposed modified-He digital signature scheme is more efficient and gives a higher level of security.