About Stability of Nonlinear Stochastic Differential Equations with State-Dependent Delay

Abstract

A nonlinear stage-structured population model with a state-dependent delay under stochastic perturbations is investigated. Delay-independent and delay-dependent conditions of stability in probability for two equilibria of the considered system are obtained via the general method of Lyapunov functionals construction and the method of linear matrix inequalities (LMIs). The model under consideration is not the aim of the work and was chosen only to demonstrate the proposed research method, which can be used for the study of other types of nonlinear systems with a state-dependent delay.

1. Introduction

Among different types of delay differential equations, in particular, stochastic delay differential equations, equations with a delay, that depends on the state of the system under consideration, play a special role and are very popular in research (see, for instance, [1,2,3,4,5,6,7,8,9] and the references therein). Here, the method of stability investigation described in [10,11] for nonlinear stochastic differential equations with usual delay is used for investigation of the following stage-structured single population model with a state-dependent delay [8].

$$\begin{array}{ll}\dot{x}\left(t\right)=\hfill & \alpha y\left(t\right)-\gamma x\left(t\right)-\alpha [1-{\tau }^{\prime }\left(z\left(t\right)\right)\dot{z}\left(t\right)]y(t-\tau \left(z\left(t\right)\right))e^{-\gamma \tau \left(z\right(t\left)\right)},\\ \dot{y}\left(t\right)=\hfill & \alpha [1-{\tau }^{\prime }\left(z\left(t\right)\right)\dot{z}\left(t\right)]y(t-\tau \left(z\left(t\right)\right))e^{-\gamma \tau \left(z\right(t\left)\right)}-\beta y^2\left(t\right),\\ \hfill & \mathrm{where}z\left(t\right)=x\left(t\right)+y\left(t\right),\\ x\left(s\right)=\hfill & \varphi \left(s\right)\ge 0,y\left(s\right)=\psi \left(s\right)\ge 0,s\in [-{\tau }_M,0].\end{array}$$

(1)

The hypotheses for model (1) are:

Hypothesis 1 (H1). 

The parameters α, β and γ are positive constants;

Hypothesis 2 (H2). 

The state-dependent maturity time delay $\tau \left(z\right)$ is an increasing twice differentiable bounded function of the total population $z=x+y$, such that $0<{\tau }_m=\tau \left(0\right)\le \tau \left(z\right)\le {\tau }_M=\tau (\infty )$ and the first and the second derivatives satisfy, respectively, the conditions ${\tau }^{\prime }\left(z\right)\ge 0$ and ${\tau }^{″}\left(z\right)\le 0$;

Hypothesis 3 (H3). 

$t-\tau \left(z\right(t\left)\right)$ is a strictly increasing function of t, i.e., $1-{\tau }^{\prime }\left(z\left(t\right)\right)\dot{z}\left(t\right)>0$, and the maturity time delay $\tau \left(z\right(t\left)\right)$ does not change arbitrarily over time.

Note that although the results obtained here are new, the stability investigation of the considered model here (1) is not the main aim of this paper. This model was chosen to demonstrate the proposed research method, which can be used for the study of many other types of nonlinear systems with a state-dependent delay under stochastic perturbations.

1.1. Equilibria

Putting in (1) $\dot{x}\left(t\right)=\dot{y}\left(t\right)=0$, we obtain the system of two algebraic equations for equilibria

$$\begin{array}{c}\alpha y(1-e^{-\gamma \tau \left(z\right)})=\gamma x,\hfill \\ y(\alpha e^{-\gamma \tau \left(z\right)}-\beta y)=0,\hfill \end{array}$$

(2)

which has two solutions: the zero equilibrium $E_0(0,0)$ and the positive equilibrium $E_1(x^{*},y^{*})$, where $x^{*}$ and $y^{*}$ are defined by the equations

$$\begin{array}{c}{x}^{*}={\displaystyle \frac{1}{\gamma }}(\alpha -\beta y^{*})y^{*}>0,\beta y^{*}=\alpha e^{-\gamma \tau \left(z^{*}\right)}<\alpha ,\mathrm{where}{z}^{*}=x^{*}+y^{*}.\hfill \end{array}$$

(3)

Theorem 1 

([8]). The system (1) has exactly one nontrivial equilibrium $E_1(x^{*},y^{*})$, and this equilibrium satisfies the condition

$$\begin{array}{c}{y}^{*}{\tau }^{\prime }\left(z^{*}\right)(2\beta y^{*}-\gamma -\alpha )<1.\hfill \end{array}$$

(4)

Remark 1. 

Note that in the case $\tau \left(z\right)=0$, system (1) splits into two separate equations $\dot{x}\left(t\right)=-\gamma x\left(t\right)$ and $\dot{y}\left(t\right)=\alpha y\left(t\right)-\beta y^2\left(t\right)$ with the equilibria $E_0(0,0)$ and $E_1(0,\alpha {\beta }^{-1})$.

Below, stability of the equilibria of system (1) is investigated under stochastic perturbations.

1.2. Auxiliary Statements

Lemma 1 

([12,13]). (Jensen’s inequality) Denote

$$G={\int }_a^{b}f\left(s\right)x\left(s\right)ds,$$

where $f\left(s\right)\ge 0$, $x\left(s\right)\in {\mathbf{R}}^n$. Then, for any positive definite matrix $R\in {\mathbf{R}}^{n\times n}$, the following inequality holds:

$$G^{T}RG\le {\int }_a^{b}f\left(s\right)ds{\int }_a^{b}f\left(s\right)x^T\left(s\right)Rx\left(s\right)ds.$$

Remark 2 

([14]). A symmetric $2\times 2$-matrix A is negative definite if and only if $Tr\left(A\right)<0$, $Det\left(A\right)>0$.

2. Stochastic Perturbations, Centering and Linearization

In this section, the necessary preliminary steps of the method under consideration are presented.

2.1. Stochastic Perturbations

Summing both Equation (1), we have

$$\begin{array}{cc}\dot{z}\left(t\right)=\hfill & \alpha y\left(t\right)-\gamma x\left(t\right)-\beta y^2\left(t\right).\end{array}$$

(5)

Substituting (5) into (1), we obtain

$$\begin{array}{ll}\dot{x}\left(t\right)=\hfill & \alpha y\left(t\right)-\gamma x\left(t\right)-f(x\left(t\right),y_t),\\ \dot{y}\left(t\right)=\hfill & -\beta y^2\left(t\right)+f(x\left(t\right),y_t),\end{array}$$

(6)

where

$$\begin{array}{ll}f(x\left(t\right),y_t)=\hfill & \alpha [1-{\tau }^{\prime }\left(z\left(t\right)\right)(\alpha y\left(t\right)-\gamma x\left(t\right)-\beta y^2\left(t\right))]y(t-\tau \left(z\left(t\right)\right))e^{-\gamma \tau \left(z\right(t\left)\right)},\\ \hfill z\left(t\right)=& x\left(t\right)+y\left(t\right),\end{array}$$

(7)

$y\left(t\right)$ is a value of the process in the time moment t, and $y_t$ is a trajectory of this process until the time moment t.

Let us assume that system (6) is exposed to stochastic perturbations that are of the white noise type, are directly proportional to the deviation of the system state $\left(x\right(t),y(t\left)\right)$ from the equilibrium $E(x^{*},y^{*})$ and influence $(\dot{x}\left(t\right),\dot{y}\left(t\right))$ immediately. Then, system (6) transforms to the following system of Ito’s stochastic delay differential Equations [15].

$$\begin{array}{ll}dx\left(t\right)=\hfill & \left[\alpha y\left(t\right)-\gamma x\left(t\right)-f(x\left(t\right),y_t)\right]dt+{\sigma }_1(x\left(t\right)-x^{*})d{w}_1\left(t\right),\\ dy\left(t\right)=\hfill & \left[-\beta y^2\left(t\right)+f(x\left(t\right),y_t)\right]dt+{\sigma }_2(y\left(t\right)-y^{*})d{w}_2\left(t\right),\end{array}$$

(8)

where ${\sigma }_1$ and ${\sigma }_2$ are constants and $w_1\left(t\right)$ and $w_2\left(t\right)$ are mutually independent standard Wiener processes.

Remark 3. 

Note that stochastic perturbations of the type of (8) for the first time were used in [16] and later in some other research (see, for instance, [14] and references therein). By that, an equilibrium $E(x^{*},y^{*})$ of the deterministic system (1) is an equilibrium of the stochastic system (8) too. In reality, $f(0,0)=0$ and via (3) $f(x^{*},y^{*})=\alpha y^{*}{e}^{-\gamma \tau \left(z^{*}\right)}$. Therefore, via (2) both equilibria $E(x^{*},y^{*})=E_0(0,0)$ and $E(x^{*},y^{*})=E_1(x^{*},y^{*})$ are solutions of system (8) too.

2.2. Centering

Let $E(x^{*},y^{*})$ be one of the two equilibria of system (8). From (2), it follows that

$$\begin{array}{c}\alpha y^{*}-\gamma x^{*}=\alpha y^{*}{e}^{-\gamma \tau \left(z^{*}\right)}=\beta {\left(y^{*}\right)}^2.\hfill \end{array}$$

(9)

Consider the new variables $x_1\left(t\right)$ and $y_1\left(t\right)$, such that

$$\begin{array}{c}x\left(t\right)=x_1\left(t\right)+x^{*},y\left(t\right)=y_1\left(t\right)+y^{*},z\left(t\right)=z_1\left(t\right)+z^{*},\hfill \\ \hfill z_1\left(t\right)=x_1\left(t\right)+y_1\left(t\right),z^{*}=x^{*}+y^{*}.\hfill \end{array}$$

(10)

Using (9) and (10), rewrite (7) as follows

$$\begin{array}{ll}f(x_1\left(t\right),y_{1t})=\hfill & \alpha [1-{\tau }^{\prime }(z_1\left(t\right)+z^{*})(\alpha y_1\left(t\right)+\alpha y^{*}-\gamma x_1\left(t\right)-\gamma x^{*}-\beta {(y_1\left(t\right)+y^{*})}^2)]\\ \hfill & \times [y_1(t-\tau (z_1\left(t\right)+z^{*}))+y^{*}]e^{-\gamma \tau (z_1\left(t\right)+z^{*})}\\ \hfill =& \alpha y_1(t-\tau (z_1\left(t\right)+z^{*}))e^{-\gamma \tau (z_1\left(t\right)+z^{*})}+\alpha y^{*}{e}^{-\gamma \tau (z_1\left(t\right)+z^{*})}\\ \hfill & -\alpha {\tau }^{\prime }(z_1\left(t\right)+z^{*})(\alpha y_1\left(t\right)-\gamma x_1\left(t\right)-\beta y_1^2\left(t\right)-2\beta y^{*}{y}_1\left(t\right))\\ \hfill & \times [y_1(t-\tau (z_1\left(t\right)+z^{*}))+y^{*}]e^{-\gamma \tau (z_1\left(t\right)+z^{*})}.\end{array}$$

(11)

Substituting (11) into system (8) and using (9), we obtain the following system of nonlinear Ito’s stochastic differential equations

$$\begin{array}{ll}d{x}_1\left(t\right)=\hfill & [-\gamma x_1\left(t\right)+\alpha y_1\left(t\right)+F(x_1\left(t\right),y_{1t})]dt+{\sigma }_1{x}_1\left(t\right)d{w}_1\left(t\right),\\ d{y}_1\left(t\right)=\hfill & [-2\beta y^{*}{y}_1\left(t\right)-\beta y_1^2\left(t\right)-F(x_1\left(t\right),y_{1t})]dt+{\sigma }_2{y}_1\left(t\right)d{w}_2\left(t\right),\end{array}$$

(12)

where

$$\begin{array}{ll}F(x_1\left(t\right),y_{1t})=\hfill & \alpha y^{*}(e^{-\gamma \tau \left(z^{*}\right)}-e^{-\gamma \tau (z_1\left(t\right)+z^{*})})-\alpha y_1(t-\tau (z_1\left(t\right)+z^{*}))e^{-\gamma \tau (z_1\left(t\right)+z^{*})}\\ \hfill & +\alpha {\tau }^{\prime }(z_1\left(t\right)+z^{*})((\alpha -2\beta y^{*})y_1\left(t\right)-\gamma x_1\left(t\right)-\beta y_1^2\left(t\right))\\ \hfill & \times [y_1(t-\tau (z_1\left(t\right)+z^{*}))+y^{*}]e^{-\gamma \tau (z_1\left(t\right)+z^{*})}.\end{array}$$

(13)

Remark 4. 

It is clear that the stability of the equilibrium $E(x^{*},y^{*})$ of system (7) and (8) is equivalent to the stability of the zero solution of system (12) and (13).

2.3. Linearization

To obtain linear approximation of system (12) and (13), note that

$$\begin{array}{ll}\hfill \tau (z_1\left(t\right)+z^{*})=& \tau \left(z^{*}\right)+{\tau }^{\prime }\left(z^{*}\right)z_1\left(t\right)+o\left(z_1\left(t\right)\right),\\ \hfill {\tau }^{\prime }(z_1\left(t\right)+z^{*})=& {\tau }^{\prime }\left(z^{*}\right)+{\tau }^{\prime \prime }\left(z^{*}\right)z_1\left(t\right)+o\left(z_1\left(t\right)\right),\\ \hfill e^{-\gamma \tau (z_1\left(t\right)+z^{*})}=& e^{-\gamma [\tau \left(z^{*}\right)+{\tau }^{\prime }\left(z^{*}\right)z_1\left(t\right)+o\left(z_1\left(t\right)\right)]}\\ \hfill =& e^{-\gamma \tau \left(z^{*}\right)}[1-\gamma {\tau }^{\prime }\left(z^{*}\right)z_1\left(t\right)+o\left(z_1\left(t\right)\right)]\\ \hfill =& e^{-\gamma \tau \left(z^{*}\right)}-\gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}{z}_1\left(t\right)+o\left(z_1\left(t\right)\right),\end{array}$$

and

$$\begin{array}{ll}{e}^{-\gamma \tau \left(z^{*}\right)}-e^{-\gamma \tau (z_1\left(t\right)+z^{*})}=& \gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}{z}_1\left(t\right)+o\left(z_1\left(t\right)\right),\end{array}$$

(14)

where $o\left(z\right)$ means that ${lim}_{z\to 0}{\displaystyle \frac{o\left(z\right)}{z}}=0$.

Substituting (14) into (13), we obtain

$$\begin{array}{ll}\hfill F(x_1\left(t\right),y_{1t})=& \alpha y^{*}\gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}{z}_1\left(t\right)-\alpha y_1(t-\tau (z_1\left(t\right)+z^{*}))[e^{-\gamma \tau \left(z^{*}\right)}-\gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}{z}_1\left(t\right)]\\ \hfill & +\alpha [{\tau }^{\prime }\left(z^{*}\right)+{\tau }^{\prime \prime }\left(z^{*}\right)z_1\left(t\right)]((\alpha -2\beta y^{*})y_1\left(t\right)-\gamma x_1\left(t\right)-\beta y_1^2\left(t\right))\\ \hfill & \times [y_1(t-\tau (z_1\left(t\right)+z^{*}))+y^{*}][e^{-\gamma \tau \left(z^{*}\right)}-\gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}{z}_1\left(t\right)]+o\left(z_1\left(t\right)\right)\\ \hfill =& \alpha y^{*}\gamma {\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}(x_1\left(t\right)+y_1\left(t\right))-\alpha e^{-\gamma \tau \left(z^{*}\right)}{y}_1(t-\tau (z_1\left(t\right)+z^{*}))\\ \hfill & +\alpha y^{*}{\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}(-\gamma x_1\left(t\right)+(\alpha -2\beta y^{*})y_1\left(t\right))+o\left(z_1\left(t\right)\right)\\ \hfill =& \alpha y^{*}{\tau }^{\prime }\left(z^{*}\right)e^{-\gamma \tau \left(z^{*}\right)}(\gamma +\alpha -2\beta y^{*})y_1\left(t\right)-\alpha e^{-\gamma \tau \left(z^{*}\right)}{y}_1(t-\tau (z_1\left(t\right)+z^{*}))+o\left(z_1\left(t\right)\right)\\ \hfill =& \nu \mu y^{*}{y}_1\left(t\right)-\nu y_1(t-\tau (z_1\left(t\right)+z^{*}))+o\left(z_1\left(t\right)\right),\end{array}$$

(15)

where

$$\begin{array}{c}\mu ={\tau }^{\prime }\left(z^{*}\right)(\gamma +\alpha -2\beta y^{*}),\nu =\alpha e^{-\gamma \tau \left(z^{*}\right)}.\hfill \end{array}$$

(16)

Following [7,8], we will solve the linearization problem of state-dependent delay differential equations by “freezing the delay” at an equilibrium, i.e., using in (15) $y_1(t-\tau \left(z^{*}\right))$ instead of $y_1(t-\tau (z_1\left(t\right)+z^{*}))$. As a result, we obtain the linear part of system (12) and (13)

$$\begin{array}{ll}d{x}_2\left(t\right)=& [-\gamma x_2\left(t\right)+(\alpha +\nu \mu y^{*})y_2\left(t\right)-\nu y_2(t-\tau \left(z^{*}\right))]dt+{\sigma }_1{x}_2\left(t\right)d{w}_1\left(t\right),\\ d{y}_2\left(t\right)=\hfill & [-(2\beta +\nu \mu )y^{*}{y}_2\left(t\right)+\nu y_2(t-\tau \left(z^{*}\right))]dt+{\sigma }_2{y}_2\left(t\right)d{w}_2\left(t\right),\end{array}$$

or in matrix form

$$\begin{gathered} dZ\left(t\right)=[AZ\left(t\right)+BZ(t-\tau \left(z^{*}\right))]dt+\sum _{i=1}^2{C}_{i}Z\left(t\right)d{w}_i\left(t\right), \\ Z\left(s\right)=Z_0\left(s\right),s\in [-\tau \left(z^{*}\right),0], \end{gathered}$$

(17)

where

$$\begin{array}{c}Z\left(t\right)=\left[\begin{array}{c}{x}_2\left(t\right)\\ y_2\left(t\right)\end{array}\right],A=\left[\begin{array}{cc}-\gamma & \alpha +\nu \mu y^{*}\\ 0& -(2\beta +\nu \mu )y^{*}\end{array}\right],B=\left[\begin{array}{cc}0& -\nu \\ 0& \nu \end{array}\right],C_1=\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& 0\end{array}\right],C_2=\left[\begin{array}{cc}0& 0\\ 0& {\sigma }_2\end{array}\right].\hfill \end{array}$$

(18)

Remark 5. 

Note that $(2\beta +\nu \mu )y^{*}>\nu >0$. From (3) and (16), it follows that $\beta y^{*}=\nu$. From this, (4) and (16), we have

$$\begin{array}{ll}(2\beta +\nu \mu )y^{*}& =2\nu +\nu \mu y^{*}\\ & =\nu (2-y^{*}{\tau }^{\prime }\left(z^{*}\right)(2\beta y^{*}-\gamma -\alpha ))\\ & >\nu (2-1)=\nu >0.\end{array}$$

3. Stability

Following Remark 4, below we consider stability or instability of the zero solution of system (12) and (13) for each of the two equilibria of the initial system (1).

3.1. Some Necessary Definitions

Let $\{\Omega ,\mathcal{F},\mathbf{P}\}$ be a complete probability space, $\{{\mathcal{F}}_t,t\ge 0\}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathcal{F}$, i.e., ${\mathcal{F}}_{t_1}\subset {\mathcal{F}}_{t_2}$ for $t_1<t_2$, and $\mathbf{E}$ be the mathematical expectation with respect to the measure $\mathbf{P}$.

Definition 1. 

The zero solution of system (12) is called stable in probability if for any ${\epsilon }_1>0$ and ${\epsilon }_2>0$ there exists $\delta >0$ such that the solution $(x_1\left(t\right),y_1\left(t\right))$ of system (12) satisfies the condition $\mathbf{P}\{{sup}_{t\ge 0}|(x_1\left(t\right),y_1\left(t\right))|>{\epsilon }_1\}<{\epsilon }_2$ provided that $\mathbf{P}\left\{{sup}_{s\in [-\tau \left(z^{*}\right),0]}\right|(x_1\left(s\right),y_1\left(s\right))|<\delta \}=1$.

Definition 2. 

The zero solution of Equation (17) is called:

-

mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that ${\mathbf{E}\left|Z\left(t\right)\right|}^2<\epsilon$, $t\ge 0$, provided that ${sup}_{s\in [-\tau \left(z^{*}\right),0]}\mathbf{E}{\left|Z\left(s\right)\right|}^2<\delta$;

-

asymptotically mean square stable if it is mean square stable and for each initial value $x\left(0\right)$ the solution $Z\left(t\right)$ of Equation (17) satisfies the condition $\underset{t\to \infty }{lim}\mathbf{E}{\left|Z\left(t\right)\right|}^2=0$.

Remark 6. 

Note that the level of nonlinearity of system (12) is higher than one. It is known [14] that in this case, a sufficient condition for asymptotic mean square stability of the zero solution of the linear approximation (17) at the same time is a sufficient condition for stability in probability of the zero solution of system (12). Via Remark 4 to obtain conditions of stability in probability for each of the two equilibria of system (8), it is enough to obtain conditions for asymptotic mean square stability of the zero solution of linear Equation (17). On the other hand, the instability of the zero solution of linear Equation (17) means the instability of the corresponding equilibrium of system (8).

3.2. Delay-Independent Condition

Theorem 2. 

Let there exist positive definite $2\times 2$-matrices P and R such that the linear matrix inequality (LMI)

$$\begin{gathered} {\Phi }_1=\left[\begin{array}{cc}{\Psi }_1\left(P\right)+R& PB\\ *& -R\end{array}\right]<0, \\ {\Psi }_1\left(P\right)=PA+A^{T}P+\sum _{i=1}^2{C}_i^{T}P{C}_i, \end{gathered}$$

(19)

holds, where the matrices A, B and $C_1$, $C_2$ are defined in (18). Then, the equilibrium $E_1(x^{*},y^{*})$ of system (7) and (8) is stable in probability.

Proof. 

Via Remarks 4 and 6, it is enough to prove that the zero solution of the linear Equation (17) is asymptotically mean square stable. Following the general method of Lyapunov functionals construction [14], let us construct the Lyapunov functional for Equation (17) in the form $V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)$, where $V_1\left(t\right)=Z^T\left(t\right)PZ\left(t\right)$, $P>0$, and the additional functional $V_2\left(t\right)$ will be chosen below.

Let L be the generator (see Appendix A) of Equation (17). Then via (19) for $V_1\left(t\right)$, we have

$$\begin{array}{ll}L{V}_1\left(t\right)& =2Z^T\left(t\right)P(AZ\left(t\right)+BZ(t-\tau \left(z^{*}\right)))+{\displaystyle \sum _{i=1}^2}{Z}^T\left(t\right)C_i^{T}P{C}_{i}Z\left(t\right)\\ & =Z^T\left(t\right){\Psi }_1\left(P\right)Z\left(t\right)+2Z^T\left(t\right)PBZ(t-\tau \left(z^{*}\right)).\end{array}$$

Using the additional functional

$$V_2\left(t\right)={\int }_{t-\tau \left(z^{*}\right)}^t{Z}^T\left(s\right)RZ\left(s\right)ds,R>0,$$

with

$$L{V}_2\left(t\right)=Z^T\left(t\right)RZ\left(t\right)-Z^T(t-\tau \left(z^{*}\right))RZ(t-\tau \left(z^{*}\right)),$$

as a result for the functional $V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)$ we obtain

$$\begin{array}{ll}LV\left(t\right)& =Z^T\left(t\right)({\Psi }_1\left(P\right)+R)Z\left(t\right)+2Z^T\left(t\right)PBZ(t-\tau \left(z^{*}\right))-Z^T(t-\tau \left(z^{*}\right))RZ(t-\tau \left(z^{*}\right))\\ & ={\eta }^T\left(t\right){\Phi }_1\eta \left(t\right),\end{array}$$

(20)

where matrix ${\Phi }_1$ is defined in (19) and ${\eta }^T\left(t\right)=(Z^T\left(t\right),Z^T(t-\tau \left(z^{*}\right)))$. The LMI (19), i.e., ${\Phi }_1<0$, holds then there exist $c>0$ such that $LV\left(t\right)\le -{c\left|Z\left(t\right)\right|}^2$. From Theorem A1 (see Appendix A), it follows that the zero solution of linear Equation (17) is asymptotically mean square stable. The proof is completed. □

Remark 7. 

It is known [12,13] that for LMI ${\Phi }_1<0$, matrix A must be negative definite. Via (18) for the equilibrium $E_0(0,0)$, we have $A=\left[\begin{array}{cc}-\gamma & \alpha \\ 0& 0\end{array}\right]$. Via Remark 2, this matrix cannot be negative definite ($Det\left(A\right)=0$). From Remark 5, we have $(2\beta +\nu \mu )y^{*}>0$. Via (18) and Remark 2, it means that for the equilibrium $E_1(x^{*},y^{*})$ matrix A is negative definite.

3.3. Delay-Dependent Condition

Rewrite Equation (17) in the neutral type form [14,17,18]

$$\begin{gathered} d(Z\left(t\right)+BG\left(t\right))=(A+B)Z\left(t\right)dt+\sum _{i=1}^2{C}_{i}Z\left(t\right)d{w}_i\left(t\right), \\ G\left(t\right)={\int }_{t-\tau \left(z^{*}\right)}^{t}Z\left(s\right)ds,Z\left(s\right)=Z_0\left(s\right),s\in [-\tau \left(z^{*}\right),0]. \end{gathered}$$

(21)

Let $\parallel B\parallel$ be the matrix norm of a matrix B, and suppose that

$$\parallel B\parallel \tau \left(z^{*}\right)<1.$$

(22)

Theorem 3. 

Suppose that condition (22) holds, and for some positive definite $2\times 2$-matrices P and R the linear matrix inequality (LMI)

$$\begin{gathered} {\Phi }_2=\left[\begin{array}{cc}{\Psi }_2\left(P\right)+\tau \left(z^{*}\right)R& {(A+B)}^{T}PB\\ *& -{\displaystyle \frac{1}{\tau \left(z^{*}\right)}}R\end{array}\right]<0, \\ {\Psi }_2\left(P\right)=P(A+B)+{(A+B)}^{T}P+\sum _{i=1}^2{C}_i^{T}P{C}_i, \end{gathered}$$

(23)

holds, where matrices A, B and $C_1$, $C_2$ are defined in (18). Then, the equilibrium $E_1(x^{*},y^{*})$ of system (7) and (8) is stable in probability.

Proof. 

Via Remarks 4 and 6 it is enough to prove that the zero solution of the linear Equation (21) is asymptotically mean square stable. Following the general method of Lyapunov functionals construction [14], let us construct the Lyapunov functional for Equation (17) in the form $V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)$, where

$$V_1\left(t\right)={(Z\left(t\right)+BG\left(t\right))}^{T}P(Z\left(t\right)+BG\left(t\right)),P>0,$$

and the additional functional $V_2\left(t\right)$ will be chosen below.

Let L be the generator (see Appendix A) of Equation (21). Then, via (23) for $V_1\left(t\right)$ we have

$$\begin{gathered} L{V}_1\left(t\right)=2{(Z\left(t\right)+BG\left(t\right))}^{T}P(A+B)Z\left(t\right)+\sum _{i=1}^2{Z}^{\prime }\left(t\right)C_i^{T}P{C}_{i}Z\left(t\right) \\ =Z^T\left(t\right){\Psi }_2\left(P\right)Z\left(t\right)+2G^T\left(t\right)B^{T}P(A+B)Z\left(t\right). \end{gathered}$$

(24)

Note that via Jensen’s inequality (Lemma 1)

$$G^T\left(t\right)RG\left(t\right)\le \tau \left(z^{*}\right){\int }_{t-\tau \left(z^{*}\right)}^t{Z}^T\left(s\right)RZ\left(s\right)ds,R>0.$$

So, for the additional functional

$$V_2\left(t\right)={\int }_{t-\tau \left(z^{*}\right)}^t(s-t+\tau \left(z^{*}\right))Z^T\left(s\right)RZ\left(s\right)ds$$

we have

$$\begin{array}{ll}L{V}_2\left(t\right)& =\tau \left(z^{*}\right)Z^T\left(t\right)RZ\left(t\right)-{\int }_{t-\tau \left(z^{*}\right)}^t{Z}^T\left(s\right)RZ\left(s\right)ds\\ & \le \tau \left(z^{*}\right)Z^T\left(t\right)RZ\left(t\right)-\frac{1}{\tau \left(z^{*}\right)}{G}^T\left(t\right)RG\left(t\right).\end{array}$$

(25)

Via (23) from (24) and (25) for the functional $V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)$ it follows that

$$LV\left(t\right)\le {\eta }^T\left(t\right){\Phi }_2\eta \left(t\right),{\eta }^T\left(t\right)=(Z^T\left(t\right),G^T\left(t\right)).$$

From this and the LMI (23) it follows that there exist $c>0$ such that $LV\left(t\right)\le -{c\left|Z\left(t\right)\right|}^2$. Via Theorem A2 (see Appendix A), it means that the zero solution of Equation (21) is asymptotically mean square stable. The proof is completed. □

Remark 8. 

Note that via (3), (16) and (18) for the equilibrium $E_1(x^{*},y^{*})$$\parallel B\parallel =\sqrt{2}\nu =\sqrt{2}\beta y^{*}$.

Remark 9. 

It is known [12,13] that for LMI ${\Phi }_2<0$, matrix $A+B$ must be negative definite. Via (18) for the equilibrium $E_0(0,0)$, we have $A+B=\left[\begin{array}{cc}-\gamma & \alpha -\nu \\ 0& \nu \end{array}\right]$ and via Remark 2 this matrix cannot be negative definite ($Det(A+B)<0$). From Remark 5, we have $(2\beta +\nu \mu )y^{*}>\nu$. Via (18) and Remark 2, it means that for the equilibrium $E_1(x^{*},y^{*})$ matrix $A+B$ is negative definite.

Remark 10. 

Note that for stability investigation of the neutral type Equation (21) it is necessary to ensure the exponential stability of the integral equation $z\left(t\right)=-BG\left(t\right)$ that follows from condition (22). Similarly to [10,19], it can be shown that instead of condition (22) the condition in the form of LMI can be used: if there exists a positive definite matrix S such that the LMI ${\tau }^2\left(z^{*}\right)B^{\prime }SB-S<0$ holds. Then, the integral equation $z\left(t\right)=-BG\left(t\right)$ is exponentially stable. Generally speaking, condition (22) is rougher than this LMI condition, but of course, it is simpler. Moreover, in the scalar case both these conditions coincide.

3.4. Examples

Example 1. 

Consider system (7) and (8) with the delay $\tau \left(z\right)={\tau }_M-({\tau }_M-{\tau }_m)e^{-\delta z}$, $\delta >0$. By that

$$\begin{gathered} \tau \left(0\right)={\tau }_m,\tau (\infty )={\tau }_M, \\ {\tau }^{\prime }\left(z\right)=\delta ({\tau }_M-{\tau }_m)e^{-\delta z}>0,{\tau }^{″}\left(z\right)=-\delta {\tau }^{\prime }\left(z\right)<0. \end{gathered}$$

Put also

$$\alpha =5,\beta =0.1,\gamma =1,{\sigma }_1=0.6,{\sigma }_2=0.5,{\tau }_m=1,{\tau }_M=3.5,\delta =5.$$

(26)

Solving system (3) with the values of the parameters given in (26), we obtain $x^{*}=7.32$, $y^{*}=1.51$, $\tau \left(z^{*}\right)=3.5$.

Via MATLAB for the LMI approach (see [12,13]), it was shown that by the values of the parameters, given in (26), for each of the matrices ${\Phi }_1$ and ${\Phi }_2$ there exist positive definite matrices P and R that the LMIs (19) and (23) hold. Moreover, $\parallel B\parallel \tau \left(z^{*}\right)=0.747<1$. So, via both Theorems 2 and 3, the equilibrium $E_1(7.32,1.51)$ of system (7) and (8) is stable in probability.

In Figure 1, 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) of the solution of system (7) and (8) are presented by the values of the parameters (26) with the initial conditions $x\left(s\right)=8.4$, $y\left(s\right)=6.5$, $s\in [-{\tau }_M,0]$. The equilibrium $E_1(7.32,1.51)$ is stable in probability, so all trajectories converge to this equilibrium.

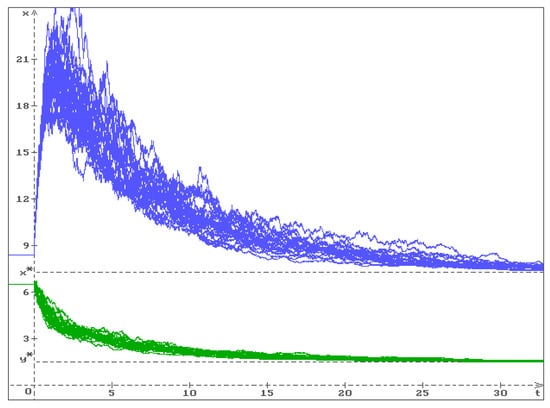
Figure 1. Stable equilibrium $E_1(7.32,1.51)$: 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) for $\alpha =5$, $\beta =0.1$, $\gamma =1$, ${\sigma }_1=0.6$, ${\sigma }_2=0.5$, ${\tau }_m=1$, ${\tau }_M=3.5$, $\delta =5$ and the initial conditions $x\left(s\right)=8.4$, $y\left(s\right)=6.5$, $s\in [-{\tau }_M,0]$. One can see that all trajectories converge to the equilibrium $E_1(7.32,1.51)$.

In Figure 2, 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) of the solution of system (7) and (8) are presented by the values of the parameters (26) with the initial conditions $x\left(s\right)=0.1$, $y\left(s\right)=0.05$, $s\in [-{\tau }_M,0]$. The equilibrium $E_0(0,0)$ is unstable, and all trajectories go out of this equilibrium.

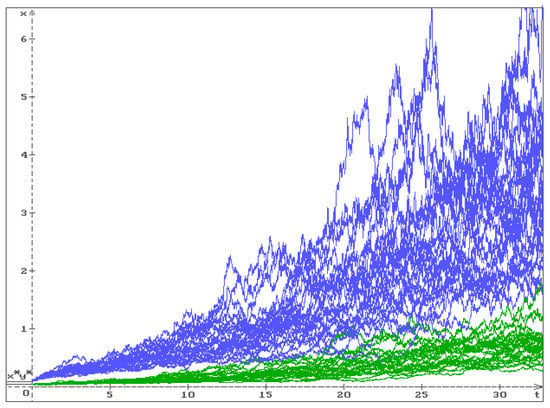
Figure 2. Unstable equilibrium $E_0(0,0)$: 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) for $\alpha =5$, $\beta =0.1$, $\gamma =1$, ${\sigma }_1=0.6$, ${\sigma }_2=0.5$, ${\tau }_m=1$, ${\tau }_M=3.5$, $\delta =5$ and the initial conditions $x\left(s\right)=0.1$, $y\left(s\right)=0.05$, $s\in [-{\tau }_M,0]$. One can see that all trajectories go out of the equilibrium $E_0(0,0)$.

Example 2. 

Consider again system (7) and (8) but with another delay $\tau \left(z\right)={\tau }_M-{\displaystyle \frac{{\tau }_M-{\tau }_m}{1+z}}$. By that, all basic delay properties are preserved:

$$\begin{gathered} \tau \left(0\right)={\tau }_m,\tau (\infty )={\tau }_M, \\ {\tau }^{\prime }\left(z\right)=\frac{{\tau }_M-{\tau }_m}{{(1+z)}^2}>0,{\tau }^{″}\left(z\right)=-2\frac{{\tau }_M-{\tau }_m}{{(1+z)}^3}<0. \end{gathered}$$

Solving again system (3) with the values of the parameters given in (26), we obtain $x^{*}=8.98$, $y^{*}=1.86$, $\tau \left(z^{*}\right)=3.29$.

Via MATLAB it was shown that by the values of the parameters, given in (26), for each of the matrices ${\Phi }_1$ and ${\Phi }_2$ there exist positive definite matrices P and R that the LMIs (19) and (23) hold. Moreover, $\parallel B\parallel \tau \left(z^{*}\right)=0.865<1$. So, via both Theorems 2 and 3, the equilibrium $E_1(8.98,1.86)$ of system (7) and (8) is stable in probability.

In Figure 3, 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) of the solution of system (7) and (8) are presented by the values of the parameters (26) with the initial conditions $x\left(s\right)=10.7$, $y\left(s\right)=5.5$, $s\in [-{\tau }_M,0]$. The equilibrium $E_1(8.98,1.86)$ is stable in probability, so all trajectories converge to this equilibrium.

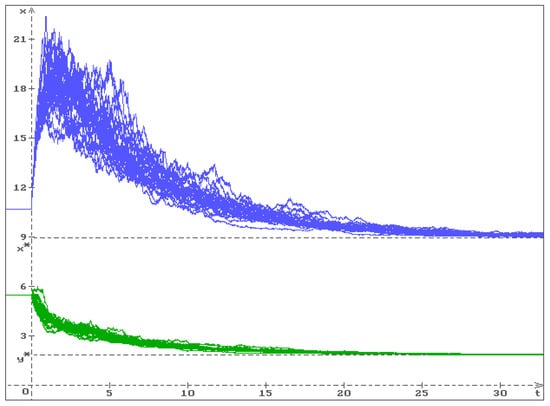
Figure 3. Stable equilibrium $E_1(7.32,1.51)$: 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) for $\alpha =5$, $\beta =0.1$, $\gamma =1$, ${\sigma }_1=0.6$, ${\sigma }_2=0.5$, ${\tau }_m=1$, ${\tau }_M=3.5$ and the initial conditions $x\left(s\right)=10.7$, $y\left(s\right)=5.5$, $s\in [-{\tau }_M,0]$. One can see that all trajectories converge to the equilibrium $E_1(7.32,1.51)$.

In Figure 4, 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) of the solution of system (7) and (8) are presented by the values of the parameters (26) with the initial conditions $x\left(s\right)=0.1$, $y\left(s\right)=0.05$, $s\in [-{\tau }_M,0]$. The equilibrium $E_0(0,0)$ is unstable, and all trajectories go out of this equilibrium.

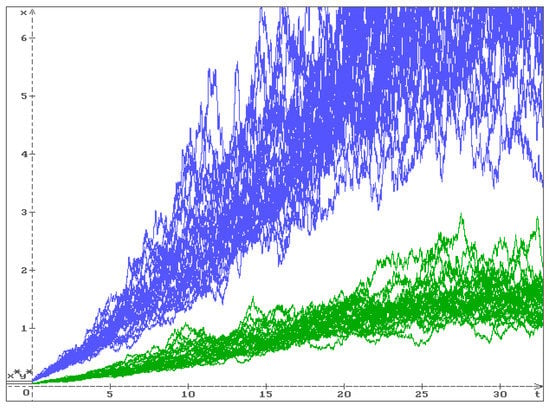
Figure 4. Unstable equilibrium $E_0(0,0)$: 25 trajectories $x\left(t\right)$ (blue) and $y\left(t\right)$ (green) for $\alpha =5$, $\beta =0.1$, $\gamma =1$, ${\sigma }_1=0.6$, ${\sigma }_2=0.5$, ${\tau }_m=1$, ${\tau }_M=3.5$ and the initial conditions $x\left(s\right)=0.1$, $y\left(s\right)=0.05$, $s\in [-{\tau }_M,0]$. One can see that all trajectories go out of the equilibrium $E_0(0,0)$.

Remark 11. 

Note that by numerical simulation of system (7) and (8) solutions for numerical simulation of trajectories of the standard Wiener processes the special algorithm described in [14] was used.

4. Conclusions

It is shown how the Lyapunov functionals construction method and the method of linear matrix inequalities (LMIs) can be used for stability and instability investigation of nonlinear systems with a state-dependent delay under stochastic perturbations. Obtained delay-independent and delay-dependent conditions of stability in probability for equilibria of the considered system are formulated in terms of linear matrix inequalities and are illustrated by numerical simulation of solutions of Ito’s stochastic differential equation. The proposed method of stability investigation can be successfully used for similar investigations of other types of nonlinear systems with state-dependent delay under stochastic perturbations.