An Insight of the Theoretical Physics of Ru-Alloyed Iron Pyrite Studied for Energy Generation

Abstract

Pyrite ${\mathrm{FeS}}_2$ has become the focus of many researchers in thin-film photovoltaics because it has some possibilities in photovoltaics. In this manuscript, we present an experimental and a theoretical study of the electronic structure of pyrite ${\mathrm{FeS}}_2$ alloyed with a small concentration of 1.19% of ruthenium (${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$) by using the Linear Muffin-Tin Orbital Method in the Atomic-Sphere approximation (LMTO-ASA) calculations and the density of states. We observed that the bandgap of ${\mathrm{FeS}}_2$ increases from $0.90508$ to $1.21586 \mathrm{eV}$ when we replace $~1.19\%$ of the $\mathrm{Fe}$ atoms with ruthenium atoms $\left(\mathrm{x}=0.0119 \mathrm{concentration} \mathrm{of} \mathrm{Ru}\right)$. We prove that this low concentration of Ru saved the gap states and the electronic and optical properties of ${\mathrm{FeS}}_2$ pyrite. Our calculated electronic bandgap is $1.21586 \mathrm{eV}$ and direct. Our results confirm that the symmetric operation of the space ${\mathrm{T}}_{\mathrm{h}}^6 \left(\mathrm{Pa}3\right)$ saves electronic structure of iron pyrite when alloyed with ruthenium.

1. Introduction

Our work is inspired by the fact that making photovoltaic cells is an interest of many researchers and this is due to the fact that these cells are used in renewable energy. So, finding a low-cost and abundant material that can be used in making such cells is very important and interesting work.

Iron pyrite ${\mathrm{FeS}}_2$ is very important among metal sulfide minerals which is recently in the focus of experimental interest because of its high abundance, its low cost, its nontoxic constituent elements, and high light absorption coefficient ($~{10}^5{ \mathrm{cm}}^{-1}$ for h$\mathsf{\nu }>1.4 \mathrm{ev}$), see [1,2]. This interesting material has been the major interest of many researchers in the field of photovoltaics because it is a promising material for photovoltaic cells [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. It has been proven that the Solid State Schottky solar cells and pyrite photoelectrochemical cells (PEC) have large short-circuit current densities (30–42 mA cm⁻²) and quantum efficiencies (up to 90%) [1,2]. Iron pyrite is a semiconductor which has a bandgap of 0.95 eV [3] which is relatively small for solar cell applications. Therefore, it is essential to introduce suitable techniques to enlarge this bandgap of iron pyrite to develop pyrite-based photovoltaic cells and photoelectrochemical solar cells. The bandgap of ${\mathrm{FeS}}_2$ pyrite can be enlarged by adding the anions of ${\mathrm{FeA}}_{\mathrm{x}}{\mathrm{S}}_{2-\mathrm{x}}$ (where A is an anion element such as As, O, etc.) or cations ${\mathrm{Fe}}_{1-\mathrm{x}}{\mathrm{M}}_{\mathrm{x}}{\mathrm{S}}_2$ where M is a cation element such as Zn, Ru, etc.). These alloying techniques have been used extensively, see [18,19]. Anion alloying of ${\mathrm{FeS}}_2$ with oxygen has been proven to increase its bandgap [20]. Furthermore, Sun in [18] claimed that ${\mathrm{FeS}}_2$ pyrite alloys with Os and Zn increases the bandgap from $0.95 \mathrm{eV}$ to $1.2–1.5 \mathrm{eV}$. One of the elements that can alloy with ${\mathrm{FeS}}_2$ pyrite to increase its bandgap is Ruthenium (Ru). Ru is an element that has been used widely for alloying and surface-coating of N-Chlorosuccinimide (NCS) due to its stability. Ruthenium sulfide $\left({\mathrm{RuS}}_2\right)$ has a bandgap of 1.8 eV [21], hence, the bandgap of Ru-alloyed ${\mathrm{FeS}}_2$ pyrite, ${\mathrm{Fe}}_{1-\mathrm{x}}{\mathrm{Ru}}_{\mathrm{x}}{\mathrm{S}}_2$, can be increased from 0.95 to $1.8 \mathrm{eV}$ if we can reach the whole alloying composition range. Sun and Ceder [22] calculated the bandgap of pyrite ${\mathrm{Fe}}_{1-\mathrm{x}}{\mathrm{Ru}}_{\mathrm{x}}{\mathrm{S}}_2$ and ${\mathrm{Fe}}_{1-\mathrm{x}}{\mathrm{O}}_{{\mathrm{s}}_{\mathrm{x}}}{\mathrm{S}}_2$ using density functional theory (DFT). They showed that it is possible to enlarge the bandgap of ${\mathrm{FeS}}_2$ pyrite if some $\mathrm{Fe}$ is replaced by $\mathrm{Os}$ or $\mathrm{Ru}$. Jun Hu et al. [18] studied iron pyrite alloyed with oxygen by DFT calculation; their calculated bandgap shows an increase from $1.02 \mathrm{eV}$ to $1.52 \mathrm{eV}$. ${\mathrm{FeS}}_2$ pyrite has a direct bandgap [23,24,25,26], while ${\mathrm{RuS}}_2$ has an indirect bandgap [27,28,29,30]. Until now, determining the properties (optical and electric) of ${\mathrm{FeS}}_2$ pyrite alloying with ruthenium $\left(\mathrm{Ru}\right)$ has been inconclusive. Ouertani et al. [23] found that the gap of Ru-alloy can increases to $1.31$ eV with a direct bandgap. There is also some new theoretical work done in [31]. In this manuscript, we used the Linear Muffin-Tin Orbital Method in the Atomic-Sphere approximation LMTO-ASA calculation to study the effect of small concentrations of $1.9\%$ of $\mathrm{Ru}$ on the bandgap, electronic structure, and optical properties of ${\mathrm{FeS}}_2$ pyrite because LMTO-ASA is imperative for calculations of the ground-state properties of compounds. It includes the effect of charge transfer which is expected to provide the main uncertainty in energy band calculations for compounds.

2. Experimental

2.1. Materials and Method

We used spray pyrolysis for fabrication of our sample. In our procedures, we chose of a solution obtained from the dissolution of 8.3 g of RuCl₃.3H₂O and FeCl₃.6H₂O with a molar ratio as FeCl₃.6H₂O: RuCl₃.3H₂O = x:1 − x (x = 0.0119) through 10 min substrates and heated at 370 $℃$. The transport rate is about 70 cm and 7 mL/min. In the aqueous solution, we have the following reactions:

$${\mathrm{FeCl}}_3.6{\mathrm{H}}_2\mathrm{O}\to {\mathrm{Fe}}^{3+}+3{\mathrm{Cl}}^{-}+6{ \mathrm{H}}_2\mathrm{O}$$

$${\mathrm{RuCl}}_3.3{\mathrm{H}}_2\mathrm{O}\to {\mathrm{Ru}}^{3+}+3{\mathrm{Cl}}^{-}+3{\mathrm{H}}_2\mathrm{O}$$

We obtained ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ phases in our Iron pyrite layers.

2.2. Characterization Techniques

The crystal structures of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ are studied by XRD (X-ray diffraction) by using Phillips D500 powder with CuK$\alpha$ radiation at $\lambda =1.42 \AA$. The XRD patterns is shown in Figure 1. Representative diffraction peaks at $2\theta$ = 32.92, 37.85, and 57.59 correspond to the (200), (210), and (311) planes. These lines were obtained by using powder diffraction data bases (JCPDS card n$°$: 00-36-1453). The resulting structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ is a cubic crystal structure belonging to the space group $\mathrm{Pa}\overline{3} \left(205\right)$. Both Iron pyrite ${\mathrm{FeS}}_2$ and Ruthenium sulfide $Ru{S}_2$ have a pyrite Pa $\overline{3}$ space group structure with 5.419 $\AA$ and 5.635$\AA$ as lattice constants, respectively. We determined the lattice parameter using the Rietveld method utilizing the PDXL program.

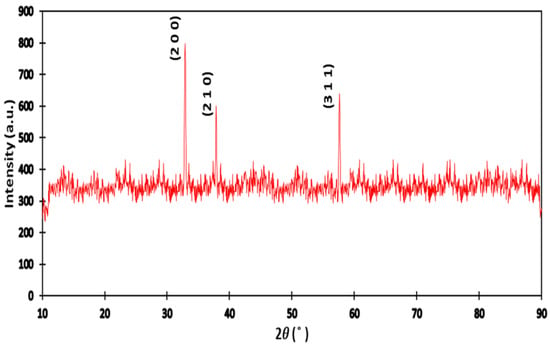
Figure 1. XRD spectrum for ${\mathrm{Fe}}_{1-\mathrm{x}}{\mathrm{Ru}}_{\mathrm{x}}{\mathrm{S}}_2$ for $\mathrm{x}=0 \mathrm{and} \mathrm{x}=0.0119$.

Moreover, this Ru-alloyed iron sulfide (${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$) exhibits cubic crystal structure in the pyrite phase. The lattice constant and the atomic positions are presented in Table 1. The pyrite structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ was presented in a cubic crystal, by replacing one Fe atom with an Ru atom in metal positions and eight positions of sulfur atoms.

Table 1. Cell Parameters.

$\mathrm{Cubic} \mathrm{lattice} \mathrm{a}$	$5.517 Å$
$\mathsf{\nu } \left(\mathrm{Position} \mathrm{paramater}\right)$	$0.113$
$\mathrm{u} \left(\mathrm{Suffer} \mathrm{position}\right)$	$0.387$
${\mathrm{Bond} \mathrm{length} \mathrm{d}}_{\mathrm{s}-\mathrm{s}}$	$2.1212 Å$

Note that compared to the pure Iron pyrite [24], we can see that the distance $\mathrm{S}-\mathrm{S}$ is similar to one in the ${\mathrm{S}}_2$ molecule and the lattice constant increases because $Ru$ ions are larger than $\mathrm{Fe}$ ions.

The optical absorption diagram of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ was carried out using a SHIMADZU 3100s spectrophotometer. Figure 2 shows ${\left(\mathsf{\alpha }\mathrm{h}\mathsf{\nu }\right)}^2$ versus the photon energy $\mathrm{h}\mathsf{\nu }$ and Figure 3 shows ${\left(\mathsf{\alpha }\mathrm{h}\mathsf{\nu }\right)}^{\frac{1}{2}}$ versus $\mathrm{h}\mathsf{\nu }$. The two graphs indicate that ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ has a direct bandgap energy of 1.23 eV.

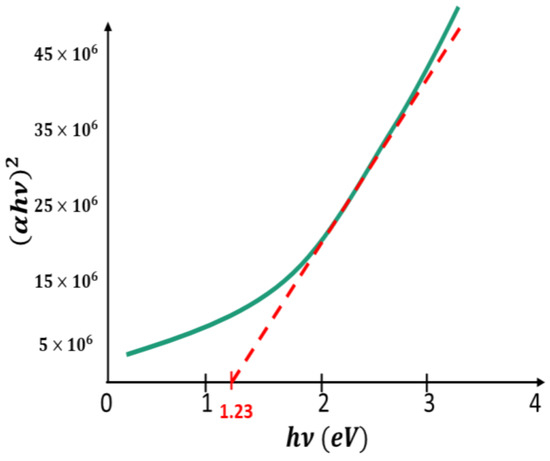
Figure 2. ${\left(\mathsf{\alpha }\mathrm{h}\mathsf{\nu }\right)}^2$ versus $\mathrm{h}\mathsf{\nu }$ gives straight line, suggesting that the Ru-alloyed FeS₂ films have a direct band gap energy.

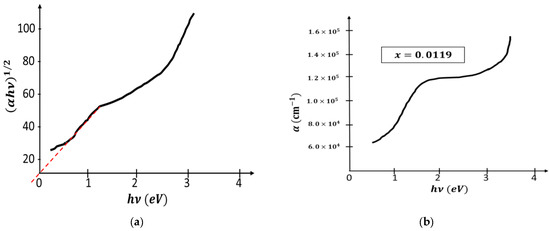
Figure 3. (a): ${\left(\mathsf{\alpha }\mathrm{h}\mathsf{\nu }\right)}^{\frac{1}{2}}$ versus $\mathrm{h}\mathsf{\nu }$. (b): $\mathsf{\alpha }$ versus $\mathrm{h}\mathsf{\nu }$.

Figure 3b shows the plot of absorption coefficients versus $\mathrm{h}\mathsf{\nu }$ and we note that the absorption coefficients are always high $(\mathsf{\alpha }>1.2\times {10}^5{ \mathrm{cm}}^{-1})$, which encourages their use in the photovoltaic domain.

3. Calculated Band Energy of $F{e}_{0.9881}R{u}_{0.0119}{S}_2$

3.1. Method

In our calculations, we apply the LMTO ASA method which has been explained in detail in several reports [32,33,34]. In our system, we have four metal atoms and eight sulfur atoms. In our case, the percentage of Ru is about 1.19$\%$ and is 25$\%$ lesser than that we have for one Ru atom and three Fe atoms and eight sulfur atoms. The data of sample are listed in the following Table 2:

Table 2. Sample Parameters.

$\mathrm{Cubic} \mathrm{lattice} \mathrm{a}$	$5.517 Å$
$\mathsf{\nu } \left(\mathrm{Position} \mathrm{paramater}\right)$	$0.113$
$\mathrm{u} \left(\mathrm{Suffer} \mathrm{position}\right)$	$0.387$
$\mathrm{Fe} \mathrm{position}$	$\left(0.5 0.5 0\right), \left(0 0.5 0.5\right),\left(0.5 0 0.5\right)$
$\mathrm{Ru} \mathrm{position}$	$\left(0 0 0\right)$
${\mathrm{Bond} \mathrm{length} \mathrm{d}}_{\mathrm{s}-\mathrm{s}}$	$2.1212 Å$

In our calculations, we employ the self-consistent band calculations. This is because it is a first-principles calculation where the density functional theory was used, see [35], using the local density approximation, see [36], and using numerical techniques which rely on the electron ion’s treatment of interaction in the pseudopotential approximation [31]. However, the ASA Hamiltonian is completely specified by the potential parameters. It will generate moments from the eigenvectors of the Hamiltonian. For a certain potential, there is a unique correspondence between the logarithmic derivative ${\mathrm{D}}_{\mathrm{v}}$ at the sphere radius and the energy Eν of the wave function $\mathsf{\phi }$. In principle, it is possible to specify either one. The potential P becomes simple because we use [37,38]

$$\mathrm{P}\left(\mathsf{\epsilon }\right)=\mathrm{const}\frac{\mathrm{D}\left(\mathsf{\epsilon }\right)+\mathrm{l}+1}{\mathrm{D}\left(\mathsf{\epsilon }\right)-\mathrm{l}}\approx {\left(\frac{{\Delta }_{\mathrm{l}}}{\mathsf{\epsilon }-{\mathrm{C}}_{\mathrm{l}}}+{\mathsf{\gamma }}_{\mathrm{l}}\right)}^{-1}$$

where ${\mathrm{C}}_1$, ${\Delta }_1$, and ${\mathsf{\gamma }}_1$, are the “potential parameters” that parameterize P. ${\mathrm{C}}_1$ corresponds to the band “center of gravity”, ${\Delta }_1$ is the “band width” parameter which corresponds approximately to the bandwidth of that l channel if it were uncoupled from the other l channels, and ${\mathsf{\gamma }}_1$ is the “band distortion parameter” which describes the deformations relative to a universal shape. Generally, a small parameterization is a perfect method to study a band structure. First, we obtain the potential parameter for all atomic spheres. The muffin-tin potential constant ${\mathrm{V}}_{\mathrm{MTZ}}$ around $\mathrm{Fe}$, $\mathrm{Ru}$, and $\mathrm{S}$ is equal to $-0.835283$. We have 24 symmetry operations. The muffin-tin MT radii are $2.939 \mathrm{a}.\mathrm{u}.$ for $\mathrm{Ru}$, $2.951 \mathrm{a}.\mathrm{u}.$ for $\mathrm{Fe}$, and $2.202 \mathrm{a}.\mathrm{u}.$ for $\mathrm{S}$. The initial sphere packing was equal to $79.2\%$, scaled to $87.9\%$. The role of these empty spheres is to reduce the number of iterations in this procedure and to reduce the overlap between the spheres centered at $\mathrm{Fe}$, $\mathrm{Ru}$, and $\mathrm{S}$.

3.2. Band Structure

Figure 4 represents energy band structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$. It shows all details of the valence and conduction bands in an energy range between −20 eV and +8 eV. Different colors are used to describe this band structure to indicate the contributions of the cations ($\mathrm{Fe}$ and $\mathrm{Ru}$) and the anion ($\mathrm{S}$). We have five distinct groups based on the order of increasing energy of this band structure. Note that the occupied bands have 80 valence electrons. First, we can see that the first two groups of bands (I, II) are associated with bonding and antibonding pairs of orbitals on ${\mathrm{S}}_2$ pairs. The two groups have a maximum energy of −11 eV and their character is $\mathrm{S}3\mathrm{s}$, where $\mathrm{S}3\mathrm{s}$ states are predominant. The structure of sulfur 3p states start approximately at −7 eV; their basic states include an extra structure due to the Fe 3d levels and a small admixture of Ru 4d levels. This group composes with bonding S 3p and Fe ${\mathrm{e}}_{\mathrm{g}}$ and Ru ${\mathrm{e}}_{\mathrm{g}}$. The Fe 3d ${\mathrm{t}}_{2\mathrm{g}}$ and Ru 4d ${\mathrm{t}}_{2\mathrm{g}}$ bands, which give us the fourth group of bands (IV), are under the Fermi level. Note that, above the Fermi level, we have a split of conduction bands; these bands have S 3p and Fe 3d ${\mathrm{e}}_{\mathrm{g}}$ and Ru 4d ${\mathrm{e}}_{\mathrm{g}}$ characters, due to the group V.

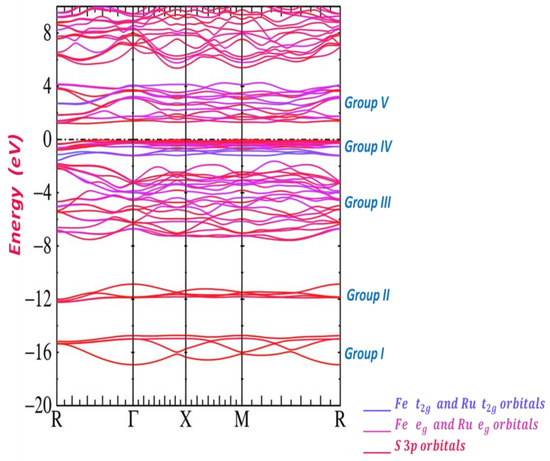
Figure 4. Band structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$.

Our calculations indicate that ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ is a direct gap semiconductor of 1.21586 eV. The valence band maximum (VBM) is −0.055993 Ry (−0.761823 eV), and the conduction band minimum (CBM) is 0.033408 Ry (0.454539 eV). The Fermi energy of −0.055993 Ry (−0.761823 eV) is very close to the maximum valence band, which leads us to deduce that we have an empty conduction band and a filled valence band. Thereby, we can conclude that our bandgap of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ is direct at the Gamma point ($\mathsf{\Gamma }$). Figure 2 and Figure 3 show that the optical measurement of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ has a direct gap of 1.23 eV, which is in good agreement with our calculations.

Figure 5a presents the band structure of ${\mathrm{FeS}}_2$ pyrite obtained by LMTO-ASA. Our calculation indicates that ${\mathrm{FeS}}_2$ pyrite is a direct-gap semiconductor, with a calculated gap of $0.90508 \mathrm{eV}$. The valence-band energy $\left(\mathrm{ev}\right)$ is $-0.000533 \mathrm{Ry}$, and the energy of the conduction band (ec) is $0.066017 \mathrm{Ry}$. The Fermi energy $-0.000533 \mathrm{Ry}$ matches the valence-band energy, which indicates that the valence band is filled while the conduction band is completely empty. Consequently, our bandgap of ${\mathrm{FeS}}_2$ is direct at the $\mathsf{\Gamma }$ gamma point$.$ The optical measurement of ${\mathrm{FeS}}_2$ pyrite has a direct gap of approximately $0.95 \mathrm{eV}$ [24], in good agreement with our calculation.

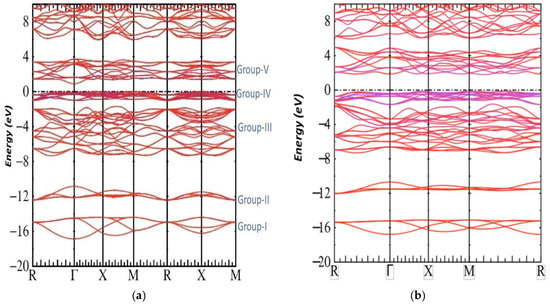
Figure 5. (a): Band structure of ${\mathrm{FeS}}_2$ pyrite. (b): Band structure of ${\mathrm{RuS}}_2$ pyrite.

Figure 5b is a structure of ${\mathrm{RuS}}_2$ pyrite obtained by LMTO-ASA. Moreover, our figures indicate that ${\mathrm{RuS}}_2$ has a bandgap semiconductor. The max valence band is at X, and the min conduction band is at $\mathsf{\Gamma }$. The indirect bandgap is between X and gamma $\mathsf{\Gamma },$ and the direct transition at $\mathsf{\Gamma }.$ We found the indirect bandgap has the following value: $1.80727 \mathrm{eV}.$ The values of the filled bands encountered $\left(\mathrm{ev}\right)$ is about −0.126036 Ry and the empty bands encountered (ec) is about 0.006851 Ry. The Fermi energy is about −0.126036 Ry. Our obtained gap energy by the linear muffin-tin is in a good agreement with an experimental bandgap of 1.8 eV [27]. Note that the band structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ is similar to the band structure of ${\mathrm{FeS}}_2$ pyrite and that is due to the fact that both have a direct bandgap and five groups of energy levels.

Figure 6 shows the energy diagram for Ru 4d, Fe 3d, and S 3p orbitals under the influences of crystal field splitting (CFS) and S-S dimerization. The bandgap Eg is denoted by the green arrow. The 3d and 4d orbitals of Fe and Ru are split into ${\mathrm{t}}_{2\mathrm{g}}$ and ${\mathrm{e}}_{\mathrm{g}}$ groups, while the 3p orbitals of S are split into $\mathrm{PP}\mathsf{\sigma }$,$\mathrm{PP}\mathsf{\pi },{ \mathrm{PP}\mathsf{\pi }}^{*}{\mathrm{and} \mathrm{PP}\mathsf{\sigma }}^{*}$ groups. This indicates that the CBM of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ alloy shifts upward toward the Fe ${\mathrm{e}}_{\mathrm{g}}$ band, the CBM still originates from ${\mathrm{PP}\mathsf{\sigma }}^{*}$.

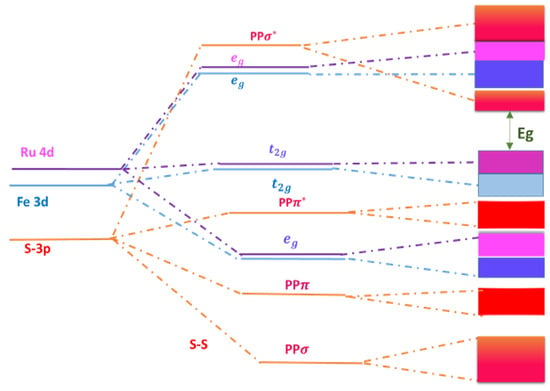
Figure 6. Energy diagram for orbitals.

The density of states (DOS) calculated below and above the Fermi level for ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ is presented in Figure 7, in which a clear hybridization between Fe, Ru, and S states is clearly seen. The two smallest peaks around −1.2 Ry and −0.8 Ry show that the S contributions are dominant. Note that the valence bands of the first two groups (I and II) are the lowest. Fe and Ru in the third group (III) have a small contribution dominance, which is mostly dominant by S. The third and the fourth groups (III, IV) are between −0.6 Ry and −0.05599 Ry. In addition, in the fourth and the fifth groups (IV, V), Fe and Ru have a dominant contribution. The highest peak in group IV lies between −0.2 Ry and −0.055993 Ry below but very close to the Fermi level, which shows that the level ${\mathrm{t}}_{2\mathrm{g}}$ is filled and all S 3p, Fe ${\mathrm{t}}_{2\mathrm{g}}$ and Ru ${\mathrm{t}}_{2\mathrm{g}}$ states (group IV states) are occupied. Hence, all S 3p and Fe ${\mathrm{e}}_{\mathrm{g}}$ and Ru ${\mathrm{e}}_{\mathrm{g}}$ states (group V) are empty indicating unoccupied ${\mathrm{e}}_{\mathrm{g}}$ states.

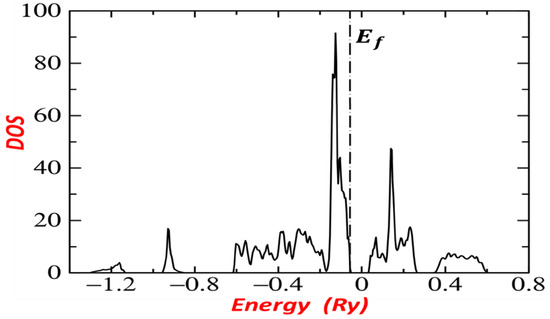
Figure 7. Density of states of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$.

In summary, the valence bands are almost completely driven from the ${\mathrm{t}}_{2\mathrm{g}}$ orbitals while the conduction band is almost pure Sp. In Figure 4, it can be clearly seen that the bottom of the conduction band is red (the S 3p states) and that the conduction band is similar to that of Iron pyrite [24]. We conclude that the presence of a low concentration of 1.19% of Ru alloy will shift the bandgap up by $~0.4 \mathrm{eV}$; at the same time, it does not change the state of Iron pyrite. Furthermore, our calculated bandgap $\mathrm{of} 1.21586 \mathrm{eV}$ is in very good agreement with the experimental value 1.23 eV.

4. Conclusions

An adequate molar ratio was chosen to fabricate ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ thin films having good properties for solar cell application. We have investigated the electronic structure of ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ using LMTO-ASA calculations. We showed that substituting ruthenium for Fe atoms is a good method to enlarge the bandgap of ${\mathrm{FeS}}_2$ pyrite while saving gap states and the optical and electrical properties of ${\mathrm{FeS}}_2$ pyrite. The small concentration of 1.19$\%$ of Ru alloy raises the maximum of the conduction band by 0.3 eV, which is considered as a desired bandgap value for solar cell applications. We note that it is highly possible to use ${\mathrm{Fe}}_{0.9881}{\mathrm{Ru}}_{0.0119}{\mathrm{S}}_2$ as multispectral photovoltaic cells (1.2–1.3 eV).