The Value of the Early-Time Lieb-Robinson Correlation Function for Qubit Arrays

Abstract

The Lieb-Robinson correlation function is one way to capture the propagation of quantum entanglement and correlations in many-body systems. We consider arrays of qubits described by the tranverse-field Ising model and examine correlations as the expanding front of entanglement first reaches a particular qubit. Rather than a new bound for the correlation function, we calculate its value, both numerically and analytically. A general analytical result is obtained that enables us to analyze very large arrays of qubits. The velocity of the entanglement front saturates to a constant value, for which an analytic expression is derived. At the leading edge of entanglement, the correlation function is well-described by an exponential reduced by the square root of the distance. This analysis is extended to arbitrary arrays with general coupling and topologies. For regular two and three dimensional qubit arrays with near-neighbor coupling we find the saturation values for the direction-dependent Lieb-Robinson velocity. The symmetry of the underlying 2D or 3D lattice is evident in the shape of surfaces of constant entanglement, even as the correlations front expands over hundreds of qubits.

1. Introduction

Entanglement in many-body quantum systems and the spread of quantum correlations has been of considerable interest for both fundamental reasons and for the possible applications in quantum computing and communication. Focus on quantum information naturally employs entropic measures derived from the von Neumann entropy of a state. Multiple measures have been proposed to capture the quantum entanglement of spatially separated systems and this remains an area of great activity [1,2,3]. Information so conceived is a property of the state of the system, characterized by either a state vector for pure states or a density operator for pure or mixed states.

Another avenue, not tied to the state of the system, considers the commutation relations between local operators that act on spatially separated subsystems. Preeminent here is investigation of the Lieb-Robinson operator [4], which quantifies the quantum correlation between a Heisenberg operator ${\widehat{A}}_j\left(t\right)$ which acts on subsystem j of the composite many-body system, and an operator ${\widehat{B}}_k$ which acts on subsystem k. The operator is given by

$${\widehat{C}}_{A_j,B_k}\left(t\right)=[{\widehat{A}}_j\left(t\right),{\widehat{B}}_k]$$

(1)

The Lieb-Robinson correlation function is then the norm of the operator.

$$C_{A_j,B_k}\left(t\right)=∥{\widehat{C}}_{A_j,B_k}\left(t\right)∥$$

(2)

If $k\ne j$, then at $t=0$ the operators $\widehat{A}$ and $\widehat{B}$ have different support and therefore commute, so the correlation function is zero. We can think of the operator ${\widehat{A}}_j\left(t\right)$ as spreading out into the system and as its support comes to include that of $\widehat{B}$, the correlation increases. This captures the quantum entanglement between the two systems which is the source of quantum correlation. The Lieb-Robinson correlation function depends only on the choice of the operators and the Hamiltonian of the system, independent of any initial state.

Lieb and Robinson established, for quite general conditions, that the correlation so defined propagates outward with a finite speed and with an exponentially bounded leading edge in space:

$$C_{AB}\left(t\right)\le c{e}^{-a(d(j,k)-v_{\mathrm{LR}}t)}$$

(3)

where $d(j,k)$ is an appropriate distance measure between the two subsystems and $v_{\mathrm{LR}}$ is the Lieb-Robinson velocity.

Because of the importance of this result, there has been a substantial effort to refine the bound in particular circumstances [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] and to understand the connection between entropic measures and correlation measures [21,22,23]. Spin models and equivalent qubit arrays have played a prominent role in studying bounds for specific systems [24] and can also be explored experimentally.

Following the work of Luitz et al. [25,26,27,28], we focus here on a specific Hamiltonian—the tranverse field Ising model–and compute the correlation function itself, rather than a bound on the correlation function. This comes at the cost of generality, of course, but yields insight into the way correlations propagate. Understanding the mechanisms and, in particular, the speed of quantum entanglement is important in the development of both quantum communication and quantum computation.

The transverse-field Ising model is a workhorse system for analyzing many-body spin systems. It is also a practically realizable system as evidenced by its use in D-Wave quantum annealing-based computers [29]. Recent results have reported measurements on one-dimensional transverse-field Ising chains using up to 2000 superconducting flux qubits in a quantum annealer [30].

For the purposes of stating a bound, the norm in Equation (3) need not be specified, but to calculate the value of the correlation function itself a particular norm must be chosen. Here we use the normalized Frobenius norm

$$∥\widehat{Q}∥=\sqrt{\frac{Tr\left({\widehat{Q}}^{†}\widehat{Q}\right)}{\mathcal{N}}},$$

(4)

where $\mathcal{N}$ is the dimension of the Hilbert space. The normalization ensures that the value is independent of the size of the space.

Our study is motivated by a desire to understand more details about how the entanglement measured by the Lieb-Robinson correlation functions spreads. Numerical time-dependent results are limited to small system sizes, so we seek analytic techniques with which we can explore much larger systems, particularly in the region near the propagating front. How long does it take for the propagation speed to reach a saturated value, and what is that value? How does the actual correlation front depart from its bound given by Equation (3)? What shape is propagation front in two and three dimensional qubit arrays?

In Section 2, we consider a linear array of near-neighbor coupled qubits—the 1D tranverse field Ising model [24], and calculate the Lieb-Robinson correlation function numerically. This is only practical for small systems. We then derive an analytical expression for the correlation function which we can compare with the numerical results. The analysis is then extended to an arbitrary array of qubits in Section 3, and subsequently applied to regular square lattices in two and three dimensions in Section 4. We conclude with a discussion of the results in Section 5.

2. Lieb-Robinson Correlation Function for a Regular Linear Array

2.1. Direct Numerical Calculation

We consider first a linear array of $N_q$ qubits with an energy $\Delta$ coupling adjacent z-components, as described by the following Hamiltonian:

$$\widehat{H}=-\gamma \sum _k^{N_q}{\widehat{\sigma }}_x^{\left(k\right)}-\frac{\Delta }{2}\sum _k^{N_q-1}{\widehat{\sigma }}_z^{\left(k\right)}{\widehat{\sigma }}_z^{(k+1)}.$$

(5)

Here ${\widehat{\sigma }}_{\alpha }^{\left(k\right)}$ is the Pauli spin operator with $\alpha =(x,y,z)$ operating on the $k^{th}$ qubit. Each operator is understood to be embedded in the full direct-product Hilbert space of the array with dimension $\mathcal{N}=2^{N_q}$. This system is the 1D transverse field Ising model. The first term represent the internal dynamics which allow each qubit to flip its state. The energy $\gamma$ sets the characteristic time for the dynamics

$$\tau \equiv \pi \hslash /\gamma .$$

(6)

We have the usual commutation relations for Pauli operators.

$$\begin{array}{ccc}\hfill \left[{\widehat{\sigma }}_x^{\left(j\right)},{\widehat{\sigma }}_y^{\left(k\right)}\right]& =& 2i{\widehat{\sigma }}_z^{\left(k\right)}{\delta }_{j,k}\hfill \\ \hfill \left[{\widehat{\sigma }}_y^{\left(j\right)},{\widehat{\sigma }}_z^{\left(k\right)}\right]& =& 2i{\widehat{\sigma }}_x^{\left(k\right)}{\delta }_{j,k}\hfill \\ \hfill \left[{\widehat{\sigma }}_z^{\left(j\right)},{\widehat{\sigma }}_x^{\left(k\right)}\right]& =& 2i{\widehat{\sigma }}_y^{\left(k\right)}{\delta }_{j,k}\hfill \end{array}$$

(7)

We consider the Lieb-Robinson operator between the z components of the first qubit and qubit k.

$${\widehat{C}}_k\left(t\right)=[{\widehat{\sigma }}_z^{\left(1\right)}\left(t\right),{\widehat{\sigma }}_z^{\left(k\right)}\left(0\right)]$$

(8)

The Lieb-Robinson correlation function is given by the norm of the operator.

$$C_k\left(t\right)=∥{\widehat{C}}_k\left(t\right)∥$$

(9)

The correlation function $C_k$ captures the quantum correlation between two qubits that are $(k-1)$ apart.

The time-development of the Heisenberg operator ${\widehat{\sigma }}_1^{\left(z\right)}$ is given by

$${\widehat{\sigma }}_z^{\left(1\right)}\left(t\right)=e^{i\frac{\widehat{H}}{\hslash }t}{\widehat{\sigma }}_z^{\left(1\right)}{e}^{-i\frac{\widehat{H}}{\hslash }t}$$

(10)

The correlation function can then be written

$$C_k\left(t\right)=∥\left[e^{i\frac{\widehat{H}}{\hslash }t}{\widehat{\sigma }}_z^{\left(1\right)}{e}^{-i\frac{\widehat{H}}{\hslash }t},{\widehat{\sigma }}_z^{\left(k\right)}\left(0\right)\right]∥.$$

(11)

The Lieb-Robinson correlation function $C_k\left(t\right)$ is a two-time correlation function that expresses the quantum correlation between qubit k at time $t=0$ and qubit 1 at time t (or equivalently, between qubit 1 at time $t=0$ and qubit k at time t). Figure 1 shows the Lieb-Robinson correlation function for a line of nine qubits calculated by direct numerical evaluation [31] of Equation (11) for the Hamiltonian in Equation (5).

Figure 1. The Lieb-Robinson correlation function between the reference qubit 1 and qubit k for a linear array of 9 qubits with near-neighbor interactions. The calculation is done by numerical evaluation of $C_q$ using Equation (11) and the Hamiltonian of Equation (5) with $\Delta /\gamma =1$.

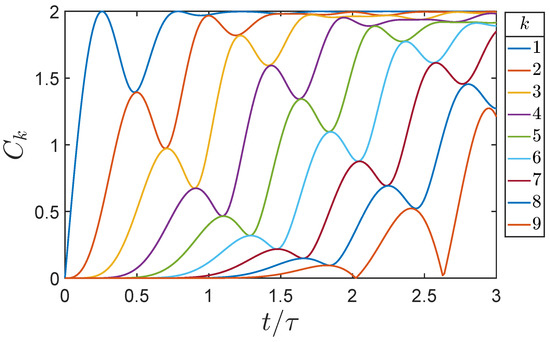
How can we understand the meaning of the self-correlation $C_1\left(t\right)$? At time $t=0$, Equation (8) yields $C_1\left(0\right)=0$ because ${\widehat{\sigma }}_z^{\left(1\right)}$ commutes with itself. As time progress, however, ${\widehat{\sigma }}_z^{\left(1\right)}\left(t\right)$ spreads out to include Pauli operators on other qubits through Equation (10). This time evolution also mixes into ${\widehat{\sigma }}_z^{\left(1\right)}\left(t\right)$ components of ${\widehat{\sigma }}_x^{\left(1\right)}$ and ${\widehat{\sigma }}_y^{\left(1\right)}$ which do not commute with ${\widehat{\sigma }}_z^{\left(1\right)}$. The quantum correlation $C_1\left(t\right)$ therefore expresses the “non-commutativity” of ${\widehat{\sigma }}_z^{\left(1\right)}\left(t\right)$ with its past self at $t=0$. Note also that the maximum non-commutativity has magnitude 2 (from Equation (7)), as seen in Figure 1.

We are interested in the early-time behavior as correlations initially spread down the line. By “early-time” behavior we mean times such that the correlation with the reference qubit 1 is small. Our focus is on the leading order term in time as the correlation between the first site and the $k^{th}$ site initially grows. Figure 2 shows a view of the correlations zoomed in to the lower left-hand corner of Figure 1.

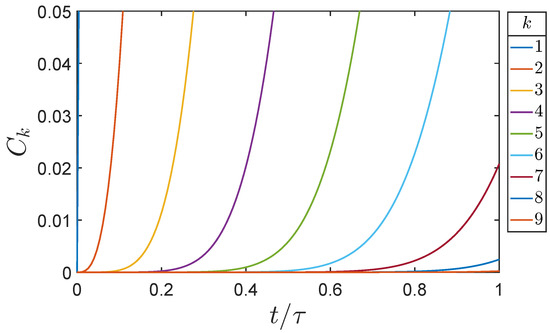
Figure 2. Detail of the early-time behavior Lieb-Robinson correlation function as the quantum correlations move down the line of nine qubits. The calculation and parameters are as in Figure 1.

The early time behavior of the Lieb-Robinson correlation function has a power-law dependence, as is evident in Figure 2 and in the log-log plot shown in Figure 3. The dots in the figure represent the numerical solution of Equation (11) for $\Delta /\gamma =1$. The lines are the results of the analytical expression derived below. Figure 4 similarly shows the numerical result for the case when $\Delta /\gamma =5$. The larger interaction strengths makes the correlations spread more rapidly down the line.

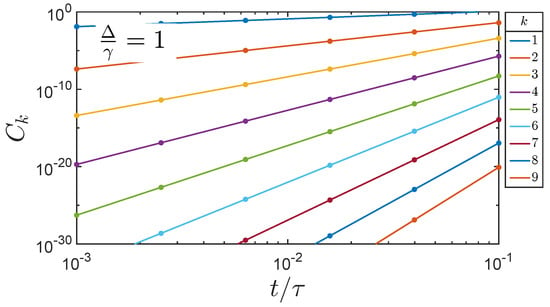
Figure 3. The Lieb-Robinson early-time correlation function for the nine qubit line demonstrates the power-law dependence on time. The qubit index is k and the dots represent numerical evaluation of Equation (11) for the Hamiltonian in Equation (5) with $\Delta /\gamma =1$. The lines represent the analytic result of Equation (30).

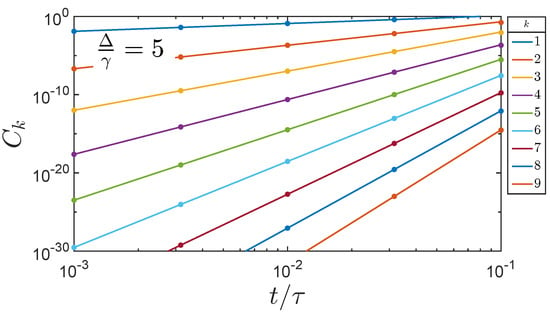
Figure 4. The Lieb-Robinson early-time correlation function for the nine qubit line with qubit index k. The dots represent the direct numerical evaluation of Equation (11) with $\Delta /\gamma =5$ and the lines represent the analytic result of Equation (30). The stronger coupling between neighboring qubits yields a faster propagation of correlations down the chain.

2.2. Analytic Solution for Early-Time Behavior

We adopt the following notation for an n-nested commutator.

$$\left[{\left(\widehat{A}\right)}^n,\widehat{B}\right]\equiv \left[\widehat{A},\left[\widehat{A},\dots \left[\widehat{A}[\widehat{A},\widehat{B}]\right]\right]\dots \right]$$

(12)

It will also be useful to define a notation for a nested commutator with a sequence of operators.

$$\left[({\widehat{\mathcal{O}}}_1,{\widehat{\mathcal{O}}}_2,\dots ,{\widehat{\mathcal{O}}}_n),\widehat{B}\right]\equiv \left[{\widehat{\mathcal{O}}}_1,\left[{\widehat{\mathcal{O}}}_2,,\dots \left[{\widehat{\mathcal{O}}}_n,\widehat{B}]\right]\right]\dots \right]$$

(13)

Using the notation of Equation (12), we can write the time dependence of any Heisenberg operator as

$$\widehat{A}\left(t\right)=\widehat{A}\left(0\right)+\sum _{n=1}^{\infty }\frac{1}{n!}{\left(\frac{it}{\hslash }\right)}^n\left[{\left(\widehat{H}\right)}^n,\widehat{A}\right].$$

(14)

Applying this to ${\widehat{\sigma }}_z^{\left(1\right)}\left(t\right)$ we have

$$\begin{array}{ccc}\hfill {\widehat{C}}_k\left(t\right)& =& \left[\left(\sum _{n=1}^{\infty }\frac{1}{n!}{\left(\frac{it}{\hslash }\right)}^n\left[{\left(\widehat{H}\right)}^n,{\widehat{\sigma }}_z^{\left(1\right)}\right]\right),{\widehat{\sigma }}_z^{\left(k\right)}\right]\hfill \end{array}$$

(15)

$$\begin{array}{ccc}& =& \sum _{n=1}^{\infty }\frac{1}{n!}{\left(\frac{it}{\hslash }\right)}^n\left[\left[{\left(\widehat{H}\right)}^n,{\widehat{\sigma }}_z^{\left(1\right)}\right],{\widehat{\sigma }}_z^{\left(k\right)}\right]\hfill \end{array}$$

(16)

$$\begin{array}{ccc}& =& \sum _{n=1}^{\infty }{\widehat{C}}_k^{\left(n\right)}{\left(\frac{t}{\tau }\right)}^n\hfill \end{array}$$

(17)

The early time Lieb-Robinson operator for qubit k is the lowest-order ${\widehat{C}}_k^{\left(n\right)}$ which is not zero. All other terms in Equation (17) will be vanishingly small for early enough times.

For convenience, we define

$${\widehat{G}}_k^{\left(n\right)}=\left[\left[{\left(\widehat{H}\right)}^{\left(n\right)},{\widehat{\sigma }}_z^{\left(1\right)}\right],{\widehat{\sigma }}_z^{\left(k\right)}\right],$$

(18)

so that,

$${\widehat{C}}_k^{\left(n\right)}=\frac{1}{n!}\frac{{\pi }^n{i}^n}{{\gamma }^n}{\widehat{G}}_k^{\left(n\right)}.$$

(19)

To calculate the self-correlation (qubit 1 with itself), we first evaluate

$$\begin{array}{ccc}\hfill \left[{\left(\widehat{H}\right)}^{\left(1\right)},{\widehat{\sigma }}_z^{\left(1\right)}\right]& =& (-\gamma )[{\widehat{\sigma }}_x^{\left(1\right)},{\widehat{\sigma }}_z^{\left(1\right)}]\hfill \\ & & -\frac{\Delta }{2}[{\widehat{\sigma }}_z^{\left(1\right)}{\widehat{\sigma }}_z^{\left(2\right)},{\widehat{\sigma }}_z^{\left(1\right)}]\hfill \\ & =& -(-2i)\gamma {\widehat{\sigma }}_y^{\left(1\right)}\hfill \end{array}$$

(20)

so

$$\begin{array}{ccc}\hfill {\widehat{G}}_1^{\left(1\right)}& =& \left[\left[{\left(\widehat{H}\right)}^{\left(1\right)},{\widehat{\sigma }}_z^{\left(1\right)}\right],{\widehat{\sigma }}_z^{\left(1\right)}\right]\hfill \\ & =& {(-2i)}^2\gamma {\widehat{\sigma }}_x^{\left(1\right)}\hfill \end{array}$$

(21)

and

$$\begin{array}{ccc}\hfill {\widehat{C}}_1^{\left(1\right)}& =& -i4\pi {\widehat{\sigma }}_x^{\left(1\right)}\hfill \\ \hfill C_1^{\left(1\right)}& =& \parallel {\widehat{C}}_k^{\left(n\right)}\parallel =4\pi .\hfill \end{array}$$

(22)

The early-time Lieb-Robinson self-correlation is therefore

$$C_1\left(t\right)\approx 4\pi \left(\frac{t}{\tau }\right)$$

(23)

where in this case the $n=1$ term is the first nonzero term which dominates at early times. The linear increase in $C_1\left(t\right)$ is evident in Figure 1, Figure 3 and Figure 4.

For the near-neighbor correlation $C_2\left(t\right)$, the first non-zero term in Equation (18) occurs for $n=3$.

$${\widehat{G}}_2^{\left(3\right)}=\left[\left[{\left(\widehat{H}\right)}^{\left(3\right)},{\widehat{\sigma }}_z^{\left(1\right)}\right],{\widehat{\sigma }}_z^{\left(2\right)}\right],$$

(24)

The term $\left[{\left(\widehat{H}\right)}^{\left(3\right)},{\widehat{\sigma }}_z^{\left(1\right)}\right]$ contains many cross terms from the three iterated commutators with $\widehat{H}$ in Equation (5). However, only one term survives the commutator with ${\widehat{\sigma }}_z^{\left(2\right)}$ in Equation (24), with the result that

$${\widehat{G}}_2^{\left(3\right)}={(-2i)}^4{(-\gamma )}^2\left(\frac{\Delta }{2}\right){\widehat{\sigma }}_x^{\left(1\right)}{\widehat{\sigma }}_x^{\left(2\right)}$$

(25)

and the early-time result for the correlation function is

$$C_2\left(t\right)\approx \frac{2^3}{3!}{\pi }^2\left(\frac{\Delta }{\gamma }\right){\left(\frac{t}{\tau }\right)}^3.$$

(26)

For $C_3$, the $n=5$ term is the leading term. The structure of the only surviving term for ${\widehat{G}}_3^{\left(5\right)}$ (Equation (18)) in this case is illustrative. We write it using the notation of Equation (13).

$${\widehat{G}}_3^{\left(5\right)}\propto \left[\left[\left({\widehat{\sigma }}_x^{\left(3\right)},{\widehat{\sigma }}_z^{\left(3\right)}{\widehat{\sigma }}_z^{\left(2\right)},{\widehat{\sigma }}_x^{\left(2\right)},{\widehat{\sigma }}_z^{\left(2\right)}{\widehat{\sigma }}_z^{\left(1\right)},{\widehat{\sigma }}_x^{\left(1\right)}\right),{\widehat{\sigma }}_z^{\left(1\right)}\right],{\widehat{\sigma }}_z^{\left(3\right)}\right]$$

(27)

The nested commutator has the structure $(X_3,Z_3{Z}_2,X_2,Z_2{Z}_1,X_1)$ traversing the shortest path (directly) between qubit 3 and qubit 1. The alternation between terms requires 5 nestings of commutators with the the Hamiltonian. A nesting of this form is necessary to avoid the whole expression becoming zero. The general feature is that to connect each pair of qubits along the path requires two nested commutators: a ${\widehat{\sigma }}_x^{\left(k\right)}$ term followed by a ${\widehat{\sigma }}_z^{\left(k\right)}{\widehat{\sigma }}_z^{(k+1)}$ term. Therefore, only odd-order terms contribute.

Each commutator in Equation (27) with ${\widehat{\sigma }}_x$ generates a factor of $(-2i)\gamma$ and each commutator with the product ${\widehat{\sigma }}_z{\widehat{\sigma }}_z$ generates a factor of $(-2i)(-\Delta /2)$ so

$${\widehat{G}}_3^{\left(5\right)}={(-2i)}^6{\gamma }^4{(-\Delta /2)}^2{\widehat{\sigma }}_x^{\left(3\right)}{\widehat{\sigma }}_x^{\left(2\right)}{\widehat{\sigma }}_x^{\left(1\right)}.$$

(28)

The norm of the Pauli string is 1. Using (19), we then obtain

$$C_3\left(t\right)\approx \frac{2^4{\pi }^5}{\left(5\right)!}{\left(\frac{\Delta }{\gamma }\right)}^2{\left(\frac{t}{\tau }\right)}^5.$$

(29)

In general, the lowest-order nonzero ${\widehat{G}}_k^{\left(n\right)}$ is proportional to a Pauli string of k${\widehat{\sigma }}_x$ terms, one for each qubit between 1 and k, and $n=2k-1$. The result for the early-time Lieb-Robinson correlation function between the reference qubit 1 and qubit k is given by:

$$C_k\left(t\right)\approx \frac{2^{k+1}{\pi }^{2k-1}}{(2k-1)!}{\left(\frac{\Delta }{\gamma }\right)}^{k-1}{\left(\frac{t}{\tau }\right)}^{2k-1}.$$

(30)

Correlations calculated with Equation (30) yield the solid lines in Figure 3 and Figure 4 and the dots show the values from numerical solution of Equation (11). The numerical calculations include all orders in time, and thus are correct at all times, not just early times, as illustrated in Figure 1. Equation (30) shows the leading order term, which is arbitrarily close to the exact result for early enough times. The excellent agreement between the two seen in Figure 3 and Figure 4 shows that the higher order terms are indeed negligible.

2.3. Asymptotic Behavior

Figure 1, Figure 2, Figure 3 and Figure 4 show the Lieb Robinson correlation $C_k\left(t\right)$ for individual qubits with index k in the linear array as a function of time. Figure 5 shows snapshots of the correlation function, computed from Equation (30), as a function of k at particular times. This lets us see the “correlation wave” propagating from the reference bit down the line. Values of $C_k$ larger than ${10}^{-2}$ are clipped and not shown here because our focus is on early-time behavior for each qubit. At the times shown in the figure, the correlation front decays rapidly in space—faster than an exponential.

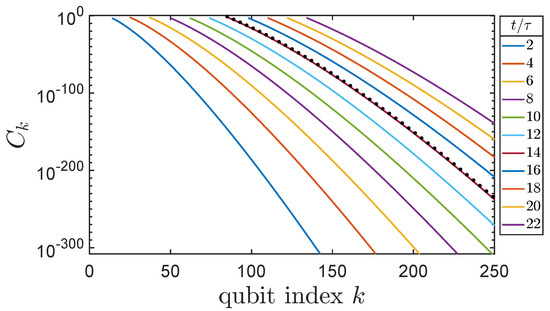
Figure 5. Snapshots of the early-time Lieb-Robinson correlation at different times for a line of qubits as a function of qubit index k. The correlation front propagates down the line and, for the times shown, the shape of the front is attenuated faster than exponentially. The solid lines are the results of Equation (30) with coupling $\Delta /\gamma =1$. The dotted line shows the correlation front at one time evaluated using Equation (31).

We examine the asymptotic shape of the correlation front propagating down the line quantitatively by taking the large k limit of Equation (30). The factorial can then be replaced by Stirlings approximation to obtain

$$C_k\left(t\right)\approx \sqrt{\frac{2}{\pi }}\sqrt{\frac{\gamma }{\Delta }}\frac{1}{\sqrt{k}}{\left(\frac{v_{\mathrm{LR}}}{(k-1/2)}\frac{t}{\tau }\right)}^{2k-1},$$

(31)

where $v_{\mathrm{LR}}$ is the Lieb-Robinson velocity given by

$$v_{\mathrm{LR}}=e\pi \sqrt{\frac{\Delta }{2\gamma }}.$$

(32)

This velocity is expressed in terms of the natural dimensionless time $t/\tau$. In dimensional form it would be $v_{\mathrm{LR}}=(e/\sqrt{2})\sqrt{\Delta \gamma }/\hslash$ qubits/s.

As the value inside the parenthesis in Equation (31) becomes less than one, the value of the correlation function drops precipitously. This occurs at the time t or qubit index k for which $v_{\mathrm{LR}}t/\tau \approx k$, which can be taken as defining the meaning of the velocity.

We can examine how the propagation of the correlation front converges to a constant speed. Let $C_{\mathrm{thresh}}$ be a threshold value of the correlation function and let $t_k/\tau$ be the time at which qubit k crosses that threshold of correlation, so $C_k(t_k/\tau )=C_{\mathrm{thresh}}$. We define the backwards finite-difference velocity of the propagating front by

$$v_k=\frac{1}{t_k/\tau -t_{k-1}/\tau }.$$

(33)

Figure 6 shows this velocity $v_k$ as a function of qubit index down the line. The velocity saturates to the value $v_{\mathrm{LR}}$ given by Equation (32). The line shows values calculated from Equation (30) for $\Delta /\gamma =1$ and $C_{\mathrm{thresh}}={10}^{-25}$. The saturated Lieb-Robinson velocity is then $e\pi /\sqrt{2}\approx 6.04$ in terms of the dimensionless time $t/\tau$. Figure 6 also shows the values of $v_k$ calculated numerically directly from the defining Equation (11).

Figure 6. Velocity saturation to the Lieb-Robinson velocity for the one-dimensional qubit line. The finite-difference velocity defined by Equation (33) is calculated from Equation (30) for for $\Delta /\gamma =1$ and $C_{\mathrm{thresh}}={10}^{-25}$. The values marked by an × are the results of numerical solution of Equation (11).

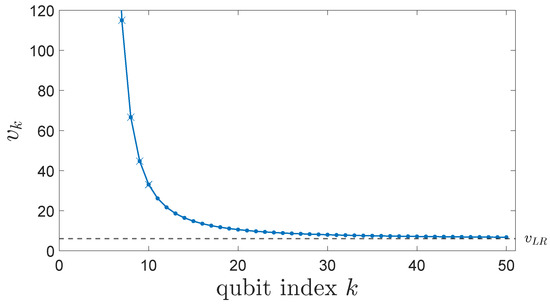
Figure 7 shows the correlation front much farther down the line (qubits with index more than 10,250) and at considerably longer times ($t/\tau$ more than 1360). By this point, the shape of the leading edge of the front is approximately exponential and moving at a steady speed. Taken together, Figure 5 and Figure 7 also illustrate that “early-time” does not refer to small values of $t/\tau$, but rather to the span of time before the quantum correlations between qubit k and the reference qubit 1 become large.

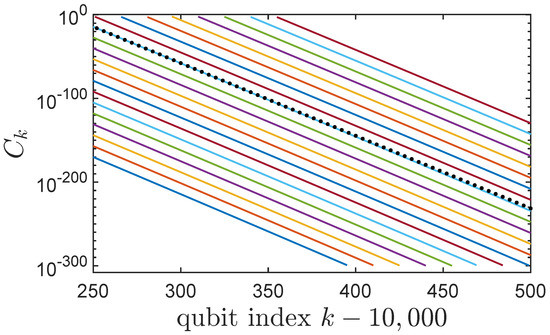
Figure 7. Snapshots of the Lieb-Robinson correlation as in Figure 5, but now for much later times and much farther down the qubit line. Snapshots are shown for even values of $t/\tau$ between 1360 and 1400. Note that the qubit index k is offset by ${10}^4$. By this point the correlation front, calculated from Equation (30), is well-approximated by the exponential dependence of Equation (34) and propagates at the saturated Lieb-Robinson velocity given by Equation (32). The dotted line shows the correlation front at one time evaluated in the limit of very large k using Equation (34).

In the region of the advancing correlation front for very large values of k, Equation (31) can be written:

$$C_k\left(t\right)\approx e\sqrt{\frac{2}{\pi }}\sqrt{\frac{\gamma }{\Delta }}\frac{1}{\sqrt{k}}{e}^{-2\left(k-v_{\mathrm{LR}}t/\tau \right)}$$

(34)

This matches the slope of the lines and the spacing in Figure 7. Comparison with Equation (3) gives precise values for the constants $a,c,d$, and $v_{LR}$ in that expression.

We note that the magnitude of early-time correlations become smaller as the front propagates down the chain because of the $k^{-1/2}$ dependence in Equation (34). This also means the shape of the front differs slightly from a simple $e^{-2k}$ in each snapshot shown in Figure 7. The attenuation of the Lieb-Robinson correlation function was also noted in Ref. [28] for the Heisenberg XXX model with short-range interactions. The $k^{-1/2}$ decay was noted in Ref. [32].

3. Correlation Function for an Arbitrary Qubit Array

The result in Equation (30) can be generalize for any network with arbitrary interaction strengths ${\Delta }_{j,k}$ between qubits j and k. The Hamiltonian for the network is

$$\widehat{H}=-\gamma \sum _k^{N_q}{\widehat{\sigma }}_x^{\left(k\right)}-\frac{1}{2}\sum _{j,k>j}^{N_q}{\Delta }_{j,k}{\widehat{\sigma }}_z^{\left(j\right)}{\widehat{\sigma }}_z^{\left(k\right)}.$$

(35)

Figure 8 shows a network of nine qubits with the strength of the coupling ${\Delta }_{j,k}$ between each indicated. The dots in Figure 9 show the result of numerical calculation of the Lieb-Robinson correlation function between the first qubit and the $k^{th}$ qubit in the array using

$$C_{1,k}\left(t\right)=∥\left[e^{i\frac{\widehat{H}}{\hslash }t}{\widehat{\sigma }}_z^{\left(1\right)}{e}^{-i\frac{\widehat{H}}{\hslash }t},{\widehat{\sigma }}_z^{\left(k\right)}\left(0\right)\right]∥.$$

(36)

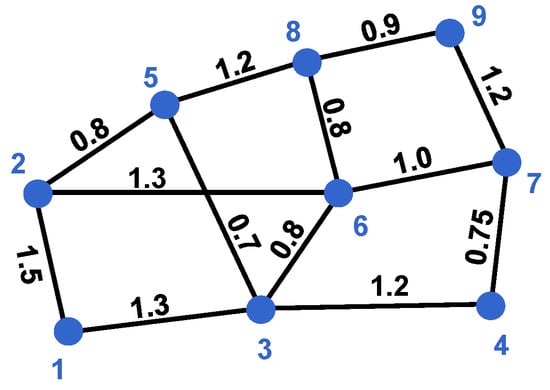
Figure 8. An arbitrary network of qubits with different coupling parameters $\Delta$.

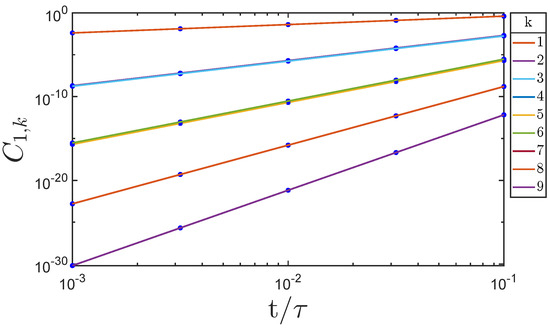
Figure 9. The Lieb-Robinson correlation function for the qubit network shown in Figure 8. $C_{1,k}$ is the correlation between qubit 1 and qubit k. The dots are the result of numerical evaluation of Equation (36) and the lines represent the general analytic result of Equation (38). Results for some values of k nearly overlap: $k=2,$ 3; $k=$ 4, 5, 6; $k=7,$ 8.

The solid lines are the result of the analytic expression derived below.

For the linear array studied in the previous section, there was one shortest path between qubit 1 and qubit k, the direct path along the line, that led to the dominant term in $\widehat{G}$ (Equation (18)). This was seen, for example, in the calculation for $G_3^{\left(5\right)}$ in Equation (27), for which the path was simply $\{1,2,3\}$. We must now generalize this analysis to include more than one path through the network. A path is then a list of indices that begin at qubit j and end at qubit k. The length of a path is the number of edges that connect successive qubits.

For an arbitrary array of interacting qubits, there can be several paths with the same minimum length L that contribute to the leading order early-time correlation function. We denote each minimum-length path by $P_{\alpha }(j,k)$ where $\alpha$ is the index of the particular path. The index of the $m^{th}$ qubit along path $P_{\alpha }(j,k)$ is denoted $q_m^{\alpha }$. The lowest order nonzero operator

$${\widehat{G}}_{j,k}^{(2L+1)}=\left[\left[{\left(\widehat{H}\right)}^{(2L+1)},{\widehat{\sigma }}_z^{\left(j\right)}\right],{\widehat{\sigma }}_z^{\left(k\right)}\right],$$

(37)

then becomes a weighted sum of Pauli strings of ${\widehat{\sigma }}_x$ operators for each qubit traversed in the path. The weights are given by the products of the couplings ${\Delta }_{q_m^{\alpha },q_{m+1}^{\alpha }}$ along the path. We then obtain for the early-time Lieb-Robinson correlation function between qubits j and k

$$C_{j,k}\left(t\right)\approx \frac{2^{L+2}{\pi }^{2L+1}}{(2L+1)!}{\left(\frac{t}{\tau }\right)}^{2L+1}\sqrt{\sum _{P_{\alpha }(j,k)}{\left(\prod _{m=1}^L\frac{{\Delta }_{q_m^{\alpha },q_{m+1}^{\alpha }}}{\gamma }\right)}^2}$$

(38)

where the sum is over all paths with the same minimum length L. Equation (38) makes no assumption about the locality of the coupling $\Delta$ between qubits, which could extend far beyond near-neighbors. Equation (38) reduces to Equation (30) when all the interaction strengths $\Delta$ are the same and connect only near neighbors. In that case, there is just the single minimum path between qubit 1 and qubit k which has length $L=k-1$. The results shown in Figure 9 are in excellent agreement with the numerical calculations.

4. Correlation Function for 2D and 3D Regular Lattices

We consider a two-dimensional square lattice of qubits with uniform near-neighbor coupling.

$$\widehat{H}=-\gamma \sum _{k_x,k_y}{\widehat{\sigma }}_x^{(k_x,k_y)}-\left(\frac{\Delta }{2}\right)\sum _{\stackrel{\mathrm{near}\mathrm{neighbors}}{\stackrel{k_x,k_y}{k_x^{\prime },k_y^{\prime }}}}{\widehat{\sigma }}_z^{(k_x,k_y)}{\widehat{\sigma }}_z^{(k_x^{\prime },k_y^{\prime })}$$

(39)

The qubit indices $k_x$ and $k_y$ go from from $-N$ to $+N$. The reference qubit is at the origin $(k_x,k_y)=(0,0)$. Clearly there is no distinction between positive and negative directions, so the value of the Lieb-Robinson correlation function at a particular qubit depends only on $(n,m)=\left(\right|k_x|,|k_y\left|\right)$. The minimum path length from the origin to $(n,m)$ is simply $m+n$, and the number of paths with that length is $(n+m)!/(n!m!)$. Applying the general result of Equation (38), we obtain for the correlation between the reference qubit at the origin and the $(n,m)$ qubit (in any quadrant):

$$C_{n,m}\left(t\right)\approx \frac{2^{n+m+2}{\pi }^{2(n+m)+1}}{\left(2\right(n+m)+1)!}\sqrt{\frac{(n+m)!}{n!m!}}\times {\left(\frac{\Delta }{\gamma }\right)}^{n+m}{\left(\frac{t}{\tau }\right)}^{2(n+m)+1}.$$

(40)

Figure 10 shown snapshots of isocontours of C evaluated using Equation (40) for several values of $t/\tau$. The Lieb-Robinson correlation front expands outward from the origin. All the minimum-length paths are Manhattan paths, with the most direct route for expanding correlations along the coordinate axes. The correlation function along coordinate axes reduces to the one-dimensional result of Equation (30). (Note that the reference qubit is here indexed $(0,0)$ rather than 1).

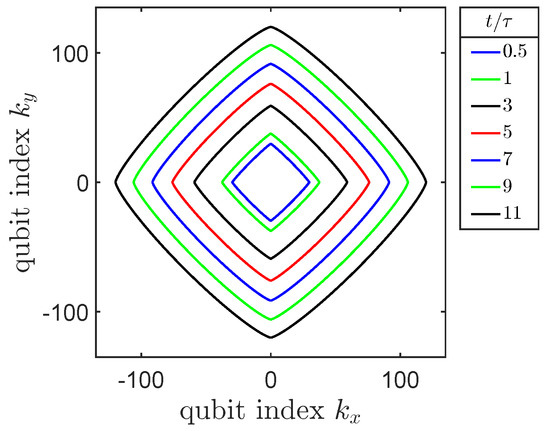
Figure 10. Isocontours of the Lieb-Robinson correlation function for a square two-dimensional array of qubits with near-neighbor coupling. Contours are shown for correlation values of ${10}^{-60}$ at several values of time.

As with the one-dimensional case, the speed of the correlation front motion saturates to the Lieb-Robinson velocity, but for for the square 2D lattice the velocity depends on direction. We can express this in terms of the angle $\theta$ with the x-axis and find:

$$v_{\mathrm{LR}}\left(\theta \right)=e\pi \left(\sqrt{\frac{\Delta }{2\gamma }}\right){\left(\frac{1+tan\left(\theta \right)}{tan{\left(\theta \right)}^{\frac{tan\left(\theta \right)}{tan\left(\theta \right)+1}}}\right)}^{\frac{1}{4}}\left(\frac{\sqrt{1+tan{\left(\theta \right)}^2}}{1+tan\left(\theta \right)}\right).$$

(41)

This expression is valid for $0\le \theta \le \pi /4$; other angles can be deduced by symmetry.

The Lieb-Robinson correlation for a three dimensional square lattice with uniform near-neighbor coupling can similarly obtained from the general result of Equation (38). The correlation function between a qubit at the origin and one with coordinates $(n,m,p)=\left(\right|k_x|,|k_y|,|k_z\left|\right)$ (in any octant) can be written

$$\begin{array}{c}{C}_{n,m,p}\left(t\right)\approx \frac{2^{n+m+p+2}{\pi }^{2(n+m+p)+1}}{\left(2\right(n+m+p)+1)!}\hfill \\ \hfill \times \sqrt{\frac{(n+m+p)!}{m!n!p!}}{\left(\frac{\Delta }{\gamma }\right)}^{(n+m+p)}{\left(\frac{t}{\tau }\right)}^{2(n+m+p)+1}.\end{array}$$

(42)

Figure 11 shows snapshots of the isosurfaces of the Lieb-Robinson correlation function C for three successive times. The influence of the Manhattan paths is clear in the rounded octahedral shape.

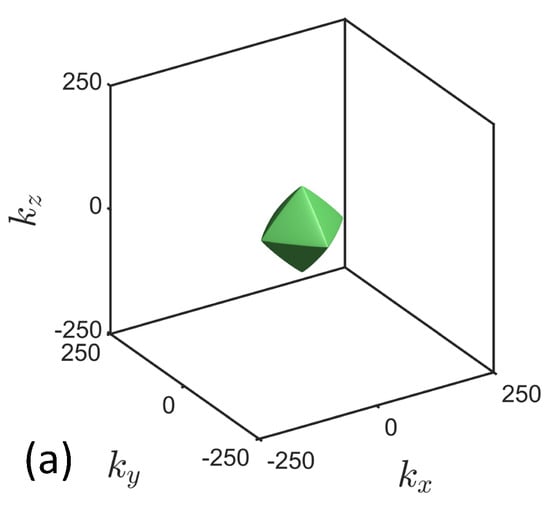
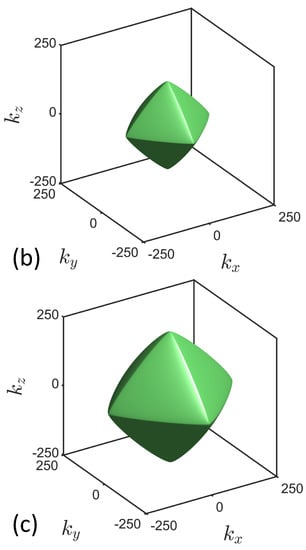
Figure 11. Isosurfaces of the early-time Lieb-Robinson correlation function for a three-dimensional regular square lattice of qubits. The surfaces are shown for near-neighbor coupling $\Delta /\gamma =1$ and $C=1\times {10}^{-170}$ at times (a) $t/\tau =1$, (b) $t/\tau =5$, and (c) $t/\tau =11$.

The direction-dependent Lieb-Robinson velocity for the 3D square lattice is expressed in terms of the polar angle $\varphi$ and azimuthal angle $\theta$:

$$v_{\mathrm{LR}}(\theta ,\varphi )=e\pi \left(\sqrt{\frac{\Delta }{2\gamma }}\right){\left(\frac{P(\theta ,\varphi )}{Q(\theta ,\varphi )}\right)}^{\frac{1}{4}}R(\theta ,\varphi ),$$

(43)

where

$$\begin{array}{c}\hfill P(\theta ,\varphi )=1+tan\left(\theta \right)+\sqrt{\frac{1+tan{\left(\theta \right)}^2}{tan{\left(\varphi \right)}^2}},\end{array}$$

(44)

$$Q(\theta ,\varphi )=tan{\left(\theta \right)}^{\left(\frac{tan\left(\theta \right)}{1+tan\left(\theta \right)+\sqrt{\frac{1+tan{\left(\theta \right)}^2}{tan{\left(\varphi \right)}^2}}}\right)}{\left(\sqrt{\frac{1+tan{\left(\theta \right)}^2}{tan{\left(\varphi \right)}^2}}\right)}^{\frac{\sqrt{\frac{1+tan{\left(\theta \right)}^2}{tan{\left(\varphi \right)}^2}}}{1+tan\left(\theta \right)+\sqrt{\frac{1+tan{\left(\theta \right)}^2}{tan{\left(\varphi \right)}^2}}}},$$

(45)

and

$$R(\theta ,\varphi )=\frac{\sqrt{1+{tan}^2\left(\theta \right)+{tan}^2\left(\varphi \right)+{tan}^2\left(\theta \right){tan}^2\left(\varphi \right)}}{tan\left(\varphi \right)+tan\left(\varphi \right)tan\left(\theta \right)+\sqrt{1+tan{\left(\theta \right)}^2}}.$$

(46)

5. Discussion

Calculating the value of the Lieb-Robinson correlation function itself, rather than a bound, for a specific Hamiltonian illuminates some aspects of the way quantum information propagates. We are able to see how the Lieb-Robinson velocity emerges as the saturation velocity of the correlation fronts propagation. A specific value for this velocity, and its angular dependence, is also obtained for regular lattices. We also see that the leading edge of the correlation front is super-exponential as the propagation starts, and acquires the exponential dependence in the bound of Equation (3) only later.

Equation (38) is the main result of this work and applies to a large class of ZZ-coupled Hamiltionians given by Equation (35) and an arbitrary network topology. We have specialized this result to address the case of regular linear one-dimensional arrays and regular square lattices in two and three dimensions with near-neighbor couplings.

There is some competition between the strength of coupling between qubits and the number of paths through intermediate qubits. However, for early times the cost of adding path length is very high because of the $2L+1$ exponent in the time exponent of Equation (38), and because of the factorial in the denominator. This latter factor also results in the decay of correlations in space as the front propagates outward. This is reflected in the $k^{-1/2}$ factor in Equation (31) for the Ising-coupled qubit line.

The expansion of the correlation is not spherically symmetric, even though it extends over hundreds of qubits; the underlying symmetry of the lattice remains apparent. This is evident in both Figure 10 and Figure 11. A single-particle wavefunction, say initially a gaussian, would expand with a circular or spherical shape on a grid of sites. The behavior we see here is more akin to the group velocity in a semiconductor crystal, or the velocity of sound in such a crystal [33]. Both exhibit the symmetry of the lattice even over macroscopic scales.

Future work could apply the general expression of Equation (38) to cases of longer-range coupling. Here we applied the general result to entanglement propagation on regular grids; this could easily be expanded to other topologies that are not simply connected. Furthermore, the limits on the velocity of propagation could be useful in establishing adiabaticity limits for annealing-based quantum computation.