Symmetries in Generalized Kaprekar’s Routine

Abstract

In this paper, algebraic relations were established that determined the invariance of a transformed number after several transformations. The restrictions that determine the group structure of these relationships were analyzed, as was the case of the Klein group. Parametric $K^r$ functions associated with the existence of cycles were presented, as well as the role of the number of their links in the grouping of numbers in higher-order equivalence classes. For this, we developed a methodology based on binary equivalence relations and the complete parameterization of the Kaprekar routine using Ki functions of parametric transformation.

1. Introduction

The process known as Kaprekar’s routine consists of sorting the digits in a number in descending order. Then, the opposite arrangement takes place, i.e., in ascending order. These two arrangements are subtracted one from another, resulting in an image of the original number. In 1949, Datlatreya Kaprekar [1] showed that when iterating such a process with four-digit numbers, the result was always 6174.

This routine of transformation has always aroused interest among fans of mathematical games [2]. However, additionally, there is important research regarding this routine has taken place among mathematicians specialized in Number Theory. Much of this effort has been directed to determining constants and cycles in various numbering systems and numbers of digits, as well as some aspects of transformation chains such as maximum distances.

Thus, the work of Prichett et al. stands out [3,4]. This group of researchers established the basic functions of numerical transformation. An n-digit is a constant of Kaprekar if and only if that number is a fixed point under Kaprekar’s routine and all numbers are transformed to that number after a finite number of applications of Kaprekar’s transformations. They determined the all one-cycle at base 10 and showed that the only decadic Kaprekar’s constants are 495 and 6174. In 2005, Walden [5] already presented some new results on the Kaprekar’s constant, establishing the unique four-adic, seven-digit and five-adic, nine-digit Kaprekar’s constant and showing that 15, 21, 27 or 33-digit Kaprekar constants do not exist. The work on the Kaprekar’s constant has continued with the interesting contributions of Dolan [6], Prince [7], Hanover [8] and Thakur [9], among others.

In addition to the study of Kaprekar’s constants, the number of transformations necessary to reach the constants or cycles has also been studied. Thus, in a recent work, Yamagami [10] collected data on the number of cycles N (b, n) and their number of links l (b, n) for some bases 2 ≤ b ≤ 15 and numbers of digits 2 ≤ n ≤ 15, many of which were calculated by the author. He noted: “It is very hard to obtain general results on b-adic n-digit Kaprekar loops for all b and n without observing any case-by-case results”. Therefore, he thinks that results with specific n or b values as in the known results above are very valuable to further research. In this article, he considers a case where b = 2 and n = 2. He proves that any two-adic Kaprekar’s constant is the two-adic expression of a product of two suitable Mersenne numbers. He also obtains some formulas for the Kaprekar distances. In 2018, together with Matsui [11], he published other paper on three-adic Kaprekar loops. They obtained the formulas for the number for all three-adic n-digit Kaprekar loops and their lengths in terms of n. Wang and Lu [12] continued Yamagami’s studies and completed them with a general solution. Meanwhile, Devlan and Zang [13] determined the maximum number of iterations required to reach a fixed point in the four-digit process.

The constant 6174 has always been surrounded by a halo of mystery [14]. The exploration of Kaprekar’s constant is a problem that allows for multiple approaches to investigation. This possibility, together with its mysterious nature, explains why it is frequently used as a didactic resource [15]. The discovery of the patterns produced by Kaprekar’s process promotes much excitement and insight into the world of mathematical discovery among students [16].

On the other hand, recent studies have investigated variations of the Kaprekar’s transformation [17,18]. In particular, we highlight the interesting paper of Bajorska-Harapinska et al. [19], which presented and discussed some variations of Kaprekar’s transformation. They were especially interested in the orbits of such transformations. For such, they understood the sets of all iterations of a transformation function on a fixed point. They provided their full description for small numbers and also proved some general properties. In 2021, Stephen et al. [20] already defined generalized α_s-Meir–Keeler contractions in S_b-metric spaces and used them to examine the existence and uniqueness of fixed points.

There is a current of opinion that understands there are important gaps in the understanding of Kaprekar’s process. We are interested in investigating the possible connections with Group Theory. We have not found previous studies on this aspect or on the existing symmetries in the transformation chains. In fact, the verification of this gap in the literature has been the main motivation of our work.

In this work, we approach the study of the transformation in base 10 with generality of the number of digits, and the following questions will be addressed:

–

What are the algebraic relations that must exist between the numbers for their images to coincide after one or several transformations? For example:

○

Why do 83,246,529 and 17,487,561 return the same transformed number?

○

Why do 8,178,382,562 and 4,774,473,809 return the same number after two transformations?

○

Why do 5,068,069 and 3,071,934 return the same number after four transformations?

–

What algebraic structures underpin these symmetries?

–

What is the relation between cycles and the algebraic architecture of the transformation schemes?

2. Design of the Investigation and Methods

Every number has an image through Kaprekar’s routine, and that image is unique. The image of a number is uniquely determined by some parameters α that characterize it (Section 3). All numbers with the same parameters give the same image. This leads to the study of Kaprekar’s routine in parametric terms.

The scheme of parametric transformations can have one or more components. An example can be seen in Scheme 1, corresponding to a 6-digit case with three components. Any component of a scheme is necessarily coalescent and contains a transformation constant (parameters whose image is themselves) or a cycle of 2 or more links. This is due to the uniqueness of the transformation and to the fact that the set of all numerical images is a subset of the multiples of 9 (Section 3). Its cardinal is much smaller than that of the set of reference numbers.

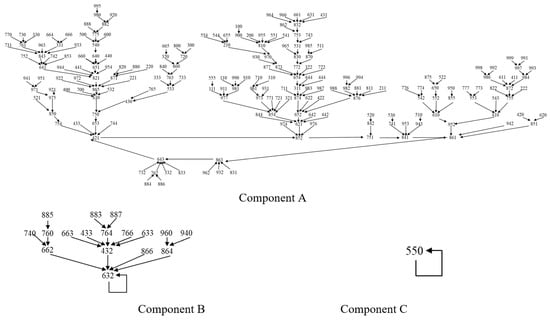
Scheme 1. Parametric transformation schemes in A₆. Each number is a class (α ß γ).

Consequently, invariances necessarily appear: sets of numbers that give the same image after one or more transformations. Or, in a dual way, these can be parameters that give the same parametric image. Our fundamental objective is to find the algebraic relations that determine these invariances, or, in other words, to identify the symmetries algebraically.

For this, we employed binary equivalence relations. These relationships, characterized by their reflexive, symmetric and transitive properties, allow one to establish partitions in a set of numbers (or of the parameters) so that all the elements of a class have the same image. We thus defined a binary equivalence relation R_r of order r as the one that exists between numbers that give the same image after r transformations (Section 7.1). As a result of what has already been said, the relation R₁ is the one that exists between numbers with the same parameters.

However, how can we determine the R₂ and higher relations? For this, we studied and developed the properties of the R_r relations. Among them, we found (33) α₁ R_r α₂ ↔ α′₁ R_r-1 α′₂, with α′ being the parametric image of α. This relationship is methodologically fundamental. It allows one to obtain the higher-order R_r relations from the lower-order ones. For example, R₃ can be obtained from R₂. For this, it is necessary to develop K_i functions of parametric transformation such that Ki (α) = α′ (Section 4). Each of these functions is associated with a permutation that reorders the digits of the transformed number in decreasing order. However, not all permutations are possible; the restriction must be met (3). This leads to a technical difficulty in the development of the functions K_i.

When parametric transformation functions K_i and e_r functions are associated with equivalences, we can algebraically determine higher-order equivalences. If an equivalence R_r is imposed on the images of two parametric classes α₁ and α₂, K_i (α₁) and K_j (α₂), the result will be an algebraic relation between α₁ and α₂ so that α₁ R_{r + 1} α₂. In summary, one of the basic methods used is (51).

(e_r × K_i) (α₁) = K_j (α₂)

Other analogous methods derive from the properties of the R_r developed in Section 7.1.

Another methodological contribution of this work is to show how K_i functions can be used to study constants and cycles.

3. The General Process

Let any number n of w digits n = a₁ a₂ … a_w belong to set A_w ⊂ ℤ, excluding numbers with identical digits. Let numbers of fewer digits be included, as long as they are completed by adding zeros to their left. Let us use the decimal numeral system, so that 0 ≤ a_i ≤ 9, I = 1, … w.

Let O_d be an operator that sorts the digits of a number in descending order:

x = O_d (n) = x₁ x₂ … x_w, x_i ≥ x_{i + 1} and let O_u be another operator which does the opposite: y = O_u (n) = x_w x_w-i … x₁.

Generalized Kaprekar’s routine is formalized through an operator K such that

K (n) = n′ = x − y = O_d (n) − O_u (n)

(1)

For example, if n = 83,246,529, O_d (n) = x = 98,654,322

O_u (n) = y = 22,345,689, n′ = K (n) = x − y = 76,308,633

The iteration of the process r times is represented by

$$K^r\left(\mathrm{n}\right)=K^{r-1}\left[\mathrm{K}\right(\mathrm{n}\left)\right] \mathrm{r}\ge 1$$

agreeing that K⁰ (n) = n and writing K¹ = K for convenience.

In our example, K² (83,246,529) = 84,326,652.

Arranging the digits through O_d allows us to define the following parameters, which result from subtracting the digits in x that are symmetrical compared to the central value.

$$\begin{gathered} {\mathsf{\alpha }}_{}^{\mathrm{s}}={\mathrm{x}}_{\mathrm{s}}-{\mathrm{x}}_{\mathrm{w}-\mathrm{s}+1} 1\le \mathrm{s}\le \mathrm{h}, \mathrm{h}=\mathrm{w}/2 \mathrm{if} \mathrm{w}=\dot{2}, \mathrm{h}=(\mathrm{w}-1)/2, \mathrm{if} \mathrm{w}=\dot{2}+1; 0<{\mathsf{\alpha }}^1\le 9, \\ 0\le {\mathsf{\alpha }}_{}^{\mathrm{s}}\le 9, 2\le \mathrm{s}\le \mathrm{h} \end{gathered}$$

(2)

α^s ≥ α ^{s + 1}, s = 1, … h − 1

(3)

must be verified as a consequence of the arrangements (1) forced by the routine.

Thus, for w = 4, α¹ = x₁ − x₄, α² = x₂ − x₃. For simplicity, these parameters are referred to as α = α¹ and ß = α² in further examples. In a similar way, the same parameters exist in A₅.

As is shown below, parameters α^s uniquely determine the image of a number. Consequently, any number is characterized by their parameters, which are represented as follows:

$$\mathrm{p} \left(\mathrm{n}\right)=({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2 \dots {\mathsf{\alpha }}^{\mathrm{h}})=\mathsf{\alpha }, \mathrm{n} \in {\mathrm{A}}_{\mathrm{w}}$$

When the situation is unambiguous, such parameters are written together as a number of h digits.

The transformation functions are the following:

(1) 

If 0 < α^s ≤ 9, s = 1, 2, … h

(1.1) 

w =$\dot{\mathbf{2}}$, h = w/2

f₁ (α¹ α² … α^h) = (x₁-x_w x₂-x_w-1 … x_w-1-x₂ x_w-x₁) = (α¹ α² … α^h -α^h …-α² -α¹) =
(α¹ α² … α^{h − 1} α^h − 1 9 − α^h 9 − α^h−1 9 − α² 10 − α¹)

(4)

So, for 6-digit numbers (w = 6)

f₁ (α¹ α² α³) = (α¹ α² α³ − 1 9 − α³ 9 − α² 10 − α¹)

which can be written as follows to avoid using superscripts:

f₁ (α ß γ) = (α ß γ−1 9−γ 9−ß 10−α), α = α¹ > 0, ß = α² > 0, γ = α³ > 0

For instance, what is the image of 631,764?

O_d (631,764) = 766,431, α = 7-1 = 6, ß = 6-3 = 3, γ = 6 − 4 = 2

p (631,764) = 632, f₁ (632) = 631,764

K (631,764) = 631,764

Apparently, this number transforms into itself. It is a transformation or balance constant in A₆.

However, note that any number with these same parameters will yield the same image n_E. For example, m = 632,000, p (m) = 632, m′ = K (m) = n_E.

Any permutation P of the digits in

(6 + a 3 + b 2 + c a b c), 0 ≤ a ≤ 3, 0 ≤ b ≤ 6, 0 ≤ c ≤ 7, a ≥ b ≥ c, a > c

will become n_E, K [P (6 + a 3 + b 2 + c a b c)] = 631,764 = n_E.

Digits a′_s in those numbers transformed by f₁ must satisfy the following restrictions:

$$\begin{gathered} {\sum }_{\mathrm{s}=1}^{\mathrm{w}} {{\mathrm{a}}^{\prime }}_{\mathrm{s}}=\dot{9}\to \mathrm{K}(\mathrm{n})=\dot{9}; {{\mathrm{a}}^{\prime }}_1+{{\mathrm{a}}^{\prime }}_{\mathrm{w}}=10; {{\mathrm{a}}^{\prime }}_{\mathrm{s}}+{{\mathrm{a}}^{\prime }}_{\mathrm{w}-\mathrm{s}+1}=9, 1<\mathrm{s}<\mathrm{h} \\ {{\mathrm{a}}^{\prime }}_{\mathrm{h}}+{{\mathrm{a}}^{\prime }}_{\mathrm{h}+1}=8 \end{gathered}$$

(5)

In the case of A₆: a′₁ + a′₆ = 10, a′₂ + a′₅ = 9, a′₃ + a′₄ = 8, ${\sum }_{\mathrm{s}=1}^6$ a_s = 27

(1.2) 

w =$\dot{\mathbf{2}}$+ 1, h = (w − 1)/2

In this case, function f₁ is similar to the last one, but it includes a 9 as a central digit in the transformed number

f₁ (α¹ α² … α^h) = (α¹ α² … α^h−1 α^h − 1 9 9 − α^h 9 − α^h−1… 9 − α² 10 − α¹)

(6)

For instance, the image of a telephone number

n = 34,326,714,825 would be

O_d = 87,654,433,221, α¹ = 7, α² = 5, α³ = 4, α⁴ = 2, α⁵ = 1

f₁ (75,421) = (7 5 4 2 1 – 1 9 9 − 1 9 − 2 9 − 4 9 − 5 10 − 7) = 75,420,987,543

Notably, for seven-digit numbers

f₁ (α ß γ) = (α ß γ − 1 9 9 − γ 9 − ß 10 − α)

The digits in the transformed number must satisfy

$$\begin{gathered} {\sum }_{\mathrm{s}=1}^{\mathrm{w}} {{\mathrm{a}}^{\prime }}_{\mathrm{s}}=\dot{9}\to \mathrm{K}(\mathrm{n})=\dot{9}; {{\mathrm{a}}^{\prime }}_1+{{\mathrm{a}}^{\prime }}_{\mathrm{w}}=10; {{\mathrm{a}}^{\prime }}_{\mathrm{s}}+{{\mathrm{a}}^{\prime }}_{\mathrm{w}-\mathrm{s}+1}=9, 1<\mathrm{s}<\mathrm{h} \\ {\mathrm{a}}_{\mathrm{h}}+{\mathrm{a}}_{\mathrm{w}-\mathrm{h}+1}=8, {\mathrm{a}}_{\mathrm{h}-1}=9 \end{gathered}$$

(7)

(2) 

If 0 < α^s ≤ 9, 1 ≤ s<r and α^s = 0, s ≥ r (r > 2)

(2.1) 

w =$\dot{\mathbf{2}}$, h = w/2

Basic function f₂ is similar to (4) but adding v = 2 (h + 1 − r) digits 9 to the middle part (two nines per null parameter):

$${\mathrm{f}}_2 ({\mathsf{\alpha }}^1 \dots {\mathsf{\alpha }}^{\mathrm{r}-1} 0 0\dots 0)=({\mathsf{\alpha }}^1 \dots {\mathsf{\alpha }}^{\mathrm{r}-2}{ }^{ }{\mathsf{\alpha }}^{\mathrm{r}-1}-1 9 \begin{array}{c}\mathrm{v}\\ \breve{\dots \dots }\\ \end{array} 9 9-{\mathsf{\alpha }}^{\mathrm{r}-1} 9-{\mathsf{\alpha }}^{\mathrm{r}-2}\dots 9-{\mathsf{\alpha }}^2 10-{\mathsf{\alpha }}^1)$$

(8)

thus satisfying the conditions

$${\sum }_{\mathrm{s}=1}^{\mathrm{w}} {{\mathrm{a}}^{\prime }}_{\mathrm{s}}=\dot{9}\to \mathrm{K}(\mathrm{n})=\dot{9}; {{\mathrm{a}}^{\prime }}_1+{{\mathrm{a}}^{\prime }}_{\mathrm{w}}=10; {{\mathrm{a}}^{\prime }}_{\mathrm{s}}+{{\mathrm{a}}^{\prime }}_{\mathrm{w}-\mathrm{s}+1}=9, 2\le \mathrm{s}\le \mathrm{r}-2$$

(9)

a′_r-1 + a′_{w-r + 2} = 8, a′_r = a′_{r + 1} = … = a′_{w-s + 1} = 9

Specifically, for A₆

f₂ (α ß 0) = (α ß-1 9 9 9-ß 10-α)

$$\sum {{\mathrm{a}}^{\prime }}_{\mathrm{s}}=36\to \mathrm{K}(\mathrm{n})=\dot{9}; {{\mathrm{a}}^{\prime }}_1+{{\mathrm{a}}^{\prime }}_6=10; {{\mathrm{a}}^{\prime }}_2+{{\mathrm{a}}^{\prime }}_5=8, {{\mathrm{a}}^{\prime }}_3={{\mathrm{a}}^{\prime }}_4=9$$

For example, let n = 549,945 have the image

O_d (n) = 995,544, p (n) = 550, f₂ (550) = 549,945, the original number itself. This is another constant in A₆.

(2.2) 

w =$\dot{\mathbf{2}}$+ 1, h = (w − 1)/2

Function f₂ is similar to the last one but adds an extra 9 as a middle digit in the transformed number:

$${\mathrm{f}}_2({\mathsf{\alpha }}^1\dots {\mathsf{\alpha }}^{\mathrm{r}-1} 0 0\dots 0)=({\mathsf{\alpha }}^1\dots {\mathsf{\alpha }}^{\mathrm{r}-2} {\mathsf{\alpha }}^{\mathrm{r}-1} -1 9\begin{array}{c}\mathrm{v}+1\\ \breve{\dots \dots }\\ \end{array}9 9-{\mathsf{\alpha }}^{\mathrm{r}-1} 9-{\mathsf{\alpha }}^{\mathrm{r}-2} \dots 9-{\mathsf{\alpha }}^2 10 -{\mathsf{\alpha }}^1)$$

(10)

adding to conditions (5), a′_{h + 1} = 9

(11)

For A₇ and γ = 0, the result is

f₂ (α ß 0) = (α ß-1 9 9 9 9-ß 10-α) with

a′₁ + a′₇ = 10, a′₂ + a′₆ = 8, a′₃ = a′₄ = a′₅ = 9

(3) 

If 0 < α¹ ≤ 9 and α^s = 0, s ≥ 2

$${\mathrm{f}}_3 ({\mathsf{\alpha }}^1 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0)=({\mathsf{\alpha }}^1-1 9 \begin{array}{c}\mathrm{w}-2\\ \breve{\dots \dots }\\ \end{array} 9 10-{\mathsf{\alpha }}^1)$$

(12)

which implies the following restrictions for the transformed numbers

a′₁ + a′_w= 9, a′₂ = … = a′_{w − 1} = 9

(13)

These two expressions are valid both for even and odd numbers of digits.

For A₆, the result is

f₃ (α 0 0) = (α − 1 9 9 9 9 10 − α)

and for A₇

f₃ (α 0 0) = (α − 1 9 9 9 9 9 10 − α)

Functions f₁, f₂ and f₃ are similar to the ones developed by (4). These functions are an epimorphism of A_W in B_W ⊂ A_W, which comprises those multiples of 9 that verify some requirement (5a.1), (5b.1) or (6.1) and that have anti images.

4. Parametric Functions

The previous development returns

p (m) = p (n) ↔ K (m) = K (n)

(14)

which suggests the transformation process should be analyzed in parametric terms. To this end, it is necessary to know the parameters of the transformed numbers.

One of the questions in the introduction is thus answered. Both numbers 83,246,529 and 17,487,561 return the same number after their transformations because both have the same parameters (7631).

Let us specify the notation used so far:

–

K, in a broad sense, refers to the transformation. Its argument is a number and its image is the transformed number K (n) = n′.

–

f_i is used in a specific sense. It acts upon parameters and yields the numerical image of all numbers whose parameters are those specified.

p (n) = α, f_i (α) = n′, α = α¹ α² …α^h

–

K can also be used broadly, by extension, to mean the parameters of some transformed number, thus transforming parameters into parameters:

K (α) = α′, α′ = p (n′)

This is the biggest problem in transformations. The digits in the transformed number are not necessarily arranged, so it is not possible to determine its parameters right away. Thus, operators O_d and O_u, which establish a permutation P_i that sorts the digits, must operate. O_d (n′) = P_i (n′). If P_i is identified, then α′ is directly discovered. A specific function K_i (α) = α′ can therefore be associated with each permutation P_i.

This is a tedious process, since the possible permutations will grow factorially as the number of digits increases:

–

With w =2 and w = 3, there are just two functions K_i (α);

–

With w = 4 and w = 5, there are 11 functions K_i (α ß) and 2 functions K_i (α 0);

–

With w = 6 and w = 7, there are two functions K_i (α 0 0), 11 functions K_i (α ß 0) and 117 functions K_i (α ß γ);

–

With w and w + 1 digits, the number of functions K_i (α¹ α² …α^s … α^h), α_s > 0, s = 1, … h approaches w!/h! by default. This is because in O_d (n′), a permutation with α^r-s to the left of α^r is, under (3), only possible if α^r = α^{r − s}.

Let us see some examples of these functions.

(1) 

Functions K_i based on (4)

w =$\dot{\mathbf{2}}$, h = w/2, f₁(α) defined in (4) and P₁ (1 2 3 …w)

P₁ is defined as the digit arrangement described in (4).

K₁(α) = [α¹ − (10 − α¹) α² − (9 − α²) … α^{h − 1} − (9 − α^h−1) α^h − 1 − (9 − α^h)] =
[2α¹ − 10 2α² − 9 … 2α^{h − 1} − 9 2α^h − 10]

(15)

The domain of existence of this function K₁ (α) = α′ is determined by the restrictions imposed by O_d (n′), with the digits being sorted in descending order (1) in permutation P₁

α¹ ≥ α², …, α^h – 1 ≥ 9 – α^h, 9 – α^h ≥ 9-α^h−1, …, 9 – α³ ≥ 9 – α², 9 – α² ≥ 10 – α¹

which implies α^h ≥ 5, and under (3), α^s ≥5, s ≥ 1, y α¹ ≥ α² + 1

Briefly, the existence conditions for K₁ (α) are

$$\mathrm{w}=\dot{2}; 5<{\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; 5\le {\mathsf{\alpha }}^{\mathrm{s}}\le 9, \mathrm{s}\ge 2$$

(16)

For instance,

n = 181,771,978,221, w = 12, h = 6, p(n) = 877,655 = α, which satisfies (16);

K₁ (877,655) = 655,310 and indeed, f₁(n) = 877,654,443,222 = n′, p(n′) = 655,310 = α′.

Note that this α′ does not satisfy (16), so it cannot be transformed through K₁. We need a function K_i based on (8), with α^h = α⁶ = 0 (see (27) in the last case in Section (3).

w =$\dot{\mathbf{2}}$, h = w/2, f₁ (α) defined in (4) and P₂ (h + 1 …w 1 2 … h)

O_d (n′) = (9-α^h 9 − α^h−1 … 9 − α² 10 − α¹ α¹ α² … α^{h − 1} α^h − 1)

K₂ (α) = (10 − 2α^h 9 − 2α^h−1 … 9 − 2α² 10-2α¹)

$$\mathrm{w}=\dot{2}; 0<{\mathsf{\alpha }}^1\le 5; {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; 0<{\mathsf{\alpha }}^{\mathrm{s}}\le 4, \mathrm{s}=2\dots \mathrm{h}, 2{\mathsf{\alpha }}^{\mathrm{h}}\le 2{\mathsf{\alpha }}^{\mathrm{h}-1}+1$$

(17)

For instance, in A₆

K₂ (541) = 810

w =$\dot{\mathbf{2}}$, h = w/2 and P₃ (h + 1 1 h + 2…w 2 3… h) in (4)

O_d (n′) = (9-α^h α¹ 9-α^h−1 9-α^h−2 … 9-α³ 9-α² 10-α¹ α² … α^h−1 α^h-1)

K₃ (α) = (10-2α^h α¹-α^h−1 9- α^h−1- α^h−2 … 9- α³-α² α¹- α²-1)

$$\mathrm{w}=\dot{2}; \mathrm{h}=\mathrm{w}/2; 1\le {\mathsf{\alpha }}^1+{\mathsf{\alpha }}^2\le 10; {\mathsf{\alpha }}^{\mathrm{s}}+{\mathsf{\alpha }}^{\mathrm{s}+1}\le 9, \mathrm{s}=2, 3,\dots \mathrm{h}-2; {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; {\mathsf{\alpha }}^1+{\mathsf{\alpha }}^{\mathrm{h}-1}\ge 9; {\mathsf{\alpha }}^1+{\mathsf{\alpha }}^{\mathrm{h}}\le 9;$$

α^h ≤ 10+ α^h−1 -2α^h; 1 ≤ α^h ≤ 4

(18)

This is an important function that generates a family of transformation constants.

(2) 

Functions K_i based on (6)

The permutations refer to the digits to the right of 9 in (6)

w =$\dot{\mathbf{2}}$+ 1, h = (w-1)/2, f₁ (α) defined in (6) and P₁

O_d (n′) = (9 α^l α² … α^{h − 1} α^h-1 9-α^h 9-α^{h − 1} … 9-α² 10-α^l)

The presence of a 9 completely changes function K₁

K₁ (α) = (α¹-1 α¹+ α²-9 α²+ α³-9 … α^{h − 1}+ α^h-9)

(19)

with the existence conditions

$$\mathrm{w}=\dot{2}+1, 5<{\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; 5\le {\mathsf{\alpha }}^{\mathrm{s}}\le 8, \mathrm{s}>1; {\mathsf{\alpha }}^{\mathrm{s}}+{\mathsf{\alpha }}^{\mathrm{s}+1}\ge 9, \mathrm{s}=1,\dots \mathrm{h}-1$$

(20)

For example, n = 8,650,000, p (n) = 865 = α

n′ = f₁ (n) = 8,649,432, O_d (n′) = 9,864,432, p (n′) = 752 = α′

α = 865 satisfies the conditions (20) and, in fact,

K₁ (α) = (8-1 8 + 6-9 6 + 5-9) = 752

w =$\dot{\mathbf{2}}$+ 1, h = (w-1)/2, and P₂ in (6)

O_d (n′) = (9 9-α^h 9-α^h−1 … 9-α² 10-α^l α^l α^{2 …} α^h−1 α^h-1)

K₂ (α) = (10-α^h 9-α^h- α^h−1 … 9-α³- α² 9- α²-α^l)

(21)

$$\mathrm{w}=\dot{2}+1, \mathrm{h}=(\mathrm{w}-1)/2; 0<{\mathsf{\alpha }}^1\le 5; {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1; {\mathsf{\alpha }}^{\mathrm{s}+1}+{\mathsf{\alpha }}^{\mathrm{s}}\le 9, \mathrm{s}=1,2,\dots \mathrm{h}-1$$

α^h−1 ≥ 1, 1 < α^h < 5

For example, n = 2,515,324 p(n) = 432

w = 7, h = 3 por (6), n′ = f₁ (n) = 4,319,766, p (n′) = 842

and in fact, since 432 satisfies the existence conditions of K₂

K₂ (432) = (10-2 9-2-3 9-3-4) = 842

w =$\dot{\mathbf{2}}$+ 1, h = (w-1)/2 ≥ 4, P₄ (1 h + 2 2 h + 3 … h + s 3 4 … s 2 h 2 h + 1 h), s = h-1 en (6)

O_d (n′) = (9 α¹ 9-α^h α² 9-α^h−1 … 9-α³ α³ … α^h−1 9-α² 10-α¹ α^h-1)

K₄(α) = (10-α^h 2α¹-10 α²-α^h α²-α^h−1 9-α^h−2-α^h−1 … 9-α⁴-α³)

(22)

h ≥ 4; 9 ≤ α¹ + α^h ≤ 11, α² + α^h ≤ 9, α² + α^h−1 ≥ 9, α³ ≤ 4

For example, in w = 15, h = 7

f₁ (α) = (α¹ α² … α⁶ α⁷-1 9 9-α⁷ 9-α⁶ … 9-α² 10-α¹) = n′

O_d (n′) = (9 α¹ 9-α⁷ α² 9-α⁶ … 9-α³ α³ … α⁶ 9- α² 10-α¹ α⁷-1)

K₄ (α) = (10- α⁷ 2α¹-10 α²-α⁷ α²-α⁶ 9-α⁵-α⁶ 9- α⁴-α⁵ 9-α³-α⁴)

K₄ (8,643,332) = 8,643,332; therefore, this number is a parametric constant in w = 15, with the numeric constant of 15 digits, 864,333,197,666,532.

Similarly, for nine digits

K₄ (α ß γ δ) = (10-δ 2α-10 ß-δ ß- γ), K₄ (8642) = 8642, which is a parametric constant in A₈.

K₄ (α), defined in a general way at w = $\dot{2}$ + 1, is an important parametric function from which one-cycles derive.

(3) 

Functions K_i based on (8)

Functions K_i based on (8), h = w/2 are complex, as they depend on the number of null parameters compared to the number of non-null parameters. If r ≤ 1 + h/2, α^r = 0, then the functions’ structure remains, since (8) provides as many nines as it provides varying digits. If there are more non-null than null parameters, r > 1 + h/2, then functions K_i will vary with each r increment.

Let us see some examples:

–

w = $\dot{\mathbf{2}}$, r ≤ 1 + h/2, α³ = 0, h ≥ 4 in (8) and P₁

$${\mathrm{n}}^{\prime }={\mathrm{f}}_2 ({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0)=({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2-1 9 \begin{array}{c}\mathrm{w}-4\\ \breve{\dots \dots }\\ \end{array} 9 9-{\mathsf{\alpha }}^2 10-{\mathsf{\alpha }}^1)$$

If permutation P₁ (1234) is used to the right of numbers 9 in O_d (n′)

$${\mathrm{O}}_{\mathrm{d}} ({\mathrm{n}}^{\prime })=(9 \begin{array}{c}\mathrm{w}-4\\ \breve{\dots \dots }\\ \end{array} 9 {\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2-1 9-{\mathsf{\alpha }}^2 10-{\mathsf{\alpha }}^1)$$

the associated function is

$$\begin{gathered} {\mathrm{K}}_{21} ({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0)=({\mathsf{\alpha }}^1-1 {\mathsf{\alpha }}^2 10-{\mathsf{\alpha }}^2 9-{\mathsf{\alpha }}^1 0 \begin{array}{c}\mathrm{h}-4\\ \breve{\dots \dots }\\ \end{array} 0), 6 \le {\mathsf{\alpha }}^1\le 9, \\ 5\le {\mathsf{\alpha }}^2\le 9, {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1 \end{gathered}$$

(23)

For example: K₂₁ (85,000) = 75,510

–

w =$\dot{\mathbf{2}}$, r ≥ 1 + h/2, α³ = 0, h = 3 in (8) and P₁

n′ = f₂ (α¹ α² 0) = (α¹ α²-1 9 9 9-α² 10-α¹)

O_d (n′) = (9 9 α¹ α²-1 9-α² 10-α¹)

K₂₂ (α¹ α² 0) = (α¹-1 α² α¹-α² + 1), 6 ≤ α¹ ≤ 9, 5 ≤ α² ≤ 9, α¹ ≥ α² + 1, 2α² ≥ α¹ + 1

(24)

a function which differs from (23)

For example: K₂₂ (850) = 754

–

w =$\dot{\mathbf{2}}$, r ≤ 1 + h/2, α³ = 0, h ≥ 4 in (8), P₂ (1423)

$$\begin{gathered} {\mathrm{O}}_{\mathrm{d}} ({\mathrm{n}}^{\prime })=(9 \begin{array}{c}\mathrm{w}-4\\ \breve{\dots \dots }\\ \end{array} 9 {\mathsf{\alpha }}^1 10-{\mathsf{\alpha }}^1{\mathsf{\alpha }}^2-1 9-{\mathsf{\alpha }}^2){\mathrm{K}}_{23}({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0)=({\mathsf{\alpha }}^{2}10-{\mathsf{\alpha }}^2{\mathsf{\alpha }}^1-1 9-{\mathsf{\alpha }}^1 0 \begin{array}{c}\mathrm{h}-4\\ \breve{\dots \dots }\\ \end{array} 0), \\ 5\le {\mathsf{\alpha }}^1\le 9, 5\le {\mathsf{\alpha }}^2\le 9, {\mathsf{\alpha }}^1+{\mathsf{\alpha }}^2\le 11 \end{gathered}$$

(25)

For example: K₂₃ (5500) = 5544

–

w =$\dot{\mathbf{2}}$, r > 1 + h/2, α³ = 0, h = 3 in (8), P₂

O_d (n′) = (9 9 α¹ 10-α¹ α²-1 9-α²)

K₂₄ (α¹ α² 0) = (α² 10-α² 2α¹-10), 5 ≤ α¹ ≤ 9, 5 ≤ α² ≤ 9, α¹ + α² ≤ 11

(26)

which only operates on parameters (550) and (650).

With r ≤ 1 + h/2, functions differ from those with r >1 + h/2

–

w = $\dot{\mathbf{2}}$, α^h = 0, h = w/2 = 6 in(8), P₃ = (6 1 7 2 3 8 9 10 4 5)

As an example of applying (15), we found:

n′ = 877,654,443,222, α′ = p (n′) = 655,310. Such α′ cannot be transformed with K₁. It is a case w = 12, h = 6, α⁶ = 0 which can be transformed with the function

K₂₅ (α ß γ δ ε 0) = (10- ε 9-δ α-ε-1 α + ß-9 γ-δ ß-γ),

α >1, α ≥ ß + 1, α + ß ≥ 9, 9 ≤ α+ δ ≤ 10, α + ε ≤ 9

α + δ-ε ≤ 10, ß + δ ≤ 9, ß + ε ≤ 8, 2γ ≥ ß + δ, γ ≥ 5, δ ≥ ε + 1, α + ß + δ-γ ≥ 9, ε ≥ 1

(27)

This function is associated with the aforementioned permutation P₃, in a specific case of (8)

f₂ (α ß γ δ ε 0) = (α ß γ δ ε -1 9 9 9-ε 9-δ 9-γ 9-ß 10-α),

f₂ (655,310) = 655,309,986,444, K₂₅ (655,310) = 964,220

(4) 

Functions K_i based on (10)

As previously stated, when the number of digits is odd, w = $\dot{2}$ + 1, h = (w-1)/2, function f₂ is similar to the one corresponding for numbers with w = $\dot{2}$, but it includes one more 9 as a middle digit in the transformed number.

Such an addition does not alter functions K_i if r ≤ 1 + h/2, α^r = 0, although it does change the last parameters of α′ if r > 1 + h/2.

In parallel with the cases considered in (3):

–

α³ = 0, w = 7, h = 3 in (10) and P₁ (1234)

K₂₆ (α¹ α² 0) = (α¹-1 α² 10- α²), 5 ≤ α¹ ≤ 9, 5 ≤ α² ≤ 9, α¹ ≥ α² + 1

(28)

a closer function to K₂₁ than to K₂₂

–

α³ = 0, w = 7, h = 3 in (10) and P₂ (1423)

K₂₇ (α¹ α² 0) = (α² 10- α² α¹-1), 5 ≤ α¹ ≤ 9, 5 ≤ α² ≤ 9, α¹ + α² ≤ 11

(29)

which is also a closer expression to K₂₃ than to K₂₄

(5) 

Functions K_i based on (12)

There are only two functions Ki based on (12):

$${\mathrm{K}}_{31} (\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0)=(\mathsf{\alpha }-1 10-\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0), 6 \le {\mathsf{\alpha }}^{ }\le 9$$

(30)

$${\mathrm{K}}_{32} (\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0)=(10-\mathsf{\alpha } \mathsf{\alpha }-1 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0), 0 \le {\mathsf{\alpha }}^{ }\le 5$$

(31)

valid both for w = $\dot{2}$ with h = w/2 and for w = $\dot{2}$ + 1 with h = (w-1)/2

Table 1 and Table 2 show some functions K_i of the different types in A₆ (w = 6) and A₇ (w = 7).

Table 1. Some functions K_i in A₆, w = 6, h = 3.

Permutation O (n′)	Associated Ki (α)	Domain of Existence
P1 (123,456)	K1 (α ß γ) = (2α-10 2ß-9 2γ-10)	6 ≤ α ≤ 9, 5 ≤ ß ≤ 9, 5 ≤ γ ≤ 9, α ≥ ß + 1
P2 (456,123)	K2 (α ß γ) = (10-2γ 9-2ß 10-2α)	0 < α ≤5, 0 < ß ≤ 4, 0 < γ ≤ 4, α ≥ ß + 1, 2γ ≤ 2ß + 1
P3 (415,623)	K3 (α ß γ) = (10-2γ α-ß α-ß-1)	9 ≤ α+ ß ≤ 10, α ≥ ß + 1, 1 ≤ γ ≤ 4 α + γ ≤ 9, α ≤ 10 + ß-2γ
P4 (142,563)	K4 (α ß γ) = (α-γ + 1 α-γ-1 2ß-9)	5 ≤ α ≤ 9, 5 ≤ ß ≤ 8, 1 ≤ γ ≤ 6 α ≥ ß + 1, 9 ≤ α + γ ≤ 11, α ≥ 2ß + γ-8
P5 (145,263)	K5 (α ß γ) = (α-γ + 1 α-γ-1 9-2ß)	6 ≤ α ≤ 9, 1 ≤ ß ≤ 4, α+ ß ≥ 10 9 ≤ α+ γ ≤ 11, α ≥ 10-2ß + γ
P6 (412,563)	K6 (α ß γ) = (10-2γ 2α-10 2ß-9)	6 ≤ α ≤ 9, 5 ≤ ß ≤ 9, 1 ≤ γ ≤ 3 α ≥ß + 1, α + γ ≤ 9
P7 (124,536)	K7 (α ß γ) = (2α-10 ß-γ + 1 ß-γ)	6 ≤ α ≤ 9, 5 ≤ ß ≤ 8, 2 ≤ γ ≤ 5 α + γ ≥ 11, 9 ≤ ß+ γ ≤ 10, 2α ≥ 11+ ß − γ
P8 (124,563)	K8 (α ß γ) = (α-γ + 1 α + ß-10 ß-γ)	6 ≤ α ≤ 9, 5 ≤ ß ≤ 8, 1 ≤ γ ≤ 5 α ≥ ß + 1, α+ ß ≥10, 10 ≤ α+ γ ≤11, 9 ≤ ß + γ ≤ 11
P9 (612,453)	K9 (α ß γ) = (11-α- γ α + ß-9 ß + γ-9)	α = 5, ß = 5 γ = 4
P1 (1234)	K22 (α ß 0) = (α-1 ß α-ß + 1)	6 ≤ α ≤ 9, 5 ≤ ß ≤ 9, α ≥ ß + 1, 2ß ≥ α + 1
P2 (1423)	K24 (α ß 0) = (ß 10- ß 2α-10)	5 ≤ α ≤ 9, 5 ≤ ß ≤ 9, α + ß ≤ 11
P1 (12)	K31 (α 0 0) = (α-1 10-α 0)	6 ≤ α ≤ 9
P2 (21)	K32 (α 0 0) = (10-α α-1 0)	0 ≤ α ≤ 5

Table 2. Some functions K_i in A₇, w = 7, h = 3.

Permutation (*)	Associated Ki (α)	Domain of Existence
P1 (123,456)	K1 (α ß γ) = (α-1 α + ß-9 ß + γ-9)	α ≥ ß + 1, γ ≥ 5
P4 (142,563)	K4 (α ß γ) = (10-γ 2α-10 ß-γ)	α ≥ ß + 1, 9 ≤ α + γ ≤ 11, ß ≥ 5, ß + γ ≤ 9
P5 (145,263)	K5 (α ß γ) = (10-γ 2α-10 9-ß-γ)	α + ß ≥ 10, ß ≤ 4, 9 ≤ α + γ ≤ 11
P6 (412,563)	K6 (α ß γ) = (10-γ α- γ-1 α + ß-9)	α ≥ ß + 1, ß ≥ 5, α + γ ≤ 9
P7 (124,536)	K7 (α ß γ) = (α-1 α- γ + 1 2ß-9)	α + γ ≥ 11, 9 ≤ ß + γ ≤ 10
P10 (123,465)	K10 (α ß γ) = (ß 2α-10 ß+γ-9)	α ≥ γ + 1, α ≤ ß + 1, γ ≥ 5
P11 (451,623)	K11 (α ß γ) = (10-γ 9-γ-ß α-ß-1)	α ≥ 5, α + ß ≤ 9
P12 (145,236)	K12 (α ß γ) = (α-1 α- γ + 1 9-ß-γ)	α + γ ≥ 11, ß ≤ 4
P13 (124,365)	K13 (α ß γ) = (ß 2α-10 ß-γ + 1)	α ≤ ß + 1, α + γ ≥ 11, γ ≤ 5
P22 (1234)	K22 (α ß 0) = (α-1 ß 10-ß)	α ≥ ß + 1, ß ≥ 5
P23 (1243)	K23 (α ß 0) = (ß α-1 10-ß)	α ≤ ß + 1, α + ß ≤ 11
P25 (1324)	K25 (α ß 0) = (α-1 10-ß ß)	α + ß ≤ 11, ß ≤ 5
P26 (1342)	K26 (α ß 0) = (10-ß α-1 ß)	α ≥ ß + 1, 9 ≤ α + ß ≤ 11
P27 (3142)	K27 (α ß 0) = (10-ß α-1 9- α)	α ≥ 5, α + ß ≤ 9
P31 (12)	K31 (α 0 0) = (α-1 10-α 0)	6 ≤ α ≤ 9
P32 (21)	K32 (α 0 0) = (10-α α-1 0)	1 ≤ α ≤ 5

* Permutation of O (n′), excluding fixed nines. Thus, P₁ (9 α ß γ-1 9-γ 9-ß 10-α), P₂₂ = (9 9 9 α ß-1 9-ß 10-α), P₃₁ = (9 9 9 9 9 α-1 10-α) and P₆ = (9 9-γ α ß 9-ß 10-α γ-1).

5. Balance: Transformation Constants

Let balance exist when there is an α_E and a K_i(α) such that K_i(α_E) = α_E or, equivalently, K (n_E) = n_E, p (n_E) = α_E.

As a corollary, $K^r$ (n_E) = n_E, $K^r$ (α_E) = α_E, ∀r ≥ 1.

Let n_E be called transformation constant and α_E parametric constant. If all the numbers n $\in$ A_w, by reiterating their transformation they become n_E; we will say that n_E is a Kaprekar constant. This is equivalent to the existence of a constant and a one-component scheme in A_w.

A transformation constant is a single-link cycle, which is why some authors call the constant a one-cycle [4]. Others call it a fixed point [5,12,13]. In relation with this fixed point and with the cycles, in general, the classic work of Prichett et al. [4] and the more recent, innovative input of Yamagami [10,11] and Bajorska-Harapinska et al. [19] should be highlighted.

In the example of (4), we see how 631,764 transforms into itself, and the same is true for α = p(n) = 632, K(632) = 632. Therefore, 631,764 = n_E and 632 = α_E.

The constants in base 10 have been exhaustively studied by Prichett et al. [3,4], who showed that in base 10, there are only two Kaprekar constants, 495 in A₃ and 6174 in A₄. They also determined one-cycles for different w-digits.

Our objective in this section is not to make a detailed study of the constants, but to show how families of constants can be derived directly from the K_i functions. In this regard, we show two examples: the family α_E = 6 3 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 3 2 in w = 2 h, h ≥ 2 and the family α_E = 8 6 4 3 $\begin{array}{c}\mathrm{h}-4\\ \breve{\dots \dots }\\ \end{array}$ 3 2 in w = 2 h + 1, h ≥ 7. We also show two singular constants, α_E = 550 in A₆ and α_E = 5 in A₃.

Constants n_E = 63$\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$3176$\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 64, α_E = 63 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$32, w = 2 h

Indeed, O_d (n_E) = 76 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 6643 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 31 and O_u (n_E) = 13 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 3466 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 67

$${{\mathrm{n}}^{\prime }}_{\mathrm{E}}={\mathrm{O}}_{\mathrm{d}} ({\mathrm{n}}_{\mathrm{E}})-{\mathrm{O}}_{\mathrm{u}} ({\mathrm{n}}_{\mathrm{E}})=63 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 3176 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 64={\mathrm{n}}_{\mathrm{E}}$$

For this expression to be valid, at least the two extreme digits and the two middle digits must be present. Such is the case with 6174, which is the renowned Kaprekar’s constant [1]. The associated parametric constants are α_E = 63 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 32.

Such constants, which generalize Kaprekar’s constant for w-digits, w = $\dot{2}$, derive from function (18) associated with permutation P₃ (h + 1 1 h + 2 … w 2 3 … h)

K₃ (α) = α → α¹ = 10-2α^h, α² = α¹-α^h−1, α³ = 9-α^h−1-α^h−2 … α^h = α¹-α²-1

with the restrictions imposed in K₃. There is a unique solution which is α_E = 6 3 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 3 2

For instance, for w = 8, h = 4

K₃ (α) = K₃ (α ß γ δ) = (10-2δ α-γ 9-ß-γ α-ß-1)

1 ≤ 10-2δ + α-γ ≤ 10; ß + γ ≤ 9; α ≥ ß + 1, α + γ ≥ 9, α ≤ 10 + γ-2δ, 1 ≤ δ ≤ 4

Imposing the equality condition

α = 10-2δ, ß = α-γ, γ = 9-ß-γ, δ = α-ß-1, there is only one solution: α = 6, ß = 3, γ = 3,

δ = 2 → α_E = 6332, which satisfies the existence conditions and f₁ (6332) = 63,317,664 = n_E.

In the case where w = 4, h = 2, P₃ = (3142), and the associated function is

K₃ (α ß) = (10-2ß 2α-10) α ≥ 5, α + ß ≤ 9

K₃ (α ß) = (α ß) → α = 10-2ß, ß = 2α-10 → α = 6, ß = 2

f₁ (6 2) = 6174, which is Kaprekar’s constant.

This family of constants cannot exist if w = $\dot{2}$ + 1, since a 9 being present in (6) completely changes function K₃. It is not valid for w = 2 either, since permutation P₃ does not make sense.

Constants n_E = 8643 $\begin{array}{c}h-4\\ \breve{\dots \dots }\\ \end{array}$ 31,976 $\begin{array}{c}h-4\\ \breve{\dots \dots }\\ \end{array}$ 532, α_E = 8643 $\begin{array}{c}h-4\\ \breve{\dots \dots }\\ \end{array}$ 32, w = 2 h + 1, h ≥ 4

They are derived from the function (22) associated with the permutation

P₄ (1 h+2 2 h+3…h+s 3 4…s 2h 2h+1), s = h + 1, h ≥ 4. De K₄ (α) = α and taking into account the domain of existence of P₄, it results in α_E.

P₄ (1 h+2 2 h+3…h+s 3 4…s 2h 2h+1)

Constant n_E = 549,945 and α_E = 550

Derives from K₂₄ in A₆ (Table 1)

α = ß, ß = 10-ß, 0 = 2α-10 → α = 5, ß = 5, γ = 0 ↔ α_E = 550

f₂ (550) = 549,945 = n_E

This constant cannot be generalized.

Constant n_E = 495 and α_E = 5

This is the other Kaprekar’s constant. If w = 3, f₁ (α) = (α-1 9 10-α) and O (n′), this allows for two permutations P₁₂ = (9 α-1 10-α) and P₂₁ = (9 10-α α-1) as well as two associated functions K₁ (α) = (α-1) and K₂ (α) = (10- α). α_E = 5 results from K₂ (α) = α and f₁ (5) = 495. It is thus another constant that cannot be generalized.

There are other functions of just one parameter. Such is the case of

–

w = 2 with f₁ (α) = (α-1 10-α) and two functions K_i,

K₁ (α) = (2α-11) and K₂ (α) = (11-2α), which obviously cannot satisfy the condition

K_i (α) = α. In A₂, there cannot be any transformation constant.

–

The same is true for functions

$$\begin{array}{c}{\mathrm{K}}_{31} (\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0)=(\mathsf{\alpha }-1 10-\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0) \mathrm{and} {\mathrm{K}}_{32} (\mathsf{\alpha } 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0)=\\ (10-\mathsf{\alpha } \mathsf{\alpha }-1 0 \begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array} 0)\end{array}$$

where condition K (α) = α leads to impossible results. In these cases, there cannot be any transformation constant either.

6. Cycles: Terminology and Functions ${\mathit{K}}^{\mathit{r}}$ (α)

There is a cycle of r links if and only if there are r parameters α_ci and r functions

K_ci (α), such that K_ci (α_ci) = α_{ci + 1} being α_ci = α_cj ↔ i ≡ j (mod r).

This amounts to the existence of r operators $K_{ci}^r$ such that $K_{ci}^r$ (α_ci) = α_ci, i = 1 …r.

In terms of numbers, it demands the existence of r numbers

$${\mathrm{n}}_{\mathrm{ci}}, \mathrm{K}\left({\mathrm{n}}_{\mathrm{ci}}\right)={\mathrm{n}}_{\mathrm{ci}+1}, {\mathrm{n}}_{\mathrm{ci}}={\mathrm{n}}_{\mathrm{cj}} \leftrightarrow \mathrm{i} \equiv \mathrm{j} (\mathrm{mod} \mathrm{r}) \mathrm{or}, \mathrm{equivalently}, K^r \left({\mathrm{n}}_{\mathrm{ci}}\right)={\mathrm{n}}_{\mathrm{ci}}, \mathrm{i}=1 \dots \mathrm{r}.$$

Let us analyze the case A₆ for six-digit numbers. The parametric transformation schemes are shown in Scheme 1.

Main component A, consisting of 201 parametric classes out of the 219 existing classes, is articulated on a seven-class cycle, which can be conventionally called

861= α_c1, 863= α_c2, 643 = α_c3, 421 = α_c4, 852 = α_c5, 751 = α_c6, 841 = α_c7

Each class becomes the following one with the functions in Table 1, indicated in the diagram:

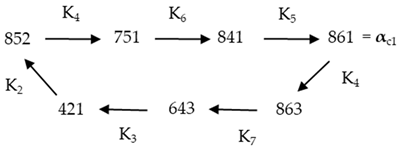
Naturally, there are seven operators $K^r$, r = 1, 2 … 7, which transform parameters separated by r links. Thus,

$$\begin{array}{c}{\mathrm{K}}_{\mathrm{c}1}^7 (\mathsf{\alpha } ß \mathsf{\gamma })={\mathrm{K}}_5 \times {\mathrm{K}}_6 \times {\mathrm{K}}_4 \times {\mathrm{K}}_2 \times {\mathrm{K}}_3 \times {\mathrm{K}}_7 \times {\mathrm{K}}_4 (\mathsf{\alpha } ß \mathsf{\gamma })=\\ (20\mathsf{\alpha }+8ß-20\mathsf{\gamma }-180 20\mathsf{\alpha }+8ß-20\mathsf{\gamma }-178 24\mathsf{\alpha }-16 ß-24\mathsf{\gamma }–71), {\mathrm{K}}_{\mathrm{c}1}^7 \left(861\right)=861.\end{array}$$

Any operator ${\mathrm{K}}_{\mathrm{ci}}^{\mathrm{s}}$ (α_ci) built with s > 7 will coincide with other ${\mathrm{K}}_{\mathrm{ci}}^{\mathrm{t}}$ (α_ci) 1 ≤ t ≤ 7 if and only if s ≡ t (mod 7). The existence of the cycle demands the coupling between functions K_i. The image of one function must belong to the domain of existence of the following one.

In numerical terms, the cycle consists of the following numbers

n_c1 = 840,852, n_c2 = 860,832, n_c3 = 862,632, n_c4 = 642,654, n_c5 = 420,876, n_c6 = 851,742,

n_c7 = 750,843, being p (n_ci) = α_ci.

In A₂, there is a five-link cycle. In A₃ and A₄, there is only one articulated on a Kaprekar’s constant. In A₅, there are two four-link cycles and one two-link cycle.

In A₇, consisting of seven-digit numbers, all 219 existing parametric classes (α ß γ) group with the following cycle formed by eight links:

7. Symmetries

7.1. Equivalence Relations

Let two numbers m and n be equivalent R_r of order r if and only if

$$\mathrm{m} {\mathrm{R}}_{\mathrm{r}} \mathrm{n} \leftrightarrow {\mathrm{K}}^{\mathrm{r}} \left(\mathrm{m}\right)={\mathrm{K}}^{\mathrm{r}} \left(\mathrm{n}\right) \mathrm{r} \ge 0$$

(32)

Since $K^r$ (m) = $K^{r-1}$ [K(m)], the following recurrence equations are found:

m R_r n ↔ K(m) R_r-1 K(n) r ≥ 1

(33)

$$\mathrm{m} \mathrm{R}{\mathrm{r}}_{ }\mathrm{n} \leftrightarrow K^s \left(\mathrm{m}\right) {\mathrm{R}}_{\mathrm{r}-\mathrm{s}} K^s \left(\mathrm{n}\right) \mathrm{s} \le \mathrm{r}$$

(34)

Note that if two numbers are equivalent, they are so for any equivalence of a higher order:

m R_r n → m R_{r + s} n s ≥ 0

(35)

It is necessary to distinguish new equivalences R_r, those which are not of a lower order:

$$\mathrm{m} {\mathbf{R}}_{\mathbf{r}} \mathrm{n} \to \cancel{\mathrm{m} {\mathrm{R}}_{\mathrm{r}-1}} \mathrm{n} \mathrm{r}>0$$

(36)

$$\mathrm{m} {\mathbf{R}}_{\mathbf{r}} \mathrm{n} \to \cancel{\mathrm{m} {\mathrm{R}}_{\mathrm{r}-\mathrm{s}}} \mathrm{n} \mathrm{s}=1,2\dots \mathrm{r}$$

(37)

from old equivalences _aR_r, those that are also of a lower order:

m (_aR_r) n→ m R_r-1 n r > 0

(38)

The notation R_r does not specify whether an equivalence is new or old.

Equivalence of an order are binary equivalence relations that have the following features:

$$\mathrm{reflexivity} \mathrm{m} {\mathrm{R}}_{\mathrm{r}} \mathrm{m} \forall \mathrm{m} \in {\mathrm{A}}_{\mathrm{w}}$$

symmetry m R_r n ↔ n R_r m ∀ m,n

transitivity m R_r n and n R_r q → m R_r q ∀ m,n,q

They allow for numbers to be grouped in equivalence classes of order r:

$${\mathrm{C}}_{\mathrm{r}}=\{\mathrm{m},\mathrm{n} \in {\mathrm{A}}_{\mathrm{w}}; \mathrm{m} {\mathrm{R}}_{\mathrm{r}} \mathrm{n}\}$$

(39)

These equivalence classes are pairwise disjoint, and their intersection is set A_w, generating a partition in A_w.

Because two numbers that are equivalent are so for any equivalence of a higher order (35), classes C_r include both the new and old equivalences. This hierarchical and inclusive feature of binary relations R_r is essential to better understand the convergence of this process.

C_r = {m,n ∈ A_w, m R_r n}, _aC_r = { p,q ∈ A_w, p R_r−1 q} C_r = C_r ∪ _aC_r

(40)

The transitive feature and relation (35) yield

m R_r n and n R_{r + s} q → m R_{r + s} q s ≥ 0

(41)

In our methodological approach to the analysis of the Kaprekar process, it is essential to extend the concept of equivalence R_r defined between numbers to sets of numbers with images in common, to equivalence classes.

Considering the last relationship, if

$$\mathrm{m} \in {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}, \mathrm{p} \in {\mathrm{C}}_{\mathrm{s}}^{\mathrm{j}} \mathrm{and} \mathrm{m} {\mathrm{R}}_{\mathrm{t}} \mathrm{p}, \mathrm{t}=\max \{\mathrm{r},\mathrm{s}\}+\mathrm{u}, \mathrm{u} \ge 0 \mathrm{then} \mathrm{if}$$

n ∈ ${\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}$ and q ∈ ${\mathrm{C}}_{\mathrm{s}}^{\mathrm{j}}$ results n R_t q. This is due to the univocal character of the transformation. All numbers belonging to a class C_v have the same image in the v-th transformation. From here on, any subsequent transformation will have the same image. Consequently, the element that best represents the transformation is not the number, but the equivalence class. Thus, we can agree to define the equivalence relation between classes according to

$$\mathrm{m} \in {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}, \mathrm{n} \in {\mathrm{C}}_{\mathrm{s}}^{\mathrm{j}} \mathrm{and} \mathrm{m} {\mathrm{R}}_{\mathrm{t}} \mathrm{p}, \mathrm{t}=\max \{\mathrm{r},\mathrm{s}\}+\mathrm{u}, \mathrm{u} \ge 0 \leftrightarrow {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}} {\mathrm{R}}_{\mathrm{t}} {\mathrm{C}}_{\mathrm{s}}^{\mathrm{j}}$$

(42)

The direction of the arrow to the left must be understood in the sense that if two classes ${\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}$ y ${\mathrm{C}}_{\mathrm{s}}^{\mathrm{j}}$ have a relation R_t, then all numbers m and n belonging to those classes have a relation R_t. In particular, it turns out

$$\mathrm{m} \in {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}, \mathrm{n} \in {\mathrm{C}}_{\mathrm{r}}^{\mathrm{j}}, \mathrm{m} {\mathrm{R}}_{\mathrm{r}+\mathrm{s}} \mathrm{n} \leftrightarrow {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}} {\mathrm{R}}_{\mathrm{r}+\mathrm{s}} {\mathrm{C}}_{\mathrm{r}}^{\mathrm{j}} \mathrm{s} \ge 0$$

(43)

From relation (14), it follows that the C₁ equivalence classes are defined by the parametric classes (we will return to this topic in Section 7.3). α represents the parameters of a number α = (α¹ α² … α^h) = p(n) and also the set of numbers that has the same parameters. As what characterizes a class C₁ are precisely these parameters, we can agree to specify each C₁ by its corresponding parameters, being able to write ${\mathrm{C}}_1^{\mathrm{i}}$ = α_i, if in the context there is no room for confusion. With this convention α has a double meaning: parameters of a number and a set of numbers with the parameters that are specified.

By extension, we say that two parametric classes α₁ and α₂ are equivalent to R_r if and only if the numbers with the respective parameters are equivalent:

α₁ R_r α₂ ↔ m R_r n, p(m) = α₁, p(n) = α₂

(44)

Expression (44) allows us to translate some of the previous relationships into a parametric class language. For example, from (43) it results

$${\mathsf{\alpha }}_1\subset {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}}, {\mathsf{\alpha }}_2 \subset {\mathrm{C}}_{\mathrm{r}}^{\mathrm{j}}, {\mathsf{\alpha }}_1 {\mathrm{R}}_{\mathrm{r}+\mathrm{s}} {\mathsf{\alpha }}_2 \to {\mathrm{C}}_{\mathrm{r}}^{\mathrm{i}} {\mathrm{R}}_{\mathrm{r}+\mathrm{s}}{\mathrm{C}}_{\mathrm{r}}^{\mathrm{j}}, s\ge 0$$

(45)

Going back to expression (14) and to definition (32), it results

$$\mathrm{m} {\mathrm{R}}_{\mathrm{r}}\mathrm{n} \leftrightarrow \mathrm{p} [{\mathrm{K}}^{\mathrm{r}-1}\left(\mathrm{m}\right)]=\mathrm{p} [{\mathrm{K}}^{\mathrm{r}-1}\left(\mathrm{n}\right)] \mathrm{r} \ge 1$$

(46)

To any equivalence R_r can be associated a function or operator e_r such that

α₁ R_r α₂ ↔ e_r (α₁) = α₂

(47)

with the domain of existence of R_r.

It is a kind of representation that facilitates notation of calculations.

7.2. Product of Equivalences

Applying an equivalence onto another one normally yields another equivalence. By using the usual representation of the product of functions

eⁱ [e^j (α)] = (eⁱ x e^j) (α) = e^k (α)

the domains of existence will have to be compatible. Thus, taking equivalences that will be later deduced

$${\mathrm{e}}_2^2 (\mathsf{\alpha } ß)=(10-\mathsf{\alpha } ß), \mathsf{\alpha }+ß \le 10; {\mathrm{e}}_2^3(\mathsf{\alpha } ß)=(\mathsf{\alpha } 10-ß), \mathsf{\alpha }+ß \ge 10$$

$${ \mathrm{e}}_2^4 (\mathsf{\alpha } ß)=({\mathrm{e}}_2^3 \times {\mathrm{e}}_2^2) (\mathsf{\alpha } ß)=(10-\mathsf{\alpha } 10-ß), \mathsf{\alpha }=ß$$

However,

$$({\mathrm{e}}_2^2 \mathrm{x} {\mathrm{e}}_2^4) (\mathsf{\alpha } ß)=(\mathsf{\alpha } 10-ß)={\mathrm{e}}_2^3, \mathrm{where} \mathrm{domains} \mathsf{\alpha }=ß \mathrm{and} \mathsf{\alpha }+ß \le 10 \mathrm{lead} \mathrm{to} \mathsf{\alpha }+ß \ge 10.$$

Moreover, the product is conditioned by restriction (3). Therefore, if α = (α ß γ),

α ≥ ß ≥ γ

$${ \mathrm{e}}_2^2 \left(\mathsf{\alpha }\right)=(\mathsf{\alpha } 9-ß \mathsf{\gamma }), \mathsf{\alpha }+ß \ge 9, ß+\mathsf{\gamma } \le 9; {\mathrm{e}}_2^3 \left(\mathsf{\alpha }\right)=(\mathsf{\alpha } ß 10-\mathsf{\gamma }), ß+\mathsf{\gamma } \ge 10$$

${\mathrm{e}}_2^6$(α) = (${\mathrm{e}}_2^3$ × ${\mathrm{e}}_2^2$) (α) = (α 9-ß 10-γ) not valid because it demands γ ≥ ß + 1, which contradicts (3).

Additionally, the other way around, the product of non-allowed equivalences can generate an allowed one. Thus,

$${\mathrm{e}}_2^7\left(\mathsf{\alpha }\right)=(10-\mathsf{\alpha } 9-ß 10-\mathsf{\gamma }), \mathrm{not} \mathrm{valid}$$

$$({\mathrm{e}}_2^6 \mathrm{x} {\mathrm{e}}_2^7) (\mathsf{\alpha })=(10-\mathsf{\alpha } ß \mathsf{\gamma })={\mathrm{e}}_2^1 (\mathsf{\alpha }) \mathrm{valid} \mathrm{if} \mathsf{\alpha }+ß \le 10$$

In summary, the product of equivalences demands that the resulting equivalence’s domain of existence be determined.

7.3. Symmetries R₀ and R₁

Symmetry R₀ has been conventionally defined as the non-transformation: m R₀ n ↔ K⁰ (m) = K⁰ (n) ↔ m = n. Each equivalence class C₀ consists of a single number. There are as many classes C₀ as there are numbers belonging to A_W.

Due to (14), symmetry R₁ is the one containing those numbers with the same parameters which return the same number after one transformation. Therefore, parametric classes, understood as the set of numbers with the same parameters, match with equivalence classes C₁. Scheme 1 shows all these classes and their transformations in the case of A₆.

As these classes uniquely determine the image of any number belonging to them, they are an essential element when understanding Kaprekar’s routine.

7.4. Symmetries R₂

R₂ symmetries are those that exist between numbers whose transformed seconds coincide.

As a result of R_r definition (32)

m R₂ n ↔ K² (m) = K² (n) and because of (46)

m R₂ n ↔ p [K (m)] = p [K (n)]

(48)

7.4.1. Permutations of the Same Sequence

If two numbers m and n, p(m) = α₁, p(n) = α₂ return images with transpositions of digits compatible with belonging to B_w, the ordered sequences will be identical O_d (m′) = O_d (n′) and their parameters will match α′₁ = α′₂, as will their numeric images

m″ = f (α′₁) = f (α′₂) = n″, thus verifying the condition of m R₂ n.

Not just any transposition is valid. Only those that respect the conditions (5) or (7) of belonging to B_w are valid.

R₂ equivalences based on (4a) and (4b)

$${\mathrm{m}}^{\prime }={\mathrm{f}}_1({\mathsf{\alpha }}_1)=({\mathsf{\alpha }}_1^1 {\mathsf{\alpha }}_1^2\dots {\mathsf{\alpha }}_1^{\mathrm{h}-1}{\mathsf{\alpha }}_1^{\mathrm{h}}-1 9-{\mathsf{\alpha }}_1^{\mathrm{h}} \dots 9-{\mathsf{\alpha }}_1^2 10-{\mathsf{\alpha }}_1^1), \mathrm{p}(\mathrm{m})={\mathsf{\alpha }}_1=({\mathsf{\alpha }}_1^1 {\mathsf{\alpha }}_1^2\dots {\mathsf{\alpha }}_1^{\mathrm{h}})$$

$$\mathrm{If} \mathrm{p} \left(\mathrm{n}\right)={\mathsf{\alpha }}_2=(10-{\mathsf{\alpha }}_1^1 {\mathsf{\alpha }}_1^2\dots {\mathsf{\alpha }}_1^{\mathrm{h}}) {\mathrm{n}}^{\prime }={\mathrm{f}}_1 ({\mathsf{\alpha }}_2)=(10-{\mathsf{\alpha }}_1^1 \dots {\mathsf{\alpha }}_1^2 \dots 9-{\mathsf{\alpha }}_1^2{\mathsf{\alpha }}_1^1)$$

n′ ∊ B_w because it meets the conditions (5) or (7) and the sequence of n′ has the same digits as that of m′, with the ends being translocated. Consequently,

O_d (m′) = O_d (n′) and p (m′) = p (n′) ↔ α₁ R₂ α₂

We used f₁ corresponding to w = $\dot{2}$, (4). The result for w = $\dot{2}$ + 1 does not change, since including a central 9 in the sequences of m′ and n′ does not modify the reasoning. Likewise, the symmetric digits can be transposed in relation to the middle ones, α^s and 9-α^s, s = 2, 3 … h-1, or the middle digits themselves, α^h-1 and 9-α^h, returning the following binary equivalences by simple transposition, where α₁ = (α¹ α² … α^h).

–

Equivalences α₁$R_{\mathbf{2}}^{\mathbf{11}}$α₂, α₂ = (10-α¹ α² …α^h), α¹ + α²≤ 10

–

Equivalences α₁$R_{\mathbf{2}}^{\mathbf{12}}$α₂, α₂ = (α¹ α² … α^s−1 9-α^s α^{s + 1} …α^h), s = 2, …h-1

α^s−1 + α^s ≥ 9, α^s + α^{s + 1} ≤ 9

For example: w = 11, α₁ = 76,632, α₂ = 76,332

f₁ (α₁) = 76,631,976,333, f₁ (α₂) = 76,331,976,633 being

f₁ (α₂) the permutation P = (1 2 9 4 5 6 7 8 3 10 11) of f₁ (α₁) and K (α₁) = K (α₂) = 84,433 consistent with (48). Besides, f₁ (8 4 4 3 3) = (8 4 4 3 2 9 6 6 5 5 2) =

= K (7 6 6 3 1 9 7 6 3 3) = K (7 6 3 3 1 9 7 6 6 3 3).

–

Equivalences α₁$R_{\mathbf{2}}^{\mathbf{13}}$α₂, α₂ = (α¹ α² …α^h−1 10-α^h), α^h−1 + α^h≥ 10

However, multiple transpositions are limited by (3):

–

Non-equivalence α₁$n_{\mathbf{2}}^{\mathbf{1}}$α₂

$${\mathsf{\alpha }}_2=({\mathsf{\alpha }}^1\dots {\mathsf{\alpha }}^{\mathrm{s}-1} 9-{\mathsf{\alpha }}^{\mathrm{s}} {\mathsf{\alpha }}^{\mathrm{s}+1}\dots {\mathsf{\alpha }}^{\mathrm{s}+\mathrm{r}-1} 9-{\mathsf{\alpha }}^{\mathrm{s}+\mathrm{r}} {\mathsf{\alpha }}^{\mathrm{s}+\mathrm{r}+1}\dots {\mathsf{\alpha }}^{\mathrm{h}}) \mathrm{impossible}, {\mathsf{\alpha }}_1 \cancel{{\mathrm{R}}_2} {\mathsf{\alpha }}_2$$

α^{s + r−1} ≤ 9- α^s and α^{s + r−1} ≥ 9-α^{s + r}

α^{s + r} ≥ 9- α^{s + r−1} ≥ α^s → α^{s + r} = α^s = α^{s + i}, i = 0, 1, … r

9- α^s ≥ α^s → α^s ≤ 4 → α^{s + r−1} = α^{s + r} ≤ 4

α^{s + r−1} ≥ 9-4 ≥ 5, which contradicts the previous expression. Therefore, α₁ $\cancel{{\mathrm{R}}_2}$ α₂ ↔ α₁ ${\mathrm{n}}_2^1$ α₂

–

Non-equivalence α₁${\mathbf{n}}_{\mathbf{2}}^{\mathbf{2}}$α₂

$${\mathsf{\alpha }}_2=({\mathsf{\alpha }}^1\dots {\mathsf{\alpha }}^{\mathrm{s}-1} 9-{\mathsf{\alpha }}^{\mathrm{s}} {\mathsf{\alpha }}^{\mathrm{s}+1}\dots 10-{\mathsf{\alpha }}^{\mathrm{h}}) \mathrm{impossible}, {\mathsf{\alpha }}_1 \cancel{{\mathrm{R}}_2} {\mathsf{\alpha }}_2$$

α^h−1 ≤ 9- α^s and α^h−1 ≥ 10-α^h

α^h ≥ 10- α^h−1 ≥ 10-(9- α^s) = 1+ α^s, impossible, since α^h ≤ α^s

$${\mathsf{\alpha }}_1 \cancel{{\mathrm{R}}_2} {\mathsf{\alpha }}_2 \leftrightarrow {\mathsf{\alpha }}_1 {\mathrm{n}}_2^2 {\mathsf{\alpha }}_2$$

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{14}}$α_2,α₂ = (10-α¹ α² … α^h−1 10-α^h) → α₂ = (5 $\begin{array}{c}h\\ \breve{\dots \dots }\\ \end{array}$ 5) = α₁

It is a specific identity solution:

$$\begin{array}{c}{\mathsf{\alpha }}^{\mathrm{h}-1}\le 10-{\mathsf{\alpha }}^1 \mathrm{y} {\mathsf{\alpha }}^{\mathrm{h}-1}\ge 10-{\mathsf{\alpha }}^{\mathrm{h}}\to {\mathsf{\alpha }}^{\mathrm{h}}\ge {\mathsf{\alpha }}^1\to {\mathsf{\alpha }}^{\mathrm{h}}={\mathsf{\alpha }}^1={\mathsf{\alpha }}^{\mathrm{s}}, \mathrm{s}=1,\dots \mathrm{h}\\ 10-{\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^1\to {\mathsf{\alpha }}^1\le 5\to {\mathsf{\alpha }}^{\mathrm{h}-1}={\mathsf{\alpha }}^{\mathrm{h}}\le 5\\ {\mathsf{\alpha }}^{\mathrm{h}-1}=5\to {\mathsf{\alpha }}^{\mathrm{s}}=5, \mathrm{s}=1\dots \mathrm{h}\\ {\mathsf{\alpha }}^{\mathrm{h}-1}\ge 10-{\mathsf{\alpha }}^{\mathrm{h}}\ge 10-5=5\end{array}\}$$

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{15}}$α₂, α₂ = (α¹ … α^s−1 9-α^s … 9-α^{s + r} α^{s + r+1} α^h)

According to (3), 9- α^s ≥ 9-α^{s + r} → α^{s + r} = α^s

Domain of existence:

α^s ≥ 9- α^{s − 1}, α^{s + r + 1} ≤ 9- α^{s + r}, α^{s + i} = α^s, i = 0, 1 … r + 1, 2 ≤ s <h

For example: w = 10:

α₁ = 75,552 and α₂ = 74,442, f₁ (α₁) = 7,555,174,443, f₁ (α₂) = 7,444,175,553, where f₁ (α₂) is the permutation P = (1 9 8 7 5 6 4 3 2 10) of f₁ (α₁) and K (α₁) = K (α₂) = 64,111 according to (48).

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{16}}$α₂, α₂ = (10-α¹ α² 9-α³ … 9-α^r α^{r + 1} α^h)

9-α³ ≤ α² ≤10- α¹→ α²≤ α³≥ α¹-1→ α¹= α² = α³ = 5

Domain of existence:

α^s = 5, s = 1, 2…r, α^{r + 1} ≤ 9- α^r

For example, α₁ = 555,532, α₂ = 554,432, w = 12:

f₁ (α₁) = 555,531,764,445, f₁ (α₂) = 554,431,765,545

where f₁ (α₂) is a permutation P = (1 2 10 9 5 6 7 8 4 3 11 12) of f₁ (α₁) and K (α₁) = K (α₂) = 631,110.

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{17}}$α₂, α₂ = (10-α¹ 9-α².…9-α^r α^{r + 1} α^h)

α¹-1 ≤ α² ≤ α¹, α^s = α², s = 2, 3, … r

For example: w = 9, α₁ = 8772, α₂ = 2222:

f₁ (α₁) = 877,197,222, f₁ (α₂) = 222,197,778, where f₁ (α₂) is the permutation

P = (9 8 74 5 6 3 2 1) of f₁ (α₁) and K (α₁) = K (α₂) = 8655.

R₂ based on (8) or (10)

$$\mathsf{\alpha }=({\mathsf{\alpha }}^1 \dots {\mathsf{\alpha }}^{\mathrm{r}} 0 \begin{array}{c}\mathrm{h}-\mathrm{r}\\ \breve{\dots \dots }\\ \end{array} 0) \mathrm{and} \mathrm{functions} {\mathrm{f}}_2 (\mathsf{\alpha }) (8) \mathrm{or} (10) \mathrm{operate}.$$

If we consider α^r as α^h, the previous equivalences are valid. For example,

$${\mathsf{\alpha }}_{\mathbf{1}} R_{\mathbf{2}}^{\mathbf{2}} ({\mathsf{\alpha }}^{\mathbf{1}}\dots {\mathsf{\alpha }}^{\mathbf{r}\mathbf{-}\mathbf{1}} \mathbf{10}-{\mathsf{\alpha }}^{\mathbf{r}} \mathbf{0} \begin{array}{c}h-r\\ \breve{\dots \dots }\\ \end{array} \mathbf{0}) {\mathsf{\alpha }}_1=\mathrm{97,400} {\mathrm{R}}_2 \mathrm{97,600}={\mathsf{\alpha }}_2, \mathrm{since} \mathrm{K} ({\mathsf{\alpha }}_1)=\mathrm{K} ({\mathsf{\alpha }}_2)=\mathrm{87,642}.$$

R₂ based on (12)

$$\mathsf{\alpha }=({\mathsf{\alpha }}^1 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0) \mathrm{and} \mathrm{the} \mathrm{function} {\mathrm{f}}_3 (\mathsf{\alpha })=({\mathsf{\alpha }}^1-1 9 \begin{array}{c}\mathrm{w}-2\\ \breve{\dots \dots }\\ \end{array} 9 10-{\mathsf{\alpha }}^1) \mathrm{operates}.$$

Only the transposition of extreme digits is possible. That is, if

$${\mathsf{\alpha }}_1=({ \mathsf{\alpha }}_{}^1 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array}0) \mathrm{and} {\mathsf{\alpha }}_2=(11-{ \mathsf{\alpha }}_{}^1 0 \begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array} 0) \mathrm{then}$$

$${\mathrm{f}}_3 ({\mathsf{\alpha }}_1)=({ \mathsf{\alpha }}_{}^1-1 9 \begin{array}{c}\mathrm{w}-2\\ \breve{\dots \dots }\\ \end{array} 9 10- {\mathsf{\alpha }}^1), {\mathrm{f}}_3 ({\mathsf{\alpha }}_2)=(10-{ \mathsf{\alpha }}_{}^1 9 \begin{array}{c}\mathrm{w}-2\\ \breve{\dots \dots }\\ \end{array} 9 { \mathsf{\alpha }}_{}^1-1)$$

which is a permutation of the same digits compatible with (13), so

O_d [f₃ (α₁)] = O_d [f₃ (α₂)] ↔ α′₁ = K (α₁) = α′₂ = K (α₂) ↔ α₁ R₂ α_2.

–

Equivalence (α 0$\begin{array}{c}h-\mathbf{1}\\ \breve{\dots \dots }\\ \end{array}$0)$R_{\mathbf{2}}^{\mathbf{3}}$(11-α 0$\begin{array}{c}h-\mathbf{1}\\ \breve{\dots \dots }\\ \end{array}$0), α≥ 2

Example: α₁ = 300, α₂ = 800, α₁ R₂ α₂ since K (α₁) = K (α₂) = 720.

7.4.2. Permutation of Different Sequences

There are equivalences where the digits from the sequence do not necessarily remain.

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{4}}$α₂

α₁ = (α¹ α² … α^h), α₂ = (10-α^h 9-α^h−1 9-α^h−2 … 9-α³ 9-α² 10-α¹),

$${\mathsf{\alpha }}^1 \ge {\mathsf{\alpha }}^2+1, \mathrm{w}=\dot{2}, \mathrm{h}=\mathrm{w}/2$$

Under (15) K₁ (α₁) = (2${ \mathsf{\alpha }}_1^1$-10 2${ \mathsf{\alpha }}_1^2$-9 … 2${ \mathsf{\alpha }}_1^{\mathrm{h}-1}$-9 2${ \mathsf{\alpha }}_1^{\mathrm{h}}$-10).

Under (17) K₂ (α₂) = (10-2${ \mathsf{\alpha }}_2^{\mathrm{h}}$ 9-2${ \mathsf{\alpha }}_2^{\mathrm{h}-1}$ … 9-2${ \mathsf{\alpha }}_2^2$ 10-2${ \mathsf{\alpha }}_2^1$).

If K₁ (α₁) = K₂ (α₂) →${ \mathsf{\alpha }}_1^1$ + ${ \mathsf{\alpha }}_2^{\mathrm{h}}$ = 10, ${ \mathsf{\alpha }}_1^{\mathrm{s}+1}$+${ \mathsf{\alpha }}_2^{\mathrm{h}-\mathrm{s}}$ = 9, s = 1, 2, … h-2.

Note that α₁ + O_u (α₂) = (10 9 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 9 10).

For example,

m = 8,178,382,562, p (m) = α₁ = 76,641, m′ = f₁ (α₁) = 7,664,085,333

n = 4,774,473,809, p (n) = α₂ = 95,333, n′ = f₁ (α₂) = 9,533,266,641

α₁ and α₂ verify the equivalence, and f₁ (α) corresponds to (4). m′ and n′ do not keep the same digits, but p (m′) = p (n′) = 84,331 and K² (m) = K² (n) = 8,433,086,652. This answers the second question in the introduction.

This equivalence, contrary to what happens with the previous ones, is not valid for odd w. In the previous example, w = 10. Let w = 11 and keep the same parameters p (m) = α₁ = 76,641, p (n) = α₂ = 95,333.

Now, the function f₁ that must be used is the one corresponding to (6):

m′ = f₁ (α₁) = 76,640,985,333, n′ = f₁ (α₂) = 95,332,966,641

which are similar to the previous ones but with a 9 in the middle position:

p (m′) = 95,432, p (n′) = 87,332.

Adding a 9 in the sequence of digits makes symmetry break.

This equivalence may generate permutations of digits from the same sequence. Such is the case of α₁ = 87,662 and α₂ = 83,322, α₁ ${ \mathrm{R}}_2^4$  α_2.

m′ = f₁ (α₁) = 8,766,173,322, n′ = f₁ (α₂) = 8,332,177,662

being O_d (m′) = O_d (n′). It is just a numeric coincidence, even if for these parameters ${ \mathrm{R}}_2^4$ does not match any of the previous equivalences.

$R_{\mathbf{2}}^{\mathbf{4}}$is a very common equivalence given the few restrictions of its domain of existence.

The product of equivalences ${\mathrm{R}}_2^1$ × ${\mathrm{R}}_2^4$ creates a family of derivative equivalences. Table 3 shows the equivalences R₂ common in A₆ and A₇, and Table 4 shows derivative equivalences in A₆. The superscripts in the equivalences are simplified by using correlative natural numbers. ${ \mathrm{n}}_2^6$ corresponds to a double translocation and ${\mathrm{n}}_2^7$ to a triple one, but none of them are an equivalence.

Table 3. Equivalences R₂ with three parameters, α = (α ß γ).

Equivalences R2 Common to A6 and A7
Group	${\mathbf{e}}_2^{\mathbf{i}} \left({\mathsf{\alpha }}_1\right)={\mathsf{\alpha }}_2$	Domain of Existence
Set I Based on (4a) or (4b) α = (α ß γ) 1 ≤ α ≤ 9 1 ≤ ß ≤ 9 1 ≤ γ ≤ 9	${ \mathrm{e}}_2^0$ (α) = (α ß γ)	1 ≤ α ≤ 9, 1 ≤ ß ≤ 9, 1 ≤ γ ≤ 9
	${ \mathrm{e}}_2^1$ (α) = (10-α ß γ)	α + ß ≤ 10
	${ \mathrm{e}}_2^2$ (α) = (α 9-ß γ)	α + ß ≥ 9, ß + γ ≤ 9
	${\mathrm{e}}_2^3$ (α) = (α ß 10-γ)	ß + γ ≥ 10
	${ \mathrm{e}}_2^4$ (α) = (10-α 9-ß γ)	α ≤ ß + 1, ß + γ ≤ 9
	${ \mathrm{e}}_2^5$ (α) = (10-α ß 10-γ)	α = ß = γ = 5
	${ \mathrm{n}}_2^6$ (α) = (α 9-ß 10-γ)	α + ß ≥ 9, γ ≥ ß + 1→ Impossible
	${ \mathrm{n}}_2^7$ (α) = (10-α 9-ß 10-γ)	α ≤ ß + 1, γ ≥ ß + 1→ Impossible
Group II Based on (5a) or (5b) α = (α ß 0)	${ \mathrm{e}}_2^0$ (α) = (α ß 0)	1 ≤ α ≤ 9, 1 ≤ ß ≤ 9, γ = 0
	${ \mathrm{e}}_2^8$ (α) = (10-α ß 0)	α + ß ≤ 10
	${ \mathrm{e}}_2^9$ (α) = (α 10-ß 0)	α + ß ≥ 10
	${ \mathrm{e}}_2^{10}$ (α) = (10-α 10-ß 0)	α = ß
Group III Based on (6) α = (α 0 0)	${ \mathrm{e}}_2^0$ (α) = (α 0 0)	1 ≤ α ≤ 9
	${ \mathrm{e}}_2^{11}$ (α) = (11-α 0 0)	2 ≤ α ≤ 9
	Equivalences R2 in A6
Group IV α = (α ß γ)	${ \mathrm{e}}_2^0$ (α) = (α ß γ)	1 ≤ α ≤ 9, 1 ≤ ß ≤ 9, 1 ≤ γ ≤ 9
	${ \mathrm{e}}_2^{12}$ (α) = (10- γ 9-ß 10-α)	1 ≤ α ≤ 9, 1 ≤ ß ≤ 8, 1 ≤ γ ≤ 8, α ≥ ß + 1

Table 4. Derivative equivalences in A₆, α = (α ß γ).

Equivalence	Domain of Existence	Example
$({\mathrm{e}}_2^1\times {\mathrm{e}}_2^{12})$ (α) = (γ 9-ß 10-α)	α ≥ ß + 1, ß + γ ≥ 9	963 R2 331
$({\mathrm{e}}_2^2\times {\mathrm{e}}_2^{12})$ (α) = (10-γ ß 10-α)	α + ß ≥ 10, ß + γ ≤ 10	963 R2 761
$({\mathrm{e}}_2^3\times {\mathrm{e}}_2^{12})$ (α) = (10-γ 9-ß α)	α + ß ≤ 9	221 R2 972
$({\mathrm{e}}_2^4\times {\mathrm{e}}_2^{12})$ (α) = (γ ß 10-α)	α + ß ≥ 10, ß = γ	933 R2 331
$({\mathrm{n}}_2^6\times {\mathrm{e}}_2^{12})$ (α) = (10-γ ß α)	α = ß, ß + γ ≤ 10	772 R2 877
$({\mathrm{n}}_2^7\times {\mathrm{e}}_2^{12})$ (α) = (γ ß α)	α = ß = γ	333 R2 333

Some of these derivative equivalences are not reciprocal, but

α₁ ${ \mathrm{R}}_2^{\mathrm{i}}$ α₂ → α₂ R₂ α₁, because K (α₁) = K (α₂). Thus, there is always another ${ \mathrm{R}}_2^{\mathrm{j}}$ such that α₂ ${ \mathrm{R}}_2^{\mathrm{j}}$ α₁.

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{51}}$α₂, α₁ = (α 0 0), α₂ = [(α + 9)/2 (19-α)/2 5], α = 5, 7, 9, w =$\dot{\mathbf{2}}$

Indeed, under (30), K₃₁ (α) = (${ \mathsf{\alpha }}_1^1$-1 10-${ \mathsf{\alpha }}_1^1$ 0 $\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$ 0) under (15) with (16),

K₁ (${ \mathsf{\alpha }}_2^1$ ${ \mathsf{\alpha }}_2^2$ $\dots { \mathsf{\alpha }}_2^h$) = (2${ \mathsf{\alpha }}_2^1$-10 2${ \mathsf{\alpha }}_2^2$-9 … 2${ \mathsf{\alpha }}_2^{h-1}$-9 2${ \mathsf{\alpha }}_2^h$-10).

$${\mathrm{K}}_{31} \left({\mathsf{\alpha }}_1\right)={\mathrm{K}}_1 \left({\mathsf{\alpha }}_2\right) \to { \mathsf{\alpha }}_1^1-1=2{ \mathsf{\alpha }}_2^1-10; 10-{ \mathsf{\alpha }}_1^1=2{ \mathsf{\alpha }}_2^2-9$$

2${ \mathsf{\alpha }}_2^s$-9 = 0, s ≥ 3, … h-1; 2${ \mathsf{\alpha }}_2^h$-10 = 0. These conditions are only possible if h = 3, yielding

$${ \mathsf{\alpha }}_2^1=({ \mathsf{\alpha }}_1^1+9)/2, { \mathsf{\alpha }}_2^2=(19-{ \mathsf{\alpha }}_1^1)/2, { \mathsf{\alpha }}_2^3=5, { \mathsf{\alpha }}_1^1=5, 7, 9$$

$$500{ \mathrm{R}}_2^{51} 775, 700 { \mathrm{R}}_2^{51} 865, 900{ \mathrm{R}}_2^{51} 955.$$

–

Equivalence α₁$R_{\mathbf{2}}^{\mathbf{52}}$α₂, α₁ = (α 0 0), α₂ = [(10-(α/2) 4 + (α/2) 5], α = 2, 4, 6, w =$\dot{\mathbf{2}}$

This results from using K₃₂ (α₁) instead of K₃₁ (α₁).

As a consequence, 200 ${ \mathrm{R}}_2^{52}$ 955, 400 ${ \mathrm{R}}_2^{52}$ 865 and 600 ${ \mathrm{R}}_2^{52}$ 775.

Note that classes 100, 300 and 800 are excluded from ${ \mathrm{R}}_2^{52}$. Class 100 does not have an equivalent R₂ different from itself and 300 ${ \mathrm{R}}_2^3 800$.

Equivalences ${ \mathrm{R}}_2^{51}$ and ${ \mathrm{R}}_2^{52}$ do not operate on numbers with w-digits, w = $\dot{2}$ + 1.

–

In A_w, w = $\dot{2}$ + 1, there are specific equivalences R₂, unshared with w = $\dot{2}$. However, such R₂ vary with w, and thus general expressions do not exist. Table 5 shows all those existing in A₇ and A₅. Some of these equivalences, such as ${ \mathrm{e}}_2^{61}$, also generate equivalences R₂ from the same sequence, e.g., 977 R₂ 973. Furthermore, if the domains of existence of K_i and K_j have classes (α ß γ) in common, they generate equivalences R₁.

Table 5. Equivalences R₂ in A_w, w = $\dot{2}$ + 1, not found in w = $\dot{2}$.

All Equivalences R2 Unique to A7 (1)
Equivalences R2	Valid for	Derives from Ki(α1) = Kj (α2)
$e_2^{61}(\mathsf{\alpha } ß \mathsf{\gamma })=[\mathsf{\alpha } (ß+\mathsf{\gamma })/2 10-ß]$	986 R2 972, 975 R2 963, 875 R2 863	K1, K7
$e_2^{62}(\mathsf{\alpha } ß \mathsf{\gamma })=\left[\right(\mathsf{\alpha }+ß+1)/2 ß+\mathsf{\gamma }-\mathsf{\alpha }+2 11-\mathsf{\alpha }]$	986 R2 972, 985 R2 962, 966 R2 852, 875 R2 863	K1, K4
$e_2^{63}(\mathsf{\alpha } ß \mathsf{\gamma })=(\mathsf{\alpha } 10-\mathsf{\gamma } 11-ß)$	981 R2 993, 971 R2 994, 972 R2 984, 961 R2 995, 962 R2 985, 872 R2 884, 862 R2 885, 863 R2 875, 763 R2 775	K4, K13
$e_2^{64}(\mathsf{\alpha } ß \mathsf{\gamma })=(\mathsf{\alpha } 10-\mathsf{\gamma } ß+2)$	931 R2 995, 921 R2 994, 911 R2 993, 932 R2 985, 922 R2 984, 832 R2 885, 822 R2 884, 833 R2 875, 733 R2 775	K5, K13
$e_2^{65}(\mathsf{\alpha } ß 0)=(11-ß \mathsf{\alpha }+ß-3 21-2\mathsf{\alpha }-ß)$	720 R2 965, 630 R2 866	K27, K1
$e_2^{66}(\mathsf{\alpha } ß 0)=(11-ß 9-\mathsf{\alpha }/2 13-\mathsf{\alpha }-ß)$	630 R2 864	K27, K7
$e_2^{67}(\mathsf{\alpha } ß 0)=(\mathsf{\alpha }+ß 18-2\mathsf{\alpha }-ß ß)$	610 R2 751, 520 R2 762	K27, K6
$e_2^{68}(\mathsf{\alpha } ß 0)=(20-2\mathsf{\alpha }-ß 10-\mathsf{\alpha }-ß ß)$	710 R2 521, 620 R2 622	K27, K11
$e_2^{69}(\mathsf{\alpha } ß 0)=(11-ß \mathsf{\alpha }+ß-3 12-\mathsf{\alpha })$	730 R2 875, 720 R2 965, 630 R2 866	K26, K1
$e_2^{70}(\mathsf{\alpha } ß 0)=(\mathsf{\alpha } 19-\mathsf{\alpha }-ß \mathsf{\alpha }+2ß-10)$	930 R2 975, 840 R2 876	K25, K1
$e_2^{71}(\mathsf{\alpha } ß 0)=(ß+1 \mathsf{\alpha }-4 ß-\mathsf{\alpha }+3)$	880 R2 943, 770 R2 833	K23, K12
$e_2^{72}(\mathsf{\alpha } ß 0)=\left[\right(\mathsf{\alpha }+9)/2 20-2ß 10-ß]$	770 R2 863	K23, K4
$e_2^{73}(\mathsf{\alpha } ß 0)=(5+ß/2 21-\mathsf{\alpha }-ß 10-\mathsf{\alpha })$	960 R2 862	K22, K4
All equivalences R2 unique to A5 (1)
$e_2^5(\mathsf{\alpha } ß)=[1/2 (\mathsf{\alpha }+ß+1) 11-\mathsf{\alpha }]$	85 R2 73, 96 R2 82	K1, K17 (2)
$e_2^6(\mathsf{\alpha } 0)=[1/2 (11-\mathsf{\alpha }) \mathsf{\alpha }]$	30 R2 43	K26, K14
$e_2^7(\mathsf{\alpha } 0)=(11-\mathsf{\alpha } 2\mathsf{\alpha }-3)$	40 R2 75	K26, K1
(2) Notation for functions Ki in A5 is independent to that one in A7. The permutations associated with Ki in A7 are shown in Table 2. The permutations associated with Ki in A3 are: P1 (1234), P17 (1342), P14 (4312) and P26 (2 1).

(1) There are no more different new R₂, except for those resulting from the transitivity (product) between R_2.

7.4.3. Equivalence Classes C₂

Equivalence classes C₂, which include numbers whose second transformations match, are an essential element in understanding the architecture of transformation trees. As an analogy, were parametric classes C₁ the leaves of a tree, classes C₂ would be the little branches that group the leaves together. The existence of equivalences R₂ contributes to new branches in the transformation schemes by means of cycles.

In Table 6, equivalence classes C₂ in A₆ are shown. Some classes C₁ do not have equivalent R₂, such as 555 $\in$ ${ \mathrm{C}}_2^{13}$, but others have up to 5 equivalents. Such is the case of ${ \mathrm{C}}_2^{74}$: any class 863, 833, 762, 732 and 332 belonging to it will become 643. Additionally, any number belonging to such classes will return the same image (642,654) after two transformations. In this example, 863 = α_c2, 643 = α_c3 and 642,654 = n_c4.

Table 6. Equivalence classes C₂ in A_6.

	Component A. Branch A
Equivalence Classes	${\mathbf{C}}_2^1$	${\mathbf{C}}_2^2$		${\mathbf{C}}_2^3$			${\mathbf{C}}_2^4$	${\mathbf{C}}_2^5$			${\mathbf{C}}_2^6$		${\mathbf{C}}_2^7$	${\mathbf{C}}_2^8$				${\mathbf{C}}_2^9$				${\mathbf{C}}_2^{10}$					${\mathbf{C}}_2^{11}$		${\mathbf{C}}_2^{12}$
Classes C1 = (α ß γ) included	966 964 661 631 431	100		832 862			655 554 544	955 900 551 541 200			753 743		810 210	965 531				985 511				970 930					870 830		877 873 772 722 322
Image of C2	832	900		753			210	810			531		970	830				870				873					772		654
αci and D *	861;14	863;14		863;14			643;14	643;14			643;14		421;14	421;14				421;14				852;14					852;14		751;14
Component A. Branch A (Continuation)
${\mathrm{C}}_2^{13}$	${\mathrm{C}}_2^{14}$	${\mathrm{C}}_2^{15}$		${\mathrm{C}}_2^{16}$			${\mathrm{C}}_2^{17}$	${\mathrm{C}}_2^{18}$			${\mathrm{C}}_2^{19}$		${\mathrm{C}}_2^{20}$	${\mathrm{C}}_2^{21}$				${\mathrm{C}}_2^{22}$				${\mathrm{C}}_2^{23}$					${\mathrm{C}}_2^{24}$
555	990 910 110	710 310		654 644 444			996 994	981 911 111			961 931		987 983 711 311	988 982 881 811 211				977 973 771 721 321				876 874 622 422					854 844 652 642 442
111	981	961		311			982	977			973		874	876				854				652					621
841;14	841;14	841;14		841;14			841;14	861;7			861;7		861;7	861;7				863;7				863;7					643;7
Component A. Branch B
${\mathrm{C}}_2^{25}$	${\mathrm{C}}_2^{26}$	${\mathrm{C}}_2^{27}$	${\mathrm{C}}_2^{28}$		${\mathrm{C}}_2^{29}$	${\mathrm{C}}_2^{30}$		${\mathrm{C}}_2^{31}$			${\mathrm{C}}_2^{32}$		${\mathrm{C}}_2^{33}$	${\mathrm{C}}_2^{34}$			${\mathrm{C}}_2^{35}$						${\mathrm{C}}_2^{36}$			${\mathrm{C}}_2^{37}$				${\mathrm{C}}_2^{38}$
995	980 920	888 882	770 730 330		666 664	775 600 500		963 933 761 731 331			540		665	800 300			853 843 752 742						660 640 440			720 320				954 944 651 641 441
980	882	775	761		331	540		843			640		320	720			641						651			860				821
751;14	841;14	861;14	863;14		863;14	863;14		643;14			643;14		643;14	643;14			421;14						421;14			421;14				852;14
Component A. Branch B (Continuation)
${\mathrm{C}}_2^{39}$	${\mathrm{C}}_2^{40}$	${\mathrm{C}}_2^{41}$	${\mathrm{C}}_2^{42}$		${\mathrm{C}}_2^{43}$	${\mathrm{C}}_2^{44}$		${\mathrm{C}}_2^{45}$			${\mathrm{C}}_2^{46}$		${\mathrm{C}}_2^{47}$	${\mathrm{C}}_2^{48}$							${\mathrm{C}}_2^{49}$				${\mathrm{C}}_2^{50}$					${\mathrm{C}}_2^{51}$
880 820 220	860 840	951 941	972 922 871 821 221		763 733 333	971 921		865 700 532 400			765 533		975 521	630 430							850				750					754 744 653 643 443
871	763	971	865		533	975		630			430		850	750							754				653					421
852;14	852;14	751;7	751;7		751;7	841;7		841;7			841;7		861;7	861;7							863;7				863;7					643;7
Component A. Branch C
Equivalence classes	${\mathrm{C}}_2^{52}$	${\mathrm{C}}_2^{53}$		${\mathrm{C}}_2^{54}$		${\mathrm{C}}_2^{55}$		${\mathrm{C}}_2^{56}$		${\mathrm{C}}_2^{57}$			${\mathrm{C}}_2^{58}$		${\mathrm{C}}_2^{59}$				${\mathrm{C}}_2^{60}$					${\mathrm{C}}_2^{61}$				${\mathrm{C}}_2^{62}$			${\mathrm{C}}_2^{63}$	${\mathrm{C}}_2^{64}$
Classes C1 = (α ß γ) incluided	999 991	998 992		997 993		875 522		986 984 611 411		776 774			650		950				777 773					872 822 222				542 552 855			755 553 543	610 410
Image of C2	997	986		984		650		872		542			552		855				553					755				610			410	952
αci and D	861;7	863;7		863;7		643;7		643;7		421;7			421;7		421;7				421;7					421;7				852;7			852;7	751;7
Component A. Cycle zone
${\mathrm{C}}_2^{65}$	${\mathrm{C}}_2^{66}$	${\mathrm{C}}_2^{67}$	${\mathrm{C}}_2^{68}$		${\mathrm{C}}_2^{69}$	${\mathrm{C}}_2^{70}$			${\mathrm{C}}_2^{71}$			${\mathrm{C}}_2^{72}$	${\mathrm{C}}_2^{73}$			${\mathrm{C}}_2^{74}$				${\mathrm{C}}_2^{75}$
520	530	510	620 420		886 884	863 833 762 732 332			976 974 621 421			852 842	953 943 751 741			952 942 851 841				962 932 861 831
842	741	943	851		762	643			852			751	841			861				863
421;7	852;7	852;7	751;7		861;7	863;7			421;7			852;7	751;7			841;7				861;7
Component B												Component C
${\mathrm{C}}_2^1$	${\mathrm{C}}_2^2$	${\mathrm{C}}_2^3$	${\mathrm{C}}_2^4$		${\mathrm{C}}_2^5$	${\mathrm{C}}_2^6$						${\mathrm{C}}_2^1$
885	887 883	760 740	766 764 663 633 433		960 940	866 864 662 432						550
760	764	662	432		864	632						550
632;3	632;3	632;2	632;2		632;2	632;1						550;0

* D stands for the number of necessary transformations so that any class C₁ belonging to a given ${\mathrm{C}}_2^{\mathrm{i}}$ becomes the stated class.

Scheme 2 shows the transformations of classes C₂ in A₆. When compared to Scheme 1, the structure of schemes stands out.

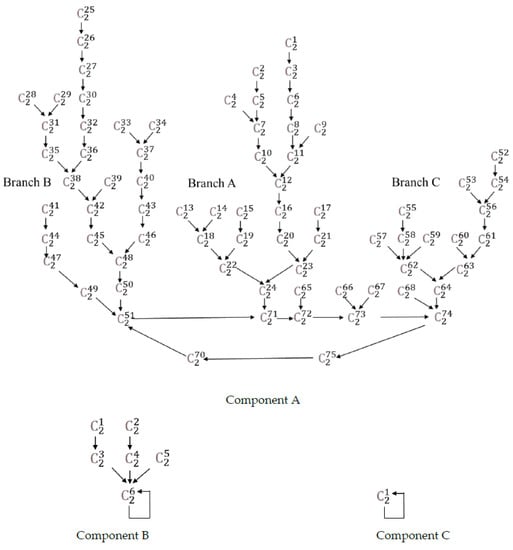
Scheme 2. Transformation scheme of equivalence classes C₂ in A_6.

7.5. Groups of Equivalence R₂

In theory, transpositions in those sequences compatible with the transformation functions should form subgroups of symmetric group S_h of all h-element possible permutations. This should be true for the product of those equivalences in Set I based on (4) or (6), those in Set II based on (8) or (10) and those in Set III based on (12).

However, generally speaking, this is not true for sets I and II. This is due to the fact that as h increases, some multiple transpositions are forbidden by (3). Such is the case of ${\mathrm{n}}_2^1{ \mathrm{and} \mathrm{n}}_2^2$ discussed in Section 7.4.1. Specifically, for A₆ and A₇, the product of equivalences e₂ and transpositions n₂ of Set I are shown in Table 7. Apart from the general associativity in the products of transpositions, as well as the existence of the neutral element $e_2^0$, it is also worth noting the involutory ${\mathrm{e}}_{2 }^{ \mathrm{i}}{\mathrm{x} \mathrm{e}}_2^{\mathrm{i}}={\mathrm{e}}_2^0$ ↔ $\left({\mathrm{e}}_2^{\mathrm{i}}\right)={\left({\mathrm{e}}_2^{\mathrm{i}}\right)}^{-1}\mathrm{and} \mathrm{abelian}$ ${\mathrm{e}}_{2 }^{ \mathrm{i}}{\mathrm{x} \mathrm{e}}_2^{\mathrm{j}}={\mathrm{e}}_{2 }^{ \mathrm{j}}{\mathrm{x} \mathrm{e}}_2^{\mathrm{i}}$ features. However, the product is no longer a closed binary relation between equivalences, since the product of some of them returns ${\mathrm{n}}_2^6{ \mathrm{or} \mathrm{n}}_2^7$, which although being transpositions, are not equivalences.

Table 7. Product of equivalences R₂ in A₆ and A₇ based on the transposition of digits from the same sequence. (f × g) (α) = f [g (α)]. (Equivalences e₂ are defined in Table 4).

Group I

$\mathrm{f}\backslash \mathrm{g}$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^5$

${\mathrm{n}}_2^6$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^5$

${\mathrm{n}}_2^6$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^3$

${\mathrm{n}}_2^7$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^0$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^1$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^5$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^0$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^1$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^0$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^3$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^1$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^2$

${\mathrm{n}}_2^6$

${\mathrm{n}}_2^6$

${\mathrm{n}}_2^7$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^1$

${\mathrm{n}}_2^7$

${\mathrm{n}}_2^7$

${\mathrm{n}}_2^6$

${\mathrm{e}}_2^5$

${\mathrm{e}}_2^4$

${\mathrm{e}}_2^3$

${\mathrm{e}}_2^2$

${\mathrm{e}}_2^1$

${\mathrm{e}}_2^0$

Group II

Group III

f\g

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^{10}$

f\g

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^{11}$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^{10}$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^{11}$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^{10}$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^{10}$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^{11}$

${\mathrm{e}}_2^{11}$

${\mathrm{e}}_2^0$

${\mathrm{e}}_2^{10}$

${\mathrm{e}}_2^{10}$

${\mathrm{e}}_2^9$

${\mathrm{e}}_2^8$

${\mathrm{e}}_2^0$

As h decreases, the forbidden general multiple transpositions ${\mathrm{n}}_2^1{ \mathrm{and} \mathrm{n}}_2^2$ disappear, and all transpositions generate equivalences. This happens when there are two non-null parameters—classes (α₁ α₂ 0$\begin{array}{c}\mathrm{h}-2\\ \breve{\dots \dots }\\ \end{array}$0) from Set II and (α₁ α₂) from Set I with h = 2. Table 7 (Group II) shows the product of equivalences for A₆ and A₇. The same is true for the four equivalences of Set I in A₄ and A₅. The product of the equivalence in these cases has an isomorph group structure of Klein group. This group is characterized because all of its elements coincide with their inverses. In addition, it is a subgroup of the symmetric group S₄ of all four-element possible permutations.

When the number of non-null parameters decreases to 1, a cyclical subgroup isomorphic to ℤ₂ appears. Such is the case of the general equivalence ${\mathrm{e}}_2^3$ (Section 7.4.1). Table 7 (Group III) shows the products for ${\mathrm{A}}_6$ and ${\mathrm{A}}_7.$ This situation also occurs in ${\mathrm{A}}_2$ and ${\mathrm{A}}_3$.

Naturally, any involutory equivalence, along with the identical, form a group isomorphic to ℤ₂. Such is the case of ${\mathrm{e}}_2^{11}$ in A₆, which in this case does not exist in A₇. However, its derivative functions (Table 4), along with the equivalence itself, do not have a subgroup structure, since the product of the former generates equivalences of Set I.

7.6. Symmetries R₃ and Higher

From (44) and (33) it results

α₁ R_r α₂ ↔ α′₁ R_r-1 α′₂, α′₁ = K_i (α₁), α′₂ = K_j (α₂)

(49)

Specifically: α₁ R₃ α₂ ↔ α′₁ R₂ α′₂

(50)

One of the approaches to obtain the algebraic expressions of equivalences R₃ is based on this expression. If an equivalence R₂ is imposed on the images of two classes α₁ and α₂, K_i (α₁) and K_j (α₂), the result will be an algebraic relation between α₁ and α₂ so that α₁ R₃ α₂:

(e₂ x K_i) (α₁) = K_j (α₂)

(51)

As a few examples, we introduce the following equivalences:

Equivalence α₁$R_{\mathbf{3}}^{\mathbf{1}}$α₂, α₁ = (α¹ α² … α^h), α₂ = (15-α¹ α² … α^h)

$$\begin{array}{c}\mathrm{w}=\dot{2}; 6\le {\mathsf{\alpha }}^1\le 9; {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1, {\mathsf{\alpha }}^1+{\mathsf{\alpha }}^2\le 14; 5\le {\mathsf{\alpha }}^{\mathrm{s}}\le 6, \mathrm{s}\ge 2;\\ \mathrm{derives} \mathrm{from} e_2^{11} \mathrm{x} {\mathrm{K}}_1 \left({\mathsf{\alpha }}_1\right)={\mathrm{K}}_1 \left({\mathsf{\alpha }}_2\right)\end{array}$$

For example, in A₆:

$$(\mathsf{\alpha } ß \mathsf{\gamma }) { \mathrm{R}}_3^1 (15-\mathsf{\alpha } ß \mathsf{\gamma })$$

Which provides the following equivalences:

$$\mathrm{Component} \mathrm{A}: 955 { \mathrm{R}}_3^1 655, 865 { \mathrm{R}}_3^1 765, 855 { \mathrm{R}}_3^1 755;$$

$$\mathrm{Component} \mathrm{B}: 866 { \mathrm{R}}_3^1 766$$

or in terms of classes C₂, for (45)

$${ \mathrm{C}}_2^5{ \mathrm{R}}_3^{}{ \mathrm{C}}_2^4, { \mathrm{C}}_2^{45}{ \mathrm{R}}_3^{}{ \mathrm{C}}_2^{46}, { \mathrm{C}}_2^{65}{ \mathrm{R}}_3^{}{ \mathrm{C}}_2^{66}, { \mathrm{C}}_2^6{ \mathrm{R}}_3^{}{ \mathrm{C}}_2^4 (\mathrm{Component} \mathrm{B}).$$

Equivalence α₁${ \mathrm{R}}_3^2$ α₂, α₁ = (α¹ α² …α^h), α₂ = (α¹ α² …α^h−1 15-α^h)

$$\mathrm{w}=\dot{2}, 6\le {\mathsf{\alpha }}^{\mathrm{h}}\le 9, {\mathsf{\alpha }}^{\mathrm{h}-1}+{\mathsf{\alpha }}^{\mathrm{h}}\ge 15, {\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1$$

derives from ${\mathrm{e}}_2^{13}$ × K₁ (α₁) = K₁ (α₂).

For example, in A₆:

$$(\mathsf{\alpha } ß \mathsf{\gamma }) R_3^2 (\mathsf{\alpha } ß 15-\mathsf{\gamma }) \mathrm{valid} \mathrm{for}$$

$$988 R_3^2 987, 987 R_3^2 988 \to {\mathrm{C}}_2^{21} {\mathrm{R}}_3 {\mathrm{C}}_2^{20}$$

Equivalence α₁${ \mathrm{R}}_3^3$ α₂, α₁ = (α¹ α² … α^h), α₂ = (α¹ α² … α^h−1 28-2α^{h − 1}-α^h)

$$\begin{gathered} \mathrm{w}=\dot{2}+1, 5<{\mathsf{\alpha }}^1\ge {\mathsf{\alpha }}^2+1, 5 \le {\mathsf{\alpha }}^{\mathrm{s}}\le 8, \mathrm{s} > 1; {\mathsf{\alpha }}^{\mathrm{s}}+{\mathsf{\alpha }}^{\mathrm{s}+1} \ge 9, \mathrm{s}=1, 2 \dots \mathrm{h}-1, 3 {\mathsf{\alpha }}^{\mathrm{h} – 1}+{\mathsf{\alpha }}^{\mathrm{h}}\ge 28 \\ 2{\mathsf{\alpha }}^{\mathrm{h}-1}+{\mathsf{\alpha }}^{\mathrm{h}}\le 23 \end{gathered}$$

derives from ${\mathrm{e}}_2^{13}$ × K₁ (α₁) = K₁ (α₂).

For example, in A₇:

$$(\mathsf{\alpha } ß \mathsf{\gamma }) {\mathrm{R}}_3^3(\mathsf{\alpha } ß 28-2ß-\mathsf{\gamma }) \mathrm{valid} \mathrm{for} \mathrm{the} \mathrm{new} \mathrm{equivalences}$$

$$987 {\mathrm{R}}_3^3 985, 985 {\mathrm{R}}_3^3 987 \mathrm{and} \mathrm{for} {\mathrm{R}}_1 986, 977 \mathrm{y} 877$$

Equivalence α₁${ \mathrm{R}}_3^4$ α₂, α₁ = (α 0 0), α₂ = [1/2 (21-α) 5 5]

Equivalence R₃ is often limited to a couple of classes. Such is the case of

$${\mathrm{e}}_2^8 \times {\mathrm{K}}_{31} \left({\mathsf{\alpha }}_1\right)={\mathrm{K}}_7 \left({\mathsf{\alpha }}_2\right) \mathrm{in} {\mathrm{A}}_6.$$

$${\mathrm{e}}_2^8 \times {\mathrm{K}}_{31} ({\mathsf{\alpha }}_1 0 0)=(11-{\mathsf{\alpha }}_1 10-{\mathsf{\alpha }}_1 0)=(2{\mathsf{\alpha }}_2-10 {ß}_2-{\mathsf{\gamma }}_2+1 {ß}_2- {\mathsf{\gamma }}_2)={\mathrm{K}}_7 \left({\mathsf{\alpha }}_2\right)$$

which entails γ₂ = ß₂, α₁ = 9, α₂ = 6, and since K₇ demands 5 ≤ ß ≤ 8 y 2 ≤ γ ≤ 5 → γ = ß = 5.

The equivalence is reduced to 900 ${\mathrm{R}}_3^4$ 655.

This situation becomes generalized when increasing the order of the equivalence. Thus, in A₇:

Equivalence α₁${ \mathrm{R}}_4^1$ α₂, α₁ = (α ß γ), α₂ = (α 48-4α-ß + 2γ γ)

derives from ${\mathrm{e}}_3^3$ x K₄ (α₁) = K₄ (α₂), only valid for 981 ${ \mathrm{R}}_4^1$ 961, which answers another of the questions in the introduction:

5,068,069 R₄ 3,071,934 because p(5,068,069) = 981 and p(3,071,934) = 961

Equivalence 533 ${ \mathrm{R}}_7^1$ 621

Indeed, $K^6$ (533) = $K^6$(621) = 864. Or, equivalently, m = 4,687,437, p(m) = 533, n = 4,693,554, p(n) = (621), $K^7$(m) = $K^7$(n) = 8,639,532 → m R₇ n.

However, the algebraic relation between 533 and 621, or between m and n, as in the two previous examples, is not extendible to other classes α₁ R₇ α_2.

As order r of equivalence R_r increases, it is less interesting to establish the determining algebraic relation.

7.7. Symmetries and Cycles

The schemes are articulated on the cycles, whether they have several links r or only one (transformation constants).

Equivalence classes C_r group numbers with the same image C_r-1. In general, α₁ R_s α₂ ↔ α′₁ R_s-1 α′₂. For example, classes C₁ 963, 933, 761, 731 and 331 all belong to ${ \mathrm{C}}_2^{31}$ because their image is the same, 843 (Table 6). Analogously, ${ \mathrm{C}}_4^4$ and ${ \mathrm{C}}_4^5$ belong to the same class C₅ because they have the same image ${ \mathrm{C}}_4^6$ (Scheme 3). This relation forces the transformation tree to swallow the leaves and little branches as s increases, and therefore, only the big branches and the trunk remain visible, using an analog language.

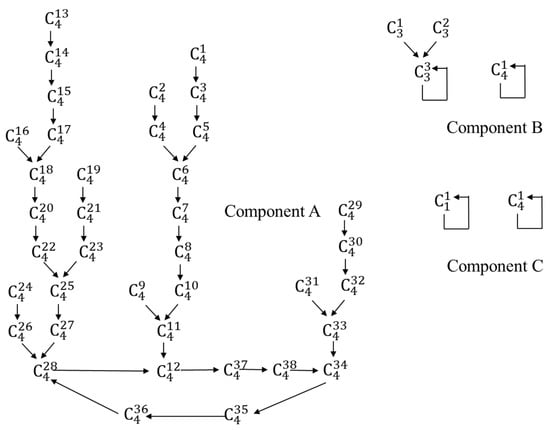
Scheme 3. Transformations between equivalence classes C₄ in A_6. (C₃ are included in component B, while C₁ appear in component C).

The absorption process occurs in the whole scheme as well as in the cycles. The latter act as black holes that swallow those classes converging with them. Each class ${ \mathrm{C}}_{\mathrm{s}}^{}$(ci) from the cycle groups with classes C_s which have ${ \mathrm{C}}_{\mathrm{s}}^{}$(ci + 1) as an image from the cycle, resulting in a new class ${ \mathrm{C}}_{\mathrm{s} +1}^{}$ (cj). The process continues until C_s = C_{s + 1} for all classes C_s in the scheme. This way, we reach the top of new equivalences R_s = R_u, where there are only as many classes C_u as there are links r in the cycle,${ \mathrm{C}}_{\mathrm{u} }^{\mathrm{i}}$, i = 1, 2, … r.

Each class ${ \mathrm{C}}_{\mathrm{u}}^{\mathrm{i}}$ belongs to the cycle and groups all classes C_s, s = 0, 1, 2…u-1, whose distance (number of transformations) to α_ci is a multiple of r. Thus, the number of links in the cycle establishes the distance pattern for the subsequent groups.

For instance, Table 8 shows the seven classes ${ \mathrm{C}}_{\mathrm{u}}^{\mathrm{i}}$ resulting from u = 13 transformations in component A from A₆. As stated several times, component A has a cycle of r = 7 links. Class 661 $\in { \mathrm{C}}_2^1$ ⊂${ \mathrm{C}}_4^1$ ⊂ ${ \mathrm{C}}_{13}^1$ and α_C1 = 861 $\in { \mathrm{C}}_2^{75}$ ⊂${ \mathrm{C}}_4^{28}$ ⊂ ${ \mathrm{C}}_{13}^1$ (Table 6). Class 661 needs 14 (2 x r) transformations to become 861—the same number of transformations that ${ \mathrm{C}}_2^1$ needs to reach ${ \mathrm{C}}_2^{75}$ (Scheme 2) or ${\mathrm{C}}_4^1$ to reach ${ \mathrm{C}}_4^{28}$ (Scheme 3). Class 430 $\in { \mathrm{C}}_2^{48}$ only requires r = 7 transformations.

Table 8. Inclusion relations C₂ ⊂ C₄ ⊂ C₁₃ in A_6.

${\mathrm{C}}_{13}^1$ *

${\mathrm{C}}_{13}^2$

${\mathrm{C}}_{13}^3$

${\mathrm{C}}_{13}^4$

${\mathrm{C}}_{13}^5$

${\mathrm{C}}_{13}^6$

${\mathrm{C}}_{13}^7$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2$

${\mathrm{C}}_4$

${\mathrm{C}}_2^1$

${\mathrm{C}}_4^1$

${\mathrm{C}}_2^2$

${\mathrm{C}}_4^2$

${\mathrm{C}}_2^4,{\mathrm{C}}_2^5$

${\mathrm{C}}_4^4$

${\mathrm{C}}_2^7,{\mathrm{C}}_2^8,{\mathrm{C}}_2^9$

${\mathrm{C}}_4^6$

${\mathrm{C}}_2^{10},{\mathrm{C}}_2^{11}$

${\mathrm{C}}_4^7$

${\mathrm{C}}_2^{12}$

${\mathrm{C}}_4^8$

${\mathrm{C}}_2^{13},{\mathrm{C}}_2^{14},{\mathrm{C}}_2^{15}$

${\mathrm{C}}_4^9$

${\mathrm{C}}_2^{18},{\mathrm{C}}_2^{19},{\mathrm{C}}_2^{20},{\mathrm{C}}_2^{21}$

${\mathrm{C}}_4^{11}$

${\mathrm{C}}_2^3$

${\mathrm{C}}_4^3$

${\mathrm{C}}_2^6$

${\mathrm{C}}_4^5$

${\mathrm{C}}_2^{35},{\mathrm{C}}_2^{36}$

${\mathrm{C}}_4^{20}$

${\mathrm{C}}_2^{38},{\mathrm{C}}_2^{39}$

${\mathrm{C}}_4^{22}$

${\mathrm{C}}_2^{25}$

${\mathrm{C}}_4^{13}$

${\mathrm{C}}_2^{16},{\mathrm{C}}_2^{17}$

${\mathrm{C}}_4^{10}$

${\mathrm{C}}_2^{27}$

${\mathrm{C}}_4^{15}$

${\mathrm{C}}_2^{28},{\mathrm{C}}_2^{29}$

${\mathrm{C}}_4^{16}$

${\mathrm{C}}_2^{24},{\mathrm{C}}_2^{51}$

${\mathrm{C}}_4^{37}$

${\mathrm{C}}_2^{37}$

${\mathrm{C}}_4^{21}$

${\mathrm{C}}_2^{40}$

${\mathrm{C}}_4^{23}$

${\mathrm{C}}_2^{41}$

${\mathrm{C}}_4^{24}$

${\mathrm{C}}_2^{26}$

${\mathrm{C}}_4^{14}$

${\mathrm{C}}_2^{52}$

${\mathrm{C}}_4^{29}$

${\mathrm{C}}_2^{30}$

${\mathrm{C}}_4^{17}$

${\mathrm{C}}_2^{31},{\mathrm{C}}_2^{32}$

${\mathrm{C}}_4^{18}$

${\mathrm{C}}_2^{57},{\mathrm{C}}_2^{58},{\mathrm{C}}_2^{59},{\mathrm{C}}_2^{60},{\mathrm{C}}_2^{61}$

${\mathrm{C}}_4^{33}$

${\mathrm{C}}_2^{62},{\mathrm{C}}_2^{63},{\mathrm{C}}_2^{66},{\mathrm{C}}_2^{67},C_2^{72}$

$C_4^{34}$

${\mathrm{C}}_2^{42},{\mathrm{C}}_2^{43}$

${\mathrm{C}}_4^{25}$

${\mathrm{C}}_2^{44}$

${\mathrm{C}}_4^{26}$

${\mathrm{C}}_2^{47},{\mathrm{C}}_2^{48},{\mathrm{C}}_2^{69},C_2^{75}$

$C_4^{28}$

${\mathrm{C}}_2^{53},{\mathrm{C}}_2^{54}$

${\mathrm{C}}_4^{20}$

${\mathrm{C}}_2^{33},{\mathrm{C}}_2^{34}$

${\mathrm{C}}_4^{19}$

${\mathrm{C}}_2^{65},C_2^{71}$

$C_4^{38}$

${\mathrm{C}}_2^{64},{\mathrm{C}}_2^{68},C_2^{73}$

$C_4^{35}$

${\mathrm{C}}_2^{45},{\mathrm{C}}_2^{46}$

${\mathrm{C}}_4^{27}$

${\mathrm{C}}_2^{22},{\mathrm{C}}_2^{23},{\mathrm{C}}_2^{49},{\mathrm{C}}_2^{50},C_2^{70}$

$C_4^{12}$

${\mathrm{C}}_2^{55}$

${\mathrm{C}}_4^{31}$

$C_2^{74}$

$C_4^{36}$

${\mathrm{C}}_2^{56}$

${\mathrm{C}}_4^{32}$

* Class ${\mathrm{C}}_{13}^{\mathrm{i}}$ includes class α_ci. ${\mathrm{C}}_{13+\mathrm{r}}^{\mathrm{i}}={\mathrm{C}}_{13}^{\mathrm{I}},$ r > 0. Classes C₂ and C₄ containing α_ci are marked in bold.

8. Discussion

We understand symmetry as invariance during transformation. This has been the aim of this paper, trying to understand why sets of different numbers return identical images, not only with a single transformation, but with any number r of them. To this end, here, binary equivalence relations of order r were used. Two numbers m and n present an equivalence relation m R_r n if and only if $K^r$ (m) = $K^r$ (n). This simple relationship allows the numbers to be grouped into C_r equivalence classes such that all their numbers give the same transform after r transformations. The use of these equivalences together with the complete parameterization of the transformation by means of K_i functions enabled us to find algebraic relations which explain the invariance of transformations.

The first step was to parameterize numbers. Any number n can have some parameters α which determine its image. We established the general functions f that conduct such transformation f (α) = n′, n′ being the image of n under Kaprekar’s routine. These functions are similar to those established by (4). From here, equivalence classes of order 1 arise—those consisting of numbers with equal parameters and give the same transformed. The transformed numbers are multiples of 9 that satisfy some strict requirements. We analyzed this aspect in detail, as it conditions the existence of symmetries.

The second step was to determine the parameters α of the transformed number. Here lies one of the main problems with transformation. The transformed number need not have its digits sorted in ascending or descending order, which is a prerequisite to determine its parameters. The permutation that arranges the digits must therefore be established. However, this is no easy task, since the number of permutations grows factorially as the number of digits increases. Once both the permutation and the domain of existence have been established, α′ is automatically defined. We established the procedure to construct the functions K_i (α) = α ‘, each one associated with a permutation. It is a novel contribution.

With these tools, we were able to approach equivalences R_r of a higher order. For this, the simple relation α₁ R_r α₂ ↔ α′₁ R_r-1 α′₂ can be very useful. Starting from equivalences R₁, we can then move onto R₂, R₃, etc.

We showed that there are some R₂—relations which must exist between numbers for their second transformation to match– that are universal. Those in sets I, II and III are valid for numbers with both an even number of digits (w = $\dot{2}$) and an odd number (w = $\dot{2}$ + 1). Others are only valid for w = $\dot{2}$. Thus, for example, the numbers whose parameters are α₁ = (α¹ α² …α^h) give the same numbers after two transformations as those with parameters α₂ = (10-α^h 9-α^h−1 9-α^h−2 … 9-α³ 9-α² 10-α¹), a¹ ≥ a² + 1. It is a α₁ R₂ α₂ valid for w = 2 h, that is, for numbers with an even number of digits. It is an involutional equivalence.

The products of equivalences I and II only have group algebraic structures for low values of w. The equivalences of set I, for w = 4 or 5, while those of set II, for w = 6 or 7. Therefore, the group is isomorphic of the Klein group. The equivalences of set III are universal, thus generating a group isomorphic to ℤ₂. The reason why there are not any more groups lies in relation (3), which forces the parameters to be arranged. Many permutations violate this arrangement, resulting in transpositions without a domain of existence in the product of equivalences.

Recently, Bajorska-Harapinska et al. [19] showed interest in these algebraic structures. In the last section of their work, they made an attempt to introduce Kaprekar-style transformation in some algebraic structures. As an example, they defined two transformations in the spirit of Kaprekar on symmetric groups S_n.

The new higher equivalence classes demand increasingly narrow domains of existence. Their algebraic relation is often only valid for a few classes C_i. With this, they are less and less interesting as r increases.

The development of functions K_i allowed us to approach another feature of transformations—the relation between cycles and symmetries. Transformation schemes are articulated on cycles. They can be leafy or not. Thus, in A₆, component A contains 201 classes C₁ and it is articulated on a seven-link cycle. Component B contains 17 classes, and it is articulated on the constant 631,764, whose parameters are α_E = 632. Component C only contains class α_E = 550, whose numeric constant is 549,945. In A₇, the 219 existing parametric classes are grouped on an eight-link cycle. How many classes make up a component of a scheme will depend on the structure of functions K₁, or equivalently, on the compatibility between successive permutations. This compatibility varies with A_w.

Additionally, dependent on each A_w is the coexistence of cycles and constants—in A₂, there is a single cycle, in A₃ and A₄, a scheme of one component with a constant (a Kaprekar constant), in A₅, three cycles, in A₆, one cycle and two constants, in A₇, a single cycle, etc.

The structuration of the schemes in equivalence classes follows a grouping pattern mediated by the number of links in the cycle. This number establishes the “meter” of distances for the successive groupings of the equivalence classes.

In short, Kaprekar’s routine raised the issue of the uniqueness of its constants. Prichett et al. [4] showed that there are only two Kaprekar constants in base 10. Additionally, in this paper, we see that there are several unique facts. The basic transformation applied to numbers in base 10 forces not only the transformed number to be a multiple of 9, but also its digits to satisfy some strict requirements (5), (7) …. In many cases, such numeric and parametric restrictions (3) lead to uniqueness. The algebraization of Kaprekar’s routine has proven the existence of universal relations as well. Such is the case of some R₂ symmetries and the existence of universal groups, such as the Klein group.

We hope that our contribution will help arouse interest in this and other numeric transformations.

9. Conclusions

The combination of binary equivalence relations and parametric transformation functions has made it possible to configure a methodology capable of identifying and characterizing symmetries. Thus, we found algebraic relationships that determine these symmetries. Of particular interest are the symmetries associated with R₂ equivalences, that is, those that generate numerical invariance after two transformations. These equivalences, together with R₁, are the most frequent. We highlight:

(a)

R₂ equivalences corresponding to transformations of digits of the same sequence (type I)

$${\mathsf{\alpha }}_1 {\mathrm{R}}_2^{1\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{i}+1}, {\mathsf{\alpha }}_1=({\mathsf{\alpha }}^1 {\mathsf{\alpha }}^2 \dots {\mathsf{\alpha }}^{\mathrm{h}}) \mathrm{i}=1, 2, 3$$

α₂ = (10-α¹ α²….α^h), α¹ + α² ≤ 10

α₃ = (α¹ α² … α^s−1 9-α^s α^{s + 1} …α^h), s = 2, …h-1 α^s−1 + α^s ≥ 9, α^s + α^{s + 1} ≤ 9

α4 = (α¹ α²…α^h-1 10- α^h ), α^h−1 + α^h ≥ 10

where w is the number of digits, and w = 2 h + z with z = 0 if w is even and z = 1 if w is odd.

All the previous equivalences correspond to simple transpositions. Only the multiple transpositions indicated in the text are possible and they lead to ${\mathrm{R}}_2^{14}$, ${\mathrm{R}}_2^{15}$, ${\mathrm{R}}_2^{16}$ y ${\mathrm{R}}_2^{17}$.

Type II

If α₁ = (α¹ … α^r 0 $\begin{array}{c}\mathrm{h}-\mathrm{r}\\ \breve{\dots \dots }\\ \end{array}$ 0) then the previous equivalences are valid if we consider α^r as α^h. This gives rise to a family of equivalences ${\mathrm{R}}_2^{2i}$.

Type III

If α₁ = (α 0 $\begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array}$ 0) then α₁${ \mathrm{R}}_2^3$ (11-α 0 $\begin{array}{c}\mathrm{h}-1\\ \breve{\dots \dots }\\ \end{array}$ 0), α ≥ 2.

All equivalences are general, regardless of the number of digits.

(b)

Equivalences R₂ corresponding to permutation of different sequences.

${ \mathrm{R}}_2^4$ stands out for presenting few restrictions. α₁ ${ \mathrm{R}}_2^4$ α₂

α₁ = (α¹ α² … α^h), α₂ = (10-α^h 9-α^{h − 1} 9-α^{h − 2} … 9-α³ 9-α² 10-α¹)

α¹ ≥ α² + 1, w even and h = w/2

The R₃ equivalencies explain the numerical invariance after scheme transformations. We highlight:

$${\mathsf{\alpha }}_1{ \mathrm{R}}_3^i {\mathsf{\alpha }}_{\mathrm{i}+1}, {\mathsf{\alpha }}_1=({{\mathsf{\alpha }}^1}_{ }{\mathsf{\alpha }}^2{ }_{\dots } {\mathsf{\alpha }}^{\mathrm{h}}), \mathrm{i}=1, 2, 3$$

α₂ = (15-α¹ α²_… α^h)

α₃ = (α¹ α² …α^{h − 1} 15-α^h)

α₄ = (α¹ α² …α^{h − 1} 28-2α^{h − 1}-α^h)

with many more restrictions than R₂, as specified in the text.

More R₃ and higher equivalences are shown in the article. In particular, all the existing R₂ for w = 6 and w = 7 are shown.

The products of equivalences I and II only have group algebraic structures for low values of w. The equivalences of set I, for w = 4 or 5, while those of set II, for w = 6 or 7. Therefore, the group is isomorphic of the Klein group. The equivalences of set III are universal, thus generating a group isomorphic to ℤ₂.

The length of the cycles—its number of links—are the pattern of distances which determines how classes are grouped around the cycle’s nodes.

Parametric transformation functions have also been useful for studying constants and cycles. We show how families of constants can be derived directly from the K_i functions.