Abstract
Continuing the study of the Moyal Higher Spin Yang–Mills theory started in our previous paper we provide a detailed discussion of matter coupling and the corresponding tree-level amplitudes. We also start the investigation of the spectrum by expanding the master fields in terms of ordinary spacetime fields. We note that the spectrum can be consistent with unitarity while still preserving Lorentz covariance, albeit not in the usual way, but by employing an infinite-dimensional unitary representation of the Lorentz group.
1. Introduction
Higher Spin (HS) particles are a natural prediction of string theory, and therefore they can be expected to play quite a crucial role whenever we attempt to include the Standard Model in a consistent theory of Quantum Gravity. In recent years, stopping a historical neglect mainly due to the difficulty of describing them by a straightforward generalization of lower spin cases and their observational elusiveness, they started playing an increasingly relevant role in phenomenological studies of both collider physics and cosmology (see e.g., [1,2,3,4] and references therein). On the theoretical side, the onset of HS degrees of freedom has been put in a close connection to the avoidance of causality problems in graviton scattering amplitudes [5,6] and to the good UV behavior of string theory. The tensionless limit of string theory in which a massless HS gauge theory is expected to emerge has been in particular at the center of the recent developments in understanding the AdS/CFT duality [7,8,9,10,11,12,13,14,15,16,17] and in possibly describing the physical string theory as a broken phase of a fundamental gauge theory [18,19,20,21]. In light of this impressive progress, the long-standing program of formulating a HS gravity that generalizes Einstein gravity and that could offer a basis for consistently quantizing gravity within the context of quantum field theory has assumed a renewed importance and urgency. Unfortunately, the problem is notoriously a very hard one. In fact, whereas it is fair to say that the free massless HS spectrum is by now well understood [22,23,24,25,26,27,28,29,30,31], the construction of consistent interactions has turned out to be a much more challenging problem. A fundamental breakthrough has come with the discovery of Vasiliev’s equations for massless HS fields on AdS background [32,33,34], but the lack of a derivation from an action principle has so far hindered the understanding of off-shell properties, and in particular of quantization. On the other hand, until recently, considering HS on flat Minkowski background has been considered a hopeless option, given the vast amount of no-go results that have appeared over the time (see [35] and references), and in particular the presence of non-localities in quartic interactions has been shown to represent an obstacle [36,37,38,39,40,41]. However, similar obstructions have lately been discussed for the case of AdS background [42,43], pointing out in particular that bulk non-locality emerges at the level of quartic interactions. The essential issue does not seem therefore to be the choice of a curved rather than flat background, but rather understanding what kind of non-locality can be allowed in HS gravity. An important step towards constructing a HS interacting theory on flat Minkowski background has come in [44,45], which, albeit characterized by a complex Hamiltonian and trivial S-matrix, can be smoothly deformed to an AdS background, where it was shown to correctly reproduce three-point correlation functions of single-trace operators of Chern-Simons Matter theories by holographic correspondence [15]. It is therefore reasonable to assume the chiral and antichiral theories could correctly describe quantum complete and local subsectors of the conjectured nonlocal full interacting theory. These results are mostly obtained in the light-front formalism, which simplifies the algebra at the expense of explicit Lorentz covariance, and assumes the HS spectrum from the start, trying to derive a consistent deformation of the linearized HS gauge symmetry. While this is surely the safest path to keep the physical content of the theory under control, it is not inconceivable that such an approach (which is also at the basis of the aforementioned no-go theorems) may fail to capture the underlying geometrical structure and the background independence that a HS gravity could be expected to possess in direct analogy to spin 2 gravity.
On the other hand, starting from previous work [46,47], itself inspired by Segal’s construction of Conformal HS theory [48], an induced action approach has been developed [49,50,51,52], based on the Noether coupling of matter HS currents to HS external sources. This approach, although leading to an effective action with an infinite number of vertices whose explicit form can hardly be determined beyond the cases with lowest number of interacting fields, has the crucial advantages of assuming a very simple gauge symmetry in a form analogous to the one of Yang–Mills (YM) gauge models and inducing a natural Moyal-product structure in terms of which the HS couplings can be compactly written in terms of master fields in a non-commutative space including the ordinary spacetime and an auxiliary space of the same dimension. The simplest model in the class of theories possessing this symmetry is the Moyal-higher-spin YM (MHSYM) one studied in [52,53,54], which naturally allows for different backgrounds, and is an ideal setup for the study of classical solutions and the description of a HS geometry. Furthermore MHSYM can be considered as the most natural starting point to study the quantization of this class of theories, which is in principle made possible by the exact knowledge of the gauge symmetry. Of course the price one has to pay is that the physical content of the theory, the spectrum in the first place, is far from obvious, making it a legitimate question to what extent MHSYM is directly related to the other previously mentioned approaches. In this paper, we continue the study we started in [54], addressing the above issue in a straightforward way, namely by starting the study of the scattering amplitudes in the context of MHSYM.
In particular, in Section 2.1, after reviewing MHSYM, we discuss in detail the coupling of a matter sector to the gauge one and show that beside standard spacetime matter fields one can introduce matter in the form of master fields. In Section 3, as a preparatory step before the computation of amplitudes, we analyze the expansion of master fields in terms of ordinary spacetime ones. A crucial aspect is that, contrary to the standard lore about non-compact groups, we highlight the possibility of avoiding the onset of negative norm ghosts while salvaging the Lorentz covariance of the spacetime action and related scattering amplitudes. In Section 4 we calculate a few basic tree-level four-point amplitudes for different types of matter in the Euclidean formulation where one can use a representation in terms of an infinite tower of finite spin spacetime fields. We show that for the “minimal” matter (described by spacetime fields) amplitudes vanish when the set of outgoing momenta is different from the set of ingoing momenta while for matter described by master fields amplitudes have an exponential fall-off. Both results are promising in the sense that the amplitudes in the MHS theory possess much softer UV behavior when compared to the Maxwell theory. Finally, in Section 5, we recap our results and put forward possible future developments.
2. MHS Theory
2.1. MHS Local Symmetry and MHSYM Model
The structure of local Moyal-higher-spin (MHS) transformations is given by the Moyal bracket
where is a general infinitesimal function on the master space parameterizing infinitesimal MHS transformations (i.e., MHS variations). Master space is (locally) defined as , where is spacetime and is an auxiliary space, both having the same dimension d. Star product is defined to be the Moyal product in the master space (see Appendix A for more details)
The Jacobi identity now implies that the MHS transformations form an infinite dimensional non-abelian Lie algebra. As we review in Section 2.3.1, one way to arrive at the MHS structure is to gauge the generalized (or super-)translations, an infinite dimensional rigid symmetry present in all free field theories, by linearly coupling to an infinite tower of HS fields [46,47,51,52].
There are two basic types of MHS covariant objects. Those that transform in the fundamental representation
and those that transform in the adjoint representation
under MHS variations. The latter we call MHS tensors. Finite (large) MHS transformations in the fundamental representation are
and in the adjoint representation are
where is the exponential function defined by using the Moyal product in the Taylor expansion.
2.2. Gauge Sector: MHSYM Model
The basic object in the gauge sector is a MHS tensor called the MHS vielbein. The latin index on the MHS vielbein is a frame-like index which means that it is raised and lowered with the Minkowski metric (or Euclid metric if one is interested in the Euclidean theory). The simplest dynamical action is the MHSYM action given by
where
is the MHS torsion (for the origins of the “geometric” naming of the objects see Section 6 of [54]). The formalism can be put in the matrix model form, in which case MHSYM action (7) becomes
The MHS vielbein is represented by a linear operator acting on a particular Hilbert space on which “position operators” and their conjugate momenta are represented (note that unlike the standard YM field theory, in which one can separate trace in the internal space from spacetime integration, here this is not the case). The operator ordering is Weyl (symmetric).
The EoM of the MHSYM theory are
where the MHS covariant derivative of the general MHS tensor is defined by
In the case (pure MHSYM theory) vacua of the theory satisfy . In particular, there is a perturbatively stable vacuum given by
which describes empty Minkowski background. Expanding around this background
one obtains that transforms as a gauge potential under MHS variations,
and the MHS covariant derivative (11)
as well as the MHS torsion
take the form as in a standard YM gauge field theory.
In some cases it is more convenient to use canonical normalized fields and parameters. This is achieved by introducing a dimensionless auxiliary coordinate with
The dimension of is (length), the same as in the standard Maxwell or Yang–Mills theories, and in it is zero. In the canonical normalization cubic terms and quartic terms in the action have the coupling given by and , respectively, where D is the total number of spacetime derivatives in a given monomial (in this normalization the Moyal product now has an additional factor of ℓ in the exponential).
2.3. Matter Sector
We present here four types of matter that can be coupled in a way that respects MHS symmetry. The first three, described in Section 2.3.1, Section 2.3.2 and Section 2.3.3, were already studied in [54].
2.3.1. Minimal Matter: Spacetime Fields
It is possible to couple an ordinary relativistic spacetime field to the MHS vielbein (the subscript r denotes both Lorentz and internal indices). This approach was originally introduced in [46,47] for the case of the Klein–Gordon field and in [51,53] for the case of the Dirac field, and generalized to all spins in [54]. The procedure goes as follows. One starts from the action for a free field in flat spacetime, which in general has the form
where is a kinetic operator, e.g., for the complex scalar field it is given by . The (minimal) coupling is achieved by substituting with the MHS vielbein in the kinetic operator and taking the action to be
This naturally accommodates the operator (matrix model) formulation, where the matter configuration is represented by a state vector in the Hilbert space on which and act as linear operators. Matter fields are then simply wave functions in the x-representation
Matter fields transform under MHS symmetry as
while is a MHS tensor. It can be shown that the master Lagrangian in (19) is a MHS tensor, which means that the corresponding action is a MHS invariant. In the matrix model language the matter action (19) has the form
In particular, for the complex Klein–Gordon field one has,
while for the Dirac field,
where are Dirac matrices.
If one uses (13) then the matter actions can be written as
where is the action of the free matter field in flat spacetime, while describe the interaction between matter and the MHS potential . This reconfirms that the configuration (12) together with describes empty flat vacuum with the flat Minkowski (or Euclid) metric. Assuming analyticity we may Taylor expand master fields around ,
Using this it can be shown that the interaction part of the action for Klein–Gordon field minimally coupled to the MHS potential is
where
and are obtained by a Taylor expansion of master field defined by
Using (13) we see that
In case of the Dirac field one gets
where the HS currents [51,53] are
The currents present in interaction terms are conserved currents of free matter actions, in their “simple” forms, related to the rigid higher spin symmetries, which transform matter fields as
Note that this variation is exactly the same as the rigid MHS variation obtained from (21) by putting and Taylor expanding (26) in the parameter . This establishes a connection between MHS symmetry and HS symmetries.
2.3.2. Master Field Matter in Adjoint Representation
One can also take the matter fields in the adjoint representation (i.e. to be a MHS tensor), for which the covariant derivative is defined by
Assuming minimal coupling we get MHS symmetric actions by substituting . Here also, as in the MHS gauge sector, the master fields are real, the actions are defined in the non-geometric phases, and can be written in the form of matrix models.
Let us apply this to the free Majorana spin-1/2 field . The MHS action for minimal coupling is (when discussing Majorana spinors, d is assumed to be such that it allows for their existence)
In the operator formulation this is
The simplest supersymmetric MHS theory can be obtained by taking the action above together with the MHSYM action.
Minimal coupling applied to a real scalar field produces the following action
2.3.3. Master Field Matter in the Fundamental Representation. I
Matter in the fundamental representation of MHS symmetry transforms as
The oddity here is that one can construct two candidates for the MHS covariant derivative. The first one is
which is natural from the standard YM perspective, but cannot be defined outside the realm of expansion around the flat Minkowski background (13). It is also not natural from the perspective of a matrix model formulation. These shortfalls can be avoided using the prescription
From the relation
it is obvious that it differs from (39). The shortfall of the latter definition is that when the covariant derivative does not assume the standard form of an ordinary spacetime gradient.
Candidates for Lagrangian terms can be built using MHS invariants where minimal coupling is assumed, as before. MHS invariants can be built by Moyal-sandwiching MHS tensors between or from the left and or from the right.
To understand the origin of the degeneracy of minimal prescriptions, let us consider the example of master Dirac field . In this case it is easy to show that
where the version of the MHS covariant derivative is the one given by (39). The first two terms on the right hand side produce the same kinetic term that would be obtained by the minimal coupling prescription based on (39)
On the left hand side of (42) is an expression which takes a natural matrix model form when used in the action
The two actions differ by the second term on the right hand side of (42), which is a MHS scalar, and nonzero even for . Note that Lagrangian terms for matter in the fundamental representation are MHS scalars and therefore can be multiplied by functions of auxiliary coordinates without breaking any of the important symmetries. The symmetry under translations in the auxiliary space is broken by such factors. It is not obvious why we should try to protect this symmetry—of course, we should be careful not to break symmetries which we would like to preserve, such as Lorentz symmetry and translations in spacetime. Also note that the action (42) is formally defined for all phases of the MHS theory and takes care of hermicity automatically.
2.3.4. Master Field Matter in the Fundamental Representation. II
The fact that the Lagrangian for matter fields in the fundamental representation is MHS invariant opens up a new possibility for constructing theories in the matter sector. One constructs candidates for Lagrangian terms by constructing MHS scalars which are also Lorentz tensors and then multiplying them by Dirac delta function or its gradients . This way all important symmetries, namely Poincaré and MHS, are preserved (such action is Poincare and MHS invariant, while the symmetry under translations in the auxiliary space is not preserved).
Let us demonstrate this on the example of the Dirac master field, by taking the action to be
Note that it preserves Poincaré symmetry of spacetime and explicitly breaks the auxiliary space translations. Observe that now there is no difference between the two forms of the minimal prescription defined above. What is outstanding is that if one Taylor-expands both and around , as in (26), then one can integrate over u in (45) to obtain a purely spacetime action, i.e., an off-shell description in terms of an infinite tower of spacetime fields in Minkowski spacetime (we remind the reader that in the case of the MHS gauge sector such description exists in the Euclidean theory, but not in Minkowski spacetime). The quadratic part of the action is non-diagonal in spacetime fields. An additional bonus is that one can construct new types of Lagrangian terms, e.g., in the case of the Dirac master field one can add the MHS Lorentz term
In the spacetime description obtained by using Taylor expansion (26) for master fields, this term supplies the standard Lorentz term for the lowest (spin-1/2) spacetime component . We leave a more detailed analysis for future work.
3. Spacetime Description
3.1. Spacetime Fields and the Free Action
As we demonstrated in [54], by integrating MHS symmetric actions over the auxiliary space u one can obtain regular spacetime actions written in terms of the spacetime fields. The question is can we understand the content of the theory in terms of Wigner’s classification of irreducible representations of the Poincaré group (and in particular using finite spin representations only). In our previous paper [54] this question was left open, so let us expand on it here. For simplicity, we analyze the theory around the empty flat configuration, so that it is natural to work with the MHS potential defined by (13). The EoM of the pure MHSYM theory are then
From the structure of the coupling of minimal (spacetime) matter to the MHS potential it seems natural to pass to the purely spacetime formulation by using Taylor expansion (26) of the MHS potential,
This leads us to a description in terms of an infinite tower of spacetime fields . By plugging this into (47) and focusing on the linear part, one obtains that the spacetime fields satisfy Maxwell-like EoM whose form naively suggests that the theory should have problems with ghosts. However, as explained in [54], that line of reasoning is flawed since such expansion does not allow for the regular off-shell spacetime description.
Instead, a more promising idea is to use a complete orthonormal set of functions in the auxiliary space (here, we use the canonical normalization (17)),
to expand the MHS potential as
Now we can perform integrations over in the action, which are finite term by term. One gets that the quadratic part of spacetime action in MHSYM theory is diagonal, every term being of the Maxwell type
There are no ghost which cannot be eliminated using the gauge symmetry, which on the linear level acts on spacetime fields as
where are obtained from MHS gauge parameter in the same fashion as in (50). If one integrates the remaining, interacting, part of the MHSYM action over u, the result is purely spacetime action which is a weakly non-local functional of spacetime fields . The problem with this sort of expansion is that there is no manifestly covariant expansion of the type (50) with discrete index r which yields a direct sum of finite dimensional irreducible representations of the Lorentz group. Interestingly, this problem does not appear in the Euclidean MHSYM theory where instead of the Lorentz group one has the group of isometries.
For example, one can use the d-dimensional Hermite functions defined by (see Appendix B for more details on the Hermite basis)
where are Hermite polynomials defined by
Due to the presence of a Euclidean product in the exponential term, the subspaces spanned by basis elements with fixed define a finite dimensional unitary representations of the group, which is relevant if one is working with the Euclidean version of the theory. However, if we are interested in the physically more relevant case of Lorentzian theory, then the Lorentz transformations of Hermite functions
provide an intrinsically infinite dimensional unitary representation of the Lorentz group, satisfying
From the general theorem we know that this representation cannot be written as a direct sum of finite dimensional representations. This representation was discussed long time ago by Dirac in [55]. The conclusion is that the vector space of square integrable functions on the auxiliary space provides an infinite dimensional unitary representation of the Lorentz group. It is a reducible representation, which follows from the fact that each sector defined by N, where
is closed under the action of the Lorentz group and thus provides a representation by itself. Note that each sector provides an irreducible representation of the larger group [56].
The expansion (50) now takes the form
From (55) it follows that provide an intrinsically infinite dimensional representation of the Lorentz group defined by
The spacetime fields carry an infinite dimensional representation of the Lorentz group, which cannot be written as a direct sum of finite dimensional IRREPs. This shows that the MHS theory differs from standard HS approaches.
It is interesting to write solutions of linearized MHSYM EoM in the helicity basis. This is most efficiently done by using a complete orthonormal basis in the auxiliary space built over spherical harmonics , e.g.,
where are Laguerre functions, are spherical harmonics, and , , , . Then the plane wave solutions for MHS potential can be expanded in the helicity basis
with . Helicity is given by , which shows that there is an infinite number of fluctuations for every value of the helicity.
3.2. MHSYM 3-Vertex in Spacetime Description
The 3-vertex is proportional to:
which we expand as
The notation is explained in the Appendix C. In particular, in this subsection and in Appendices Appendix B and Appendix C we work in Euclidean and do not write the bar on u, i.e., we choose . (The restriction to Euclidean is due to simplicity. In principle it would be possible to carry out the calculations in Lorentzian signature. As explained in the text around (55), even in Lorentzian case one would need to use Euclidean version of in the exponent of the weight function of the Hermite polynomials. In addition one would need to use (distingishing and ) even though it breaks manifest Lorentz symmetry. As explained in the previous subsection, the Lorentz symmetry would remain in the form of infinite dimensional unitary representations.) Using (A41), we get
where . The coefficient can be read out from (A50). Taking traces of and plugging it in into (64), we get
where
and is a sum over all integer symmetric matrices (i.e., it represents 10 sums for , and where for convenience we have ) for which and . The indices in the last two lines of (65) contract with the term in the second line. Note that the number of indices in the last two lines is , i.e., they all contract. The sums are the same as in (A50).
By similar techniques an explicit expression for the four vertex can also be derived.
4. Calculation of Amplitudes
The idea here is to perform a few sample perturbative calculations in the realm of the MHSYM theory coupled to matter, to see if the MHSYM theory produces mathematically sensible results when quantized. First, we must first calculate the Feynman rules. For this we shall use canonical normalization (17) and expand all master fields in an orthonormal basis in auxiliary space, as described in (49) and (50). A benefit of this representation is that the MHS propagator is simple and obtained immediately from (51),
where we use the Feynman gauge.
As for the propagators and vertices which include matter, they depend on the type of matter, and are discussed below independently for all cases.
4.1. Minimal Spacetime Matter
4.1.1. Feynman Rules
Here matter is described by standard spacetime fields, as described in Section 2.3.1, so the propagators are of the usual form. To make the demonstration as simple as possible, we take matter to be a single Dirac field minimally coupled to the MHS vielbein.
To calculate vertices we use (19) with (24), which after using (50) and normalization (17), leads to the following form for the interacting part of the action
From this follows the expression for the interacting part of the Lagrangian density
where the currents are given by
There is only one type of vertex, depicted in Figure 1. If we denote by the outgoing fermion momentum and with q the ingoing fermion momentum, then the vertex contribution is
where the vertex factor is the MHS contribution to the standard QED result, and is given by
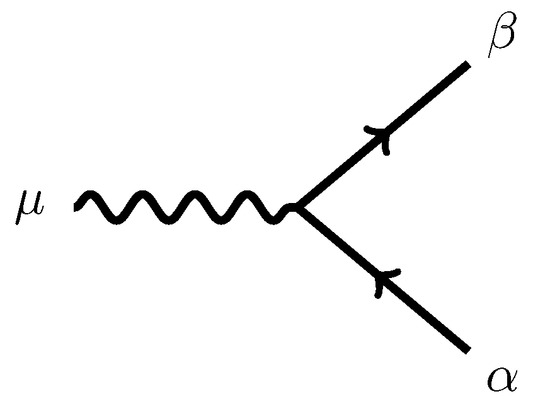
Figure 1.
Interaction vertex for the minimal coupling.
Comparing it to QED, we see that the difference is in the vertex functions given by the basis functions in the auxiliary space evaluated at
The basis functions vanish in the limit faster than any power, making the UV limit soft. The formula for the MHS vertex factor (71) suggests that the UV behavior of the MHSYM should be better than in QED.
4.1.2. Example: Four-Point Amplitude
As an example, we take the tree-level four-point amplitude for the Dirac field. There is effectively one Feynman diagram, shown in Figure 2, which has two channels: t and u.
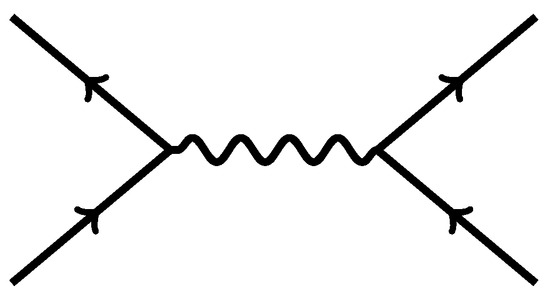
Figure 2.
Tree-level four-point amplitude Feynman diagram.
Let us start with the t-channel. Using the vertex (71) and the propagator (67) whose momentum is , the t-channel contribution reads
where is the QED result and is given by
In the last line we used the completeness relation
Finally, using the energy-momentum conservation condition
we obtain
The u-channel Feynman diagram is obtained simply by exchanging in the results for the t-channel, which means that the momentum of the propagator is , and
where
The full tree-level amplitude is then
It is vanishing unless the set of momenta in the final state is the same as the set of momenta in the initial state. This result is expected from the viewpoint of the Coleman-Mandula theorem, despite the fact that MHS theory does not fulfill all assumptions of the theorem. The result is also interesting from the perspective of the search for dark matter candidates in cosmology (for recent speculations that higher-spin particles may describe dark matter see [3]).
The MHSYM theory can be consistently truncated if we require (“truncation to spin-even sector”). In this case the basis functions are also odd, , and the completeness relation becomes
The t-channel amplitude is now
The main conclusion, that the amplitude is ultralocal in the momentum space, remains the same.
4.2. Master Space Matter in the Fundamental Representation
4.2.1. Feynman Rules
Now we assume that matter is represented by a single master Dirac field in the fundamental representation of the MHS symmetry (see Section 2.3.3). The free action is
while the interaction term is
where denotes the trace over spinor indices. Then we also expand the master Dirac field in the orthonormal basis in the auxiliary space
where is a spinor index. The basis used for the matter field does not have to be the same as the one used for the MHS potential. Using (85) in (83) gives us the propagator for the Dirac spacetime fields
where the first term on the RHS is the usual propagator for the Dirac field. Using (85) and (50) in (84) we obtain that the vertex is
where the QED vertex is
and the MHS vertex factor is given by
This completes the knowledge of Feynman rules in this theory. Again, compared to QED the difference is the presence of a vertex factor that softens the UV behavior.
4.2.2. Example: Four-Point Amplitude
We want to calculate the tree-level four-point amplitude with matter fields on all legs. Again, there is essentially one diagram, depicted in Figure 2, which has two channels. Let us first calculate the t-channel diagram. From Feynman rules calculated above we obtain the amplitude
where
In passing from second to third line the completeness relation was used. The u-channel contribution to the amplitude is obtained from (90) and (91) by exchanging and . The total tree-level amplitude is
There are no Dirac-delta functions which are present in the case of simple spacetime matter. The integral in (91) is convergent and, due to the asymptotic fall-off of functions when , the MHS contribution certainly makes the UV behavior softer when compared to the standard spinor QED. The basis functions are of the form
where are polynomials. Using this in (91) we obtain
where , and are polynomial functions. The exponential factor makes the UV behaviour much softer when compared to QED.
5. Conclusions
MHSYM is a novel approach to the construction of HS gravity, where, contrary to the standard Noether procedure, a specific form of the gauge symmetry, constrained by the coupling to matter HS currents, is assumed rather than the ordinary massless HS free spectrum. This makes the model the ideal setup to answer a wide range of questions that are hard to approach in the absence of an explicit action, as it happens in most of HS literature, such as the ones about background dependence, the HS-induced geometry, classical solutions, and the UV behavior of the theory after quantization. In this paper, we have set up the stage for such studies discussing the coupling to matter and the corresponding tree-level amplitudes. Our results suggest that the presence of master fields including gauge fields with unbounded spin can lead to non-standard couplings and produce scattering amplitudes with remarkable simplification properties that are unattainable when a finite number of HS particles is included. In particular we saw that in the case of ordinary spacetime matter one gets a four-particles scattering amplitudes ultralocal in momentum space, a result which is interesting from a perspective of the dark matter searches. In the case of master space matter in the fundamental representation, the ultralocal behavior is absent and the amplitudes are exponentially softened. We have singled out a physically relevant class of bases in the auxiliary space (orthonormal bases) for the Lorentzian MHSYM theory, which not only leads to a regular spacetime action but also furnishes an infinite dimensional unitary representation of the Lorentz group and is therefore free of the negative norm ghosts that affect finite dimensional representations in the absence of an explicit gauge symmetry.
In the future, it would be interesting to consider scattering amplitudes between HS-like particles. In this perspective we started analyzing the spectrum and pointing how unitarity may be preserved while keeping Lorentz covariance, at least at the perturbative level. We emphasize that when the theory is written in terms of spacetime fields, the Lorentz representations acting on fields are inherently infinite dimensional, which makes the MHS construction more akin to infinite spin theories than to more standard HS constructions which are based on (an infinite tower of) finite dimensional HS fields. This property of the MHS construction may be why the MHSYM theory apparently avoids the standard no-go theorems. Of course, the full study of S-matrix could provide the definitive confirmation of this expectation. It will be also interesting to pursue the Fadeev–Popov quantization of the theory along the lines already described in [53], the next step being the computation of one-loop quantum effective action, where the UV properties of MHSYM could be studied. In particular these results could be compared with the one-loop finiteness observed in [57,58]. One can also figure out that, by considering this model on an AdS background, one can provide an explicit bulk action to compare with the correlation functions of vector models on the AdS boundary, analogously to what was done in [15]. Of course, it would be crucial to be able to identify a consistent truncation to the chiral theory studied in [44].
Author Contributions
Conceptualization, M.C., P.D.P., S.G.G., M.P. and I.V.; methodology, M.C., P.D.P., S.G.G., M.P. and I.V.; software, M.C., P.D.P., S.G.G., M.P. and I.V.; validation, M.C., P.D.P., S.G.G., M.P. and I.V.; formal analysis, M.C., P.D.P., S.G.G., M.P. and I.V.; investigation, M.C., P.D.P., S.G.G., M.P. and I.V.; writing—original draft preparation, M.C., P.D.P., S.G.G., M.P. and I.V.; writing—review and editing, M.C., P.D.P., S.G.G., M.P. and I.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the University of Rijeka under the project uniri-prirod-18-256. The research of S.G. has been supported by the Israel Science Foundation (ISF), grant No. 244/17.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
P.D.P. would like to thank Erwin Schroedinger Institute for Mathematics and Physics (University of Vienna) for support during the visit under the framework of ESI Programme and Workshop “Higher Spins and Holography”, and Evgeny Skvortsov and Per Sundell for stimulating discussions. S.G is also grateful to Dario Francia, Per Sundell, Massimo Taronna, Konstantin Alkalaev, Alexey Sharapov, Evgeny Skvortsov, Xavier Bekaert, Euihun Joung and to the organizers and participants of the workshop “Higher Spin Gravity: Chaotic, Conformal and Algebraic Aspects” at the Asia Pacific Center for Theoretical Physics for discussions and comments on topics relevant to the paper. We especially thank Loriano Bonora as this work evolved from our mutual collaboration.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Properties of the Moyal Product
We use the following definition for the Moyal product of functions on the master space with coordinates :
The partial derivatives are defined in the usual way, i.e.,
The Moyal product is associative
and Hermitian under the complex conjugation
The Moyal product can, for a class of functions with well behaved fall of conditions, be calculated in the integral form
Note that the Moyal commutator of real functions is purely imaginary, while the Moyal anticommutator of real functions is real. It is important to note that the Moyal commutator obeys the Jacobi identity
and the derivation (or Leibniz) property
The same properties are obeyed by the ordinary (matrix) commutator. From (A7) it follows
The Moyal product satisfies the adjoint property under integration
where a, b and c are square-integrable functions on the master space. If we put we obtain
It is convenient to define deformations on standard functions on the master space by using Moyal instead of ordinary product in the Taylor expansion. We denote such functions with the ★ subscript, e.g.,
where is the Moyal product with n factors of
Appendix B. Hermite Basis
Let us consider the kinetic term
where
We can use condensed notation as in [59] (cf. also [60])
where . For the time being, just for the sake of simplicity, we choose . We define the weight function
such that
We now define the Hermite polynomial of order n as
where We can prove that
and, for generic order n,
where we are using the condensed notation
One can prove the orthogonality relation
where the subscripts and stand for m-tuples and n-tuples of indices taken respectively from the two sets and , and
Now one can readily write down the expansion
where
We see that
Using the facts that
and that
and
we see that
where
One can now see that the kinetic term can be written in the diagonal form
Appendix C. Further Hermite Basis
Here we develop necessary formulas to write the Moyal commutator of two MHS potentials. The notation is slightly different than in Appendix B.
Appendix C.1. Notation
Here the notation includes symmetrization with weight one, i.e., repeated indices (that are all down or all up, and are not dummy indices as in the product on the right hand side in the Equation (A37) below) are symmetrized. The number of indices is written in parenthesis i.e., is the same as . Some examples are: . Note that, contrary to the Appendix B, no other factors are implied in the notation. Similarly, and . If is symmetric we write the previous expression as . The trace is denoted by square brackets in the superscript . We give two more examples:
With respect to (A21), for further convenience we add a label denoting total number of indices
where instead of (A17) and (A18) the (multidimensional) Hermite polynomials are now written as
with given by (A15). These satisfy othogonality relations now written as
e.g., for Equation (A33) reads:
Sometimes we need to count how many of the indices have a value . The count is denoted by
and, by definition, has the property
Using we can e.g., write the product of m terms, , as the product of d terms, , with the corresponding powers:
Using this notation one can express multi-dimensional Hermite polynomials (A32) as a product of the standard one-dimensional (usually denoted by in the literature)
Using this (and knowing the inversion formula for one-dimensional Hermite polynomials) one can easily find the inversion formula for the multi-dimensional Hermite polynomials
Similarly, one gets the multiplication formula:
from which one obtains “orthogonality” relations with an adjusted power for the weight
where
The following relations are useful for the calculations of the next subsection
For reference we write also
Appendix C.2. Moyal Commutator in Hermite Basis
To calculate the 3-vertex, we need to expand the Moyal product of two MHS potentials using the Hermite basis. As a first step, we expand the potentials and the product and express the result using a single Hermite polynomial. Note that here the weight function is (each of the potentials contributes with ). We will deal with it in the integration in the next subsection. The product of the two potentials is:
where
and is a function that is 1 if and is even, and zero otherwise. The first few terms of this expansion are as follows
References
- Criado, J.C.; Djouadi, A.; Koivunen, N.; Raidal, M.; Veermäe, H. Higher-spin particles at high-energy colliders. JHEP 2021, 5, 254. [Google Scholar] [CrossRef]
- Falkowski, A.; Isabella, G.; Machado, C.S. On-shell effective theory for higher-spin dark matter. SciPost Phys. 2021, 10, 101. [Google Scholar] [CrossRef]
- Alexander, S.; Jenks, L.; McDonough, E. Higher Spin Dark Matter. Phys. Lett. B 2021, 819, 136436. [Google Scholar] [CrossRef]
- Criado, J.C.; Koivunen, N.; Raidal, M.; Veermäe, H. Dark matter of any spin–an effective field theory and applications. Phys. Rev. D 2020, 102, 125031. [Google Scholar] [CrossRef]
- Camanho, X.O.; Edelstein, J.D.; Maldacena, J.; Zhiboedov, A. Causality Constraints on Corrections to the Graviton Three-Point Coupling. JHEP 2016, 2016, 1–62. [Google Scholar] [CrossRef]
- Afkhami-Jeddi, N.; Kundu, S.; Tajdini, A. A Bound on Massive Higher Spin Particles. JHEP 2019, 4, 056. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213. [Google Scholar] [CrossRef]
- Petkou, A.C. Evaluating the AdS dual of the critical O(N) vector model. JHEP 2003, 3, 049. [Google Scholar] [CrossRef][Green Version]
- Giombi, S.; Yin, X. Higher Spin Gauge Theory and Holography: The Three-Point Functions. JHEP 2010, 9, 115. [Google Scholar] [CrossRef]
- Giombi, S.; Minwalla, S.; Prakash, S.; Trivedi, S.P.; Wadia, S.R.; Yin, X. Chern-Simons Theory with Vector Fermion Matter. Eur. Phys. J. C 2012, 72, 2112. [Google Scholar] [CrossRef]
- Aharony, O.; Gur-Ari, G.; Yacoby, R. d = 3 Bosonic Vector Models Coupled to Chern-Simons Gauge Theories. JHEP 2012, 3, 037. [Google Scholar] [CrossRef]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Towards holographic higher-spin interactions: Four-point functions and higher-spin exchange. JHEP 2015, 3, 170. [Google Scholar] [CrossRef]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Quartic AdS Interactions in Higher-Spin Gravity from Conformal Field Theory. JHEP 2015, 11, 149. [Google Scholar] [CrossRef]
- Sleight, C.; Taronna, M. Higher Spin Interactions from Conformal Field Theory: The Complete Cubic Couplings. Phys. Rev. Lett. 2016, 116, 181602. [Google Scholar] [CrossRef]
- Skvortsov, E. Light-Front Bootstrap for Chern-Simons Matter Theories. JHEP 2019, 6, 058. [Google Scholar] [CrossRef]
- Eberhardt, L.; Gaberdiel, M.R.; Gopakumar, R. Deriving the AdS3/CFT2 correspondence. JHEP 2020, 2, 136. [Google Scholar] [CrossRef]
- Aharony, O.; Chester, S.M.; Urbach, E.Y. A Derivation of AdS/CFT for Vector Models. JHEP 2021, 3, 208. [Google Scholar] [CrossRef]
- Gaberdiel, M.R.; Gopakumar, R. String Theory as a Higher Spin Theory. JHEP 2016, 9, 085. [Google Scholar] [CrossRef]
- Polyakov, D. Higher Spins and Open Strings: Quartic Interactions. Phys. Rev. D 2011, 83, 046005. [Google Scholar] [CrossRef]
- Polyakov, D. Gravitational Couplings of Higher Spins from String Theory. Int. J. Mod. Phys. A 2010, 25, 4623–4640. [Google Scholar] [CrossRef]
- Polyakov, D. Interactions of Massless Higher Spin Fields From String Theory. Phys. Rev. D 2010, 82, 066005. [Google Scholar] [CrossRef]
- Majorana, E. Relativistic theory of particles with arbitrary intrinsic angular momentum. Nuovo Cim. 1932, 9, 335–344. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Relativistic wave equations. Proc. R. Soc. Lond. A 1936, 155, 447–459. [Google Scholar] [CrossRef]
- Fierz, M. Force-free particles with any spin. Helv. Phys. Acta 1939, 12, 3–37. [Google Scholar]
- Pauli, W.; Fierz, M. On Relativistic Field Equations of Particles With Arbitrary Spin in an Electromagnetic Field. Helv. Phys. Acta 1939, 12, 297–300. [Google Scholar]
- Wigner, E.P. On Unitary Representations of the Inhomogeneous Lorentz Group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Fronsdal, C. Massless Fields with Integer Spin. Phys. Rev. D 1978, 18, 3624. [Google Scholar] [CrossRef]
- Francia, D.; Sagnotti, A. Free geometric equations for higher spins. Phys. Lett. B 2002, 543, 303–310. [Google Scholar] [CrossRef]
- Francia, D.; Mourad, J.; Sagnotti, A. Current Exchanges and Unconstrained Higher Spins. Nucl. Phys. B 2007, 773, 203–237. [Google Scholar] [CrossRef]
- Francia, D. Geometric Lagrangians for massive higher-spin fields. Nucl. Phys. B 2008, 796, 77–122. [Google Scholar] [CrossRef][Green Version]
- Campoleoni, A.; Francia, D. Maxwell-like Lagrangians for higher spins. JHEP 2013, 3, 168. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Consistent equation for interacting gauge fields of all spins in (3+1)-dimensions. Phys. Lett. B 1990, 243, 378–382. [Google Scholar] [CrossRef]
- Vasiliev, M.A. More on equations of motion for interacting massless fields of all spins in (3+1)-dimensions. Phys. Lett. B 1992, 285, 225–234. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Higher spin gauge theories in four-dimensions, three-dimensions, and two-dimensions. Int. J. Mod. Phys. D 1996, 5, 763–797. [Google Scholar] [CrossRef]
- Bekaert, X.; Boulanger, N.; Sundell, P. How higher-spin gravity surpasses the spin two barrier: No-go theorems versus yes-go examples. Rev. Mod. Phys. 2012, 84, 987. [Google Scholar] [CrossRef]
- Metsaev, R.R. Poincare invariant dynamics of massless higher spins: Fourth order analysis on mass shell. Mod. Phys. Lett. A 1991, 6, 359–367. [Google Scholar] [CrossRef]
- Taronna, M. Higher-Spin Interactions: Four-point functions and beyond. JHEP 2012, 4, 029. [Google Scholar] [CrossRef]
- Taronna, M. Higher-Spin Interactions: Three-point functions and beyond. arXiv 2012, arXiv:1209.5755. [Google Scholar]
- Joung, E.; Taronna, M. Cubic interaction induced deformations of higher-spin symmetries. JHEP 2014, 3, 103. [Google Scholar] [CrossRef]
- Taronna, M. On the Non-Local Obstruction to Interacting Higher Spins in Flat Space. JHEP 2017, 5, 026. [Google Scholar] [CrossRef]
- Roiban, R.; Tseytlin, A.A. On four-point interactions in massless higher spin theory in flat space. JHEP 2017, 4, 139. [Google Scholar] [CrossRef]
- Boulanger, N.; Kessel, P.; Skvortsov, E.D.; Taronna, M. Higher spin interactions in four-dimensions: Vasiliev versus Fronsdal. J. Phys. A 2016, 49, 095402. [Google Scholar] [CrossRef]
- Sleight, C.; Taronna, M. Higher-Spin Gauge Theories and Bulk Locality. Phys. Rev. Lett. 2018, 121, 171604. [Google Scholar] [CrossRef]
- Ponomarev, D.; Skvortsov, E.D. Light-Front Higher-Spin Theories in Flat Space. J. Phys. A 2017, 50, 095401. [Google Scholar] [CrossRef]
- Ponomarev, D. Chiral Higher Spin Theories and Self-Duality. JHEP 2017, 12, 141. [Google Scholar] [CrossRef]
- Bekaert, X.; Joung, E.; Mourad, J. On higher spin interactions with matter. JHEP 2009, 0905, 126. [Google Scholar] [CrossRef]
- Bekaert, X.; Joung, E.; Mourad, J. Effective action in a higher-spin background. JHEP 2011, 1102, 048. [Google Scholar] [CrossRef]
- Segal, A.Y. Conformal higher spin theory. Nucl. Phys. B 2003, 664, 59–130. [Google Scholar] [CrossRef]
- Bonora, L.; Cvitan, M.; Dominis Prester, P.; Giaccari, S.; De Souza, B.L.; Štemberga, T. One-loop effective actions and higher spins. JHEP 2016, 1612, 084. [Google Scholar] [CrossRef]
- Bonora, L.; Cvitan, M.; Dominis Prester, P.; Giaccari, S.; Štemberga, T. One-loop effective actions and higher spins. Part II. JHEP 2018, 1801, 080. [Google Scholar] [CrossRef]
- Bonora, L.; Cvitan, M.; Dominis Prester, P.; Giaccari, S.; Paulisic, M.; Stemberga, T. Worldline quantization of field theory, effective actions and L∞ structure. JHEP 2018, 1804, 095. [Google Scholar] [CrossRef]
- Bonora, L.; Cvitan, M.; Dominis Prester, P.; Giaccari, S.; Stemberga, T. HS in flat spacetime. The effective action method. Eur. Phys. J. C 2019, 79, 258. [Google Scholar] [CrossRef]
- Bonora, L.; Cvitan, M.; Dominis Prester, P.; Giaccari, S.; Stemberga, T. HS in flat spacetime. YM-like models. arXiv 2018, arXiv:1812.05030. [Google Scholar]
- Cvitan, M.; Dominis Prester, P.; Giaccari, S.; Paulišić, M.; Vuković, I. Gauging the higher-spin-like symmetries by the Moyal product. JHEP 2021, 6, 144. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Unitary Representations of the Lorentz Group. Proc. R. Soc. Lond. A 1945, 183, 284–295. [Google Scholar]
- Bars, I. Relativistic Harmonic Oscillator Revisited. Phys. Rev. D 2009, 79, 045009. [Google Scholar] [CrossRef]
- Skvortsov, E.; Tran, T. One-loop Finiteness of Chiral Higher Spin Gravity. JHEP 2020, 7, 021. [Google Scholar] [CrossRef]
- Skvortsov, E.; Tran, T.; Tsulaia, M. More on Quantum Chiral Higher Spin Gravity. Phys. Rev. D 2020, 101, 106001. [Google Scholar] [CrossRef]
- Grad, H. Note on N-dimensional Hermite polynomials. Commun. Pure Appl. Math. 1949, 2, 325–330. [Google Scholar] [CrossRef]
- Patarroyo, K.Y. A digression on Hermite polynomials. arXiv 2019, arXiv:1901.01648. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).