A Simple Semi-Analytic Contact Mechanical Model for Tangential and Torsional Fretting Wear of Axisymmetric Contacts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fundamental Assumptions
2.2. Elementary Axisymmetric Contact Solutions
2.3. Numerical Implementation of the Abel-Like Integral Transforms
3. Results
3.1. Model for Tangential Fretting Wear
3.2. Comparison with a Contact Mechanically More Rigorous Model
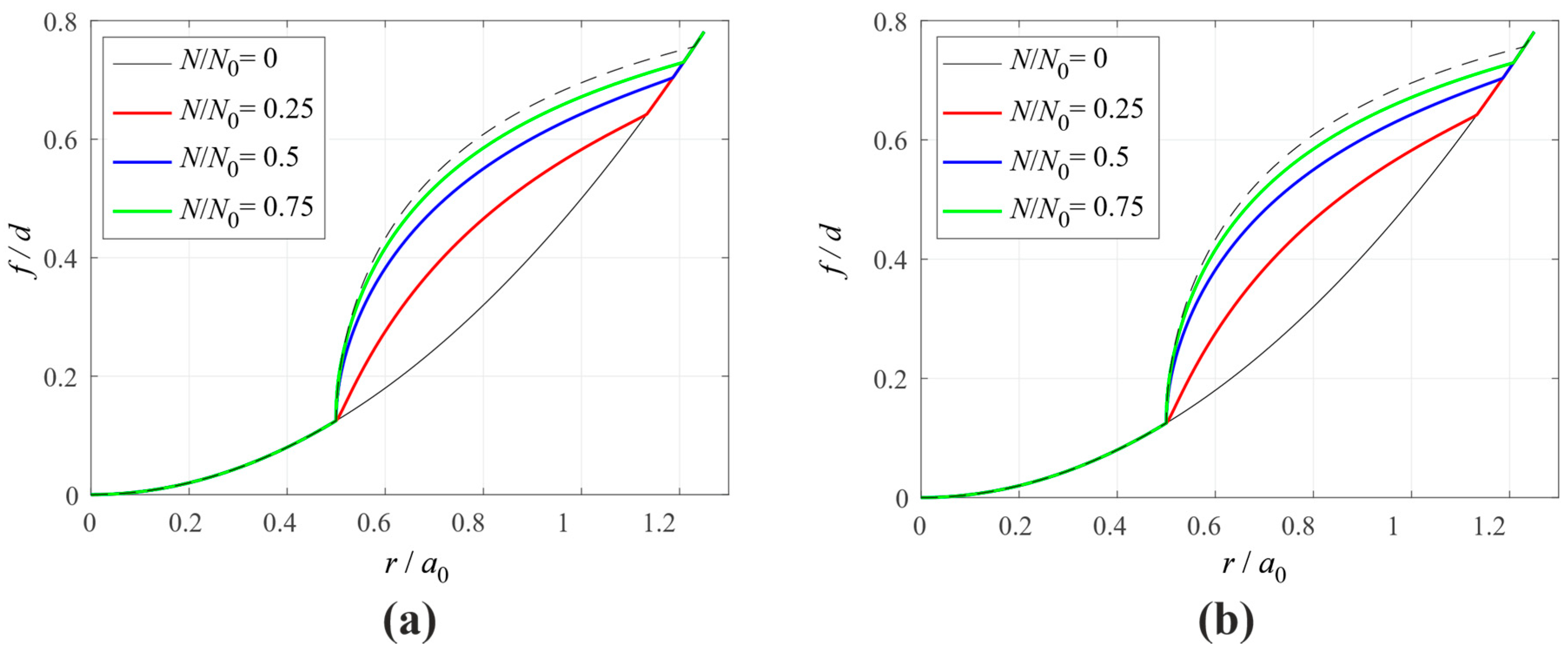
3.3. Model for Torsional Fretting Wear
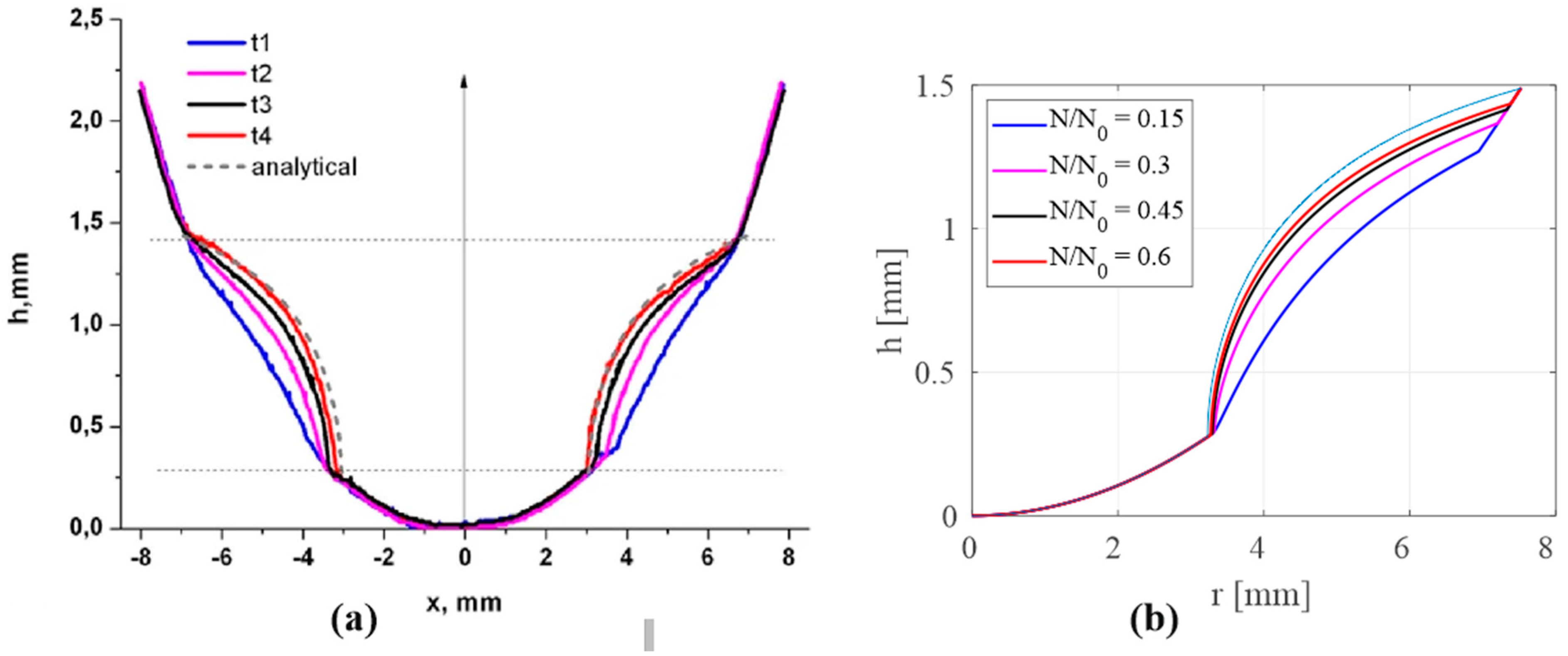
3.4. Comparison with Experimental Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Antler, M. Survey of contact fretting in electrical connectors. Compon. Hybrids Manuf. Technol. 1985, 8, 87–104. [Google Scholar] [CrossRef]
- Rajasekaran, R.; Nowell, D. Fretting fatigue in dovetail blade roots: Experiment and analysis. Tribol. Int. 2006, 39, 1277–1285. [Google Scholar] [CrossRef]
- Collier, J.P.; Mayor, M.B.; Jensen, R.E.; Surprenant, V.A.; Surprenant, H.P.; McNamar, J.L.; Belec, L. Mechanisms of failure of modular prostheses. Clin. Orthop. Relat. Res. 1992, 285, 129–139. [Google Scholar] [CrossRef]
- Li, J.; Lu, Y.H. Effects of displacement amplitude on fretting wear behaviors and mechanism of Inconel 600 alloy. Wear 2013, 304, 223–230. [Google Scholar] [CrossRef]
- Madge, J.J.; Leen, S.B.; Shipway, P.H. The critical role of fretting wear in the analysis of fretting fatigue. Wear 2007, 263, 542–551. [Google Scholar] [CrossRef]
- Ciavarella, M.; Demelio, G. A review of analytical aspects of fretting fatigue, with extension to damage parameters, and application to dovetail joints. Int. J. Solids Struct. 2001, 38, 1791–1811. [Google Scholar] [CrossRef] [Green Version]
- Goryacheva, I.G.; Rajeev, P.T.; Farris, T.N. Wear in Partial Slip Contact. J. Tribol. 2001, 123, 848–856. [Google Scholar] [CrossRef]
- McColl, I.R.; Ding, J.; Leen, S.B. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Gallego, L.; Nélias, D. Modeling of Fretting Wear under Gross Slip and Partial Slip Conditions. J. Tribol. 2007, 129, 528–535. [Google Scholar] [CrossRef]
- Pereira, K.; Yue, T.; Wahab, M.A. Multiscale analysis of the effect of roughness on fretting wear. Tribol. Int. 2017, 110, 222–231. [Google Scholar] [CrossRef] [Green Version]
- Hills, D.; Nowell, D. Mechanics of Fretting Fatigue; Springer: Dordrecht, The Netherlands, 1994; 246p. [Google Scholar]
- Fouvry, S.; Elleuch, K.; Simeon, G. Prediction of crack initiation under partial slip fretting conditions. J. Strain Anal. Eng. Des. 2002, 37, 549–564. [Google Scholar] [CrossRef]
- Pereira, K.; Wahab, M.A. Fretting fatigue lifetime estimation using a cyclic cohesive zone model. Tribol. Int. 2020, 141, 105899. [Google Scholar] [CrossRef]
- Llavori, I.; Zabala, A.; Urchegui, M.A.; Tato, W.; Gómez, X. A coupled crack initiation and propagation numerical procedure for combined fretting wear and fretting fatigue lifetime assessment. Ther. Appl. Fract. Mech. 2019, 101, 294–305. [Google Scholar] [CrossRef]
- Aleshin, V.V. On Applications of Semi-Analytical Methods of Contact Mechanics. Front. Mech. Eng. 2020, 6, 30. [Google Scholar] [CrossRef]
- Done, V.; Kesavan, D.; Chaise, T.; Nélias, D. Semi analytical fretting wear simulation including wear debris. Tribol. Int. 2017, 109, 1–9. [Google Scholar] [CrossRef]
- Boussinesq, J. Application des Potentiels a L’etude de L’Equilibre et du Mouvement des Solides Elastiques; Imprimerie, L. Danel: Lille, France, 1885; 727p. [Google Scholar]
- Cerruti, V. Ricerche intorno all’equilibrio de’ corpi elastici isotropi. Accad. Lincei Rend. 1882, 3, 81–122. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; 452p. [Google Scholar]
- Hertz, H. Über die Berührung fester elastischer Körper. J. die Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Fouvry, S.; Paulin, C.; Liskiewicz, T. Application of an energy wear approach to quantify fretting contact durability: Introduction of a wear energy capacity concept. Tribol. Int. 2007, 40, 1428–1440. [Google Scholar] [CrossRef]
- Schubert, G. Zur Frage der Druckverteilung unter elastisch gelagerten Tragwerken. Ing. Arch. 1942, 13, 132–147. [Google Scholar] [CrossRef]
- Galin, L.A. Three-Dimensional Contact Problems of the Theory of Elasticity for Punches with a Circular Planform. Prikl. Mat. I Mekhanika 1946, 10, 425–448. [Google Scholar]
- Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems; Springer: Berlin/Heidelberg, Germany, 2019; 347p. [Google Scholar]
- Cattaneo, C. Sul Contatto di due Corpore Elastici: Distribuzione degli sforzi. Accad. Lincei Rend. 1938, 27, 342–348, 434–436, 474–478. [Google Scholar]
- Ciavarella, M. Tangential Loading of General Three-Dimensional Contacts. J. Appl. Mech. 1998, 65, 998–1003. [Google Scholar] [CrossRef] [Green Version]
- Jäger, J. A New Principle in Contact Mechanics. J. Tribol. 1998, 120, 677–684. [Google Scholar] [CrossRef]
- Jäger, J. Axi-symmetric bodies of equal material in contact under torsion or shift. Arch. Appl. Mech. 1995, 65, 478–487. [Google Scholar] [CrossRef]
- Lubkin, J.L. The torsion of elastic spheres in contact. J. Appl. Math. Mech. 1951, 73, 183–187. [Google Scholar]
- Willert, E.; Popov, V.L. Exact one-dimensional mapping of axially symmetric elastic contacts with superimposed normal and torsional loading. J. Angew. Math. Mech. 2017, 97, 173–182. [Google Scholar] [CrossRef]
- Benad, J. Fast numerical implementation of the MDR transformations. Facta Univers. Ser. Mech. Eng. 2018, 16, 127–138. [Google Scholar] [CrossRef]
- Jäger, J. Elastic contact of equal spheres under oblique forces. Arch. Appl. Mech. 1993, 63, 402–412. [Google Scholar] [CrossRef]
- Varenberg, M.; Etsion, I.; Halperin, G. Slip Index: A New Unified Approach to Fretting. Tribol. Lett. 2004, 17, 569–573. [Google Scholar] [CrossRef]
- Heredia, S.; Fouvry, S. Introduction of a new sliding regime criterion to quantify partial, mixed and gross slip fretting regimes: Correlation with wear and cracking processes. Wear 2010, 269, 515–524. [Google Scholar] [CrossRef]
- Dimaki, A.V.; Dmitriev, A.I.; Chai, Y.S.; Popov, V.L. Rapid simulation procedure for fretting wear on the basis of the method of dimensionality reduction. Int. J. Solids Struct. 2014, 51, 4215–4220. [Google Scholar] [CrossRef] [Green Version]
- Popov, V.L.; Heß, M. Method of Dimensionality Reduction in Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2015; 265p. [Google Scholar]
- Popov, V.L. Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 2014, 4, 3749. [Google Scholar] [CrossRef] [Green Version]
- Jäger, J. Torsional impact of elastic spheres. Arch. Appl. Mech. 1994, 64, 235–248. [Google Scholar]
- Dmitriev, A.I.; Voll, L.B.; Psakhie, S.G.; Popov, V.L. Universal limiting shape of worn profile under multiple-mode fretting conditions: Theory and experimental evidence. Sci. Rep. 2016, 6, 23231. [Google Scholar] [CrossRef] [Green Version]
- Varenberg, M.; Halperin, G.; Etsion, I. Different aspects of the role of wear debris in fretting wear. Wear 2002, 252, 902–910. [Google Scholar] [CrossRef]
- Meng, H.C.; Ludema, K.C. Wear models and predictive equations: Their form and content. Wear 1995, 181–183(Pt. 2), 443–457. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, J.; Jin, Z.; Prakash, B.; Hu, Y. A review of recent advances in tribology. Friction 2020, 8, 221–300. [Google Scholar] [CrossRef] [Green Version]
- Yoon, Y.; Etsion, I.; Take, F.E. The evolution of fretting wear in a micro-spherical contact. Wear 2011, 270, 567–575. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, W.; Thouless, M.D.; Barber, J.R. Effect of plastic deformation on the evolution of wear and local stress fields in fretting. Int. J. Solids Struct. 2016, 82, 1–8. [Google Scholar] [CrossRef]
- Munisamy, R.L.; Hills, D.A.; Nowell, D. Static Axisymmetric Hertzian Contacts Subject to Shearing Forces. J. Appl. Mech. 1994, 61, 278–283. [Google Scholar] [CrossRef]
- Barber, J.R. Contact Mechanics; Springer: Basel, Switzerland, 2018; 585p. [Google Scholar]
- Willert, E. FFT-based Implementation of the MDR transformations for homogeneous and power-law graded materials. Facta Univers. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Forsbach, F. Stress Tensor and Gradient of Hydrostatic Pressure in the Half-Space Beneath Axisymmetric Bodies in Normal and Tangential Contact. Front. Mech. Eng. 2020, 6, 39. [Google Scholar] [CrossRef]
- Heß, M.; Popov, V.L. Method of Dimensionality Reduction in Contact Mechanics and Friction: A User’s Handbook. II. Power-Law Graded Materials. Facta Univers. Ser. Mech. Eng. 2016, 14, 251–268. [Google Scholar] [CrossRef] [Green Version]
- Willert, E.; Dmitriev, A.I.; Psakhie, S.G.; Popov, V.L. Effect of elastic grading on fretting wear. Sci. Rep. 2019, 9, 7791. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Willert, E. A Simple Semi-Analytic Contact Mechanical Model for Tangential and Torsional Fretting Wear of Axisymmetric Contacts. Symmetry 2021, 13, 1582. https://doi.org/10.3390/sym13091582
Willert E. A Simple Semi-Analytic Contact Mechanical Model for Tangential and Torsional Fretting Wear of Axisymmetric Contacts. Symmetry. 2021; 13(9):1582. https://doi.org/10.3390/sym13091582
Chicago/Turabian StyleWillert, Emanuel. 2021. "A Simple Semi-Analytic Contact Mechanical Model for Tangential and Torsional Fretting Wear of Axisymmetric Contacts" Symmetry 13, no. 9: 1582. https://doi.org/10.3390/sym13091582
APA StyleWillert, E. (2021). A Simple Semi-Analytic Contact Mechanical Model for Tangential and Torsional Fretting Wear of Axisymmetric Contacts. Symmetry, 13(9), 1582. https://doi.org/10.3390/sym13091582




