Monitoring Persistence Change in Heavy-Tailed Observations

Abstract

In this paper, a ratio test based on bootstrap approximation is proposed to detect the persistence change in heavy-tailed observations. This paper focuses on the symmetry testing problems of $I\left(1\right)$-to-$I\left(0\right)$ and $I\left(0\right)$-to-$I\left(1\right)$. On the basis of residual CUSUM, the test statistic is constructed in a ratio form. I prove the null distribution of the test statistic. The consistency under alternative hypothesis is also discussed. However, the null distribution of the test statistic contains an unknown tail index. To address this challenge, I present a bootstrap approximation method for determining the rejection region of this test. Simulation studies of artificial data are conducted to assess the finite sample performance, which shows that our method is better than the kernel method in all listed cases. The analysis of real data also demonstrates the excellent performance of this method.

1. Introduction

Change point analysis is used in a wide range of fields such as biology, medicine, finance, etc. The hot research topics in change point analysis are how to test structural changes of the statistical model and how to estimate the change points. The detection of a change point is very meaningful, which can help in building a more reasonable model. Over the past few decades, many economic and financial data have displayed changes in persistence. This type of change causes substantial practical problems, especially concerning inflation rates, short-term interest rates, and government budget deficits. There is a rich literature on the detection of such change points. Kim [1] and Kim et al. [2] proposed the ratio test for a change in persistence. Leybourne et al. [3] discussed the ADF test method. The LBI test was also considered, such as by Busetti and Taylor [4] and by Leybourne and Taylor [5]. More recently, Leybourne et al. [6] proposed a CUSUM test. Sibbertsen and Kruse [7] studied the change point problem of long-range dependence series. Belaire-Franch and Contreras [8] presented a nonparametric unit root test. Halunga and Osborn [9] summarized the ratio-based estimators of persistence change points. Kejriwal et al. [10] considered the Wald tests for detecting multiple persistence changes. Perron et al. [11] proposed a test for the presence of a nonlinear deterministic trend to determine whether the noise component is stationary or contains an autoregressive unit root. In [12], the unit root test on the panel $AR\left(1\right)$ model was discussed. Kejriwal et al. [13] presented bootstrap procedures for detecting multiple persistence shifts. The abovementioned work has a common limitation: they are for a time series with finite variance.

It is also important to studying the sequences of infinite variance. This type of sequence has many interesting mathematical properties. In this paper, we present a new approach to test persistence change in heavy-tailed sequences. We assume that the innovation follows a heavy-tailed distribution. This distribution regularly varies with tail index $\kappa$ satisfying $1<\kappa <2$, so that the mean exists but the variance is infinite for the sequence. There are a lot of heavy-tailed models in economics and finance; see, for example, Davis and Mikosch [14], Kokoszka and Wolf [15], Soohan et al. [16], etc. Such data sets are well explained by a heavy-tailed model rather than a Gaussian model. Therefore, testing for change within this sequence has also attracted significant research interests. Horváth and Kokoszka [17] tested unit root in such an innovation case. Wang et al. [18] presented a detection and estimation method of structural change in heavy-tailed sequence.

This paper focuses on symmetric $I\left(1\right)$-to-$I\left(0\right)$ and $I\left(0\right)$-to-$I\left(1\right)$ persistence change detection problems for observations in heavy-tailed distribution. A bootstrap method is proposed to test changes in persistence. First, we construct the test statistic into a ratio form with residual CUSUM. The proposed statistic is a completely new attempt. It is different from the traditional ratio statistic of Kim [1]. Then, we prove the null distribution of the test statistic. We present its consistency under an alternative hypothesis. Moreover, a bootstrap procedure is proposed for determining the rejection region of this test because the null distribution contains an unknown tail index. Finally, the simulation results of artificial and real data sets demonstrate the good performance of our method.

The remainder of this paper is organized as follows. Section 2 first introduces the statistical model. Then, Section 3 presents the test method and theoretical results. Section 4 contains the simulation studies. The simulation shows the performance of our method is excellent. Section 5 and Section 6 present the discussion and the conclusions, respectively.

2. Statistical Model

The model discussed in this paper is as follows:

$$y_t={\mu }_t+{\epsilon }_t,$$

(1)

$${\epsilon }_t={\rho }_t{\epsilon }_{t-1}+e_t,t=1,\cdots ,T,$$

(2)

where${\mu }_t=E\left(y_t\right)={\delta }^T{d}_t$is a linear combination for a vector of nonrandom regressors $d_t$. We assume three different typical scenarios: $d_t=0,d_t=1$, and $d_t={(1,t)}^T$.  $\left\{e_t\right\}$ is a heavy-tailed sequence satisfying the following assumption.

Assumption 1.

The sequence $\left\{e_t\right\}$ is strictly stationary with symmetric univariate marginal distributions, which satisfy

$$T\times P(e_1/a_T\in ·)⟹\mu (·),$$

(3)

where $a_T$ is defined by $T\times P\left(\right|e_1|>a_T)\to 1$, the notation ¡°⟹¡± means weak convergence, and the measure $\mu (·)$ is given by

$$2\mu \left(dx\right)={\kappa \left|x\right|}^{-\kappa -1}I\{x<0\}dx+\kappa x^{-\kappa -1}I\{x>0\}dx,$$

(4)

where $1<\kappa <2.$

Lemma 1.

If Assumption 1 holds, then

$$\left(a_T^{-1}\sum _{t=1}^{\left[T\tau \right]}{e}_t,a_T^{-2}\sum _{t=1}^{\left[T\tau \right]}{e}_t^2\right)\stackrel{d}{⟶}\left(U_1\left(\tau \right),U_2\left(\tau \right)\right),$$

(5)

where $\left\{U_1\left(\tau \right)\right\}$ is a κ-stable and $\left\{U_2\left(\tau \right)\right\}$ is a $\kappa /2$-stable Lévy process in $[0,1]$. The notation ¡°$\stackrel{d}{⟶}$¡± stands for convergence in distribution.

Remark 1.

This result was obtained by Resnick [19] and by Kokoszka and Wolf [15]. The quantities $a_T$ can be denoted as $a_T=T^{1/\kappa }L\left(T\right)$ for some slowly varying function L.

Consider the following null hypothesis:

$$H_0:y_t\sim I\left(1\right),t=1,\cdots ,T,$$

(6)

against the alternative hypothesis

$$H_1:y_t\sim I\left(1\right),t=1,\cdots ,\left[T{\tau }_0\right],$$

(7)

$$y_t\sim I\left(0\right),t=\left[T{\tau }_0\right]+1,\cdots ,T,$$

(8)

where ${\tau }_0\in (0,1),$ T is the sample size and $[·]$ is the rounding function.

We also deal with the following test problem:

$$H_0^{{}^{\prime }}:y_t\sim I\left(0\right),t=1,\cdots ,T,$$

(9)

against the alternative hypothesis

$$H_1^{{}^{\prime }}:y_t\sim I\left(0\right),t=1,\cdots ,\left[T{\tau }_0^{{}^{\prime }}\right],$$

(10)

$$y_t\sim I\left(1\right),t=\left[T{\tau }_0^{{}^{\prime }}\right]+1,\cdots ,T,$$

(11)

where ${\tau }_0^{{}^{\prime }}\in (0,1)$.

The goal of our paper is to detect $H_0$ against $H_1$ or to test $H_0^{{}^{\prime }}$ against $H_1^{{}^{\prime }}$. These are two symmetry test problems. In model (1), the process $\left\{y_t\right\}$ is $I\left(0\right)$ if $|{\rho }_t|<1$, the process $\left\{y_t\right\}$ is $I\left(1\right)$ if $|{\rho }_t|=1$. In this paper, we detect whether the process $\left\{y_t\right\}$ is $I\left(1\right)$ throughout the sample period or a change occurs from $I\left(1\right)$ to $I\left(0\right)$. We also test whether the process $\left\{y_t\right\}$ is $I\left(0\right)$ throughout the sample period or a change occurs from $I\left(0\right)$ to $I\left(1\right)$.

3. Monitoring Change in Persistence

In this section, we establish the ratio and bootstrap tests for persistence change problems. We demonstrate the construction of statistics and their good theoretical properties.

3.1. Detecting $I\left(1\right)$ to $I\left(0\right)$

Let $\left\{{\widehat{\epsilon }}_{0,t}\right\}$ be the OLS residuals from the regression of $y_t$ on $d_t$, $t=1,\cdots ,\left[T\tau \right],$ and let $\left\{{\widehat{\epsilon }}_{1,t}\right\}$ be the OLS residuals from the regression of $y_t$ on $d_t$ , $t=\left[T\tau \right]+1,\cdots ,T$. Under $H_0$, the average information of the sequence $\{{\widehat{\epsilon }}_{0,t},t=1,\cdots ,\left[T\tau \right]\}$ should no be very different from the average information of the sequence $\{{\widehat{\epsilon }}_{1,t},t=\left[T\tau \right]+1,\cdots ,T\}$. Take the average of these two parts. The numerator and the denominator of the ratio should be close to each other if there is no persistence change. On the other hand, the numerator and the denominator are very different under $H_1$. The ratio-form statistic is constructed as follows:

$$R_T\left(\tau \right)=\frac{{\left[\tau T\right]}^{-2}{\displaystyle \sum _{t=1}^{\left[T\tau \right]}}{\widehat{\epsilon }}_{0,t}^2}{{\left[(1-\tau )T\right]}^{-2}{\displaystyle \sum _{t=\left[T\tau \right]+1}^T}{\widehat{\epsilon }}_{1,t}^2}.$$

(12)

Based on (12), we can obtain three test statistics: maximum-chow statistic in Andrews [20]:

$$\underset{\tau \in \mathsf{\Theta }}{max}{R}_T\left(\tau \right),$$

(13)

mean-score statistic in Hansen [21]:

$${\int }_{\tau \in \mathsf{\Theta }}{R}_T\left(\tau \right)d\tau ,$$

(14)

mean-exponential statistic in Andrews and Ploberger [22]:

$$log\{{\int }_{\tau \in \mathsf{\Theta }}exp\left(R_T\left(\tau \right)\right)d\tau \},$$

(15)

where $\tau \in \mathsf{\Theta }$, $\mathsf{\Theta }$ is a compact subset in $[0,1]$.

Theorem 1.

If Assumption 1 and the null hypothesis $H_0$ hold,

$$R_T\left(\tau \right)⟹\frac{{\tau }^{-2}{V}_{j,0}\left(\tau \right)}{{(1-\tau )}^{-2}{V}_{j,1}\left(\tau \right)}\equiv R_{\infty }\left(\tau \right)$$

(16)

and

$$H\left(R_T\right)⟹H\left(R_{\infty }\right),$$

(17)

where $H(·)$ denotes the statistics (13)–(15). The notation $j=1$ signifies the model with $d_t=0$, $j=2$, and $j=3$ denote $d_t=1$ and $d_t={(1,t)}^T$ respectively.

$$V_{1,1}\left(\tau \right)={\int }_{\tau }^1{U}_1{\left(r\right)}^{2}dr,V_{1,0}\left(\tau \right)={\int }_0^{\tau }{U}_1{\left(r\right)}^{2}dr;$$

(18)

$$V_{2,1}\left(\tau \right)=V_{1,1}\left(\tau \right)-\frac{1}{1-\tau }{G}_1{\left(\tau \right)}^2,V_{2,0}\left(\tau \right)=V_{1,0}\left(\tau \right)-\frac{1}{\tau }{K}_1{\left(\tau \right)}^2;$$

(19)

$$V_{3,1}\left(\tau \right)=V_{1,1}\left(\tau \right)+4{(1-\tau )}^{-1}\left(3{(1-\tau )}^{-1}{G}_1\left(\tau \right)G_2\left(\tau \right)-G_1{\left(\tau \right)}^2-3{(1-\tau )}^{-2}{G}_2{\left(\tau \right)}^2\right);$$

(20)

$$V_{3,0}\left(\tau \right)=V_{1,0}\left(\tau \right)+4{\tau }^{-1}(3{\tau }^{-1}{K}_1\left(\tau \right)K_2\left(\tau \right)-K_1{\left(\tau \right)}^2-3{\tau }^{-2}{K}_2{\left(\tau \right)}^2);$$

(21)

$$K_1\left(\tau \right)={\int }_0^{\tau }{U}_1\left(r\right)dr,K_2\left(\tau \right)={\int }_0^{\tau }r{U}_1\left(r\right)dr;$$

(22)

$$G_1\left(\tau \right)=K_1\left(1\right)-K_1\left(\tau \right),G_2\left(\tau \right)=K_2\left(1\right)-K_2\left(\tau \right).$$

(23)

The following Theorem 2 shows the consistency of the test.

Theorem 2.

If Assumption 1 and the alternative hypothesis $H_1$ hold, then $R_T\left(\tau \right)=O_P\left(1\right)$ when $0<\tau <{\tau }_0$, $R_T\left(\tau \right)=O_P\left(T\right)$ when ${\tau }_0\le \tau <1$. Thus, if $[{\tau }_0,1]\cap \mathsf{\Theta }\ne$, $H\left(R_T\right)=O_P\left(T\right)$.

3.2. Detecting $I\left(0\right)$ to $I\left(1\right)$

The notations ${\widehat{\epsilon }}_{0,t}$ and ${\widehat{\epsilon }}_{1,t}$ have similar meanings as before. The statistic is constructed symmetrically as follows:

$$M_T\left(\tau \right)=\frac{{\left[(1-\tau )T\right]}^{-2}{\displaystyle \sum _{t=\left[T\tau \right]+1}^T}{\widehat{\epsilon }}_{1,t}^2}{{\left[\tau T\right]}^{-2}{\displaystyle \sum _{t=1}^{\left[T\tau \right]}}{\widehat{\epsilon }}_{0,t}^2}.$$

(24)

Based on (24), we can obtain three analogous test statistics:

$$\underset{\tau \in \mathsf{\Theta }}{max}{M}_T\left(\tau \right),$$

(25)

$${\int }_{\tau \in \mathsf{\Theta }}{M}_T\left(\tau \right)d\tau ,$$

(26)

$$log\{{\int }_{\tau \in \mathsf{\Theta }}exp\left(M_T\left(\tau \right)\right)d\tau \},$$

(27)

where $\tau \in \mathsf{\Theta }$, $\mathsf{\Theta }$ is a compact subset in $[0,1]$.

Theorem 3.

If Assumption 1 and the null hypothesis $H_0^{{}^{\prime }}$ hold (assuming that $|{\rho }_t|=|\rho |<1$), we have

$$M_T\left(\tau \right)⟹\frac{{(1-\tau )}^{-2}{W}_{j,1}\left(\tau \right)}{{\tau }^{-2}{W}_{j,0}\left(\tau \right)}\equiv M_{\infty }\left(\tau \right)$$

(28)

and

$$H\left(M_T\right)⟹H\left(M_{\infty }\right),$$

(29)

where $H(·)$ denotes the statistics (25)–(27). The notation $j=1$ signifies the model with $d_t=0$, $j=2$, and $j=3$ denote $d_t=1$ and $d_t={(1,t)}^T$ respectively.

$$W_{1,0}\left(\tau \right)=W_{2,0}\left(\tau \right)=W_{3,0}\left(\tau \right)={\mathsf{\Psi }}_2^2{U}_2\left(\tau \right),$$

(30)

$$W_{1,1}\left(\tau \right)=W_{2,1}\left(\tau \right)=W_{3,1}\left(\tau \right)={\mathsf{\Psi }}_2^2{U}_2(1-\tau ),$$

(31)

where ${\mathsf{\Psi }}_2$ denotes $l_2$ norm of sequence $\left\{{\phi }_j\right\}$ and ${\phi }_j={\rho }^j$.

The following Theorem 4 shows the consistency of the test.

Theorem 4.

If Assumption 1 and the alternative hypothesis $H_1^{{}^{\prime }}$ hold, then $M_T\left(\tau \right)=O_P\left(T\right)$ when $0<\tau <{\tau }_0^{{}^{\prime }}$ and $M_T\left(\tau \right)=O_P\left(1\right)$ when ${\tau }_0^{{}^{\prime }}\le \tau <1$. Thus, if $[0,{\tau }_0^{{}^{\prime }}]\cap \mathsf{\Theta }\ne$, $H\left(M_T\right)=O_P\left(T\right)$.

3.3. Bootstrap Approximation

The drawback of statistics $R_T\left(\tau \right)$ and $M_T\left(\tau \right)$ is that the asymptotic distributions depend on the tail index $\kappa$. Mandelbrot [23] proposed a method for estimating the tail index. However, the accuracy of this method was not good enough. In order to solve this problem, we present the bootstrap method. The goal of this section is to discuss an approximation rejection region of this test based on the statistic $R_T\left(\tau \right)$, even if $\kappa$ is unknown. Take the case with $I\left(1\right)$ changing into $I\left(0\right)$ as an example.

The algorithm is as follows:

Step 1: Compute the centered residuals

$${\tilde{e}}_i={\widehat{e}}_i-\frac{1}{T}\sum _{i=1}^T{\widehat{e}}_i,1\le i\le T,$$

(32)

where ${\widehat{e}}_i={\widehat{\epsilon }}_i-\widehat{\rho }{\widehat{\epsilon }}_{i-1}.$$\widehat{\rho }$ is the OLS estimator of $\rho$ on residuals ${\widehat{\epsilon }}_1,{\widehat{\epsilon }}_2,...,{\widehat{\epsilon }}_T.$

Step 2: For a fixed $N\le T$, select with replacement a bootstrap sample $\{e_i^{\ast },i=1,...,N\}$ from $\{{\tilde{e}}_i,i=1,...,T\}$.

Step 3: Calculate the bootstrap process

$${\widehat{\epsilon }}_i^{\ast }=\widehat{\rho }{\widehat{\epsilon }}_{i-1}^{\ast }+e_i^{\ast },i=1,...,N$$

(33)

$${\tilde{y}}_i={\widehat{\delta }}^T{d}_i+{\widehat{\epsilon }}_i^{\ast },i=1,...,N$$

(34)

and the statistic

$${\tilde{R}}_N\left(\tau \right)=\frac{{\left[\tau N\right]}^{-2}{\displaystyle \sum _{t=1}^{\left[N\tau \right]}}{\widehat{\eta }}_{0,t}^2}{{\left[(1-\tau )N\right]}^{-2}{\displaystyle \sum _{t=\left[N\tau \right]+1}^N}{\widehat{\eta }}_{1,t}^2},$$

(35)

where $\left\{{\widehat{\eta }}_{0,t}\right\}$ is the OLS residuals from the regression of ${\tilde{y}}_t$ on $d_t$, $t=1,\cdots ,\left[N\tau \right]$ and $\left\{{\widehat{\eta }}_{1,t}\right\}$ is the OLS residuals from the regression of ${\tilde{y}}_t$ on $d_t$ , $t=\left[N\tau \right]+1,\cdots ,N$.

Step 4: Repeat Step 2 and Step 3 B times. The asymptotic critical value $H\left(R\right)$ of statistic $H\left(R_T\right)$ can be approximated by the empirical quantile of $H(\tilde{R})$. We reject the null hypothesis if $H\left(R_T\right)>H\left(R\right)$.

In order to prove the convergence of ${\tilde{R}}_N\left(\tau \right)$, we consider the following assumption:

Assumption 2.

As $T\to \infty$, then $N\to \infty$ and $N/T\to 0.$

Theorem 5.

If Assumption 1 and 2 hold, then for every real x,

$$P_{ϵ}({\tilde{R}}_N\left(\tau \right)\le x)\stackrel{P}{⟶}P(R_{\infty }\left(\tau \right)\le x),$$

(36)

where $ϵ=\sigma ({\epsilon }_j,j\ge 1)$, $P_{ϵ}$ is the conditional probability with respect to ϵ and ¡°$\stackrel{P}{⟶}$¡± stands for convergence in probability.

Remark 2.

Theorem 5 implies that the bootstrap test has an asymptotically correct size. Additionally, it also shows that the test with bootstrap add-on is consistent.

We can finish the bootstrap algorithm of detecting $H_0^{{}^{\prime }}$ against $H_1^{{}^{\prime }}$ similarly. We construct the statistic

$${\tilde{M}}_N\left(\tau \right)=\frac{{\left[(1-\tau )N\right]}^{-2}{\displaystyle \sum _{t=\left[N\tau \right]+1}^N}{\widehat{\eta }}_{1,t}^2}{{\left[\tau N\right]}^{-2}{\displaystyle \sum _{t=1}^{\left[N\tau \right]}}{\widehat{\eta }}_{0,t}^2}.$$

(37)

We can also obtain the corresponding conclusion of Theorem 5.

Theorem 6.

If Assumptions 1 and 2 hold, then for every real x,

$$P_{ϵ}({\tilde{M}}_N\left(\tau \right)\le x)\stackrel{P}{⟶}P(M_{\infty }\left(\tau \right)\le x),$$

(38)

where $ϵ=\sigma ({\epsilon }_j,j\ge 1)$, $P_{ϵ}$ is the conditional probability with respect to ϵ and ¡°$\stackrel{P}{⟶}$¡± stands for convergence in probability.

Appendix A presents the mathematical proofs.

4. Simulation and Real-Data Analysis

In this section, simulation studies of artificial data are conducted to assess the finite sample performance. The empirical sizes and powers perform well. Simulation results show that our method is better than the kernel method in all listed cases. The analysis of real data also demonstrates that this method is effective.

4.1. Simulation

We use R software to complete the simulation. To save computational time, we simply show the results for $d_t=1$. The results for the $d_t=0$ and $d_t={(1,t)}^T$ cases are quite similar.

To investigate the size and power property of the test, we consider the following data generating process:

$$y_t=r_0+{\epsilon }_t,{\epsilon }_t=\rho {\epsilon }_{t-1}+e_t,t=1,\cdots ,T.$$

(39)

Null hypothesis:

$$H_0:\rho =1,t=1,\cdots ,T,$$

(40)

against the alternative hypothesis:

$$H_1:\rho =1,t=1,\cdots ,\left[T{\tau }_0\right],$$

(41)

$$\rho ={\rho }_0,t=\left[T{\tau }_0\right]+1,\cdots ,T,$$

(42)

another null hypothesis:

$$H_0^{{}^{\prime }}:\rho ={\rho }_0,t=1,\cdots ,T,$$

(43)

against the corresponding alternative hypothesis:

$$H_1^{{}^{\prime }}:\rho ={\rho }_0,t=1,\cdots ,[T{\tau }_0^{{}^{\prime }}],$$

(44)

$$\rho =1,t=[T{\tau }_0^{{}^{\prime }}]+1,\cdots ,T,$$

(45)

where $r_0=0.1$, ${\rho }_0=0.2,0.5,0.8$, ${\tau }_0=0.25,0.35$, and ${\tau }_0^{{}^{\prime }}=0.3,0.5$. The innovation $\left\{e_t\right\}$ satisfies Assumption 1. We set the tail index $\kappa =1.14,1.43,1.97$. This heavy-tailed sequence is generated by a small program that can be downloaded from Professor Nolan’s website: https://edspace.american.edu/jpnolan/, accessed on 20 May 2021.

The simulation study is based on different sample sizes $T=200,500,800$ at nominal levels $\alpha =0.1$ or $\alpha =0.05$. We consider the test statistic (13) and (25). We choose the appropriate bootstrap sample sizes N, which is not given in detail. Let $N=\{20,25,35\},\{30,35,40\},$ $\{70,100,120\}$, respectively, and the bootstrap frequency $B=500$ in this section.

In the case of detecting $H_0$ against $H_1$, the algorithm to calculate empirical sizes is as follows (Algorithm 1):

Algorithm 1. Calculate empirical sizes detecting $H_0$ against $H_1$.

initialize count variable $k=0$ repeat     Step A: Generate the data $y_t,t=1,...,T$ under $H_0$ and calculate the statistics $R_T\left(\tau \right)$ and $H\left(R_T\right)=\underset{0.2\le \tau \le 0.8}{max}{R}_T\left(\tau \right).$     Step B: Repeat the Step 1, 2 and 3 in the bootstrap algorithm for $B=500$ times in Section 3.3. Calculate the empirical quantile of $H({\tilde{R}}_N)=\underset{0.2\le \tau \le 0.8}{max}{\tilde{R}}_N\left(\tau \right)$, which can be denoted as $R_{T,N}$.     Step C: If $H\left(R_T\right)>R_{T,N}$, we reject $H_0$ and let $k=k+1$. until   for 5000 times      return   $k/5000$

The empirical sizes can be approximated by the frequency, which the null hypothesis rejects with 5000 replications. Calculating the empirical powers is similar to the above algorithm. Only change the data generating process under $H_1$. The method to obtain the empirical sizes and powers is also similar in the case of testing $H_0^{{}^{\prime }}$ against $H_1^{{}^{\prime }}$.

The empirical sizes and powers of the $I\left(1\right)$ to $I\left(0\right)$ test are provided in Table 1, Table 2, Table 3 and Table 4. The data in parentheses are the corresponding standard errors. We analyze the main conclusions that can be drawn from Table 1, Table 2, Table 3 and Table 4.

(1)

The empirical sizes are almost close to the nominal level $\alpha$ in Table 1.

(2)

From Table 2, Table 3 and Table 4, we can find the powers increase when the value of T is larger for the same ${\rho }_0$ and ${\tau }_0$. For fixed numbers T and ${\tau }_0$, the powers raise gradually with the decrease in ${\rho }_0$. The earlier change gives higher empirical power for the same T and ${\rho }_0$. This is a famous result in the detection of change points. Some powers are equal to 1 in Table 4.

(3)

The larger tail index $\kappa$, the higher empirical powers. This is due to the special properties of heavy-tailed sequences. The smaller tail index $\kappa$, the more likely the sequence is to contain ‘outliers’. The test statistics behave differently before and after such points, which could seriously affect the performance of this test.

Table 1. Empirical sizes (${\rho }_0=0.5$).

T	N	$\mathit{\kappa }=1.14$		$\mathit{\kappa }=1.43$		$\mathit{\kappa }=1.97$
		$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$
	20	0.132 (0.024)	0.045 (0.014)	0.087 (0.019)	0.057 (0.016)	0.088 (0.020)	0.045 (0.014)
200	25	0.096 (0.020)	0.062 (0.017)	0.114 (0.022)	0.055 (0.016)	0.095 (0.020)	0.060 (0.017)
	35	0.115 (0.022)	0.041 (0.014)	0.110 (0.022)	0.053 (0.016)	0.106 (0.022)	0.057 (0.016)
	30	0.096 (0.013)	0.043 (0.009)	0.110 (0.014)	0.049 (0.009)	0.103 (0.013)	0.053 (0.010)
500	35	0.106 (0.014)	0.052 (0.010)	0.114 (0.014)	0.053 (0.010)	0.091 (0.013)	0.047 (0.009)
	40	0.105 (0.014)	0.047 (0.009)	0.090 (0.013)	0.052 (0.010)	0.098 (0.013)	0.052 (0.010)
	70	0.097 (0.010)	0.053 (0.008)	0.105 (0.011)	0.048 (0.008)	0.102 (0.010)	0.049 (0.008)
800	100	0.102 (0.010)	0.048 (0.008)	0.097 (0.010)	0.049 (0.008)	0.099 (0.010)	0.050 (0.008)
	120	0.101 (0.010)	0.051 (0.008)	0.099 (0.010)	0.050 (0.008)	0.100 (0.010)	0.050 (0.008)

Table 2. Empirical powers $\kappa =1.14,\alpha =0.05$.

${\mathit{\tau }}_0$	T	N	${\mathit{\rho }}_0=0.8$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.2$
		20	0.588 (0.035)	0.697 (0.033)	0.735 (0.031)
${\tau }_0$ = 0.35	200	25	0.591 (0.035)	0.703 (0.032)	0.700 (0.033)
		35	0.612 (0.035)	0.706 (0.032)	0.717 (0.032)
		20	0.712 (0.032)	0.823 (0.026)	0.847 (0.025)
${\tau }_0$ = 0.25	200	25	0.724 (0.032)	0.828 (0.026)	0.839 (0.026)
		35	0.725 (0.032)	0.822 (0.026)	0.846 (0.025)
		30	0.743 (0.019)	0.780 (0.018)	0.807 (0.018)
${\tau }_0$ = 0.35	500	35	0.744 (0.019)	0.800 (0.018)	0.792 (0.018)
		40	0.746 (0.019)	0.794 (0.018)	0.805 (0.018)
		30	0.879 (0.014)	0.937 (0.011)	0.953 (0.009)
${\tau }_0$ = 0.25	500	35	0.888 (0.014)	0.937 (0.011)	0.954 (0.009)
		40	0.881 (0.014)	0.942 (0.010)	0.949 (0.010)
		70	0.756 (0.015)	0.808 (0.014)	0.810 (0.014)
${\tau }_0$ = 0.35	800	100	0.772 (0.015)	0.806 (0.014)	0.815 (0.014)
		120	0.760 (0.015)	0.804 (0.014)	0.813 (0.014)
		70	0.925 (0.009)	0.952 (0.008)	0.964 (0.007)
${\tau }_0$ = 0.25	800	100	0.921 (0.010)	0.954 (0.007)	0.965 (0.006)
		120	0.924 (0.009)	0.952 (0.008)	0.963 (0.007)

Table 3. Empirical powers $\kappa =1.43,\alpha =0.05$.

${\mathit{\tau }}_0$	T	N	${\mathit{\rho }}_0=0.8$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.2$
		20	0.619 (0.035)	0.731 (0.031)	0.754 (0.030)
${\tau }_0$ = 0.35	200	25	0.613 (0.035)	0.737 (0.031)	0.749 (0.031)
		35	0.615 (0.035)	0.739 (0.031)	0.750 (0.031)
		20	0.795 (0.028)	0.897 (0.021)	0.930 (0.018)
${\tau }_0$ = 0.25	200	25	0.813 (0.028)	0.905 (0.021)	0.924 (0.019)
		35	0.804 (0.028)	0.894 (0.022)	0.929 (0.018)
		30	0.760 (0.019)	0.806 (0.018)	0.813 (0.017)
${\tau }_0$ = 0.35	500	35	0.764 (0.019)	0.801 (0.018)	0.813 (0.017)
		40	0.761 (0.019)	0.804 (0.018)	0.815 (0.017)
		30	0.901 (0.013)	0.955 (0.009)	0.976 (0.007)
${\tau }_0$ = 0.25	500	35	0.902 (0.013)	0.958 (0.009)	0.976 (0.007)
		40	0.904 (0.013)	0.960 (0.009)	0.974 (0.007)
		70	0.789 (0.014)	0.816 (0.014)	0.824 (0.013)
${\tau }_0$ = 0.35	800	100	0.794 (0.014)	0.815 (0.014)	0.826 (0.013)
		120	0.790 (0.014)	0.810 (0.014)	0.823 (0.013)
		70	0.945 (0.008)	0.971 (0.006)	0.980 (0.005)
${\tau }_0$ = 0.25	800	100	0.949 (0.008)	0.975 (0.005)	0.982 (0.005)
		120	0.941 (0.008)	0.975 (0.005)	0.984 (0.004)

Table 4. Empirical powers $\kappa$ = 1.97, $\alpha$ = 0.05.

${\mathit{\tau }}_0$	T	N	${\mathit{\rho }}_0=0.8$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.2$
		20	0.695 (0.033)	0.742 (0.031)	0.792 (0.028)
${\tau }_0$ = 0.35	200	25	0.698 (0.033)	0.746 (0.031)	0.778 (0.029)
		35	0.695 (0.033)	0.745 (0.031)	0.777 (0.029)
		20	0.862 (0.024)	0.949 (0.015)	0.966 (0.013)
${\tau }_0$ = 0.25	200	25	0.877 (0.023)	0.951 (0.015)	0.969 (0.012)
		35	0.870 (0.024)	0.963 (0.013)	0.968 (0.012)
		30	0.775 (0.019)	0.814 (0.017)	0.823 (0.017)
${\tau }_0$ = 0.35	500	35	0.766 (0.019)	0.812 (0.018)	0.824 (0.017)
		40	0.777 (0.019)	0.810 (0.018)	0.823 (0.017)
		30	0.975 (0.007)	0.988 (0.005)	0.995 (0.003)
${\tau }_0$ = 0.25	500	35	0.974 (0.007)	0.990 (0.004)	1 (0)
		40	0.970 (0.008)	0.991 (0.004)	1 (0)
		70	0.806 (0.014)	0.823 (0.013)	0.835 (0.013)
${\tau }_0$ = 0.35	800	100	0.803 (0.014)	0.826 (0.013)	0.837 (0.013)
		120	0.805 (0.014)	0.829 (0.013)	0.838 (0.013)
		70	0.990 (0.003)	0.995 (0.002)	1 (0)
${\tau }_0$ = 0.25	800	100	0.989 (0.004)	0.996 (0.002)	1(0)
		120	0.987 (0.004)	1 (0)	1 (0)

The empirical sizes and powers of the $I\left(0\right)$ to $I\left(1\right)$ test are provided in Table 5, Table 6, Table 7 and Table 8. The data in parentheses is the corresponding standard errors.We now present the main conclusions of the simulation.

Table 5. Empirical sizes (${\rho }_0=0.5$).

T	N	$\mathit{\kappa }=1.14$		$\mathit{\kappa }=1.43$		$\mathit{\kappa }=1.97$
		$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathit{\alpha }=\mathbf{0}.\mathbf{05}$
	20	0.083 (0.019)	0.062 (0.017)	0.088 (0.020)	0.058 (0.016)	0.115 (0.022)	0.043 (0.014)
200	25	0.122 (0.023)	0.053 (0.016)	0.102 (0.021)	0.059 (0.017)	0.102 (0.021)	0.067 (0.018)
	35	0.095 (0.020)	0.055 (0.016)	0.096 (0.020)	0.052 (0.016)	0.086 (0.019)	0.055 (0.016)
	30	0.097 (0.013)	0.052 (0.010)	0.095 (0.013)	0.053 (0.010)	0.107 (0.014)	0.058 (0.010)
500	35	0.110 (0.014)	0.049 (0.009)	0.114 (0.014)	0.054 (0.010)	0.089 (0.013)	0.045 (0.009)
	40	0.110 (0.014)	0.050 (0.010)	0.092 (0.013)	0.043 (0.009)	0.096 (0.013)	0.052 (0.010)
	70	0.098 (0.010)	0.058 (0.008)	0.094 (0.010)	0.051 (0.008)	0.100 (0.010)	0.050 (0.008)
800	100	0.102 (0.010)	0.047 (0.007)	0.107 (0.011)	0.049 (0.008)	0.101 (0.010)	0.051 (0.008)
	120	0.097 (0.010)	0.054 (0.008)	0.098 (0.010)	0.052 (0.008)	0.099 (0.010)	0.050 (0.008)

Table 6. Empirical powers $\kappa =1.14,\alpha =0.05$.

${\mathit{\tau }}_0^{{}^{\prime }}$	T	N	${\mathit{\rho }}_0=0.2$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.8$
		20	0.895 (0.022)	0.883 (0.023)	0.817 (0.027)
${\tau }_0^{{}^{\prime }}$ = 0.5	200	25	0.897 (0.021)	0.881 (0.023)	0.827 (0.027)
		35	0.910 (0.020)	0.882 (0.023)	0.825 (0.027)
		20	0.922 (0.019)	0.894 (0.022)	0.834 (0.026)
${\tau }_0^{{}^{\prime }}$ = 0.3	200	25	0.926 (0.018)	0.894 (0.022)	0.832 (0.026)
		35	0.925 (0.019)	0.893 (0.022)	0.833 (0.026)
		30	0.920 (0.012)	0.890 (0.014)	0.843 (0.016)
${\tau }_0^{{}^{\prime }}$ = 0.5	500	35	0.922 (0.012)	0.891 (0.014)	0.840 (0.016)
		40	0.921 (0.012)	0.892 (0.014)	0.845 (0.016)
		30	0.944 (0.010)	0.928 (0.011)	0.865 (0.015)
${\tau }_0^{{}^{\prime }}$ = 0.3	500	35	0.939 (0.010)	0.931 (0.011)	0.868 (0.015)
		40	0.940 (0.010)	0.932 (0.011)	0.866 (0.015)
		70	0.935 (0.009)	0.928 (0.009)	0.858 (0.012)
${\tau }_0^{{}^{\prime }}$ = 0.5	800	100	0.938 (0.009)	0.928 (0.009)	0.856 (0.012)
		120	0.940 (0.008)	0.929 (0.009)	0.856 (0.012)
		70	0.959 (0.007)	0.945 (0.008)	0.905 (0.010)
${\tau }_0^{{}^{\prime }}$ = 0.3	800	100	0.960 (0.007)	0.944 (0.008)	0.905 (0.010)
		120	0.956 (0.007)	0.942 (0.008)	0.906 (0.010)

Table 7. Empirical powers $\kappa =1.43,\alpha =0.05$.

${\mathit{\tau }}_0^{{}^{\prime }}$	T	N	${\mathit{\rho }}_0=0.2$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.8$
		20	0.915 (0.020)	0.890 (0.022)	0.844 (0.026)
${\tau }_0^{{}^{\prime }}$ = 0.5	200	25	0.917 (0.019)	0.891 (0.022)	0.841 (0.026)
		35	0.913 (0.020)	0.887 (0.023)	0.833 (0.026)
		20	0.954 (0.015)	0.937 (0.017)	0.847 (0.025)
${\tau }_0^{{}^{\prime }}$ = 0.3	200	25	0.950 (0.015)	0.934 (0.018)	0.851 (0.025)
		35	0.951 (0.015)	0.935 (0.018)	0.851 (0.025)
		30	0.950 (0.010)	0.935 (0.011)	0.880 (0.014)
${\tau }_0^{{}^{\prime }}$ = 0.5	500	35	0.945 (0.010)	0.933 (0.011)	0.888 (0.014)
		40	0.943 (0.010)	0.928 (0.011)	0.885 (0.014)
		30	0.961 (0.009)	0.952 (0.010)	0.912 (0.013)
${\tau }_0^{{}^{\prime }}$ = 0.3	500	35	0.961 (0.009)	0.955 (0.009)	0.901 (0.013)
		40	0.962 (0.009)	0.954 (0.009)	0.909 (0.013)
		70	0.951 (0.008)	0.936 (0.009)	0.872 (0.012)
${\tau }_0^{{}^{\prime }}$ = 0.5	800	100	0.953 (0.007)	0.930 (0.009)	0.878 (0.011)
		120	0.947 (0.008)	0.929 (0.009)	0.877 (0.011)
		70	0.966 (0.006)	0.955 (0.007)	0.933 (0.009)
${\tau }_0^{{}^{\prime }}$ = 0.3	800	100	0.970 (0.006)	0.959 (0.007)	0.919 (0.010)
		120	0.968 (0.006)	0.957 (0.007)	0.927 (0.009)

Table 8. Empirical powers $\kappa =1.97,\alpha =0.05$.

${\mathit{\tau }}_0^{{}^{\prime }}$	T	N	${\mathit{\rho }}_0=0.2$	${\mathit{\rho }}_0=0.5$	${\mathit{\rho }}_0=0.8$
		20	0.922 (0.019)	0.895 (0.022)	0.863 (0.024)
${\tau }_0^{{}^{\prime }}$ = 0.5	200	25	0.921 (0.019)	0.897 (0.021)	0.866 (0.024)
		35	0.925 (0.019)	0.896 (0.022)	0.850 (0.0225)
		20	0.955 (0.014)	0.949 (0.015)	0.877 (0.023)
${\tau }_0^{{}^{\prime }}$ = 0.3	200	25	0.959 (0.014)	0.954 (0.015)	0.885 (0.023)
		35	0.956 (0.014)	0.946 (0.016)	0.888 (0.022)
		30	0.958 (0.009)	0.941 (0.010)	0.892 (0.014)
${\tau }_0^{{}^{\prime }}$ = 0.5	500	35	0.957 (0.009)	0.940 (0.010)	0.895 (0.014)
		40	0.957 (0.009)	0.942 (0.010)	0.890 (0.014)
		30	0.976 (0.007)	0.957 (0.009)	0.923 (0.012)
${\tau }_0^{{}^{\prime }}$ = 0.3	500	35	0.975 (0.007)	0.962 (0.009)	0.921 (0.012)
		40	0.973 (0.007)	0.961 (0.009)	0.925 (0.012)
		70	0.958 (0.007)	0.944 (0.008)	0.881 (0.011)
${\tau }_0^{{}^{\prime }}$ = 0.5	800	100	0.959 (0.007)	0.942 (0.008)	0.883 (0.011)
		120	0.959 (0.007)	0.946 (0.008)	0.884 (0.011)
		70	0.978 (0.005)	0.964 (0.007)	0.942 (0.008)
${\tau }_0^{{}^{\prime }}$ = 0.3	800	100	0.973 (0.006)	0.965 (0.006)	0.941 (0.008)
		120	0.973 (0.006)	0.966 (0.006)	0.945 (0.008)

(1) The empirical sizes are almost the same as the nominal level $\alpha$ in Table 5.

(2) From Table 6, Table 7 and Table 8, we find that the powers increase when the value of T is larger for the same ${\rho }_0$ and ${\tau }_0$. For fixed numbers T and ${\tau }_0$, the powers raise gradually with the decrease in ${\rho }_0$. An earlier location of the change point results in a higher empirical power. This is a famous result in the detection of change points.

(3) The larger tail index $\kappa$, the higher empirical powers. This is due to the special properties of heavy-tailed sequences. The smaller tail index $\kappa$, the more likely the sequence is to contain ‘outliers’. The test statistics behave differently before and after such points, which could seriously affect the performance of this test.

We compare our method with the kernel-weighted ratio method (Chen et al. [24]). The empirical powers of the $I\left(0\right)$ to $I\left(1\right)$ tests are provided in Table 9. We let $T=200,500$, $\kappa =1.43$ and the location of change point ${\tau }_0^{{}^{\prime }}=0.5$. The other parameters are set as before. In the kernel method, we choose bandwidth $h=0.2M$, where the start time M is set to be $0.2T$ or $0.3T$.

Table 9. Empirical powers of our method and the kernel method.

T	N	${\mathit{\rho }}_0$	Our Method	Kernel Method
				$\mathit{M}=\mathbf{0}.\mathbf{2}\mathit{T}$	$\mathit{M}=\mathbf{0}.\mathbf{3}\mathit{T}$
$T=200$	$N=20$	0.2	0.915	0.784	0.751
		0.5	0.890	0.766	0.679
		0.8	0.844	0.757	0.644
	$N=25$	0.2	0.917	0.785	0.755
		0.5	0.891	0.765	0.677
		0.8	0.841	0.755	0.642
	$N=35$	0.2	0.913	0.786	0.752
		0.5	0.887	0.766	0.676
		0.8	0.833	0.752	0.641
$T=500$	$N=30$	0.2	0.950	0.934	0.910
		0.5	0.935	0.880	0.847
		0.8	0.880	0.849	0.731
	$N=35$	0.2	0.945	0.936	0.911
		0.5	0.933	0.888	0.845
		0.8	0.888	0.851	0.729
	$N=40$	0.2	0.943	0.933	0.910
		0.5	0.928	0.886	0.848
		0.8	0.885	0.850	0.730

Table 9 shows that our test method is better than the kernel-weighted test method in all listed cases. The empirical powers of our method are always greater than that of the kernel method at two different start times. The powers increase when the value of T is larger for the same ${\rho }_0$. For fixed number T, the powers raise gradually with the decrease of ${\rho }_0$. In particular, our advantage is more obvious when the sample size is 200. In other words, we can obtain high empirical powers with a small sample size. Our method is more efficient. The numerical simulation shows excellent performance of our method.

4.2. Real-Data Analysis

There is growing evidence to indicate that many economic and financial time sequences have heavy-tailed features. Sometimes, the data contains changes in persistence. We apply the ratio test method to analyze the foreign exchange rate data. The data set contains 300 monthly foreign exchange rates for Sweden/US from January 1971 to December 1995. Figure 1 shows the real data. The data used here can be found on the website of the Federal Reserve Bank of St. Louis. Figure 2 describes the first-order difference of the original data in Figure 1. From Figure 2, we can see that there exist many ’outliers’.

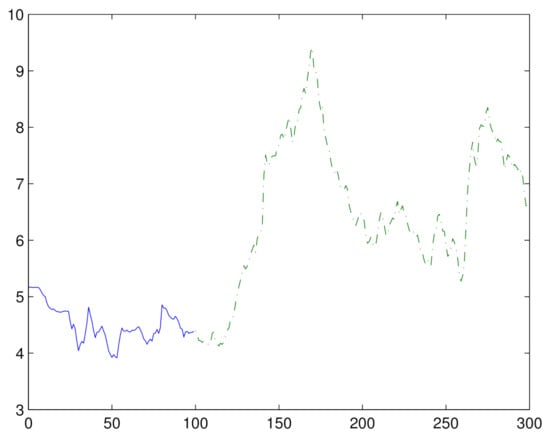
Figure 1. Monthly exchange rate data for Sweden/US.

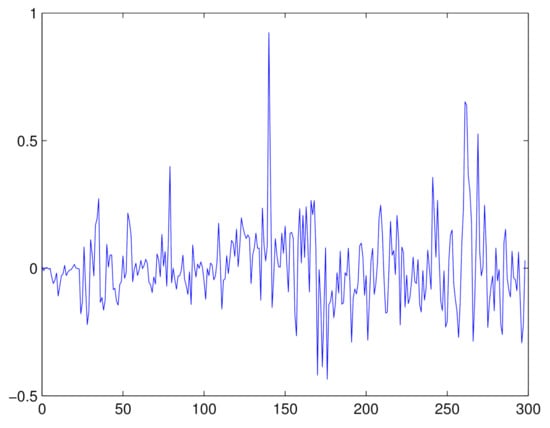
Figure 2. First order difference data for Figure 1.

According to Figure 1, the real data maybe has a persistence change from $I\left(0\right)$ to $I\left(1\right)$. We apply our method to detect persistence change in this sequence. First, we used the bootstrap approximation method to determine the rejection domain by the statistic (37). Then, we discovered that the test statistic is larger than the critical value. Therefore, we reject the null hypothesis. This means there could be a change point in persistence from $I\left(0\right)$ to $I\left(1\right)$. Based on Kim’s [1] method, the change point estimation is 104. This coincides with our detection results.

One question we have is whether the conclusion of a rejection is caused by persistence change points or by ’outliers’. In order to solve this problem and to make our conclusion more reliable, we also tested the first-order difference data in Figure 2. The monitoring process that used the same parameters as before does not discover changes in persistence. This result shows that the initial data contains a possible change point and that the first-order difference series is stationary.

Furthermore, we conclude that there could be a change point in persistence from $I\left(0\right)$ to $I\left(1\right)$. The estimated change point 104 is located at the point August, 1979. Referring to the history of the American economic policy, this estimated location can be well interpreted. In the second half of the 1970s, the US government decided to adopt an expansionary fiscal policy and a monetary policy to stimulate the economy due to the high inflation, high unemployment rate, and economic growth rate of the US economy. After President Reagan took office, the dollar began to strengthen and the foreign exchange rate for Sweden/US reached its highest point in July 1985. Thus, this implies that the sequence goes from stationary to nonstationary because of the stimulus of the economic policy.

5. Discussion

We focused on the symmetric $I\left(1\right)$-to-$I\left(0\right)$ and $I\left(0\right)$-to-$I\left(1\right)$ persistence change testing problems in this paper. A ratio test based on bootstrap approximation was proposed to detect this type of change in heavy-tailed observations. On the basis of residual CUSUM, the test statistic was constructed in a ratio form. We proved the null distribution of the test statistic. The consistency under alternative hypothesis was also discussed. However, the null distribution of the test statistic contains an unknown tail index. Then, we presented the bootstrap methodology.

Over the past few decades, many economic and financial data have displayed changes in persistence. This type of changes causes substantial practical problems concerning inflation rates, short-term interest rates, and government budget deficits, especially the issue of inflation persistence that plays a key role in the formulation and evaluation of quantitative macroeconomic models; see Korenok et al. [25]. Furthermore, a possible application of testing persistence change is to predictive regression, predicting a low-persistence $I\left(0\right)$ variable such as stock returns using a highly persistent predictor; see Kejriwal et al. [13] and Verdickt et al. [26].

Our study thus offers a new strategy to treat persistence change detecting problems. There are still some shortcomings in our work: for example, how to select the bootstrap sample sizes N for a fixed T, how to determine the direction of the persistence change, etc. We will conduct further research into these questions.

6. Conclusions

In this paper, the new ratio and bootstrap test for persistence change with heavy-tailed innovations was proposed. This paper focuses on the $I\left(1\right)$-to-$I\left(0\right)$ and $I\left(0\right)$-to-$I\left(1\right)$ persistence change detecting problems. We derived the asymptotic distributions of the ratio tests under the corresponding null hypothesises. However, the asymptotic distributions are dependent on tail index $\kappa$, which is unknown and difficult to estimate. To solve this problem, we presented an approximate method based on the bootstrap methodology. As most subsampling methods, our approach relies on the choice of the subsample size N. Under the alternative, we proved the consistency of the ratio and bootstrap test. The simulation results show that the empirical sizes and powers perform well. In conclusion, the ratio test based on bootstrap method constitutes an effective tool for detecting persistence change with heavy-tailed sequence.