Fixed-Point Iterative Method with Eighth-Order Constructed by Undetermined Parameter Technique for Solving Nonlinear Systems

Abstract

In this manuscript, by using undetermined parameter method, an efficient iterative method with eighth-order is designed to solve nonlinear systems. The new method requires one matrix inversion per iteration, which means that computational cost of our method is low. The theoretical efficiency of the proposed method is analyzed, which is superior to other methods. Numerical results show that the proposed method can reduce the computational time, remarkably. New method is applied to solve the numerical solution of nonlinear ordinary differential equations (ODEs) and partial differential equations (PDEs). The nonlinear ODEs and PDEs are discretized by finite difference method. The validity of the new method is verified by comparison with analytic solutions.

1. Introduction

Symmetry is a fundamental topic in many areas of physics and mathematics. Many problems from engineering and mathematics possess symmetry, which can be transformed into the nonlinear systems $F\left(z\right)=0$. Some nonlinear ODEs and PDEs can be discretized into nonlinear systems. Using the iterative method to solve these nonlinear systems, we can find the numerical solution of ODEs and PDEs. Newton’s method [1,2] is the oldest and famous iterative method for the numerical solution of nonlinear systems,

$$z^{(j+1)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),$$

(1)

where $J_j=F^{\prime }\left(z^{\left(j\right)}\right)$ is the Jacobin matrix. Newton’s method is one-point iterative method, which is convergent quadratically. Any one-point iterative method which is constructed by F and its first $r-1$ derivatives cannot get higher order than r. Researchers try to improve the computational efficiency of one-point method by different ways. One effective way is to increase the iteration step of iterative method. This kind of methods are called multistep or multipoint iterative methods. It has better efficiency than one-point iterative method. For example, based on a quadrature formulae, Darvishi et al. [3] suggested an efficient multipoint method with order four that requires two F, two matrix inversions and three $F^{\prime }$. Grau-Sánchez et al. [4] proposed a variant of Ostrowski’s method, which needs two matrix inversions, three F, two $F^{\prime }$ and one first-order divided difference. Using the pseudocompostion technique, Cordero et al. [5] presented a sixth-order Jarratt-type method that uses three $F^{\prime }$, two matrix inversions and three F. They [6] also presented a four-step eighth-order method that requires the same computational cost as their sixth-order Jarratt-type method. Using the weight function technique, Sharma and Arora [7] suggested a Jarratt-type method with order six, which requires one matrix inversion, three F and two $F^{\prime }$. Behl and Cordero [8] designed a sixth-order scheme that needs two matrix inversions, two F and one first-order divided difference. Behl and Arora [9] proposed a derivative-free scheme with order seven for solving nonlinear systems, which needs one matrix inversion, five F and two first-order divided differences. Using the interpolation technique, we [10] obtained a seventh-order method that is extendible to solve nonlinear systems. This method requires three matrix inversions, four F and five first-order divided differences. We [11] also obtained another seventh-order fixed-point method that needs one matrix inversion, five F and three first-order divided differences. Sharma and Aroa [12] obtained a seventh-order derivative-free method. This method requires two matrix inversions, four F and five first-order divided differences. Using the undetermined parameter technique, Narang et al. [13] designed a seventh-order method, which needs one matrix inversion, three F and two first-order divided differences per iteration.

Many efficient multipoint iterative methods for solving nonlinear equations have been proposed, see [14,15,16,17,18,19,20]. However, not all multipoint iterative methods can be extended to solve nonlinear systems. Therefore, it is an interesting research to construct multipoint iterative method for solving systems of nonlinear equations. Ham and Chun [14] proposed the following fifth-order method for solving nonlinear equations

$$\{\begin{array}{c}{t}_j=z_j-\frac{f\left(z_j\right)}{f^{\prime }\left(z_j\right)},\\ z_{j+1}=t_j-\frac{f^{\prime }\left(t_j\right)+3f^{\prime }\left(z_j\right)}{5f^{\prime }\left(t_j\right)-f^{\prime }\left(z_j\right)}\frac{f\left(t_j\right)}{f^{\prime }\left(z_j\right)},\end{array}$$

(2)

which is called Ham-Chun’s method. We generalize Ham-Chun’s method to Banach space to solve nonlinear systems and obtain the following iterative scheme

$$\{\begin{array}{c}{t}^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-N_j^{-1}\left[F^{\prime }\left(t^{\left(j\right)}\right)+3J_j\right]J_j^{-1}F\left(t^{\left(j\right)}\right),\end{array}$$

(3)

where $N_j=5F^{\prime }\left(t^{\left(j\right)}\right)-J_j$ and $J_j=F^{\prime }\left(z^{\left(j\right)}\right)$. Method (3) is called HM5 in this paper, which requires two F, two matrix inversions and two $F^{\prime }$ per iteration. Method HM5 is not the fixed-point iterative method, so its computational efficiency is low.

In this paper, we propose an eighth-order fixed-point iterative method for the numerical solution of nonlinear systems. First, we prove the order of convergence of method HM5 in Section 2. Inspired by method HM5, we propose an eighth-order fixed-point method by using the undetermined parameter method in Section 3. The proposed method requires one LU decomposition per iteration, which means that this method has low computational cost. The computational efficiency of iterative method is analyzed in Section 4. The proposed method is used to solve the solution of nonlinear systems, nonlinear ODEs and PDEs in Section 5. Section 6 gives a short conclusion.

2. Iterative Method with Order Five for Solving Nonlinear Systems

Theorem 1.

Let $\xi \in {\mathbb{R}}^m$ be the zero of F: $\mathbf{D}\subset {\mathbb{R}}^m\to {\mathbb{R}}^m$, $F\left(z\right)$ be sufficiently Fréchet differentiable and $F^{\prime }\left(z\right)$ be continuous and nonsingular at $\mathbf{D}$. Then, method HM5 converges to ξ with order five, if initial guess $z^{\left(0\right)}$ close to ξ.

Proof. 

Let $B_i=\frac{1}{i!}{F}^{\prime }{\left(\xi \right)}^{-1}{F}^{\left(i\right)}\left(\xi \right)\in L_i({\mathbb{R}}^m,{\mathbb{R}}^m)$ and $e=z^{\left(j\right)}-\xi .$ By using the results in [15], we get

$$F\left(z^{\left(j\right)}\right)=F^{\prime }\left(\xi \right)[e+B_2{e}^2+B_3{e}^3+O\left(e^4\right)],$$

(4)

$$F^{\prime }\left(z^{\left(j\right)}\right)=F^{\prime }\left(\xi \right)[I+2B_{2}e+3B_3{e}^2+4B_4{e}^3+O\left(e^4\right)],$$

(5)

and

$$F^{\prime }{\left(z^{\left(j\right)}\right)}^{-1}=[I-2B_{2}e+(4B_2^2-3B_3)e^2-(8B_2^3-6B_2{B}_3-6B_3{B}_2+4B_4)e^3+O\left(e^4\right)]F^{\prime }{\left(\xi \right)}^{-1}.$$

(6)

Let $E=t^{\left(j\right)}-\xi .$ From (4)–(6), we get

$$E=t^{\left(j\right)}-\xi =e-F^{\prime }{\left(z^{\left(j\right)}\right)}^{-1}F\left(z^{\left(j\right)}\right)=B_2{e}^2-2(B_2^2-B_3)e^3+O\left(e^4\right).$$

(7)

Similar argument to (4), we arrive at

$$F\left(t^{\left(j\right)}\right)=F^{\prime }\left(\xi \right)[E+B_2{E}^2+O\left(E^3\right)],$$

(8)

$$F^{\prime }\left(t^{\left(j\right)}\right)=F^{\prime }\left(\xi \right)[I+2B_{2}E+O\left(E^2\right)],$$

(9)

$$N_j=F^{\prime }\left(\xi \right)[4I-2B_{2}e-(10B_2^2-3B_3)e^2+4(5B_2^3-5B_2{B}_3+B_4)e^3+O\left(e^4\right)],$$

(10)

and

$$N_j^{-1}=[\frac{1}{4}I-\frac{1}{8}{B}_{2}e+\frac{1}{16}(-9B_2^2+3B_3)e^2+\frac{1}{32}(21B_2^3-34B_2{B}_3+8B_4)e^3+O\left(e^4\right)]F^{\prime }{\left(\xi \right)}^{-1},$$

(11)

Using (3), (5), (6), (9) and (11), we obtain the error equation:

$$e_{n+1}=(\frac{3}{2}{B}_2^4-B_2^2{B}_3)e^5+O\left(e^6\right)$$

(12)

It is easy to see that method HM5 is of fifth-order convergence. □

Based on method HM5, we will give a new fixed-point method with order eight in the following section.

3. Fixed-Point Iterative Method with Order Eight

Inspired by method HM5, we design a fixed-point iterative method by using the undetermined parameter technique as follows:

$$\{\begin{array}{c}{t}^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),\\ w^{\left(j\right)}=t^{\left(j\right)}-[I+(I+g_1{M}^{\left(j\right)})M^{\left(j\right)}[J_j^{-1}F\left(t^{\left(j\right)}\right),\\ z^{(j+1)}=w^{\left(j\right)}-[I+(I+g_2{M}^{\left(j\right)})M^{\left(j\right)}]J_j^{-1}F\left(w^{\left(j\right)}\right),\end{array}$$

(13)

where $M^{\left(j\right)}=J_j^{-1}(J_j-F^{\prime }\left(t^{\left(j\right)}\right))$, I is an identity matrix and $g_i,(i=1,2)$ are constant parameters to be determined.

Theorem 2.

Let $\xi \in {\mathbb{R}}^m$ be the zero of $F\left(z\right): \mathbf{D}\subset {\mathbb{R}}^m\to {\mathbb{R}}^m$, $F\left(z\right)$ be sufficiently Fréchet differentiable and $F^{\prime }\left(z\right)$ be continuous and nonsingular at $\mathbf{D}$. If $g_1=\frac{5}{4}$, $g_2=\frac{3}{2}$ and initial guess $z^{\left(0\right)}$ is close to ξ, then method (13) reaches eighth-order convergence.

Proof. 

From (5), (6) and (9), we obtain

$$M^{\left(j\right)}=2B_{2}e-(6B_2^2-3B_3)e^2+4(4B_2^3-4B_2{B}_3+B_4)e^3+O\left(e^4\right).$$

(14)

Let $\epsilon =w^{\left(j\right)}-\xi .$ Using (6), (8) and (14), we arrive at

$$\epsilon =w^{\left(j\right)}-\xi =B_2^3(5-4g_1)e^4+4B_2^2(B_3(6-5g_1)+A_2^2(-9+10g_1))e^5+O\left(e^6\right),$$

(15)

and

$$F\left(w^{\left(j\right)}\right)=F^{\prime }\left(\alpha \right)[\epsilon +B_2{\epsilon }^2+O\left({\epsilon }^3\right)].$$

(16)

Using (13)–(16), we can get the error equation of method (13)

$$e_{n+1}=z^{(j+1)}-\xi =2B_2^5(-5+4g_1)(-3+2g_2)e^6-4\left(B_2^4\right(B_3(-56+g_1(46-32g_2)+39g_2)$$

$$+B_2^2(89-76g_2+8g_1(-11+9g_2))\left)\right)e^7+B_2^3(2B_2{B}_4(157-108g_2+8g_1$$

$$(-16+11g_2\left)\right)+B_2^4(2483-16g_1^2-2652g_2+24g_1(-123+122g_2))$$

$$+B_3^2(651-481g_2+g_1(-554+408g_2))+B_2^2{B}_3(-3123$$

$$+2760g_2-4g_1(-789+668g_2)\left)\right)e^8+O\left(e^9\right)$$

(17)

Taking $g_1=\frac{5}{4}$ and $g_2=\frac{3}{2}$, we get

$$e_{n+1}=(280B_2^7-48B_2^5{B}_3+2B_2^3{B}_3^2)e^8+O\left(e^9\right)$$

(18)

It is easy see that the order of method (13) is eight. Per iteration, method (13) requires three F, two $F^{\prime }$ and twice LU decompositions. Compared to method HM5, method (13) only increases one function evaluation $F\left(z\right)$.

Thus, we get an iterative method with eighth-order as follows

$$\{\begin{array}{c}{t}^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),\\ w^{\left(j\right)}=t^{\left(j\right)}-[I+(I+\frac{5}{4}{M}^{\left(j\right)})M^{\left(j\right)}]J_j^{-1}F\left(t^{\left(j\right)}\right),\\ z^{(j+1)}=w^{\left(j\right)}-[I+(I+\frac{3}{2}{M}^{\left(j\right)})M^{\left(j\right)}]J_j^{-1}F\left(w^{\left(j\right)}\right),\end{array}$$

(19)

where $M^{\left(j\right)}=J_j^{-1}(J_j-F^{\prime }\left(t^{\left(j\right)}\right))$ and $J_j=F^{\prime }\left(z^{\left(j\right)}\right)$. Method (19) is called NM8 in this paper. □

4. Computational Efficiency

The computational efficiency indexes $CEI$ is proposed by Grau-Sánchez et al. [4,16,17]:

$$CEI({\nu }_0,{\nu }_1,m)={\rho }^{\frac{1}{C({\nu }_0,{\nu }_1,m)}},$$

(20)

where

$$C({\nu }_0,{\nu }_1,m)=S_0\left(m\right){\nu }_0+S_1\left(m\right){\nu }_1+S(m,l).$$

(21)

In per iteration, $C({\nu }_0,{\nu }_1,m)$ represents the cost of iterative method. Parameter $S_0\left(m\right)$ is the number of the scalar functions used in F and $[y,x;F]$. Parameter $S_1\left(m\right)$ is the number of scalar functions used in $F^{\prime }$. $S(m,l)$ is the number of products. The parameter l in (21) is the ratio between the divisions and products. The parameters ${\nu }_0$ and ${\nu }_1$ in (21) are the ratios between products and evaluations that are required to express $C({\nu }_0,{\nu }_1,m)$ in terms of products. $\rho$ represents the convergence order. The LU decomposition is used to solve linear systems in the processing of iteration. The following methods are used to compared the computational efficiency:

Darvishi et al. fourth-order method [3] (DM4)

$$\{\begin{array}{c}\hfill w^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),\hfill \\ \hfill t^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}(F\left(z^{\left(j\right)}\right)+F\left(w^{\left(j\right)}\right)),\hfill \\ \hfill z^{(j+1)}=z^{\left(j\right)}-6{(J_j+4F^{\prime }\left(\frac{z^{\left(j\right)}+t^{\left(j\right)}}{2}\right)+F^{\prime }\left(t^{\left(j\right)}\right))}^{-1}F\left(t^{\left(j\right)}\right).\hfill \end{array}$$

(22)

Grau-Sánchez et al. sixth-order method [4] (GM6)

$$\{\begin{array}{c}\hfill w^{\left(j\right)}=z^{\left(j\right)}-J_j^{-1}F\left(z^{\left(j\right)}\right),\hfill \\ \hfill t^{\left(j\right)}=w^{\left(j\right)}-{\mu }_{1}F\left(w^{\left(j\right)}\right),\hfill \\ \hfill z^{(j+1)}=t^{\left(j\right)}-{\mu }_{1}F\left(t^{\left(j\right)}\right),\hfill \end{array}$$

(23)

where ${\mu }_1=2{[z^{\left(j\right)},w^{\left(j\right)};F]}^{-1}-J_j^{-1}$ and $[w^{\left(j\right)},z^{\left(j\right)};F]$ is the first-order divided difference operator.

Cordero et al. sixth-order method [5] (CM6)

$$\{\begin{array}{c}\hfill w^{\left(j\right)}=z^{\left(j\right)}-\frac{1}{2}{J}_j^{-1}F\left(z^{\left(j\right)}\right),\hfill \\ \hfill t^{\left(j\right)}=z^{\left(j\right)}+{\mu }_2[3J_j-4F\left(w^{\left(j\right)}\right)],\hfill \\ \hfill z^{(j+1)}=t^{\left(j\right)}+{\mu }_{2}F\left(t^{\left(j\right)}\right).\hfill \end{array}$$

(24)

where ${\mu }_2={[J_j-2F^{\prime }\left(w^{\left(j\right)}\right)]}^{-1}$.

Cordero et al. eighth-order method [6] (CM8)

$$\{\begin{array}{c}\hfill w^{\left(j\right)}=z^{\left(j\right)}-\frac{1}{2}{J}_j^{-1}F\left(z^{\left(j\right)}\right),\hfill \\ \hfill u^{\left(j\right)}=\frac{1}{3}(4w^{\left(j\right)}-z^{\left(j\right)})+{\mu }_{3}F\left(z^{\left(j\right)}\right),\hfill \\ \hfill v^{\left(j\right)}=u^{\left(j\right)}+2{\mu }_{3}F\left(u^{\left(j\right)}\right),\hfill \\ \hfill z^{(j+1)}=v^{\left(j\right)}+2{\mu }_{3}F\left(v^{\left(j\right)}\right).\hfill \end{array}$$

(25)

where ${\mu }_3={[J_j-3F^{\prime }\left(t^{\left(j\right)}\right)]}^{-1}$.

The C and $CEI$ of different iterative methods are given below:

$$C_{DM4}=2m{\nu }_0+3m^2{\nu }_1+\frac{m}{3}(2m^2+9m-5+3(m+2)l)$$

(26)

$$CE{I}_{DM4}=4^{1/C_{DM4}}.$$

(27)

$$C_{GM6}=(m^2+2m){\nu }_0+m^2{\nu }_1+\frac{2m}{3}(m^2+6m-4+3(m+2)l)$$

(28)

$$CE{I}_{GM6}=6^{1/C_{GM6}}.$$

(29)

$$C_{CM6}=3m{\nu }_0+2m^2{\nu }_1+\frac{m}{3}(2m^2+9m+1+3(m+2)l)$$

(30)

$$CE{I}_{CM6}=6^{1/C_{CM6}}.$$

(31)

$$C_{CM8}=3m{\nu }_0+2m^2{\nu }_1+\frac{m}{3}(2m^2+12m+4+3(m+3)l)$$

(32)

$$CE{I}_{CM8}=8^{1/C_{CM8}}.$$

(33)

$$C_{HM5}=2m{\nu }_0+2m^2{\nu }_1+\frac{m}{3}(2m^2+12m-8+3(m+2)l)$$

(34)

$$CE{I}_{HM5}=5^{1/C_{HM5}}.$$

(35)

$$C_{NM8}=3m{\nu }_0+2m^2{\nu }_1+\frac{m}{6}(2m^2+63m-29+3(m+13)l)$$

(36)

$$CE{I}_{NM8}=8^{1/C_{NM8}}.$$

(37)

The computational efficiencies of different methods are compared by the ratio $R_{A,B}$ [4,10]

$$R_{A,B}=\frac{lnCE{I}_A}{lnCE{I}_B}=\frac{ln\left({\rho }_A\right)C_B({\nu }_0,{\nu }_1,m)}{ln\left({\rho }_B\right)C_A({\nu }_0,{\nu }_1,m)}.$$

(38)

If $R_{A,B}>1$, then method B is less efficient than method A. $R_{A,B}=1$ is the boundary between the computational efficiencies, which is an equation of ${\nu }_0$ as a function of m, l and ${\nu }_1$. Parameters in (38) satisfy ${\nu }_0>0$, ${\nu }_1>0$, $l\ge 1$ and $m\ge 2$, the $CEI$ of different methods is studied in the following result.

Theorem 3.

 

1. For all ${\nu }_0,{\nu }_1>0$ and $l\ge 1$, we arrive at:

(a) 

$CE{I}_{NM8}>CE{I}_{DM4}$ for all $m\ge 8$.

(b) 

$CE{I}_{NM8}>CE{I}_{CM6}$ for all $m\ge 2$.

(c) 

$CE{I}_{NM8}>CE{I}_{HM5}$ for all $m\ge 11$.

(d) 

$CE{I}_{NM8}>CE{I}_{CM8}$ for all $m\ge 18$.

2. We have $CE{I}_{NM8}>CE{I}_{GM6}$ for all $m\ge 2$ and ${\nu }_0>H$, where $H=\frac{6(2r-q)m{\nu }_1+2(r-5q)m^2+(63r-9q+(3r-33q)l)m+43q-5r+(39r-33q)l}{18(mq+q-r)}.$

Proof. 

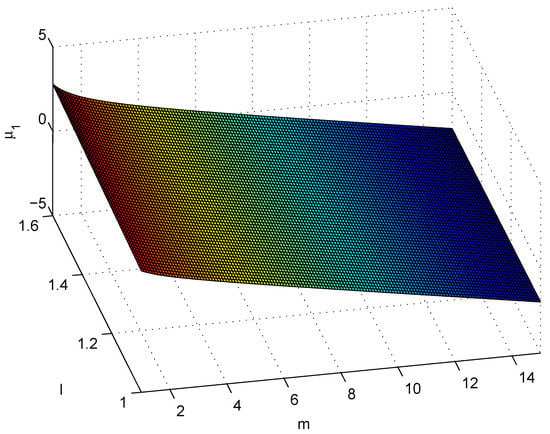
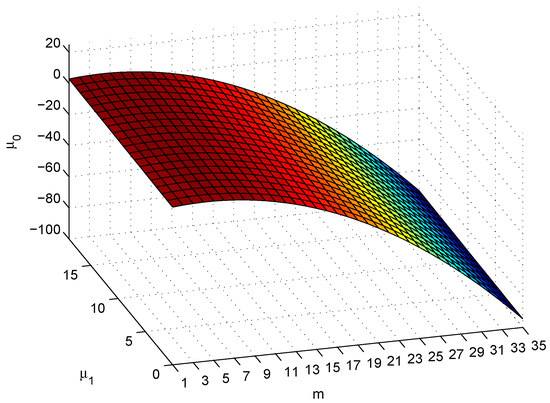
1. From (26), (27) and (36)–(38), we get the boundary $R_{NM8,DM4}=1$ that is given by

$${\nu }_1=\frac{-4(m-9)m-14+(21-6m)l}{15m}.$$

(39)

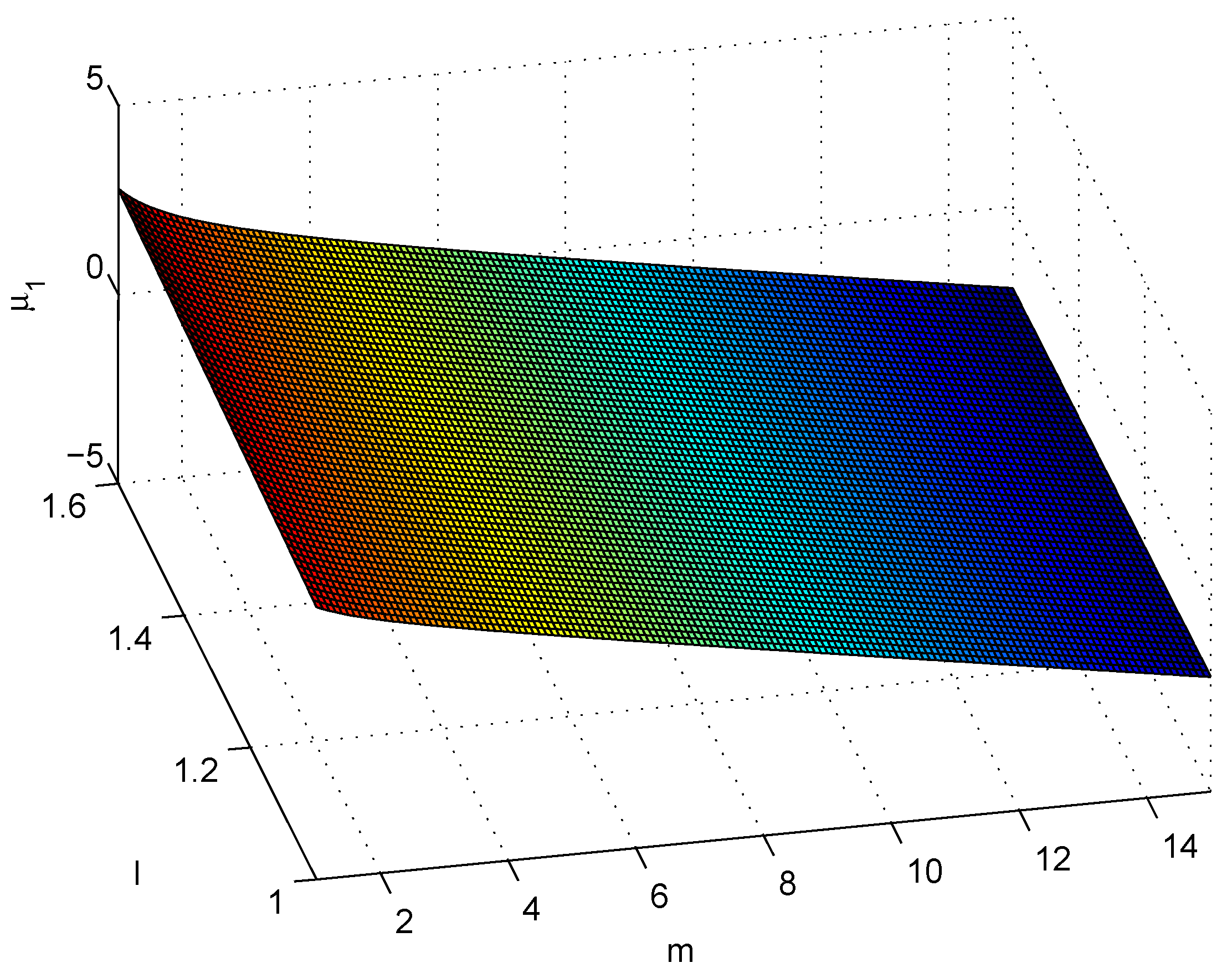
Figure 1 shows the boundary $R_{NM8,DM4}=1$, which implies that $CE{I}_{NM8}>CE{I}_{DM4}$ on the above and $CE{I}_{NM8}<CE{I}_{DM4}$ on the below of boundary plane. Parameter $m\ge 8$, ${\nu }_1$ is always negative which means that DM4 is less efficient than NM8 for all $m\ge 8$ and $l\ge 1.$

Figure 1. Boundary plane of $R_{NM8,DM4}=1$.

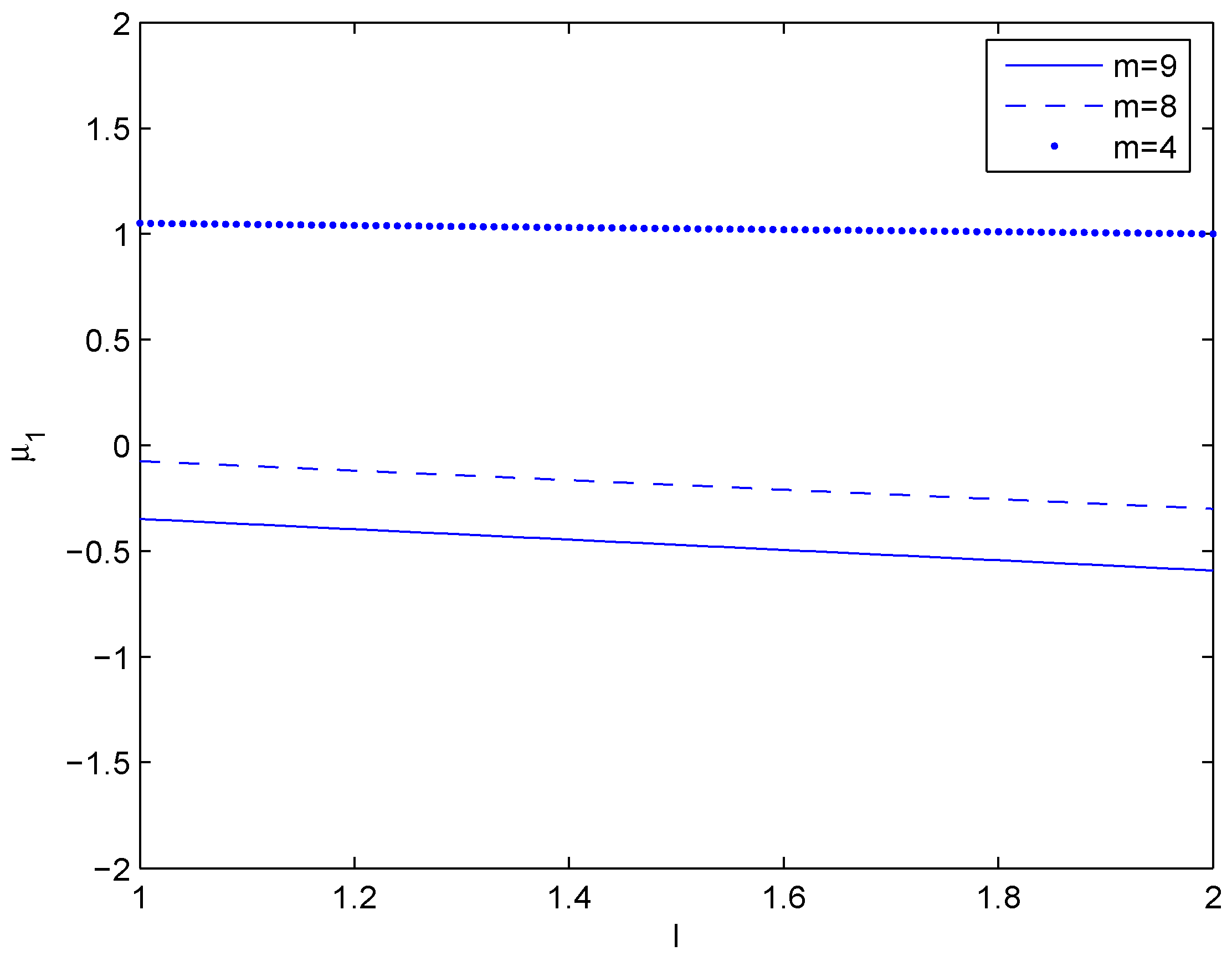
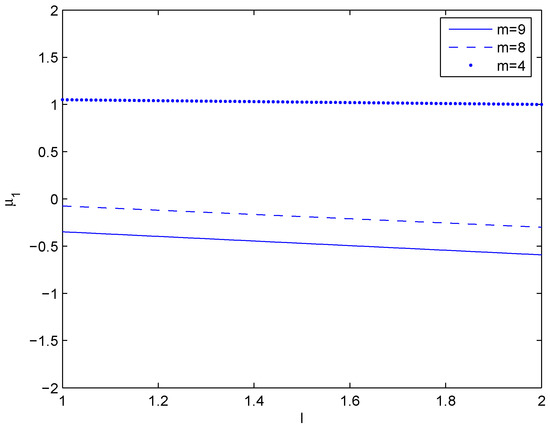
Figure 2 shows the boundary lines in $(l,{\nu }_1)$-plane for $m=4,8$ and 9 which means that $CE{I}_{NM8}>CE{I}_{DM4}$ for $m=8,m=9$ and $l\ge 1.$ For $m<4$, $CE{I}_{NM8}>CE{I}_{DM4}$ on the above of boundary line and $CE{I}_{NM8}<CE{I}_{DM4}$ on the below of boundary line.

Figure 2. Boundary lines in $(l,{\nu }_1)$-plane for m = 4, 8 and 9.

From (28), (29) and (36)–(38), we get the boundary $R_{NM8,CM6}=1$ that is given by

$${\nu }_0=\frac{12(ln3-2ln2)m{\nu }_1+2(ln3-35ln2)m^2+(63+9ln2+(3ln3-15ln2)l)m-35ln2-29ln3+(39ln3+3ln2)l}{18(2ln2-ln3)},$$

(40)

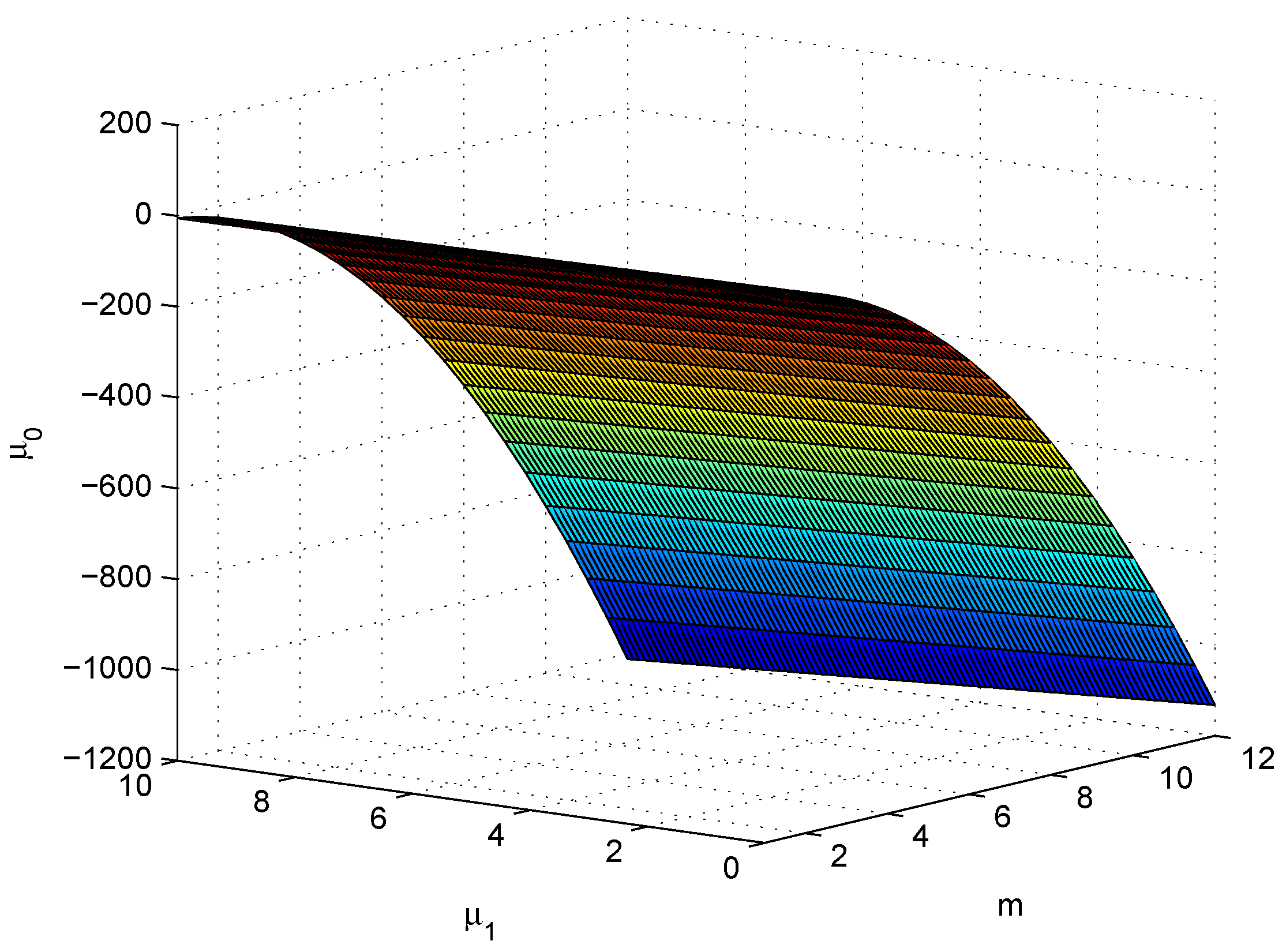
For $m\ge 2$, ${\nu }_0$ is always negative. Figure 3 shows the boundary for $l=1$, which means that CM6 is less efficient than N8 for all $m\ge 2$ and ${\nu }_1\ge 0$.

Figure 3. Boundary plane of $R_{NM8,CM6}=1$.

Using (35)–(38), we obtain the boundary $R_{NM8,HM5}=1$ that is written by

$${\nu }_0=\frac{2(p-6q)m^2+63mp-72mq+48q-29p+[3(m+13)p-18(m+2)q]l+12(q-3p)m{\nu }_1}{18(2q-p)},$$

(41)

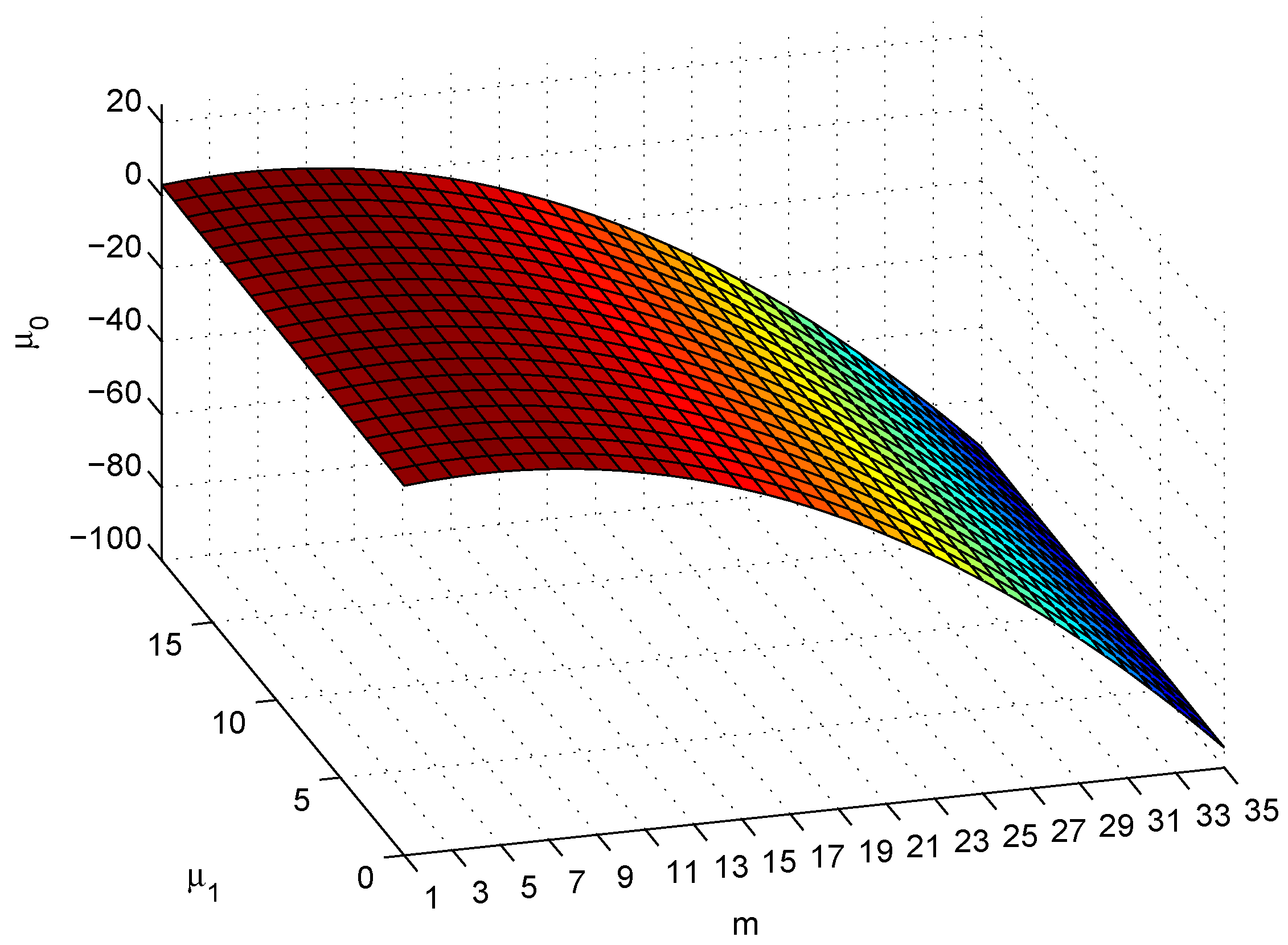
where $p=ln5$ and $q=ln2$. For $m\ge 11$, ${\nu }_0$ is always negative. Figure 4 shows the boundary for $l=1$, which implies that method NM8 is more efficient than method HM5 for all $m\ge 11$, ${\nu }_1\ge 0$ and $l=1.$

Figure 4. Boundary plane of $R_{NM8,HM5}=1$.

Using (32), (33) and (36)–(38), we obtain the following relation between NM8 and CM8:

$$R_{NM8,CM8}=\frac{ln\left({\rho }_{NM8}\right)C_{CM8}}{ln\left({\rho }_{CM8}\right)C_{NM8}}=\frac{3{\nu }_0+2m{\nu }_1+\frac{1}{3}(2m^2+12m+4+3(m+3)l)}{3{\nu }_0+2m{\nu }_1+\frac{1}{6}(2m^2+63m-29+3(m+13)l)}.$$

(42)

Using the numerator to subtract the denominator of (42), we get

$$\frac{1}{6}((2m-39)m+37+3(m-7)l).$$

(43)

If the expression (43) is more than zero then $R_{NM8,CM8}>1$. Thus, we obtain that $CE{I}_{NM8}>CE{I}_{CM8}$ for all $m\ge 18$ and $l\ge 1$.

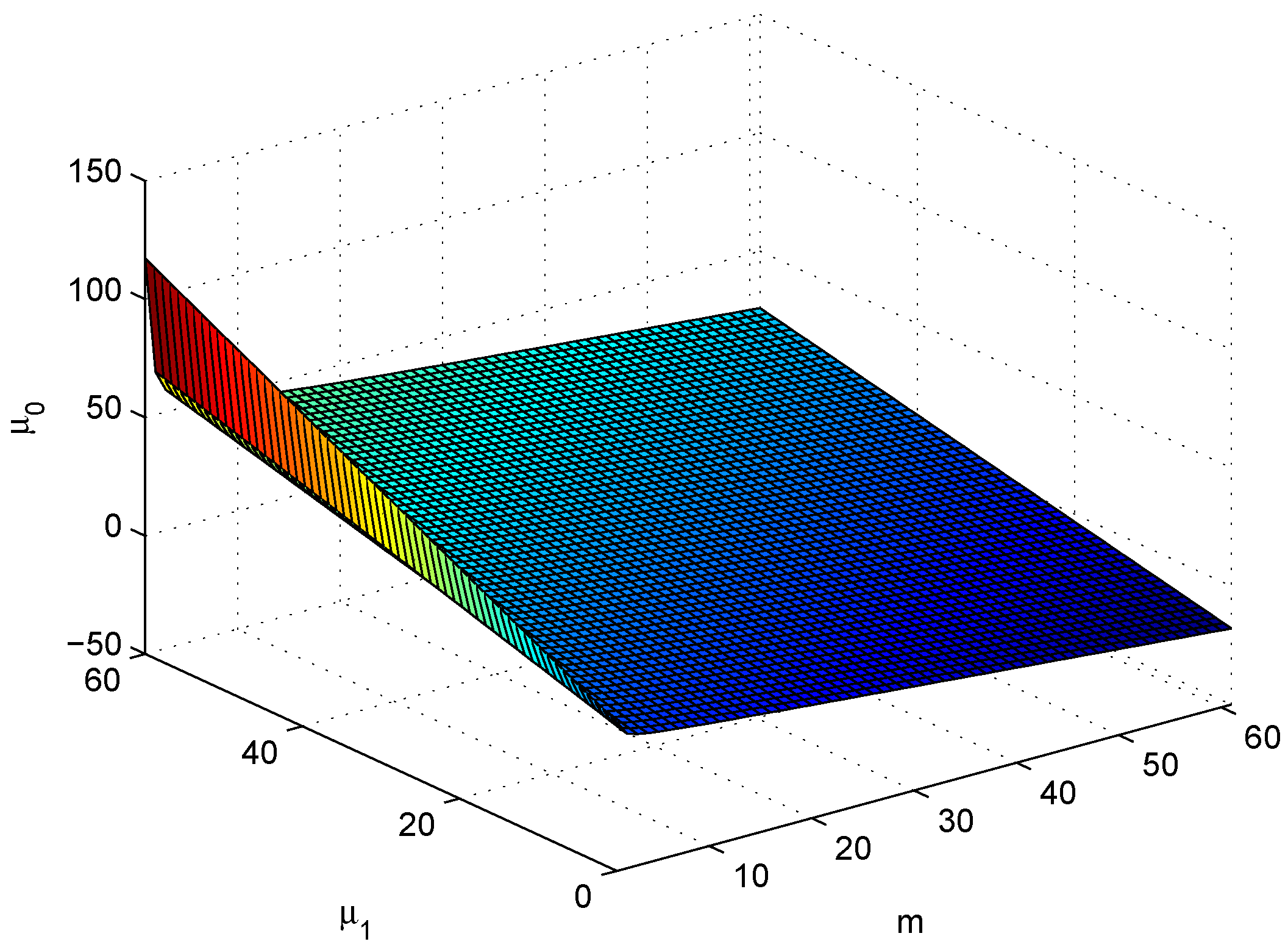
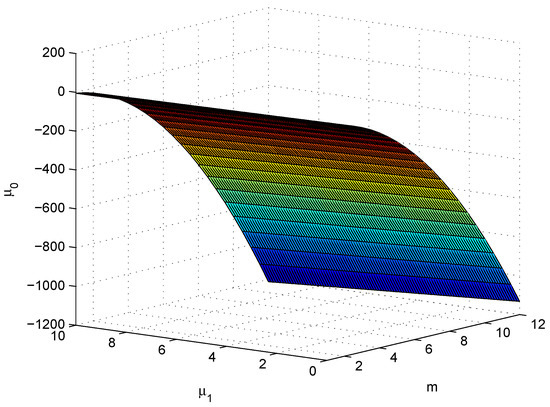
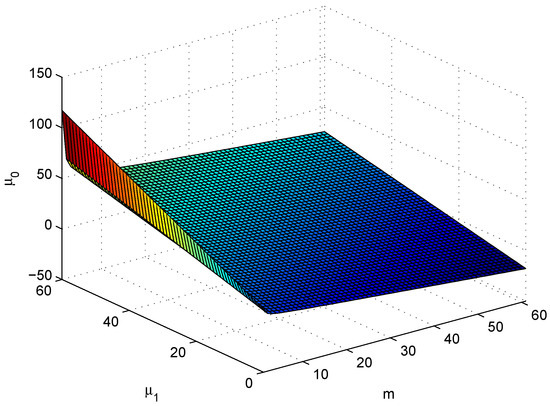
2. From (28), (29) and (36)–(38), we get the boundary $R_{NM8,GM6}=1$ that is given by

$${\nu }_0=\frac{6(2r-q)m{\nu }_1+2(r-5q)m^2+(63r-9q+(3r+3q)l)m+19q-29r+(39-33q)l}{18(mq+q-r)}$$

(44)

where $r=ln3$ and $q=ln2.$

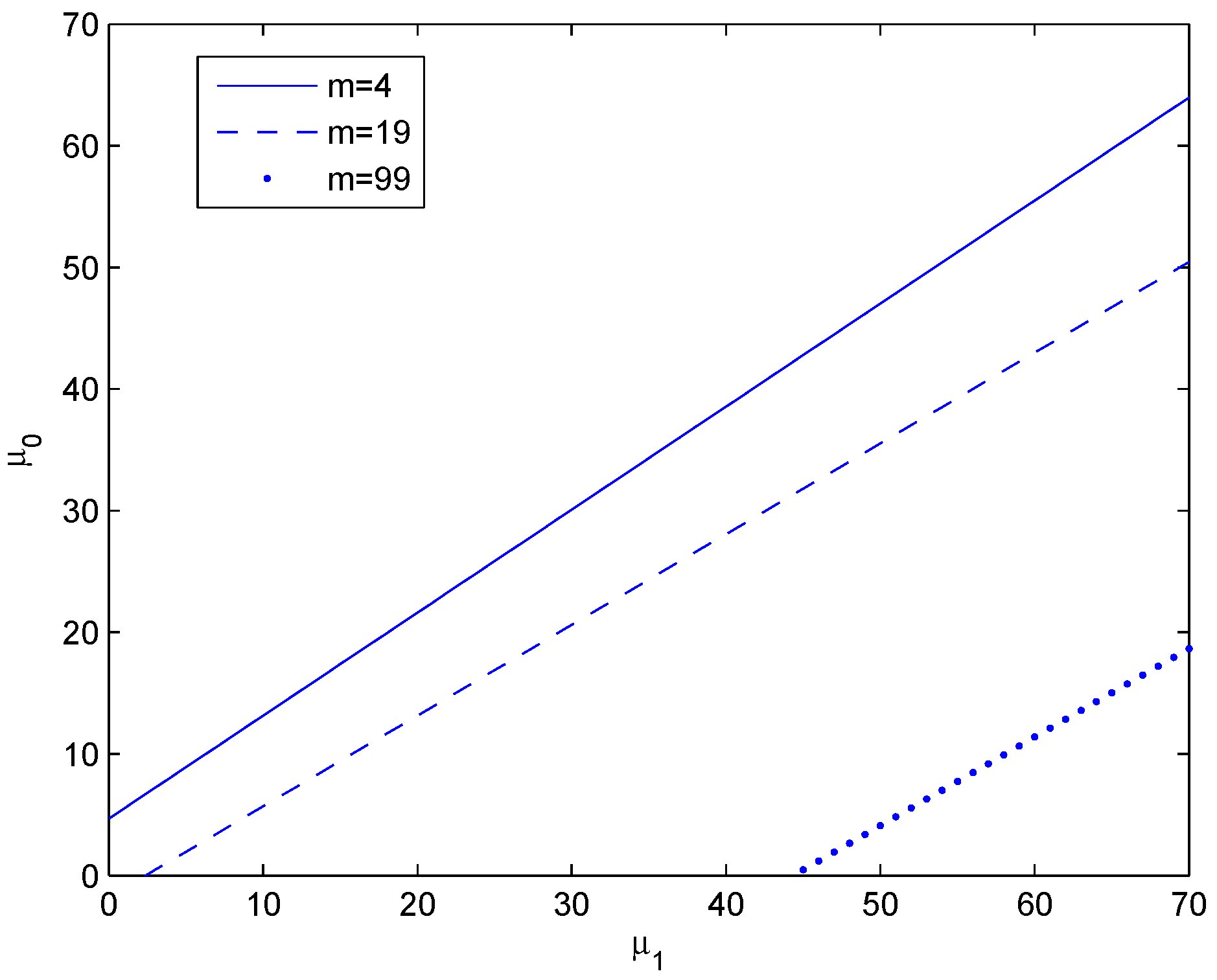
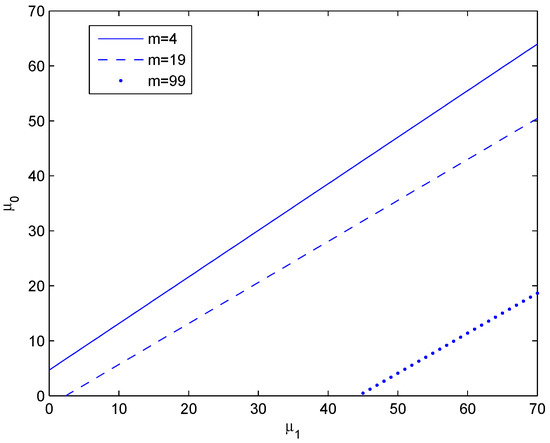
Figure 5 shows the boundary plane for Equation (44). Taking $l=1$, Figure 6 shows some particular boundaries corresponding to $m=4,19$ and 99, wherein $CE{I}_{NM8}>CE{I}_{GM6}$ on the above and $CE{I}_{NM8}<CE{I}_{GM6}$ on the below of each line. □

Figure 5. Boundary plane of $R_{NM8,GM6}=1$.

Figure 6. Boundary lines in $({\nu }_1,{\nu }_0)$-plane for $m=4,19$ and 99.

5. Numerical Results

New methods HM5 and NM8 are compared with methods DM4, GM6, CM6 and CM8 for solving some nonlinear systems. Numerical algorithms are written by the Maple 14. Table 1 shows an estimate of the cost of functions in product units.

Table 1. Estimation of cost of elementary functions, where $z=\sqrt{3}-1$ and $p=\sqrt{5}$.

Function	$\mathit{z}\ast \mathit{p}$	$\mathit{z}/\mathit{p}$	$\sqrt{\mathit{z}}$	$ln\left(\mathit{z}\right)$	$exp\left(\mathit{z}\right)$	$arctan\left(\mathit{z}\right)$	$sin\left(\mathit{z}\right)$	$cos\left(\mathit{z}\right)$
Cost	0.110 ms	1	5	12	53	95.03	112	110

The computational cost of elementary functions based on product is showed in Table 1. Estimation of computing time of elementary functions are computed with Maple 14 in a processor Intel R Core (TM) i3-2350M CPU, 1.79 GHz (32-bit Machine) Microsoft Windows 7 Professional. Table 1 shows that the computing time of one product is 0.110 milliseconds (ms). The computational cost of division with respect to product is $l=1$ and the computational cost of function $\sqrt{x}$ with respect to product is $l=5$.

In Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, $EF$ represents the errors of function values at the last step, $NI$ represents the number of iterations, $CC$ represents the computational cost, $EV$ represents the errors values of $\Vert z^{\left(j\right)}-z^{(j-1)}\Vert$, $CEI$ represents the computational efficiency index, $ACOC$ [17] represents the approximated computational order of convergence, $e-Time$ represents the mean CPU time. We choose the tolerance $\Vert z^{\left(j\right)}-z^{(j-1)}\Vert <{10}^{-200}$ for implementing the methods.

Table 2. Numerical results in Example 1.

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	$\mathit{ACOC}$	C	$\mathit{CEI}$	e-Time
DM4	5	1.118 $\times {10}^{-239}$	4.630 $\times {10}^{-957}$	4	2560	1.000541668	1.0293
HM5	5	8.158 $\times {10}^{-518}$	7.000 $\times {10}^{-2048}$	5	1896	1.000849220	0.671
GM6	4	1.343 $\times {10}^{-277}$	3.887 $\times {10}^{-830}$	6	3232	1.000554535	1.2756
CM6	5	2.458 $\times {10}^{-770}$	5.000 $\times {10}^{-2048}$	6	2332	1.000768631	1.0525
CM8	4	1.549 $\times {10}^{-314}$	4.000 $\times {10}^{-2048}$	8	2356	1.000883005	0.7890
NM8	4	1.824 $\times {10}^{-369}$	1.500 $\times {10}^{-2047}$	8	2436	1.000853994	0.8794

Table 3. Numerical results in Example 2 ($m=8$).

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	$\mathit{ACOC}$	C	$\mathit{CEI}$	e-Time
DM4	6	1.884 $\times {10}^{-525}$	1.000 $\times {10}^{-2048}$	4	3944	1.000351556	1.1695
HM5	5	2.008 $\times {10}^{-566}$	4.000 $\times {10}^{-2048}$	5	2352	1.000684519	0.573
GM6	4	7.608 $\times {10}^{-313}$	6.299 $\times {10}^{-938}$	6	5400	1.000331862	1.9465
CM6	5	1.355 $\times {10}^{-726}$	2.000 $\times {10}^{-2048}$	6	2736	1.000655097	0.8530
CM8	4	1.038 $\times {10}^{-304}$	1.000 $\times {10}^{-2048}$	8	2816	1.000738710	0.6985
NM8	4	1.491 $\times {10}^{-551}$	2.000 $\times {10}^{-2048}$	8	3040	1.000684261	0.7189

Table 4. Numerical results in Example 2 $(m=19)$.

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	$\mathit{ACOC}$	C	$\mathit{CEI}$	e-Time
DM4	6	2.331 $\times {10}^{-770}$	2.600 $\times {10}^{-2048}$	4	23,161	1.000059856	5.9182
HM5	5	3.121 $\times {10}^{-803}$	2.000 $\times {10}^{-2048}$	5	10,392	1.000154875	4.1079
GM6	4	2.862 $\times {10}^{-471}$	2.676 $\times {10}^{-1412}$	6	28,918	1.000061962	1.0168
CM6	5	1.191 $\times {10}^{-1191}$	2.300 $\times {10}^{-2048}$	6	11,096	1.000161491	4.2287
CM8	4	1.167 $\times {10}^{-511}$	2.700 $\times {10}^{-2048}$	8	11,495	1.000180916	4.1368
NM8	4	5.143 $\times {10}^{-671}$	1.900 $\times {10}^{-2048}$	8	11,400	1.000182424	3.3269

Table 5. Numerical results in Example 3 $(m=99)$.

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	$\mathit{ACOC}$	C	$\mathit{CEI}$	e-Time
DM4	7	3.538 $\times {10}^{-652}$	0.000e+00	4	2,058,804	1.0000006733	10.233
HM5	6	4.138 $\times {10}^{-507}$	4.000 $\times {10}^{-2048}$	5	696,003	1.000002312	9.078
GM6	5	3.033 $\times {10}^{-271}$	1.674 $\times {10}^{-811}$	6	715,803	1.0000025031	15.178
CM6	6	2.054 $\times {10}^{-1148}$	0.000e+00	6	686,598	1.0000026096	7.924
CM8	5	1.071 $\times {10}^{-555}$	0.000e+00	8	696,597	1.0000029851	7.144
NM8	5	1.686 $\times {10}^{-302}$	4.000 $\times {10}^{-2048}$	8	432,102	1.0000048124	6.130

Table 6. The $e-Time$ (in seconds) in Example 3.

Methods	DM4	HM5	GM6	CM6	CM8	NM8
m = 199	62.759	54.562	72.899	52.213	45.287	28.797
m = 299	199.369	192.386	204.688	169.853	144.924	82.898

Table 7. Numerical results in Example 4.

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	$\mathit{ACOC}$	C	$\mathit{CEI}$	e-Time
DM4	6	3.318 $\times {10}^{-249}$	2.152 $\times {10}^{-994}$	15,200,200	1.00000009120238	103.849
HM5	6	8.878 $\times {10}^{-727}$	8.845 $\times {10}^{-2048}$	12,020,400	1.00000013389222	89.560
GM6	7	1.765 $\times {10}^{-614}$	8.828 $\times {10}^{-2048}$	13,641,200	1.00000013134912	2708.988
CM6	6	1.843 $\times {10}^{-1167}$	9.282 $\times {10}^{-2048}$	12,005,000	1.00000014925111	100.137
CM8	5	1.220 $\times {10}^{-1287}$	7.138 $\times {10}^{-2048}$	12,045,400	1.00000017263368	88.889
NM8	5	1.370 $\times {10}^{-793}$	9.248 $\times {10}^{-2048}$	9,618,200	1.00000021619864	75.036

Table 8. Numerical results in Example 5.

Methods	$\mathit{NI}$	$\mathit{EV}$	$\mathit{EF}$	C	$\mathit{CEI}$	e-Time
DM4	6	4.850 $\times {10}^{-693}$	1.096 $\times {10}^{-2047}$	767,500	1.00000180624836	6.583
HM5	5	9.508 $\times {10}^{-457}$	2.676 $\times {10}^{-1831}$	757,400	1.00000212495329	5.304
GM6	6	3.823 $\times {10}^{-201}$	3.593 $\times {10}^{-802}$	787,600	1.00000227496382	149.324
CM6	4	4.521 $\times {10}^{-328}$	1.381 $\times {10}^{-1972}$	748,100	1.00000239508303	4.009
CM8	4	5.505 $\times {10}^{-765}$	9.052 $\times {10}^{-2048}$	758,300	1.00000274224501	4.399
NM8	4	4.472 $\times {10}^{-356}$	8.581 $\times {10}^{-2048}$	484,700	1.00000429017124	3.728

Table 9. Numerical results in Example 6.

Methods	DM4	HM5	GM6	CM6	CM8	NM8
$NI$	5	4	4	4	3	3
$e-Time$	22.5	18.7	19.6	19.8	16.3	15.5

Example 1.

Nonlinear system [16]:

$$z_j-cos(2z_j-\sum _{i=1}^m{z}_i)=0,1\le j\le m.$$

For this problem, we choose the parameter $m=4$. For $m=4$, we require four scalar cosine functions in the evaluation of vector functions F and four scalar sine functions in the evaluation of matrix $F^{\prime }$. Base on (21) and Table 1, we get parameters ${\nu }_0=\frac{110\times 4}{4}=110$ and ${\nu }_1=\frac{112\times 4}{16}=28$. For this example, we can get the computational cost of different methods by using parameters $l=1,m=4,{\nu }_0=110$ and ${\nu }_1=28$. The solution $\xi \approx {(0.5149,\cdots ,0.5149)}^T$ is founded by initial guess $z^{\left(0\right)}={(1.0,\cdots 1.0)}^T$. The results of comparisons for this example are displayed in Table 2.

Example 2.

Nonlinear system [17]:

$$\sum _{k=1,k\ne j}^m{z}_k-exp(-z_k)=0,k=1,\dots ,m$$

First, we choose the parameter $m=8$. Using the same calculation method as example 1, we obtain parameters ${\nu }_0=53$ and ${\nu }_1=0.625$. For $m=8$, the solution $\xi \approx {(0.125951,\cdots ,0.125951)}^T$ is founded by the initial guess $x^{\left(0\right)}={(5.0,\cdots 5.0)}^T$. Secondly, we choose the parameters $m=19$ and get ${\nu }_0=53$ and ${\nu }_1=0.20789$. For $m=19,$ the solution $\xi \approx {(0.0527,\cdots ,0.0527)}^T$ is founded by the initial guess is $z^{\left(0\right)}={(2.0,\cdots 2.0)}^T.$ Table 3 and Table 4 display the numerical results.

Example 3.

Nonlinear system [8]:

$$\{\begin{array}{c}\hfill z_j{z}_{j+1}-1=0,j=1,\dots ,m-1\hfill \\ \hfill z_m{z}_1-1=0.\hfill \end{array}$$

The initial guess chosen $z^{\left(0\right)}={\{5,5,\cdots ,5\}}^t$ is used for finding the solution $\xi ={\{1,1,\cdots ,1\}}^t.$ We choose the parameters $m=99,199$ and 299 in (25), respectively. In this problem, the parameters ${\nu }_0=1$ and ${\nu }_1=0$ are not dependent of m. Table 5 and Table 6 show the numerical results.

Example 4.

Boundary-value problem [13]:

$$\begin{array}{c}{u}^{\prime \prime }\left(z\right)=u{\left(z\right)}^3+sin\left(u^{\prime }{\left(z\right)}^2\right),z\in [0,1],\\ u\left(0\right)=0,u\left(1\right)=1.\end{array}$$

The first and second derivatives in this problem are discretized by difference method

$$\begin{array}{c}{u}_j^{\prime \prime }=\frac{u_{j+1}-2u_j+u_{j-1}}{h^2},j=1,2,3,\cdots ,n-1,\end{array}$$

and

$$\begin{array}{c}{u}_j^{\prime }=\frac{u_{j+1}-u_{j-1}}{2h},j=1,2,3,\cdots ,n-1,\end{array}$$

The interval $[0,1]$ is partitioned into n smaller intervals with end points $0=z_0<z_1<\cdots <z_{n-1}<z_n=1$. The partition is regular, this is $\Delta x_j=1/n$ for all j. We get the following nonlinear systems

$$\begin{array}{c}{u}_{j-1}-2u_j+u_{j+1}-h^2{u}_j^3-h^{2}sin\left({\left(\frac{u_{j-1}-u_{j+1}}{2h}\right)}^2\right)=0,j=1,2,3,\dots ,n-1.\end{array}$$

For $n=201,$ the solution ${(0.003239,0.006488,0.009748,\dots ,0.9922)}^T$ is founded by the initial guess $z^{\left(0\right)}={(0.5,\cdots 0.5)}^T.$ Parameters ${\nu }_0=120$ and ${\nu }_1=80.54$. Table 7 display the numerical results.

Example 5.

Boundary-value problem:

$$\begin{array}{c}-u^{\prime \prime }\left(z\right)=y{\left(z\right)}^2,z\in [0,1],\\ u\left(0\right)=0,u\left(1\right)=1.\end{array}$$

Using the same discretization method as problem 4, we obtain the nonlinear systems as follows:

$$\begin{array}{c}{u}_{j-1}-2u_j+u_{j+1}-h^2{u}_j^2=0,j=1,2,3,\dots ,n-1.\end{array}$$

For $n=101,$ the solution ${(0.01084,0.02168,0.03252,\dots ,0.9854)}^T$ is founded by the initial value $z^{\left(0\right)}={(0.5,\cdots 0.5)}^T.$ Parameters ${\nu }_0=4$ and ${\nu }_1=2$. Table 8 display the numerical results.

Example 6.

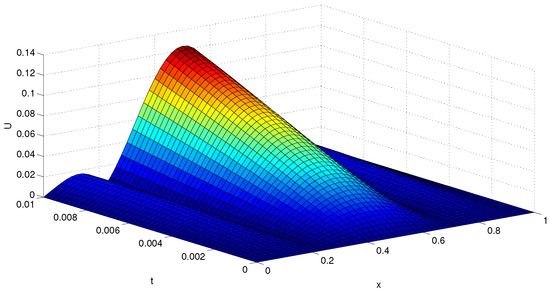
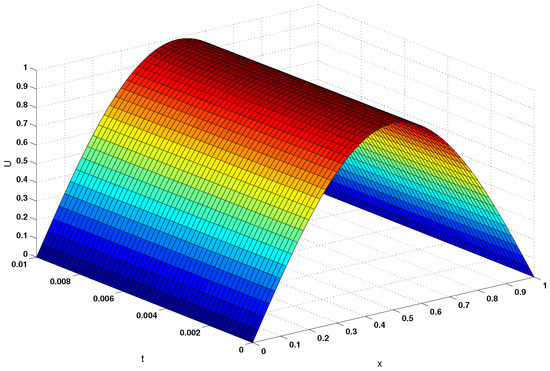
Nonlinear PDE problem [18]:

$$\begin{array}{c}{u}_{zz}=u_t+u_z-u^2+f(z,t),z\in [0,1],t\ge 0,\\ u(0,t)=0,u(1,t)=0.\\ f(z,t)=e^{(-t)}(-\pi \ast cos(\pi \ast z)-({\pi }^2-2)\ast sin(\pi \ast z))\end{array}$$

This PDE problem is a Heat Conduction Problems. We transform this problem to the nonlinear systems by using finite differences. The intervals $[0,1]$ and $[0,T]$ are partitioned into N smaller intervals, and get step size $h=1/N$ and $k=T/N$ in z and t directions. Let $u=u(z,t)$ be the exact solution and $u_{i,j}\approx u(z_i,t_j)$. Using difference method, we use obtain approximations $u_z(z,t)\approx \frac{u(z+h,t)-u(z-h,t)}{2h}$, $u_t(z,t)\approx \frac{u(z,t)-u(z,t-k)}{k}$ and $u_{zz}(z,t)\approx \frac{u(z+h,t)-2u(z,t)+u(z-h,t)}{h^2}$. We get a nonlinear system as follows:

$$\begin{array}{c}(2k+kh)u_{i-1,j}+(-4k-2h^2)u_{i,j}+(2k-kh)u_{i+1,j}+2k{h}^2{u}_{i,j}^2+2h^2{u}_{i,j-1}-2k{h}^{2}f(z_i,t_j)=0\end{array}$$

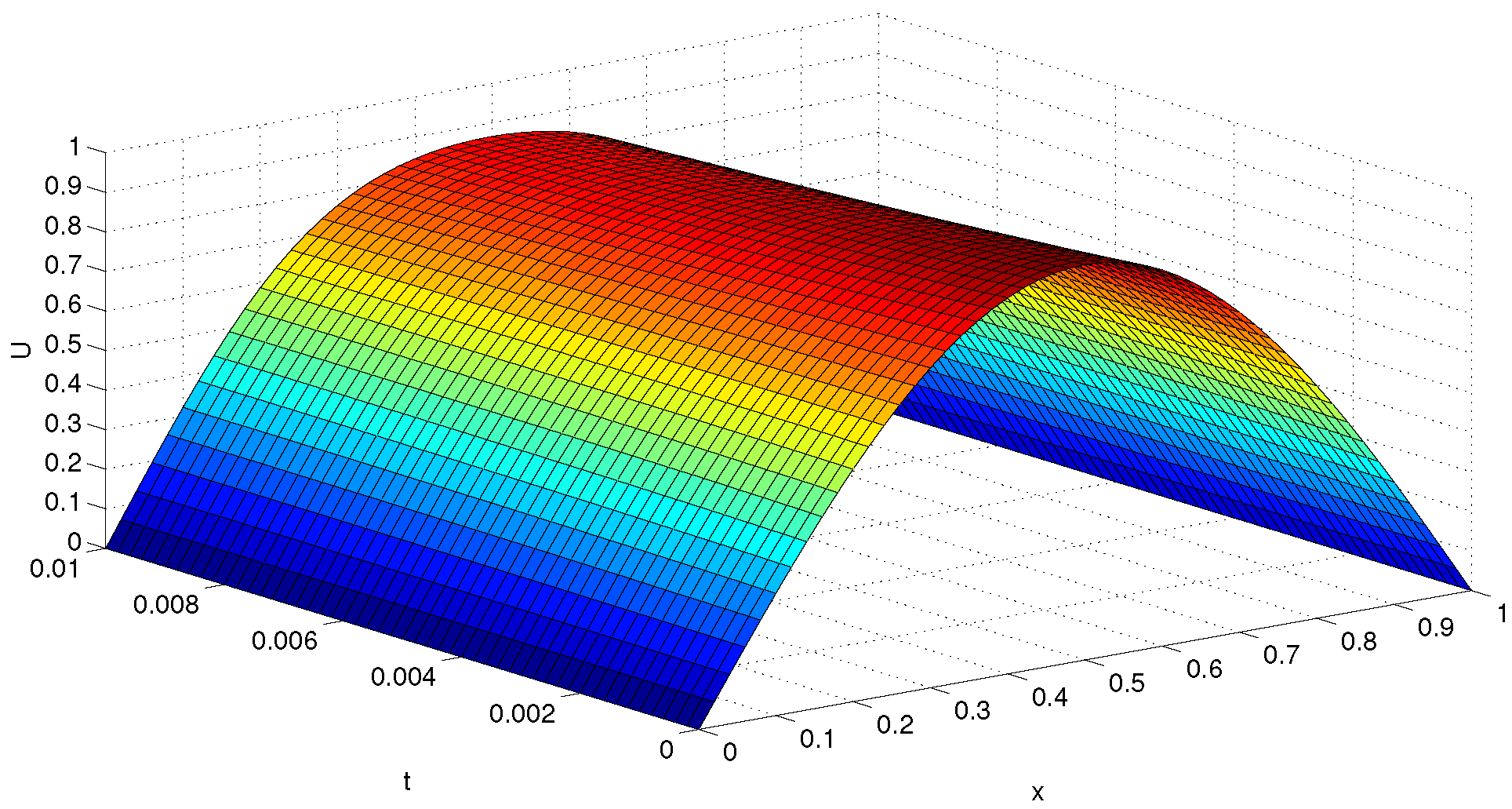
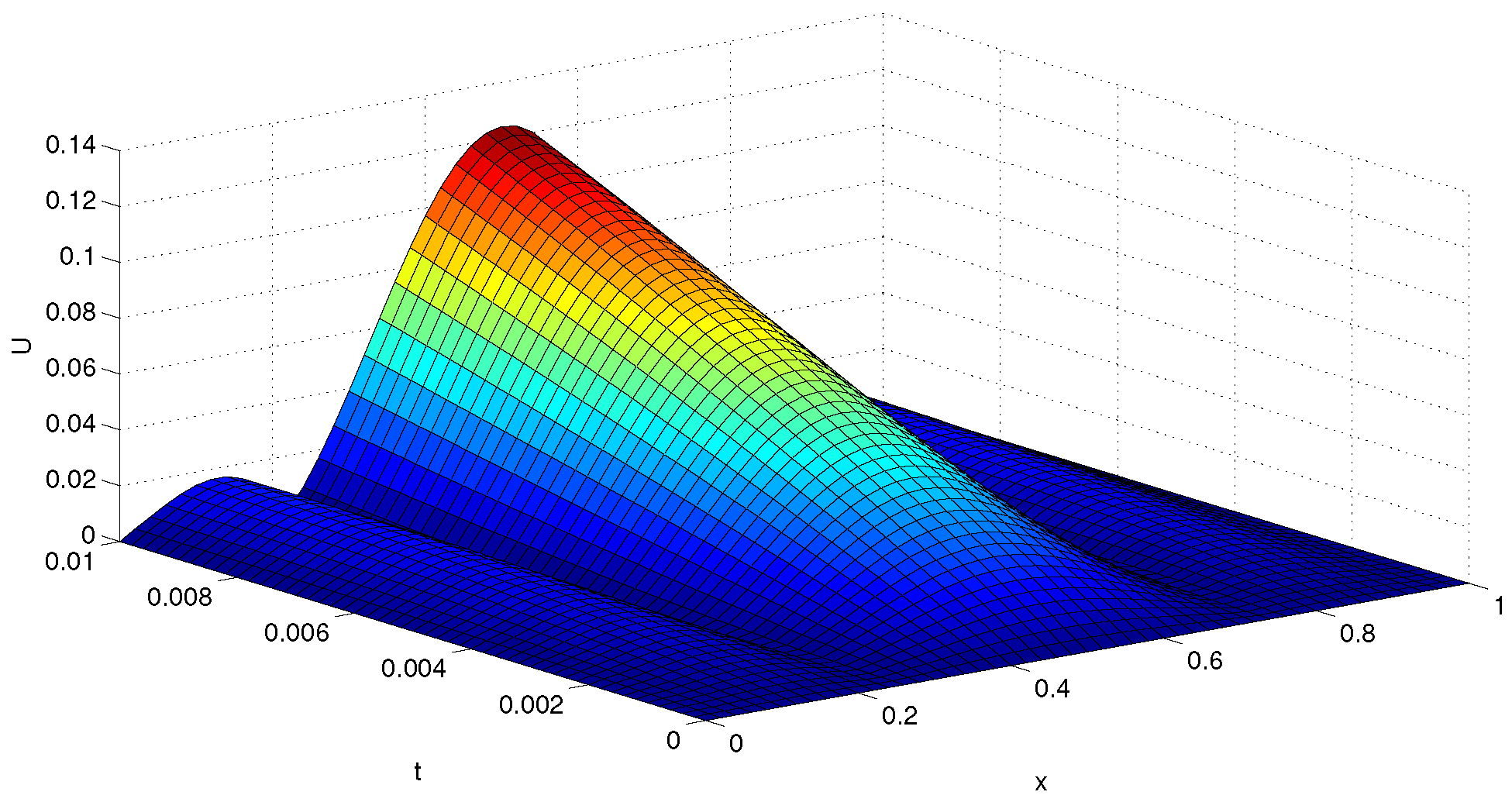
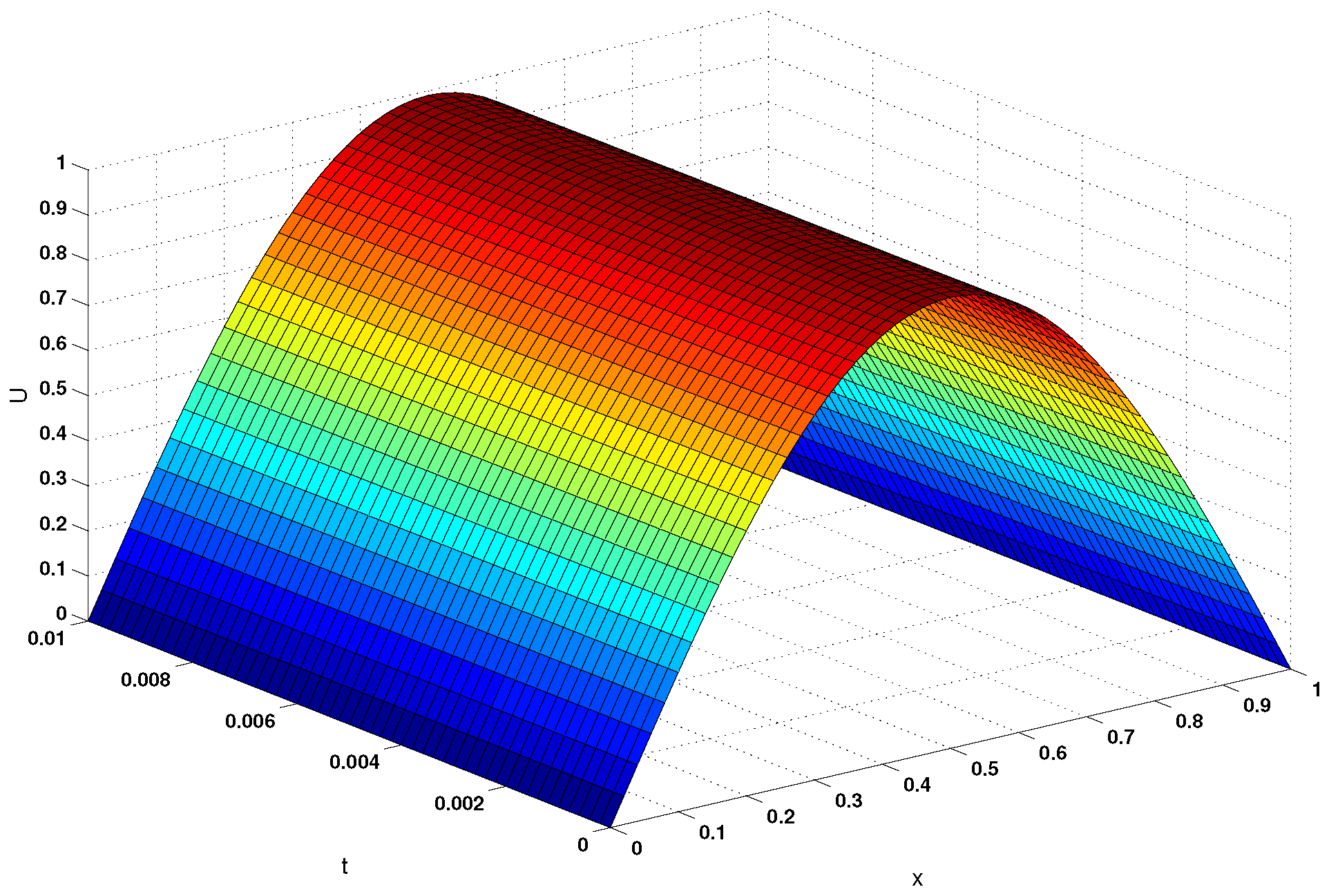
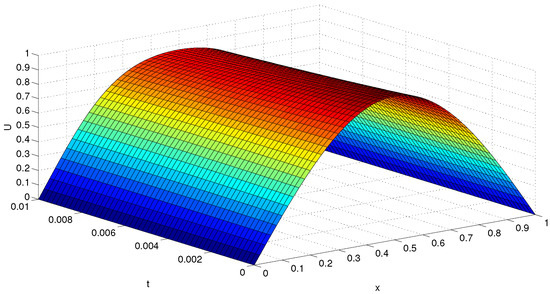
for $i=1,2,\dots ,N-1$ and $j=1,2,\dots ,N$ For fixed j, we get some nonlinear systems with size $(N-1)\times (N-1)$. Choosing different N and T, we solve this problem by different methods. The results are given in Table 9, where $NI$ represents the number of iteration and $e-Time$ represents the CUP time. The approximate solution and absolute value of error of this problem are shown in Figure 7 and Figure 8, when $T=0.01$ and $N=50$. Figure 9 shows the exact solutions of this problems.

Figure 7. Approximate solutions of Heat conduction equation.

Figure 8. Absolute error of u for $t\in [0,0.01]$.

Figure 9. The exact solutions of Heat conduction equation.

Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 show that compared with other methods, method NM8 has lower computational cost and higher computational efficiency. We find that method NM8 costs less computing time than other methods. This advantage is obvious for solving large scale nonlinear systems. Figure 7, Figure 8 and Figure 9 show that method NM8 can be used to solve nonlinear PDE equations with high accuracy.

6. Conclusions

We have extended the fifth-order Ham-Chun’s method to Banach space and developed an efficient method with eighth-order for solving standard nonlinear systems, nonlinear ODEs and PDEs. Our method requires three functions F, two derivatives $F^{\prime }$ and one matrix inversion $F^{\prime -1}$ per iteration. Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 show that our method NM8 show a highly efficient especially in large scale nonlinear systems. Numerical results verify that our method NM8 is better than other methods in this paper.