Abstract
The Augmented Lagrangian Smoothed Particle Hydrodynamics (ALSPH) method is a novel incompressible Smoothed Particle Hydrodynamics (SPH) approach that solves Navier–Stokes equations by an iterative augmented Lagrangian scheme through enforcing the divergence-free coupling of velocity and pressure fields. This study aims to systematically investigate the time step size and the number of inner iteration parameters to boost the performance of the ALSPH method. Additionally, the effects of computing spatial derivatives with two alternative schemes on the accuracy of numerical results are also scrutinized. Namely, the first scheme computes spatial derivatives on the updated particle positions at each iteration, whereas the second one employs the updated pressure and velocity fields on the initial particle positions to compute the gradients and divergences throughout the iterations. These two schemes are implemented to the solution of a flow over a circular cylinder at Reynolds numbers of 200 in two dimensions. Initially, simulations are performed in order to determine the optimum time step sizes by utilizing a maximum number of five iterations per time step. Subsequently, the optimum number of inner iterations is investigated by employing the predetermined optimum time step size under the same flow conditions. Finally, the schemes are tested on the same flow problem with different Reynolds numbers using the best performing combination of the aforementioned parameters. It is observed that the ALSPH method can enable one to increase the time step size without deteriorating the numerical accuracy as a consequence of imposing larger ALSPH penalty terms in larger time step sizes, which, overall, leads to improved computational efficiency. When considering the hydrodynamic flow characteristics, it can be stated that two spatial derivative schemes perform very similarly. However, the results indicate that the derivative operation with the updated particle positions produces slightly lower velocity divergence magnitudes at larger time step sizes.
1. Introduction
Smoothed particle hydrodynamics (SPH) method is a mesh free, particle based, Lagrangian computational method that was introduced simultaneously by Lucy [] and Gingold and Monaghan [] for solving astrophysics problems. Following its introduction to hydrodynamics studies by Monaghan [], the SPH method has become a fast growing computational fluid dynamics (CFD) approach. The initial SPH formulation employed a weakly compressible velocity–pressure coupling scheme, in which the pressure field is numerically computed from the density variation through an equation of state. Although this explicit Weakly Compressible SPH (WCSPH) scheme has clear advantages in tackling various types of violent free-surface hydrodynamics problems, which have large and non-linear deformations [,,], it always requires additional numerical treatments to prevent the occurrence of noisy and oscillatory pressure fields [,,].
Therefore, for dealing with incompressible fluid flow accurately, a fully incompressible SPH (ISPH) approach [,] is proposed through being inspired from the algorithm originally developed for a mesh based method []. In ISPH, the velocity-pressure coupling scheme is based on the projection method, wherein a computationally expensive implicit solution of pressure Poisson equation is required []. Many challenging incompressible fluid mechanics problems were successfully simulated with the conventional ISPH method, including free surface flows [,], multiphase flows [,], electrohydrodynamics [,], among others. The ISPH methodology has also been implemented with hybrid Lagrangian–Eulerian discretization approaches [] and Eulerian SPH [] in order to achieve a more consistent and stable numerical framework for the SPH method in general []. Moreover, in order to reduce the computational costs, explicit incompressible SPH formulations are also present in the literature [,,], which introduce simplifying assumptions for solving the pressure Poisson equation in an explicit fashion. Augmented Lagrangian SPH (ALSPH) is the most recent and novel explicit incompressible SPH method that has been recently introduced and further improved by the authors [,].
In general framework, Augmented Lagrangian method is an optimization method [], which utilizes Lagrange multipliers, together with penalty functions, in order to minimize (or maximize) an objective function. With this combination, constrained optimization problems are solved as unconstrained sets of equations in a manner that the penalty terms are modified at each iteration with respect to the Lagrangian multipliers defined for the mathematical model. Inspired from this mathematical optimization perspective, the ALSPH method utilizes suitable augmented Lagrangian penalty terms on the pressure and velocity fields decoupled by the projection principle [] and it performs iterations to minimize velocity divergence without solving implicit Poisson equation for pressure.
Fortin and Glowinski pioneered the idea of solving Navier–Stokes equations as an optimization problem with the help of the Augmented Lagrangian method []. Fortin and Glowinski [] introduced augmented Lagrangian algorithms for solving Navier–Stokes equations and other engineering problems. Followingly, Desai and Ito [] applied the method for optimal control problems that are governed by steady state Navier-Stokes equations. The method is employed on solving 2D lid-driven cavity and channel flow with sudden expansion problems utilizing a grid based discretization approach. Again, with a grid based approach, Vincent and Caltagirone [] solved 2D and 3D unsteady fluid flow problems with an incompressible projective augmented Lagrangian application. Vincent et al. [] applied an adaptive augmented Lagrangian method on 3D direct numerical simulation (DNS) with a multiphase, volume of fluid (VOF) framework, where the augmented Lagrangian is implemented in the predictor step of the projection approach. The adaptivity is provided by evaluating the augmented Lagrangian penalty term locally over a conditional penalty coefficient that is based on the dominant flow characteristics. There are also meshless applications of the approach in solid mechanics field for the solution of material and crack discontinuity problems [] and on elastic solids [] to enforce boundary conditions.
To this end, the ALSPH method is the first meshless implementation of the augmented Lagrangian approach to the solution of the Navier–Stokes equations. The augmented Lagrangian penalty term in the ALSPH method is designed to mimic the bulk viscosity term of the Navier–Stokes equations, which should normally be equal to zero for an incompressible flow problem. In this regard, the ALSPH method tries to ensure that this term be zero through its iterative scheme. The penalty term is modified (or augmented) at each iteration while the bulk viscosity term diminishes. Fatehi et al. [] performed simulations with the ALSPH method on 2D flow over the backward facing step and 2D pressure jump problems, when comparing the results with the weakly compressible SPH (WCSPH) method. In our recent study [], along with algorithm enhancements and a simple adaptive scheme for the penalty term estimation, we have further investigated the performance of the ALSPH method through solving a challenging incompressible flow problem, namely, 2D flow past a circular cylinder under low to moderate Reynolds numbers. The authors [,] demonstrated the advantage of ALSPH over WCSPH in terms of rendering smoother pressure fields and smaller velocity divergences at the expense of a larger computational cost. The findings of our study [] have further indicated the accuracy of the ALSPH method, especially in higher Reynolds numbers, as compared to the WCSPH method at same particle resolutions and time step sizes. In our previous study [], the effects of the time step size or the maximum number of iterations per time step were not investigated. When considering higher particle resolution requirements of the WCSPH method at higher Reynolds numbers [,,], our results have also pointed out the advantage of the ALSPH method over WCSPH in terms of computational costs, even without optimizing these temporal and iterative discretization parameters [].
Given the fact that the ALSPH is a relatively new approach to enforcing the incompressibility condition in particle based simulations, it is important to scrutinize its all aspects to be able to make it a versatile pressure-velocity coupling algorithm. To this end, it is essential to understand the effect of various parameters (i.e., time step, number of iterations and locations of derivative operations) on the accuracy of the ALSPH results. Hence, the main focus of the current study is to determine the optimum time step size, and a practical iteration procedure for the ALSPH method, which involves the number of inner iteration for each time step and the identification of the most effective particle location for computing spatial derivatives during each inner iteration. With n representing temporal discretization in the scheme, the first approach computes the spatial derivatives at by utilizing the displaced particle position results of the previous iteration []. In the second approach, the derivatives are always computed with respect to the initial particle positions at n []. The velocity and pressure values are approximated with the same SPH procedures in both of the schemes.
Simulations are performed on the benchmark problem of 2D incompressible flow past a circular cylinder using the in-house C++ code in order to examine the numerical performances of both ALSPH schemes and to obtain the optimum time step and number of inner iteration values. The results are compared in terms of the dynamic properties (force and pressure coefficients), the wake kinematics (Strouhal number analysis), and the velocity divergence as a measure of error in enforcing incompressibility condition in the flow domain. Initially, a series of simulations employing the two derivative estimation schemes are performed to determine an optimum dimensionless time step size by limiting the maximum number of iterations per time step to five. Subsequently, utilizing the best applicable dimensionless time step size, the schemes are tested for the iteration number of two, five, and twenty. Finally, the two schemes are examined under Reynolds numbers varying from 100 to 300 utilizing the optimum combination of the aforementioned parameters. Ultimately, the novelty of this paper lies in the detailed and systematic investigations of the above stated parameters, so that the ALSPH method can be reliably used to model incompressible flow problems. The key findings of this research are elaborated within the numerical results section and concisely stated in the conclusion.
2. Governing Equations and ALSPH Methodology
Continuity and linear momentum equations which govern the fluid motion are written as;
where is the material time derivative, t is the time, is the density, is the velocity vector, p is the thermodynamic pressure, is the viscous stress tensor, and is the gravitational acceleration vector. The viscous force expressed as the divergence of the viscous stress tensor in Equation (2) can be written for a Newtonian fluid, as
where and represent the dynamic and bulk viscosity coefficients, respectively. With an incompressible flow assumption, the divergence of velocity becomes zero and the bulk viscosity (volume viscosity) vanishes. Accordingly, the conservation of linear momentum for incompressible flow is written as
2.1. Derivation of the ALSPH Formulation
In the ALSPH method, the velocity and pressure fields are decoupled via the projection approach []. The Helmholtz-Hodge decomposition theorem states that any arbitrary sufficiently smooth vector field can be written as the sum of a divergence-free vector field and the gradient of a scalar field, such that
Differing from the conventional projective ISPH schemes, ALSPH utilizes the orthogonal projection operator on the momentum balance equation in Equation (2), rather than the one in Equation (4), such that
where is the kinematic viscosity that is defined as . As a result of the projection operation, the pressure gradient term presented in Equation (2) vanishes since it is perpendicular to the divergence-free subspace. Hence, the predicted velocity field is an intermediate velocity field without the contribution of pressure forces. The aim of this decomposition approach is to obtain the velocity field that ensures the divergence-free condition. Therefore, upon taking divergence of Equation (5), with the assumption of , the pressure Poisson equation is obtained as
The augmented Lagrangian method is employed onto Equation (6) by replacing the bulk viscosity coefficient with an augmented Lagrangian penalty coefficient , transforming the volume viscosity force into the augmented Lagrangian penalty term that diminishes through iterations as the gradient of velocity divergence declines. With the superscripts n and m representing the time step and iterations, respectively, initializing the iterations with and , the ALSPH algorithm predicts the intermediate velocity as
Here, is the penalty coefficient that is defined as , while being the maximum velocity magnitude in the domain and is a constant with a value between 1 and 100 []. In this study, is taken as 100. The value of is only updated at the beginning of time step and it stays constant through iterations. The angle bracket “⟨⟩” in Equation (8) instructs that the derivative operation is to be performed based on the particle positions at the time n and iteration m frames that are designated by its superscripts.
ALSPH utilizes an equation of state approach to fulfill the divergence-free condition in order to avoid an implicit solution of Equation (7). Approximating in Equation (1), a velocity divergence is obtained, as
where c is the speed of sound parameter. Taking divergence of Equation (5) and replacing with Equation (9), prospective pressure field is obtained in the iterative form as;
In obtaining Equation (10), one can clearly see that the value replaces . Upon setting equal to the above definition of , it can be shown that . For any flow to be treated incompressible, the ratio of the speed of the flow to the speed of sound should be smaller than 0.3. To be on the safe side, the ratio of 0.1 is utilized, which leads to of 100.
After obtaining new pressures, the velocity field is updated utilizing Equation (5), as follows:
Respectively, new positions of particles are obtained by
where represents the position vector of the particle .
The convergence criteria is imposed either ensuring a satisfactory velocity divergence value that is defined by the parameter ;
or reaching a predefined maximum number of iterations per time step. In this study, is taken as . Section 2.4 provides the iterative algorithm for a given time step for the ALSPH method.
2.2. Spatial Derivatives of Field Functions
The value of any field function in the computational domain can be approximated by utilizing SPH interpolation, as follows [];
Here, represents the value of any vector valued or scalar function at the spatial coordinates of particle . Subscript designates the variables associated with the neighbor particles of , which reside within a support domain that is limited by the radius h. Hereby, the neighbors constitute a total number N that varies for each particle . , or in full form is a smoothing kernel/an interpolation weight factor, which is a function of relative particle positions and the smoothing length h. As another interpolation factor, is the volume of each neighbor particle computed by the inverse of the summed kernel function as . This study employs the quintic kernel function used in the reference [].
In the ALSPH method, flow domain is discretized with particles. Accordingly, the gradient and the Laplacian terms in the ALSPH formulation are evaluated by a corrected SPH approach [], as follows;
where is a second rank correction tensor.
2.3. Artificial Particle Displacement
Before moving to the next time step, the particle positions are shifted by the artificial particle displacement method [,] in order to prevent non-physical particle clustering effect. The corrected particle position is calculated as:
where , and is the position displacement vector. Accordingly, the velocity and pressure of the particle are also corrected, as []:
2.4. Derivative Estimation Schemes
The original ALSPH algorithm that was developed by Fatehi et al. [] is explained at the beginning of this section. In our previous study [], we proposed dropping the computationally expensive, repeating neighbor searching operation during the iterations. Furthermore, the algorithm on the estimation of the spatial derivatives was modified. The aim of the present study is to compare two derivative estimation schemes, performing a single neighbor searching operation in each time step.
The first scheme can be considered to be a modified version (without a repetitive neighbor search) of the scheme that was introduced by Fatehi et al. [], utilizing the updated particle positions as . The second one is the same scheme employed in our previous study [], which uses the particle positions at the beginning of the time step as . The aforementioned schemes will respectively be referred to as Algorithms 1 and 2 hereafter. The superscripts belonging to the angle brackets in Equations (8), (10) and (11), corresponding to Algorithm 1, are changed from to the form , hence constructing Algorithm 2, as given below as pseudo codes.
| Algorithm 1 The pseudo code for the algorithm that computes spatial derivatives on updated particle positions |
|
| Algorithm 2 The pseudo code for the algorithm that computes spatial derivatives on initial particle positions |
|
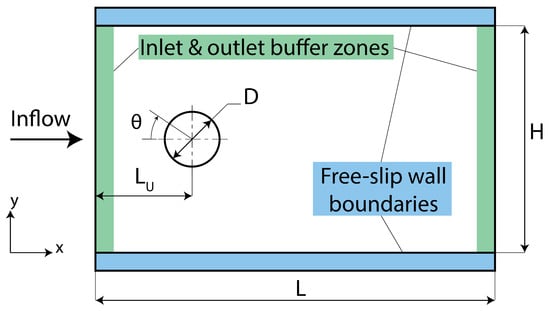
Figure 1.
Computational domain.
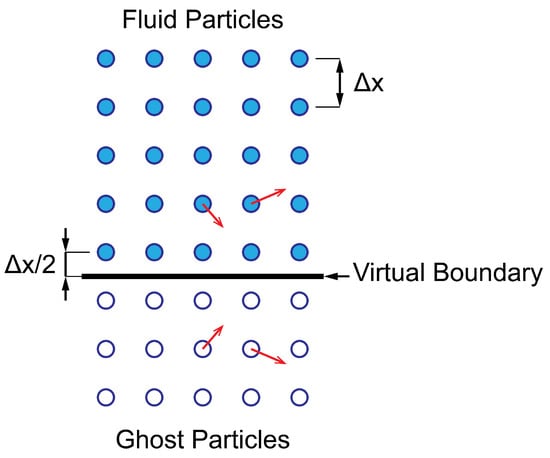
Figure 2.
Free slip ghost particles for channel boundaries [].
3. Problem Definition
In this study, 2D incompressible channel flow past circular cylinder is simulated to determine the best possible ALSPH parameters in terms of accuracy and computational costs. Channel geometry is given in Figure 1, where D is the cylinder diameter and , , and .
Reynolds number is defined as with uniform inlet velocity U. The initial particle discretization is realized by uniform orthogonal fluid particles with equal particle distances of in both x and y axes. Channel walls are represented by ghost fluid particles with a free-slip boundary condition, as illustrated in Figure 2 []. Two buffer zones with lengths of 6 h are defined along the inlet and outlet regions to ensure mass conservation within the channel (Figure 1). Particles of the inlet buffer zone enters into the flow domain with the constant velocity U. Fluid particles reaching the outlet buffer zone are enforced to preserve the normal component of their velocity to the boundary until they travel beyond 6 h thick outlet buffer zone. Fixed solid cylinder particles are radially distributed with respect to the same scale. An additional pressure term is imposed upon the cylinder particles in order to ensure no-slip and Neumann boundary conditions for flow around the solid obstacle;
where is a pseudo-velocity for the solid particles computed using Equation (8), is the outwards facing surface normal, is the modified pressure, and is the pseudo-displacement along the normal direction.
The instantaneous values of drag coefficient and lift coefficient for the cylinder are computed by integrating the forces acting on the solid particles of the cylinder as , where and is the number of cylinder particles. Similarly, the pressure coefficient is computed over the cylinder surface as , where is the angular coordinate with respect to the center of the cylinder (Figure 1) and is the instantaneous mean inlet pressure. Because the flow is oscillatory, the mean values of the drag and pressure coefficients as well as the root mean square of lift coefficient, respectively, , , and are computed over the averaging period T in accordance with the following relations;
The mean velocity divergence in the domain is computed as , where is the total number of fluid particles.
4. Numerical Results
There are three main investigations in the present study. The first one is the comparison of the spatial derivative Algorithms 1 and 2. To this end, all other investigations are realized for both Algorithms 1 and 2. Two different particle resolutions, namely, and are utilized for all relevant simulations in order to understand the effect of spatial resolution on the numerical results. The second one is to determine the maximum applicable time step size, written in a dimensionless form as . Accordingly, time step size is incrementally tested. Finally, after determining an optimum dimensionless time step size for the problem at hand with five iterations per time step, the effect of the number of iterations on the accuracy of the results are examined by utilizing the iteration number of two and 20 per time step. All three investigations to find the optimum parameters are realized at . Ultimately, having determined the best performing time step size and the number of iterations, both 1 and 2 algorithms are tested under with to examine how these parameters respond to the Reynolds number of the flow. It should be emphasized that the algorithms are equivalent in terms of computational cost. In the figures of the following subsections, the results of Algorithms 1 and 2 will be designated as (1) and (2), respectively.
4.1. Time Step Size
The mean force coefficients and vortex shedding characteristics are investigated and presented in Figure 3 and Figure 4, respectively, in order to capture both dynamics and kinematics of the problem. It must be restated that the simulations in this subsection are always performed with a maximum of five iterations per time step.
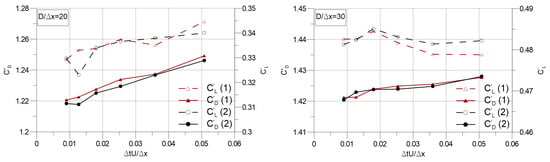
Figure 3.
Mean drag and lift coefficients versus dimensionless time step size.
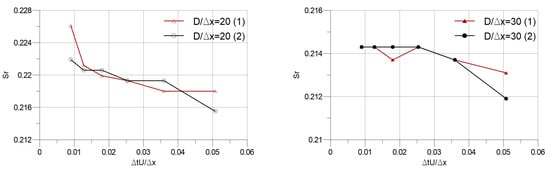
Figure 4.
Strouhal number versus dimensionless time step size.
Figure 3 shows the values of mean drag and lift coefficients varying with the dimensionless time step sizes (). Algorithms 1 and 2 are in tune with each other, as it can be seen from both and results. As for the kinematics, periodic vortex shedding characteristics are compared over Strouhal number "” versus dimensionless time step size in Figure 4, where , with f being vortex shedding frequency in Hz. Similarly, Algorithms 1 and 2 yield coherent results in this aspect. The noticeable difference between the force coefficient values for and indicates that cannot provide a sufficient particle resolution. Yet, it can be inferred from Figure 5 that the mean velocity divergence, hence the continuity error, is comparable for these two particle resolutions. Figure 5 also indicates that increasing the time step sizes results in a better achievement of overall incompressibility in the domain. This is due to the fact that, since the time step size is a term in the penalty coefficient as , the larger the time step size, the larger is the penalty coefficient, which affects the iterative guesses of the intermediate velocity field and the pressure field through Equations (8) and (10), respectively. Consequently, the penalty coefficient naturally influences the convergence characteristics of the iterative process. It should be stated that for simulations with five iterations per time step, the utilization of the time step beyond the maximum value that is represented in Figure 5 yields diverging simulations for both particle resolutions and both algorithms. Algorithms 1 and 2 show generally similar trend with increasing time step sizes. However, Algorithm 1 performs slightly better than Algorithm 2 in larger time step sizes.
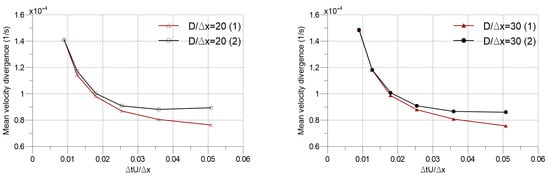
Figure 5.
Mean velocity divergence of flow domain versus dimensionless time step size.
It should also be noted that the simulations in our previous study [] were performed with a lower dimensionless time step size as , which corresponds to the lower ends on the x axes of Figure 3, Figure 4 and Figure 5. Therefore, it is reasonable to conclude that the algorithm distinction does not noticeably affect the results of the previous study [] due to the unoptimized time step sizes.
For the sake of completeness, in Table 1, the results of two algorithms are compared with the 2D numerical findings of the literature in terms of mean drag and root mean square of lift coefficient as well as the Strouhal number for , where the simulations are performed with and .

Table 1.
Comparison with two-dimensional (2D) numerical simulation results of literature for .
At inner iterations, Algorithm 1 updates the particle positions by computing the derivative terms on previously predicted particle positions, whereas Algorithm 2 calculates the derivatives at initial particle positions with the updated field function values of and p, as explained in Section 2.4. The effect of derivative locations on the accuracy is negligibly small because both schemes compute the new positions of particle for the inner iteration using Equation (12) based on .
4.2. Number of Iterations
In the previous subsection, it was concluded that the best performing dimensionless time step size is the largest applicable one for the simulations with five iterations per time step. Thus, the effect of the maximum iteration number on the results is investigated, utilizing this dimensionless time step value, namely for the forthcoming simulations.
The same analysis pattern as the previous Section 4.2 is adopted in Figure 6, Figure 7 and Figure 8, investigating, respectively, force coefficients, Strouhal number, and the mean velocity divergence against the number of iterations per time step. Figure 6 and Figure 7 do not indicate any clear distinction between the two algorithms both in terms of force coefficients and Strouhal numbers with an increasing number of iterations. In Figure 8 a decreasing trend of mean continuity error is observed with an increasing number of iterations per time step for both resolutions.
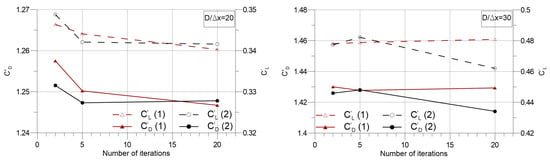
Figure 6.
Mean drag and lift coefficients versus number of iterations per time step.
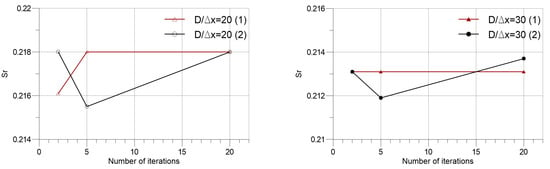
Figure 7.
Strouhal number versus number of iterations per time step.
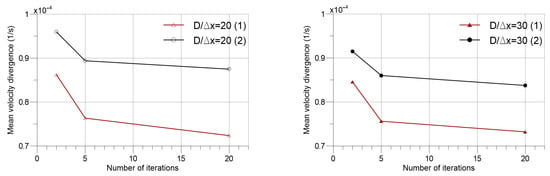
Figure 8.
Mean velocity divergence of flow domain versus number of iterations per time step.
In Figure 9, spatial variations of the velocity divergence and the magnitude of vorticity at similar lift extremities (around for each case) are given for . Despite the almost identical results of vorticities for Algorithms 1 and 2, there are distinguishable differences for velocity divergences as the mean values that are depicted in Figure 8 suggest. Notwithstanding the fact that twenty iterations per time step yields the best results for both algorithms in general, five iterations per time step is an expedient choice, given the trade off between admissible accuracy and computational cost.
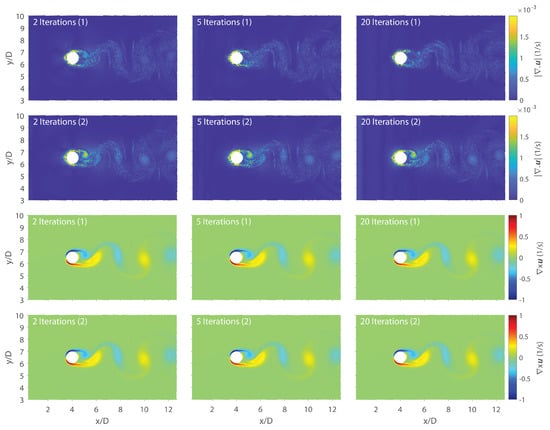
Figure 9.
Comparison of instantaneous spatial velocity divergence and vorticity with a different number of iterations per time step.
In Figure 10, pressure coefficients for Algorithms 1 and 2 with two, five, and 20 iterations are compared over the simulations with . The results of for the Algorithm 1 are unaffected by the number of iterations per time step, yielding overlapping mean pressure coefficients along the cylinder surface. Additionally, the differences between the results of Algorithms 1 and 2 are trivial for a kind of flow characteristic, which is fairly unsteady. It can be noticed that the mean drag and lift coefficient results of resolution in Figure 6 also support the findings of pressure coefficients, since they both demonstrate almost insensitive responses to the number of iterations per time step for Algorithm 1. The finite volume method results of Rajani et al. [] and experimental results of Thom [] are also included in this comparison to present supplementary information.
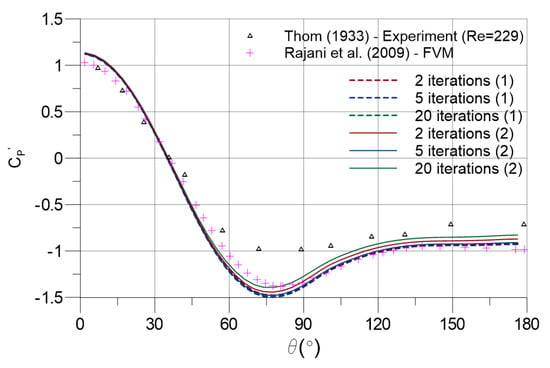
Figure 10.
Mean pressure coefficient acting on the surface of the cylinder.
4.3. Reynolds Number
Following a thorough investigation of flow characteristics at , the two algorithms are compared at Reynolds numbers that range from 100 to 300. All of the simulations are performed utilizing with a maximum of five iterations per time step, except for the cases, which produce unstable simulations. Thus, for only at cases, time step sizes are reduced to .
In Figure 11, the mean drag and lift coefficients against Reynolds numbers are presented. It can be observed that both and series are almost identical. Higher particle resolutions are required with increasing Reynolds numbers, which can be inferred through comparing the results of the current study with that of Zhang et al. based on the finite difference approach []. Moreover, the Strouhal number results of the two algorithms at different Reynolds numbers are compared in Figure 12. Correspondingly to the results of force coefficients (Figure 11), the Strouhal number results of Algorithms 1 and 2 match with each other. The mean velocity divergences of the flow fields display similar behaviour with the overall outlook of the results that were classified in the previous subsection. Figure 13 shows that Algorithm 1 produces slightly lower mean velocity divergence in the flow domain at all Reynolds numbers covered.
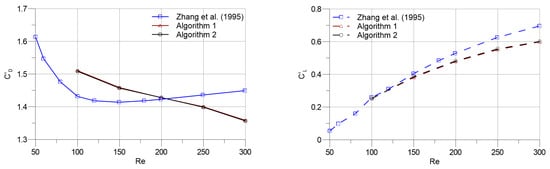
Figure 11.
Mean drag and lift coefficients versus Reynolds number.
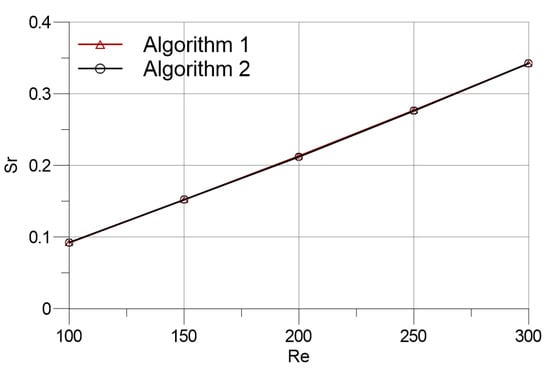
Figure 12.
Strouhal number versus Reynolds number.
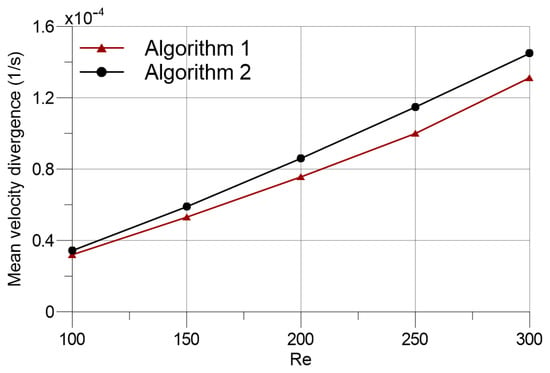
Figure 13.
Mean velocity divergence of flow domain versus Reynolds number.
5. Conclusions
The aim of the current study is to investigate in detail the effect of time step size, number of inner iterations, and two different algorithms as to the calculation of spatial derivatives on the robustness, accuracy, and computational cost of the augmented Lagrangian SPH method. To be clear, Algorithm 1 utilizes the particle positions of the previous iteration to compute gradients and divergences of pressure and velocity fields, whereas Algorithm 2 employs the initial particle positions of the time step for these computations. As for the time step, a smaller numerical error is observed at larger time step sizes for both algorithms, which is associated with fact that the time step size is embedded in the penalty coefficient , which augments the prediction of the optimum pressure and velocity fields at each iteration. The largest applicable and best performing dimensionless time step size is found to be around for . The further increase in the dimensionless time step size leads to instability and divergence in both of the algorithms, hence blowing up the simulation. The findings of the present study indicate that the dimensionless time step size that is utilized in our previous study based on the Algorithm 2 is in a safe range, such that it does not produce any difference from the Algorithm 1. It is observed that increasing the number of inner iterations improves the accuracy of simulations for both algorithms, as expected. Nevertheless, the accuracy that is gained by increasing the maximum number of iterations from five to twenty is not notably high to justify the additional computational cost.
Finally, the most efficient combination of the dimensionless time step size and the maximum number of iterations per time step, which are and five iterations respectively, are tested at to 300. Algorithms 1 and 2 yield overlapping results in terms of both force coefficients acting on the cylinder and periodic vortex shedding characteristics of the downstream. Overall, the results of the two algorithms do not meaningfully differ in terms of the dynamics and kinematics of the flow. However, Algorithm 1 can be deemed to be better, since it produces slightly smaller computational error at larger time step sizes.
Although in this study, the ALSPH method is extensively tested against time step size, the number of iterations, and locations of derivative operations for incompressible laminar flow, it is expedient to test it further for challenging free surface and turbulent flow problems, which will form the future direction of the current study.
Author Contributions
Conceptualization, M.Y., M.O. and D.C.K.; methodology, M.Y., M.O. and D.C.K.; software, D.C.K., M.O. and M.Y.; validation, M.O. and D.C.K.; formal analysis, M.O. and D.C.K.; investigation, M.O. and D.C.K.; resources, M.Y.; data curation, D.C.K. and M.O.; writing—original draft preparation, D.C.K. and M.O.; writing—review and editing, M.Y. and M.O.; visualization, D.C.K.; supervision, M.Y.; project administration, M.Y.; funding acquisition, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Scientific and Technological Research Council of Turkey grant number 117M091. The article processing charge for open access publication was funded by personal research fund provided by Sabanci University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lucy, L.B. Numerical Approach to Testing of Fission Hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics—Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free-Surface Flows with Sph. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touze, D.; Graziani, G. delta-SPH model for simulating violent impact flows. Comput. Method Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Ozbulut, M.; Yildiz, M.; Goren, O. A numerical investigation into the correction algorithms for SPH method in modeling violent free surface flows. Int. J. Mech. Sci. 2014, 79, 56–65. [Google Scholar] [CrossRef]
- Ozbulut, M.; Ramezanzadeh, S.; Yildiz, M.; Goren, O. Modelling of wave generation in a numerical tank by SPH method. J. Ocean Eng. Mar. Energy 2020, 6. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainali, A.; Sadek, S.H.; Yildiz, M. Improved Incompressible Smoothed Particle Hydrodynamics method for simulating flow around bluff bodies. Comput. Method Appl. Mech. Eng. 2011, 200, 1008–1020. [Google Scholar] [CrossRef]
- Cummins, S.J.; Rudman, M. An SPH projection method. J. Comput. Phys. 1999, 152, 584–607. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S.D. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical Solution of Navier-Stokes Equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Colagrossi, A. A Meshless Lagrangian Method for Free-Surface and Interface Flows with Fragmentation. Ph.D. Thesis, University of Rome, Rome, Italy, 2005. [Google Scholar]
- Shao, S. Incompressible SPH simulation of water entry of a free-falling object. Int. J. Numer. Methods Fluids 2009, 59, 91–115. [Google Scholar] [CrossRef]
- Chow, A.D.; Rogers, B.D.; Lind, S.J.; Stansby, P.K. Incompressible SPH (ISPH) with fast Poisson solver on a GPU. Comput. Phys. Commun. 2018, 226, 81–103. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainali, A.; Yildiz, M. Numerical modeling of Kelvin–Helmholtz instability using smoothed particle hydrodynamics. Int. J. Numer. Meth. Eng. 2011, 87, 988–1006. [Google Scholar] [CrossRef]
- Shadloo, M.; Zainali, A.; Yildiz, M. Simulation of single mode Rayleigh–Taylor instability by SPH method. Comput. Mech. 2013, 51, 699–715. [Google Scholar] [CrossRef]
- Rahmat, A.; Yildiz, M. A multiphase ISPH method for simulation of droplet coalescence and electro-coalescence. Int. J. Multiph. Flow 2018, 105, 32–44. [Google Scholar] [CrossRef]
- Saghatchi, R.; Rahmat, A.; Yildiz, M. Electrohydrodynamics of a droplet in a highly confined domain: A numerical study. Phys. Fluids 2020, 32, 123305. [Google Scholar] [CrossRef]
- Oger, G.; Marrone, S.; Le Touzé, D.; de Leffe, M. SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms. J. Comput. Phys. 2016, 313, 76–98. [Google Scholar] [CrossRef]
- Lind, S.; Stansby, P. High-order Eulerian incompressible smoothed particle hydrodynamics with transition to Lagrangian free-surface motion. J. Comput. Phys. 2016, 326, 290–311. [Google Scholar] [CrossRef]
- Vacondio, R.; Altomare, C.; De Leffe, M.; Hu, X.; Le Touzé, D.; Lind, S.; Marongiu, J.C.; Marrone, S.; Rogers, B.D.; Souto-Iglesias, A. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comput. Part. Mech. 2020, 1–14. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Manzari, M.T.; Hannani, S.K. A fully explicit three-step SPH algorithm for simulation of non-Newtonian fluid flow. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 715–735. [Google Scholar] [CrossRef]
- Rafiee, A.; Thiagarajan, K.P. An SPH projection method for simulating fluid-hypoelastic structure interaction. Comput. Methods Appl. Mech. Eng. 2009, 198, 2785–2795. [Google Scholar] [CrossRef]
- Barcarolo, D.A.; Touze, D.L.; Vuyst, F.D. Incompressible smoothed particle hydrodynamics: Proposition and validation of a fully-explicit algorithm. In Proceedings of the Seventh International SPHERIC Workshop, Prato, Italy, 29–31 May 2012; pp. 99–106. [Google Scholar]
- Fatehi, R.; Rahmat, A.; Tofighi, N.; Yildiz, M.; Shadloo, M.S. Density-based smoothed particle hydrodynamics methods for incompressible flows. Comput. Fluids 2019, 185, 22–33. [Google Scholar] [CrossRef]
- Kolukisa, D.C.; Ozbulut, M.; Pesman, E.; Yildiz, M. Development of computationally efficient augmented Lagrangian SPH for incompressible flows and its quantitative comparison with WCSPH simulating flow past a circular cylinder. Int. J. Numer. Methods Eng. 2020, 121, 4187–4207. [Google Scholar] [CrossRef]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Fortin, M.; Glowinski, R. Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems; Studies in Mathematics and Its Applications; North-Holland: Amsterdam, The Netherlands, 1983; Volume 15. [Google Scholar]
- Desai, M.; Ito, K. Optimal Controls of Navier-Stokes Equations. SIAM J. Control Optim. 1994, 32, 1428–1446. [Google Scholar] [CrossRef]
- Vincent, S.; Caltagirone, J.P. Efficient solving method for unsteady incompressible interfacial flow problems. Int. J. Numer. Methods Fluids 1999, 30, 795–811. [Google Scholar] [CrossRef]
- Vincent, S.; Caltagirone, J.P.; Lubin, P.; Randrianarivelo, T.N. An adaptative augmented Lagranglan method for three-dimensional multimaterial flows. Comput. Fluids 2004, 33, 1273–1289. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ferro, G.; Ventura, G. Material and crack discontinuities: Application of an element free augmented Lagrangian method. In Proceedings of the International Conference on Damage and Fracture Mechanics; WIT Press: Southampton, UK, 1998; pp. 237–246. [Google Scholar] [CrossRef]
- Ventura, G. An augmented Lagrangian approach to essential boundary conditions in meshless methods. Int. J. Numer. Methods Eng. 2002, 53, 825–842. [Google Scholar] [CrossRef]
- Marrone, S.; Colagrossi, A.; Antuono, M.; Colicchio, G.; Graziani, G. An accurate SPH modeling of viscous flows around bodies at low and moderate Reynolds numbers. J. Comput. Phys. 2013, 245, 456–475. [Google Scholar] [CrossRef]
- Ayyildiz, M.; Saydam, A.Z.; Ozbulut, M. A Numerical study on the hydrodynamic performance of an immersed foil: Uncertainty quantification of RANS and SPH methods. Comput. Fluids 2019, 191, 104248. [Google Scholar] [CrossRef]
- Colagrossi, A.; Nikolov, G.; Durante, D.; Marrone, S.; Souto-Iglesias, A. Viscous flow past a cylinder close to a free surface: Benchmarks with steady, periodic and metastable responses, solved by meshfree and mesh-based schemes. Comput. Fluids 2019, 181, 345–363. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G.; Carney, T.C.; Hipp, J.R.; Allahdadi, F.A. High-Strain Lagrangian Hydrodynamics—A 3-Dimensional Sph Code for Dynamic Material Response. J. Comput. Phys. 1993, 109, 67–75. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods E 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainali, A.; Yildiz, M.; Suleman, A. A robust weakly compressible SPH method and its comparison with an incompressible SPH. Int. J. Numer. Methods Eng. 2012, 89, 939–956. [Google Scholar] [CrossRef]
- Ozbulut, M.; Tofighi, N.; Goren, O.; Yildiz, M. Investigation of Wave Characteristics in Oscillatory Motion of Partially Filled Rectangular Tanks. J. Fluids Eng. 2018, 140, 041204. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Fey, U.; Noack, B.R.; Konig, M.; Eckelmann, H. On the Transition of the Cylinder Wake. Phys. Fluids 1995, 7, 779–794. [Google Scholar] [CrossRef]
- Rajani, B.N.; Kandasamy, A.; Majumdar, S. Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model 2009, 33, 1228–1247. [Google Scholar] [CrossRef]
- Thom, A. The Flow Past Circular Cylinders at Low Speeds. Proc. R. Soc. Lond. Ser. A 1933, 141, 651–669. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).