Recent Developments of the Lauricella String Scattering Amplitudes and Their Exact SL(K + 3,C) Symmetry

Abstract

In this review, we propose a new perspective to demonstrate the Gross conjecture regarding the high-energy symmetry of string theory. We review the construction of the exact string scattering amplitudes (SSAs) of three tachyons and one arbitrary string state, or the Lauricella SSA (LSSA), in the $26D$ open bosonic string theory. These LSSAs form an infinite dimensional representation of the $SL(K+3,\mathbb{C})$ group. Moreover, we show that the $SL(K+3,\mathbb{C})$ group can be used to solve all the LSSAs and express them in terms of one amplitude. As an application in the hard scattering limit, the LSSA can be used to directly prove the Gross conjecture, which was previously corrected and proved by the method of the decoupling of zero norm states (ZNS). Finally, the exact LSSA can be used to rederive the recurrence relations of SSA in the Regge scattering limit with associated $SL(5,\mathbb{C})$ symmetry and the extended recurrence relations (including the mass and spin dependent string BCJ relations) in the nonrelativistic scattering limit with the associated $SL(4,\mathbb{C})$ symmetry discovered recently.

1. Introduction

In contrast to low-energy string theory, many issues regarding high-energy behavior of string theory have not yet been well understood. Historically, it was first conjectured by Gross [1,2,3,4,5] that there exist infinite linear relations among hard string scattering amplitudes (HSSA) of different string states. Moreover, these linear relations are so powerful that they can be used to solve all HSSAs and express them in terms of one amplitude. This conjecture was later (slightly) corrected and proved by using the decoupling of zero norm states [6,7,8,9] in [10,11,12,13,14,15,16]. For more details, see the recent review articles [17,18].

In this paper, we review another perspective to understand the high-energy behavior of strings and demonstrate the Gross conjecture regarding the high-energy symmetry of string theory. Since the theory of strings, as a quantum theory, consists of an infinite number of particles with arbitrarily high spins and masses, one first crucial step to uncovering its high-energy behavior is to exactly calculate a class of SSA that contains the whole spectrum valid for all energies. Recently, the present authors constructed a class of such an exact SSA that contains three tachyons and one arbitrary string state in the spectrum, or the Lauricella SSA (LSSA), in the $26D$ open bosonic string theory.

There are many works based on the research of tensionless strings (${\alpha }^{\prime }\to \infty$) [19,20,21,22,23,24,25,26,27,28,29] that are related to our works on high-energy symmetry of string theory. However, as presented in Section 4, in our high-energy calculation, we keep the mass level parameter M of the string spectrum fixed as a finite constant at each mass level. In contrast, in the calculation of tensionless strings in the literature, all string states are massless in the limit ${\alpha }^{\prime }\to \infty$. We believe that by keeping M fixed as a finite constant, one can obtain more information about the high-energy behavior of string theory.

More recently, other interesting approaches have been proposed in the literature which deal with higher spin string states [30,31,32,33,34,35]. More works need to be done on higher spin string states, especially higher massive fermionic string states in the R-sector of superstrings, before one can fully understand the high-energy behavior of superstring theory.

In Section 2 of this review, we calculate the LSSAs and express them in terms of D-type Lauricella functions. As an application, we easily reproduce the string BCJ relation [36,37,38,39]. As an illustration of LSSA, we give two simple examples to demonstrate the complicated notation. We then proceed to show that the LSSAs form an infinite dimensional representation of the $SL(K+3,C)$ group. For simplicity, and as an warm up exercise, we begin with the case of $K=1$ or the $SL(4,C)$ group.

In Section 3, we first show that there exist $K+2$ recurrence relations among the D-type Lauricella functions. We then show that the corresponding $K+2$ recurrence relations among the LSSAs can be used to reproduce the Cartan subalgebra and simple root system of the $SL(K+3,\mathbb{C})$ group with rank $K+2$. As a result, the $SL(K+3,\mathbb{C})$ group can be used to solve all the LSSAs and express them in terms of one amplitude. We stress that these exact nonlinear relations among the exact LSSAs are generalizations of the linear relations among HSSAs in the hard scattering limit conjectured by Gross. Finally, we show that, for the first few mass levels, the Lauricella recurrence relations imply the validity of Ward identities derived from the decoupling of Lauricella ZNS. However, these Lauricella Ward identities are not good enough to solve all the LSSAs and express them in terms of one amplitude.

In Section 4 of this review, we calculate symmetries or relations among the LSSAs of different string states at various scattering limits. These include the linear relations first conjectured by Gross [1,2,3,4,5] and later corrected and proved in [10,12,13,14,15,16] in the hard scattering limit, the recurrence relations in the Regge scattering limit with associated $SL(5,\mathbb{C})$ symmetry [40,41,42] and the extended recurrence relations (including the mass and spin dependent string BCJ relations) in the nonrelativistic scattering limit with associated $SL(4,\mathbb{C})$ symmetry [37] discovered recently.

In Section 5, we give a brief conclusion and suggest some future works. Finally, in the Appendix A, we present detailed calculations of the LSSAs presented in Section 2 of the text.

2. The Exact LSSAs and Their $\mathit{SL}(\mathit{K}+\mathbf{3},\mathit{C})$ Symmetry

2.1. The Exact LSSAs

One important observation of calculating LSSAs is to first note that the SSAs of three tachyons and one arbitrary string state with polarizations orthogonal to the scattering plane vanish. This observation greatly simplifies the calculation of the LSSA. In the CM frame, we define the kinematics as

$$\begin{array}{cc}\hfill k_1& =\left(\sqrt{M_1^2+{\left|\overrightarrow{k_1}\right|}^2},-\left|\overrightarrow{k_1}\right|,0\right),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill k_2& =\left(\sqrt{M_2+{\left|\overrightarrow{k_1}\right|}^2},+\left|\overrightarrow{k_1}\right|,0\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill k_3& =\left(-\sqrt{M_3^2+{\left|\overrightarrow{k_3}\right|}^2},-|\overrightarrow{k_3}|cos\varphi ,-|\overrightarrow{k_3}|sin\varphi \right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill k_4& =\left(-\sqrt{M_4^2+{\left|\overrightarrow{k_3}\right|}^2},+|\overrightarrow{k_3}|cos\varphi ,+|\overrightarrow{k_3}|sin\varphi \right)\hfill \end{array}$$

(4)

with $M_1^2=M_3^2=M_4^2=-2$ and $\varphi$ is the scattering angle. The Mandelstam variables are $s=-{\left(k_1+k_2\right)}^2$, $t=-{\left(k_2+k_3\right)}^2$ and $u=-{\left(k_1+k_3\right)}^2$. There are three polarizations on the scattering plane, and they are defined to be [10,12]

$$\begin{array}{cc}\hfill e^T& =(0,0,1),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill e^L& =\frac{1}{M_2}\left(|\overrightarrow{k_1}|,\sqrt{M_2+{\left|\overrightarrow{k_1}\right|}^2},0\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill e^P& =\frac{1}{M_2}\left(\sqrt{M_2+{\left|\overrightarrow{k_1}\right|}^2},\left|\overrightarrow{k_1}\right|,0\right)\hfill \end{array}$$

(7)

where $e^P=\frac{1}{M_2}(E_2,{\mathrm{k}}_2,0)=\frac{k_2}{M_2}$ is the momentum polarization, $e^L=\frac{1}{M_2}({\mathrm{k}}_2,E_2,0)$ is the longitudinal polarization and $e^T=(0,0,1)$ is the transverse polarization. For later use, we also define

$$k_i^X\equiv e^X·k_i\mathrm{for}X=\left(T,P,L\right).$$

(8)

We now proceed to calculate the LSSAs of three tachyons and one arbitrary string state in the $26D$ open bosonic string theory. The general states at mass level $M_2^2=2(N-1)$, $N={\sum }_{n,m,l>0}\left(n{r}_n^T+m{r}_m^P+l{r}_l^L\right)$ with polarizations on the scattering plane are of the following form:

$$\left|r_n^T,r_m^P,r_l^L\right.〉=\prod _{n>0}{\left({\alpha }_{-n}^T\right)}^{r_n^T}\prod _{m>0}{\left({\alpha }_{-m}^P\right)}^{r_m^P}\prod _{l>0}{\left({\alpha }_{-l}^L\right)}^{r_l^L}|0,k\rangle .$$

(9)

The $\left(s,t\right)$ channel of the LSSA can be calculated to be [43]

$$\begin{array}{cc}\hfill A_{st}^{(r_n^T,r_m^P,r_l^L)}& =\prod _{n=1}{\left[-(n-1)!k_3^T\right]}^{r_n^T}·\prod _{m=1}{\left[-(m-1)!k_3^P\right]}^{r_m^P}\prod _{l=1}{\left[-(l-1)!k_3^L\right]}^{r_l^L}\hfill \\ \hfill & ·B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)F_D^{\left(K\right)}\left(-\frac{t}{2}-1;R_n^T,R_m^P,R_l^L;\frac{u}{2}+2-N;{\tilde{Z}}_n^T,{\tilde{Z}}_m^P,{\tilde{Z}}_l^L\right)\hfill \end{array}$$

(10)

where we have defined

$$R_k^X\equiv {\left\{-r_1^X\right\}}^1,\dots ,{\left\{-r_k^X\right\}}^k\mathrm{with}{\left\{a\right\}}^n=\underset{n}{\underbrace{a,a,\dots ,a}}.$$

(11)

and

$$Z_k^X\equiv \left[z_1^X\right],\dots ,\left[z_k^X\right]\mathrm{with}\left[z_k^X\right]=z_{k0}^X,\dots ,z_{k\left(k-1\right)}^X.$$

(12)

In Equation (12), we have defined

$$\begin{array}{cc}\hfill z_k^X& =\left|{\left(-\frac{k_1^X}{k_3^X}\right)}^{\frac{1}{k}}\right|,z_{k{k}^{\prime }}^X=z_k^X{e}^{\frac{2\pi i{k}^{\prime }}{k}},{\tilde{z}}_{k{k}^{\prime }}^X\equiv 1-z_{k{k}^{\prime }}^X\mathrm{for}{k}^{\prime }=0,\dots ,k-1\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \mathrm{or}\left[z_k^X\right]& =z_k^X,z_k^X{\omega }_k,\dots ,z_k^X{\omega }_k^{k-1},{\omega }_k=e^{\frac{2\pi i}{k}}.\hfill \end{array}$$

(14)

The integer K in Equation (10) is defined to be

$$K=\underset{\{\mathrm{for}\mathrm{all}{r}_j^T\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^P\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^L\ne 0\}}{\sum j}.$$

(15)

The D-type Lauricella function $F_D^{\left(K\right)}$ in Equation (10) is one of the four extensions of the Gauss hypergeometric function to K variables and is defined to be

$$\begin{array}{cc}\hfill & F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)\hfill \\ \hfill & =\sum _{n_1,\dots ,n_K=0}^{\infty }\frac{{\left(\alpha \right)}_{n_1+\dots +n_K}}{{\left(\gamma \right)}_{n_1+\dots +n_K}}\frac{{\left({\beta }_1\right)}_{n_1}\dots {\left({\beta }_K\right)}_{n_K}}{n_1!\dots n_K!}{x}_1^{n_1}\dots x_K^{n_K}\hfill \end{array}$$

(16)

where ${\left(\alpha \right)}_n=\alpha ·\left(\alpha +1\right)\dots \left(\alpha +n-1\right)$ is the Pochhammer symbol. An integral representation of the Lauricella function $F_D^{\left(K\right)}$ was discovered by Appell and Kampe de Feriet (1926) [44],

$$\begin{array}{cc}\hfill & F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)\hfill \\ \hfill & =\frac{\Gamma \left(\gamma \right)}{\Gamma \left(\alpha \right)\Gamma (\gamma -\alpha )}{\int }_0^{1}dt{t}^{\alpha -1}{(1-t)}^{\gamma -\alpha -1}·{(1-x_{1}t)}^{-{\beta }_1}{(1-x_{2}t)}^{-{\beta }_2}\dots {(1-x_{K}t)}^{-{\beta }_K},\hfill \end{array}$$

(17)

which was used to calculate Equation (10).

2.2. String BCJ Relation as a By-Product

Alternatively, by using the identity of the Lauricella function for $b_i\in Z^{-}$,

$$\begin{array}{cc}\hfill & F_D^{\left(K\right)}\left(a;b_1,\dots ,b_K;c;x_1,\dots ,x_K\right)=\frac{\Gamma \left(c\right)\Gamma \left(c-a-\sum b_i\right)}{\Gamma \left(c-a\right)\Gamma \left(c-\sum b_i\right)}\hfill \\ \hfill ·& F_D^{\left(K\right)}\left(a;b_1,\dots ,b_K;1+a+\sum b_i-c;1-x_1,\dots ,1-x_K\right),\hfill \end{array}$$

(18)

one can rederive the string BCJ relations [36,37,38,39]:

$$\begin{array}{cc}\hfill \frac{A_{st}^{(r_n^T,r_m^P,r_l^L)}}{A_{tu}^{(r_n^T,r_m^P,r_l^L)}}& =\frac{{(-)}^N\Gamma \left(-\frac{s}{2}-1\right)\Gamma \left(\frac{s}{2}+2\right)}{\Gamma \left(\frac{u}{2}+2-N\right)\Gamma \left(-\frac{u}{2}-1+N\right)}\hfill \\ \hfill & =\frac{sin\left(\frac{\pi u}{2}\right)}{sin\left(\frac{\pi s}{2}\right)}=\frac{sin\left(\pi k_2·k_4\right)}{sin\left(\pi k_1·k_2\right)}.\hfill \end{array}$$

(19)

This gives another form of the $\left(s,t\right)$ channel amplitude:

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_m^P,r_l^L)}\hfill \\ \hfill & =B\left(-\frac{t}{2}-1,-\frac{s}{2}-1+N\right)\prod _{n=1}{\left[-(n-1)!k_3^T\right]}^{r_n^T}\hfill \\ \hfill & ·\prod _{m=1}{\left[-(m-1)!k_3^P\right]}^{r_m^P}\prod _{l=1}{\left[-(l-1)!k_3^L\right]}^{r_l^L}\hfill \\ \hfill & ·F_D^{\left(K\right)}\left(-\frac{t}{2}-1;R_n^T,R_m^P,R_l^L;\frac{s}{2}+2-N;Z_n^T,Z_m^P,Z_l^L\right).\hfill \end{array}$$

(20)

Similarly, the $\left(t,u\right)$ channel amplitude can be calculated to be

$$\begin{array}{cc}\hfill & A_{tu}^{(r_n^T,r_m^P,r_l^L)}\hfill \\ \hfill & =B\left(-\frac{t}{2}-1,-\frac{u}{2}-1\right)\prod _{n=1}{\left[-(n-1)!k_3^T\right]}^{r_n^T}\hfill \\ \hfill & ·\prod _{m=1}{\left[-(m-1)!k_3^P\right]}^{r_m^P}\prod _{l=1}{\left[-(l-1)!k_3^L\right]}^{r_l^L}\hfill \\ \hfill & ·F_D^{\left(K\right)}\left(-\frac{t}{2}-1;R_n^T,R_m^P,R_l^L;\frac{s}{2}+2-N;Z_n^T,Z_m^P,Z_l^L\right).\hfill \end{array}$$

(21)

The detailed calculation of all the above results can be found in the appendix. To illustrate the complicated notations used in Equation (10), we give two explicit examples of the LSSA in the following subsection.

2.3. Two Simple Examples of the LSSA

2.3.1. Example One

We take the tensor state of the second vertex to be

$$\left|\mathrm{state}\right.〉={\left({\alpha }_{-1}^T\right)}^{r_1^T}{\left({\alpha }_{-1}^P\right)}^{r_1^P}{\left({\alpha }_{-1}^L\right)}^{r_1^L}|0,k\rangle .$$

(22)

The LSSA in Equation (10) can then be calculated to be

$$\begin{array}{cc}\hfill A_{st}^{(r_1^T,r_1^P,r_l^L)}& ={\left(-k_3^T\right)}^{r_1^T}{\left(-k_3^P\right)}^{r_1^P}{\left(-k_3^L\right)}^{r_1^L}B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\hfill \\ \hfill & ·F_D^{\left(3\right)}\left(-\frac{t}{2}-1;-r_1^T,-r_1^P,-r_1^L;\frac{u}{2}+2-N;{\tilde{z}}_{10}^T,{\tilde{z}}_{10}^P,{\tilde{z}}_{10}^L\right)\hfill \end{array}$$

(23)

where the arguments in $F_D^{\left(3\right)}$ are calculated to be

$$\begin{array}{cc}\hfill R_n^T& ={\left\{-r_1^T\right\}}^1,\dots ,{\left\{-r_n^T\right\}}^k={\left\{-r_1^T\right\}}^1=-r_1^T,\hfill \\ \hfill R_m^P& ={\left\{-r_1^P\right\}}^1,\dots ,{\left\{-r_m^P\right\}}^k={\left\{-r_1^P\right\}}^1=-r_1^P,\hfill \\ \hfill R_l^L& ={\left\{-r_1^L\right\}}^1,\dots ,{\left\{-r_l^L\right\}}^k={\left\{-r_1^L\right\}}^1=-r_1^L,\hfill \\ \hfill {\tilde{Z}}_n^T& =\left[{\tilde{z}}_1^T\right],\dots ,\left[{\tilde{z}}_n^T\right]=\left[{\tilde{z}}_1^T\right]={\tilde{z}}_{10}^T=1-z_{10}^T=1-z_k^T{e}^{\frac{2\pi i0}{1}}=1-\left|-\frac{k_1^T}{k_3^T}\right|,\hfill \\ \hfill {\tilde{Z}}_n^P& =\left[{\tilde{z}}_1^P\right],\dots ,\left[{\tilde{z}}_n^P\right]=\left[{\tilde{z}}_1^P\right]={\tilde{z}}_{10}^P=1-\left|-\frac{k_1^P}{k_3^P}\right|,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\tilde{Z}}_n^L& =\left[{\tilde{z}}_1^L\right],\dots ,\left[{\tilde{z}}_n^L\right]=\left[{\tilde{z}}_1^L\right]={\tilde{z}}_{10}^L=1-\left|-\frac{k_1^L}{k_3^L}\right|\hfill \end{array}$$

(25)

and the order K in Equation (15) is

$$\begin{array}{cc}\hfill K& =\underset{\{\mathrm{for}\mathrm{all}{r}_j^T\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^P\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^L\ne 0\}}{\sum j}\hfill \\ \hfill & =1+1+1=3.\hfill \end{array}$$

(26)

2.3.2. Example Two

We take the tensor state to be

$$\left|\mathrm{state}\right.〉={\left({\alpha }_{-1}^T\right)}^{r_1^T}{\left({\alpha }_{-2}^T\right)}^{r_2^T}{\left({\alpha }_{-5}^T\right)}^{r_5^T}{\left({\alpha }_{-6}^T\right)}^{r_6^T}|0,k\rangle .$$

(27)

The LSSA in Equation (10) can be calculated to be

$$\begin{array}{cc}\hfill A_{st}^{(r_1^T,r_1^P,r_l^L)}& ={\left(-k_3^T\right)}^{r_1^T}{\left(-k_3^T\right)}^{r_2^T}{\left(-4!k_3^T\right)}^{r_5^T}{\left(-5!k_3^T\right)}^{r_6^T}B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\hfill \\ \hfill & ·F_D^{\left(14\right)}\left(\begin{array}{c}-\frac{t}{2}-1;-r_1^T,\underset{2}{\underbrace{-r_2^T,-r_2^T}},\underset{5}{\underbrace{-r_5^T,-r_5^T,-r_5^T,-r_5^T,-r_5^T}},\underset{6}{\underbrace{-r_6^T,-r_6^T,-r_6^T,-r_6^T,-r_6^T,-r_6^T}};\\ \frac{u}{2}+2-N;{\tilde{z}}_{10}^T,\underset{2}{\underbrace{{\tilde{z}}_{20}^T,{\tilde{z}}_{21}^T}},\underset{5}{\underbrace{{\tilde{z}}_{50}^T,{\tilde{z}}_{51}^T,{\tilde{z}}_{52}^T,{\tilde{z}}_{53}^T,{\tilde{z}}_{54}^T}},\underset{6}{\underbrace{{\tilde{z}}_{60}^T,{\tilde{z}}_{61}^T,{\tilde{z}}_{62}^T,{\tilde{z}}_{63}^T,{\tilde{z}}_{64}^T,{\tilde{z}}_{65}^T}}\end{array}\right)\hfill \end{array}$$

(28)

where the arguments in $F_D^{\left(14\right)}$ are calculated to be

$$\begin{array}{cc}\hfill R_n^T& ={\left\{-r_1^T\right\}}^1,\dots ,{\left\{-r_n^T\right\}}^k={\left\{-r_1^T\right\}}^1,{\left\{-r_2^T\right\}}^2,{\left\{-r_5^T\right\}}^5,{\left\{-r_6^T\right\}}^6\hfill \\ \hfill & =-r_1^T,\underset{2}{\underbrace{-r_2^T,-r_2^T}},\underset{5}{\underbrace{-r_5^T,-r_5^T,-r_5^T,-r_5^T,-r_5^T}},\underset{6}{\underbrace{-r_6^T,-r_6^T,-r_6^T,-r_6^T,-r_6^T,-r_6^T}}\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\tilde{Z}}_n^T& =\left[{\tilde{z}}_1^T\right],\dots ,\left[{\tilde{z}}_n^T\right]=\left[{\tilde{z}}_1^T\right],\left[{\tilde{z}}_2^T\right],\left[{\tilde{z}}_5^T\right],\left[{\tilde{z}}_6^T\right]\hfill \\ \hfill & ={\tilde{z}}_{10}^T,\underset{2}{\underbrace{{\tilde{z}}_{20}^T,{\tilde{z}}_{21}^T}},\underset{5}{\underbrace{{\tilde{z}}_{50}^T,{\tilde{z}}_{51}^T,{\tilde{z}}_{52}^T,{\tilde{z}}_{53}^T,{\tilde{z}}_{54}^T}},\underset{6}{\underbrace{{\tilde{z}}_{60}^T,{\tilde{z}}_{61}^T,{\tilde{z}}_{62}^T,{\tilde{z}}_{63}^T,{\tilde{z}}_{64}^T,{\tilde{z}}_{65}^T}}\hfill \end{array}$$

(30)

and

$$\begin{array}{cc}\hfill K& =\underset{\{\mathrm{for}\mathrm{all}{r}_j^T\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^P\ne 0\}}{\sum j}+\underset{\{\mathrm{for}\mathrm{all}{r}_j^L\ne 0\}}{\sum j}\hfill \\ \hfill & =\left(1+2+5+6\right)+0+0=14.\hfill \end{array}$$

(31)

In the following subsections, we discuss the exact $SL(K+3,C)$ symmetry of the LSSA. For simplicity, we begin with the simple $SL(4,C)$ symmetry with $K=1.$

2.4. The $SL(4,C)$ Symmetry

In this section, for illustration, we first consider the simplest $K=1$ case with $SL(4,C)$ symmetry. For a given K, there can be LSSAs with different mass levels N. As an example, for the case of $K=1$, there are three types of LSSA:

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1},F_D^{\left(1\right)}\left(-\frac{t}{2}-1,-p_1,\frac{u}{2}+2-p_1,1\right),N& =p_1,\hfill \\ \hfill {\left({\alpha }_{-1}^P\right)}^{q_1},F_D^{\left(1\right)}\left(-\frac{t}{2}-1,-q_1,\frac{u}{2}+2-q_1,\left[{\tilde{z}}_1^P\right]\right),N& =q_1,\hfill \\ \hfill {\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(1\right)}\left(-\frac{t}{2}-1,-r_1,\frac{u}{2}+2-r_1,\left[{\tilde{z}}_1^L\right]\right),N& =r_1.\hfill \end{array}$$

(32)

To calculate the group representation of the LSSA for $K=1$, we define [45]

$$f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=B\left(\gamma -\alpha ,\alpha \right)F_D^{\left(1\right)}\left(\alpha ;\beta ;\gamma ;x\right)a^{\alpha }{b}^{\beta }{c}^{\gamma }.$$

(33)

We see that the LSSA in Equation (10) for the case of $K=1$ corresponds to the case $a=1=c$, and can be written as

$$A_{st}^{R^X}=f_{11}^{-k_3^X}\left(-\frac{t}{2}-1;R^X;\frac{u}{2}+2-N;{\tilde{Z}}^X\right).$$

(34)

We can now introduce the ${(K+3)}^2-1={(1+3)}^2-1=15$ generators of $SL(4,C)$ group [45,46]

$$\begin{array}{cc}\hfill E_{\alpha }& =a\left(x{\partial }_x+a{\partial }_a\right),\hfill \\ \hfill E_{-\alpha }& =\frac{1}{a}\left[x\left(1-x\right){\partial }_x+c{\partial }_c-a{\partial }_a-xb{\partial }_b\right],\hfill \\ \hfill E_{\beta }& =b\left(x{\partial }_x+b{\partial }_b\right),\hfill \\ \hfill E_{-\beta }& =\frac{1}{b}\left[x\left(1-x\right){\partial }_x+c{\partial }_c-b{\partial }_b-xa{\partial }_a\right],\hfill \\ \hfill E_{\gamma }& =c\left[\left(1-x\right){\partial }_x+c{\partial }_c-a{\partial }_a-b{\partial }_b\right],\hfill \\ \hfill E_{-\gamma }& =-\frac{1}{c}\left(x{\partial }_x+c{\partial }_c-1\right),\hfill \\ \hfill E_{\beta \gamma }& =bc\left[\left(x-1\right){\partial }_x+b{\partial }_b\right],\hfill \\ \hfill E_{-\beta ,-\gamma }& =\frac{1}{bc}\left[x\left(x-1\right){\partial }_x+xa{\partial }_a-c{\partial }_c+1\right],\hfill \\ \hfill E_{\alpha \gamma }& =ac\left[\left(1-x\right){\partial }_x-a{\partial }_a\right],\hfill \\ \hfill E_{-\alpha ,-\gamma }& =\frac{1}{ac}\left[x\left(1-x\right){\partial }_x-xb{\partial }_b+c{\partial }_c-1\right],\hfill \\ \hfill E_{\alpha \beta \gamma }& =abc{\partial }_x,\hfill \\ \hfill E_{-\alpha ,-\beta ,-\gamma }& =\frac{1}{abc}\left[x\left(x-1\right){\partial }_x-c{\partial }_c+xb{\partial }_b+xa{\partial }_a-x+1\right],\hfill \\ \hfill J_{\alpha }& =a{\partial }_a,\hfill \\ \hfill J_{\beta }& =b{\partial }_b,\hfill \\ \hfill J_{\gamma }& =c{\partial }_c,\hfill \end{array}$$

(35)

and calculate their operations on the basis of functions [45,46]

$$\begin{array}{cc}\hfill E_{\alpha }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\gamma -\alpha -1\right)f_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right),\hfill \\ \hfill E_{\beta }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\beta f_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right),\hfill \\ \hfill E_{\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\gamma -\beta \right)f_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right),\hfill \\ \hfill E_{\beta \gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\beta f_{ac}^b\left(\alpha ;\beta +1;\gamma +1;x\right),\hfill \\ \hfill E_{\alpha \gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\beta -\gamma \right)f_{ac}^b\left(\alpha +1;\beta ;\gamma +1;x\right),\hfill \\ \hfill E_{\alpha \beta \gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\beta f_{ac}^b\left(\alpha +1;\beta +1;\gamma +1;x\right),\hfill \\ \hfill E_{-\alpha }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\alpha -1\right)f_{ac}^b\left(\alpha -1;\beta ;\gamma ;x\right),\hfill \\ \hfill E_{-\beta }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\gamma -\beta \right)f_{ac}^b\left(\alpha ;\beta -1;\gamma ;x\right),\hfill \\ \hfill E_{-\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\alpha +1-\gamma \right)f_{ac}^b\left(\alpha ;\beta ;\gamma -1;x\right),\hfill \\ \hfill E_{-\beta ,-\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\alpha -\gamma +1\right)f_{ac}^b\left(\alpha ;\beta -1;\gamma -1;x\right),\hfill \\ \hfill E_{-\alpha ,-\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(\alpha -1\right)f_{ac}^b\left(\alpha -1;\beta ;\gamma -1;x\right),\hfill \\ \hfill E_{-\alpha ,-\beta ,-\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\left(-\alpha +1\right)f_{ac}^b\left(\alpha -1;\beta -1;\gamma -1;x\right),\hfill \\ \hfill J_{\alpha }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\alpha f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right),\hfill \\ \hfill J_{\beta }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\beta f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right),\hfill \\ \hfill J_{\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\gamma f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right).\hfill \end{array}$$

(36)

It is important to note, for example, that since $\beta$ is a nonpositive integer, the operation by $E_{-\beta }$ will not be terminated as in the case of the finite dimensional representation of a compact Lie group. Here the representation is infinite-dimensional. On the other hand, a simple calculation gives

$$\begin{array}{cc}\hfill \left[E_{\alpha },E_{-\alpha }\right]& =2J_{\alpha }-J_{\gamma },\hfill \\ \hfill \left[E_{\beta },E_{-\beta }\right]& =2J_{\beta }-J_{\gamma },\hfill \\ \hfill \left[E_{\gamma },E_{-\gamma }\right]& =2J_{\gamma }-\left(J_{\alpha }+J_{\beta }+1\right),\hfill \end{array}$$

which suggests the Cartan subalgebra

$$\left[J_{\alpha },J_{\beta }\right]=0,\left[J_{\beta },J_{\gamma }\right]=0,\left[J_{\alpha },J_{\gamma }\right]=0.$$

(37)

Indeed, if we redefine

$$\begin{array}{cc}\hfill J_{\alpha }^{\prime }& =J_{\alpha }-\frac{1}{2}{J}_{\gamma },\hfill \\ \hfill J_{\beta }^{\prime }& =J_{\beta }-\frac{1}{2}{J}_{\gamma },\hfill \\ \hfill J_{\gamma }^{\prime }& =J_{\gamma }-\frac{1}{2}\left(J_{\alpha }+J_{\beta }+1\right),\hfill \end{array}$$

we discover that each of the following six triplets [45,46]

$$\begin{array}{cc}\hfill & \left\{J^{+},J^{-},J^0\right\}\equiv \left\{E_{\alpha },E_{-\alpha },J_{\alpha }^{\prime }\right\},\left\{E_{\beta },E_{-\beta },J_{\beta }^{\prime }\right\},\hfill \\ \hfill & \left\{E_{\gamma },E_{-\gamma },J_{\gamma }^{\prime }\right\},\left\{E_{\alpha ,\beta ,\gamma },E_{-\alpha ,-\beta ,-\gamma },J_{\alpha }^{\prime }+J_{\beta }^{\prime }+J_{\gamma }^{\prime }\right\},\hfill \\ \hfill & \left\{E_{\alpha \gamma },E_{-\alpha ,-\gamma },J_{\alpha }^{\prime }+J_{\gamma }^{\prime }\right\},\left\{E_{\alpha \beta },E_{-\alpha ,-\beta },J_{\alpha }^{\prime }+J_{\beta }^{\prime }\right\}\hfill \end{array}$$

constitutes the well-known commutation relations

$$\left[J^0,J^{\pm }\right]=\pm J^{\pm },\left[J^{+},J^{-}\right]=2J^0$$

(38)

.

2.5. The General SL($K+3$,C) Symmetry

We are now ready to generalize the calculation of the previous section and calculate the group representation of the LSSA for general K. We first define [45]

$$\begin{array}{cc}\hfill & f_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)\hfill \\ \hfill & =B\left(\gamma -\alpha ,\alpha \right)F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)a^{\alpha }{b}_1^{{\beta }_1}\dots b_K^{{\beta }_K}{c}^{\gamma }.\hfill \end{array}$$

(39)

Note that the LSSA in Equation (10) corresponds to the case $a=1=c$ and can be written as

$$A_{st}^{(r_n^T,r_m^P,r_l^L)}=f_{11}^{-(n-1)!k_3^T,-(m-1)!k_3^P,-(l-1)!k_3^L}\left(-\frac{t}{2}-1;R_n^T,R_m^P,R_l^L;\frac{u}{2}+2-N;{\tilde{Z}}_n^T,{\tilde{Z}}_m^P,{\tilde{Z}}_l^L\right).$$

(40)

It is possible to extend the calculation of the $SL(4,\mathbb{C})$ symmetry group for the $K=1$ case discussed in the previous section to the general $SL(K+3,\mathbb{C})$ group. We first introduce the ${(K+3)}^2-1$ generators of the $SL(K+3,C)$ group ($k=1,2,\dots K$) [45,46]

$$\begin{array}{cc}\hfill E^{\alpha }& =a\left({\displaystyle \sum }_j{x}_j{\partial }_j+a{\partial }_a\right),\hfill \\ \hfill E^{{\beta }_k}& =b_k\left(x_k{\partial }_k+b_k{\partial }_{b_k}\right),\hfill \\ \hfill E^{\gamma }& =c\left({\displaystyle \sum }_j\left(1-x_j\right){\partial }_{x_j}+c{\partial }_c-a{\partial }_a-{\displaystyle \sum }_j{b}_j{\partial }_{b_j}\right),\hfill \\ \hfill E^{\alpha \gamma }& =ac\left({\displaystyle \sum }_j\left(1-x_j\right){\partial }_{x_j}-a{\partial }_a\right),\hfill \\ \hfill E^{{\beta }_k\gamma }& =b_{k}c\left[\left(x_k-1\right){\partial }_{x_k}+b_k{\partial }_{b_k}\right],\hfill \\ \hfill E^{\alpha {\beta }_k\gamma }& =a{b}_{k}c{\partial }_{x_k},\hfill \\ \hfill E_{\alpha }& =\frac{1}{a}\left[{\displaystyle \sum }_j{x}_j\left(1-x_j\right){\partial }_{x_j}+c{\partial }_c-a{\partial }_a-{\displaystyle \sum }_j{x}_j{b}_j{\partial }_{b_j}\right],\hfill \\ \hfill E_{{\beta }_k}& =\frac{1}{b_k}\left[x_k\left(1-x_k\right){\partial }_{x_k}+x_k{\displaystyle \sum }_{j\ne k}\left(1-x_j\right)x_j{\partial }_{x_j}+c{\partial }_c-x_{k}a{\partial }_a-{\displaystyle \sum }_j{b}_j{\partial }_{u_j}\right],\hfill \\ \hfill E_{\gamma }& =-\frac{1}{c}\left({\displaystyle \sum }_j{x}_j{\partial }_{x_j}+c{\partial }_c-1\right),\hfill \\ \hfill E_{\alpha \gamma }& =\frac{1}{ac}\left[{\displaystyle \sum }_j{x}_j\left(1-x_j\right){\partial }_{x_j}-{\displaystyle \sum }_j{x}_j{b}_j{\partial }_{b_j}+c{\partial }_c-1\right],\hfill \\ \hfill E_{{\beta }_k\gamma }& =\frac{1}{b_{k}c}\left[x_k\left(x_k-1\right){\partial }_{x_k}+{\displaystyle \sum }_{j\ne k}\left(x_j-1\right)x_j{\partial }_{x_j}+x_{k}a{\partial }_a-c{\partial }_c+1\right],\hfill \\ \hfill E_{\alpha {\beta }_k\gamma }& =\frac{1}{a{b}_{k}c}\left[{\displaystyle \sum }_j{x}_j\left(x_j-1\right){\partial }_{x_j}-c{\partial }_c+x_{k}a{\partial }_a+{\displaystyle \sum }_j{x}_j{b}_j{\partial }_{b_j}-x_k+1\right],\hfill \\ \hfill E_{{\beta }_p}^{{\beta }_k}& =\frac{b_k}{b_p}\left[\left(x_k-x_p\right){\partial }_{z_k}+b_k{\partial }_{b_k}\right],(k\ne p),\hfill \\ \hfill J_{\alpha }& =a{\partial }_a,\hfill \\ \hfill J_{{\beta }_k}& =b_k{\partial }_{b_k},\hfill \\ \hfill J_{\gamma }& =c{\partial }_c.\hfill \end{array}$$

(41)

Note that we have used the upper indices to denote the “raising operators” and the lower indices to denote the “lowering operators”. The number of generators can be counted in the following way. There are 1 $E^{\alpha }$, K $E^{{\beta }_k}$, 1 $E^{\gamma }$,1 $E^{\alpha \gamma }$,K$E^{{\beta }_k\gamma }$ and K$E^{\alpha {\beta }_k\gamma }$ which sum up to $3K+3$ raising generators. There are also $3K+3$ lowering operators. In addition, there are $K\left(K-1\right)$ $E_{{\beta }_p}^{{\beta }_k}$ and $K+2$ $J$, corresponding to the Cartan subalgebra. In summary, the total number of generators is $2(3K+3)+K(K-1)+K+2={(K+3)}^2-1$. It is straightforward to calculate the operation of these generators on the basis of functions ($k=1,2,\dots ,K$) [45]

$$\begin{array}{cc}\hfill E^{\alpha }{f}_{ac}^{b_1\dots b_K}\left(\alpha \right)& =\left(\gamma -\alpha -1\right)f_{ac}^{b_1\dots b_K}\left(\alpha +1\right),\hfill \\ \hfill E^{{\beta }_k}{f}_{ac}^{b_1\dots b_K}\left({\beta }_k\right)& ={\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1\right),\hfill \\ \hfill E^{\gamma }{f}_{ac}^{b_1\dots b_K}\left(\gamma \right)& =\left(\gamma -{\displaystyle \sum }_j{\beta }_j\right)f_{ac}^{b_1\dots b_K}\left(\gamma +1\right),\hfill \\ \hfill E^{\alpha \gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;\gamma \right)& =\left({\displaystyle \sum }_j{\beta }_j-\gamma \right)f_{ac}^{b_1\dots b_K}\left(\alpha +1;\gamma +1\right),\hfill \\ \hfill E^{{\beta }_k\gamma }{f}_{ac}^{b_1\dots b_K}\left({\beta }_k;\gamma \right)& ={\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1;\gamma +1\right),\hfill \\ \hfill E^{\alpha {\beta }_k\gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)& ={\beta }_k{f}_{ac}^{b_1\dots b_K}\left(\alpha +1;{\beta }_k+1;\gamma +1\right),\hfill \\ \hfill E_{\alpha }{f}_{ac}^{b_1\dots b_K}\left(\alpha \right)& =\left(\alpha -1\right)f_{ac}^{b_1\dots b_K}\left(\alpha -1\right),\hfill \\ \hfill E_{{\beta }_k}{f}_{ac}^{b_1\dots b_K}\left({\beta }_k\right)& =\left(\gamma -{\displaystyle \sum }_j{\beta }_j\right)f_{ac}^{b_1\dots b_K}\left({\beta }_k-1\right),\hfill \\ \hfill E_{\gamma }{f}_{ac}^{b_1\dots b_K}\left(\gamma \right)& =\left(\alpha -\gamma +1\right)f_{ac}^{b_1\dots b_K}\left(\gamma -1\right),\hfill \\ \hfill E_{\alpha \gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;\gamma \right)& =\left(\alpha -1\right)f_{ac}^{b_1\dots b_K}\left(\alpha -1;\gamma -1\right),\hfill \\ \hfill E_{{\beta }_k\gamma }{f}_{ac}^{b_1\dots b_K}\left({\beta }_k;\gamma \right)& =\left(\alpha -\gamma +1\right)f_{ac}^{b_1\dots b_K}\left({\beta }_k-1;\gamma -1\right),\hfill \\ \hfill E_{\alpha {\beta }_k\gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)& =\left(1-\alpha \right)f_{ac}^{b_1\dots b_K}\left(\alpha -1;{\beta }_k-1;\gamma -1\right),\hfill \\ \hfill E_{{\beta }_p}^{{\beta }_k}{f}_{ac}^{b_1\dots b_K}\left({\beta }_k;{\beta }_p\right)& ={\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1;{\beta }_p-1\right),\hfill \\ \hfill J_{\alpha }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)& =\alpha f_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right),\hfill \\ \hfill J_{{\beta }_k}{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)& ={\beta }_k{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right),\hfill \\ \hfill J_{\gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)& =\gamma f_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_k;\gamma \right)\hfill \end{array}$$

(42)

where, for simplicity, we have omitted those arguments in $f_{ac}^{b_1\dots b_K}$ that remain the same after the operation. The commutation relations of the $SL(K+3)$ Lie algebra can be calculated in the following way. In addition to the Cartan subalgebra for the $K+2$ generators $\left\{J_{\alpha },J_{{\beta }_k},J_{\gamma }\right\}$, we redefine

$$\begin{array}{cc}\hfill J_{\alpha }^{\prime }& =J_{\alpha }-\frac{1}{2}{J}_{\gamma },\hfill \\ \hfill J_{{\beta }_k}^{\prime }& =J_{{\beta }_k}-\frac{1}{2}{J}_{\gamma }+\sum _{j\ne k}{J}_{{\beta }_j},\hfill \\ \hfill J_{\gamma }^{\prime }& =J_{\gamma }-\frac{1}{2}\left(J_{\alpha }+\sum _j{J}_{{\beta }_j}+1\right).\hfill \end{array}$$

(43)

We discover that each of the following seven triplets [45]

$$\begin{array}{cc}\hfill & \left\{J^{+},J^{-},J^0\right\}\equiv \left\{E^{\alpha },E_{\alpha },J_{\alpha }^{\prime }\right\},\left\{E^{{\beta }_k},E_{{\beta }_k},J_{{\beta }_k}^{\prime }\right\},\hfill \\ \hfill & \left\{E^{\gamma },E_{\gamma },J_{\gamma }^{\prime }\right\},\left\{E^{\alpha {\beta }_k\gamma },E_{\alpha {\beta }_k\gamma },J_{\alpha }^{\prime }+J_{{\beta }_k}^{\prime }+J_{\gamma }^{\prime }\right\},\hfill \\ \hfill & \left\{E^{\alpha \gamma },E_{\alpha \gamma },J_{\alpha }^{\prime }+J_{\gamma }^{\prime }\right\},\left\{E^{\alpha {\beta }_k},E_{\alpha {\beta }_k},J_{\alpha }^{\prime }+J_{{\beta }_k}^{\prime }\right\},\hfill \\ \hfill & \left\{E_{{\beta }_p}^{{\beta }_l},E_{{\beta }_l}^{{\beta }_p},J_{{\beta }_l}^{\prime }-J_{{\beta }_p}^{\prime }\right\}\hfill \end{array}$$

(44)

satisfies the commutation relations in Equation (38).

Finally, in addition to Equation (44), there is another compact way to write the Lie algebra commutation relations of $SL(K+3,C).$ Indeed, one can check that the Lie algebra commutation relations of $SL(K+3,C)$ can be written as [45]

$$\left[{\mathit{\epsilon }}_{ij},{\mathit{\epsilon }}_{kl}\right]={\delta }_{jk}{\mathit{\epsilon }}_{il}-{\delta }_{li}{\mathit{\epsilon }}_{kj}$$

(45)

with the following identifications:

$$\begin{array}{cc}\hfill E^{\alpha }& ={\mathit{\epsilon }}_{12},E_{\alpha }={\mathit{\epsilon }}_{21},E^{{\beta }_k}={\mathit{\epsilon }}_{k+3,3},E_{\beta }={\mathit{\epsilon }}_{3,k+3},\hfill \\ \hfill E^{\gamma }& ={\mathit{\epsilon }}_{31},E_{\gamma }={\mathit{\epsilon }}_{13},E^{\alpha \gamma }={\mathit{\epsilon }}_{32},E_{\alpha \gamma }={\mathit{\epsilon }}_{23},\hfill \\ \hfill E^{{\beta }_k\gamma }& =-{\mathit{\epsilon }}_{k+3,1},E_{{\beta }_k\gamma }=-{\mathit{\epsilon }}_{1,k+3},E_{\alpha {\beta }_k\gamma }=-{\mathit{\epsilon }}_{k+3,2},\hfill \\ \hfill E_{\alpha {\beta }_k\gamma }& =-{\mathit{\epsilon }}_{2,k+3},J_{\alpha }^{\prime }=\frac{1}{2}\left({\mathit{\epsilon }}_{11}-{\mathit{\epsilon }}_{22}\right),J_{{\beta }_k}^{\prime }=\frac{1}{2}\left({\mathit{\epsilon }}_{k+3,k+3}-{\mathit{\epsilon }}_{33}\right),J_{\gamma }^{\prime }=\frac{1}{2}\left({\mathit{\epsilon }}_{33}-{\mathit{\epsilon }}_{11}\right).\hfill \end{array}$$

(46)

2.6. Discussion

There are some special properties in the $SL(K+3,\mathbb{C})$ group representation of the LSSA that make it different from the usual symmetry group representation of a physical system. First, the set of LSSA does not fill up the whole representation space V. For example, states $f_{ac}^{b_1\dots b_K}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)$ in V with $a\ne 1$ or $c\ne 1$ are not LSSAs.

Indeed, there are more states in V with $K\ge 2$ that are not LSSAs either. We give one example in the following. For $K=2$, there are six types of LSSAs: $(\omega =-1)$

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-1}^P\right)}^{q_1},F_D^{\left(2\right)}(a,-p_1,-q_1,c-p_1-q_1,1,\left[{\tilde{z}}_1^P\right]),N& =p_1+q_1,\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(2\right)}(a,-p_1,-r_1,c-p_1-r_1,1,\left[{\tilde{z}}_1^L\right]),N& =p_1+r_1,\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^P\right)}^{q_1}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(2\right)}(a,-q_1,-r_1,c-q_1-r_1,\left[{\tilde{z}}_1^P\right],\left[{\tilde{z}}_1^L\right]),N& =q_1+r_1,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^T\right)}^{p_2},F_D^{\left(2\right)}(a,-p_2,-p_2,c-2p_2,1,1),N& =2p_2,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^P\right)}^{q_2},F_D^{\left(2\right)}(a,-q_2,-q_2,c-2q_2,1-z_2^P,1-\omega z_2^P),N& =2q_2,\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^L\right)}^{r_2},F_D^{\left(2\right)}(a,-r_2,-r_2,c-2r_2,1-z_2^L,1-\omega z_2^L),N& =2r_2.\hfill \end{array}$$

(52)

One can show that those states obtained from the operation by $E_{\beta }$ in either states in Equations (50)–(52) are not LSSAs. However, it is shown in Section 3 that all states in V, including those “auxiliary states” which are not LSSAs as stated above, can be exactly solved by recurrence relations or the $SL(K+3,\mathbb{C})$ group and expressed in terms of one amplitude. These “auxiliary states” and states with $a\ne 1$ or $c\ne 1$ in V may represent other SSAs—e.g., SSAs of two tachyons and two arbitrary string states, etc.—which will be considered in the near future.

3. Solving LSSA through Recurrence Relations

In the previous section, the string scattering amplitudes of three tachyons and one arbitrary string states in the 26D open bosonic string theory were obtained in terms of the D-type Lauricella functions; i.e., the LSSA in Equation (10). The symmetry of the LSSA was also discussed by constructing the $SL(K+3,\mathbb{C})$ group for the D-type Lauricella functions $F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)$. It is natural to suspect that the LSSAs are dependent on each other due to the symmetry between them. In fact, we are able to show that all the LSSAs are related to a single LSSA by the recurrence relations of the D-type Lauricella functions.

To solve all the LSSAs, a key observation is that all arguments ${\beta }_m$ in the Lauricella functions $F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)$ in the LSSA (10) are nonpositive integers. We show that this plays a key role in proving the solvability of all the LSSAs below.

The generalization of the $2+2$ recurrence relations of the Appell functions to the $K+2$ recurrence relations of the Lauricella functions was given in [47]. One can use these $K+2$ recurrence relations to reduce all the Lauricella functions $F_D^{\left(K\right)}$ in the LSSA (10) to the Gauss hypergeometry functions ${}_2{F}_1(\alpha ,\beta ,\gamma )$. Then, all the LSSAs can be solved by deriving a multiplication theorem for the Gauss hypergeometry functions.

In this section, we will review the steps presented in [47].

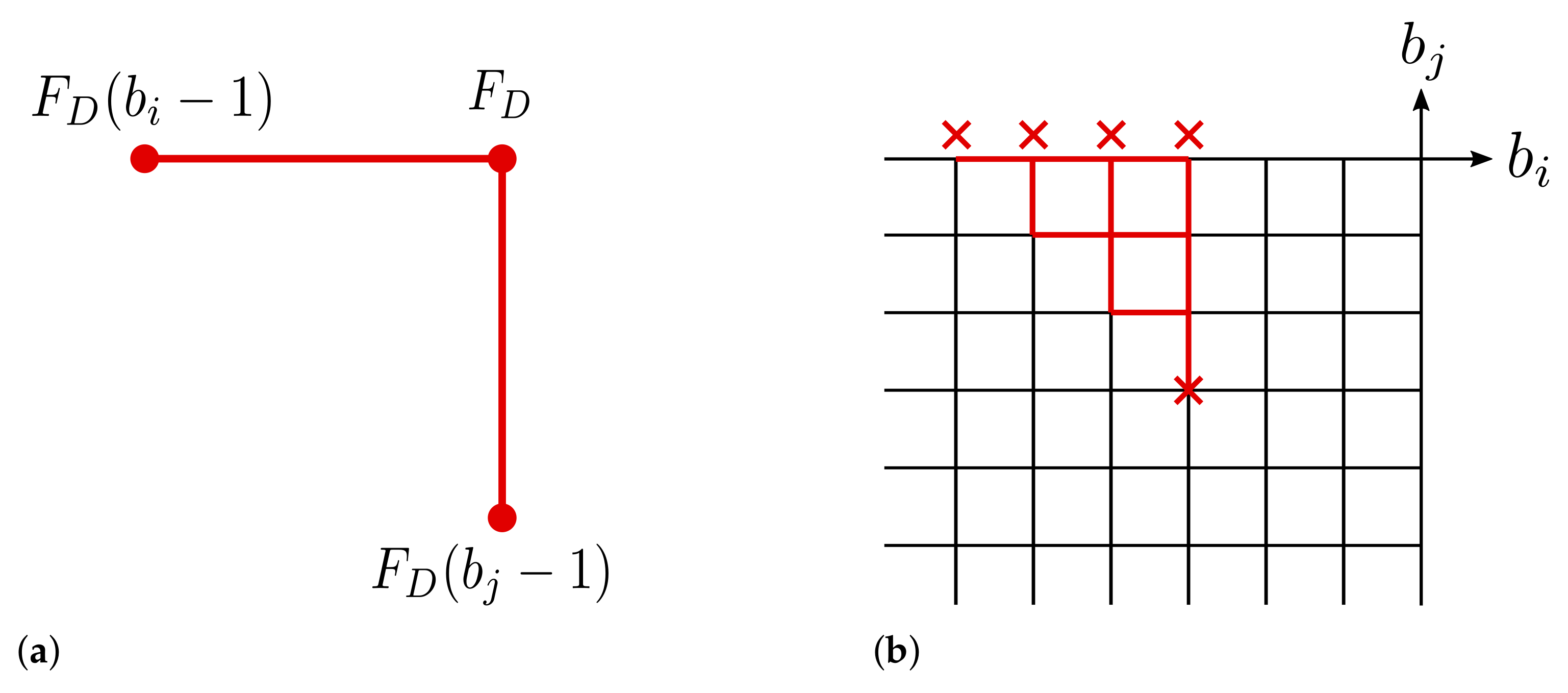
3.1. Recurrence Relations of the LSSA

For $K=2$, the Lauricella functions D-type $F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)$ reduce to the type-1Appell functions $F_1\left(\alpha ;b_1,{\beta }_2;\gamma ,x,y\right)$. The four fundamental recurrence relations which link the contiguous functions are

$$\begin{array}{c}\hfill \left(\alpha -{\beta }_1-{\beta }_2\right)F_1\left(\alpha ;{\beta }_1,{\beta }_2;\gamma ,x,y\right)-\alpha F_1\left(\alpha +1;{\beta }_1,{\beta }_2;\gamma ,x,y\right)\\ \hfill +{\beta }_1{F}_1\left(\alpha ;{\beta }_1+1,{\beta }_2;\gamma ,x,y\right)+{\beta }_2{F}_1\left(\alpha ;{\beta }_1,{\beta }_2+1;\gamma ,x,y\right)& =0,\hfill \end{array}$$

(53)

$$\begin{array}{c}\hfill \gamma F_1\left(\alpha ;{\beta }_1,{\beta }_2;\gamma ,x,y\right)-\left(\gamma -\alpha \right)F_1\left(\alpha ;{\beta }_1,{\beta }_2;\gamma +1,x,y\right)\\ \hfill -\alpha F_1\left(\alpha +1;{\beta }_1,{\beta }_2;\gamma +1,x,y\right)& =0,\hfill \end{array}$$

(54)

$$\begin{array}{c}\hfill \gamma F_1\left(\alpha ;{\beta }_1,{\beta }_2;\gamma ,x,y\right)+\gamma \left(x-1\right)F_1\left(\alpha ;{\beta }_1+1,{\beta }_2;\gamma ,x,y\right)\\ \hfill -\left(\gamma -\alpha \right)x{F}_1\left(\alpha ;{\beta }_1+1,{\beta }_2;\gamma +1,x,y\right)& =0,\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill \gamma F_1\left(\alpha ;{\beta }_1,{\beta }_2;\gamma ,x,y\right)+\gamma \left(y-1\right)F_1\left(\alpha ;{\beta }_1,{\beta }_2+1;\gamma ,x,y\right)& \hfill \\ \hfill -\left(\gamma -\alpha \right)y{F}_1\left(\alpha ;{\beta }_1,{\beta }_2+1;\gamma +1,x,y\right)& =0.\hfill \end{array}$$

(56)

It is straightforward to generalize the above relations and prove the following $K+2$ recurrence relations for the D-type Lauricella functions: [47]

$$\begin{array}{c}\hfill \left(\alpha -\sum _i{\beta }_i\right)F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)-\alpha F_D^{\left(K\right)}\left(\alpha +1;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)\\ \hfill +{\beta }_1{F}_D^{\left(K\right)}\left(\alpha ;{\beta }_1+1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)+\dots +{\beta }_K{F}_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K+1;\gamma ;x_1,\dots ,x_K\right)& =0,\hfill \end{array}$$

(57)

$$\begin{array}{c}\hfill \gamma F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)-\left(\gamma -\alpha \right)F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma +1;x_1,\dots ,x_K\right)\\ \hfill -\alpha F_D^{\left(K\right)}\left(\alpha +1;{\beta }_1,\dots ,{\beta }_K;\gamma +1;x_1,\dots ,x_K\right)& =0,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \gamma F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_m,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_m,\dots ,x_K\right)& \hfill \\ \hfill +\gamma (x_m-1)F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_m+1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_m,\dots ,x_K\right)\\ \hfill +(\alpha -\gamma )x_m{F}_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_m+1,\dots ,{\beta }_K;\gamma +1;x_1,\dots ,x_m,\dots ,x_K\right)& =0,\hfill \end{array}$$

(59)

where $m=1,2,\dots ,K$. In the case of $K=2$, Equation (59) reduces to the Appell recurrence relations in Equations (55) and (56).

To simplify the notation, we omit those arguments of $F_D^{\left(K\right)}$ that remain the same in the rest of the paper. Then, the above $K+2$ recurrence relations can be expressed as

$$\begin{array}{cc}\hfill \left(\alpha -\sum _i{\beta }_i\right)F_D^{\left(K\right)}-\alpha F_D^{\left(K\right)}\left(\alpha +1\right)+{\beta }_1{F}_D^{\left(K\right)}\left({\beta }_1+1\right)+\dots +{\beta }_K{F}_D^{\left(K\right)}\left({\beta }_K+1\right)& =0,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill \gamma F_D^{\left(K\right)}-\left(\gamma -\alpha \right)F_D^{\left(K\right)}\left(\gamma +1\right)-\alpha F_D^{\left(K\right)}\left(\alpha +1;\gamma +1\right)& =0,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill \gamma F_D^{\left(K\right)}+\gamma (x_m-1)F_D^{\left(K\right)}\left({\beta }_m+1\right)+(\alpha -\gamma )x_m{F}_D^{\left(K\right)}\left({\beta }_m+1,;\gamma +1\right)& =0.\hfill \end{array}$$

(62)

To proceed, we first consider the two recurrence relations from Equation (62) for $m=i$, j with $i\ne j$,

$$c{F}_D^{\left(K\right)}+\gamma (x_i-1)F_D^{\left(K\right)}\left({\beta }_i+1\right)+(\alpha -\gamma )x_i{F}_D^{\left(K\right)}\left({\beta }_i+1;\gamma +1\right)=0,$$

(63)

$$\gamma F_D^{\left(K\right)}+\gamma (x_j-1)F_D^{\left(K\right)}\left({\beta }_j+1\right)+(\alpha -\gamma )x_j{F}_D^{\left(K\right)}\left({\beta }_j+1;\gamma +1\right)=0,$$

(64)

By shifting ${\beta }_{i,j}$ to ${\beta }_{i,j}-1$ and combining the above two equations to eliminate the $F_D^{\left(K\right)}\left(c+1\right)$ term, we obtain the following key recurrence relation [47]:

$$x_j{F}_D^{\left(K\right)}\left({\beta }_i-1\right)-x_i{F}_D^{\left(K\right)}\left({\beta }_j-1\right)+\left(x_i-x_j\right)F_D^{\left(K\right)}=0.$$

(65)

One can repeatedly apply Equation (65) to the Lauricella functions in the LSSA in Equation (10) and end up with an expression that expresses $F_D^{\left(K\right)}({\beta }_1,{\beta }_2,\dots {\beta }_K)$ in terms of $F_D^{(K-1)}\left({\beta }_1,\dots {\beta }_{i-1},{\beta }_{i+1}\dots {\beta }_j^{\prime },\dots {\beta }_K\right)$, ${\beta }_j^{\prime }={\beta }_j,{\beta }_j-1,\dots ,{\beta }_j-\left|{\beta }_i\right|$ or $F_D^{(K-1)}({\beta }_1,\dots {\beta }_i^{\prime },\dots {\beta }_{j-1},{\beta }_{j+1},\dots {\beta }_K)$, ${\beta }_i^{\prime }={\beta }_i,{\beta }_i-1,\dots ,{\beta }_i-\left|{\beta }_j\right|$ (assume $i<j$). We can repeat the above process to decrease the value of K and reduce all the Lauricella functions $F_D^{\left(K\right)}$ in the LSSA to the Gauss hypergeometry functions $F_D^{\left(1\right)}=$${}_2{F}_1(\alpha ,\beta ,\gamma ,x)$ as shown in Figure 1.

3.2. Solving all the LSSAs

In the last subsection, we expressed all the LSSAs in terms of the Gauss hypergeometry functions $F_D^{\left(1\right)}={}_2{F}_1(\alpha ,\beta ,\gamma ,x)$. In this subsection, we further reduce the Gauss hypergeometry functions by deriving a multiplication theorem for them and solve all the LSSAs in terms of one single amplitude.

We begin with Taylor’s theorem:

$$f(x+y)=\sum _{n=0}^{\infty }\frac{y^n}{n!}\frac{d^n}{d{x}^n}f\left(x\right).$$

(66)

By replacing y by $(y-1)x$, we get the identity

$$f\left(xy\right)=\sum _{n=0}^{\infty }\frac{{(y-1)}^n{x}^n}{n!}\frac{d^n}{d{x}^n}f\left(x\right).$$

(67)

One can then use the derivative relation of the Gauss hypergeometry function

$$\frac{d^n}{d{x}^n}{}_2{F}_1(\alpha ,\beta ,\gamma ,x)=\frac{{\left(\alpha \right)}_n{\left(\beta \right)}_n}{{\left(\gamma \right)}_n}{}_2{F}_1(\alpha +n,\beta +n,\gamma +n,x),$$

(68)

where ${\left(\alpha \right)}_n=\alpha ·\left(\alpha +1\right)\dots \left(\alpha +n-1\right)$ is the Pochhammer symbol, to obtain the following multiplication theorem:

$${}_2{F}_1(\alpha ,\beta ,\gamma ,xy)=\sum _{n=0}^{\left|\beta \right|}\frac{{(y-1)}^n{x}^n}{n!}\frac{{\left(\alpha \right)}_n{\left(\beta \right)}_n}{{\left(\gamma \right)}_n}{}_2{F}_1(\alpha +n,\beta +n,\gamma +n,x).$$

(69)

It is important to note that the summation in the above equation is up to a finite integer $\left|\beta \right|$ given that $\beta$ is a nonpositive integer for the cases of LSSA.

In particular, if we take $x=1$ in Equation (69), we get the following relation:

$$\begin{array}{cc}\hfill {}_2{F}_1(\alpha ,\beta ,\gamma ,y)& =\sum _{n=0}^{\left|\beta \right|}\frac{{(y-1)}^n}{n!}\frac{{\left(\alpha \right)}_n{\left(\beta \right)}_n}{{\left(\gamma \right)}_n}{}_2{F}_1(\alpha +n,\beta +n,\gamma +n,1)\hfill \\ \hfill & =\sum _{n=0}^{\left|\beta \right|}\frac{{(y-1)}^n}{n!}\frac{{\left(\alpha \right)}_n{\left(\beta \right)}_n}{{\left(\gamma \right)}_n}\frac{{(-)}^n{\left(\gamma \right)}_n}{{(\gamma -\alpha -\beta )}_n}{}_2{F}_1(\alpha ,\beta ,\gamma ,1).\hfill \end{array}$$

(70)

By using the following example of the 15 Gauss contiguous relations

$${\{\gamma -2\beta +(\beta -\alpha )x\}}_2{F}_1+\beta {(1-x)}_2{F}_1(\beta +1)+{(\beta -\gamma )}_2{F}_1(\beta -1)=0,$$

(71)

and setting $x=1$, which eliminates the second term of Equation (71), we can reduce the argument $\beta$ in ${}_2{F}_1(\alpha ,\beta ,c,1)$ to $\beta =-1$ or 0, which corresponds to vector or tachyon amplitudes in the LSSA. This completes the proof that all the LSSAs calculated in Equation (10) can be solved through various recurrence relations of Lauricella functions. Moreover, all the LSSAs can be expressed in terms of one single four tachyon amplitude.

3.3. Examples of Solving LSSA

For illustration, in this subsection, we calculate the Lauricella functions which correspond to the LSSA for levels $K=1,2,3$.

For $K=1$, there are three type of LSSA $(\alpha =-\frac{t}{2}-1,\gamma =\frac{u}{2}+2)$

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1},F_D^{\left(1\right)}(\alpha ,-p_1,\gamma -p_1,1),N& =p_1,\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^P\right)}^{q_1},F_D^{\left(1\right)}(\alpha ,-q_1,\gamma -q_1,\left[{\tilde{z}}_1^P\right]),N& =q_1,\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(1\right)}(\alpha ,-r_1,\gamma -r_1,\left[{\tilde{z}}_1^L\right]),N& =r_1.\hfill \end{array}$$

(74)

For $K=2$, there are six type of LSSA $(\omega =-1)$

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-1}^P\right)}^{q_1},F_D^{\left(2\right)}(\alpha ,-p_1,-q_1,\gamma -p_1-q_1,1,\left[{\tilde{z}}_1^P\right]),N& =p_1+q_1,\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(2\right)}(\alpha ,-p_1,-r_1,\gamma -p_1-r_1,1,\left[{\tilde{z}}_1^L\right]),N& =p_1+r_1,\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^P\right)}^{q_1}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(2\right)}(\alpha ,-q_1,-r_1,\gamma -q_1-r_1,\left[{\tilde{z}}_1^P\right],\left[{\tilde{z}}_1^L\right]),N& =q_1+r_1,\hfill \end{array}$$

(77)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^T\right)}^{p_2},F_D^{\left(2\right)}(\alpha ,-p_2,-p_2,\gamma -2p_2,1,1),N& =2p_2,\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^P\right)}^{q_2},F_D^{\left(2\right)}(\alpha ,-q_2,-q_2,\gamma -2q_2,1-Z_2^P,1-\omega Z_2^P),N& =2q_2,\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^L\right)}^{r_2},F_D^{\left(2\right)}(\alpha ,-r_2,-r_2,\gamma -2r_2,1-Z_2^L,1-\omega Z_2^L),N& =2r_2.\hfill \end{array}$$

(80)

For $K=3$, there are 10 types of LSSA $({\omega }_1=-1,{\omega }_2=\frac{\left(-1+i\sqrt{3}\right)/2}{2})$

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-1}^P\right)}^{q_1}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(3\right)}(\alpha ,-p_1,-q_1,-r_1,\gamma -p_1-q_1-r_1,1,\left[{\tilde{z}}_1^P\right],\left[{\tilde{z}}_1^L\right]),N& =p_1+q_1+r_1,\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^T\right)}^{p_2}{\left({\alpha }_{-1}^P\right)}^{q_1},F_D^{\left(3\right)}(\alpha ,-p_2,-p_2,-q_1,\gamma -2p_2-q_1,1,1,\left[{\tilde{z}}_1^P\right]),N& =2p_2+q_1,\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^T\right)}^{p_2}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(3\right)}(\alpha ,-p_2,-p_2,-r_1,\gamma -2p_2-r_1,1,1,\left[{\tilde{z}}_1^L\right]),N& =2p_2+r_1,\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-2}^P\right)}^{q_2},F_D^{\left(3\right)}(\alpha ,-p_1,-q_2,-q_2,\gamma -2q_2-p_1,1,1-Z_2^P,1-{\omega }_1{Z}_2^P),N& =2q_2+p_1,\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-2}^P\right)}^{q_2}{\left({\alpha }_{-1}^L\right)}^{r_1},F_D^{\left(3\right)}(\alpha ,-q_2,-q_2,-r_1,\gamma -2q_2-r_1,1-Z_2^P,1-{\omega }_1{Z}_2^P,\left[{\tilde{z}}_1^L\right]),N& =2q_2+r_1,\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^T\right)}^{p_1}{\left({\alpha }_{-2}^L\right)}^{r_2},F_D^{\left(3\right)}(\alpha ,,-p_1,-r_2,-r_2,\gamma -2r_2-p_1,1,1-Z_2^L,1-{\omega }_1{Z}_2^L),N& =2r_2+p_1.\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-1}^P\right)}^{q_1}{\left({\alpha }_{-2}^L\right)}^{r_2},F_D^{\left(3\right)}(\alpha ,,-q_1,-r_2,-r_2,\gamma -2r_2-q_1,\left[{\tilde{z}}_1^P\right],1-Z_2^L,1-{\omega }_1{Z}_2^L),N& =2r_2+q_1.\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-3}^T\right)}^{p_3},F_D^{\left(3\right)}(\alpha ,-p_3,-p_3,-p_3,\gamma -3p_3,1,1,1),N& =3p_3,\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-3}^P\right)}^{q_3},F_D^{\left(3\right)}(\alpha ,-q_3,-q_3,-q_3,\gamma -3q_3,1-Z_3^P,1-{\omega }_2{Z}_3^P,1-{\omega }_2^2{Z}_3^P),N& =3q_3,\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill {\left({\alpha }_{-3}^L\right)}^{r_3},F_D^{\left(3\right)}(\alpha ,-r_3,-r_3,-r_3,\gamma -3r_3,1-Z_3^L,1-{\omega }_2{Z}_3^L,1-{\omega }_2^2{Z}_3^L),N& =3r_3.\hfill \end{array}$$

(90)

All the LSSAs for $K=2,3$ can be reduced through the recurrence relations in Equation (65) and expressed in terms of those of $K=1.$ Furthermore, all resulting LSSAs for $K=1$ can be further reduced by applying Equations (70) and (71) and finally expressed in terms of one single LSSA.

3.4. SL($K+3$,C) Symmetry and Recurrence Relations

In this subsection, we use the recurrence relations of the D-type $F_D^{\left(K\right)}\left(\alpha ;{\beta }_1,\dots ,{\beta }_K;\gamma ;x_1,\dots ,x_K\right)$ to reproduce the Cartan subalgebra and simple root system of $SL(K+3,\mathbb{C})$ with rank $K+2$. We first review the case of the $SL(4,\mathbb{C})$ symmetry group, and then extend it to the general case of $SL(K+3,\mathbb{C})$ Symmetry.

3.4.1. $SL(4,\mathbb{C})$ Symmetry

We first relate the $SL(4,\mathbb{C})$ group to the recurrence relations of $F_D^{\left(1\right)}\left(\alpha ;\beta ;\gamma ;x\right)$ or of the LSSA in Equation (32). For our purpose, there are $K+2=1+2=3$ recurrence relations among $F_D^{\left(1\right)}\left(\alpha ;\beta ;\gamma ;x\right)$ or Gauss hypergeometry functions

$$\begin{array}{cc}\hfill \left(\alpha -\beta \right)F_D^{\left(1\right)}-\alpha F_D^{\left(1\right)}\left(\alpha +1\right)+\beta F_D^{\left(1\right)}\left(\beta +1\right)& =0,\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill \gamma F_D^{\left(1\right)}-\left(\gamma -\alpha \right)F_D^{\left(1\right)}\left(\gamma +1\right)-\alpha F_D^{\left(1\right)}\left(\alpha +1;\gamma +1\right)& =0,\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill \gamma F_D^{\left(1\right)}+\gamma \left(x-1\right)F_D^{\left(1\right)}\left(\beta +1\right)-\left(\gamma -\alpha \right)x{F}_D^{\left(1\right)}\left(\beta +1;\gamma +1\right)& =0,\hfill \end{array}$$

(93)

which can be used to reproduce the Cartan subalgebra and simple root system of the $SL(4,\mathbb{C})$ group with rank 3.

With the identification in Equation (33), the first recurrence relation in Equation (91) can be rewritten as

$$\frac{\left(\alpha -\beta \right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)}{B\left(\gamma -\alpha ,\alpha \right)a^{\alpha }{b}^{\beta }{c}^{\gamma }}-\frac{\alpha f_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right)}{B\left(\gamma -\alpha -1,\alpha +1\right)a^{\alpha +1}{b}^{\beta }{c}^{\gamma }}+\frac{\beta f_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right)}{B\left(\gamma -\alpha ,\alpha \right)a^{\alpha }{b}^{\beta +1}{c}^{\gamma }}=0.$$

(94)

By using the identity

$$B\left(\gamma -\alpha -1,\alpha +1\right)=\frac{\Gamma \left(\gamma -\alpha -1\right)\Gamma \left(\alpha +1\right)}{\Gamma \left(\gamma \right)}=\frac{\alpha }{\gamma -\alpha -1}\frac{\Gamma \left(\gamma -\alpha \right)\Gamma \left(\alpha \right)}{\Gamma \left(\gamma \right)},$$

(95)

the recurrence relation then becomes

$$\left(\alpha -\beta \right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)-\frac{\gamma -\alpha -1}{a}{f}_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right)+\frac{\beta }{b}{f}_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right)=0,$$

(96)

or

$$\left(\alpha -\beta -\frac{E_{\alpha }}{a}+\frac{E_{\beta }}{b}\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0,$$

(97)

which means

$$\left[\alpha -\beta -\left(x{\partial }_x+a{\partial }_a\right)+\left(x{\partial }_x+b{\partial }_b\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0,$$

(98)

or

$$\left[\left(\alpha -J_{\alpha }\right)-\left(\beta -J_{\beta }\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0.$$

(99)

Similarly, for the second recurrence relation in Equation (92), we obtain

$$\left[c\left(\gamma -\beta \right)-E_{\gamma }+\frac{E_{\alpha \gamma }}{a}\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0.$$

(100)

which means

$$\left[\left(\gamma -c{\partial }_c\right)-\left(\beta -b{\partial }_b\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0,$$

(101)

or

$$\left[\left(\gamma -J_{\gamma }\right)-\left(\beta -J_{\beta }\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0.$$

(102)

Finally, the third recurrence relation in Equation (93) can be rewritten as

$$\left[b\beta +\left(x-1\right)E_{\beta }-\frac{x{E}_{\beta \gamma }}{c}\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0,$$

(103)

which gives after some computation

$$\left(\beta -J_{\beta }\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0.$$

(104)

It is easy to see that Equations (99), (102) and (104) imply the last three equations of Equation (36) or the Cartan subalgebra in Equation (37), as expected.

In addition to the Cartan subalgebra, we need to derive the operations of the $\{E_{\alpha },E_{\beta },E_{\gamma }\}$ from the recurrence relations. With the operations of Cartan subalgebra and $\{E_{\alpha },E_{\beta },E_{\gamma }\}$, one can reproduce the entirety of $SL(4,\mathbb{C})$ algebra.

We first use the operation of $E_{\alpha ,\beta }$ in Equation (36) to express Equation (91) in the following two ways:

$$\begin{array}{cc}\hfill \left(\alpha -\beta -\frac{E_a}{a}\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)+\frac{\beta }{b}{f}_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right)& =0,\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill \left(\alpha -\beta +\frac{E_{\beta }}{b}\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)-\frac{\left(\gamma -\alpha -1\right)}{a}{f}_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right)& =0,\hfill \end{array}$$

(106)

which, by using the definition of $E_{\alpha ,\beta }$ in Equation (35), become

$$\begin{array}{cc}\hfill \left(\alpha -\beta -\frac{a\left(x{\partial }_x+a{\partial }_a\right)}{a}\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =-\frac{\beta f_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right)}{b},\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill \left(\alpha -\beta +\frac{b\left(x{\partial }_x+b{\partial }_b\right)}{b}\right)f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =\frac{\left(\gamma -\alpha -1\right)f_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right)}{a},\hfill \end{array}$$

(108)

which in turn imply

$$\begin{array}{cc}\hfill \left[b\left(b{\partial }_b+x{\partial }_x\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =E_{\beta }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=\beta f_{ac}^b\left(\alpha ;\beta +1;\gamma ;x\right),\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill \left[a\left(a{\partial }_a+x{\partial }_x\right)\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)& =E_{\alpha }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=\left(\gamma -\alpha -1\right)f_{ac}^b\left(\alpha +1;\beta ;\gamma ;x\right),\hfill \end{array}$$

(110)

The above Equations (109) and (110) are consistent with the operation of $E_{\alpha ,\beta }$ in Equation (36).

Finally, we check the operation of $E_{\gamma }$. Note that Equation (92) can be written as

$$\frac{\gamma f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)}{B\left(\gamma -\alpha ,\alpha \right)a^{\alpha }{b}^{\beta }{c}^{\gamma }}-\frac{\left(\gamma -\alpha \right)f_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right)}{\frac{\left(\gamma -\alpha \right)}{\gamma }B\left(\gamma -\alpha ,\alpha \right)a^{\alpha }{b}^{\beta }{c}^{\gamma +1}}-\frac{\alpha f_{ac}^b\left(\alpha +1;\beta ;\gamma +1;x\right)}{\frac{\alpha }{\gamma }B\left(\gamma -\alpha ,\alpha \right)a^{\alpha +1}{b}^{\beta }{c}^{\gamma +1}}=0,$$

(111)

which gives

$$f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)-\frac{1}{c}{f}_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right)-\frac{1}{ac}{f}_{ac}^b\left(\alpha +1;\beta ;\gamma +1;x\right)=0.$$

(112)

Using the definition and operation of $E_{\alpha \gamma }$ in Equation (35), we obtain

$$f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)-\frac{1}{c}{f}_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right)-\frac{E_{\alpha \gamma }}{ac\left(\beta -\gamma \right)}{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=0,$$

which gives

$$f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)-\frac{ac\left[\left(1-x\right){\partial }_x-a{\partial }_a\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)}{ac\left(\beta -\gamma \right)}=\frac{f_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right)}{c}.$$

(113)

After some simple computation, we get

$$-c\left[b{\partial }_b-c{\partial }_c-\left(1-x\right){\partial }_x+a{\partial }_a\right]f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=E_{\gamma }{f}_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)=\left(\gamma -\beta \right)f_{ac}^b\left(\alpha ;\beta ;\gamma +1;x\right),$$

which is consistent with the operation of $E_{\gamma }$ in Equation (36).

Thus, we have shown that the extended LSSAs $f_{ac}^b\left(\alpha ;\beta ;\gamma ;x\right)$ in Equation (33) with arbitrary a and c form an infinite-dimensional representation of the $SL(4,\mathbb{C})$ group. Moreover, the 3 recurrence relations among the LSSAs can be used to reproduce the Cartan subalgebra and simple root system of the $SL(4,\mathbb{C})$ group with rank 3. The recurrence relations are thus equivalent to the representation of the $SL(4,\mathbb{C})$ symmetry group.

3.4.2. $SL(K+3,\mathbb{C})$ Symmetry

The $K+2$ fundamental recurrence relations among $F_D^{\left(K\right)}\left(\alpha ;\beta ;\gamma ;x\right)$ or the Lauricella functions are listed in Equations (60)–(62). In the following, we show that the three types of recurrence relations above imply the Cartan subalgebra of the $SL(K+3,\mathbb{C})$ group with rank $K+2$.

With the identification in Equation (39), the first type of recurrence relation in Equation (60) can be rewritten as

$$\left(\alpha -\sum _j{\beta }_j\right)f_{ac}^{b_1\dots b_K}-\frac{E^{\alpha }{f}_{ac}^{b_1\dots b_K}\left(\alpha \right)}{a}+{\displaystyle \sum }_j\frac{E^{{\beta }_j}{f}_{ac}^{b_1\dots b_K}\left({\beta }_j\right)}{b_j}=0,$$

(114)

which gives

$$\left(\alpha -\sum _j{\beta }_j\right)f_{ac}^{b_1\dots b_K}-\left({\displaystyle \sum }_j{x}_j{\partial }_j+a{\partial }_a\right)f_{ac}^{b_1\dots b_K}+{\displaystyle \sum }_j\left(x_j{\partial }_j+b_j{\partial }_{b_j}\right)f_{ac}^{b_1\dots b_K}=0$$

(115)

or

$$\left[\left(\alpha -a{\partial }_a\right)+\sum _j\left({\beta }_j-b_j{\partial }_{b_j}\right)\right]f_{ac}^{b_1\dots b_K}=0,$$

(116)

which means

$$\left[\left(\alpha -J_{\alpha }\right)+\sum _j\left({\beta }_j-J_{{\beta }_j}\right)\right]f_{ac}^{b_1\dots b_K}=0.$$

(117)

The second type of recurrence relation in Equation (61) can be rewritten as

$$f_{ac}^{b_1\dots b_K}-\frac{E^{\gamma }{f}_{ac}^{b_1\dots b_K}\left(\gamma \right)}{c\left(\gamma -{\displaystyle \sum }_j{\beta }_j\right)}-\frac{E^{\alpha \gamma }{f}_{ac}^{b_1\dots b_K}\left(\alpha ;\gamma \right)}{ac\left({\displaystyle \sum }_j{\beta }_j-\gamma \right)}=0,$$

(118)

which gives

$$\left[\gamma -{\displaystyle \sum }_j{\beta }_j-\left({\displaystyle \sum }_j\left(1-x_j\right){\partial }_{x_j}+c{\partial }_c-a{\partial }_a-{\displaystyle \sum }_j{b}_j{\partial }_{b_j}\right)+\left({\displaystyle \sum }_j\left(1-x_j\right){\partial }_{x_j}-a{\partial }_a\right)\right]f_{ac}^{b_1\dots b_K}=0$$

(119)

or

$$\left[\left(\gamma -c{\partial }_c\right)-{\displaystyle \sum }_j\left({\beta }_j-b_j{\partial }_{b_j}\right)\right]f_{ac}^{b_1\dots b_K}=0.$$

(120)

Equation (120) can be written as

$$\left[\left(\gamma -J_{\gamma }\right)-{\displaystyle \sum }_j\left({\beta }_j-J_{{\beta }_j}\right)\right]f_{ac}^{b_1\dots b_K}=0.$$

(121)

The third type of recurrence relation in Equation (62) can be rewritten as ($m=1,2,\dots K$)

$$f_{ac}^{b_1\dots b_K}+\frac{(x_m-1)E^{{\beta }_m}{f}_{ac}^{b_1\dots b_K}}{b_m{\beta }_m}-\frac{x_m{E}^{{\beta }_m\gamma }{f}_{ac}^{b_1\dots b_K}}{b_{m}c{\beta }_m}=0,$$

(122)

which gives

$${\beta }_m{f}_{ac}^{b_1\dots b_K}+(x_m-1)\left(x_m{\partial }_m+b_m{\partial }_{b_m}\right)f_{ac}^{b_1\dots b_K}-x_m\left[\left(x_m-1\right){\partial }_{x_m}+b_m{\partial }_{b_m}\right]f_{ac}^{b_1\dots b_K}=0$$

(123)

or

$$\left({\beta }_m-b_m{\partial }_{b_m}\right)f_{ac}^{b_1\dots b_K}=0.$$

(124)

In the above calculation, we have used the definition and operation of $E^{{\beta }_m\gamma }$ in Equation (41) and Equation (42), respectively.

Equation (124) can be written as

$$\left({\beta }_m-J_{{\beta }_m}\right)f_{ac}^{b_1\dots b_K}=0,m=1,2,\dots K.$$

(125)

It is important to see that Equations (117), (121) and (125) imply the last three equations of Equation (42) or the Cartan subalgebra of $SL(K+3,\mathbb{C})$ as expected.

In addition to the Cartan subalgebra, we need to derive the operations of the $\{E^{\alpha },E^{{\beta }_k},E^{\gamma }\}$ from the recurrence relations. With the operations of Cartan subalgebra and $\{E^{\alpha },E^{{\beta }_k},E^{\gamma }\}$, one can reproduce the whole $SL(K+3,\mathbb{C})$ algebra. The calculations of $E^{\alpha }$ and $E^{\gamma }$ are straightforward and are similar to the case of $SL(4,\mathbb{C})$ in the previous section. Here, we present only the calculation of $E^{{\beta }_k}$. The recurrence relation in Equation (60) can be rewritten as

$$\left(\alpha -\sum _j{\beta }_j\right)f_{ac}^{b_1\dots b_K}-\frac{E^{\alpha }{f}_{ac}^{b_1\dots b_K}\left(\alpha \right)}{a}+{\displaystyle \sum }_{j\ne k}\frac{E^{{\beta }_j}{f}_{ac}^{b_1\dots b_K}\left({\beta }_j\right)}{b_j}+\frac{{\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1\right)}{b_k}=0.$$

(126)

After the operation of $E^{{\beta }_j}$, we obtain

$$\left(\alpha -\sum _j{\beta }_j\right)f_{ac}^{b_1\dots b_K}-\left({\displaystyle \sum }_j{x}_j{\partial }_j+a{\partial }_a\right)f_{ac}^{b_1\dots b_K}+{\displaystyle \sum }_{j\ne k}\left(x_j{\partial }_j+b_j{\partial }_{b_j}\right)f_{ac}^{b_1\dots b_K}=\frac{-{\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1\right)}{b_k},$$

which gives the consistent result

$$b_k\left(b_k{\partial }_{b_k}+x_k{\partial }_k\right)f_{ac}^{b_1\dots b_K}\left({\beta }_k\right)=E^{{\beta }_k}{f}_{ac}^{b_1\dots b_K}={\beta }_k{f}_{ac}^{b_1\dots b_K}\left({\beta }_k+1\right),k=1,2,\dots K.$$

(127)

In the above calculation, we have used the definitions and operations of $E^{{\beta }_k}$ and $E^{\alpha }$ in Equation (41) and Equation (42), respectively.

The $K+2$ equations in Equations (117), (121) and (125) together with $K+2$ equations for the operations $\{E^{\alpha },E^{{\beta }_k},E^{\gamma }\}$ are equivalent to the Cartan subalgebra and the simple root system of $SL(K+3,\mathbb{C})$ with rank $K+2.$ With the Cartan subalgebra and the simple roots, one can easily write the whole Lie algebra of the $SL(K+3,\mathbb{C})$ group. Thus, one can construct the Lie algebra from the recurrence relations and vice versa.

In the previous subsections, it was shown that [47] the $K+2$ recurrence relations among $F_D^{\left(K\right)}$ can be used to derive recurrence relations among LSSAs and reduce the number of independent LSSAs from ∞ down to 1. We conclude that the $SL(K+3,\mathbb{C})$ group can be used to derive an infinite number of recurrence relations among LSSAs, and one can solve all the LSSA sand express them in terms of one amplitude.

3.5. Lauricella Zero Norm States and Ward Identities

In addition to the recurrence relations among LSSAs, there are on-shell stringy Ward identities among LSSAs. These Ward identities can be derived from the decoupling of two types of zero norm states (ZNS) in the old covariant first quantized string spectrum. However, we show below that these Lauricella zero norm states (LZNS) or the corresponding Lauricella Ward identities are not good enough to solve all the LSSAs and express them in terms of one amplitude.

On the other hand, in the last section, we have shown that by using (A) recurrence relations of the LSSAs, (B) the multiplication theorem of the Gauss hypergeometry function and (C) the explicit calculation of four tachyon amplitudes, one can explicitly solve and calculate all LSSAs. This means that the solvability of LSSAs through the calculations of (A), (B) and (C) implies the validity of Ward identities. Ward identities cannot be independent of the recurrence relations used in the last section; otherwise, there will be a contradiction with the solvability of LSSAs.

In this section, we study some examples of Ward identities of LSSAs from this point of view. Incidentally, high-energy zero norm states (HZNS) [10,12,13,14,15,16] and the corresponding stringy Ward identities at the fixed angle regime, Regge zero norm states (RZNS) [41,42] and the corresponding Regge Ward identities at the Regge regime have been studied previously. In particular, HZNS at the fixed angle regime can be used to solve all the high energy SSAs [10,12,13,14,15,16].

3.5.1. The Lauricella Zero Norm States

We consider the set of Ward identities of the LSSA with three tachyons and one arbitrary string state. Thus, we only need to consider polarizations of the tensor states on the scattering plane since the amplitudes with polarizations orthogonal to the scattering plane vanish.

There are two types of zero norm states (ZNS) in the old covariant first quantum string spectrum:

$$\begin{array}{cc}\hfill \mathrm{Type}\mathrm{I}& :L_{-1}\left|x\right.〉,\mathrm{where}{L}_1\left|x\right.〉=L_2\left|x\right.〉=0,L_0\left|x\right.〉=0;\hfill \end{array}$$

(128)

$$\begin{array}{cc}\hfill \mathrm{Type}\mathrm{II}& :\left(L_{-2}+\frac{3}{2}{L}_{-1}^2\right)\left|\tilde{x}\right.〉,\mathrm{where}{L}_1\left|\tilde{x}\right.〉=L_2\left|\tilde{x}\right.〉=0,(L_0+1)\left|\tilde{x}\right.〉=0.\hfill \end{array}$$

(129)

While type I ZNS exists at any spacetime dimension, type II ZNS only exists at $D=26$.

We begin with the case of mass level $M^2=2$. There is a type II ZNS

$$\left[\frac{1}{2}{\alpha }_{-1}·{\alpha }_{-1}+\frac{5}{2}k·{\alpha }_{-2}+\frac{3}{2}{(k·{\alpha }_{-1})}^2\right]\left|0,k\right.〉,$$

(130)

and a type I ZNS

$$[\theta ·{\alpha }_{-2}+(k·{\alpha }_{-1})(\theta ·{\alpha }_{-1})]\left|0,k\right.〉,\theta ·k=0.$$

(131)

The three polarizations defined in Equations (5)–(7) of the second tensor state with momentum $k_2$ on the scattering plane satisfy the completeness relation

$${\eta }_{\mu \nu }=\sum _{\alpha ,\beta }{e}_{\mu }^{\alpha }{e}_{\nu }^{\beta }{\eta }_{\alpha \beta }=diag(-1,1,1)$$

(132)

where $\mu ,\nu =0,1,2$ and $\alpha ,\beta =P,L,T$. And ${\alpha }_{-1}^T={\sum }_{\mu }{e}_{\mu }^T{\alpha }_{-1}^{\mu }$, ${\alpha }_{-1}^T{\alpha }_{-2}^L={\sum }_{\mu ,\nu }{e}_{\mu }^T{e}_{\nu }^L{\alpha }_{-1}^{\mu }{\alpha }_{-2}^{\nu }$ etc.

The type II ZNS in Equation (130) gives the LZNS

$$\left(\sqrt{2}{\alpha }_{-2}^P+{\alpha }_{-1}^P{\alpha }_{-1}^P+\frac{1}{5}{\alpha }_{-1}^L{\alpha }_{-1}^L+\frac{1}{5}{\alpha }_{-1}^T{\alpha }_{-1}^T\right)|0,k\rangle .$$

(133)

The type I ZNS in Equation (131) gives two LZNSs:

$$({\alpha }_{-2}^T+\sqrt{2}{\alpha }_{-1}^P{\alpha }_{-1}^T)|0,k\rangle ,$$

(134)

$$({\alpha }_{-2}^L+\sqrt{2}{\alpha }_{-1}^P{\alpha }_{-1}^L)|0,k\rangle .$$

(135)

where ${\alpha }_{-1}^T={\sum }_{\mu }{e}_{\mu }^T{\alpha }_{-1}^{\mu }$, ${\alpha }_{-1}^T{\alpha }_{-2}^L={\sum }_{\mu ,\nu }{e}_{\mu }^T{e}_{\nu }^L{\alpha }_{-1}^{\mu }{\alpha }_{-2}^{\nu }$ etc. The LZNSs in Equations (134) and (135) correspond to choosing ${\theta }^{\mu }=e^T$ and ${\theta }^{\mu }=e^L$, respectively. In conclusion, there are 3 LZNSs at the mass level $M^2=2$.

At the second massive level $M^2=4,$ there is a type I scalar ZNS,

$$\left[\frac{17}{4}{(k·{\alpha }_{-1})}^3+\frac{9}{2}(k·{\alpha }_{-1})({\alpha }_{-1}·{\alpha }_{-1})+9({\alpha }_{-1}·{\alpha }_{-2})+21(k·{\alpha }_{-1})(k·{\alpha }_{-2})+25(k·{\alpha }_{-3})\right]\left|0,k\right.〉,$$

(136)

a symmetric type I spin two ZNS,

$$[2{\theta }_{\mu \nu }{\alpha }_{-1}^{(\mu }{\alpha }_{-2}^{\nu )}+k_{\lambda }{\theta }_{\mu \nu }{\alpha }_{-1}^{\lambda \mu \nu }]\left|0,k\right.〉,k·\theta ={\eta }^{\mu \nu }{\theta }_{\mu \nu }=0,{\theta }_{\mu \nu }={\theta }_{\nu \mu },$$

(137)

where ${\alpha }_{-1}^{\lambda \mu \nu }\equiv {\alpha }_{-1}^{\lambda }{\alpha }_{-1}^{\mu }{\alpha }_{-1}^{\nu }$, and two vector ZNSs,

$$\begin{array}{cc}\hfill \left[\left(\frac{5}{2}{k}_{\mu }{k}_{\nu }{\theta }_{\lambda }^{\prime }+{\eta }_{\mu \nu }{\theta }_{\lambda }^{\prime }\right){\mathcal{\alpha }}_{-1}^{\left(\mu \nu \lambda \right)}+9k_{\mu }{\theta }_{\nu }^{\prime }{\mathcal{\alpha }}_{-1}^{\left(\mu \nu \right)}+6{\theta }_{\mu }^{\prime }{\mathcal{\alpha }}_{-1}^{\mu }\right]\left|0,k\right.〉,\theta ·k& =0,\hfill \end{array}$$

(138)

$$\begin{array}{cc}\hfill \left[\left(\frac{1}{2}{k}_{\mu }{k}_{\nu }{\theta }_{\lambda }+2{\eta }_{\mu \nu }{\theta }_{\lambda }\right){\mathcal{\alpha }}_{-1}^{\left(\mu \nu \lambda \right)}+9k_{\mu }{\theta }_{\nu }{\mathcal{\alpha }}_{-1}^{\left[\mu \nu \right]}-6{\theta }_{\mu }{\mathcal{\alpha }}_{-1}^{\mu }\right]\left|0,k\right.〉,\theta ·k& =0.\hfill \end{array}$$

(139)

Note that Equations (138) and (139) are linear combinations of a type I and a type II ZNS. This completes the four ZNSs at the second massive level $M^2=$ 4.

The scalar ZNS in Equation (136) gives the LZNS

$$\left[25{\left({\alpha }_{-1}^P\right)}^3+9{\alpha }_{-1}^P{\left({\alpha }_{-1}^L\right)}^2+9{\alpha }_{-1}^P{\left({\alpha }_{-1}^T\right)}^2+9{\alpha }_{-2}^L{\alpha }_{-1}^L+9{\alpha }_{-2}^T{\alpha }_{-1}^T+75{\alpha }_{-2}^P{\alpha }_{-1}^P+50{\alpha }_{-3}^P\right]\left|0,k\right.〉.$$

(140)

For the two type I spin ZN7 in Equation (137), we define

$${\theta }_{\mu \nu }=\sum _{\alpha ,\beta }{e}_{\mu }^{\alpha }{e}_{\nu }^{\beta }{u}_{\alpha \beta }.$$

(141)

The transverse and traceless conditions on ${\theta }_{\mu \nu }$ then imply

$$u_{PP}=u_{PL}=u_{PT}=0\mathrm{and}{u}_{PP}-u_{LL}-u_{TT}=0,$$

(142)

which gives two LZNSs:

$$\begin{array}{cc}\hfill ({\alpha }_{-1}^L{\alpha }_{-2}^L+{\alpha }_{-1}^P{\alpha }_{-1}^L{\alpha }_{-1}^L-{\alpha }_{-1}^T{\alpha }_{-2}^T-{\alpha }_{-1}^P{\alpha }_{-1}^T{\alpha }_{-1}^T)|0,k\rangle & ,\hfill \end{array}$$

(143)

$$\begin{array}{cc}\hfill ({\alpha }_{-1}^{(L}{\alpha }_{-2}^{T)}+{\alpha }_{-1}^P{\alpha }_{-1}^L{\alpha }_{-1}^T)|0,k\rangle & .\hfill \end{array}$$

(144)

The vector ZNS in Equation (138) gives two LZNSs:

$$[6{\alpha }_{-3}^T+18{\alpha }_{-1}^{(P}{\alpha }_{-2}^{T)}+9{\alpha }_{-1}^P{\alpha }_{-1}^P{\alpha }_{-1}^T+{\alpha }_{-1}^L{\alpha }_{-1}^L{\alpha }_{-1}^T+{\alpha }_{-1}^T{\alpha }_{-1}^T{\alpha }_{-1}^T]|0,k\rangle ,$$

(145)

$$[6{\alpha }_{-3}^L+18{\alpha }_{-1}^{(P}{\alpha }_{-2}^{L)}+9{\alpha }_{-1}^P{\alpha }_{-1}^P{\alpha }_{-1}^L+{\alpha }_{-1}^L{\alpha }_{-1}^L{\alpha }_{-1}^L+{\alpha }_{-1}^L{\alpha }_{-1}^T{\alpha }_{-1}^T]|0,k\rangle .$$

(146)

The vector ZNS in Equation (139) gives two LZNS:

$$[3{\alpha }_{-3}^T-9{\alpha }_{-1}^{[P}{\alpha }_{-2}^{T]}-{\alpha }_{-1}^L{\alpha }_{-1}^L{\alpha }_{-1}^T-{\alpha }_{-1}^T{\alpha }_{-1}^T{\alpha }_{-1}^T]|0,k\rangle ,$$

(147)

$$[3{\alpha }_{-3}^L-9{\alpha }_{-1}^{[P}{\alpha }_{-2}^{L]}-{\alpha }_{-1}^L{\alpha }_{-1}^L{\alpha }_{-1}^L-{\alpha }_{-1}^L{\alpha }_{-1}^T{\alpha }_{-1}^T]|0,k\rangle .$$

(148)

In conclusion, there are seven LZNSs in total at the mass level $M^2=4$.

It is important to note that there are nine LSSAs at mass level $M^2=2$ with only three LZNSs, and 22 LSSAs at mass level $M^2=4$ with only seven LZNSs. Thus, in contrast to the recurrence relations calculated in Equations (65) and (69), these Ward identities are not enough to solve all the LSSAs and express them in terms of one amplitude.

3.5.2. The Lauricella Ward Identities

In this subsection, we explicitly verify some examples of Ward identities through processes (A), (B) and (C). Process (C) is implicitly used through the kinematics. Ward identities cannot be independent of the recurrence relations used in processes (A), (B) and (C) in the last section.

For $M^2=2$, we define the following kinematics variables:

$$\begin{array}{cc}\hfill \alpha & =\frac{-t}{2}-1=M{k}_3^P-N+1=\sqrt{2}{k}_3^P-1,\hfill \end{array}$$

(149)

$$\begin{array}{cc}\hfill \gamma & =\frac{s}{2}+2-N=-M{k}_1^P=-\sqrt{2}{k}_1^P,\hfill \end{array}$$

(150)

$$\begin{array}{cc}\hfill d& ={\left(\frac{-k_1^L}{k_3^L}\right)}^{\frac{1}{2}},1-\left(\frac{-k_1^P}{k_3^P}\right)=\frac{\alpha -\gamma +1}{\alpha +1},\hfill \end{array}$$

(151)

then

$$\frac{u}{2}+2-N=\alpha -\gamma +1-N=\alpha -\gamma -1.$$

(152)

As examples, we calculate the Ward identities associated with the LZNSs in Equations (134) and (135). The calculation is based on processes (A) and (B). By using Equation (10), the Ward identities we want to prove are

$$\begin{array}{cc}\hfill \left(-k_3^T\right)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;1-{\left(\frac{-k_1^T}{k_3^T}\right)}^{\frac{1}{2}},1+{\left(\frac{-k_1^T}{k_3^T}\right)}^{\frac{1}{2}}\right)& \hfill \\ \hfill +\sqrt{2}\left(-k_3^P\right)\left(-k_3^T\right)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;1-\left(\frac{-k_1^P}{k_3^P}\right),1-\left(\frac{-k_1^T}{k_3^T}\right)\right)& =0,\hfill \end{array}$$

(153)

$$\begin{array}{cc}\hfill \left(-k_3^L\right)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;1-{\left(\frac{-k_1^L}{k_3^L}\right)}^{\frac{1}{2}},1+{\left(\frac{-k_1^L}{k_3^L}\right)}^{\frac{1}{2}}\right)& \hfill \\ \hfill +\sqrt{2}\left(-k_3^P\right)\left(-k_3^L\right)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;1-\left(\frac{-k_1^P}{k_3^P}\right),1-\left(\frac{-k_1^L}{k_3^L}\right)\right)& =0\hfill \end{array}$$

(154)

or, using the kinematics variables just defined,

$$\begin{array}{cc}\hfill F_D^{\left(2\right)}(a;-1,-1;\alpha -\gamma -1;1,1)-(\alpha +1)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;\frac{\alpha -\gamma +1}{\alpha +1},1\right)& =0,\hfill \end{array}$$

(155)

$$\begin{array}{cc}\hfill F_D^{\left(2\right)}(\alpha ;-1,-1;\alpha -\gamma -1;1-d,1+d)-(\alpha +1)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;\frac{\alpha -\gamma +1}{\alpha +1},1-d^2\right)& =0.\hfill \end{array}$$

(156)

Equations (155) and (156) can be explicitly proved as

$$\begin{array}{c}{F}_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;1,1\right)-(\alpha +1)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;\frac{\alpha -\gamma +1}{\alpha +1},1\right)\hfill \\ =F_D^{\left(1\right)}\left(\alpha ;-2;\alpha -\gamma -1;1\right)-(\alpha +1)\left[\begin{array}{c}\frac{\alpha -\gamma +1}{\alpha +1}{F}_D^{\left(1\right)}\left(\alpha ;-2;\alpha -\gamma -1;1\right)\hfill \\ +\frac{\gamma }{\alpha +1}{F}_D^{\left(1\right)}\left(\alpha ;-1;\alpha -\gamma -1;1\right)\hfill \end{array}\right]\hfill \end{array}$$

(157)

$$\begin{array}{c}\left(\gamma -\alpha \right)F_D^{\left(1\right)}\left(\alpha ;-2;\alpha -\gamma -1;1\right)-\gamma F_D^{\left(1\right)}\left(\alpha ;-1;\alpha -\gamma -1;1\right)\hfill \\ =0\hfill \end{array}$$

(158)

and

$$\begin{array}{c}{F}_D^{\left(2\right)}(\alpha ;-1,-1;\alpha -\gamma -1;1-d,1+d)-(\alpha +1)F_D^{\left(2\right)}\left(\alpha ;-1,-1;\alpha -\gamma -1;\frac{\alpha -\gamma +1}{\alpha +1},1-d^2\right)\hfill \\ =\frac{1-d}{1+d}{F}_D^{\left(1\right)}(\alpha ;-2;\alpha -\gamma -1;1+d)-\frac{2d}{1+d}{F}_D^{\left(1\right)}(\alpha ;-1;\alpha -\gamma -1,1+d)\hfill \\ -(\alpha +1)\left[\begin{array}{c}\frac{\alpha -\gamma +1}{(\alpha +1)(1-d^2)}{F}_D^{\left(1\right)}\left(\alpha ;-2;\alpha -\gamma -1;1-d^2\right)\\ +\left(\frac{\alpha -\gamma +1}{(\alpha +1)(1-d^2)}-(1-d)\right)F_D^{\left(1\right)}(\alpha ;-1;\alpha -\gamma -1;1-d^2)\end{array}\right]\hfill \end{array}$$

(159)

$$\begin{array}{cc}\hfill & =\frac{1-d}{1+d}\left(1-\frac{2\alpha d}{\gamma -1}+\frac{\alpha {(\alpha +1)}^2}{(\gamma -1)(\gamma -2)}\right)F_D^{\left(1\right)}(\alpha ;-2;\alpha -\gamma -1;1)\hfill \\ \hfill & -\frac{2d}{1+d}\left(1-\frac{\alpha d}{\gamma }\right)F_D^{\left(1\right)}(\alpha ;-1;\alpha -\gamma -1;1)\hfill \end{array}$$

(160)

$$\begin{array}{cc}\hfill & -(\alpha +1)\left[\begin{array}{c}\frac{\alpha -\gamma +1}{(\alpha +1)(1-d^2)}\left(1+\frac{2\alpha d^2}{\gamma -1}+\frac{\alpha (\alpha +1)d^4}{(\gamma -1)(\gamma -2)}\right)F_D^{\left(1\right)}(\alpha ;-2;\alpha -\gamma -1;1)\\ +\left(\frac{\alpha -\gamma +1}{(\alpha +1)(1-d^2)}-(1-d)\right)\left(1+\frac{\alpha d^2}{\gamma }\right)F_D^{\left(1\right)}(\alpha ;-1;\alpha -\gamma -1;1)\end{array}\right]=0,\hfill \end{array}$$

(161)

where we used Equation (65) in process (A) to get Equations (157) and (159) and Equation (70) in process (B) to get Equation (160). The last last lines of the above equations were obtained by using Equation (71).

3.6. Summary

In this section, we have shown that there is an infinite number of recurrence relations valid for all energies among the LSSA of three tachyons and one arbitrary string state. Moreover, this infinite number of recurrence relations can be used to solve all the LSSAs and express them in terms of one single four tachyon amplitude. In addition, we find that the $K+2$ recurrence relations among the LSSA can be used to reproduce the Cartan subalgebra and simple root system of the $SL(K+3,\mathbb{C})$ group with rank $K+2$. Thus, the recurrence relations are equivalent to the representation of $SL(K+3,\mathbb{C})$ group of the LSSA. As a result, the $SL(K+3,\mathbb{C})$ group can be used to solve all LSSAs and express them in terms of one amplitude [47].

We have also shown that, for the first few mass levels, the solvability of LSSAs through the calculations of recurrence relations implies the validity of Ward identities derived from the decoupling of LZNS. However, the Lauricella Ward identities are not good enough to solve all the LSSAs and express them in terms of one amplitude.

4. Relations among LSSAs in Various Scattering Limits

In this section, we show that there exist relations or symmetries among SSAs of different string states at various scattering limits. In the first subsection, we show that the linear relations [1,2,3,4,5] conjectured by Gross among the hard SSAs (HSSAs) at each fixed mass level in the hard scattering limit can be rederived from the LSSA. These relations reduce the number of independent HSSAs from ∞ down to 1.

In the second subsection, we show that the Regge SSA (RSSA) in the Regge scattering limit can be rederived from the LSSA. All the RSSAs can be expressed in terms of the Appell functions with associated $SL(5,\mathbb{C})$ symmetry [40,41,42]. Moreover, the recurrence relations of the Appell functions can be used to reduce the number of independent RSSAs from ∞ down to 1.

Finally, in the nonrelativistic scattering limit, we show that the nonrelativistic SSAs (NSSAs) and various extended recurrence relations among them an be rederived from the LSSA. In addition, we also derive the nonrelativistic level $M_2$-dependent string BCJ relations, which are the stringy generalization of the massless field theory BCJ relation [48] to the higher spin stringy particles. These NSSAs can be expressed in terms of the Gauss hypergeometry functions with associated $SL(4,\mathbb{C})$ symmetry [40,41,42].

4.1. Hard Scattering Limit—Proving the Gross Conjecture from LSSAs

In this subsection, we show that the linear relations conjectured by Gross [1,2,3,4,5] in the hard scattering limit can be rederived from the LSSA. First, we briefly review the results discussed in [17,18] for the linear relations among HSSAs. It was first observed that for each fixed mass level N with $M^2=2(N-1)$, the following states are of a leading order in energy at the hard scattering limit [14,15]

$$\left|N,2m,q\right.〉\equiv {\left({\alpha }_{-1}^T\right)}^{N-2m-2q}{\left({\alpha }_{-1}^L\right)}^{2m}{\left({\alpha }_{-2}^L\right)}^q|0,k\rangle .$$

(162)

Note that in Equation (162), only even powers $2m$ in ${\alpha }_{-1}^L$ [10,11,12] survive, and the naive energy order of the amplitudes will drop by an even number of energy powers in general. The HSSAs with vertices corresponding to states with an odd power in ${\left({\alpha }_{-1}^L\right)}^{2m+1}$ turn out to be of a subleading order in energy and can be ignored. By using the stringy Ward identities or the decoupling of two types of zero norm states (ZNSs) in the hard scattering limit, the linear relations among HSSAs of different string states at each fixed mass level N were calculated to be [14,15]

$$\frac{A_{st}^{(N,2m,q)}}{A_{st}^{(N,0,0)}}={\left(-\frac{1}{M}\right)}^{2m+q}{\left(\frac{1}{2}\right)}^{m+q}(2m-1)!!.$$

(163)

Exactly the same result can be obtained by using two other techniques: the Virasoro constraint calculation and the corrected saddle-point calculation [14,15]. The calculation of of Equation (163) was first done for one high-energy vertex in Equation (162) and could then be easily generalized to four high-energy vertices. In the decoupling of ZNS calculations at the mass level $M^2=4$, for example, there are four leading order HSSAs [10,12]

$$A_{TTT}:A_{LLT}:A_{\left(LT\right)}:A_{\left[LT\right]}=8:1:-1:-1$$

(164)

which are proportional to each other. However. the saddle point calculation of [5] gave $A_{TTT}\propto A_{\left[LT\right]},$ and $A_{LLT}=0$, which are inconsistent with the decoupling of ZNS or unitarity of the theory. Indeed, a sample calculation was done [10,12] to explicitly verify the ratios in Equation (164).

One interesting application of Equation (163) was the derivation of the ratio between $A_{st}^{(N,2m,q)}$ and $A_{tu}^{(N,2m,q)}$ in the hard scattering limit [36]

$$A_{st}^{(N,2m,q)}\simeq {(-)}^N\frac{sin(\pi k_2·k_4)}{sin(\pi k_1·k_2)}{A}_{tu}^{(N,2m,q)}$$

(165)

where $A_{tu}^{(N,2m,q)}$ is the corresponding $(t,u)$ channel HSSA.

Equation (165) was shown to be valid for scatterings of four arbitrary string states in the hard scattering limit and was obtained in 2006. This result was obtained earlier than the discovery of four-point field theory BCJ relations in [48] and “string BCJ relations” in Equation (19) [37,38,39]. In contrast to the the calculation of string BCJ relations in [38,39], which was motivated by the field theory BCJ relations in [48], the result of Equation (165) was inspired by the calculation of hard closed SSAs [36] by using the KLT relation [49]. More detailed discussion can be found in [18,36].

Thus, we are ready to rederive Equations (162) and (163) from the LSSA in Equation (10). The relevant kinematics are

$$\begin{array}{cc}\hfill k_1^T& =0,k_3^T\simeq -Esin\varphi ,\hfill \end{array}$$

(166)

$$\begin{array}{cc}\hfill k_1^L& \simeq -\frac{2p^2}{M_2}\simeq -\frac{2E^2}{M_2},\hfill \end{array}$$

(167)

$$\begin{array}{cc}\hfill k_3^L& \simeq \frac{2E^2}{M_2}{sin}^2\frac{\varphi }{2}.\hfill \end{array}$$

(168)

where E and $\varphi$ are the CM frame energy and scattering angle, respectively. One can calculate

$${\tilde{z}}_{k{k}^{\prime }}^T=1,{\tilde{z}}_{k{k}^{\prime }}^L=1-{\left(-\frac{s}{t}\right)}^{1/k}{e}^{\frac{i2\pi k^{\prime }}{k}}\sim O\left(1\right).$$

(169)

The LSSA in Equation (10) reduces to

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_l^L)}=B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\hfill \\ \hfill & ·\prod _{n=1}{\left[(n-1)!Esin\varphi \right]}^{r_n^T}\prod _{l=1}{\left[-(l-1)!\frac{2E^2}{M_2}{sin}^2\frac{\varphi }{2}\right]}^{r_l^L}\hfill \\ \hfill & ·F_D^{\left(K\right)}\left(-\frac{t}{2}-1;R_n^T,R_l^L;\frac{u}{2}+2-N;{\left(1\right)}_n,{\tilde{Z}}_l^L\right).\hfill \end{array}$$

(170)

As mentioned above, in the hard scattering limit, there was a difference between the naive energy order and the real energy order corresponding to the ${\left({\alpha }_{-1}^L\right)}^{r_1^L}$ operator in Equation (9). Thus, it is important to pay attention to the corresponding summation and write

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_l^L)}=B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\hfill \\ \hfill & ·\prod _{n=1}{\left[(n-1)!Esin\varphi \right]}^{r_n^T}\prod _{l=1}{\left[-(l-1)!\frac{2E^2}{M_2}{sin}^2\frac{\varphi }{2}\right]}^{r_l^L}\hfill \\ \hfill & ·\sum _{k_r}\frac{{\left(-\frac{t}{2}-1\right)}_{k_r}}{{\left(\frac{u}{2}+2-N\right)}_{k_r}}\frac{{\left(-r_1^L\right)}_{k_r}}{k_r!}{\left(1+\frac{s}{t}\right)}^{k_r}·\left(\dots \right)\hfill \end{array}$$

(171)

where ${\left(a\right)}_{n+m}={\left(a\right)}_n{\left(a+n\right)}_m$ and $\left(\dots \right)$ are terms which are not relevant to the following discussion. We then propose the following formula:

$$\begin{array}{cc}\hfill & \sum _{k_r=0}^{r_1^L}\frac{{\left(-\frac{t}{2}-1\right)}_{k_r}}{{\left(\frac{u}{2}+2-N\right)}_{k_r}}\frac{{\left(-r_1^L\right)}_{k_r}}{k_r!}{\left(1+\frac{s}{t}\right)}^{k_r}\hfill \\ \hfill =& 0·{\left(\frac{tu}{s}\right)}^0+0·{\left(\frac{tu}{s}\right)}^{-1}+\dots +0·{\left(\frac{tu}{s}\right)}^{-\left[\frac{r_1^L+1}{2}\right]-1}\hfill \\ \hfill & +C_{r_1^L}{\left(\frac{tu}{s}\right)}^{-\left[\frac{r_1^L+1}{2}\right]}+\mathit{O}\left\{{\left(\frac{tu}{s}\right)}^{-\left[\frac{r_1^L+1}{2}\right]+1}\right\}.\hfill \end{array}$$

(172)

where [] stands for the Gauss symbol, $C_{r_1^L}$ is independent of energy E and depends on $r_1^L$ and possibly the scattering angle $\varphi$. When $r_1^L=2m$ is an even number, we further propose that $C_{r_1^L}=\frac{\left(2m\right)!}{m!}$ and is $\varphi$ independent. We have verified Equation (172) for $r_1^L=0,1,2,\dots ,10$.

Notice that Equation (172) reduces to the Stirling number identity by taking the Regge limit ($s\to \infty$ with t fixed) and setting $r_1^L=2m$,

$$\begin{array}{c}\sum _{k_r=0}^{2m}\frac{{\left(-\frac{t}{2}-1\right)}_{k_r}}{{\left(-\frac{s}{2}\right)}_{k_r}}\frac{{\left(-2m\right)}_{k_r}}{k_r!}{\left(\frac{s}{t}\right)}^{k_r}\simeq \sum _{k_r=0}^{2m}{\left(-2m\right)}_{k_r}{\left(-\frac{t}{2}-1\right)}_{k_r}\frac{{\left(-2/t\right)}^{k_r}}{k_r!}\\ =0·{\left(-t\right)}^0+0·{\left(-t\right)}^{-1}+\dots +0·{\left(-t\right)}^{-m+1}+\frac{\left(2m\right)!}{m!}{\left(-t\right)}^{-m}+\mathit{O}\left\{{\left(\frac{1}{t}\right)}^{m+1}\right\},\end{array}$$

(173)

which was proposed in [40] and proved in [50].

It was demonstrated in [40] that the ratios in the hard scattering limit in Equation (163) can be reproduced from a class of Regge string scattering amplitudes presented in Equation (181). The key of the proof of this relationship between HSSA and RSSA was the new Stirling number identity proposed in Equation (173) and mathematical proved in [50]. On the other hand, the mathematical proof of Equation (172), which is a generalization of the identity in Equation (173), is an open question and may be an interesting one to study.

The zero terms in Equation (172) correspond to the naive leading energy orders in the HSSA calculation. In the hard scattering limit, the true leading order SSA can then be identified:

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_l^L)}\simeq B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\hfill \\ \hfill & ·\prod _{n=1}{\left[(n-1)!Esin\varphi \right]}^{r_n^T}\prod _{l=1}{\left[-(l-1)!\frac{2E^2}{M_2}{sin}^2\frac{\varphi }{2}\right]}^{r_l^L}\hfill \\ \hfill & ·C_{r_1^L}{\left(Esin\varphi \right)}^{-2\left[\frac{r_1^L+1}{2}\right]}·\left(\dots \right)\hfill \\ \hfill & \sim E^{N-{\sum }_{n\ge 2}n{r}_n^T-\left(2\left[\frac{r_1^L+1}{2}\right]-r_1^L\right)-{\sum }_{l\ge 3}l{r}_l^L},\hfill \end{array}$$

(174)

which means that SSA reaches its highest energy when $r_{n\ge 2}^T=r_{l\ge 3}^L=0$ and $r_1^L=2m$—an even number. This result is consistent with the previous result presented in Equation (162) [10,11,12,13,14,15,16].

Finally, the leading order SSA in the hard scattering limit, i.e., $r_1^T=N-2m-2q$, $r_1^L=2m$ and $r_2^L=q$, can be calculated to be

$$\begin{array}{cc}\hfill & A_{st}^{(N-2m-2q,2m,q)}\hfill \\ \hfill & \simeq B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right){\left(Esin\varphi \right)}^N\frac{\left(2m\right)!}{m!}{\left(-\frac{1}{2M_2}\right)}^{2m+q}\hfill \\ \hfill & =(2m-1)!!{\left(-\frac{1}{M_2}\right)}^{2m+q}{\left(\frac{1}{2}\right)}^{m+q}{A}_{st}^{(N,0,0)}\hfill \end{array}$$

(175)

which reproduces the ratios in Equation (163), and is consistent with the previous result [10,11,12,13,14,15,16].

4.2. Regge Scattering Limit

There is another important high-energy limit of SSA: the RSSA in the Regge scattering limit. The relevant kinematics in the Regge limit are

$$\begin{array}{cc}\hfill k_1^T& =0,k_3^T\simeq -\sqrt{-t},\hfill \end{array}$$

(176)

$$\begin{array}{cc}\hfill k_1^P& \simeq -\frac{s}{2M_2},k_3^P\simeq -\frac{\tilde{t}}{2M_2}=-\frac{t-M_2^2-M_3^2}{2M_2},\hfill \end{array}$$

(177)

$$\begin{array}{cc}\hfill k_1^L& \simeq -\frac{s}{2M_2},k_3^L\simeq -\frac{{\tilde{t}}^{\prime }}{2M_2}=-\frac{t+M_2^2-M_3^2}{2M_2}.\hfill \end{array}$$

(178)

One can easily calculate

$${\tilde{z}}_{k{k}^{\prime }}^T=1,{\tilde{z}}_{k{k}^{\prime }}^P=1-{\left(-\frac{s}{\tilde{t}}\right)}^{1/k}{e}^{\frac{i2\pi k^{\prime }}{k}}\sim s^{1/k}$$

(179)

and

$${\tilde{z}}_{k{k}^{\prime }}^L=1-{\left(-\frac{s}{{\tilde{t}}^{\prime }}\right)}^{1/k}{e}^{\frac{i2\pi k^{\prime }}{k}}\sim s^{1/k}.$$

(180)

In the Regge limit, the SSA in Equation (20) reduces to

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_m^P,r_l^L)}\hfill \\ \hfill \simeq & B\left(-\frac{t}{2}-1,-\frac{s}{2}-1\right)\prod _{n=1}{\left[(n-1)!\sqrt{-t}\right]}^{r_n^T}\hfill \\ \hfill ·& \prod _{m=1}{\left[(m-1)!\frac{\tilde{t}}{2M_2}\right]}^{r_m^P}\prod _{l=1}{\left[(l-1)!\frac{{\tilde{t}}^{\prime }}{2M_2}\right]}^{r_l^L}\hfill \\ \hfill ·& F_1\left(-\frac{t}{2}-1;-q_1,-r_1;-\frac{s}{2};\frac{s}{\tilde{t}},\frac{s}{{\tilde{t}}^{\prime }}\right).\hfill \end{array}$$

(181)

where $F_1$ is the Appell function. Equation (181) agrees with the result obtained in [42] previously.

The recurrence relations of the Appell functions can be used to reduce the number of independent RSSAs from ∞ down to 1. One can also calculate the string BCJ relation in the Regge scattering limit and study the extended recurrence relation in the Regge limit [37].

4.3. Nonrelativistic Scattering Limit and Extended Recurrence Relations

In this section, we discuss nonrelativistic string scattering amplitudes (NSSAs) and the extended recurrence relations among them. In addition, we will also derive the nonrelativistic level $M_2$-dependent string BCJ relations which are the stringy generalization of the massless field theory BCJ relation [48] to the higher spin stringy particles.

We employ the nonrelativistic string scattering limit or $|\overrightarrow{k_2}|<<M_2$ limit to calculate the mass level and spin dependent low-energy SSA. In contrast to the zero slope ${\alpha }^{\prime }$ limit used in the literature to calculate the massless Yang–Mills couplings [51,52] for superstrings and the three point ${\phi }^3$ scalar field coupling [53,54,55] for bosonic strings, we found it appropriate to take the nonrelativistic limit to calculate low-energy SSAs for string states with both higher spins and finite mass gaps.

4.3.1. Nonrelavistic LSSA

In this subsection, we first calculate the NSSA from the LSSA. In the nonrelativistic limit $|\overrightarrow{k_1}|\ll M_2$, we have

$$\begin{array}{cc}\hfill k_1^T& =0,k_3^T=-\left[\frac{ϵ}{2}+\frac{{(M_1+M_2)}^2}{4M_1{M}_2ϵ}{\left|\overrightarrow{k_1}\right|}^2\right]sin\varphi ,\hfill \end{array}$$

(182)

$$\begin{array}{cc}\hfill k_1^L& =-\frac{M_1+M_2}{M_2}\left|\overrightarrow{k_1}\right|+O\left(|\overrightarrow{k_1}{|}^2\right),\hfill \end{array}$$

(183)

$$\begin{array}{cc}\hfill k_3^L& =-\frac{ϵ}{2}cos\varphi +\frac{M_1+M_2}{2M_2}\left|\overrightarrow{k_1}\right|+O\left(|\overrightarrow{k_1}{|}^2\right),\hfill \end{array}$$

(184)

$$\begin{array}{cc}\hfill k_1^P& =-M_1+O\left(|\overrightarrow{k_1}{|}^2\right),\hfill \end{array}$$

(185)

$$\begin{array}{cc}\hfill k_3^P& =\frac{M_1+M_2}{2}-\frac{ϵ}{2M_2}cos\varphi \left|\overrightarrow{k_1}\right|+O\left(|\overrightarrow{k_1}{|}^2\right)\hfill \end{array}$$

(186)

where $ϵ=\sqrt{{(M_1+M_2)}^2-4M_3^2}$ and $M_1=M_3=M_4=M_{tachyon}$. One can easily calculate

$$z_k^T=z_k^L=0,z_k^P\simeq \left|{\left(\frac{2M_1}{M_1+M_2}\right)}^{\frac{1}{k}}\right|.$$

(187)

The SSA in Equation (20) reduces to

$$\begin{array}{cc}\hfill & A_{st}^{(r_n^T,r_m^P,r_l^L)}\hfill \\ \hfill & \simeq \prod _{n=1}{\left[(n-1)!\frac{ϵ}{2}sin\varphi \right]}^{r_n^T}\prod _{m=1}{\left[-(m-1)!\frac{M_1+M_2}{2}\right]}^{r_m^P}\hfill \\ \hfill & ·\prod _{l=1}{\left[(l-1)!\frac{ϵ}{2}cos\varphi \right]}^{r_l^L}B\left(\frac{M_1{M}_2}{2},1-M_1{M}_2\right)\hfill \\ \hfill & ·F_D^{\left(K\right)}\left(\frac{M_1{M}_2}{2};R_m^P;M_1{M}_2;{\left(\frac{2M_1}{M_1+M_2}\right)}_m\right)\hfill \end{array}$$

(188)

where

$$K=\underset{\{\mathrm{for}\mathrm{all}{r}_m^P\ne 0\}}{\sum m}.$$

(189)

4.3.2. Nonrelativistic String BCJ Relations

Note that for string states with $r_k^P=0$ in Equation (20) for all $k\ge 2$, one has $K=1$, and the Lauricella functions in the low-energy nonrelativistic SSA reduce to the Gauss hypergeometric functions $F_D^{\left(1\right)}={}_{2}F_1$ with the associated $SL(4,C)$ symmetry. In particular, for the case of the leading trajectory string state in the second vertex with mass level $N=N_1+N_2+N_3$ where $r_1^T=N_1$, $r_1^P=N_3$, $r_1^L=N_2$, and $r_k^X=0$ for all $k\ge 2$, the SSA reduces to

$$\begin{array}{cc}\hfill & A_{st}^{(N_1,N_2,N_3)}={\left(\frac{ϵ}{2}sin\varphi \right)}^{N_1}{\left(\frac{ϵ}{2}cos\varphi \right)}^{N_2}\hfill \\ \hfill ·& {\left(-\frac{M_1+M_2}{2}\right)}^{N_3}B\left(\frac{M_1{M}_2}{2},1-M_1{M}_2\right)\hfill \\ \hfill ·& {}_2{F}_1\left(\frac{M_1{M}_2}{2};-N_3;M_1{M}_2;\frac{2M_1}{M_1+M_2}\right),\hfill \end{array}$$

(190)

which agrees with the result obtained in [37] previously. Similarly, one can calculate the corresponding nonrelativistic $t-u$ channel amplitude as

$$\begin{array}{cc}\hfill A_{tu}^{(N_1,N_2,N_3)}=& {\left(-1\right)}^N{\left(\frac{ϵ}{2}sin\varphi \right)}^{N_1}{\left(\frac{ϵ}{2}cos\varphi \right)}^{N_2}\hfill \\ \hfill & ·{\left(-\frac{M_1+M_2}{2}\right)}^{N_3}B\left(\frac{M_1{M}_2}{2},\frac{M_1{M}_2}{2}\right)\hfill \\ \hfill & ·{}_2{F}_1\left(\frac{M_1{M}_2}{2};-N_3;M_1{M}_2;\frac{2M_1}{M_1+M_2}\right).\hfill \end{array}$$

(191)

Finally, the ratio of $s-t$ and $t-u$ channel amplitudes is [37]

$$\begin{array}{cc}\hfill \frac{A_{st}^{(N_1,N_2,N_3)}}{A_{tu}^{(N_1,N_2,N_3)}}& ={\left(-1\right)}^N\frac{B\left(-M_1{M}_2+1,\frac{M_1{M}_2}{2}\right)}{B\left(\frac{M_1{M}_2}{2},\frac{M_1{M}_2}{2}\right)}\hfill \\ \hfill & ={(-1)}^N\frac{\Gamma \left(M_1{M}_2\right)\Gamma \left(-M_1{M}_2+1\right)}{\Gamma \left(\frac{M_1{M}_2}{2}\right)\Gamma \left(-\frac{M_1{M}_2}{2}+1\right)}\simeq \frac{sin\pi \left(k_2·k_4\right)}{sin\pi \left(k_1·k_2\right)}\hfill \end{array}$$

(192)

where, in the nonrelativistic limit, we have

$$\begin{array}{cc}\hfill k_1·k_2& \simeq -M_1{M}_2,\hfill \end{array}$$

(193a)

$$\begin{array}{cc}\hfill k_2·k_4& \simeq \frac{\left(M_1+M_2\right)M_2}{2}.\hfill \end{array}$$

(193b)

We thus obtain consistent nonrelativistic level $M_2$-dependent string BCJ relations. Similar relations for $t-u$ and $s-u$ channel amplitudes can be calculated. We stress that the above relation is the stringy generalization of the massless field theory BCJ relation [48] to the higher spin stringy particles. Moreover, as shown in the next subsection, there are much more relations among the NSSAs.

4.3.3. Extended Recurrence Relations in the Nonrelativistic Scattering Limit

Leading Trajectory String States

In this subsection, we derive two examples of extended recurrence relations among NSSAs. We first note that there is a recurrence relation of the Gauss hypergeometry function,

$${}_2{F}_1(a;b;c;z)=\frac{c-2b+2+(b-a-1)z}{(b-1)(z-1)}{}_2{F}_1(a;b-1;c;z)+\frac{b-c-1}{(b-1)(z-1)}{}_2{F}_1(a;b-2;c;z),$$

(194)

which can be used to derive the recurrence relation,

$$\begin{array}{cc}\hfill \left(-\frac{M_1+M_2}{2}\right)A_{st}^{(p,r,q)}=& \frac{M_2\left(M_1{M}_2+2q+2\right)}{\left(q+1\right)\left(M_2-M_1\right)}{\left(\frac{ϵ}{2}sin\varphi \right)}^{p-p^{\prime }}{\left(\frac{ϵ}{2}cos\varphi \right)}^{p^{\prime }-p+1}{A}_{st}^{\left(p^{\prime },p+r-p^{\prime }-1,q+1\right)}\hfill \\ \hfill +& \frac{2\left(M_1{M}_2+q+1\right)}{\left(q+1\right)\left(M_2-M_1\right)}{\left(\frac{ϵ}{2}sin\varphi \right)}^{p-p^{″}}{\left(\frac{ϵ}{2}cos\varphi \right)}^{p^{″}-p+2}{A}_{st}^{\left(p^{″},p+r-p^{″}-2,q+2\right)}\hfill \end{array}$$

(195)

where $p^{\prime }$ and $p^{″}$ are the polarization parameters of the second and third amplitudes on the right-hand side of Equation (195). For example, for a fixed mass level $N=4$, one can derive many recurrence relations for either $s-t$ channel or $t-u$ channel amplitudes with $q=0,1,2$. For example, for $q=2,$$(p,r)=(2,0),(1,1),(0,2)$, we have $p^{\prime }=0,1$ and $p^{″}=0.$ We can thus derive—for example, for $(p,r)=(2,0)$ and $p^{\prime }=1$—the recurrence relation among amplitudes $A_{st}^{(2,0,2)}{A}_{st}^{(1,0,3)}{A}_{st}^{(0,0,4)}$ as follows:

$$\left(-\frac{M_1+M_2}{2}\right)A_{st}^{(2,0,2)}=\frac{M_2\left(M_1{M}_2+6\right)}{3\left(M_2-M_1\right)}\left(\frac{ϵ}{2}sin\varphi \right)A_{st}^{(1,0,3)}+\frac{2\left(M_1{M}_2+4\right)}{3\left(M_2-M_1\right)}{\left(\frac{ϵ}{2}sin\varphi \right)}^2{A}_{st}^{(0,0,4)}.$$

(196)

Exactly the same relation can be obtained for $t-u$ channel amplitudes since the ${}_2{F}_1(a;b;c;z)$ dependence in the $s-t$ and $t-u$ channel amplitudes calculated above are the same. Moreover, we can, for example, replace the $A_{st}^{(2,0,2)}$ amplitude above by the corresponding $t-u$ channel amplitude $A_{tu}^{(2,0,2)}$ through Equation (192) and obtain

$$\begin{array}{cc}\hfill \frac{{\left(-1\right)}^N}{2cos\frac{\pi M_1{M}_2}{2}}\left(-\frac{M_1+M_2}{2}\right)A_{tu}^{(2,0,2)}& =\frac{M_2\left(M_1{M}_2+6\right)}{3\left(M_2-M_1\right)}\left(\frac{ϵ}{2}sin\varphi \right)A_{st}^{(1,0,3)}\hfill \\ \hfill & +\frac{2\left(M_1{M}_2+4\right)}{3\left(M_2-M_1\right)}{\left(\frac{ϵ}{2}sin\varphi \right)}^2{A}_{st}^{(0,0,4)},\hfill \end{array}$$

(197)

which relates higher spin nonrelativistic string amplitudes in both $s-t$ and $t-u$ channels. Equation (197) is one example of the extended recurrence relations in the nonrelativistic string scattering limit.

General String States

Equation (197) relates the NSSAs of different polarizations of a fixed leading trajectory string state. In the next sample calculation, we calculate one example of an extended recurrence relation that relates the NSS amplitudes of different higher spin particles for each fixed mass level $M_2$. In particular, the $s-t$ channel of the NSS amplitudes of three tachyons and one higher spin massive string state at mass level $N=3p_1+q_1+3$ corresponding to the following three higher spin string states,

$$\begin{array}{cc}\hfill & A_1{\left(i{\partial }^3{X}^T\right)}^{p_1}{\left(i\partial X^P\right)}^1{\left(i\partial X^L\right)}^{q_1+2},\hfill \end{array}$$

(198)

$$\begin{array}{cc}\hfill & A_2{\left(i{\partial }^2{X}^T\right)}^{p_1}{\left(i\partial X^P\right)}^2{\left(i\partial X^L\right)}^{p_1+q_1+1},\hfill \end{array}$$

(199)

$$\begin{array}{cc}\hfill & A_3{\left(i\partial X^T\right)}^{p_1}{\left(i\partial X^P\right)}^3{\left(i\partial X^L\right)}^{2p_1+q_1},\hfill \end{array}$$

(200)

can be calculated to be

$$\begin{array}{cc}\hfill A_1& ={\left[2!\frac{ϵ}{2}sin\varphi \right]}^{p_1}{\left[-\left(1-1\right)!\frac{M_1+M_2}{2}\right]}^1{\left[0!\frac{ϵ}{2}cos\varphi \right]}^{q_1+2}\hfill \\ \hfill & \times B\left(\frac{M_1{M}_2}{2},1-M_1{M}_2\right){}_2{F}_1\left(\frac{M_1{M}_2}{2},-1,M_1{M}_2,\frac{-2M_1}{M_1+M_2}\right),\hfill \end{array}$$

(201)

$$\begin{array}{cc}\hfill A_2& ={\left[1!\frac{ϵ}{2}sin\varphi \right]}^{p_1}{\left[-\left(2-1\right)!\frac{M_1+M_2}{2}\right]}^2{\left[0!\frac{ϵ}{2}cos\varphi \right]}^{p_1+q_1+1}\hfill \\ \hfill & \times B\left(\frac{M_1{M}_2}{2},1-M_1{M}_2\right){}_2{F}_1\left(\frac{M_1{M}_2}{2},-2,M_1{M}_2,\frac{-2M_1}{M_1+M_2}\right),\hfill \end{array}$$

(202)

$$\begin{array}{cc}\hfill A_3& ={\left[0!\frac{ϵ}{2}sin\varphi \right]}^{p_1}{\left[-\left(3-1\right)!\frac{M_1+M_2}{2}\right]}^3{\left[0!\frac{ϵ}{2}cos\varphi \right]}^{2p_1+q_1}\hfill \\ \hfill & \times B\left(\frac{M_1{M}_2}{2},1-M_1{M}_2\right){}_2{F}_1\left(\frac{M_1{M}_2}{2},-3,M_1{M}_2,\frac{-2M_1}{M_1+M_2}\right).\hfill \end{array}$$

(203)

To apply the recurrence relation in Equation (194) for Gauss hypergeometry functions, we choose

$$a=\frac{M_1{M}_2}{2},b=-1,c=M_1{M}_2,z=\frac{-2M_1}{M_1+M_2}.$$

(204)

One can then calculate the extended recurrence relation

$$\begin{array}{cc}\hfill & 16\left(\frac{2M_1}{M_1+M_2}+1\right){\left(-\frac{M_1+M_2}{2}\right)}^2{\left(\frac{ϵ}{2}cos\varphi \right)}^{2p_1}{A}_1\hfill \\ \hfill & =8·2^{P_1}\left(\frac{M_1{M}_2}{2}+2\right)\left(\frac{2M_1}{M_1+M_2}+2\right)\left(-\frac{M_1+M_2}{2}\right){\left(\frac{ϵ}{2}cos\varphi \right)}^{p_1+1}{A}_2\hfill \\ \hfill & -2^{P_1}\left(M_1{M}_2+2\right){\left(\frac{ϵ}{2}cos\varphi \right)}^2{A}_3\hfill \end{array}$$

(205)

where ${\mathit{p}}_1$ is an arbitrary integer. More extended recurrence relations can be similarly derived.

The existence of these low-energy stringy symmetries comes as a surprise in terms of the perspective of Gross’s high-energy symmetries [1,3,5]. Finally, in contrast to the Regge string spacetime symmetry, which was shown to be related to $SL(5,C)$ of the Appell function $F_1$, we found that the low-energy stringy symmetry is related to $SL(4,C)$ [46] of the Gauss hypergeometry functions ${}_2{F}_1.$

4.4. Summary

In this section, we rederive from the LSSAs the relations or symmetries among SSAs of different string states at three different scattering limits. We first reproduce the linear relations [14,15] of the HSSA from the LSSA in the hard scattering limit. We also obtain Appell functions $F_1$ and Gauss hypergeometric functions ${}_2{F}_1$ with $SL(5,C)$ and $SL(4,C)$ symmetry in the Regge and the nonrelativistic limits, respectively. In contrast to the linear relations in the hard scattering limit, we obtain extended recurrence relations for the cases of RSSAs and NSSAs. These two classes of recurrence relations are closely related to those of the LSSAs with $K=2$ and $K=1$, respectively. In the end, we also show that with the nonrelativistic string BCJ relations [37], the extended recurrence relations we obtained can be used to connect SSAs with different spin states and different channels.

5. Conclusions and Future Works

In this review, we provide a different perspective to demonstrate the Gross conjecture regarding the high-energy symmetry of string theory [1,2,3,4,5]. We review our recent construction of the exact SSAs of three tachyons and one arbitrary string state, or the LSSAs, in the $26D$ open bosonic string theory. In addition, we discover that these LSSAs form an infinite-dimensional representation of the $SL(K+3,\mathbb{C})$ group. Moreover, we show that the $SL(K+3,\mathbb{C})$ group can be used to solve all the LSSAs and express them in terms of one amplitude.

As an important application in the hard scattering limit, the LSSAs can be used to prove the Gross conjecture regarding the high-energy symmetry of string theory, which was previously corrected and proved by the method of decoupling of zero norm states (ZNSs) [6,7,8,9,10,11,12,13,14,15,16]. In this sense, the results of the LSSAs presented in this review extend the Gross conjecture to all kinematic regimes. Finally, the exact LSSA can be used to rederive the recurrence relations of SSAs in the Regge scattering limit with associated $SL(5,\mathbb{C})$ symmetry and the extended recurrence relations (including the mass and spin dependent string BCJ relations) in the nonrelativistic scattering limit with associated $SL(4,\mathbb{C})$ symmetry. These results were first discovered without knowing the exact LSSA.

There are many important related issues that remain to be studied. To name some examples, how can the LSSA be generalized to multitensor cases? Can one calculate exactly five-point, six-point and even higher point functions for arbitrary higher spin string states? Solving these issues would be important to uncover the whole spacetime symmetry structure of string theory. Presumably, the $SL(K+3,\mathbb{C})$ symmetry of the LSSA is only a small part of the whole spacetime symmetry of string theory.

Another important issue is the construction of massive fermion SSAs for the R-sector of superstrings. Recently, the present authors calculated a class of polarized fermion string scattering amplitudes (PFSSAs) at arbitrary mass levels [56]. They discovered that, in the hard scattering limit, the functional forms of the non-vanishing PFSSAs at each fixed mass level are independent of the choices of spin polarizations. This result agrees with the Gross conjecture regarding the high-energy string scattering amplitudes extended to the R-sector. In addition, this peculiar property of hard PFSSAs should be compared with the usual spin polarization-dependence of the hard-polarized fermion field theory scatterings. However, the construction of the PFSSA involved only the leading Regge trajectory fermion string state of the R sector [57,58]. It is a nontrivial task to construct the general massive fermion string vertex operators [59,60,61,62].

Many questions related to the construction of SSA involving the general massive fermion string states need to be answered before we can better understand the high-energy behavior of superstring theory.