Abstract
High-precision and high-density three-dimensional point cloud models usually contain redundant data, which implies extra time and hardware costs in the subsequent data processing stage. To analyze and extract data more effectively, the point cloud must be simplified before data processing. Given that point cloud simplification must be sensitive to features to ensure that more valid information can be saved, in this paper, a new simplification algorithm for scattered point clouds with feature preservation, which can reduce the amount of data while retaining the features of data, is proposed. First, the Delaunay neighborhood of the point cloud is constructed, and then the edge points of the point cloud are extracted by the edge distribution characteristics of the point cloud. Second, the moving least-square method is used to obtain the normal vector of the point cloud and the valley ridge points of the model. Then, potential feature points are identified further and retained on the basis of the discrete gradient idea. Finally, non-feature points are extracted. Experimental results show that our method can be applied to models with different curvatures and effectively avoid the hole phenomenon in the simplification process. To further improve the robustness and anti-noise ability of the method, the neighborhood of the point cloud can be extended to multiple levels, and a balance between simplification speed and accuracy needs to be found.
1. Introduction
Three-dimensional (3D) scanning technology has always been the focus of research on computer vision, reverse engineering, and computer graphics [1]. A point cloud is the most basic and popular data type collected through 3D scanning technology [2]. With the development of 3D scanning technology, the accuracy and density of 3D point cloud models have increased continuously. This study focuses on the scattered data point cloud, which is distributed irregularly and unordered. However, these 3D point cloud models contain huge amounts of redundant data. If all point cloud data are processed, the computer will inevitably consume a large amount of running time and occupy huge storage space, seriously affecting the efficiency of modeling and rendering. Therefore, on the premise of ensuring the features of the point cloud model, simplifying the point cloud in the early stage of point cloud processing is very important and practical.
Currently, the commonly used point cloud simplification methods include the bounding box algorithm [3,4], the uniform grid method [5], the curvature sampling method [6], the clustering method [7], the triangular grid method [8], etc. [9,10,11,12]. However, these methods have some shortcomings. To make the density of the point cloud more uniform, some methods ignore local details, which leads to inaccurate reconstruction results. Some methods, such as the curvature sampling method, can retain the original details of the point cloud well, but they are computationally intensive and inefficient. Based on this, many scholars have studied the simplification of the point cloud and proposed several algorithms. For a structured point cloud, Markovic et al. [13] proposed a simplified point cloud method that uses ε-insensitive support vector regression with spline and b-spline kernels to find the significant points from high curvature areas in scanned lines, thereby retaining the high level of initial information about the shape and structure of the scanned object. However, a scattered data point cloud lacks a natural topological connection and often experiences problems, such as uneven sampling, noise, and missing data. The simplified point cloud can easily have a bad impact on the appearance, modeling, and accurate expression of the geometric model. Consequently, feature extraction and retention are essential when a scattered data point cloud is simplified. For the feature extraction of a point cloud model, scholars have done a lot of research [14,15,16]. On this basis, many scholars have proposed point cloud simplification algorithms with feature preservation. According to the neighborhood distribution characteristics of the model, some scholars have proposed K-neighborhood-related simplification methods. Li et al. [17] first used a k-d tree to segment point cloud data to establish a spatial topology and then combined the change of the local normal vector and the reserved points as the threshold to simplify the point cloud in the region. This algorithm prevents holes when the simplification ratio is extremely high. Ji et al. [18] proposed a new K-neighborhood search method based on distance and density, and feature points are selected according to their geometric features. This method is named as the detail feature points simplified algorithm (DFPSA) for a 3D point cloud. According to the morphological characteristics of the model, some scholars put forward the simplification method of geometric algebra. Mahdaoui et al. [19] proposed a point cloud iterative simplification method based on the density function and Shannon entropy estimation. The algorithm is suitable for different point clouds with different densities, and the reconstruction effect of the simplified point cloud is near the original point cloud model. Yuan et al. [20] proposed a simplified algorithm based on conformal geometric algebra. The spherical tree is used to construct multi-resolution subdivision, and K-means clustering is used to calculate the minimum boundary sphere, and then the adaptive point cloud simplification is carried out. Bernard et al. [21] used the associated point distribution model to represent the statistical shape model, but due to the heteroscedasticity of point cloud data, the surface generated using only the reconstruction method of the probability model will have a certain deviation, resulting in a low-accuracy curvature calculation value. Some scholars pay attention to the noise variables in the point cloud model, such as Zhu et al. [22], who proposed a noisy three-dimensional model data simplification approach. The core idea of this approach is to use the guided filter algorithm, often used in 2D images, to reposition point cloud data, especially noisy point cloud data, to enhance the features and geometric details.
Starting from what is already known in this field, a new simplification algorithm for scattered point clouds with feature preservation is proposed, so that it can simplify the point cloud and save as much information as possible. Based on the point cloud model’s own morphological characteristics to divide its characteristics, based on the Delaunay neighborhood of the point cloud, this paper uses the moving least-square (MLS) method and discrete gradient ideas to extract the important points in point cloud mode, that is, feature points, thereby simplifying the point cloud. The experimental results show that this method can be applied to point cloud models with different shapes, noises, and orders of magnitude.
The rest of this paper is organized as follows. Section 2 introduces the implementation of our method and related formulas and describes the acquisition of the Delaunay neighborhood of the point cloud and how to use the MLS method and the discrete gradient to obtain the feature points of each part of the point cloud. Section 3 elaborates on the experimental results, including the simplified results of our method under different models and the conclusions after comparison with the other three methods. In the last section, some conclusions and future work directions are given by observing the experimental results.
2. Methodology
The core idea of point cloud simplification is to remove a large amount of redundant data and retain feature data to ensure that the original model can be restored with as few points as possible. Point cloud features include global and potential features. Global features include edge and non-edge features. Potential features are the space divided after global features are extracted.
The flowchart of the proposed point cloud simplification method comprises four stages, as shown in Figure 1. We assume that P is the original point cloud model, which can be defined as P = {pi(x,y,z)}, i∈[1, n], where pi is the i-th point and n is the size of P. The simplified point cloud set is denoted as R. Specifically, after preprocessing the point cloud, we construct the Delaunay neighborhood of the point cloud P. According to the edge distribution characteristics of the points, the edge points are judged, which is Step 1 in the figure. Then, the MLS method is used to calculate the normal vector of the point cloud, and the valley ridge feature points are extracted according to the maximum curvature threshold, which is Step 2. Then, according to the discrete gradient, the potential feature points are further judged and retained, which is Step 3. Finally, in Step 4, the non-feature points are extracted by the uniform sampling method, and the sampling interval is s.
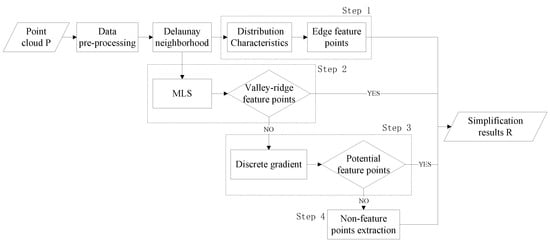
Figure 1.
Algorithm flowchart.
2.1. Extraction of the Point Cloud Edge
Generally, edge point clouds have more features than valley-ridge point clouds. Thus, these edge points must be retained in the process of point cloud simplification.
2.1.1. Delaunay Neighborhood
The most significant feature of the point cloud model is the lack of topological connections between point data. Therefore, taking the point cloud model as the research object, the neighborhood points of the point data should be calculated first.
For the point cloud model with a uniform sampling density, the k-nearest neighbors of a point can be selected to represent its neighborhood. However, the sampling density of many point cloud models varies, and the k-nearest neighbors of feature points may be located in one side of the area. Thus, the Delaunay neighborhood [23] is adopted in this study, that is, the local plane is fitted to point pi in the sphere neighborhood and projected to the plane to obtain projection point qi. Then, we perform Delaunay triangulation on projection point qi to obtain the Delaunay neighborhood () of point p. As shown in Figure 2, the first-order Delaunay neighborhood of p is recorded as .
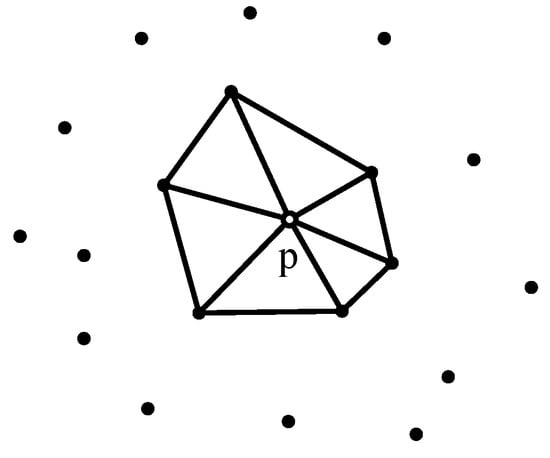
Figure 2.
First-order Delaunay neighborhood of point p.
2.1.2. The Edge Distribution Characteristics
The edge points of the point cloud can be obtained by constructing the Delaunay neighborhood of the point cloud and combining the edge distribution characteristics of the point cloud.
As shown in Figure 3, generally, for non-edge points, the points in the neighborhood are distributed around the point. In addition, for edge points, the points in the neighborhood gather in a certain direction. According to the above rules, we use the edge coefficient Fp to measure the aggregation degree of the point distribution in the neighborhood of point p. That is, the unit normal vector composed of a point and its neighbors is superimposed. After the superposition of non-edge points, it tends to a zero vector in theory, while the edge point is a non-zero vector, so the boundary points can be quickly and roughly extracted according to the superposition normal vector. The formula of Fp is shown below:
where pi is the i-th neighborhood point of point p and D is the number of points in the neighborhood of p. The larger the edge coefficient Fp is, the more non-uniform the point distribution around point p is, the more detached it is from the point cloud body and has the characteristics of edge points.

Figure 3.
The edge distribution characteristics of the point cloud. (a) Neighborhood distribution of non-edge points; (b) Neighborhood distribution of edge points.
To improve the adaptability of the algorithm, after calculating the boundary point index F of the point, if the boundary point index Fp of a point satisfies Equation (2), the point is judged to be the boundary point.
where mF is the mean value and F is the standard deviation of Fp.
Edge point clouds have many characteristics of the model, so these points must be retained in the process of point cloud simplification.
2.2. Determination of Valley-Ridge Feature Points
Valley-ridge and potential feature points are evaluated based on normal vectors. This section discusses the extraction of valley-ridge feature points. The MLS method [24,25] is used to fit the points in the first-order Delaunay neighborhood of point pi to a plane, and the normal direction of the plane is the normal vector of pi. Given that the direction of the normal vectors obtained in this manner is uncertain, these normal vectors must be unified. Unification must be performed according to the direction of the line of sight to ensure the consistency of the direction of the normal vector. Generally, the origin is regarded as the viewpoint position, and the line of sight is = (−x,−y,−z)T. The normal vector of the point cloud is adjusted, such that ∙ > 0. Finally, according to the adjusted normal vector, the Gaussian curvature (kg) and average curvature (kh) of each point are calculated. The principal curvature, k = kn ± of the surface can be obtained, and k takes the larger absolute value as the curvature value. The threshold CT is set. When the absolute value (|k|) of the principal curvature of a point is larger than CT∙mean(sum(|k|)), that is |k| > CT∙mean(sum(|k|)), this point is the valley-ridge point of the model, which is recorded as V.
2.3. Determination of Potential Feature Points
The previous chapter discusses the extraction of global features. The threshold setting is large. Thus, only the obvious feature points in the model can be extracted. To avoid ignoring the potential feature points, we assume that V is the first kind of potential feature points, and then extract the second kind of potential feature points based on the discrete gradient from the point cloud in P.
First, we define discrete function fp, which is a feature detection operator at a point. Then, the discrete gradient at that point is calculated by using the operator. As shown in Figure 4, θpi is the angle formed by point p and its neighborhood point pi in the principal direction and can measure the degree of bending of a potential surface at a point. The principal direction in this work is the direction of eigenvector v0 corresponding to the minimum eigenvalue of the covariance matrix of a point and its local neighborhood points. The formula of covariance matrix T is as follows:
where c = pi is the centroid of Np. Np is the Delaunay neighborhood of point p, and the eigenvalues of covariance matrix T are λ0 < λ1 < λ2.
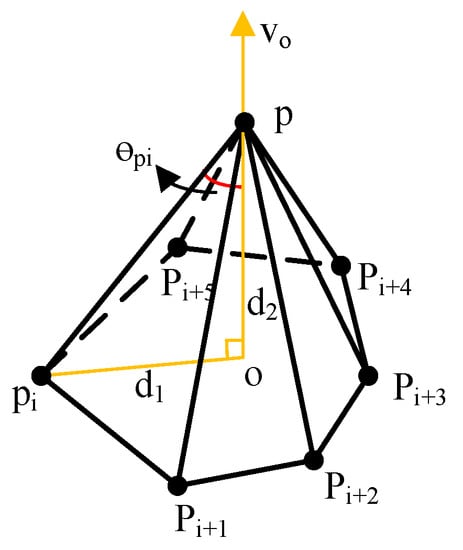
Figure 4.
Illustration of the angle θpi.
Angle θpi can be expressed as
where ‖p − pi‖ is the Euclidean distance between p and pi and pi is the point in the Delaunay neighborhood of p. cosθpi decreases monotonously in the interval 0 < pi < 180, that is, the larger the value of pi is, the smaller the value of cosθpi is, and the smoother the feature is at this point; on the contrary, the larger the value of cosθpi is, the sharper the feature at this point is. Therefore, the local feature detection operator (fp) of point p is defined as
where the larger the value of fp is, the greater the bending degree of the potential surface in the local neighborhood of point p is.
The discrete gradient (Gi) between points p and pi in its neighborhood is set as
where p − pi is the shortest path length between points p and pi, which is defined as the geodesic distance between two points.
According to discrete Morse theory, discrete gradient Gi is used as the criterion to extract the second type of potential feature points. The specific criterion is
When the above condition is satisfied, the corresponding points in the neighborhood are selected. Then, according to the number of times (Ui) this point appears as the neighborhood of the first kind of potential feature points, the second kind of potential feature points are screened and distinguished, that is,
where Mgi = (Tg × Ui), Tg∈[0, 1] is the threshold value.
3. Experimental and Discussion
3.1. Preparation
MATLAB R2016a was used to program the algorithm. The computer was configured with a Winl0 system, 3.4 GHz Intel Core i7, 16 G memory, and NVDIA GeForceGtX960M graphics card. To verify the effectiveness of the proposed point cloud simplification algorithm, we selected four groups of point cloud data with different characteristics for simplification analysis. The feature sharpness characteristics of these four data vary, and their potential surfaces are uneven. The experiment evaluated the method from two aspects, namely simplification and reconstruction effects, and compared it with the grid-based, curvature-based simplification methods in Geomagic and feature-preserving [20] simplification methods.
As shown in Figure 5a,b, the point cloud data of Bunny and Dragon models are all from the 3D point cloud database established by Stanford University. The Dragon model has 437,645 points, while the Bunny model has 35,947 points. The point cloud data of the Mask model are obtained from the 3D measurement system built in our laboratory, and the measured object is shown in Figure 6a. This system is shown in Figure 6b, consisting of one projector and four cameras. Group A’s camera model is Manta G-504, with a 2452 × 2056 resolution and a pixel size of 3.45 μm; Group B’s camera model is MER-500-14GM /CP, with a 2592 × 1944 resolution and a pixel size of 2.2 μm. The lens is OPT-165M. The projector is DLP Light Crafter 4500. The Mask point cloud model obtained by Group A’s cameras has 2,194,425 points, and that obtained by Group B’s cameras has 3,367,616 points.

Figure 5.
(a) Bunny and (b) dragon.

Figure 6.
(a) Mask and (b) experimental setup.
3.2. Results and Analysis
The simplification of a point cloud requires deleting redundant points and retaining global and local features as much as possible on the premise of meeting the requirements of the simplification rate. The formula of simplification rate is as follows:
where ρ is the simplification rate, and the bigger the value is, the more points are deleted, that is, the greater the simplification degree is; otherwise, fewer points are deleted, that is, the simplification degree is lower.
When the simplification rate is too low, the appearance and details of the simplified model and the original model will not be very different. When the simplification rate is too high, the simplified model is prone to holes after reconstruction. Therefore, we determine the approximate range of ρ according to the number of the original model point clouds. The Bunny and Dragon models’ ρ ranges from 20% to 80%, and that of Mask A and Mask B models ranges from 35% to 90%.
The entire point cloud simplification process of the proposed method is divided into four stages: edge point detection, valley-ridge feature point estimation, potential feature point recognition, and non-feature point extraction. Taking the Bunny model as an example, when ρ = 53%, the point cloud data obtained by each step of our method are shown in Figure 7. For convenience of distinguishing, the point clouds obtained at different stages are displayed in different colors. Edge points are purple, valley-ridge points are green, potential feature points are blue, and non-feature points are red. It can be seen that valley-ridge feature point estimation and potential feature point recognition complement each other, obtaining good model details (such as ears, torso, and face), while edge point detection and non-feature point extraction are good for filling smooth areas (such as the back). Thus, the final result can be preserved well regardless of the feature (i.e., contour or detail feature).

Figure 7.
(a) Edge points, (b) valley-ridge feature points, (c) potential feature points, (d) non-feature points, (e) simplified results, and (f) reconstruction results.
3.2.1. Setting Parameters
At the beginning of the study, we hoped to reduce the influence of artificial parameter adjustment in the algorithm on point cloud simplification as much as possible, so the number of artificial thresholds was set as low as possible. According to the introduction in Section 2, we can know from the formula that the parameters to be adjusted are CT, Tg, and s. Different parameters have different effects on different types of point clouds. According to the definition of each threshold, if the value of CT is between 0 to 1, too many points with inconspicuous valley and ridge features will be stored, which will affect the extraction of potential feature points, so the value of CT should be greater than 1. An excessively large CT will also affect the subsequent simplification steps. Depending on the size and shape of the point cloud model, the upper limit of CT value is also different. After repeated trials and comparison, the maximum value of CT is about 5, otherwise there are too few valley-ridge feature points. Tg is a weight coefficient, and generally, its value range is (0,1). However, depending on the number of original point clouds, the value range is also different. In the case of a small number of original point clouds, the value of Tg is (0,0.5). s is the sampling interval of the non-feature point cloud, and its value depends on the number of feature points retained after the first three steps of simplification and the target simplification rate of the point cloud. Therefore, in the following discussion, we only focus on the selection of CT and Tg.
Figure 8 shows the effect of the selection of Ct and Tg values on the final simplified result of the Bunny model when the non-feature point sampling interval s is fixed at 50. Each line of images, from left to right, are edge points, valley-ridge points, potential feature points, non-feature points, the final simplified point cloud model, and its reconstruction model. It can be seen that the larger the values of Ct and Tg are, the less points are saved. Each step of our method is interlocking. The selection of valley-ridge points and the preservation of potential feature points are complementary to each other, and they can extract the details of the model very well. The appropriate adjusting of the number of non-feature points can help reshape the entire simplified model. In summary, for a point cloud model with uniform sampling and distinctive features, Ct and Tg are set to small values, and s can be selected according to the requirements of the simplification rate. If there is no special requirement, s can be set to a medium value.

Figure 8.
The effect of different threshold selections on the Bunny model, where s = 50. (a) CT = 1.1, Tg = 0.1; (b) CT = 1.1, Tg = 0.5; (c) CT = 5, Tg = 0.1; and (d) CT = 5, Tg = 0.4.
3.2.2. The Self-Adapting Experiment Parameters
Due to the various forms of point cloud data acquisition, there are also many differences in point cloud models. The method in this paper simplifies the four different types of models in Figure 5 and Figure 6 to ensure the applicability and feasibility of the method.
The point cloud model of the simplified results at different simplification rates and the corresponding reconstruction effects are shown in Figure 9, where Figure 9a–d are Bunny, Dragon, Mask A, and Mask B models, respectively. When ρ = 0, it means that the corresponding model in Figure 8 is the original model. With an increase in the simplification rate, the simplified model will lose some texture information and local detail features with too few point clouds after simplification. For example, when ρ = 71.4%, the ear part of the Bunny model is slightly missing. However, it can be seen from Table 1 that the maximum error, average error, and root-mean-square (RMS) error are kept at a small level, indicating that the simplified model basically retains the geometric features and contour appearance of the original model. Therefore, the proposed point cloud simplification algorithm effectively retains the geometric information in different models, such as the boundary, high curvature points, and local features.
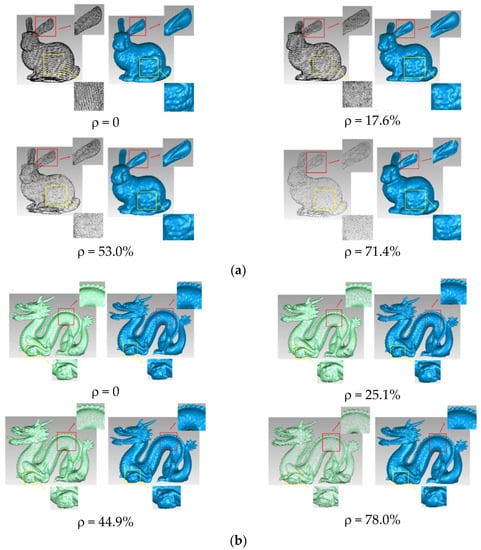

Figure 9.
Simplification results of our method: (a) Bunny, (b) Dragon, (c) Mask A, and (d) Mask B models.

Table 1.
Simplification rate and evaluation of results.
3.2.3. Comparison of the Simplification Effect with Other Methods
To further verify the effectiveness of our method, in this chapter, we used the grid-based, curvature-based simplification methods in Geomagic and feature-preserving [20] simplification methods to simplify the data of Bunny and Mask A models and compared the results with our method.
The simplified results are shown in Figure 10. The surface of the Bunny model has many wrinkles. The geometric details show that the feature points retained by our method are more continuous and uniform, whereas the other three methods lose a lot of feature information when the simplification rates are high. Especially for bunny ears, the difference is most obvious. Because the number of point clouds in the ear part is not very large, it is easy to have holes and deformations if we do not pay attention to feature preservation during the simplification process. For the Mask A model with an uneven feature distribution, the proposed method retains more points in the concave and convex changes, while the curvature-based simplification method focuses on feature retention and ignores the extraction of points in the smoother area, resulting in more holes. The grid-based and the feature-preserving simplification methods retain too many non-feature points in a few flat regions, which makes the face of Mask A too smooth, but the real face of Mask A is uneven.

Figure 10.
Simplification results of the grid method: (a) Bunny and (d) Mask A models. Simplification result of the curvature adaptive method: (b) Bunny and (e) Mask A models. Simplification results of the feature-preserving method [18]: (c) Bunny and (f) Mask A models.
The above is the intuitive visual impression of the simplified results obtained by the four methods. The following is a detailed analysis of the error comparison of the four methods based on numerical calculation.
Table 2 shows the error comparison between the simplified model and the original Bunny and Mask A models under different simplification rates of different methods. It can be seen that the error of our proposed method is the smallest, followed by the feature-preserving method, and the results of the other two methods are relatively poor. Since their simplification rates are similar but not exactly the same, it is not easy to observe in the table, and Figure 10 was drawn to make the numerical comparison more intuitive.

Table 2.
Error evaluation of the simplified result of Bunny and Mask A models.
It can be seen that Figure 11 shows the error relationship between the simplified model and the original model under different methods. In the simplification of the Bunny model, the error results of the four methods are similar when their simplification rate is small, and our method is slightly better. When the simplification rate increases gradually, the errors of these four methods all increase, but obviously, the error of our method is much smaller. In the simplification of the Mask A model, the feature-preserving method and our method have greater advantages, and our method is better overall. In summary, our method can detect and extract the features of different point cloud models better, while retaining the edge points, making the 3D point cloud model more realistic and comprehensive.
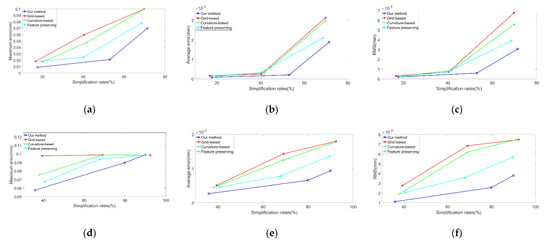
Figure 11.
Simplified error comparison of the Bunny model: (a) maximum error, (b) average error, and (c) RMS error. Simplified error comparison of the Mask A model: (d) maximum error, (e) average error, and (f) RMS error.
4. Conclusions
To retain as many feature points as possible when removing a large amount of redundant information in high-precision and high-density point clouds, this paper proposes a new simplification algorithm for scattered point clouds with feature preservation. The simplified method makes full use of the feature information about the original point cloud. First, the Delaunay neighborhood of the point cloud is established, and the contour of the model is extracted according to the edge distribution characteristics of the point cloud. Second, the valley-ridge points are preserved by the curvature using the MLS method. Then, according to the discrete gradient idea, the potential feature points are found. Finally, the non-feature points are sampled simply and comprehensively. The proposed method has good expansibility and adaptability. For future work, we would like to extend the first-order Delaunay neighborhood to a multi-order neighborhood to further improve the robustness and anti-noise ability of the algorithm. However, in the discrete gradient calculation, the shortest path length between two points is usually taken as the approximate geodesic distance, which is time consuming and thus requires further research and optimization to find a balance between simplified speed and accuracy.
Author Contributions
Conceptualization, Z.Z. and D.Z.; methodology, M.G., Z.Z. and D.Z.; software, M.G.; validation, M.G.; formal analysis, M.G.; investigation, M.G.; resources, Z.Z.; data curation, M.G.; writing—original draft preparation, M.G.; writing—review and editing, M.G., Z.Z. and D.Z.; visualization, M.G.; supervision, Z.Z. and D.Z.; project administration, M.G.; funding acquisition, Z.Z. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (61572307).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thanou, D.; Chou, P.A.; Frossard, P. Graph-Based Compression of Dynamic 3D Point Cloud Sequences. IEEE Trans. Image Process. 2016, 25, 1765–1778. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Qiao, S.; Wang, X.; Yang, Y.; Zhang, Y. Feature-Preserved Point Cloud Simplification Based on Natural Quadric Shape Models. Appl. Sci. 2019, 9, 2130. [Google Scholar] [CrossRef]
- Sun, W.; Bradley, C.; Zhang, Y.; Loh, H. Cloud data modelling employing a unified, non-redundant triangular mesh. Comput. Des. 2001, 33, 183–193. [Google Scholar] [CrossRef]
- Weir, D.J.; Milroy, M.; Bradley, C. Reverse engineering physical models empolying wrap-aroud B-spline surfaces and quadrics. J. Eng. Manuf. 1996, 210, 147–157. [Google Scholar] [CrossRef]
- Martin, R.R.; Stroud, I.A.; Marshall, A.D. Data reduction for reverse engineering. Proc. Inf. Geometers Conf. 1997, 10, 85–100. [Google Scholar]
- Kim, S.-J.; Kim, C.-H.; Levin, D. Surface simplification using a discrete curvature norm. Comput. Graph. 2002, 26, 657–663. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Hu, Q. A feature preserving algorithm for point cloud simplification based on hierarchical clustering. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5581–5584. [Google Scholar] [CrossRef]
- Chen, Y.H.; Ng, C.; Wang, Y. Data reduction in integrated reverse engineering and rapid prototyping. Int. J. Comput. Integr. Manuf. 1999, 12, 97–103. [Google Scholar] [CrossRef]
- Han, H.; Han, X.; Sun, F.; Huang, C. Point cloud simplification with preserved edge based on normal vector. Optik 2015, 126, 2157–2162. [Google Scholar] [CrossRef]
- Tonini, M.; Abellán, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–110. [Google Scholar] [CrossRef]
- Chen, Z.; Da, F. 3D point cloud simplification algorithm based on fuzzy entropy iteration. Acta Opt. Sinica 2013, 33, 0815001. [Google Scholar] [CrossRef]
- Turk, G. Texture synthesis on surfaces. Proc. Annu. Conf. Comput. Graph. Interact. Tech. SIGGRAPH 2001, 347–354. [Google Scholar] [CrossRef]
- Markovic, V.; Jakovljevic, Z.; Miljkovic, Z. Feature Sensitive Three-Dimensional Point Cloud Simplification using Support Vector Regression. Teh. Vjesn. Tech. Gaz. 2019, 26, 985–994. [Google Scholar] [CrossRef]
- Chen, S.; Tian, D.; Feng, C.; Vetro, A.; Kovacevic, J. Contour-enhanced resampling of 3D point clouds via graphs. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2941–2945. [Google Scholar]
- Xia, S.; Wang, R. A Fast Edge Extraction Method for Mobile Lidar Point Clouds. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1288–1292. [Google Scholar] [CrossRef]
- Elkhrachy, I. Feature Extraction of Laser Scan Data Based on Geometric Properties. J. Indian Soc. Remote Sens. 2017, 45, 1–10. [Google Scholar] [CrossRef]
- Li, T.; Pan, Q.; Gao, L.; Li, P. A novel simplification method of point cloud with directed Hausdorff distance. In Proceedings of the 2017 IEEE 21st International Conference on Computer Supported Cooperative Work in Design (CSCWD), Wellington, New Zealand, 26–28 April 2017; pp. 469–474. [Google Scholar]
- Ji, C.; Li, Y.; Fan, J.; Lan, S. A Novel Simplification Method for 3D Geometric Point Cloud Based on the Importance of Point. IEEE Access 2019, 7, 129029–129042. [Google Scholar] [CrossRef]
- Mahdaoui, A.; Bouazi, A.; Hsaini, A.M.; Sbai, E.H. Entropic Method for 3D Point Cloud Simplification. In Computers and Devices for Communication; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 613–621. [Google Scholar]
- Yuan, S.; Zhu, S.; Luo, W.; Yu, Z.-Y.; Yuan, L.-W.; Li, D.-S. Feature preserving multiresolution subdivision and simplification of point clouds: A conformal geometric algebra approach. Math. Methods Appl. Sci. 2018, 41, 4074–4087. [Google Scholar] [CrossRef]
- Bernard, F.; Salamanca, L.; Thunberg, J.; Tack, A.; Jentsch, D.; Lamecker, H.; Zachow, S.; Hertel, F.; Goncalves, J.; Gemmar, P. Shape-aware surface reconstruction from sparse 3D point-clouds. Med. Image Anal. 2017, 38, 77–89. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Ma, S.; Xu, D. Guided Filter Simplification Method for Noisy Point Cloud Data. In Proceedings of the 2020 Chinese Automation Congress (CAC), Xi’an, China, 7–8 November 2020; pp. 6951–6955. [Google Scholar]
- Floater, M.S.; Reimers, M. Meshless parameterization and surface reconstruction. Comput. Aided Geom. Des. 2001, 18, 77–92. [Google Scholar] [CrossRef]
- Dey, T.K.; Sun, J. An Adaptive M LS Surface for Reconstruction with Guarantees. In Proceedings of the Third Eurographics Symposium on Geometry Processing, Vienna, Austria, 4–6 July 2005; pp. 43–52. [Google Scholar]
- Wang, H.; Scheidegger, C.; Silva, C. Bandwidth Selection and Reconstruction Quality in Point-Based Surfaces. IEEE Trans. Vis. Comput. Graph. 2009, 15, 572–582. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).