Abstract
We present a review of the possibilities to conduct experiments of high efficiency in the nuclear and high energy physics with spin-polarized beams in a collider complex, configuration of which includes Siberian snakes or figure-8 collider ring. Special attention is given to the recently elicited advantageous possibility to conduct high precision experiments in a regime of the spin transparency (ST) when the design global spin tune is close to zero. In this regime, the polarization control is realized by use of spin navigators (SN), which are compact special insertions of magnets dedicated to a high flexibility spin manipulation including frequent spin flips.
1. Introduction
Experiments with polarized beams have been and remain a crucial tool in understanding particle and nuclear structure and reactions from the first principles []. The necessity of fundamental studies of the matter microstructure with polarized beams in accelerators can be justified in general by an irrefutable argument that one needs to characterize the state of the incident colliding particles by a complete set of the involved dynamical parameters, and the particle spin orientation (longitudinal and transverse) is one of them. The search for new physics beyond the Standard model necessitates high-precision experiment with polarized beams. The search for CP- and T-violations in semi-strong hadron interactions [,,] belongs to this category. In particular, the extension of the Standard model including CP- and T-violations may explain the anomalously large baryonic asymmetry of the Universe where the Standard model of the elementary particle physics disagrees with the experimental results by many orders of magnitude []. The study of the nucleon spin structure is one of the main goals of the Electron-Ion Collider EIC (BNL, Brookhaven, NY, USA) [] and the NICA collider (JINR, Dubna, Russia) []. Recent advances in spin physics have led to a proposal of using storage rings for the search of axion-like particles, which are one of the candidates for explaining the dark matter in the Universe []. The aforementioned projects require precise control of the longitudinal and transverse polarizations in colliders and storage rings [,,].
The presented article is a review of the related accelerator aspects of the polarized beam instrumentation, namely acceleration, maintenance, control and spin manipulation of the polarized beams. Based on earlier established methods and concepts of the coherent spin preservation and control such as Siberian Snakes (SibS) [] and Figure-8 synchrotrons (F8S) [,], here we mainly focus on the newly discovered possibilities of further enhancing the flexibility and precision strength of the polarized beams operation in colliders, which we call the spin transparency (ST) [].
The content of this paper is exposed in the historical order of developments in the area from the early 1960s until the recent years. During the preceding period (starting in the 20th century) associated crucially with the arriving and setting of quantum mechanics, electrodynamics (QED) and atomic and nuclear physics, a fundamental role of spin as an intrinsic feature of the subatomic particles has been elicited through numerous series of critical observations, measurements and breakthroughs in the theory and experiments. Lighting up this heroic era should complement our review of the accelerator problematics, although adding the related material would make the paper volume much bigger. By the way, to the fortune of the authors and potential readers, an excellent description of the spin physics history including this period, together with profound exposition of motivations for critical experiments with polarized beams, was presented to the nuclear and high energy physics community several years ago by Prof. R. Milner []. Acquainting with his remarkable article would benefit a reader with more complete perception of history and destinies of the spin physics, so we recommend it to the reader.
2. General Requirements to Polarized Colliders
Polarized sources. The existing polarized ion source technology meets the requirements of the existing and planned polarized beam colliders []. The current state of the polarized source technology is briefly discussed in Section 3.1.
Figure of Merit (FOM). This characteristic of colliding beams is defined as the product of the experiment’s luminosity L and of the two particle polarizations and squared: []. This parameter quantifies the overall performance of a polarized beam experiments involving collisions of two polarized particles, such as polarized beam collider experiments and experiments with a polarized beam on a polarized target. Its statistical uncertainties scale as . The fourth-power dependence of the on the polarizations motivates the development of techniques for generation and preservation of the highest beam polarization degree.
Beam polarization degree preservation through acceleration. After a polarized beam is generated by a polarized source, the first challenge is to preserve the beam polarization in the process of its acceleration to the final energy. The main difficulties with preserving the polarization are associated with crossing of numerous spin resonances [,,,,,,,,,,,].
Spin rotators. Polarized beam experiments typically require adjustment of a certain polarization orientation at the interaction point and its variability []. Two spin rotators are placed around each IP in RHIC to provide longitudinal polarization at that IP []. The ST mode offers the capability of manipulating the polarization direction at the IP including spin flip by adjusting small magnetic field integrals. Polarization in the ST mode can be manipulated in real time during an experiment.
Polarimetry. Adequately fast and accurate polarimetry is necessary for polarized beam setup and monitoring of polarization evolution during the store and collider experimental program. Recently proposed experiments require accuracy of absolute polarization measurement at the level of ∼1% on a time scale of 1 h. Some of the experiments also require bunch-by-bunch polarization measurement []. The general concept of hadron polarimetry is presented in Section 3.2.
Capability of a frequent spin flipping. This is another typical requirement of polarized beam experiments crucial for minimizing their systematic errors, as discussed in Section 3.3. Spin flipping has been demonstrated experimentally by a slow ramp of an RF magnet’s frequency through a spin resonance tune [,,,,,]. This technique is used in RHIC for spin flipping with a high efficiency of 97% in the energy range of 24–255 GeV []. Reference [] proposed the method of a trapped spin flip allowing one to reverse the spin every particle turn using RF fields. Single-, many-, and multi-turn spin-flipping systems have been considered for figure-8 rings and racetrack synchrotrons with and without Siberian snakes []. A multi-turn spin-flipping scheme using quasi-stationary magnetic fields has been proposed for reversing the ion spins in a figure-8 collider [].
Long term maintenance of beam polarization in the collision mode. A typical collider run takes on the order of 10 h. Decay of the beam spin coherence can hen be caused by high-order stationary spin resonances. Polarization loss during this time should not exceed a few percent.
3. Polarized Sources, Polarimetry and Spin Flipping
3.1. Polarized Sources
Polarized light ions can be provided by an Atomic Beam Polarized Ion Source (ABPIS) [,,,]. In these sources, electron-polarized negatively-charged ions are produced by electron-polarized neutral atoms capturing an electron from unpolarized ions through resonant charge exchange. The neutral hydrogen atoms are selected based on their electron polarization using permanent-magnet sextupoles, which focus two of the hyperfine states with the lowest energies in magnetic field and defocus the other two states. The beam is then fully nucleus polarized by hyperfine transitions. Ionizing species are provided by a plasma source. Such sources have been demonstrated to generate appropriate levels of , , and ion currents and may allow one to generate polarized and beams in the future with appropriate R&D []. JINR currently operates an ABPIS to generate a polarized beam for injection into the Nuclotron and into the NICA collider [] in the future.
Such sources have been shown to provide several milliampere currents in hundred-microsecond pulses and even higher polarized protons intensities []. An advantage of this type of source is the ability to provide both and (or their positive counterparts) from a single device. Additionally, development of the RF transition units has made accessible virtually any polarization state for polarized H or D ions, including the tensor polarization states of ions []. ions from ABPIS have demonstrated polarization over 90%.
Another type of a polarized source is an Optically-Pumped Polarized Ion Source (OPPIS), such as that used at RHIC [,]. In RHIC’s OPPIS, protons capture polarized electrons from laser-polarized rubidium atoms and get converted into electron-polarized neutral hydrogen atoms. The electron polarization is converted into the nuclear polarization in the Sona transition region with magnetic field configuration optimized for polarization transfer. Electron-polarized atomic hydrogen is finally negatively-ionized a sodium vapor cell, being converted into a nuclear-polarized ion.
The RHIC OPPIS has been routinely used in collider operation since 2000. Its intensity is being continuously upgraded. A maximum polarization of 85% has been measured at the linac exit at a beam energy of 200 MeV.
Polarized beams are of increasing interest, and significant progress has been made to develop a source of polarized ions for RHIC [,]. atoms are polarized by the metastability-exchange optical pumping (MEOP) process [] and then transferred to an Electron Beam Ion Source (EBIS) for ionization. The source has demonstrated over 80% polarization of gas, and further development for ionization tests is ongoing.
3.2. Polarimetry
The differential spin-dependent cross section, for an elastic scattering reaction initiated by a polarized beam, is given by []
where is the unpolarized cross section, is the vector analyzing power and is the vector polarization component along the y-axis. If the beam consists of spin-1 particles, are the tensor polarization components and are the tensor analyzing powers. Equation (1) uses the Madison Convention coordinate system, which is a right-handed system with its axes defined with respect to the scattering plane: the positive z-axis is along the beam momentum while the positive y-axis is along where is momentum of the forward-scattered particle.
The procedure for measuring the beam polarizations is to collide it with a target, detect a reaction with known analyzing powers, such as , and elastic scattering, and then extract the polarizations using Equation (1). The analyzing power of elastic scattering as a function of the beam momentum p and the center-of-mass polar scattering angle can be precisely measured, for example, using an unpolarized beam and a polarized atomic hydrogen beam target.
Taking exclusive elastic scattering data can be slow due to the required data processing time. Polarimetry can sometimes be sped up significantly by calibrating the detector’s effective analyzing powers
where is the analyzing power of pp elastic scattering, is the inclusive two-prong left-right ring scaler asymmetry and is the exclusive pp elastic scattering asymmetry. Furthermore, can be averaged over the detector acceptance in for extracting the polarization from an inclusive left-right scattering asymmetry measurement.
3.3. Spin Flipping
Measuring the scattering asymmetry, with the beam polarization always oriented in the same direction, could lead to a systematic false asymmetry associated with errors, such as unequal efficiencies of different detectors, polarimeter misalignment, beam current fluctuations from cycle to cycle, etc. Most of these systematic errors can be eliminated by reversing the beam polarization several times during the measurement. This can be done by alternating the source polarization or flipping the polarization direction of a stored beam. Such a reversal is equivalent to turning the detector over. Then, for instance, a proton scattered to the left, with the beam polarization up, is equivalent to a proton scattered to the right, with the beam polarization down.
The vertical polarization is calculated as
where is the angle-weighted average analyzing power and is the total number of events scattered into the left (right) quadrant with the beam polarization up (down). Similarly, the radial beam polarization is calculated using
where is the total number of events scattered into the up (down) quadrant with the source polarization up (down). Using this method of determining the polarization greatly reduces most systematic errors caused by the false asymmetry. The largest remaining source of the measured polarization’s systematic error is the uncertainty in the analyzing power . For example, the average analyzing power for elastic scattering at 120 MeV is about 0.3.
4. Spin Resonances
The behavior of a particle’s spin in a magnetic field and electric field is a precession with an angular frequency and is described by the Thomas–BMT (Bargmann, Michel, Telegdi) equation [,]:
where q is the particle’s electric charge, m is its rest mass, c is the speed of light, is the particle’s velocity, is , is the relativistic Lorentz energy factor, G is the particle’s anomalous magnetic moment ( for protons, for electrons, and for deuterons) and and are the magnetic field components perpendicular and parallel to , respectively. In Equation (5), the magnetic and electric fields and time are measured in the laboratory frame, while the spin vector is defined in the particle’s rest frame to avoid complex Lorentz transformation of the spin. In circular accelerators, the effect of the electric fields on the spin motion is usually negligible compared to the magnetic fields; thus, the last term inside the square brackets in Equation (5) can usually be ignored when describing spin evolution.
Equation (5) describes the spin evolution in magnetic fields in a semi-classical way. To analyze the spin dynamics in a periodic magnetic structure of a synchrotron, it is sometimes more convenient to use the quantum mechanical spinor formalism [,]. The spin state of a spin-1/2 particle can be represented by a two-component vector called a spinor:
where and are the complex probability amplitudes for the particle’s two possible spin states and , respectively. In the spinor formalism, the spin vector is given by
where is a vector, whose components are the Pauli spin matrices.
Resonance tune equation. In a circular accelerator, it is sometimes convenient to replace the time variable t with the particle’s orbital angle . The transformation between and t is defined by , where is the local radius of curvature of the particle’s orbit. In terms of the orbital angle and two-component spinor , assuming vertical guiding field and absence of coupling, the Thomas–BMT equation (Equation (5)) [,] can be written as [,]
where the diagonal matrix elements describe spin precession around the vertical fields of the bending dipoles, while the off-diagonal element characterizes the spin-perturbing kick, which couples the up and down components of the spinor.
The quantity is given by
where and are the radial and longitudinal perturbing fields, respectively. Due to the periodic nature of a particle’s motion in a synchrotron, can be expanded in a Fourier series
where the Fourier amplitude is called the resonance strength and the harmonic is called the resonance tune, which is the frequency of the spin-perturbing kicks. When the spin precession frequency is equal to the resonance tune , the beam may be depolarized by the coherent spin perturbations caused by these kicks. Note that the spin resonance fenomenon in synchrotrons is similar to the Nuclear Magnetic Resonance (NMR) phenomenon observed earlier in atomic physics.
The second term in Equation (11) can usually be neglected. The radial perturbing field arises from the beam’s displacement from the center of the ring’s quadrupoles and higher-order multipoles:
The first term in Equation (12) is usually the most significant. Inserting it into Equation (11) and ignoring the and higher-order multipole contributions gives
The vertical displacement of a particle y can be decomposed into three parts:
where is the closed orbit displacement due to misalignment of the ring’s elements, describes the particle’s vertical betatron motion and the coupling coefficient characterizes the degree of coupling of the particle’s vertical motion to its horizontal betatron oscillations . Let us consider spin resonance effects, due to each of the y components in Equation (14), separately.
By definition of the closed orbit, is periodic in with a period of . Thus, it contains only integer Fourier harmonics. Therefore, its contribution to is non-zero only when
where n is an integer. These spin resonances, arising from the closed orbit errors , are called the imperfection depolarizing resonances. Note that, for a given closed orbit error, the imperfection resonance’s strength increases with energy as .
Let us next consider the part of Equation (14). Following the basic beam dynamics, the particle’s vertical betatron motion is described by
where is the vertical betatron function, is the beam’s vertical geometric rms emittance, is the vertical betatron tune and is the vertical betatron phase. Due to periodic structure of the integrand, the integral in Equation (13) is non-zero only for harmonics
where m is an integer, while P is the super-periodicity of a synchrotron, i.e., the number of identical periodic building blocks in the accelerator. However, realistic synchrotrons do not have a perfect super-periodicity due to errors in the magnetic fields of each super-period. Thus, spin resonances can also occur at
for any integer n even if it is not an integer multiple of the super-periodicity P. Nevertheless, for , resonances are generally much weaker. These spin resonances, occurring due to the vertical betatron motion , are called the vertical betatron or intrinsic resonances. Note that the intrinsic resonance’s strength is proportional to .
The last term in Equation (14) becomes important when the particle’s horizontal and vertical betatron oscillations are coupled. Then, the coupling coefficient . Betatron coupling happens, to some extent, in all realistic synchrotrons and may be caused, for example, by the presence of skew quadrupoles and/or solenoids. Similar to the vertical intrinsic resonance case, the integral in Equation (13) is significant when . When a strong betatron coupling is introduced, the lattice super-periodicity becomes one and the spin resonances are located at
for all integer n. However, the resonances with may still be more important. These resonances are called the horizontal betatron or intrinsic coupling resonances. The intrinsic coupling resonance strength is proportional to . Depending on and , the horizontal betatron resonances may be as strong as the vertical ones.
Similar harmonic analysis accounting for the spin effect of higher-order magnetic multipoles and non-linearity of the beam dynamics leads to the spin resonance condition
where n, m, h and j are all integers. These spin resonances are called the non-linear or higher-order intrinsic resonances. The order of the resonance in Equation (20) is defined as .
Another effect of the spin–orbit coupling in circular accelerators is that the particle’s synchrotron oscillations may cause frequency modulation of the spin tune. The frequency spectrum of the spin motion then contains not only the normal unperturbed spin tune but also additional harmonics with where l is an integer and is the synchrotron tune. Each of these harmonics may itself satisfy a spin resonance condition. Then, several synchrotron side-band resonances may appear on each side of any spin resonance of the previously discussed types. Finally, by combining Equations (15) and (18)–(20) and taking into account the synchrotron side-band resonances, the general spin resonance condition can be written as
Resonance crossing and Froissart–Stora formula. In the case of a single isolated spin resonance, the resonance driving term , given by Equation (10), is
The Thomas–BMT equation (Equation (5)) for the two-component spinor then becomes
In general, and/or in Equation (23) may be functions of . A practically important case is that of a constant-rate crossing of a single isolated resonance when , where is the constant crossing speed, changes from to and the resonance is crossed at . In this case, Equation (23) can be solved analytically. The solution is given by
where and are the initial and final polarizations, respectively. Equation (24) is the Froissart–Stora formula []. It gives the beam’s final polarization after passing through an isolated spin resonance either by ramping through or by ramping through or by ramping both and at the same time. Equation (24) shows that, if a resonance is weak and/or it is crossed quickly, i.e., , there is no polarization loss. When it is strong and/or it is crossed slowly, i.e., , the polarization is flipped and there is again no polarization loss. Polarization loss occurs for the intermediate cases when .
The Froissart–Stora theory has been extended to the case of correlated periodic crossing (CPC) of a single spin resonance [] based on the general theory of spin motion in a periodic field []. Theory was applied to design of a spin depolarizer []. On the other hand, the CPC theory can also be applied to the design of a spin flipper.
Resonance depolarization. When not applying special polarization preservation techniques, polarization loss during acceleration in a conventional ring is caused primarily by spin resonances [], i.e., when the spin tune is in sync with an integer-multiple combination of the orbital tunes given by Equation (21). Since the spin tune in conventional racetrack synchrotron changes proportionally to the beam energy, spin resonances are unavoidably crossed in the process of beam acceleration. The number of resonances increases with energy leading to beam depolarization, while it is accelerated to high energies.
Compensation techniques (ZGS and AGS). Several techniques have been proposed to preserve polarization when crossing a spin resonance [,,,,,]. Some of them are based on changing the crossing speed or the resonance strength to provide fast or slow resonance crossing [,]. All of these techniques may only reduce, but not completely eliminate, beam depolarization during resonance crossing. Thus, there could still be a significant polarization loss when crossing too many resonances.
One technique, transparent crossing, is based on control of the spin motion directly in the resonance region [,,,]. In principle, it allows one to eliminate depolarization when crossing resonances. However, its effectiveness depends on the beam momentum spread and the use of quickly changing magnetic fields, which alter the spin dynamics during crossing of the effective resonance region.
5. Spin Dynamics in Stationary Conditions: General Theory
5.1. Spin Dynamics on a Closed Orbit in a Ring
According to the above shown analysis, small magnetic fields associated with errors do not demolish the coherent spin of a polarized beam unless they enter in resonances with spin precession in the vertical field. Being sufficiently small, they cause only small periodic shaking of the coherent spin following the behavior of the perturbative field. However, strictly speaking, this result was obtained only in the first order of the perturbation method. A question that was raised back in 1970 is the following: What happens to spin dynamics if we increase the horizontal fields, while the beam closed orbit (disturbed or not disturbed) still exists? Surprisingly, it became possible to solve this interesting problem not only in examples (e.g., a beam passing through a strong solenoid) but also in general. The result is striking: the periodic spin motion exists once a (stable) closed orbit exists; in rest, field behavior is not a matter. Thus, general spin motion is then a precession around the periodic solution with some global tune []. Periodic polarization is unique if . In the case , any polarization is periodic, i.e., this is a degenerate situation.
An ultimate illustration of this statement is a case of a solenoid insertion causing a maximum spin disturbance, i.e., flip of the vertical spin (Figure 1): in this case, periodic spin is horizontal outside of the solenoid, while the global spin tune is equal to independent of the spin precession phase advance over the arcs of . However, it is symptomatic that, being viewed in the straight opposite to the solenoid, the periodic spin is longitudinal.
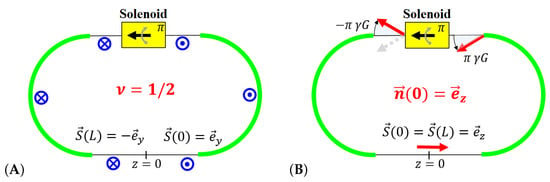
Figure 1.
Spin in a ring with a -solenoid showing: flip of the vertical polarization (A); and behavior of the periodic polarization (B).
The statement about existence of a periodic polarization has been derived based not on examples such as that but by applying a fundamental method of proper vectors of spin transformations matrix as for rotations. This matrix is characterized by three independent parameters corresponding to three elementary rotations in three orthogonal planes. Finally, there is an equivalent visualization for any rotation in a three-dimensional space for an ensemble of vectors (or a solid body): the axis of rotation (two parameters) and the angle of rotation of the spin ensemble about it. Specifically this axis arrives as the periodic spin direction driven by the TBMT spin law, Equation (5), over the closed orbit in an accelerator ring.
5.2. Spin Field and Adiabatic Invariant
When considering particle motion along a periodic closed orbit, one can introduce spin projection on the periodic solution: as an invariant []. In reality, particles experience oscillations near a reference orbit. At stability, there are three adiabatic invariants (partial action integrals) of particle orbital motion . Correspondently, for the spin degrees of freedom, we may introduce a spin invariant action as a function (a certain form) of the spin and orbital variables:
It follows from the definition of this form as a dynamical invariant that the vector function taken along the particle trajectory should satisfy the TBMT equation, i.e., it should be a special solution of Equation (5), which is expressed as a unique function of the orbital variables. Thus, it can be found by calculating the spin deviation from the periodical vector enforced by particle oscillations relative to the closed orbit [,].
Thus, the spin dynamics in synchrotrons can be described similarly to the orbital motion where one first specifies the design closed orbit. A particle moving the closed orbit repeats its velocity every turn. In the case of stable motion, particles deviating from the closed orbit experience betatron and synchrotron oscillations while remaining near the closed orbit.
The role of the closed orbit for the spin is played by the periodic spin precession axis (n axis). When moving along the design closed orbit, the particle spins oriented along the n axis repeat their directions every turn. As illustrated in Figure 2, a spin oriented transversely to the n axis rotates by an angle in one turn along the closed orbit where is the spin tune.
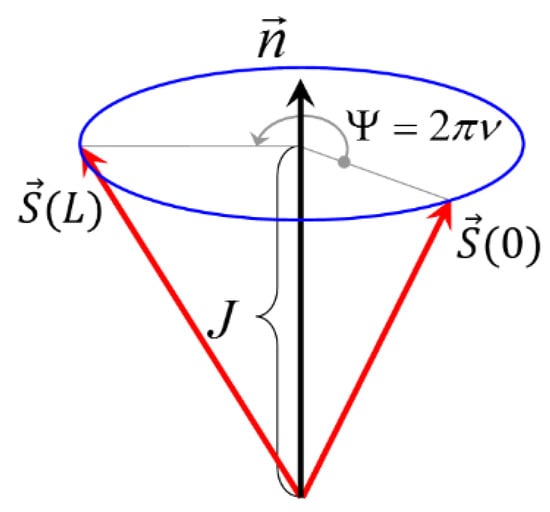
Figure 2.
Spin precession about the n axis in one turn.
A necessary condition for a high degree of the beam polarization in a stationary situation is smallness of the spread. Polarization remains stable only along the n axis, since the spin tune spread completely smears the particle spins initially transverse to the n axis in about turns.
We thus have acquired a general canonic representation of the beam polarization dynamics for cyclic motion in a synchrotron. Now, let us return to the intriguing observation in the above example with a spin flip in a straight with a solenoid insertion: the classical phase advance over arcs due to the anomalous magnetic moment effectively occurs out of the spin global cycling. What does such a trick do to the problem of the coherent spin preservation during acceleration, maintenance, etc.?
6. Spin Echo Techniques for Spin Stabilization in Synchrotrons
6.1. Siberian Snakes
The above example with spin flip through a solenoid actually has played a role of a bifurcation point for arriving at the Siberian Snakes (name given by E. Courant, abbreviation SibS is used below), the invention of which [] is considered to be a major advance in the endeavors on preserving beam polarization in high energy accelerators and storage rings.
What is a Siberian Snake? Our definition here is: a SibS is a helical chain of dipole magnets (or simply a solenoid at low energies) that rotates the spin of a particle by about an axis , while it does not disturb the beam orbit outside of the snake. Insertion of a single Siberian snake into a collider ring completely rearranges the spin motion. The stable polarization is no longer vertical but lies in the collider plane, while the spin tune (the global tune ) is independent of energy and equals one half. This dramatic rearrangement changes totally the treatment of the spin resonances problem in acceleration and long term maintenance of the polarized beams in synchrotrons.
SibS effect as Spin Echo implemented in an accelerator ring. In the above example with vertical spin flip through a solenoid, the axis is directed along the beam velocity. Below, we show examples of snakes composed of dipole magnets, with axes transverse or parallel to the beam direction or oriented in another desired direction. From the point of view of the global effect of a SibS on the spin motion in a synchrotron, the snake axis should lie in the plane of the design orbit of a synchrotron. Other than that, the choice of a specific direction of the snake axis can be determined by the desired orientation of the periodic polarization in the straight opposite to the snake-dedicated straight (see Figure 4). For a more clear yet profound perception of this circumstance, it may be useful to look at the diagram of spin motion presented in Figure 3 in terms of the Spin Echo, a phenomenon of the spin ensemble dynamics in inhomogeneous magnetic field revealed in studies of the nuclear magnetic resonance (NMR). In our case of a spin ensemble of a charge particle beam in a synchrotron, the role of the inhomogeneity factor is played (basically) by the energy spread of the beam, which leads to a spread in the spin precession phase in the arcs proportional to the anomalous magnetic factor G:
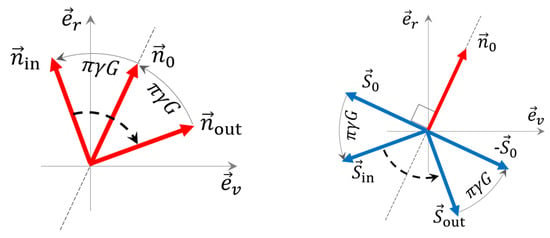
Figure 3.
Spin Echo schematics. Notations and are for the periodic spin and horizontal spin transverse to that, respectively. The starting point is the straight opposite to the straight with the snake. The “in” and “out” indexes denote the spin orientations at the entrance and exit of the snake, respectively. and are the radial and velocity direction unit vectors, respectively.
This spread gets canceled over one beam turn, together with the “automatic” cancellation of the overall phase advance in a single beam turn, thanks to the vertical spin flip through the SibS. We would like to underline that, in the context of the SibS phenomenon as suppression (cancellation) of the harmful impact of the spin precession in the arcs that grows with energy, the direction of the SibS axis is not of the first importance, but the spin flip carried out by a SibS is crucial in protection of the spin coherence against spin depolarizing resonances.
Figure 4 illustrates the change of the global spin dynamics in a ring with an installed snake producing a flip of the vertical spin around the snake axis.

Figure 4.
Spin in a ring with a single snake.
The red arrows in Figure 4A show the dynamics of a spin oriented along the periodic polarization direction (n axis). In the straight opposite to the SibS, the n axis is parallel to the snake axis . When going through one arc, the polarization lies in the collider’s plane and rotates about the vertical field. It then rotates by about the snake axis and restores its original direction after rotation in the second arc. One might say that the snake “compensates” the spin effect of the arcs at any particle energy.
The blue arrows in Figure 4B illustrate the dynamics of a spin oriented transversely to the n axis. The spin is vertical at the entrance into the first arc and flips after passing the snake. As a result, the snake sets the spin tune of the accelerator to one half for all beam energies, thus avoiding crossing of spin resonances during acceleration.
It is worth noting that the SibS case is not the only possible situation in synchrotrons when such an intrinsic feature of the spin dynamics as the spin echo manifests itself. Another example of this kind is an adiabatic crossing of a spin resonance. The spin echo in that case is considered in a dedicated paper [].
Snake zoo. A solenoid rotating the spin by 180 degrees about the longitudinal axis (Figure 1) is an elementary example of a SibS []. Use of solenoids is preferable at low energies because they do not perturb the closed orbit. The longitudinal field integral of a solenoidal snake depends on the particle momentum and is given for protons and deuterons by
During acceleration, the solenoid field must change proportionally to the beam momentum. Therefore, solenoidal snakes can in practice be used in the momentum range of up to ∼10 GeV/c.
For proton momenta above ∼10 GeV/c, it is more adequate to use transverse fields, since their integral required for a snake is proportional to the particle velocity and is practically independent of the beam momentum. There are many proposals of snake designs for protons using transverse fields of dipole and helical magnets.
Let us give examples of snakes based on use of dipole magnets where it is easy to follow the spin evolution along the snake. The following schematics illustrate the SibS design principles. Figure 5 shows the schematics of snakes composed as a chain of dipole magnets [,]. Figure 6 illustrates snake design using helical transverse field [,,].
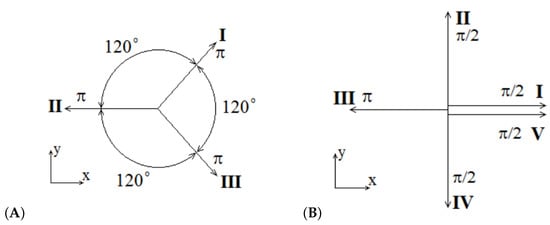
Figure 5.
Schematics of dipole snakes with radial (A) and longitudinal (B) axes. The particle velocity is transverse to the picture’s plane. The arrows indicate the field directions.
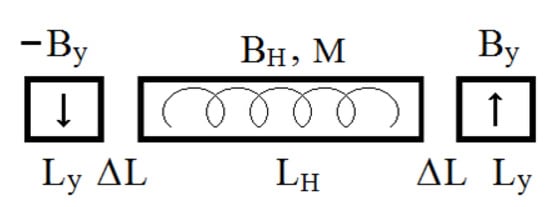
Figure 6.
Snake schematic with an M-turn helical magnet.
The design of a snake with a radial axis (Figure 5A) uses three dipole magnets in the three consecutive snake sections (I–III). The field direction in each section is indicated in the figure. In each section, the spin rotates by an angle about the field direction. The scheme of a snake with a longitudinal axis (Figure 5B) uses five dipole magnets. Four of them rotate the spin by an angle . The central section with a radial field rotates the spin by an angle . The net field integral is independent of energy and is 16.5 T·m for each snake. In both snake designs, the beam velocity direction is restored. The orbital shift generated by the snake in the orbital plane can be compensated, for example, in a near-by section using a pair of dipoles with vertical fields of opposite direction.
In the ultra-relativistic limit, the dipole field integrals required to rotate the proton and deuteron spins by are
It is worth noting that it is not practical to use transverse fields in the design of snakes for deuterons due to the small anomalous part of their gyro-magnetic ratio. To preserve the deuteron polarization at high energies, it is more adequate to use a figure-8 ring configuration [,].
Helical field is efficient for use in snake design. When the transverse field of a helical magnet makes a full number of turns, the velocity direction is restored automatically. The orbit offset can be compensated by a pair of dipoles placed, for example, around the helical magnet. Use of multi-turn helical magnets allows one to significantly reduce the maximum orbit deflection inside the snake, which is inversely proportional to the number of field turns M.
When using a helical magnet with M full turns, the total integral of the snake’s transverse field in the ultra-relativistic limit equals []
Two SibS in a ring. With two snakes located in opposite straight sections of a race-track type storage ring, the n axis is vertical, as shown in Figure 7, and the spin tune depends on the angle between the two snake axes
and equals one half if the angle is [].
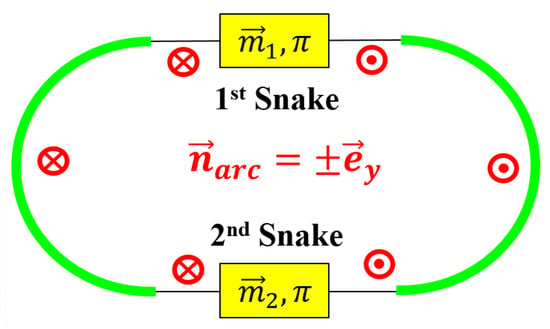
Figure 7.
Spin dynamics in a collider with two SibS.
Polarized beams at ultra-high energies. At hadron (proton, ) energies well above 100 GeV, one may need to install more than one pair of SibS in a collider ring in order to suppress the growing depolarizing power of the characteristic depolarizing resonances due to collider imperfections []. Such a conceptual design was actually undertaken about 30 years ago []. Here, we use a quotation from Reference []: “In the 1980s, a new 20 TeV on 20 TeV proton–proton collider was being planned in the U.S. Each 20 TeV SSC ring would have about 36,000 resonances. It was concluded that it should be possible to accelerate and maintain the polarization of 20 TeV protons in the SSC, only if the new Siberian-snake concept ...really worked. This motivated the development at IUCF. Twenty six empty spaces for Siberian snakes were added in each SSC ring. The SSC was canceled in 1993”. Here, we can readdress such an enterprise as polarized super-high energy (100 TeV range) hadron beams to the today thought and planned future hadron supercolliders. We are sure it is doable when requested. For super-high energies (beyond 1 TeV), spin-compensated quadrupole technique has been proposed []. One can then significantly reduce the required number of snakes.
Long-Term Spin Stability in Collider with Siberian Snakes. One of the critical issues for any collider is a potential depolarization caused by higher order stationary spin resonances associated, in particular, with the beam–beam space charge interaction in the presence of a large spin tune spread. It was pointed out in earlier studies that insertion of SibSs also provides compensation of the spin tune spread caused by the beam emittance [,], thus giving one the capability of a high-precision spin tune control. A long-term polarization maintenance was experimentally demonstrated in RHIC with two Siberian Snakes, where the polarization of colliding proton beams is sustained for many hours []. This success is achieved due to compensation of the spin tune spread by the snakes and a fine selection of the betatron tunes.
Polarized beam facilities and projects with Siberian Snakes. As examples, let us consider the snake designs which have been realized at IUCF and in the RHIC collider and are under development for the NICA project and FermiLab’s Main Injector.
Solenoidal snake in the IUCF Cooling Ring. A solenoidal snake was used in the IUCF Cooler Ring to test the snake concept []. With the snake off, polarized protons were depolarized during acceleration when the imperfection ( MeV) and intrinsic ( MeV) resonances were crossed. Turning of the snake on completely changed the situation, beam depolarization was completely eliminated during acceleration of polarized protons.
Figure 8 shows a schematic of the solenoidal Siberian snake of the IUCF Cooler Ring.

Figure 8.
Solenoidal Siberian snake of the IUCF Cooler Ring.
The main element of the design is a solenoid with a maximum field integral of 2 T·m. Besides its effect on the spin, the solenoid introduces coupling of the transverse orbital motion. This coupling was compensated by two pairs of skew quadrupoles . The design also used two pairs of normal quadrupoles Q for optical match of the snake to the ring. The total length of the snake including the additional quadrupoles was about 10 m.
Solenoidal snake in Nuclotron. It is planned to use the super-conducting synchrophasotron Nuclotron as an injector of polarized protons in the NICA collider []. It is proposed to insert a solenoidal snake into the Nuclotron lattice to preserve the proton polarization during acceleration to 6 GeV/c. The difficulty with insertion of a solenoid snake is limited space availability in the accelerator; the snake must fit in two empty straights of 3.5 m each.
The problem of placing a solenoidal snake in Nuclotron is solved [] by omitting compensation of betatron coupling and employing super-conducting solenoids with a high field ramp rate of ∼1 T/s, which can be built at JINR. Figure 9 shows a schematic of placement of the Siberian snake solenoids among focusing and defocusing structural quadrupoles.
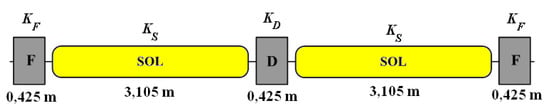
Figure 9.
Schematic of placement of the Siberian snake solenoidsin Nuclotron without compensating quadrupoles.
The longitudinal field integral of the snake is T·m at a momentum of 6 GeV/c. The corresponding solenoid field is 3.6 T.
Helical snake in RHIC.Figure 10 demonstrates a schematic of the helical snake of the RHIC collider [,,,]. The snake consists of four sections of 2.4 m each. The dipole field makes a full turn in each section. The magnetic fields at the entrance into each section are vertical and pair-wise opposite in sign for compensation of the orbit excursion at the exit from the snake. The full length of the Siberian snake is 10.2 m with gaps of m. The direction of the spin rotation axis of such a snake is controlled by the magnetic fields and of the inner and outer helix pairs. A full Siberian snake with a rotation axis oriented at an angle of to the particle velocity is set at 25 GeV using the fields of T and T.
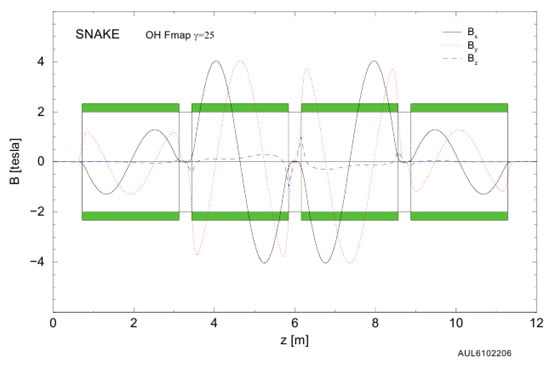
Figure 10.
Schematic of the helical snake of the RHIC collider.
Such fields result in a “snake”-line beam trajectory inside each snake of the RHIC collider as illustrated in Figure 11. The orbit deflection is and 3.3 cm in the horizontal and vertical directions, respectively. The term “Siberian snake” was introduced by E.D. Courant who noted that the closed orbit oscillates in the changing transverse fields of the snake resembling a moving snake []. The term “Siberian snake” was also adopted for use with longitudinal fields, even though, strictly speaking, a solenoid does not distort the closed orbit.
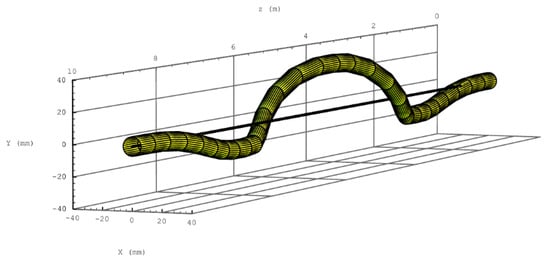
Figure 11.
Orbit deflection inside one of the helical snakes of the RHIC collider.
Multi-turn helical snake proposed for FermiLab’s Main Injector. The helical snakes developed for the RHIC collider can be used starting with an energy of ∼20 GeV due to their closed orbit excursion.
A helical dipole with M field turns allows one to reduce the orbit deflection inside a snake by several times [,,]. A snake design using a single such helical dipole is shown in Figure 6. Two corrector dipoles with vertical fields of opposite directions are placed around the helical dipole for compensation of the radial orbit shift. A design of a helical snake with 4 field turns has been proposed for acceleration of polarized protons from 9 to 120 GeV in FermiLab’s Main Injector [].
The axis of such a helical snake is practically longitudinal. The limitation on the minimum energy due to the magnet aperture goes down to a few GeV. Figure 12 shows a graph of the orbit deflection in the snake scheme with a four-turn helical dipole. The snake is 6.8 m long and has the following parameters: , T, m, T and m. The maximum orbit excursion is about 1.5 cm for particles with a momentum of 8.9 GeV/c.
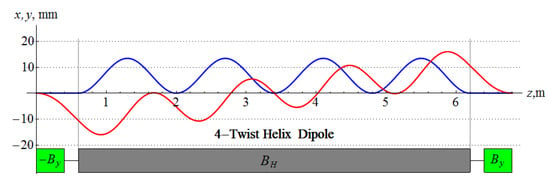
Figure 12.
Orbit deflection inside a four-turn helical snake proposed for FermiLab’s Main Injector.
Increasing the number of periods of a helical snake allows one to lower the injection energy of polarized protons into a collider.
SibS constraints. The challenges of using a Siberian snake are its proper realization and mitigation of its orbital effects. A Siberian snake can be built using either longitudinal or transverse fields. A longitudinal field does not change the beam orbit but its spin rotation is inversely proportional to the beam momentum. Therefore, application of this type of snakes is limited to relatively low energies. In helical and dipole snakes, the integral of the transverse field is almost independent of the beam energy. The limitation of using such snakes is associated with the beam’s closed orbit excursion and transverse focusing, which becomes acceptably small only at relatively high energies. Thus, use of Siberian snakes is problematic in the medium energy range from a few GeV to a few tens of GeV.
Besides its effect on the spin, transverse field also deflects the closed orbit. This leads to increase of the total integral of the snake field, which can vary for protons within a range of 16 to 30 T·m. The value of the total integral of the snake field depends on the maximum closed orbit deflection at the beam injection energy and on the direction of the snake axis . The closed orbit distortion is inversely proportional to the particle energy and thus reduces with energy increase.
In addition, due to a small value of the deuteron anomalous magnetic moment (), use of Siberian snakes with transverse fields for deuterons would require an integrated transverse field of the order of 600 T·m even in the medium energy range. Therefore, it requires impractically high field and/or long snake magnets.
6.2. Figure-8 Ring
An elegant solution for low and medium relativistic energies free of SibS technical challenges while equally effective for any species including deuterons is to use an accelerator in a figure-8 ring configuration [,]. In this type of an accelerator configuration, rotation of spins in one direction in one arc is compensated by rotation of the spins in the opposite direction in the other arc. For a perfectly flat orbit at a constant energy, this cancellation is exact regardless of the guiding (vertical) field behavior along the arcs:
This feature of the energy independence of the net spin procession in one turn (i.e., the spin tune) is a topological property of a figure-8 ring, which means that it is independent of the dimension and shape of the arcs as well as of the local bending angles, as long as the accelerator is completely flat. Such a topological cancellation of the phase advance of the spin precession in the vertical field of a figure-8 synchrotron (F8S) is, again, manifestation of the spin echo—a fundamental property of the spin dynamics. However, in this case, it results from the spin gymnastics that is rather rudimentary compared to the SibS.
An important difference between the F8S and SibS cases is that the global spin tune of an ideal figure-8 accelerator is not 1/2 or other fixed number but zero for any beam energy, i.e., the particles are constantly in the region of the zero-integer spin resonance. Therefore, to stabilize the polarization direction against influence of radial fields of imperfections, instead of strong snake fields, it is now sufficient to introduce weak design fields to overcome the effect of the zero-integer spin resonance strength []. As an example, a longitudinal field integral as low as 1 T·m provides preservation of the polarization during acceleration up to 100 GeV of both protons and deuterons. To keep the spin tune constant during acceleration, thus avoiding spin resonance crossing, the solenoid field should change proportionally to the beam momentum.
Figure-8 rings in the energy range of ∼20–30 GeV may serve as universal polarized beam boosters for all hadron species. A figure-8 collider configuration is an efficient solution for all polarized species but especially for deuterons in the sense that such a collider ring can be additionally equipped with SibSs to serve the polarized proton and 3He beams operation. Such a collider is practically free of the polarized beam acceleration and maintenance issues. This is a substantial advantage of the figure-8 design over the conventional one in terms of simplicity, required technology and operational robustness of a polarized hadron beam facility.
Let us note that potential applications of SibS and F8S are not limited to just highly-efficient preservation of the beam spin coherence in accelerator and collider facilities.
7. Spin Transparency
7.1. General Idea
Energy independence of the spin tune due to the spin echo effect and sensitivity of the spin motion to weak magnetic fields near a zero spin tune open an avenue for a new spin control technique, called a Spin Transparency (ST) method []. The idea of the ST method is in compensation of the spin effect of the synchrotron’s magnetic elements when the particle is moving on the design orbit, i.e., the synchrotron lattice is designed in such a way to provide repeatability of any spin direction after every particle turn. Such a lattice becomes effectively “transparent” to the spin, i.e., the spin effect of the synchrotron lattice over a particle turn is equivalent to that of a drift space. This formally means that the particles are in the region of a spin resonance (the ST resonance). This means that spin motion is governed, to the first order, by ring imperfections causing closed orbit excursion and, to the second order, by the particle’s betatron and synchrotron motions. However, at least up to modest energies of a few hundred GeV, these effects are relatively small and are further suppressed for deuterons due to their small G.
In the ST-resonance region, even weak perturbing fields can substantially change the spin orientation. However, such a high sensitivity to small fields can be used to create an efficient polarization control system by means of a special device called a “Spin Navigator” (SN). The role of the SN is shift the spin tune from the ST resonance by a small value of the SN tune and to set the required stable polarization direction at the selected orbital location. Therefore, a spin pointing along is repeated every particle turn while a spin oriented transversely to the direction rotates by a small angle of in one particle turn. The only requirement is that the spin rotation due to the SN should be much greater than that due to imperfections, i.e., the zero integer spin resonance strength. Such a navigator has practically no effect on the orbital beam dynamics [,].
Since, in the spin transparent mode, the polarization is stabilized by weak magnetic fields of the order of a few Tm, it becomes possible to set any polarization orientation at any location in the ring by making a small rotation about an appropriate axis. Moreover, the polarization direction can be adiabatically adjusted while keeping the spin tune constant thus avoiding any depolarization. Spin flip is a particular example of such a spin manipulation []. More generally, in the spin transparent mode, one has full control of the polarization direction and the spin tune. For example, one can change polarization from transverse to longitudinal.
Spin navigators allow one to drastically reconsider the methodology of the spin orientation control when performing polarized beam experiments.
Traditionally, in colliders with preferred spin direction, polarization is controlled using a pair of spin rotators with “strong” fields. Such rotators introduce noticeable distortions of the beam orbital characteristics as a result leading to variation of the experimental running conditions for different polarization directions. Adjustment of the polarization orientation using strong-field spin rotators while conducting an experiment is a complex technical problem.
In colliders with spin transparency, ion polarization can be efficiently controlled using “weak” fields, which have essentially no effect on the beam’s orbital characteristics. It does not present a problem to manipulate the spin orientation while running an experiment by varying the SN fields. It becomes feasible to implement a spin-flipping system with a spin reversal time of less than 1 s that allows for polarized beam experiments at a new precision level.
7.2. Spin Transparency of Figure-8
The most natural representative of a ST collider is an accelerator in the shape of a figure-8 []. In such a collider, the effect of one arc on the spin is compensated by the other arc. As an example, Figure 13 shows a scheme for setting the longitudinal ion polarization in the experimental straight section of JLEIC by activating a weak solenoid of a universal 3D spin navigator []. Since the effect of the whole ring on the polarization over one particle turn is reduced to zero, the spin motion is stabilized by the solenoid, which “forces” the longitudinal polarization direction at the solenoid location. The subsequent polarization dynamics along the collider ring is determined by strong arc fields, which rotate the spins in the collider’s plane returning them to the longitudinal polarization after a full particle turn.
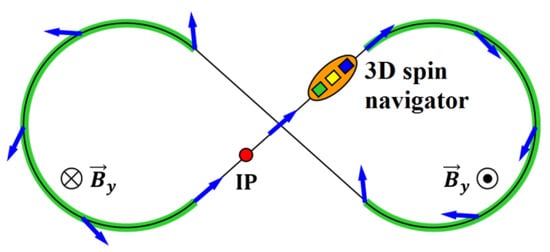
Figure 13.
Schematic of polarization dynamics in JLEIC.
To obtain any polarization direction at the collision point for any ion species including deuterons, the universal 3D spin navigator includes three modules, which can rotate the spin about three orthogonal axes . They are built using weak solenoids and stabilize a given polarization direction .
It is sufficient to use a 10 T·m solenoid to stabilize the polarization of any particles including deuterons in the longitudinal direction at the solenoid location in a figure-8 TS collider up to an energy of about 100 GeV. Besides, such a scheme is universal for all particle species including both protons and deuterons. What especially stands out in the case of a figure-8 ring is the possibility of complete polarization using weak solenoids, which do not distort the closed orbit. Obtaining longitudinally-polarized deuterons in the energy range of up to 100 GeV using a single Siberian snake with a longitudinal axis would require a longitudinal field integral of about 1300 T·m or a transverse field integral of about 500 T·m.
7.3. Spin Transparency in a Racetrack with Two Identical Siberian Snakes
Insertion of two identical Siberian snakes in the opposite straights of a racetrack-shaped synchrotron results in a zero value of the spin tune in its entire energy range and the synchrotron goes into the spin transparency regime.
ST mode in the NICA collider. It is proposed [] to control the proton and deuteron polarizations in the NICA collider in the momentum range of up to 13.5 GeV/c using two solenoidal Siberian snakes. The scheme of ion polarization control in the NICA collider is presented in Figure 14.
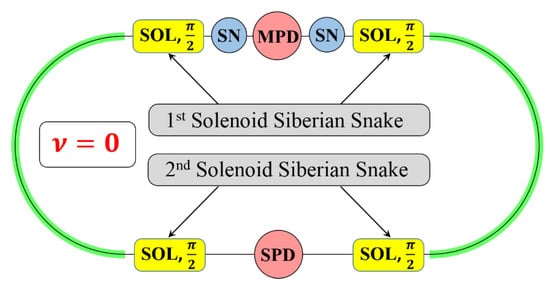
Figure 14.
Scheme of realization of the ST regime in the NICA collider.
Two solenoidal snakes installed symmetrically in respect to both MPD and SPD set-ups will provide ST regime in NICA collider. Two spin navigator insertions (SN) symmetrically placed near MPD are used to stabilize the needed polarization direction at any point of the collider ring, including the collision points, at injection, etc. In this snake configuration, the spin navigator allows one to control the polarization in the vertical plane at the interaction points of the MPD and SPD detectors, while polarization lies in the collider’s plane in the arcs.
ST mode in RHIC (see Figure 15) The existing snakes can also be used for operation of RHIC in the ST mode []. The spin rotation axes of the helical snakes lie in the collider’s plane and are set by the snakes’ magnetic fields []. The spin tune is determined by the angle between the snake axes and the stable polarization in the collider’s arcs is vertical. The spin tune equals one half (RHIC’s regular mode of operation) if the angle between the snake axes is . To convert RHIC to the TS mode, when the spin tune is zero (or one), the angle between the snake axes must be set to zero (or ), i.e., the snakes must be identical. The effect of the strong fields in the arcs and snakes on the spin reduces to zero over one orbit turn, any polarization direction repeats after each orbit turn.
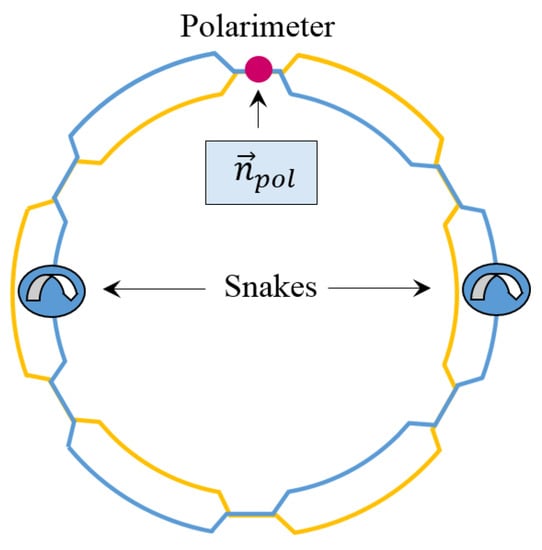
Figure 15.
RHIC ring with two helical snakes.
Thus, two identical snakes convert RHIC to the ST mode. and, from the spin dynamics point of view, it becomes equivalent to a figure-8 collider. While geometrically obviously still different, the two kinds of rings have identical topologies of the spin motion. The two snakes located opposite to each other in a circular ring divide the ring into two arcs. Due to the action of the snakes, the spin sees opposite fields in the two arcs in exactly the same way as it happens in a figure-8 ring. JINR (Dubna, Russia) develops the NICA collider project with two solenoidal snakes set in the TS mode [].
From the above example, we see that a collider of one type can be easily transformed into a collider of the other type. For instance, insertion of a Siberian snake into a spin-transparent collider converts it into a collider with preferred spin direction. Inversely, addition of a second identical snake to a single-snake collider with preferred spin direction converts it into a spin-transparent collider.
7.4. Spin Navigators
SN can be designed on the basis of magnetic elements with longitudinal as well as transverse fields [,]. Longitudinal fields do not change the closed orbit but their required field integral grows proportionally to the beam momentum. Transverse fields distort the closed orbit but their required field integral is independent of energy. The orbit excursion reduces with energy increase. Thus, longitudinal fields are most suitable for use at low and medium energies and with deuterons. As energy increases, use of transverse fields becomes more adequate. Let us next present the schemes of SN navigators proposed for the JLEIC, NICA and RHIC colliders.
SN in the JLEIC collider. The ion collider ring of JLEIC employs a universal 3D spin navigator designed on the basis of solenoids with small field integrals (weak solenoids), which allows for manipulating the polarization of any particle species (protons, deuterons, helium-3, etc.) [].
The weak solenoids do not change the design orbit and allow one to control the beam polarization essentially without affecting parameters of the orbital motion. The navigator consists of three sections: those for control of the radial , vertical and longitudinal polarization components (see Figure 16).

Figure 16.
3D spin navigator schematic.
The section for control of the longitudinal polarization component consists of a single solenoid, which does not change the design orbit (Figure 17c). Control of the radial (Figure 17a) and vertical (Figure 17b) polarization components is done using fixed orbit bumps, which are realized using magnetic dipoles with vertical and radial fields. Their strengths scale proportionally to the beam momentum. The radial and vertical polarization components are controlled using two pairs of opposite-field solenoids placed between the dipoles in the bumps, as illustrated in Figure 17. Note that the described sections can be placed in any order in any available space of the straight section.

Figure 17.
Modules for control of the spin components: radial (a); vertical (b); and longitudinal (c).
Schematic placement of the 3D navigator elements in the collider ring’s experimental straight is shown in Figure 18. The black, blue and green colors indicate the structural quadrupoles and radial- and vertical-field dipoles, respectively, while yellow identifies the weak control solenoids. For the dipole and solenoid lengths of m and m, respectively, the total length of each section is about 8 m. The fixed orbit deviation in the bumps is mm in the whole momentum range of the collider. Placement of each bump between lattice quadrupoles keeps the experimental straight dispersion-free.
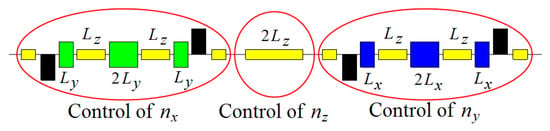
Figure 18.
Placement of the 3D spin navigator elements.
The SN maintains the spin tunes of 0.01 for protons and for deuterons in the entire JLEIC energy range with the maximum dipole and solenoid field strengths of 3 and 2 T, respectively.
SN in the NICA collider. A detailed scheme of the SN insertions is presented in Figure 19 []. The SN solenoids, and , generate longitudinal magnetic fields . They are placed between the collider structural magnets indicated as 3 and 4. The structural magnets generate radial fields deflecting the beams to the collision plane of the MPD.
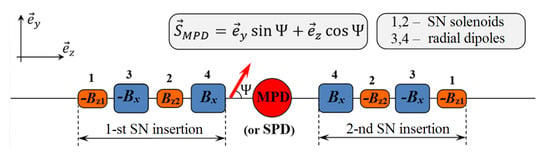
Figure 19.
Schematic of the spin navigator insertions for the ST mode of the NICA collider.
The described scheme allows for control of the ion polarization direction in the vertical plane of the MPD (SPD) detector. is the angle between the polarization direction and particle velocity. A field integral of 0.6 T·m of one of the navigator solenoids provides stable operation of the scheme in the entire energy range. The spin tunes are then for protons and for deuterons.
The spin rotation angles of the navigator solenoids in each SN section are calculated for small values of the spin tune according to
where is the spin rotation angle by the radial-field dipole, is the orbital bending angle of the radial-field dipole, and is the magnetic rigidity.
The required field integrals of the navigator solenoids are
Thus, the navigator solenoid fields and allow for setting the required spin tune and n axis orientation at the detector of the NICA collider:
where
SN in RHIC. Small adjustments of the snake parameters can perform all of the functions of an SN []. The polarization can be set to the required orientation by adjusting a small angle between the snake axes and small offsets and of the snakes’ spin rotation angles from :
where is the spin tune induced by the snakes serving as a 3D SN. Equation (38) assumes that both snake axes are longitudinal. The described navigator allows one to set any 3D polarization direction at the polarimeter by small variation of the snake currents. Exceptions are points where the snake rotators allows one to set any 2D polarization orientation in the plane for even k and in the plane for odd k.
The ST mode eliminates the need for strong-field rotators around an interaction point by readjusting the global spin dynamics to provide the required spin orientation at the interaction point rather than modifying the spin dynamics locally as with strong spin rotators.
Compensation of lattice imperfection. SNs can be used not only to stabilize the polarization but to empirically compensate the effect of the imperfections as well []. The spin rotation due to imperfections, the ST resonance strength, can be determined experimentally by polarization measurements. The SN can next be set to provide an equal but opposite spin rotation. After such a compensation, from the spin dynamics point of view, a real synchrotron with lattice imperfections behaves as a synchrotron where all magnetic elements are fabricated and installed perfectly. In this case, depolarizing effects are primarily associated with betatron and synchrotron oscillations of the beam particles and spin manipulation requires an SN with ultimately small field integral values. It becomes possible to significantly increase the maximum energy for conducting experiments with polarized beams in the ST mode. It is also possible to suppress higher-order spin effects by an appropriate lattice design. This opens opportunities for ultra-high precision polarized beam experiments such as a search for a permanent electric dipole moment of an ion.
7.5. Spin Response Function in the ST Mode
As noted above, the spin dynamics in the ST mode is strongly influenced by perturbing magnetic fields and it becomes particularly important to properly account their effect on the beam polarization. In practical situations, the main sources of perturbing fields are associated with fabrication and alignment errors of the synchrotron’s magnetic elements that are random in nature. Besides the direct effect on the spin occurring when a particle passes an element with perturbing field, it is important to account for the integral effect of the entire ring related to motion of the particle on the trajectory distorted by this element. In practice, the integral effect of the entire ring through the distorted orbit is typically much greater than the direct effect of the perturbing lattice element. Reference [] described the response-function technique for the ST mode allowing one to account for the integral effect of the whole synchrotron ring on the spin.
In the general case, the spin effect of periodic perturbing fields , and in the ST mode is described by three vector response functions, the radial , vertical and longitudinal , respectively, which are determined by the ring optics []
where is the magnetic rigidity and L is the orbit length.
In the spin reference frame, the spin motion is rotation about the averaged spin field , whose magnitude is equal to the ST-resonance strength: .
Besides calculation of the ST resonance strength due to lattice imperfections, the response functions allow one to address the question of compensating the spin tune spread associated with betatron and synchrotron oscillations as well as to reduce the depolarizing effects at the interaction points related to the non-linearity of the fields of the colliding bunches, etc. The response functions allow for development of optimal spin navigator designs using weak transverse and longitudinal fields. Thus, the response functions are a valuable tool for calculation of the optics parameters of ST synchrotrons necessary for completion of high-precision measurements in experiments with polarized beams.
7.6. Long-Term Spin Stability in ST Collider Mode
Given RHIC experience of multi-hour polarization maintenance [] achieved by compensation of the spin tune spread by the snakes and a fine selection of the betatron tunes, there is no doubt that, with a proper tuning of the orbital oscillations, one will observe a similar stabilizing effect of the figure-8 configuration for all polarized ion species of an ST collider.
7.7. Deuteron Tensor Polarization
The ST technique described above allows for acceleration and spin control of a polarized deuteron beam up to energies of interest to nuclear physics []. Polarized deuterons are indispensable for understanding of the QCD structure of the Nucleon–Nucleon (NN) interaction. The NN force is strongly spin-dependent. Tensor-polarization dependent measurements uniquely determine the quark–gluon distributions of the interacting NN pair, and they cannot be described by the incoherent sum of the two nucleons.
Dynamics of the deuteron vector polarization in a synchrotron is identical to that of the polarization of spin-1/2 particles. The spin-1 dynamics and therefore the deuteron tensor polarization dynamics in a synchrotron can be completely described by the spin dynamics of a system of two spin-1/2 particles []. Thus, fundamentally, by developing an understanding of the vector polarization dynamics in a synchrotron, for example, using the tools discussed above, one at the same provides full description of the tensor polarization behavior. This is, of course, only true for semi-classical spin-1 dynamics in electro-magnetic fields of an accelerator and does not apply to nuclear interactions.
7.8. Spin Transparency Benefits
Let us summarize the beneficial features of the spin transparent ring design:
- Energy-independent spin tune
- Preservation of polarization of any ion species including deuterons during acceleration by maintaining a small constant spin tune using weak magnetic fields
- Extendibility to arbitrary energy through compensation of the zero-integer spin resonance strength and/or use of pairs of compact Siberian snakes
- Ease of polarization control by weak magnetic fields
- Adiabatic spin manipulation including spin flip without polarization loss
- Manipulation of the polarization with no impact on the orbital dynamics
- Possibility of ultra-high precision polarized beam experiments
- Equalization of the up and down polarization life times for electron beams
8. Conclusions
The purpose of the presented review is to light up the current state of the polarized beam techniques both existing and under development applicable to polarized hadron beams in colliders. The reality of our days is the polarized proton–proton collider complex RHIC at Brookhaven National Laboratory where Siberian snakes have been implemented and operated successfully. Further conceptual development presented in this paper has been essentially stimulated by the designs of the two collider projects, now under construction: the Electron-Ion Collider at BNL and the NICA collider at JINR. The presented post-SibS conceptual advances such as figure-8 and, especially, the Spin Transparency concept are aimed at expanding the possibilities of flexible control, manipulation and flipping of the hadron polarization in these and future high-energy collider projects under consideration.
Author Contributions
All authors contributed equally to the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Contract No. DE-AC05-06OR23177.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this review are available within the article and referenced materials.
Acknowledgments
We are grateful to S. Troshin for his encouragement of this paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.-B.; et al. Electron Ion Collider: The Next QCD Frontier. Eur. Phys. J. A 2016, 52, 268. [Google Scholar] [CrossRef]
- Okun, L.B. Note concerning CP parity. Yad. Fiz. 1965, 1, 938. [Google Scholar]
- Prentki, J.; Veltman, M.J.G. Possibility of CP violation in semistrong interactions. Phys. Lett. 1965, 15, 88. [Google Scholar] [CrossRef]
- Lee, T.D.; Wolfenstein, L. Analysis of CP Noninvariant Interactions and the K0(1), K0(2) System. Phys. Rev. 1965, 138, B1490. [Google Scholar] [CrossRef]
- Bernreuther, W. CP violation and baryogenesis. In CP Violation in Particle, Nuclear and Astrophysics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 237–293. [Google Scholar]
- Aschenauer, E.C.; Baker, M.D.; Bazilevsky, A.; Boyle, K.; Belomestnykh, S.; Ben-Zvi, I.; Brooks, S.; Brutus, C.; Burton, T.; Fazio, S.; et al. eRHIC design study: An electron-ion collider at BNL. arXiv 2014, arXiv:1409.1633. [Google Scholar]
- Kekelidze, V.D.; Lednicky, R.; Matveev, V.A.; Meshkov, I.N.; Sorin, A.S.; Trubnikov, G.V. Three stages of the NICA accelerator complex. Eur. Phys. J. A 2016, 52, 211. [Google Scholar] [CrossRef]
- Semertzidis, Y. Axion dark matter searches. PoS ICHEP 2019, 2018, 729. [Google Scholar]
- Chen, X. A Plan for EIC in China. arXiv 2018, arXiv:1809.00448. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. Polarized particle acceleration. Dokl. Acad. Nauk SSSR 1975, 223, 830. [Google Scholar]
- Derbenev, Y.S. University of Michigan Report; UM HE 96-05; University of Michigan: Ann Arbor, Michigan, 1996. [Google Scholar]
- Abeyratne, S.; Accardi, A.; Ahmed, S.; Barber, D.; Bisognano, J.; Bogacz, A.; Castilla, A.; Chevtsov, P.; Corneliussen, S.; Deconinck, W.; et al. Science Requirements and Conceptual Design for a Polarized Medium Energy Electron-Ion Collider at Jefferson Lab. arXiv 2012, arXiv:1209.0757. [Google Scholar]
- Filatov, Y.N.; Kondratenko, A.M.; Kondratenko, M.A.; Derbenev, Y.S.; Morozov, V.S. Transparent spin method for spin control of hadron beams in colliders. Phys. Rev. Lett. 2020, 124, 194801. [Google Scholar] [CrossRef]
- Milner, R.G. PoS PSTP2013. arXiv 2013, arXiv:1311.5016. [Google Scholar]
- Sy, A. ICFA-BD Newsletter; International Committee for Future Accelerators: Batavia, IL, USA, 2018; Volume 74, p. 99. [Google Scholar]
- Fischer, W.; Bazilevsky, A. Impact of three-dimensional polarization profiles on spin-dependent measurements in colliding beam experiments. Phys. Rev. ST Accel. Beams 2012, 15, 041001. [Google Scholar] [CrossRef]
- Froisart, M.; Stora, R. Depolarisation d’un faisceau de protons polarises dans un synchrotron. Nucl. Instrum. Methods 1960, 7, 297. [Google Scholar] [CrossRef]
- Cohen, D. Feasibility of Accelerating Polarized Protons with the Argonne ZGS. Rev. Sci. Instrum. 1962, 33, 161. [Google Scholar] [CrossRef]
- Simonyan, K.A.; Orlov, Y.F. Anomalous Resonance Spin Flip of a Particle in a Magnetic Field. Zh. Eksp. Teor. Fiz. 1963, 45, 173. [Google Scholar]
- Plis, Y.A.; Soroko, L.M. The current state of the physics and technology of obtaining polarized particle beams. Uspekhi Fiz. Nauk 1972, 107, 281. [Google Scholar] [CrossRef]
- Khoe, T.; Ratner, L.G.; Martin, R.L.; Parker, E.F.; Potts, C.W.; Ratner, L.G.; Timm, R.E. Acceleration of polarized protons to 8.5 GeV/c. Part. Accel. 1975, 6, 213. [Google Scholar]
- Montague, B.W. Polarized beams in high energy storage rings. Phys. Rep. 1984, 113, 1. [Google Scholar] [CrossRef]
- Khiari, F.Z.; Cameron, P.R.; Crabb, D.G.; Fujisaki, M.; Gialas, I. Acceleration of polarized protons to 22 GeV/c and the measurement of spin-spin effects in p↑+p↑→p+p. Phys. Rev. D 1989, 39, 45. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y. Spin-depolarization mechanisms due to overlapping spin resonances in synchrotrons. Phys. Rev. E 1993, 47, 3631. [Google Scholar] [CrossRef]
- Lee, S.Y. Spin Dynamics and Snakes in Synchrotrons; World Scientific: Singapore, 1997. [Google Scholar]
- Ranjbar, V.H.; Lee, S.Y.; Huang, H.; Luccio, A.U.; MacKay, W.W.; Ptitsyn, V.; Roser, T.; Tepikian, S. Observation of higher-order snake resonances in polarized proton acceleration in RHIC. Phys. Rev. Lett. 2003, 91, 034801. [Google Scholar] [CrossRef]
- Hoffstaetter, G.H.; Vogt, M. Strength of higher-order spin-orbit resonances. Phys. Rev. E 2004, 70, 056501. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Kewisch, J.; Huang, H.; Minty, M. Minimization of spin tune spread for preservation of spin polarization at RHIC. Phys. Rev. Accel. Beams 2019, 22, 061002. [Google Scholar] [CrossRef]
- Ptitsin, V.I.; Shatunov, Y.M. Helical spin rotators and snakes. Nucl. Instrum. Methods Phys. Res. Sect. A 1997, 398, 126. [Google Scholar] [CrossRef]
- Caussyn, D.D.; Derbenev, Y.S.; Ellison, T.J.P.; Lee, S.Y.; Rinckel, T.; Schwandt, P.; Sperisen, F.; Stephenson, E.J.; von Przewoski, B.; Blinov, B.B.; et al. Spin Flipping a Stored Polarized Proton Beam. Phys. Rev. Lett. 1994, 73, 2857. [Google Scholar] [CrossRef] [PubMed]
- Koop, I.; Shatunov, Y. Spin flip by RF-field at storage rings with Siberian snakes. AIP Conf. Proc. 1995, 343, 317. [Google Scholar]
- Blinov, B.B.; Etienne, Z.B.; Krisch, A.D.; Leonova, M.A.; Lorenzon, W.; Morozov, V.S.; Peters, C.C.; Wong, K.V.; Yonehara, K.; Anferov, V.A.; et al. 99.6% Spin-Flip Efficiency in the Presence of a Strong Siberian Snake. Phys. Rev. Lett. 2001, 88, 014801. [Google Scholar] [CrossRef]
- Morozov, V.S.; Etienne, Z.B.; Kandes, M.C.; Krisch, A.D.; Leonova, M.A.; Sivers, D.W.; Wong, V.K.; Yonehara, K.; Anferov, V.A.; Meyer, H.O.; et al. First Spin Flipping of a Stored Spin-1 Polarized Beam. Phys. Rev. Lett. 2003, 91, 214801. [Google Scholar] [CrossRef] [PubMed]
- Mane, S.R. Spin flipping in rings with Siberian snakes. Nucl. Instrum. Methods Phys. Res. Sect. A 2009, 605, 266. [Google Scholar] [CrossRef]
- Shatunov, Y.M. Spin control by rf fields at accelerators and storage rings. In XIII Advanced Research Workshop on High Energy Spin Physics (DSPIN-09); 2011; Available online: https://inspirehep.net/files/fc8db800ac20136cdbd0f7269faea0db (accessed on 18 December 2020).
- Huang, H.; Kewisch, J.; Liu, C.; Marusic, A.; Meng, W.; Méot, F.; Oddo, P.; Ptitsyn, V.; Ranjbar, V. and Roser, T. High Spin-Flip Efficiency at 255 GeV for Polarized Protons in a Ring With Two Full Siberian Snakes. Phys. Rev. Lett. 2018, 120, 264804. [Google Scholar] [CrossRef] [PubMed]
- Derbenev, Y.S.; Anferov, V.A. RF driven stable spin-flipping motion of a stored polarized beam. Phys. Rev. ST Accel. Beams 2000, 3, 094001. [Google Scholar] [CrossRef]
- Derbenev, Y.; Kondratenko, A.; Kondratenko, M.; Morozov, V.; Filatov, Y. Spin-flipping systems for storage rings. In Proceedings of the XIV Advanced Research Workshop on High Energy Spin Physics (DSPIN-11), JINR, Dubna, Russia, 20–24 September 2011; p. 377. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N.; Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y. Spin Flipping System in the JLEIC Collider Ring. In Proceedings of the NAPAC’16, Chicago, IL, USA, 9–14 October 2016. [Google Scholar]
- Belov, A.S.; Esin, S.K.; Netchaeva, L.P.; Plokhinski, Y.V.; Vasil’ev, G.A.; Klenov, V.S.; Turbabin, A.V.; Yakushev, V.P. High-intensity source of polarized negative hydrogen ions with a resonant charge-exchange plasma ionizer. Rev. Sci. Instrum. 1996, 67, 1293. [Google Scholar] [CrossRef]
- Belov, A.S.; Netchaeva, L.P.; Turbabin, A.V. Intensity improvements of pulsed source of polarized negative hydrogen ions. Rev. Sci. Instrum. 2006, 77, 03A522. [Google Scholar] [CrossRef]
- Belov, A.S. Production of Polarized Ions with Nearly Resonant Charge-Exchange Collisions in Plasma. AIP Conf. Proc. 2008, 980, 209. [Google Scholar]
- Belov, A.S.; Donets, D.E.; Fimushkin, V.V.; Kovalenko, A.D.; Kutuzova, L.V.; Prokofichev, Y.V.; Shutov, V.B.; Turbabin, A.V.; Zubets, V.N. Source of polarized ions for the JINR accelerator complex. J. Phys. Conf. Ser. 2017, 938, 012017. [Google Scholar] [CrossRef]
- Belov, A.S. A scheme for a polarized 3He ion source with a resonant charge-exchange plasma ionizer. Nucl. Instrum. Methods Phys. Res. Sect. A 1998, 402, 205. [Google Scholar] [CrossRef]
- Zelenski, A.; Kponou, A.; Ritter, J.; Belov, A.; Zubets, V. The RHIC polarized H− source. Rev. Sci. Instrum. 2016, 87, 02B705. [Google Scholar] [CrossRef]
- Zelenski, A. Optically-Pumped Polarized H− and 3He++ Ion Sources Development at RHIC. In Proceedings of the IPAC’18, TUYGBE4, Vancouver, BC, Canada, 29 April 29–4 May 2018. [Google Scholar]
- Maxwell, J.; Epstein, C.; Milner, R.; Alessi, J.; Beebe, E.; Pikin, A.; Ritter, J.; Zelenski, A. Development of a Polarized Helium-3 Source for RHIC and eRHIC. Int. J. Mod. Phys. Conf. Ser. 2016, 40, 1660102. [Google Scholar] [CrossRef]
- Colegrove, F.D.; Schearer, L.D.; K, G. Walters, Polarization of 3He Gas by Optical Pumping. Phys. Rev. 1963, 132, 2561. [Google Scholar] [CrossRef]
- Barschall, H.H.; Haeberli, W. (Eds.) Madison Convention. In Proceedings of the 3rd International Symposium on Polarization Phenomena in Nuclear Physics, Madison, WI, USA, 31 August–4 September 1970; University of Wisconsin Press: Madison, WI, USA, 1971; p. xxv. [Google Scholar]
- Thomas, L.H.I. The kinematics of an electron with an axis. Philos. Mag. 1927, 3, 1. [Google Scholar] [CrossRef]
- Bargmann, V.; Michel, L.; Telegdi, V.L. Precession of the polarization of particles moving in a homogeneous electromagnetic field. Phys. Rev. Lett. 1959, 2, 435. [Google Scholar] [CrossRef]
- Courant, E.D. The ultrastructure of pulmonary lymphatic capillaries of newborn rabbits and of human infants. Bull. Am. Phys. Soc. 1962, 7, 33. [Google Scholar]
- Courant, E.D.; Ruth, R.D. BNL Report; BNL-51270. 1980. Available online: https://www.osti.gov/servlets/purl/7034691 (accessed on 25 December 2020).
- Derbenev, Y.S.; Kondratenko, A.M.; Skrinskii, A.N. Dynamics of the Polarization of Particles Near Spin Resonances. Zh. Eksp. Teor. Fiz. 1971, 60, 1216. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M.; Skrinsky, A.N. Particle spin motion in storage ring with arbitrary field. Dokl. Akad. Nauk SSSR 1970, 192, 1255. [Google Scholar]
- Derbenev, Y.S.; Serednyakov, S.I.; Shatunov, Y.M.; Kondratenko, A.M.; Skrinsky, A.N.; Tumaikin, G.M.; Shatunov, Y.M. Accurate calibration of the beam energy in a storage ring based on measurement of spin precession frequency of polarized particles. Part. Accel. 1980, 10, 177. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. Compensation for Particle Beam Depolarization of Spin Resonance Intersection at Accelerators. Part. Nucl. Lett. 2004, 1, 266. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. On Compensation of Beam Depolarization at Crossing of a Spin Resonance, in Proc. SPIN’17, Kyoto, Japan. AIP Conf. Proc. 2007, 915, 874. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. Multiple Spin Resonance Crossing in Accelerators. AIP Conf. Proc. 2009, 1149, 789. [Google Scholar]
- Morozov, V.S.; Chao, A.W.; Krisch, A.D.; Leonova, M.A.; Raymond, R.S.; Sivers, D.W.; Wong, V.K.; Garishvili, A.; Gebel, R.; Lehrach, A.; et al. Experimental Test of a New Technique to Overcome Spin-Depolarizing Resonances. Phys. Rev. Lett. 2009, 102, 244801. [Google Scholar] [CrossRef]
- Derbenev, Y.S.; Kondratenko, A.M. Particle spin diffusion in storage rings. Zh. Eksp. Teor. Fiz. 1972, 62, 430. [Google Scholar]
- Barber, D.P.; Ellison, J.A.; Heinemann, K. Quasiperiodic spin-orbit motion and spin tunes in storage rings. Phys. Rev. ST Accel. Beams 2004, 7, 124002. [Google Scholar] [CrossRef]
- Chao, A.W.; Courant, E.D. Spin echo in synchrotrons. Phys. Rev. Accel. Beams 2007, 10, 014001. [Google Scholar] [CrossRef]
- Derbenev, Y.S.; Kondratenko, A.M. Acceleration of polarized particles in synchrotrons to high energies. In Proceedings of the 10th International Conference on High Energy Accelerators, Protvino, Russia, 11–17 July 1977; pp. 70–75. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. On the Possibilities to Obtain High-Energy Polarized Particles in Accelerators and Storage Rings. AIP Conf. Proc. 1979, 51, 292. [Google Scholar]
- Kondratenko, A.M. Polarized Beams in Storage Rings and Cyclic Accelerators. Ph.D. Thesis, INP, Siberian Branch of the Academy of Sciences of USSR, Novosibirsk, Russia, 1982. [Google Scholar]
- Courant, E.D. Helical Siberian snakes. AIP Conf. Proc. 1989, 187, 1085. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. On polarization preservation criteria in accelerator with Siberian snakes. J. Tech. Phys. 1989, 59, 104. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. Possibilities of polarized protons acceleration up to energy 1 TeV and above. In Proceedings of the XII Int. Conference on High Energy Accelerators, Fermilab, Batavia, 11–16 August 1983; pp. 413–415. [Google Scholar]
- Lee, S.Y.; Courant, E.D. Tolerance of imperfections in high-energy circular accelerators for polarized protons. Phys. Rev. D 1990, 41, 292. [Google Scholar] [CrossRef] [PubMed]
- Chao, A.W.; Derbenev, Y.S. Cancellation of the Quadrupole Effect on Spin in High-Energy Accelerators. Part. Accel. 1991, 36, 25. [Google Scholar]
- Mane, S.R.; Shatunov, Y.M.; Yokoya, K. Siberian Snakes in high-energy accelerators. J. Phys. G Nucl. Part. Phys. 2005, 31, R151. [Google Scholar] [CrossRef]
- Harrison, M.; Peggs, S.; Roser, T. The RHIC accelerator. Annu. Rev. Nucl. Part. Sci. 2002, 52, 425–469. [Google Scholar] [CrossRef]
- Krisch, A.D.; Mane, S.R.; Raymond, R.S.; Roser, T.; Stewart, J.A.; Terwilliger, K.M.; Vuaridel, B.; Goodwin, J.E.; Meyer, H.-O.; Minty, M.G.; et al. First test of the Siberian snake magnet arrangement to overcome depolarizing resonances in a circular accelerator. Phys. Rev. Lett. 1989, 63, 1137. [Google Scholar] [CrossRef]
- Kovalenko, A.; Agapov, N.; Kekelidze, V.; Kekelidze, V.; Lednicky, R.; Meshkov, I.; Mikhaylov, V.; Sidorin, A.; Sorin, A.; Trubnikov, G. The NICA Facility in polarized proton operation mode. In Proceedings of the IPAC’11, San Sebastian, Spain, 4–9 September 2011. [Google Scholar]
- Kovalenko, A.D.; Butenko, A.V.; Kekelidze, V.D.; Mikhaylov, V.A.; Kondratenko, M.A.; Kondratenko, A.M.; Filatov, Y.N. Orbital Parameters of Proton and Deuteron Beams in NICA Collider with Solenoid Siberian Snakes. J. Phys. Conf. Ser. 2016, 678, 012022. [Google Scholar] [CrossRef]
- Ptitsin, V.I.; Shatunov, Y.M.; Peggs, G. 1996, pp. 3331–3333. Available online: https://accelconf.web.cern.ch/p95/ARTICLES/RAQ/RAQ21.PDF (accessed on 25 December 2020).
- Courant, E.D.; Fischer, W.; Luccio, A.; Mariam, F.; Okamura, M.; Peggs, S.; Pilat, F.; Ptitsin, V.; Roser, T.; Shatunov, Y.; et al. The use of helical dipole magnets in the RHIC spin project. In Proceedings of the 12th International Symposium on High Energy Spin Physics, Amsterdam, The Netherlands, 10–14 September 1996; pp. 579–581. [Google Scholar]
- Ptitsyn, V.I. Polarized Beams in Accelerators and Storage Rings with Siberian Snakes. Ph.D. Dissertation, INP, Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russia, 2005. [Google Scholar]
- Courant, E.D.; Ratner, L.G. Depolarization during acceleration and storage of polarized protons and deuterons. AIP Conf. Proc. 1978, 42, 101. [Google Scholar]
- Antoulinakis, F.; Chen, Y.; Dutton, A.; De La Fuente, E.R.; Haupert, S.; Ljungman, E.A.; Myers, P.D.; Thompson, J.K.; Tai, A.; Aidala, C.A.; et al. 4-twist helix snake to maintain polarization in multi-GeV proton rings. Phys. Rev. Accel. Beams 2017, 20, 091003. [Google Scholar] [CrossRef]
- Filatov, Y.N.; Kondratenko, A.M.; Kondratenko, M.A. Spin response function technique in spin-transparent synchrotrons. Eur. Phys. J. C 2020, 80, 778. [Google Scholar] [CrossRef]
- Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y.; Kondratenko, A.; Kondratenko, M.; Filatov, Y. Ion polarization control in MEIC rings using small magnetic fields integrals. PoS (PSTP 2013) 2014, 182, 026. [Google Scholar]
- Kovalenko, A.D.; Butenko, A.V.; Kekelidze, V.D.; Mikhaylov, V.A.; Filatov, Y.; Kondratenko, A.M.; Kondratenko, M.A. Ion polarization control in the MPD and SPD detectors of the NICA collider. In Proceedings of the IPAC’15, Richmond, VA, USA, 3–8 May 2015; pp. 2031–2033. [Google Scholar]
- Kondratenko, A.M.; Derbenev, Y.S.; Filatov, Y.N.; Lin, F.; Morozov, V.S.; Kondratenko, M.A.; Zhang, Y. Preservation And Control Of The Proton And Deuteron Polarizations In The Proposed Electron-Ion Collider At Jefferson Lab. Phys. Part. Nucl. 2014, 45, 319. [Google Scholar] [CrossRef]
- Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y.; Filatov, Y.; Kondratenko, A.M.; Kondratenko, M.A. Baseline Scheme for Polarization Preservation and Control in the MEIC Ion Complex. In Proceedings of the IPAC’15, Richmond, VA, USA, 3–8 May 2015; pp. 2301–2303. [Google Scholar]
- Filatov, Y.N.; Kovalenko, A.D.; Butenko, A.V.; Syresin, E.M.; Mikhailov, V.A.; Shimanskiy, S.S.; Kondratenko, A.M.; Kondratenko, M.A. Spin transparency mode in the NICA collider. EPJ Web Conf. 2019, 204, 10014. [Google Scholar] [CrossRef]
- Morozov, V.S.; Adams, P.; Derbenev, Y.S.; Filatov, Y.; Huang, H.; Kondratenko, A.M.; Kondratenko, M.A.; Lin, F.; Méot, F.; Ptitsyn, V.; et al. Experimental verification of transparent spin mode in RHIC. In Proceedings of the IPAC’19, Melbourne, Australia, 19–24 May 2019; pp. 2783–2786. [Google Scholar]
- Basdevant, J.-L. Lectures on Quantum Mechanics; Springer: New York, NY, USA, 2007; p. 232. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).