Application of the Efros Theorem to the Function Represented by the Inverse Laplace Transform of s^−μ exp(−s^ν)

Abstract

Using a special case of the Efros theorem which was derived by Wlodarski, and operational calculus, it was possible to derive many infinite integrals, finite integrals and integral identities for the function represented by the inverse Laplace transform. The integral identities are mainly in terms of convolution integrals with the Mittag–Leffler and Volterra functions. The integrands of determined integrals include elementary functions (power, exponential, logarithmic, trigonometric and hyperbolic functions) and the error functions, the Mittag–Leffler functions and the Volterra functions. Some properties of the inverse Laplace transform of $s^{-\mu }\exp (-s^{\nu })$ with $\mu \ge 0$ and $0<\nu <1$ are presented.

1. Introduction

Inversions of the Laplace transforms of exponential functions

$$\begin{array}{c}{f}_{\nu ,\mu }\left(t\right)={\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\int }_{c-i\infty }^{c+i\infty }}{\mathrm{e}}^{st}F\left(s\right)ds;c>0,\hfill \\ F\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu }}};0<\nu <1;\mu \ge 0,\hfill \end{array}$$

(1)

were during the 1945–1970 period in a focus of attention of a number of well-known mathematicians like Humbert [1], Pollard [2], Wlodarski [3], Mikusinski [4,5,6,7], Wintner [8], Ragab [9] and Stankovič [10]. In the case $\mu =0$, Mikusinski was able to obtain the inverse Laplace transform in terms of integral representations [7]

$$\begin{array}{c}\mathcal{L}\left\{f_{\nu ,0}\left(t\right)\right\}={\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-st}{f}_{\nu ,0}\left(t\right)dt={\mathrm{e}}^{-s^{\nu }};0<\nu <1;t>0,\hfill \\ f_{\nu ,0}\left(t\right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-ut}{\mathrm{e}}^{-u^{\nu }cos\left(\pi \nu \right)}sin[u^{\nu }sin\left(\pi \nu \right)]du,\hfill \\ f_{\nu ,0}\left(t\right)={\displaystyle \frac{2}{\pi }}{\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-u^{\nu }cos\left(\frac{\pi \nu }{2}\right)}cos[u^{\nu }cos\left(\frac{\pi \nu }{2}\right)]cos\left(ut\right)du,\hfill \end{array}$$

(2)

and also as the finite trigonometric integral

$$\begin{array}{c}{f}_{\nu ,0}\left(t\right)={\displaystyle \frac{\nu }{\pi (1-\nu )t}}{\displaystyle {\int }_0^{\pi }}\xi {\mathrm{e}}^{-\xi }du;0<\nu <1;t>0\hfill \\ \xi ={\displaystyle \frac{1}{t^{\nu /(1-\nu )}}}{\left({\displaystyle \frac{sin\left(\nu u\right)}{sinu}}\right)}^{\nu /(1-\nu )}{\displaystyle \frac{sin\left[\right(1-\nu \left)u\right]}{sinu}}.\hfill \end{array}$$

(3)

It was established that the functions $f_{\nu ,0}\left(t\right)$ can be expressed in terms of exponential and parabolic cylinder functions when $\nu =1/2$ [9,11] and by help of the Airy functions and their first derivatives for $\nu =1/3$ and $\nu =2/3$ [9,12]. For $\nu =1/4$, the solution was deduced by Barkai [13] in 2001 using Mathematica as a sum of three generalized hypergeometric functions, but the numerical result was uncertain, presumably for a bag in the computing program. In 2010–2012 Gorska and Penson [14,15] were able to represent $f_{\nu ,0}\left(t\right)$ in terms of Mejer G functions. Earlier, in 1958 Ragab [9] expressed $f_{\nu ,0}\left(t\right)$ in terms of MacRobert E functions for $\nu =1/n$.

In 1952 Wlodarski [3] showed that when the generalized product Efros theorem [16] is applied to the Laplace transform of $f_{\nu ,\mu }\left(t\right)$ which is given in (1), then it is possible to derive the following formula

$$\begin{array}{c}\mathcal{L}\left\{g\left(t\right)\right\}=G\left(s\right);0<\nu <1;\mu \ge 0,\hfill \\ {\mathcal{L}}^{-1}\left\{\frac{G\left(s^{\nu }\right)}{s^{\mu }}\right\}={\displaystyle {\int }_0^{\infty }}g\left(u\right){\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}du=\hfill \\ {\displaystyle {\int }_0^{\infty }}g\left(u\right){\mathcal{L}}^{-1}\left\{\frac{{\mathrm{e}}^{-u{s}^{\nu }}}{s^{\mu }}\right\}du={\displaystyle {\int }_0^{\infty }}g\left(u\right)f_{\nu ,\mu }\left(u\right)du.\hfill \end{array}$$

(4)

It was established in our recent paper [17] that for $\mu =0$ and $\mu =1-\nu$ this functional expression can be written in terms of specific Wright functions $W_{\nu ,\mu }(-t)$, sometimes referred to as the Mainardi functions

$$\begin{array}{c}{F}_{\nu }\left(t\right)=W_{-\nu ,0}(-t);0<\nu <1,\hfill \\ M_{\nu }\left(t\right)=W_{-\nu ,1-\nu }(-t),\hfill \end{array}$$

(5)

in the following way

$$\begin{array}{c}\nu {\mathcal{L}}^{-1}\left\{\frac{G\left(s^{\nu }\right)}{s^{1-\nu }}\right\}={\displaystyle {\int }_0^{\infty }}g\left(u\right)F_{\nu }\left(\frac{u}{t^{\nu }}\right)\frac{du}{u};0<\nu <1,\hfill \\ t^{\nu }{\mathcal{L}}^{-1}\left\{\frac{G\left(s^{\nu }\right)}{s^{1-\nu }}\right\}={\displaystyle {\int }_0^{\infty }}g\left(u\right)M_{\nu }\left(\frac{u}{t^{\nu }}\right)du.\hfill \end{array}$$

(6)

This follows from the fact that the functions $F_{\nu }\left(t\right)$ and $M_{\nu }\left(t\right)$ satisfy

$$\begin{array}{c}\mathcal{L}\left\{{\displaystyle \frac{1}{\mathit{\lambda }\nu }}{F}_{\nu }\left({\displaystyle \frac{\mathit{\lambda }}{t^{\nu }}}\right)\right\}=\mathcal{L}\left\{{\displaystyle \frac{1}{t^{\nu }}}{M}_{\nu }\left({\displaystyle \frac{\mathit{\lambda }}{t^{\nu }}}\right)\right\}={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{1-\nu }}},\hfill \\ 0<\nu <1;\mathit{\lambda }>0.\hfill \end{array}$$

(7)

It was also illustrated by us in [17], that in many cases, by using standard tables of the Laplace transforms [18,19,20,21], the left hand side Laplace transforms in (6) can be inverted and numerous infinite integrals, finite integrals and integral identities for the functions $F_{\nu }\left(t\right)$ and $M_{\nu }\left(t\right)$ can be derived.

Let us recall that the Wright functions [22,23], considered initially as a some kind generalization of the Bessel functions, are defined as an entire functions of the argument $z\in \mathbb{C}$ and parameters $\mathit{\lambda }>-1$ and $\mu \in \mathbb{C}$ by

$$W_{\mathit{\lambda },\mu }\left(z\right)={\displaystyle \sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{k!\mathrm{\Gamma }(\mathit{\lambda }k+\mu )}}};\mathit{\lambda }>-1,\mu \in \mathbb{C}.$$

(8)

It is usual to distinguish them in two kinds, the first kind with $\mathit{\lambda }\ge 0$ and the second kind with $\mathit{\lambda }=-\nu$ and $\nu \in (0,1)$, see, e.g., [11].

Restricting our attention to positive argument $t>0$, the Mainardi functions turn out to be particular Wright functions of the second kind expressed by the following series

$$\begin{array}{c}{F}_{\nu }\left(t\right)={\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \frac{{(-t)}^k}{k!\mathrm{\Gamma }(-\nu k)}}={\displaystyle \frac{1}{\pi }}{\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \frac{{(-1)}^{k+1}{t}^k}{k!}}\mathrm{\Gamma }(\nu k+1)sin\left(\pi \nu k\right),\hfill \\ M_{\nu }\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{(-t)}^k}{k!\mathrm{\Gamma }\left(-\nu (k+1)+1\right)}}={\displaystyle \frac{1}{\pi }}{\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \frac{{(-t)}^{k-1}}{(k-1)!}}\mathrm{\Gamma }\left(\nu k\right)sin\left(\pi \nu k\right),\hfill \\ F_{\nu }\left(t\right)=\nu t{M}_{\nu }\left(t\right).\hfill \end{array}$$

(9)

The interest in the Wright functions of the second kind comes from the fact that they play an important role in solution of the linear partial differential equations of fractional order which describe a wide spectrum of phenomena including probability distributions, anomalous diffusion and diffusive waves [24,25,26,27,28,29,30,31,32,33].

In Section 2, of this paper, by using the complex inversion formula in (1) and the Bromwich contour, the integral representation of $f_{\nu ,\mu }\left(t\right)$ with $0<\nu <1$ and $0\le \mu <1$ is derived and some basic properties of this inverse transform are established. The cases $\mu \ge 1$ can be dealt as well, see Appendix A for details.

The next two Section 3 and Section 4 are devoted to evaluation of infinite, finite and convolution integrals by using the Efros theorem in the Wlodarski form. The integrands of these integrals or integral identities include the elementary functions (power, exponential, logarithmic, trigonometric and hyperbolic functions) and the special functions (the error function, Mittag–Leffler functions and the Volterra functions). The last section provides concluding remarks.

In derivations of these integrals direct and inverse Laplace transforms which are taken from tables of transforms [18,19,20,21] are always presented in mathematical expressions. All mathematical operations and manipulations with elementary and special functions, integrals and transforms are formal and their validity is assured by considering the restrictions usually imposed in the operational calculus.

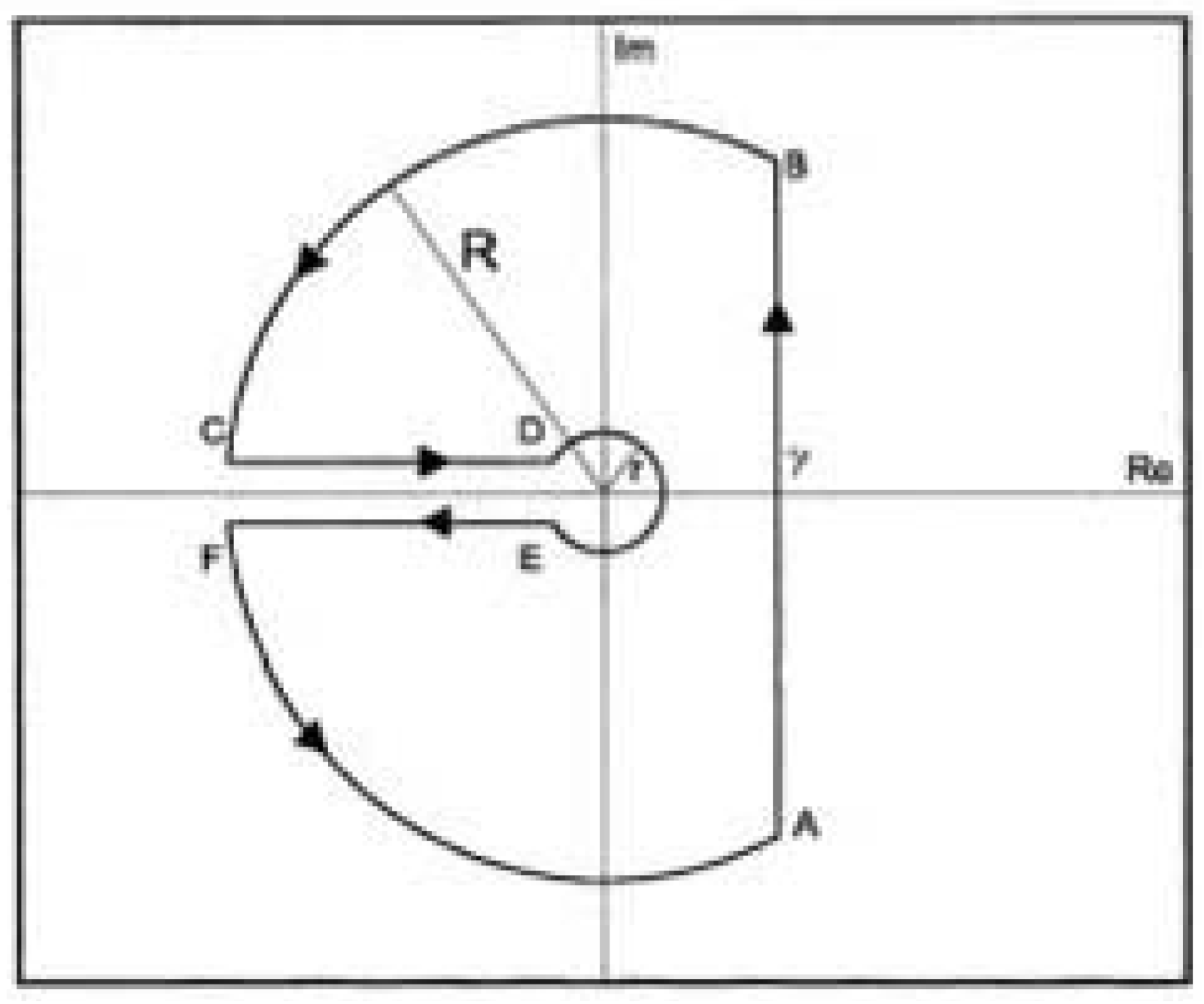
2. Integral Representations of the Inverse Laplace Transform of ${\mathit{s}}^{-\mathbf{\mu }}\mathbf{exp}(-{\mathit{s}}^{\mathbf{\nu }})$

Before infinite integrals in (6) will be evaluated, it is of interest to derive the function $f_{\nu ,\mu }\left(t\right)$ by performing the complex integration from (1). In investigated case, the branch point of the integrand exists and is located at the origin $s=0$ and therefore the equivalent Bromwich contour is plotted in Figure 1. The closed contour of integration ABCDEFA includes the line AB, the arcs BC and FA of a circle of radius $R\to \infty$ with center at origin, the arc DE of a circle of radius $r\to 0$ with center at origin, and two parallel lines CD and EF. The the cut along the negative axis ensures that $F\left(s\right)$ is a single-valued function. However, according to the Cauchy lemma the integrals along the arcs BC and FA vanish as $R\to \infty$.

Figure 1. The equivalent Bromwich contour.

As a consequence there are only three contributions coming from integrals on the CD and EF lines and from the small circle round origin, DE, so we have

$$\begin{array}{c}F\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu }}};0<\nu <1;\mu \ge 0,\hfill \\ f_{\nu ,\mu }\left(t\right)={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-ut}\left[F\left(u{\mathrm{e}}^{-\pi i}\right)-F\left(u{\mathrm{e}}^{\pi i}\right)\right]du+{\displaystyle \frac{1}{2\pi i}}\underset{r\to 0}{lim}{\displaystyle {\int }_{-\pi }^{\pi }}{\mathrm{e}}^{tr{\mathrm{e}}^{i\theta }}F\left(r{\mathrm{e}}^{i\theta }\right)r{\mathrm{e}}^{i\theta }dr.\hfill \end{array}$$

(10)

However, the last trigonometric integral vanishes for $\mu <1$ and therefore the final result of the complex integration from (10) is

$$\begin{array}{c}{f}_{\nu ,\mu }\left(t\right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut-u^{\nu }cos\left(\pi \nu \right)}}{u^{\mu }}}sin[u^{\nu }sin\left(\pi \nu \right)+\pi \mu ]du,\hfill \\ t>0;0<\nu <1;\mu <1.\hfill \end{array}$$

(11)

The same integral representation has been derived in 1970 by Stankoviċ [10] for the Wright function, but on the negative values of the argument t and which is presented here in our notation

$$\begin{array}{c}{t}^{\mu -1}{W}_{\nu ,\mu }\left(-{\displaystyle \frac{1}{t^{\nu }}}\right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut-u^{\nu }cos\left(\pi \nu \right)}}{u^{\mu }}}sin[u^{\nu }sin\left(\pi \nu \right)+\pi \mu ]du,\hfill \\ t>0;0<\nu <1;\mu <1,\hfill \end{array}$$

(12)

and comparing (11) with (12) we have that the inverse exponential functions can be expressed in terms of the Wright functions, in agreement with the survey analysis by Mainardi and Consiglio [33] where also plots are presented,

$$f_{\nu ,\mu }\left(t\right)=t^{\mu -1}{W}_{\nu ,\mu }\left(-{\displaystyle \frac{1}{t^{\nu }}}\right);0<\nu <1;\mu \ge 0,.$$

(13)

In particular, for $\mu =1-\nu$ the Wright functions are reduced to the Mainardi functions $F_{\nu }\left(t\right)$ and $M_{\nu }\left(t\right)$ [11]

$$f_{\nu ,1-\nu }\left(t\right)={\displaystyle \frac{1}{\nu }}{F}_{\nu }\left({\displaystyle \frac{1}{t^{\nu }}}\right)={\displaystyle \frac{1}{t^{\nu }}}{M}_{\nu }\left({\displaystyle \frac{1}{t^{\nu }}}\right);0<\nu <1.$$

(14)

For $\nu =1/2,\mu =0$ and $\nu =\mu =1/2$, the integrals in (11) become the Laplace transforms of trigonometric functions [18,19,20,21]

$$\begin{array}{c}{f}_{1/2,0}\left(t\right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-ut}sin\left(u^{1/2}\right)du={\displaystyle \frac{{\mathrm{e}}^{-1/4t}}{2\sqrt{\pi }{t}^{3/2}}},\hfill \\ f_{1/2,1/2}\left(t\right)={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut}}{u^{1/2}}}sin(u^{1/2}+{\displaystyle \frac{\pi }{2}})du={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut}}{u^{1/2}}}cos\left(u^{1/2}\right)du={\displaystyle \frac{{\mathrm{e}}^{-1/4t}}{\sqrt{\pi }}}.\hfill \end{array}$$

(15)

Since [11,12]

$$F_{1/3}\left({\displaystyle \frac{1}{t^{1/3}}}\right)={\displaystyle \frac{1}{3\pi t^{1/2}}}{K}_{1/3}\left({\displaystyle \frac{2}{\sqrt{27t}}}\right),$$

(16)

it follows from (11) and (14) that

$$\begin{array}{c}{f}_{1/3,2/3}\left(t\right)={\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut-u^{1/3}/2}}{u^{2/3}}}\left[\sqrt{3}cos\left({\displaystyle \frac{\sqrt{3}}{2}}{u}^{1/3}\right)-sin\left({\displaystyle \frac{\sqrt{3}}{2}}{u}^{1/3}\right)\right]du=\hfill \\ {\displaystyle \frac{1}{\pi }}\sqrt{{\displaystyle \frac{\mathit{\lambda }}{t}}}{K}_{1/3}\left({\displaystyle \frac{2}{\sqrt{27t}}}\right).\hfill \end{array}$$

(17)

Differentiation of the integral (11) with respect to the argument t gives

$$\begin{array}{c}{\displaystyle \frac{d^n{f}_{\nu ,\mu }\left(t\right)}{d{t}^n}}=f_{\nu ,\mu -n}\left(t\right)={\displaystyle \frac{{(-1)}^n}{\pi }}{\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{{\mathrm{e}}^{-ut-u^{\nu }cos\left(\pi \nu \right)}}{u^{\mu -n}}}sin[u^{\nu }sin\left(\pi \nu \right)+\pi \mu ]du,\hfill \\ t>0;0<\nu <1;\mu <1;n=0,1,2,3,\dots ,\hfill \end{array}$$

(18)

and using rules of the operational calculus we have the initial and final values of the function from [33]

$$\begin{array}{c}{f}_{\nu ,\mu }(t\to +0)=\underset{s\to \infty }{lim}\left[sF\left(s\right)\right]=s^{1-\mu }{\mathrm{e}}^{-s^{\nu }}=0;0<\nu <1;\mu <1,\hfill \\ f_{\nu ,\mu }(t\to \infty )=\underset{s\to 0}{lim}\left[sF\left(s\right)\right]=s^{1-\mu }{\mathrm{e}}^{-s^{\nu }}=0.\hfill \end{array}$$

(19)

This is in an agreement with the finding of Pollard [2] that for $\mu =0$, the inverse Laplace transform $f_{\nu ,0}$ is positive almost everywhere, but for $\mu <0$ Stankoviċ [10] postulated that in a some interval this function is negative and has at least one zero. Expanding the exponent in $F\left(s\right)$ into series it is possible to obtain the behaviour of the function for large values of the argument t

$$\begin{array}{c}{\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}\left[1-{\displaystyle \frac{s^{\nu }}{1!}}+{\displaystyle \frac{s^{2\nu }}{2!}}-\dots \right]\right\}.\hfill \\ f_{\nu ,\mu }(t\to \infty )\sim {\displaystyle \frac{1}{t^{1-\mu }}}\left\{{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\mu \right)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\mu -\nu )t^{\nu }}}+{\displaystyle \frac{1}{2\mathrm{\Gamma }(\mu -2\nu )t^{2\nu }}}-\dots \right\}\hfill \end{array}$$

(20)

The integral of the $f_{\nu ,\mu }$ can be derived directly from

$${\int }_0^t{f}_{\nu ,\mu }\left(u\right)du={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{1+\mu }}}\right\}=f_{\nu ,\mu +1}\left(t\right).$$

(21)

In order to obtain the recurrence relations the following operational rule can be applied

$$\mathcal{L}\left\{t{f}_{\nu ,\mu -1}\left(t\right)\right\}=-{\displaystyle \frac{d}{ds}}\left[F\left(s\right)\right]=-{\displaystyle \frac{d}{ds}}\left\{{\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu -1}}}\right\}=(\mu -1){\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu }}}+\nu {\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{\mu -\nu }}},$$

(22)

and the inverse transforms in (22) are

$$t{f}_{\nu ,\mu -1}\left(t\right)=(\mu -1)f_{\nu ,\mu }\left(t\right)+\nu f_{\nu ,\mu -\nu }\left(t\right).$$

(23)

However, from (18) with n = 1, we have

$${\displaystyle \frac{d{f}_{\nu ,\mu }\left(t\right)}{dt}}=f_{\nu ,\mu -1}\left(t\right),$$

(24)

and therefore

$$t{\displaystyle \frac{d{f}_{\nu ,\mu }\left(t\right)}{dt}}=(\mu -1)f_{\nu ,\mu }\left(t\right)+\nu f_{\nu ,\mu -\nu }\left(t\right).$$

(25)

3. Integrals of the Inverse Laplace Transform of ${\mathit{s}}^{-\mathbf{\mu }}\mathbf{exp}\left({\mathit{s}}^{\mathbf{\nu }}\right)$ with Elementary Functions

In the first example the Wlodarski integral formula (4) is applied to the power function $g\left(t\right)=t^{\mathit{\lambda }}$,

$$\begin{array}{c}g\left(t\right)=t^{\mathit{\lambda }};\mathit{\lambda }>0,\hfill \\ G\left(s\right)={\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)}{s^{\mathit{\lambda }+1}}};G\left(s^{\nu }\right)={\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)}{s^{(\mathit{\lambda }+1)\nu }}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)}{s^{(\mathit{\lambda }+1)\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)}{s^{(\mathit{\lambda }+1)\nu +\mu }}}\right\}={\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)t^{(\mathit{\lambda }+1)\nu +\mu -1}}{\mathrm{\Gamma }\left[\right(\mathit{\lambda }+1)\nu +\mu )]}},\hfill \end{array}$$

(26)

and therefore we have

$${\displaystyle {\int }_0^{\infty }}{u}^{\mathit{\lambda }}{f}_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{\mathrm{\Gamma }(\mathit{\lambda }+1)t^{(\mathit{\lambda }+1)\nu +\mu -1}}{\mathrm{\Gamma }\left[\right(\mathit{\lambda }+1)\nu +\mu )]}};0<\nu <1;\mu <1;\mathit{\lambda }>0.$$

(27)

The above results can be extended to functions $g\left(t\right)$ which are defined at finite intervals and to step functions jumping at integral values of variable t. Let start with

$$\begin{array}{c}g\left(t\right)=\left\{\begin{array}{c}1;0<t<\mathit{\lambda }\hfill \\ 0;t>\mathit{\lambda }\hfill \end{array}\right..\hfill \\ G\left(s\right)={\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }s}}{s}};G\left(s^{\nu }\right)={\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{\nu }}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu }}}-{\displaystyle \frac{{\mathit{\lambda }}^{(\mu /\nu +1)}{\mathrm{e}}^{-{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{\nu }}}{{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{\nu +\mu }}}\right\}=\hfill \\ {\displaystyle \frac{t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}-{\mathit{\lambda }}^{\left[\right(\mu -1)/\nu +1]}{f}_{\nu ,\nu +\mu }\left({\displaystyle \frac{t}{{\mathit{\lambda }}^{1/\nu }}}\right),\hfill \end{array}$$

(28)

which leads to the finite integral

$$\begin{array}{c}{\displaystyle {\int }_0^{\mathit{\lambda }}}{f}_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}-{\mathit{\lambda }}^{\left[\right(\mu -1)/\nu +1]}{f}_{\nu ,\nu +\mu }\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right),\hfill \\ 0<\nu <1;\mu <1;\mathit{\lambda }>0.\hfill \end{array}$$

(29)

In the next example, from

$$\begin{array}{c}g\left(t\right)=\left\{\begin{array}{c}1-t;0<t<1\hfill \\ 0;t>1\hfill \end{array}\right.,\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-s}+s-1}{s^2}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}+s^{\nu }-1}{s^{2\nu }}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}+s^{\nu }-1}{s^{2\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{2\nu +\mu }}}-{\displaystyle \frac{1}{s^{\nu +\mu }}}+{\displaystyle \frac{{\mathrm{e}}^{-s^{\nu }}}{s^{2\nu +\mu }}}\right\}=\hfill \\ {\displaystyle \frac{t^{2\nu +\mu -1}}{\mathrm{\Gamma }(2\nu +\mu )}}-{\displaystyle \frac{t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}+f_{\nu ,2\nu +\mu }\left(t\right),\hfill \end{array}$$

(30)

we have

$${\displaystyle {\int }_0^1}(1-u)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{2\nu +\mu -1}}{\mathrm{\Gamma }(2\nu +\mu )}}-{\displaystyle \frac{t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}+f_{\nu ,2\nu +\mu }\left(t\right).$$

(31)

Using

$$\begin{array}{c}g\left(t\right)=\left\{\begin{array}{c}0;0<t<\mathit{\lambda }\hfill \\ {\displaystyle \frac{{(t-\mathit{\lambda })}^{\mu }}{\mathrm{\Gamma }(\mu +1)}};t>\mathit{\lambda }\hfill \end{array}\right.,\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }s}}{s^{\mu +1}}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{(\mu +1)\nu }}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{(\mu +1)\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{{\mathit{\lambda }}^{\left[\right(1/\nu +1)\mu +1]}{\mathrm{e}}^{-{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{\nu }}}{{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{(\mu +1)\nu +\mu }}}\right\}=\hfill \\ ={\mathit{\lambda }}^{\left[\right(1/\nu +1)\mu -1/\nu +1]}{f}_{\nu ,\nu +\nu \mu +\mu }\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right),\hfill \end{array}$$

(32)

it is possible to derive

$${\displaystyle {\int }_{\mathit{\lambda }}^{\infty }}{(t-\mathit{\lambda })}^{\mu }{f}_{\nu ,\mu }\left(u\right)du={\mathit{\lambda }}^{\left[\right(1/\nu +1)\mu -1/\nu +1]}{f}_{\nu ,\nu +\nu \mu +\mu }\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right).$$

(33)

In the next example the case of exponential function is considered:

$$\begin{array}{c}g\left(t\right)={\mathrm{e}}^{-\alpha t};\alpha >0,\hfill \\ G\left(s\right)={\displaystyle \frac{1}{s+\alpha }};G\left(s^{\nu }\right)={\displaystyle \frac{1}{s^{\nu }+\alpha }},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{\nu }+\alpha }}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{s^{\nu -1}}{s^{\nu }+\alpha }}\right\}={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{\nu }(-\alpha t^{\nu }).\hfill \end{array}$$

(34)

From (4) and (34) the convolution integral with the Mittag–Leffler function

$$\begin{array}{c}{E}_{\nu }\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{t^k}{\mathrm{\Gamma }(k\nu +1)}},\hfill \\ \mathcal{L}\left\{E_{\nu }(-\alpha t^{\nu })\right\}={\displaystyle \frac{s^{\nu -1}}{s^{\nu }+\alpha }},\hfill \end{array}$$

(35)

is derived

$$\begin{array}{c}{\displaystyle {\int }_0^{\infty }}{\mathrm{e}}^{-}{}^{\alpha u}{f}_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{\nu }(-\alpha t^{\nu }),\hfill \\ 0<\nu <1;\mu <1;\alpha >0.\hfill \end{array}$$

(36)

By changing variable of integration $x=t{\left(cos\theta \right)}^2$, all convolution integrals can be expressed as in terms of finite trigonometric integrals. The shifted increasing and decreasing exponential functions are considered in the following two examples. From

$$\begin{array}{c}g\left(t\right)=\left\{\begin{array}{c}0;0<t<\mathit{\lambda };0<\nu <1\hfill \\ 1-{\mathrm{e}}^{-(t-\mathit{\lambda })};t>\mathit{\lambda }\hfill \end{array}\right.,\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }s}}{s(s+1)}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{\nu }(s^{\nu }+1)}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{s^{\nu }(s^{\nu }+1)}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{s^{\nu -1}}{(s^{\nu }+1)}}·{\displaystyle \frac{{\mathit{\lambda }}^{(2\nu +\mu -1)/\nu }{\mathrm{e}}^{-{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{\nu }}}{{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{(2\nu +\mu -1)}}}\right\}=\hfill \\ {\mathit{\lambda }}^{(\nu +\mu -1)/\nu }{E}_{\nu }(-t^{\nu })\ast f_{\nu ,}{}_{2\nu +\mu -1}\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right),\hfill \end{array}$$

(37)

we have the convolution of two functions.

$${\displaystyle {\int }_{\mathit{\lambda }}^{\infty }}\left[1-{\mathrm{e}}^{-(u-\mathit{\lambda })}\right]f_{\nu ,\mu }\left(u\right)du={\mathit{\lambda }}^{(\nu +\mu -1)/\nu }{E}_{\nu }(-t^{\nu })\star f_{\nu ,}{}_{2\nu +\mu -1}\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right).$$

(38)

Similarly from

$$\begin{array}{c}g\left(t\right)=\left\{\begin{array}{c}0;0<t<\mathit{\lambda };0<\nu <1\hfill \\ {\mathrm{e}}^{-(t-\mathit{\lambda })};t>\mathit{\lambda }\hfill \end{array}\right.;\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }s}}{(s+1)}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{(s^{\nu }+1)}};\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu }}}{(s^{\nu }+1)}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{s^{\nu -1}}{(s^{\nu }+1)}}·{\displaystyle \frac{{\mathit{\lambda }}^{(\nu +\mu -1)/\nu }{\mathrm{e}}^{-{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{\nu }}}{{\left({\mathit{\lambda }}^{1/\nu }s\right)}^{(\nu +\mu -1)}}}\right\}=\hfill \\ {\mathit{\lambda }}^{(\nu +\mu -2)/\nu }{E}_{\nu }(-t^{\nu })\ast f_{\nu ,}{}_{\nu +\mu -1}\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right),\hfill \end{array}$$

(39)

it is possible to obtain

$${\displaystyle {\int }_{\mathit{\lambda }}^{\infty }}{\mathrm{e}}^{-(u-\mathit{\lambda })}{f}_{\nu ,\mu }\left(u\right)du={\mathit{\lambda }}^{(\nu +\mu -2)/\nu }{E}_{\nu }(-t^{\nu })\star f_{\nu ,}{}_{\nu +\mu -1}\left(\frac{t}{{\mathit{\lambda }}^{1/\nu }}\right).$$

(40)

The logarithmic functions are the next group of elementary functions to be considered. In the simplest case from

$$\begin{array}{c}g\left(t\right)=lnt;C={\mathrm{e}}^{\gamma };\hfill \\ G\left(s\right)=-{\displaystyle \frac{ln\left(Cs\right)}{s}};G\left(s^{\nu }\right)=-{\displaystyle \frac{ln\left(C{s}^{\nu }\right)}{s^{\nu }}};\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{-ln\left(C{s}^{\nu }\right)}{s^{\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{-\nu ln\left(Cs\right)+(\nu -1)\gamma }{s}}\right\}=\hfill \\ {\displaystyle \frac{(\nu -1)\gamma t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}+{\displaystyle \frac{\nu t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star lnt\hfill \end{array}$$

(41)

where $\gamma$ is the Euler constant, it follows that

$${\displaystyle {\int }_0^{\infty }}lnu{f}_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{(\nu -1)\gamma t^{\nu +\mu -1}}{\mathrm{\Gamma }(\nu +\mu )}}+{\displaystyle \frac{\nu t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star lnt.$$

(42)

In the more general case

$$\begin{array}{c}g\left(t\right)=t^{\mathit{\lambda }-1}lnt;\mathit{\lambda }>0;0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)}{s^{\mathit{\lambda }}}}\left[\psi \left(\mathit{\lambda }\right)-lns\right];G\left(s^{\nu }\right)={\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)\left[\psi \right(\mathit{\lambda })-\nu lns]}{s^{\mathit{\lambda }\nu }}};\hfill \\ \mathrm{\Gamma }\left(\mathit{\lambda }\right){\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{\left[\psi \right(\mathit{\lambda })-\nu lns]}{s^{\mathit{\lambda }\nu }}}\right\}=\mathrm{\Gamma }\left(\mathit{\lambda }\right){\mathcal{L}}^{-1}\left\{{\displaystyle \frac{\psi \left(\mathit{\lambda }\right)+\gamma \nu }{s^{(\mathit{\lambda }\nu +\mu )}}}-{\displaystyle \frac{\nu }{s^{(\mathit{\lambda }\nu +\mu -1)}}}·{\displaystyle \frac{ln\left(Cs\right)}{s}}\right\}=\hfill \\ {\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)[\psi \left(\mathit{\lambda }\right)+\gamma \nu ]t^{(\mathit{\lambda }\nu +\mu -1)}}{\mathrm{\Gamma }(\mathit{\lambda }\nu +\mu )}}+{\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)\nu t^{(\mathit{\lambda }\nu +\mu -2)}}{\mathrm{\Gamma }(\mathit{\lambda }\nu +\mu -1)}}\star ln{t}^{\nu },\hfill \end{array}$$

(43)

we have

$${\displaystyle {\int }_0^{\infty }}{u}^{\mathit{\lambda }-1}lnu{f}_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)\left[\psi \left(\mathit{\lambda }\right)+\gamma \nu \right]t^{(\mathit{\lambda }\nu +\mu -1)}}{\mathrm{\Gamma }(\mathit{\lambda }\nu +\mu )}}+{\displaystyle \frac{\mathrm{\Gamma }\left(\mathit{\lambda }\right)\nu t^{(\mathit{\lambda }\nu +\mu -2)}}{\mathrm{\Gamma }(\mathit{\lambda }\nu +\mu -1)}}\star ln{t}^{\nu }.$$

(44)

Trigonometric and hyperbolic functions is the last groups of elementary functions to be considered. From:

$$\begin{array}{c}g\left(t\right)=sin\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{\mathit{\lambda }}{s^2+{\mathit{\lambda }}^2}};G\left(s^{\nu }\right)={\displaystyle \frac{\mathit{\lambda }}{s^{2\nu }+{\mathit{\lambda }}^2}};\hfill \\ \mathit{\lambda }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{2\nu }+{\mathit{\lambda }}^2}}\right\}=\mathit{\lambda }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{2\nu +\mu -1}}}·{\displaystyle \frac{s^{2\nu -1}}{s^{2\nu }+{\mathit{\lambda }}^2}}\right\}={\displaystyle \frac{\mathit{\lambda }{t}^{2\nu +\mu -2}}{\mathrm{\Gamma }(2\nu +\mu -1)}}\star E_{2\nu }(-{\mathit{\lambda }}^2{t}^{2\nu }),\hfill \end{array}$$

(45)

the following integral identity is derived

$${\displaystyle {\int }_0^{\infty }}sin\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{\mathit{\lambda }{t}^{2\nu +\mu -2}}{\mathrm{\Gamma }(2\nu +\mu -1)}}\star E_{2\nu }(-{\mathit{\lambda }}^2{t}^{2\nu }).$$

(46)

Similarly as in (45), for the hyperbolic sine function, the change is only in the sign

$$\begin{array}{c}g\left(t\right)=sinh\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{\mathit{\lambda }}{s^2-{\mathit{\lambda }}^2}};G\left(s^{\nu }\right)={\displaystyle \frac{\mathit{\lambda }}{s^{2\nu }-{\mathit{\lambda }}^2}};\hfill \\ \mathit{\lambda }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{2\nu }-{\mathit{\lambda }}^2}}\right\}=\mathit{\lambda }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{2\nu +\mu -1}}}·{\displaystyle \frac{s^{2\nu -1}}{s^{2\nu }-{\mathit{\lambda }}^2}}\right\}={\displaystyle \frac{\mathit{\lambda }{t}^{2\nu +\mu -2}}{\mathrm{\Gamma }(2\nu +\mu -1)}}\star E_{2\nu }\left({\mathit{\lambda }}^2{t}^{2\nu }\right),\hfill \end{array}$$

(47)

and therefore we have

$${\displaystyle {\int }_0^{\infty }}sinh\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{\mathit{\lambda }{t}^{2\nu +\mu -2}}{\mathrm{\Gamma }(2\nu +\mu -1)}}\star E_{2\nu }\left({\mathit{\lambda }}^2{t}^{2\nu }\right).$$

(48)

In the case of cosine function, from;

$$\begin{array}{c}g\left(t\right)=cos\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{s}{s^2+{\mathit{\lambda }}^2}};G\left(s^{\nu }\right)={\displaystyle \frac{s^{\nu }}{s^{2\nu }+{\mathit{\lambda }}^2}};\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{s^{\nu }}{s^{2\nu }+{\mathit{\lambda }}^2}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{s^{2\nu -1}}{s^{2\nu }+{\mathit{\lambda }}^2}}\right\}={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{2\nu }(-{\mathit{\lambda }}^2{t}^{2\nu }),\hfill \end{array}$$

(49)

we have

$${\displaystyle {\int }_0^{\infty }}cos\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{2\nu }(-{\mathit{\lambda }}^2{t}^{2\nu }).$$

(50)

Similarly as in (47) and (48)

$$\begin{array}{c}g\left(t\right)=cosh\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{s}{s^2-{\mathit{\lambda }}^2}};G\left(s^{\nu }\right)={\displaystyle \frac{s^{\nu }}{s^{2\nu }-{\mathit{\lambda }}^2}};\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{s^{\nu }}{s^{2\nu }-{\mathit{\lambda }}^2}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{s^{2\nu -1}}{s^{2\nu }-{\mathit{\lambda }}^2}}\right\}={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{2\nu }\left({\mathit{\lambda }}^2{t}^{2\nu }\right),\hfill \end{array}$$

(51)

for the hyperbolic cosine function we have

$${\displaystyle {\int }_0^{\infty }}cosh\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{2\nu }\left({\mathit{\lambda }}^2{t}^{2\nu }\right).$$

(52)

In the case of the product of trigonometric and hyperbolic sine functions the direct and inverse Laplace transforms are

$$\begin{array}{c}g\left(t\right)=sin\left(\mathit{\lambda }t\right)sinh\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{2{\mathit{\lambda }}^{2}s}{s^4+4{\mathit{\lambda }}^4}};G\left(s^{\nu }\right)={\displaystyle \frac{2{\mathit{\lambda }}^2{s}^{\nu }}{s^{4\nu }+4{\mathit{\lambda }}^4}};\hfill \\ 2{\mathit{\lambda }}^2{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{s^{\nu }}{s^{4\nu }+4{\mathit{\lambda }}^4}}\right\}=2{\mathit{\lambda }}^2{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{3\nu +\mu -1}}}·{\displaystyle \frac{s^{4\nu -1}}{(s^{4\nu }+4{\mathit{\lambda }}^4)}}\right\}=\hfill \\ \frac{2{\mathit{\lambda }}^2}{\mathrm{\Gamma }(3\nu +\mu -1)}[t^{(3\nu +\mu -2)}\star E_{4\nu }(-4{\mathit{\lambda }}^4{t}^{4\nu })],\hfill \end{array}$$

(53)

and therefore

$${\int }_0^{\infty }sin\left(\mathit{\lambda }u\right)sinh\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du=\frac{2{\mathit{\lambda }}^2}{\mathrm{\Gamma }(3\nu +\mu -1)}[t^{(3\nu +\mu -2)}\star E_{4\nu }(-4{\mathit{\lambda }}^4{t}^{4\nu })].$$

(54)

For the product of trigonometric and hyperbolic sine functions we have

$$\begin{array}{c}g\left(t\right)=cos\left(\mathit{\lambda }t\right)cosh\left(\mathit{\lambda }t\right);0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{s^3}{s^4+4{\mathit{\lambda }}^4}};G\left(s^{\nu }\right)={\displaystyle \frac{s^{3\nu }}{s^{4\nu }+4{\mathit{\lambda }}^4}};\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{s^{3\nu }}{s^4+4{\mathit{\lambda }}^4}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{s^{4\nu -1}}{s^{4\nu }+4{\mathit{\lambda }}^4}}\right\}={\displaystyle \frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}}\star E_{4\nu }(-4{\mathit{\lambda }}^4{t}^{4\nu }),\hfill \end{array}$$

(55)

and therefore

$${\displaystyle {\int }_0^{\infty }}cos\left(\mathit{\lambda }u\right)(cosh\left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du=\frac{t^{\nu +\mu -2}}{\mathrm{\Gamma }(\nu +\mu -1)}\star E_{4\nu }(-4{\mathit{\lambda }}^4{t}^{4\nu }).$$

(56)

4. Integrals of the Inverse Laplace Transform of ${\mathit{s}}^{-\mathbf{\mu }}\mathbf{exp}(-{\mathit{s}}^{\mathbf{\nu }})$ with the Mitag-Leffler, Error and Volterra Functions

The Laplace transform of the two parameter Mittag–Leffler function is [11,34,35,36]

$$\begin{array}{c}\mathcal{L}\left\{t^{\beta -1}{E}_{\alpha ,\beta }(\pm \mathit{\lambda }{t}^{\alpha })\right\}={\displaystyle \frac{s^{\alpha -\beta }}{s^{\alpha }\mp \mathit{\lambda }}},\hfill \\ E_{\alpha ,\beta }\left(z\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{z^k}{\mathrm{\Gamma }(k\alpha +\beta )}},\hfill \end{array}$$

(57)

and this permits to obtain

$$\begin{array}{c}g\left(t\right)=t^{\beta -1}{E}_{\alpha ,\beta }(\pm \mathit{\lambda }{t}^{\alpha });0<\nu <1;\hfill \\ G\left(s\right)={\displaystyle \frac{s^{\alpha -\beta }}{s^{\alpha }\mp \mathit{\lambda }}};G\left(s^{\nu }\right)={\displaystyle \frac{s^{(\alpha -\beta )\nu }}{s^{\alpha \nu }\mp \mathit{\lambda }}};\hfill \\ \left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{s^{(\alpha -\beta )\nu }}{s^{\alpha \nu }\mp \mathit{\lambda }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{s^{\alpha \nu -(\beta \nu +\mu )}}{s^{\alpha \nu }\mp \mathit{\lambda }}}\right\}=t^{(\beta \nu +\mu -1)}{E}_{\alpha \nu ,\beta \nu +\mu }(\pm \mathit{\lambda }{t}^{\alpha }),\hfill \end{array}$$

(58)

and

$${\displaystyle {\int }_0^{\infty }}{u}^{\beta -1}{E}_{\alpha ,\beta }(\pm \mathit{\lambda }{u}^{\alpha })f_{\nu ,\mu }\left(u\right)du=t^{(\beta \nu +\mu -1)}{E}_{\alpha \nu ,\beta \nu +\mu }(\pm \mathit{\lambda }{t}^{\alpha }).$$

(59)

Thus, in both sides of expressions (59) appear the Mittag–Leffler functions. Evidently, for $\beta =1$ they are reduced to the classical Mittag–Leffler functions.

$${\displaystyle {\int }_0^{\infty }}{E}_{\alpha ,1}(\pm \mathit{\lambda }{u}^{\alpha })f_{\nu ,\mu }\left(u\right)du=t^{(\nu +\mu -1)}{E}_{\alpha \nu ,\nu +\mu }(\pm \mathit{\lambda }{t}^{\alpha }),$$

(60)

and for $\beta =\alpha$ and $\beta =\alpha +1$ we have

$$\begin{array}{c}{\displaystyle {\int }_0^{\infty }}{u}^{\alpha -1}{E}_{\alpha ,\alpha }(\pm \mathit{\lambda }{u}^{\alpha })f_{\nu ,\mu }\left(u\right)du=t^{(\alpha \nu +\mu -1)}{E}_{\alpha \nu ,\alpha \nu +\mu }(\pm \mathit{\lambda }{t}^{\alpha }),\hfill \\ {\displaystyle {\int }_0^{\infty }}{u}^{\alpha }{E}_{\alpha ,\alpha +1}(\pm \mathit{\lambda }{u}^{\alpha })f_{\nu ,\mu }\left(u\right)du=t^{\left[\right(\alpha +1)\nu +\mu -1]}{E}_{\alpha \nu ,(\alpha +1)\nu +\mu }(\pm \mathit{\lambda }{t}^{\alpha }).\hfill \end{array}$$

(61)

If $\beta =1/2$, in the integrands of (61) the Mittag–Leffler functions are expressed then by the error functions [35,36]

$$\begin{array}{c}{E}_{1/2}(\pm z)={\mathrm{e}}^{z^2}[1\pm \mathrm{erf}\left(z\right)];z=\mathit{\lambda }{u}^{\alpha },\hfill \\ E_{1/2,1/2}(\pm z)=\left\{{\displaystyle \frac{1}{\sqrt{z}}}\pm z{\mathrm{e}}^{z^2}[1\pm \mathrm{erf}\left(z\right)]\right\},\hfill \\ E_{1/2,3/2}\left(z\right)={\displaystyle \frac{{\mathrm{e}}^z}{\sqrt{z}}}\mathrm{erf}\left(z\right).\hfill \end{array}$$

(62)

If $\beta$ is positive integer, the Mittag–Leffler functions are expressed by elementary functions [36]. In particular cases, with $\nu =1/2,\mu =0$. $\nu =\mu =1/2$ and $\nu =1/3,\mu =2/3$ the explicit form of the inverse transforms of exponential functions is known (see (15) and (17)).

The Laplace transform of the error function is

$$\begin{array}{c}g\left(t\right)=\mathrm{erf}\left({\displaystyle \frac{\mathit{\lambda }}{2t^{1/2}}}\right);0<\nu <1,\hfill \\ G\left(s\right)={\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }{s}^{1/2}}}{s}};G\left(s^{\nu }\right)={\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu /2}}}{s^{\nu }}},\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1-{\mathrm{e}}^{-\mathit{\lambda }{s}^{\nu /2}}}{s^{\nu }}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}-{\displaystyle \frac{{\mathit{\lambda }}^{2\mu /\nu }{\mathrm{e}}^{-{\left({\mathit{\lambda }}^{2/\nu }s\right)}^{\nu /2}}}{{\left({\mathit{\lambda }}^{2/\nu }s\right)}^{\mu }}}\right\}=\hfill \\ {\displaystyle \frac{t^{\mu -1}}{\mathrm{\Gamma }\left(\mu \right)}}-{\mathit{\lambda }}^{2(\mu -1)/\nu }{f}_{\nu /2,\mu }\left({\displaystyle \frac{t^{\nu /2}}{{\mathit{\lambda }}^{2/\nu }}}\right),\hfill \end{array}$$

(63)

which yields

$${\displaystyle {\int }_0^{\infty }}\mathrm{erf}\left({\displaystyle \frac{\mathit{\lambda }}{2u^{1/2}}}\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\mu -1}}{\mathrm{\Gamma }\left(\mu \right)}}-{\mathit{\lambda }}^{2(\mu -1)/\nu }{f}_{\nu /2,\mu }\left({\displaystyle \frac{t^{\nu /2}}{{\mathit{\lambda }}^{2/\nu }}}\right).$$

(64)

The Volterra functions are defined by the following integrals [37]:

$$\begin{array}{c}\nu \left(t\right)={\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{t^u}{\mathrm{\Gamma }(u+1)}}du,\hfill \\ \nu (t,\alpha )={\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{t^{u+\alpha }}{\mathrm{\Gamma }(u+\alpha +1)}}du,\hfill \\ \mu (t,\beta ,\alpha )={\displaystyle {\int }_0^{\infty }}{\displaystyle \frac{u^{\beta }{t}^{u+\alpha }}{\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(u+\alpha +1)}}du,\hfill \end{array}$$

(65)

and their Laplace transforms are

$$\begin{array}{c}\mathcal{L}\left\{\nu \left(\mathit{\lambda }t\right)\right\}={\displaystyle \frac{1}{sln\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)}};\mathit{\lambda }>0,\hfill \\ \mathcal{L}\left\{\nu (\mathit{\lambda }t,\alpha )\right\}={\displaystyle \frac{{\mathit{\lambda }}^{\alpha }}{s^{\alpha +1}ln\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)}},\hfill \\ \mathcal{L}\left\{\mu \left(\right(\mathit{\lambda }t,\beta ,\alpha )\right\}={\displaystyle \frac{{\mathit{\lambda }}^{\alpha }}{s^{\alpha +1}ln{\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)}^{\beta +1}}}.\hfill \end{array}$$

(66)

The logarithmic functions in the Laplace transforms permit to express the integrals of the Volterra functions with inverse Laplace transform of exponential function in terms of convolution integrals. From

$$\begin{array}{c}g\left(t\right)=\nu \left(\mathit{\lambda }t\right);\mathit{\lambda }>0,\hfill \\ G\left(s\right)={\displaystyle \frac{1}{sln\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)}};G\left(s^{\nu }\right)={\displaystyle \frac{1}{s^{\nu }ln\left({\displaystyle \frac{s^{\nu }}{\mathit{\lambda }}}\right)}};0<\nu <1,\hfill \\ {\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{\nu }ln\left[{(s/{\mathit{\lambda }}^{1/\nu })}^{\nu }\right]}}\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\nu +\mu -1}}}·{\displaystyle \frac{1}{\nu sln(s/{\mathit{\lambda }}^{1/\nu })}}\right\}=\hfill \\ {\displaystyle \frac{t^{\nu +\mu -2}}{\nu \mathrm{\Gamma }(\nu +\mu -1)}}\ast \nu \left({\mathit{\lambda }}^{1/\nu }t\right),\hfill \end{array}$$

(67)

it follows that

$${\displaystyle {\int }_0^{\infty }}\nu \left(\mathit{\lambda }u\right)f_{\nu ,\mu }\left(u\right)du={\displaystyle \frac{t^{\nu +\mu -2}}{\nu \mathrm{\Gamma }(\nu +\mu -1)}}\star \nu \left({\mathit{\lambda }}^{1/\nu }t\right).$$

(68)

Similarly from

$$\begin{array}{c}g\left(t\right)=\nu (\mathit{\lambda }t,\rho );\mathit{\lambda },\rho >0\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathit{\lambda }}^{\rho }}{s^{\rho +1}ln\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathit{\lambda }}^{\rho }}{s^{(\rho +1)\nu }ln\left({\displaystyle \frac{s^{\nu }}{\mathit{\lambda }}}\right)}};0<\nu <1,\hfill \\ {\mathit{\lambda }}^{\rho }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{(\rho +1)\nu }ln\left[{(s/{\mathit{\lambda }}^{1/\nu })}^{\nu }\right]}}\right\}={\mathit{\lambda }}^{\rho }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu -1}}}·{\displaystyle \frac{1}{\nu s^{(\rho +1)\nu +1}ln(s/{\mathit{\lambda }}^{1/\nu })}}\right\}=\hfill \\ {\displaystyle \frac{t^{\mu -2}}{\mathrm{\Gamma }(\mu -1)\nu \mathit{\lambda }}}\star ,\nu [{\mathit{\lambda }}^{1/\nu }t,(\rho +1)\nu ],\hfill \end{array}$$

(69)

we have

$${\displaystyle {\int }_0^{\infty }}\nu (\mathit{\lambda }u,\rho )f_{\nu ,\mu }du={\displaystyle \frac{t^{\mu -2}}{\mathrm{\Gamma }(\mu -1)\nu \mathit{\lambda }}}\star \nu [{\mathit{\lambda }}^{1/\nu }t,(\rho +1)\nu ].$$

(70)

Finally, the Laplace transform of the generalized Volterra function is

$$\begin{array}{c}g\left(t\right)=\mu (\mathit{\lambda }t,\xi ,\rho );\mathit{\lambda },\rho ,\xi >0\hfill \\ G\left(s\right)={\displaystyle \frac{{\mathit{\lambda }}^{\rho }}{s^{\rho +1}{[ln\left({\displaystyle \frac{s}{\mathit{\lambda }}}\right)]}^{\xi +1}}};G\left(s^{\nu }\right)={\displaystyle \frac{{\mathit{\lambda }}^{\rho }}{s^{(\rho +1)\nu }{[ln\left({\displaystyle \frac{s^{\nu }}{\mathit{\lambda }}}\right)]}^{\xi +1}}};0<\nu <1,\hfill \\ {\mathit{\lambda }}^{\rho }{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu }}}·{\displaystyle \frac{1}{s^{(\rho +1)\nu }{\{ln\left[{(s/{\mathit{\lambda }}^{1/\nu })}^{\nu }\right]\}}^{\xi +1}}}\right\}=\hfill \\ {\displaystyle \frac{{\mathit{\lambda }}^{\rho }}{{\nu }^{\xi +1}}}{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{1}{s^{\mu -1}}}·{\displaystyle \frac{1}{s^{(\rho +1)\nu +1}{[ln(s/{\mathit{\lambda }}^{1/\nu })]}^{\xi +1}}}\right\}=\hfill \\ {\displaystyle \frac{t^{\mu -2}}{\mathrm{\Gamma }(\mu -1)\mathit{\lambda }{\nu }^{\xi +1}}}\star \mu [{\mathit{\lambda }}^{1/\nu }t,\xi ,(\rho +1)\nu ],\hfill \end{array}$$

(71)

and (65) yields

$${\displaystyle {\int }_0^{\infty }}\mu (\mathit{\lambda }u,\xi ,\rho )f_{\nu ,\mu }du={\displaystyle \frac{t^{\mu -2}}{\mathrm{\Gamma }(\mu -1)\mathit{\lambda }{\nu }^{\xi +1}}}\star \mu [{\mathit{\lambda }}^{1/\nu }t,\xi ,(\rho +1)\nu ].$$

(72)

The number of similar convolution integrals can be significantly enlarged if the Volterra functions are multiplied by $t^n$ with $n=1,2,3,\dots$, then their Laplace transforms should be differentiated n times. The result of such differentiations are linear combinations of these functions [34,35,36]. For example, with $n=1$ and $\mathit{\lambda }=1$ we have

$$\begin{array}{c}t\nu (t,\rho )={\mathcal{L}}^{-1}\left\{-{\displaystyle \frac{d}{ds}}\left[{\displaystyle \frac{1}{s^{\rho +1}lns}}\right]\right\}={\mathcal{L}}^{-1}\left\{{\displaystyle \frac{\rho +1}{s^{\rho +2}lns}}+{\displaystyle \frac{1}{s^{\rho +2}{(lns)}^2}}\right\}=\hfill \\ (\rho +1)\nu [t,(\rho +1\left)\nu \right]+\mu [t,1,(\rho +1\left)\nu \right].\hfill \end{array}$$

(73)

5. Conclusions

By applying the Efros theorem in the form established by Wlodarski it was possible to derive a number of infinite integrals, finite integrals and integral identities with the function which represent the Laplace inverse transform of $s^{-\mu }\exp (-s^{\nu })$ with $0<\nu <1$ and $0\le \mu <1$. The extension to the cases $\mu \ge 1$ is dealt in Appendix A Derived by us integrals include in integrands elementary functions (power, exponential, logarithmic, trigonometric and hyperbolic functions) and the error functions, the Mittag–Leffler functions and the Volterra functions. Many results appear in form of the convolution integrals. Performing the inversion by the complex integration, it was possible to show that the inverse Laplace inverse transform, which means the original function, can be also expressed in terms of the Wright functions and for particular values of parameters by the Mainardi functions. Using rules of operational calculus some properties of the inverse Laplace transform were derived.