Quantum Fisher Information and Bures Distance Correlations of Coupled Two Charge-Qubits Inside a Coherent Cavity with the Intrinsic Decoherence
Abstract
1. Introduction
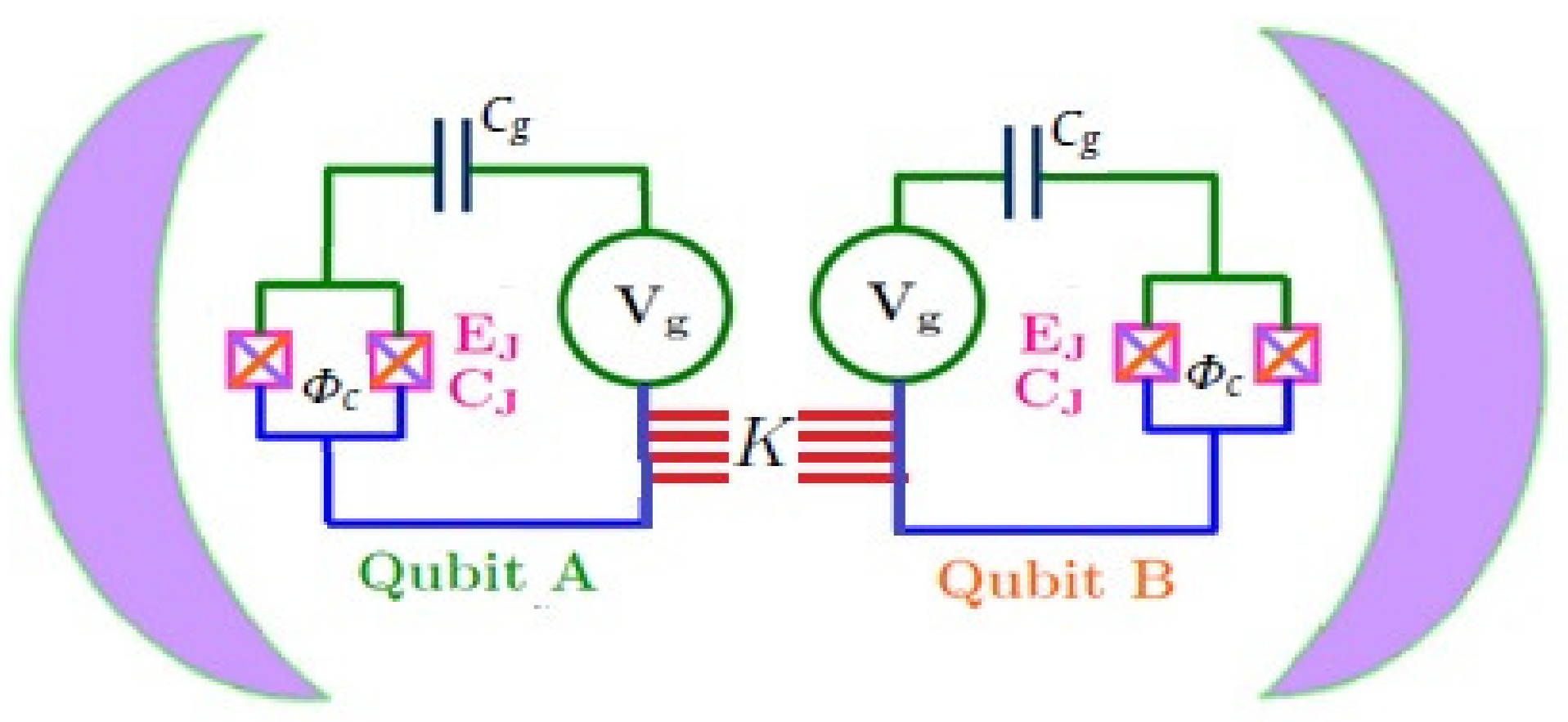
2. Time Evolution of the Physical Model
3. Quantum Fisher Information and Bures Distance Entanglement
3.1. Local Quantum Fisher Information
3.2. Bures Distance Entanglement
4. Dynamics of the Correlation Quantifiers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Yu, H.; McCuller, L.; Tse, M.; Kijbunchoo, N.; Barsotti, L.; Mavalvala, N. Quantum correlations between light and the kilogram-mass mirrors of LIGO. Nature 2020, 583, 43. [Google Scholar] [CrossRef]
- He, X. Quantum correlation alignment for unsupervised domain adaptation. Phys. Rev. A 2020, 102, 032410. [Google Scholar] [CrossRef]
- Coulamy, I.B.; Warnes, J.H.; Sarandy, M.S.; Saguia, A. Scaling of the local quantum uncertainty at quantum phase transitions. Phys. Lett. A 2016, 380, 1724. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Homid, A.H.; Abdel-Aty, M.; Eleuch, H. Trace-norm correlation beyond entanglement in InAs nanowire system with spin-orbit interaction and external electric field. J. Opt. Soc. Am. B 2019, 36, 926. [Google Scholar] [CrossRef]
- Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Dakic, B.; Vedral, V.; Brukner, C. Necessary and Sufficient Condition for Nonzero Quantum Discord. Phys. Rev. Lett. 2010, 105, 190502. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Metwally, N. Enhancing non-local correlations in a dissipative two-qubit system via dipole dipole interplay. Quantum. Inf. Process. 2019, 18, 79. [Google Scholar] [CrossRef]
- Streltsov, A.; Kampermann, H.; Bruss, D. Linking a distance measure of entanglement to its convex roof. New J. Phys. 2010, 12, 123004. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing Nonclassical Correlations via Local Quantum Uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H. High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys. Rev. A 2015, 91, 032309. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Generation and robustness of bipartite non-classical correlations in two nonlinear microcavities coupled by an optical fiber. J. Opt. Soc. Am. B 2018, 35, 47. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Non-local correlation and quantum discord in two atoms in the non-degenerate model. Ann. Phys. 2012, 327, 3130. [Google Scholar] [CrossRef]
- Wei, T.-C.; Nemoto, K.; Goldbart, P.M.; Kwiat, P.G.; Munro, W.J.; Verstraete, F. Maximal entanglement versus entropy for mixed quantum states. Phys. Rev. A 2003, 67, 022110. [Google Scholar] [CrossRef]
- Costa, A.C.S.; Beims, M.W.; Angelo, R.M. Generalized discord, entanglement, Einstein Podolsky Rosen steering, and Bell nonlocality in two-qubit systems under (non-) Markovian channels: Hierarchy of quantum resources and chronology of deaths and births. Phys. A Stat. Mech. Appl. 2016, 461, 469. [Google Scholar] [CrossRef]
- Tóth, G. Multipartite entanglement and high-precision metrology. Phys. Rev. A 2012, 85, 022322. [Google Scholar] [CrossRef]
- Taddei, M.M.; Escher, B.M.; Davidovich, L.; de Matos Filho, R.L. Quantum Speed Limit for Physical Processes. Phys. Rev. Lett. 2013, 110, 050402. [Google Scholar] [CrossRef]
- Karpat, G.; Çakmak, B.; Fanchini, F.F. Quantum coherence and uncertainty in the anisotropic XY chain. Phys. Rev. B 2014, 90, 104431. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, J.; Lu, X.-M.; Wang, X. Fisher information in a quantum-critical environment. Phys. Rev. A 2010, 82, 022306. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222. [Google Scholar] [CrossRef]
- Zhang, Y.-R.; Zeng, Y.; Fan, H.; You, J.Q.; Nori, F. Characterization of Topological States via Dual Multipartite Entanglement. Phys. Rev. Lett. 2018, 120, 250501. [Google Scholar] [CrossRef]
- Jafari, R.; Akbari, A. Dynamics of quantum coherence and quantum Fisher information after a sudden quench. Phys. Rev. A 2020, 101, 062105. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum Metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef] [PubMed]
- Metwally, N. Fisher information of accelerated two-qubit systems. Int. J. M. Phys. B 2018, 32, 1850050. [Google Scholar] [CrossRef]
- Wang, C.; Fang, M.-F. Enhancing the precision of parameter estimation in a dissipative qutrit via quantum feedback control and classical driving. Quantum. Inf. Process. 2020, 19, 112. [Google Scholar] [CrossRef]
- Genoni, M.G.; Olivares, S.; Paris, M.G. Optical Phase Estimation in the Presence of Phase Diffusion. Phys. Rev. Lett. 2011, 106, 153603. [Google Scholar] [CrossRef]
- Chapeau-Blondeau, F. Entanglement-assisted quantum parameter estimation from a noisy qubit pair: A Fisher information analysis. Phys. Lett. A 2017, 381, 1369. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef]
- Dhar, H.S.; Bera, M.N.; Adesso, G. Characterizing non-Markovianity via quantum interferometric power. Phys. Rev. A 2015, 991, 032115. [Google Scholar] [CrossRef]
- Slaoui, A.; Bakmou, L.; Daoud, M.; AhlLaamara, R. A comparative study of local quantum Fisher information and local quantum uncertainty in Heisenberg XY model. Phys. Lett. A 2019, 83, 2241. [Google Scholar] [CrossRef]
- Kim, S.; Li, L.; Kumar, A.; Wu, J. Characterizing nonclassical correlations via local quantum Fisher information. Phys. Rev. A 2018, 97, 032326. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Long-time death of nonclassicality of a cavity field interacting with a charge qubit and its own reservoir. Phys. Lett. A 2010, 2010 374, 4115. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Clustering of exceptional points and dynamical phase transitions. Phys. Rev. A 2016, 93, 042116. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Skew information correlations beyond entanglement in dissipative two Su (2)-systems. Results Phys. 2019, 15, 102614. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Bipartite non-classical correlations for a lossy two connected qubit-cavity systems: Trace distance discord and Bell’s non-locality. Quantum. Inf. Process. 2018, 17, 96. [Google Scholar] [CrossRef]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef] [PubMed]
- Ng, H.T.; Nori, F. Quantum phase measurement and Gauss sum factorization of large integers in a superconducting circuit. Phys. Rev. A 2010, 82, 042317. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.-X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar]
- MacQuarrie, E.R.; Neyens, S.F.; Dodson, J.P.; Corrigan, J.; Thorgrimsson, B.; Holman, N.; Palma, M.; Edge, L.F.; Friesen, M.; Coppersmith, S.N.; et al. Progress toward a capacitively mediated CNOT between two charge qubits in Si/SiGe. NPJ Quantum Inf. 2020, 6, 81. [Google Scholar] [CrossRef]
- Stassi, R.; Cirio, M.; Nori, F. Scalable quantum computer with superconducting circuits in the ultrastrong coupling regime. NPJ Quantum Inf. 2020, 6, 67. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A.; Homid, A.H. Implementing discrete quantum Fourier transform via superconducting qubits coupled to a superconducting cavity. J. Opt. Soc. Am. B 2013, 30, 1178. [Google Scholar] [CrossRef]
- AObada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A.; Homid, A.H. fficient protocol of N-bit discrete quantum Fourier transform via transmon qubits coupled to a resonator. Quantum Inf. Process. 2014, 13, 475. [Google Scholar] [CrossRef]
- Mirza, I.M. Strong coupling optical spectra in dipole dipole interacting optomechanical Tavis-Cummings models. Opt. Lett. 2016, 41, 2422. [Google Scholar] [CrossRef] [PubMed]
- Vanegas-Giraldo, J.J.; Vinck-Posada, H.; Echeverri-Arteaga, S.; Gómez, E.A. The strange attraction phenomenon induced by phonon-mediated off-resonant coupling in a biexciton-cavity system. Phys. Lett. A 2020, 384, 126481. [Google Scholar] [CrossRef]
- You, J.Q.; Nori, F. Quantum information processing with superconducting qubits in a microwave field. Phys. Rev. B 2003, 68, 064509. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Życzkowski, K.; Horodecki, P.; Horodecki, M.; Horodecki, R. Dynamics of quantum entanglement. Phys. Rev. A 2001, 65, 012101. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H.; Ooi, C.H.R. Non-locality Correlation in Two Driven Qubits Inside an Open Coherent Cavity: Trace Norm Distance and Maximum Bell Function. Sci. Rep. 2019, 9, 19632. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Luo, S.; Fu, S. Quantum criticality from Fisher information. Quantum Inf. Process. 2017, 16, 91. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Farouk, A.; Yassen, M.F.; Eleuch, H. Quantum Correlation via Skew Information and Bell Function Beyond Entanglement in a Two-Qubit Heisenberg XYZ Model: Effect of the Phase Damping. Appl. Sci. 2020, 10, 3782. [Google Scholar] [CrossRef]
- You, B.; Cen, L. Necessary and sufficient conditions for the freezing phenomena of quantum discord under phase damping. Phys. Rev. A 2012, 86, 012102. [Google Scholar] [CrossRef]
- Chanda, T.; Das, T.; Sadhukhan, D.; Pa, A.K.; Sen(De), A.; Sen, U. Scale-invariant freezing of entanglement. Phys. Rev. A 2018, 97, 062324. [Google Scholar] [CrossRef]
- Li, X.-Y.; Zhu, Q.-S.; Zhu, M.-Z.; Wu, H.; Wu, S.-Y.; Zhu, M.-C. The freezing Rnyi quantum discord. Sci. Rep. 2019, 9, 14739. [Google Scholar] [CrossRef]
- Xu, J.-S.; Xu, X.-Y.; Li, C.-F.; Zhang, C.-J.; Zou, X.-B.; Guo, G.-C. Experimental investigation of classical and quantum correlations under decoherence. Nat. Commun. 2010, 1, 7. [Google Scholar] [CrossRef] [PubMed]
- Paula, F.M.; Silva, I.A.; Montealegre, J.D.; Souza, A.M.; deAzevedo, E.R.; Sarthour, R.S.; Saguia, A.; Oliveira, I.S.; Soares-Pinto, D.O.; Adesso, G.; et al. Observation of Environment-Induced Double Sudden Transitions in Geometric Quantum Correlations. Phys. Rev. Lett. 2013, 111, 250401. [Google Scholar] [CrossRef] [PubMed]
- Yu, A.; Pashkin, T.; Yamamoto, O.; Astafiev, Y.; Nakamura, D.; Averin, V.; Tsai, J.S. Quantum oscillations in two coupled charge qubits. Nature 2003, 421, 823. [Google Scholar]
- Xu, J.-S.; Sun, K.; Li, C.-F.; Xu, X.-Y.; Guo, G.-C.; Andersson, E.; Franco, R.L.; Compagno, G. Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 2013, 4, 2851. [Google Scholar] [CrossRef]
- von Lüpke, U.; Beaudoin, F.; Norris, L.M.; Sung, Y.; Winik, R.; Qiu, J.Y.; Kjaergaard, M.; Kim, D.; Yoder, J.; Gustavsson, S.; et al. Two-Qubit Spectroscopy of Spatiotemporally Correlated Quantum Noise in Superconducting Qubits. PRX Quantum 2020, 1, 010305. [Google Scholar] [CrossRef]
- Hong, S.; Park, C.H.; Choi, Y.-H.; Kim, Y.-S.; Cho, Y.-W.; Oh, K.; Limm, H.-T. Experimental implementation of arbitrary entangled operations. New J. Phys. 2020, 22, 093070. [Google Scholar] [CrossRef]
- Liu, S.; Yu, R.; Li, J.; Wu, Y. Generation of a multi-qubit W entangled state through spatially separated semiconductor quantum-dot-molecules in cavity-quantum electrodynamics arrays. J. Appl. Phys. 2014, 115, 134312. [Google Scholar] [CrossRef]
- Bugu, S.; Ozaydin, F.; Ferrus, T.; Kodera, T. Preparing Multipartite Entangled Spin Qubits via Pauli Spin Blockade. Sci. Rep. 2020, 10, 3481. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.A.; Vitanov, N.V. Two-qubit quantum gate and entanglement protected by circulant symmetry. Sci. Rep. 2020, 10, 5030. [Google Scholar] [CrossRef] [PubMed]

| LQFI | BDE | The Observations | Figs. | |
|---|---|---|---|---|
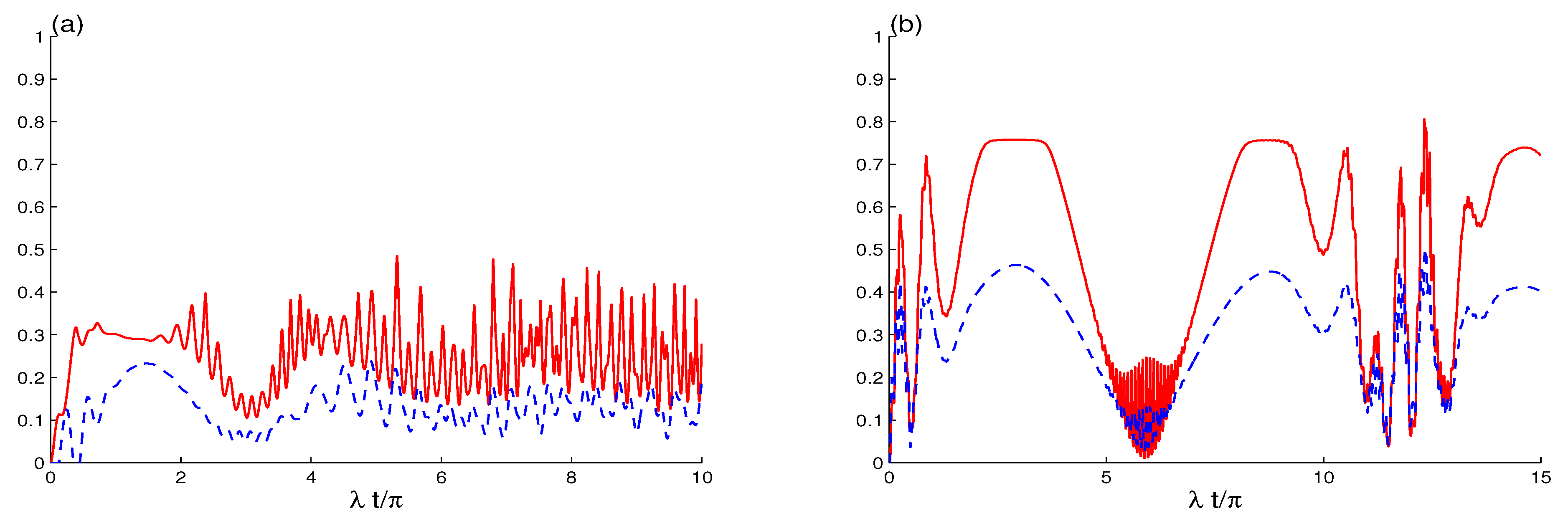
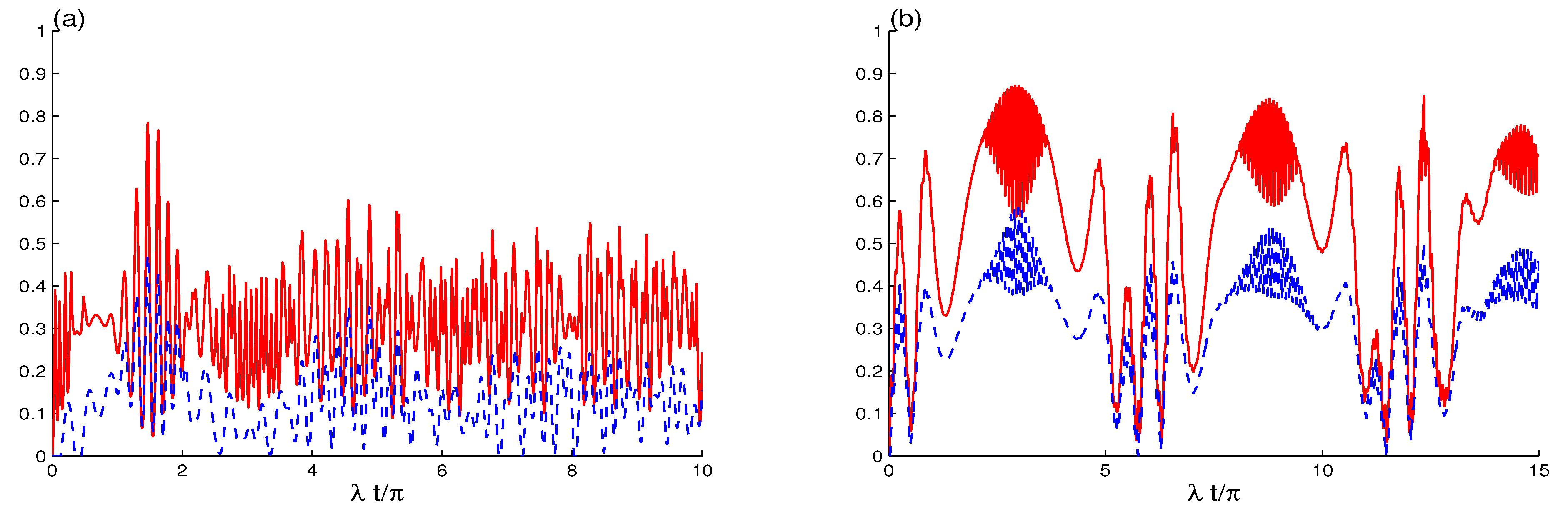
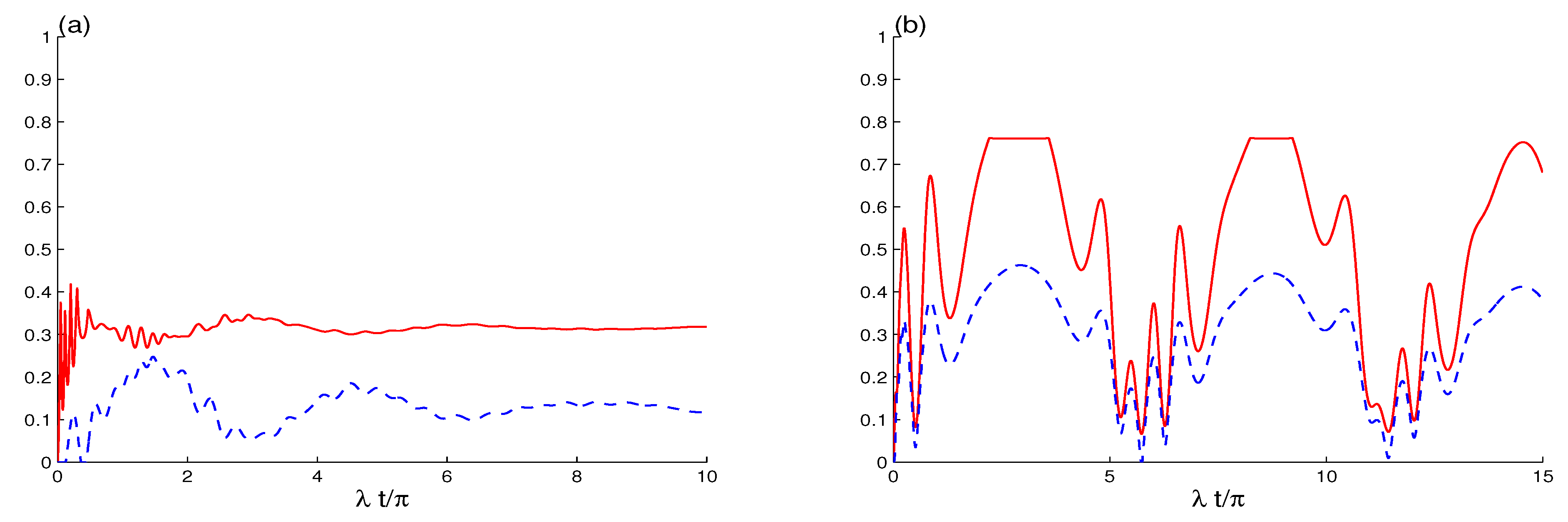
| OF | Yes | Yes | OF of is more than of | Figure 2 and Figure 4 |
| OA | Yes | Yes | OA of are larger than of | All |
| SD | No | Yes | SD is only in | Figure 4a and Figure 5a |
| SC | Yes | No | SC are only in | Figure 5b |
| FC | Yes | No | FC is only in | Figure 2b, Figure 3b and Figure 5b |
| SC | Yes | Yes | SC of is more than of | Figure 3a and Figure 5a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-B.A.; Khalil, E.M.; Selim, M.M.; Eleuch, H. Quantum Fisher Information and Bures Distance Correlations of Coupled Two Charge-Qubits Inside a Coherent Cavity with the Intrinsic Decoherence. Symmetry 2021, 13, 352. https://doi.org/10.3390/sym13020352
Mohamed A-BA, Khalil EM, Selim MM, Eleuch H. Quantum Fisher Information and Bures Distance Correlations of Coupled Two Charge-Qubits Inside a Coherent Cavity with the Intrinsic Decoherence. Symmetry. 2021; 13(2):352. https://doi.org/10.3390/sym13020352
Chicago/Turabian StyleMohamed, Abdel-Baset A., Eied. M. Khalil, Mahmoud M. Selim, and Hichem Eleuch. 2021. "Quantum Fisher Information and Bures Distance Correlations of Coupled Two Charge-Qubits Inside a Coherent Cavity with the Intrinsic Decoherence" Symmetry 13, no. 2: 352. https://doi.org/10.3390/sym13020352
APA StyleMohamed, A.-B. A., Khalil, E. M., Selim, M. M., & Eleuch, H. (2021). Quantum Fisher Information and Bures Distance Correlations of Coupled Two Charge-Qubits Inside a Coherent Cavity with the Intrinsic Decoherence. Symmetry, 13(2), 352. https://doi.org/10.3390/sym13020352






