Abstract
The complexity of a mathematical expression is a measure that can be used to compare the expression with other mathematical expressions and judge which one is simpler. In the paper, we analyze three effect factors for the complexity of a mathematical expression: representational length, computational time, and intelligibility. Mainly, the paper introduces a binary-lambda-calculus based calculation method for representational complexity and a rule based calculation method for algebraic computation complexity. In the process of calculating the representation complexity of mathematical expressions, we transform the de bruijn notation into the binary lambda calculus of mathematical expressions that is inspired by compressing symmetry strings in Kolmogorov complexity theorem. Furthermore, the application of complexity of mathematical expressions in MACP, a mathematics answer checking protocol, is also addressed. MACP can be used in a computer aided assessment system in order to compute correct answers, verify equivalence of expressions, check user answers whether in a simplification form, and give automatic partial grades.
1. Introduction
The application of information technology in education has become ubiquitous in modern life [1,2,3,4,5]. A computer aided assessment (CAA) is extremely useful in assessing the abilities of students. In recent years, some computer aided assessments of mathematics employ computer algebra system (CAS) in order to evaluate the work of students [6,7,8,9,10,11,12].
A modern intelligent Web-based mathematics assessment system, called MathPASS [13], was developed by Lanzhou University (LZU) and Kent State University (KSU). MathPASS, as shown in Figure 1, is a practical system that has more than 10,000 registered student and teacher users in mathematical courses of KSU. As a part of MathPASS, LZU and KSU are jointly designing and developing a mathematics answer checking protocol (MACP) [14]. Figure 2 shows the system structure of MACP. MACP is an access protocol for communication between mathematics assessment system server and its client. MACP service is a Web service for checking answers and grading questions to mathematics of middle-school and college. The MACP service aims to grade user answers through verifying the equivalence of expressions and checking the expression forms of the answers. The standard answer could be provided by the CAA system, which is using MACP or automatically generated and computed by the MACP service. The implementation of MACP is based on Representational State Transfer (REST). The request data and service response of MACP are encapsulated into JSON (JavaScript Object Notation) code. In the interior, MACP service uses the computer algebra system (CAS) to verify the equivalence of expressions and compute correct answers. A CAA system could use the MACP service to evaluate the work of students on the Internet. As a simple illustration, imagine a student interacting with a CAA system and, in some way, entering a mathematical expression as an answer to a question. The CAA system could make a primary judgment for the correctness of a student answer by comparing the string of the student answer with the one of standard answer. If the two strings do not match, the CAA sends the two answers to MACP service. The MACP service calls for a CAS to perform a expression subtraction of the student answer from the standard answer. If the result of subtraction is zero, then the system has established an algebraic equivalence between the student answer and the standard answer. Subsequently, the MACP service judges whether the student answer is in a simplest form or a correct form automatically. The checking result of MACP service returns to the CAA in a predefined format. The CAA could use this grade result to make further process.
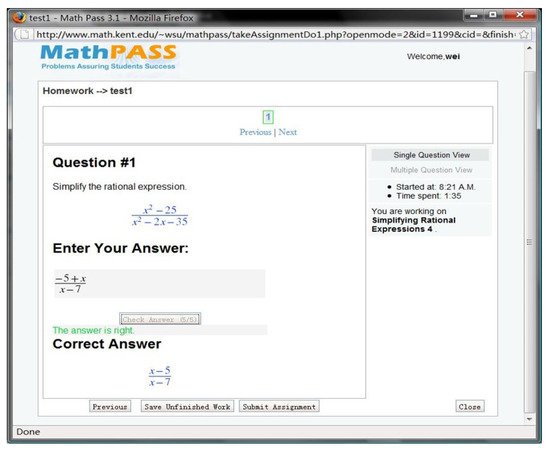
Figure 1.
MathPASS system.
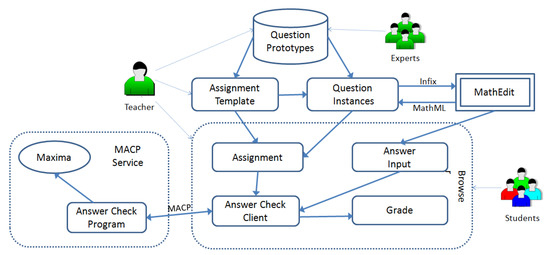
Figure 2.
The system structure of mathematics answer checking protocol (MACP).
Our goal is to give accuracy scores for answers that are submitted by students. The algebraic equivalence between two expressions of the student answer and the standard answer is important to evaluate correctness of an student answer. However, different from in research and the engineering area of computer algebra, a mathematical expression may be partially correct as an answer though it is equivalent to the standard answer in the education area. In the paper, we propose a method for calculating the scores of different mathematical expressions. The paper discusses complexity of mathematical expressions and how to apply the complexity on giving partial credit in automatic answer checking for mathematics. In the following, Section 2 describes the data communication formats of MACP. In Section 3 and Section 4, we give and analyze two key problems of automatic answer checking: what kinds of answers are right, wrong, or partially right? Why do we ask students to enter the answer in the simplified form? Section 5, Section 6 and Section 7 present our computation method of complexity of mathematical expressions in detail. Section 8 gives a method of computing partial credit that is based on the complexity of mathematical expressions. Section 9 describes the conclusion and future work of the paper.
2. Data Format of MACP
As a communication protocol, MACP uses standard HTTP protocol in order to transfer data between CAA and MACP Web service. This section will introduce the request and response data format of MACP. In MACP, each service request could include multi-questions for checking together. Each question could also contain multi mathematical expressions of the user answer, multi mathematical expressions of the standard answer, and the question itself. The following is the main syntax rules of the request data with JSON encoding.
[{
"name":"<check item name>",
"cmd":"<check command>",
"response":"<response list>",
"exprs":[{
"expr":"<expression name>",
"encoding":"<encoding format>",
"role":"<expression role>",
"value":"<expression itself>",
"form":"<required expression form>",
"op":"<question operation>",
"var":"<variables>"
},…]
},…]
The cmd parameter in the request data is to set answer checking command in each check item. The symbols of =, ~, &, and | could be used in the answer checking command to express the logic relationship of expressions. The following is an example of a check rule command.
(u1=s1 & u2=s2)|(u1=s2 & u2=s1)
In the example u1 and u2 are two expressions of a user answer and s1 and s2 are two expressions of a standard answer. The MACP service verifies the equivalence of the user answer and standard answer under the logical sequence of the check rule command. The check rule command in above example could be used in the questions of solving quadratic equations.
MACP service could also convert a mathematical expression among MathML Presentation (http://www.w3.org/Math (accessed on 24 January 2021)), MathML Content, OpenMath (http://www.openmath.org/ (accessed on 24 January 2021)), and Standard Infix Format [15]. The response parameter lists all of the response data that a client wants to get. It may include MathML, infix, or OpenMath code of any expression. The request data of MACP could contain answer grade rules: the given syntax form or simplest form (see Section 3 for details). The following is an example of the response parameter.
s1.mmlp,u2.openmath,q1.answer.mmlc,u1.sim
In the example, the MathML Presentation code of expression s1, the OpenMath code of expression u2, the MathML content code of the answer expression of question q1, and the result of whether u1 being in the simplest form are included in the response data.
When a CAA calls MACP to check an answer, the standard answer may or may not be given as an input to MACP service. If not, then MACP could compute and generate the standard answer automatically. The op parameter could be written in the request data to specify what types of operations should be implemented in order to generate standard answers. Table 1 lists a series of operation types in MACP. The following is a real example of MACP request data that is to check user answers
and of an equation question 2x2 + 4x = 8.

Table 1.
The functions of answer generation.
Example 1.
A real example of MACP request data
checkcmd=’[{
name:c1,
cmd:"[s1,s2]=solve(q1) & ((u1=s1&u2=s2)|(u1=s2&u2=s1))",
response:"s1.mmlp,s2.mmlp",
exprs:[
{expr:u1,encoding:infix,role:usrAnswer,value:"(-4-sqrt(80))/4)"},
{expr:u2,encoding:infix,role:usrAnswer,value:"sqrt(5)-1"},
{expr:q1,encoding:infix,role:Question,value:"2*x^2+4*x=8"}]}]’;
params="checkcmd="+ encodeURIComponent(checkcmd);
var murl="http://boar.cs.kent.edu/aacs.php";
send_request(murl,params,prca);
The response data is also encoded in JSON. The following is the main syntax rules for MACP response data. The response parameter lists every value for each request item.
[{
"name":"<check item name>",
"status":"<status>",
"correctness":"<correctness>",
"details":"<details>",
"response":[
{
"rname":"<response item name>",
"value":"<response item value>"
},…]
},…
]
The following is an example of response data in MACP for example 1:
Example 2.
A real example of the MACP response data
[{
"name":"c1",
"status":"normal",
"correctness":"90%",
"details":"<u1> is not simplest",
"response":[
{"rname":"s1.mmlp",
"value":"<math><mrow><mo>-</mo><mn>1</mn><mo>-</mo><msqrt><mn>5</mn></msqrt>
</mrow></math>"},
{"rname":"s2.mmlp",
"value":"<math><mrow><mo>-</mo><mn>1</mn><mo>+</mo><msqrt><mn>5</mn></msqrt>
</mrow></math>"
}]
}]
In the response data, the standard answers and are given in the format of MathML Presentation.
3. Answer Grade Rule
When can we say an answer is “right”? The student answer can be compared with the standard answer by CAS. Obviously, the answer is wrong if the comparing result is not equivalence in algebra. However, we cannot easily say that the answer is right, even though they are equal. In the paper, the standard answer and the user answer only infer those answers that are one or more mathematical expressions.
During the maintenance of MathPASS, the authors received hundreds of emails from students to report that the answers they entered are correct, but the system graded them wrong. On the other hand, some mathematical teachers also report that some student answers should be treated as “wrong” or “partial right”; however. the system grade them right. To make a better answer grade rule, the authors of this paper looked into all of the standard answers in MathPASS and some other CAA systems, such as CourseCompass (http://www.coursecompass.com (accessed on 24 January 2021)) and Stack [8,16,17]. With the analysis of correct answer or best answer, a phenomenon is found that most of the answers in CAA systems could be classified into two broad categories: simplified form and special syntax form. This taxonomy does not strictly separate all of the answers into two totally different categories. One part of the answer with special syntax form may also be required as a simplified form. However this taxonomy has been found to be useful for evaluating the answer of students and solving the issues of partial credit. In a simplified form, the MACP service not only compares the algebraic equivalence, but it also checks the answer whether in a full simplification form. A partial credit for how “right” of the answer could return to host CAA in order to denote the correctness. While in special syntax form, the MACP service may check the answer according to the syntax form that was described in the request data. The paper will introduce how to check answer in simplified form.
4. Overview of Simplified Form
The first category of correct answer is to ask the student to enter the answer with a full simplification form. The questions in this category include simplification, calculation, writing the equation of a function, writing the domain of expression, etc. Particularly, students are desired to reduce their answers to the lowest terms. The purpose of this kind of question is not only to assess the ability of calculation, but to also assess the ability of simplifying a mathematical expression. The following gives some examples of this kind of question.
Example 3.
Calculate.
- (a)
- (b)
- (c)
Although most teachers want students to write a particular algebraic expression in the simplified possible form, it is difficult to know exactly what means in all cases the simplified form. The concept of simplified form has been mentioned in many earlier papers when they talked about expression simplification [18,19,20,21,22]. However, these papers discuss the problem only under the field of general computer algebra systems and not under the field of mathematical assessment or not under the field of answer checking for elementary algebra. Although finding the simplest form of any mathematical expression may be impossible [19], it is meaningful and feasible to define a method in order to verify simplest form for an expression of elementary algebra, especially for the answer expression of an elementary mathematical question. The paper in the following will give a method of verifying simplest form of a mathematical expression.
Before we go into the details of simplified form, let us first look at one interesting question: why do we ask student to enter the answer in the simplified form? Both Caviness [19] and Fitch [20] gave three reasons for algebra simplification in the research field of computer algebra and symbolic computing, including: less store memory, faster processing, and easier to identify. For mathematical answers in the educational field, we also find at least three important reasons to ask student to enter an answer in a simplified form:
- To assess the ability of students to simplify a mathematical expression. The process of algebra simplification requires various mathematical knowledge and abilities. Otherwise, for learning, mathematics have the particular serial character, and earlier knowledge is required as a prerequisite for a later one. The implicit aim of expression simplification is to assess the mastery of earlier knowledge.
- To put the answer in a form in which it is easier to justify the correctness of the answer. For the simplified form of an answer, it is mostly a canonical form or a simpler form, and it is easy to compare with the standard answer. The amount of possible totally correct answers is less in the simplified form.
- In general, a simplified expression is much easier for human beings to understand and more convenient for human beings to process, such as writing it on the paper and communication with other people. One of important purpose of mathematics itself is to use some easy forms to express complicated problems.
5. The Complexity of a Mathematical Expression
The simplified form of a mathematical expression denotes that simplification manipulations have been carried out on the expression. More formally, let be a class of mathematical expressions and let ∼ be an equivalence relation on .
Definition 1.
A mathematical expression is the simplified form of a mathematical expression if it meets the following specification:
and there does not exist such a that
where C is the function to compute the complexity of the mathematical expression.
The complexity of a mathematical expression is a measure that can be used to compare the expression with other mathematical expressions and judge which one is simpler. The problem of what is “simpler” for expressions has been addressed by many literatures. Fenichel [23] figured that the simplification of an expression is to arrange the expression in an intelligible form. Moses [22] argued that the simplification form of an expression is a form in which the remaining steps of a computation on the expression can be most efficiently performed. Buchberger [18] expressed the concept of simplicity by saying: “expression s is shorter than expression t”, “s needs less memory for representation in computer storage than t”, “the evaluation of s is less complex than that of t”, “numerically, s is more stable than t”, or “the structure of s is more intelligible than that of t”. Jacques gave a definition for simpler in [21]: an expression A is simpler than an expression B if, in all contexts where A and B can be used, they mean the same thing, and the length of the description A is shorter than the length of the description of B. He put emphasis on the representational complexity of a mathematical expression. Billing [24] gave a specific value, depending on the type of each symbol of a mathematical expression and reckoned the complexity as the sum of each symbol. Ali computed the complexity of the expression according the number of operands, operators and depth of the expression tree in [25]. It is worthwhile to mention that what Ali addressed regardinf the complexity of expressions is not only for the equivalent expressions, but also for two arbitrary mathematical expressions that are not equivalence in algebra. From the analysis of the above literatures, we can see that they mainly discuss the complexity of a expression from three views: representational view, computational view, and intelligible view. Indeed, the three views cover most parameters of the complexity of an expression.
One of the main contributions of this paper is to show how to calculate the complexity with different parameters. The complexity of an expression can be evaluated according three parameters: representation complexity, computation complexity, and intelligibility. Formally, the complexity of a mathematical expression E can be computed as
where is the representation complexity of E, is the computation complexity of E, and is the intelligibility of E. The Formula (1) gives a general computation method for the complexity of an expression. The complexity computation has a wide application, such as simplification in computer algebra system, answer checking in CAA, indexing expression in mathematics search, and splitting mathematical expressions in systems for visually impaired users, etc. The parameters of , , and in the Formula (1) can be different for different applications. For example, in a CAS or theorem proving system, the complexity of a mathematical expression may mainly depend on computation and intelligibility. Accordingly, the parameters of and will be much greater than . While, in a speech system for visually impaired users, the parameters of and will be much greater than , since such a system has major emphasis on the complexity of representation and intelligibility. In general, the sum of these three parameters is 1. Here, the intelligibility of an expression mainly depends on the conventional lexicographic ordering, symmetry, and context of the expression. In terms of answer checking, the different lexicographic ordering does not change the result of answer grade. For example, if the standard answer is , the user answer will be treated totally right. Although the context of the expression may partially affect answer grading, the parameter is hard to calculate, for it is mainly related with nature language. Thus, in the field of answer checking the coefficient is set as 0 and the Formula (1) is changed to
The following sections will introduce the calculation methods of representation complexity and computation complexity.
6. Representation Complexity
In the paper, the calculation method of representation complexity is inspired by theories of Kolmogorov complexity [26] and binary lambda calculus [27]. Kolmogorov complexity is a theoretical tool that is used in order to define “simplicity”. Binary lambda calculus can be used as the calculation tool for the length of an expression. The section is organized, as follows: the first subsection will give a quick introduction to Kolmogorov complexity, lambda calculus [28,29], De Bruijn notation [30], and binary lambda calculus. The second subsection will address the calculation method for representation complexity of a mathematical expression.
6.1. Kolmogorov Complexity and Binary Lambda Calculus
Andrei N. Kolmogorov (1965), Ray Solomonoff (1964), and Gregory Chaitin (1966) developed the concept of Kolmogorov complexity independently with different motivation. In computer science, the Kolmogorov complexity of an object is a measure of the computational resources that are needed to specify the object. The Kolmogorov complexity of a string S is the size of the smallest program of an optimal University Turing Machine U generating S, thus
For example, consider the following two strings of length 33, each containing only lowercase letters and numbers:
weiweiweiweiweiweiweiweiweiweiwei
x8rx2y39umgw5q85s4c1j5b2p0cv4w17u.
Kolmogrov complexity deals with randomness and symmetry of information [31]. Roughly speaking, the symmetry of information states that, for any two strings x and y, the information contained in x about y is equal to the information that is contained in y about x, up to logarithmic factors. In the above examples, the first string possesses symmetry structure of characters and it has a short English-language description, namely “wei 11 times”, which consists of 12 characters. The second one does not possess symmetric feature and it has no obvious simple description other than writing down the string itself, which has 33 characters. In the Kolmogorov complexity, it does not matter which optimal Universal Turing Machine is chosen.
Church (1936) invented a formal system called the lambda calculus and defined the notion of computable function via this system.
Definition 2.
The set of-terms (notation Λ) is built up from an infinite set of variables while using application and (function) abstraction, as following.
Thus, are all -terms.
The mathematician De Bruijn invented the De Bruijn notation [30] to represent terms in the calculus with the purpose of eliminating the names of the variable from the notation. Terms that are written using these notations are invariant with respect to conversion, so the check for -equivalence is the same as that for syntactic equality. Each De Bruijn notation is a natural number that represents an occurrence of a variable in a -term, and denotes the number of binders that are in scope between that occurrence and its corresponding binder. The De Bruijn notation of calculus term is .
The binary lambda calculus adopt a standard binary encoding to calculus term in a de bruijn notation. The code for a term in de Bruijn notation is inductively defined, as follows:
For instance,
6.2. Calculation Method of Representation Complexity
The representation complexityof a mathematical expression E is the shortest length of the computer program s in a specify language that can store and produce this mathematical expression on the Universal Turing Machine and then halt. Intuitively, the representation complexity of an expression is a sense of long or short to the expression for human being feeling. It is mainly related to the syntax and symmetry of the mathematical expression. To compute representation complexity, we must first specify an encoding for Turing machines, where an encoding is a function that associates to each Turing machine M a bit string . If M is a Turing machine, which, on input w outputs string x, then the concatenated string is a description of x. One of the important directions of this calculation method is to crush the expression object into pieces that are as small as possible.
A mathematical expression can be rewritten to the function form. For example, the expression
can be rewritten to
From the view of syntax composition, a mathematical expression could consist of three elements: operators (functions), operands, and combination rules for operators and operands. For example, the expression (3) contains five operators (, +, −, /, ⌃), four operands (x, 3, 2, ) and a combination rule, as shown in the Figure 3. Thus, the representation complexity of a mathematical expression is calculated as the sum of the storage length of operands, operators and combination rule. In the paper, we use binary as the storage length unit.
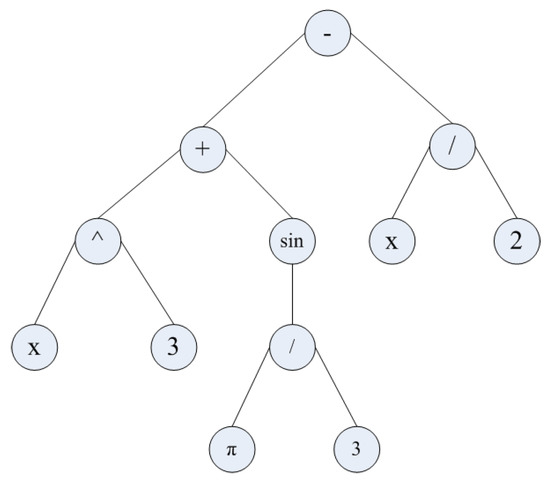
Figure 3.
The syntax tree of mathematical expression.
There are three types of operands: number, variable, and symbol constant. A number may be an integer, a decimal, or a fraction. From the view of representation, the complexity of a big integer is larger than a small one. For example, the expression 230528 + 34923 is more complex than the expression . The representation complexity of an integer is the binary length of the integer. Suppose that I is an integer, the representation complexity of I is
The representation complexity of a decimal mainly depends on the length of the decimal. Suppose that D is a decimal, is the decimal that is obtained by changing the rightmost digit of D to 5, is the integral part length of the binary of , is the decimal part length of the binary of , and is the location where the first one occurs from left to right, and then the representation complexity of D is
Suppose that F is a fraction, is the numerator of F, and is the denominator of F, then the representation complexity of F is
If there is a negative or positive sign in a number N, then the representation complexity of N is
Intuitively, the different variables (x, y, etc.) and symbolic constant (, a, b, , etc.) have the same complexity to a human being and computer. Thus, a constant value 8 (the binary length of ASCII) is predefined for all of the variables and symbolic constant.
In computer, computational symmetry is defined as using computers to model, analyze, synthesize, and manipulate symmetries in digital forms, imagery or otherwise [32]. Here, we use computational symmetry to simplify the storage length and then give computational complexity of mathematical expressions. In computer, if a number, variable, symbolic constant, or symmetry structure occurs more than once in an expression, then a pointer can be used to reduce the storage length. Correspondingly, the complexity of an expression decreases if less different numbers, variables, symbolic constants, and sub-expressions occur in the expression. For example, a human being will feel that is more complex than . Thus, suppose that O is a number, variable, or symbolic constant, and O occurs i times in an expression, the total representation complexity of all Os in the expression is
where is the representation complexity of single O.
To store the combination rule, all of the variables, constants, functions, and sub-expressions in the expression are replaced by type-free symbols. Figure 4 shows the object after the replacement of the variables, constants, functions, and sub-expressions in Figure 3. In the lambda calculus, a unitary function can be expressed by ., a binary function can be ., and an ternary function can be .. Thus, the object shown in the Figure 4 can be written as
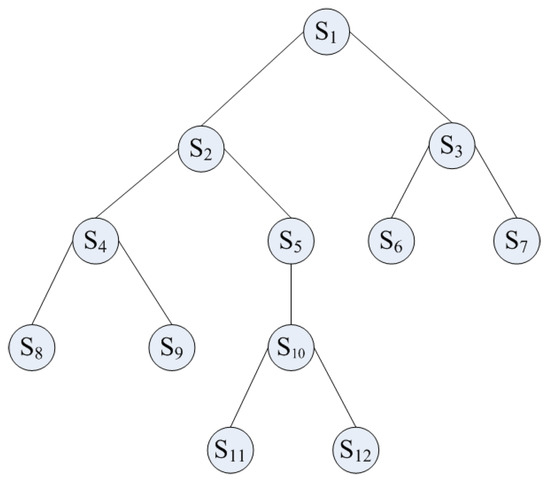
Figure 4.
The tree structure for combination rule with type-free symbols.
Accordingly, the De Bruijn notation of the combination rule for the expression is
Afterwards, it can be converted to the binary lambda calculus as
7. Computation Complexity
Let £ is a specified language on the Universal Turing Machine, U is the set of programs that can manipulate on E to produce , let , thus
where the running time of P is the shortest in U, the computational complexity of a mathematical expression E is the running time of P. A problem is regarded as inherently difficult if solving the problem requires a large amount of resources, independent of the algorithm used for solving it. Generally speaking, the computation complexity of the expression is larger than the one of . However, though the representation complexity of the expression is much larger than the , the computation complexity of the first one is much smaller than the later one. When computing or manipulating an expression, there are normally two steps: the first step is to simplify the expression and the second one is to substitute the variables with input values. The simplification process is to execute rewriting and simple numerical computation in order to make the expression into the simplest form. For example, if there is an expression in a computer program, then the compile program will first optimize the expression to . Thus, the computational complexity of an expression should contain two parts: the time spent for algebraic simplification and the time spent for further computing. Accordingly, the computation complexity of an expression E can be represented as
where is the algebraic simplification complexity and is the further computation complexity. Next, let us focus on the computational complexity under the condition of equivalent expressions and answer checking.
Theorem 1.
Assume that E and are two equivalent expressions (), and then the further computation complexity of E and are same.
The proof is obvious. For , there must exist to satisfy and , where is the simplified form for E and . The further computation complexity of E and are both equal with .The literature (https://en.wikipedia.org/wiki/Computational_complexity_of_mathematical_operations (accessed on 24 January 2021)) collected the computation complexity of various algorithms for common mathematical operations, which can be used to estimate the further computation complexity of an expression. Because the value of further computation complexity can be eliminated during evaluation the score in answer checking, the paper will not discuss the further computation complexity in detail. To obtain the algebraic simplification complexity of an expression, lots of rewrite rules for expression simplification are defined. All of these rewrite rules can be regarded as an one-hop computation with a predefined computation complexity. Table 2 lists some common rewrite rules and their computation complexity. In the table, some asterisk wildcards of Mathematics Query Language (MQL), which is a language in an ongoing project named MathSearch (http://wme.lzu.edu.cn/mathsearch (accessed on 24 January 2021)), are used in order to represent mathematical patterns. In MQL, the A_ denotes a pattern object that can stand for any algebraic expression with a name A. m_Num can stand for any expression with a qualification of number. The number can be a real, integer, or fraction. The computation complexity of common numeric computation, including addition, subtraction, multiplication, division, exponent, and root, are defined in Table 3.

Table 2.
Some rewrite rules for expression simplification.

Table 3.
Evaluation method for computation complexity of a numeric computation.
By the application of these rewritten rules and numerical computation, an expression can be manipulated into its simpliest form. However, with the application of different rules and orders, the manipulation process may be various for the simplification of one expression. Thus, the algebraic simplification process of an expression E to its simplest form can be considered to be a weighted directed graph, where a vertex denotes a mathematical expression and an edge represents an application of an one-hop rewritten rule or a simple numeric computation. One path from start vertex to end vertex indicates a simplification process for the expression. Because there may exist infinite methods for simplification of a complex mathematical expression, the paths of the graph may be infinite. A constant value is predefined as an upper limit of the numbers of the paths in order to solve the problem. In practice, we found that the simplification methods for most expressions in elementary algebra are not more than 200 by analyzing mathematical expression answers that were submitted by students in MathPASS. Thus usually 200 is the constant value. The symbolic simplification complexity of an expression can be denoted by the shortest path in the weighted directed graph within finite paths.
Formally, let G be the weighted directed graph from vertex E to vertex , where E is a mathematical expression and is the simplest form of E. The length of a path P from E to is the sum of the weights of the edges of P. Suppose that P consists of edges , , …, , the length of P can be defined as
where is the computation complexity of . The algebraic simplification complexity of the expression E can be denoted as
Figure 5 shows an example of the weighted directed-graph for algebraic simplification. The numbers in the figure represent the mathematical expressions that are shown in Table 4. From Figure 5, we can see easily that the path ①–④–⑥–⑦–⑬–⑰–⑲, ①–④–⑥–⑦–⑬–⑱–⑲ and ①–④–⑥–⑦–⑭–⑱–⑲ are three shortest paths for the simplification of the expression ① in Table 4. Thus, the algebraic simplification complexity of the expression is 34, which is the sum of the shortest path length.
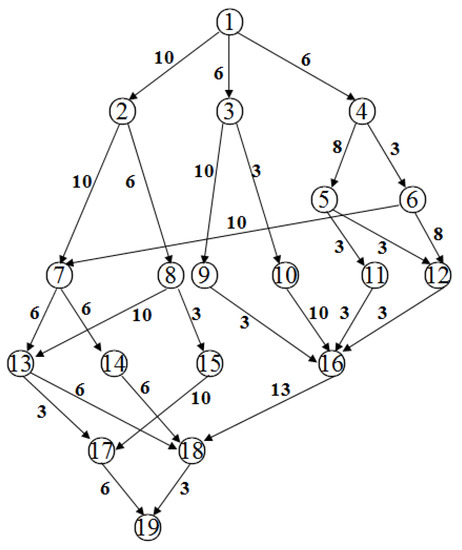
Figure 5.
The weighted directed-graph for algebraic simplification.

Table 4.
The mathematical expressions for algebraic simplification.
8. Answer and Score
Let us first focus on the problem of the standard answer. Does a standard answer exist definitely for any mathematical problems? What is a standard answer and how to get a standard answer? To answer these questions, let us look back into the grade rule which a teacher would adopt. For (b) in Example 3, the standard answer is , while the teacher may treat it as totally correct when students enter , , as the answer. If a student answer is , or , the teacher will argue that the answer is not completely correct and it will give a score of or . However, if the student answer is totally same with the question or the student answer is
teachers will mark it as a wrong answer.
A referenced answer of a question is a mathematical expression that satisfies the requirement of a mathematical problem. A referenced answer class of a question is a set that includes all of the referenced answers of a question. An equivalent class of a referenced answer is a class of all expressions that are equivalent to the referenced answer.
Definition 3.
Let E be an a-expression of a question T and ξ be the equivalent class of E, a canonical form of E is a computable mapping m from ξ into ξ that satisfies:
- ,
- if , , and
- for all and , .
The canonical form of E is the standard answer for the question T. The referenced answer and standard answer can be either entered in the MACP request data or computed in the CAS. The standard answer, which is usually given by teachers or experts, is a better one among the reference answers.
Definition 4.
Suppose that T is a mathematical question. The complexity of referenced answer of T, denoted , is the max complexity value in all the referenced answers.
Suppose that the question T is a mathematical expression and U is the expression of a user answer. Subsequently, the score for U can be computed as
The score value can be used to assign the partial grades in automatic correction. Let us substitute the Formula (2) into the above Formula (4). Subsequently, we can get
When calculating the score, the computation complexity takes greater effect than the representation complexity. According to the principle of symmetry, if the representation complexity of mathematical expressions is greater, then its computation complexity is also greater. Thus, in practice, we take the value of coefficients as 0.4 and the value of as 0.6. Let us look into the example that is shown in Table 4. If a student enters the expression ⑯ in Table 4 as an answer, the representation complexity of expression ⑯ in Table 4 is 94 and the algebraic simplification complexity is 16, and he/she gets a score 69%. The expression ⑨ in Table 4 gets 20%, expression ⑥ in Table 4 gets 27%, and expression ⑱ in Table 4 gets 70%.
The score presented in Formula (5) is obtained under the condition where the question is provided in the MACP request data. However, if the question T is not entered in the request data, we can not get the value. Accordingly, in such a case, the MACP service can only give the “full right” or “full wrong” result instead of partial score.
9. Conclusions
The paper presents a way to calculate the complexity of mathematical expressions. In the paper, we analyze three effect factors for the complexity of a mathematical expression: representational length, computational time, and intelligibility. Inspired by theories of Kolmogorov complexity and binary lambda calculus, we compress the symmetry data and then convert a mathematical expression to the least binary data that can be used to compute its representational length. A shortest path method in the weighted directed graph of simplifying an mathematical expression is also used to calculate the expression computational complexity in the paper. Furthermore, the application of complexity of mathematical expressions in MACP, a mathematics answer checking protocol, has excellent performance in verifying the equivalence of expressions, checking user answers whether in a simplification form, and giving automatic partial grades.
With the analysis of correct answer or best answer, the paper addresses a phenomenon that most of the answers in CAA systems could be classified into two broad categories: simplified form and special syntax form. The paper gives three reasons for why do we ask student to enter the answer in the simplified form. In the paper, we mainly focus on how to judge an answer in a simplified form. While, for the other category, we also need to give a solution on how to judge an answer in a right syntax form. In the future work, we will study the classification of special syntax forms in mathematical education and computation methods of partial grades for different types of questions.
Author Contributions
Conceptualization, W.S., P.S.W., H.L. and Z.H.; Formal analysis, W.S.; Methodology, W.S., P.S.W., H.L. and Z.H.; Project administration, W.S.; Software, W.S. and C.C.; Writing—original draft, W.S.; Writing—review & editing, Q.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the CCF-AFSG Research Fund (No. RF20200014), National Natural Science Foundation of China (No. 61772006), the Science and Technology Foundation of Guangxi (No. AA17204096, AB17129012), the Talents Foundation of Lanzhou (No. 2020-RC-13), and the Special Fund for Bagui Scholars of Guangxi.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, K.; Lally, V. Rhetorical relationships with students: A higher education case study of perceptions of online assessment in mathematics. Res. Comp. Int. Educ. 2018, 13, 7–26. [Google Scholar] [CrossRef]
- Erabadda, B.; Ranathunga, S.; Dias, G. Computer aided evaluation of multi-step answers to algebra questions. In Proceedings of the 2016 IEEE 16th International Conference on Advanced Learning Technologies, Austin, TX, USA, 25–28 July 2016; pp. 199–201. [Google Scholar]
- Hoogland, K.; Tout, D. Computer-based assessment of mathematics into the twenty-first century: Pressures and tensions. ZDM Math. Educ. 2018, 675–686. [Google Scholar] [CrossRef]
- Ruijter, M.K.; Draaijer, S. Digital exams in engineering education. In Technology Enhanced Assessment; Springer: Cham, Switzerland, 2018; pp. 140–164. [Google Scholar]
- Wang, P.; Mikusa, M.; Al-shomrani, S.; Chiu, D.; Lai, X.; Zou, X. Features and advantages of wme: A web-based mathematics education system. In Proceedings of the IEEE SoutheastCon, Ft. Lauderdale, FL, USA, 8–10 April 2005. [Google Scholar]
- Helen, S.A.; Cliff, E.B.; Athol, A.K.; Martin, A.Y. Incorporating partial credit in computer aided assessment of mathematics in secondary education. Br. J. Educ. Technol. 2006, 37, 93–119. [Google Scholar]
- Chaachoua, H.; Nicaud, J.F.; Bronner, A.; Bouhineau, D. APLUSIX, A learning environment for algebra, actual use and benefits. In Proceedings of the International Congress on Mathematics Education, Copenhagen, Denmark, 4–11 July 2004. [Google Scholar]
- Christopher, J.S. Assessing elementary algebra with stack. Int. J. Math. Educ. Sci. Technol. 2007, 38, 987–1002. [Google Scholar]
- Christopher, J.S. Implementing computer algebra enabled questions for the assessment and learning of mathematics. Int. J. Technol. Math. Educ. 2008, 15, 3–18. [Google Scholar]
- Genemo, H.; Miah, S.J.; McAndrew, A. A design science research methodology for developing a computer-aided assessment approach using method marking concept. Educ. Inf. Technol. 2016, 21, 1769–1784. [Google Scholar] [CrossRef]
- Ashton, H.; Wood, C. Use of online assessment to enhance teaching and learning: The pass-it project. Eur. Educ. Res. J. 2006, 5, 122–130. [Google Scholar] [CrossRef]
- Nicaud, J.; Bouhineau, D.; Chaachoua, H. Mixing microworld and cas features in building computer systems that help students learn algebra. Int. J. Comput. Math. Learn. 2004, 9, 169–211. [Google Scholar] [CrossRef]
- Su, W.; Li, L.; Cai, C.; Wang, P.S. An intelligent mathematics assessment system. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; pp. 1–4. [Google Scholar]
- Wang, P.S. On automatic mathematical answer checking. In Presentation in ECCAD; Shepherd University: Shepherdstown, WV, USA, 2008. [Google Scholar]
- Su, W.; Wang, P.S.; Li, L. An on-line mathML editing tool for web applications. In Proceedings of the International Multi-Symposiums on Computer and Computational Sciences, Iowa City, IA, USA, 13–15 August 2007. [Google Scholar]
- Christopher, J.S.; Nadine, K. Automation of mathematics examinations. Comput. Educ. 2016, 94, 215–227. [Google Scholar]
- Sangwin, C.J. Practice and practise in university: What defines success and how does online assessment support achieving this. In Success in Higher Education; Springer: Singapore, 2017; pp. 111–130. [Google Scholar]
- Buchberger, B.; Collins, G.E.; Loos, R.; Albrecht, R. Computer algebra symbolic and algebraic computation. ACM SIGSAM Bull. 1982, 16, 11–44. [Google Scholar] [CrossRef]
- Caviness, B.F. On canonical forms and simplification. J. Assoc. Comput. Mach. 1970, 17, 385–396. [Google Scholar] [CrossRef]
- Fitch, J.P. On algebraic simplification. Algebr. Simpl. 1973, 16, 23–27. [Google Scholar] [CrossRef][Green Version]
- Carette, J. Understanding expression simplification. In Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, Santander, Spain, 4–7 July 2004; pp. 72–79. [Google Scholar]
- Moses, J. Algebraic simplification a guide for the perplexed. In Proceedings of the Second ACM Symposium on Symbolic and Algebraic Manipulation, New York, NY, USA; 1971; pp. 282–304. [Google Scholar]
- Fenichel, R.R. An On-Line System for Algebraic Manipulation. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 2008. MAC-TR-35. [Google Scholar]
- Billing, J.; Wehmeier, S. Rule-Based Simplification of Expressions. mathPAD Band. 2002, pp. 36–43. Available online: http://msdl.cs.mcgill.ca/people/indrani/mupad_doc.pdf (accessed on 24 January 2021).
- Awde, A.; Bellik, Y.; Tadj, C. Complexity of mathematical expressions in adaptive multimodal multimedia system ensuring access to mathematics for visually impaired users. Int. J. Comput. Inf. Sci. Eng. 2008, 2, 152–195. [Google Scholar]
- Li, M.; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Tromp, J. Binary lambda calculus and combinatory logic. In Randomness and Complexity, From Leibniz to Chaitin; University of Auckland: Auckland, New Zealand, 2007; pp. 237–260. Available online: https://www.worldscientific.com/worldscibooks/10.1142/6577 (accessed on 24 January 2021).
- Henk, B. The lambda calculus: Its syntax and semantics. In Studies in Logic and the Foundations of Mathematics; North-Holland: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Henk, B. Lambda calculi with types. In Handbook of Logic in Computer Science; Oxford University Press: Oxford, UK, 2008; Volume II. [Google Scholar]
- de Bruijn, N.G. Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the church-rosser theorem. In Studies in Logic and the Foundations of Mathematics; North-Holland: Amsterdam, The Netherlands, 1994; Volume 133, pp. 375–388. [Google Scholar]
- Vereshchagin, N.; Vitanyi, P. Kolmogorov structure function with an application to the foundations of model selection. In Proceedings of the 47th IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 19 November 2002; IEEE: New York, NY, USA, 2002; pp. 751–760. [Google Scholar]
- Liu, Y. Computational symmetry. Symmetry 2000 2002, 80, 231–245. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).