A Model of Diameter Measurement Based on the Machine Vision
Abstract
1. Introduction
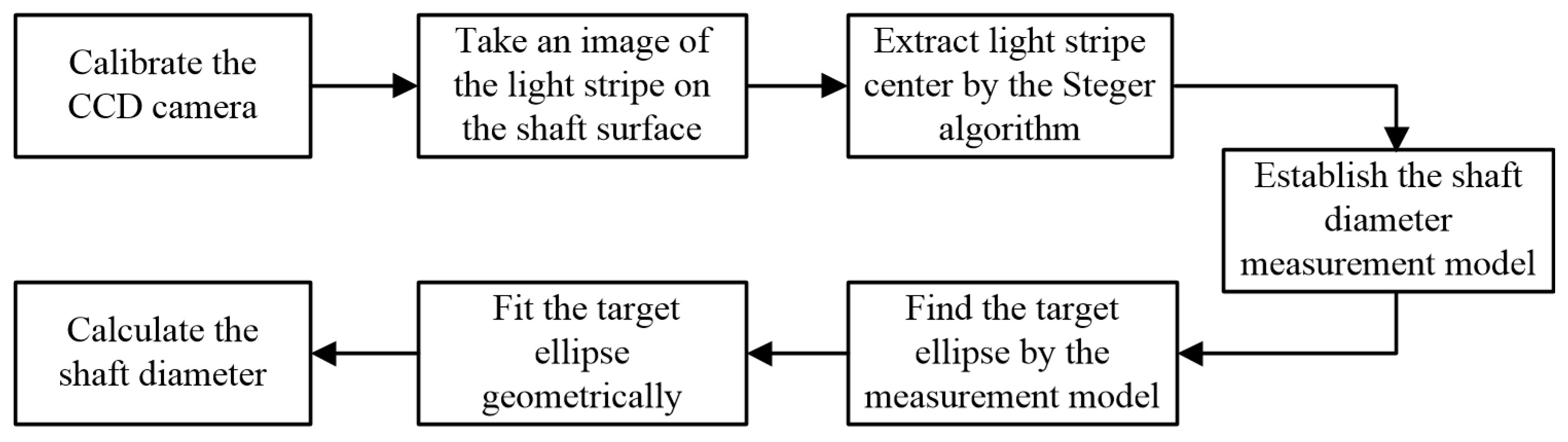
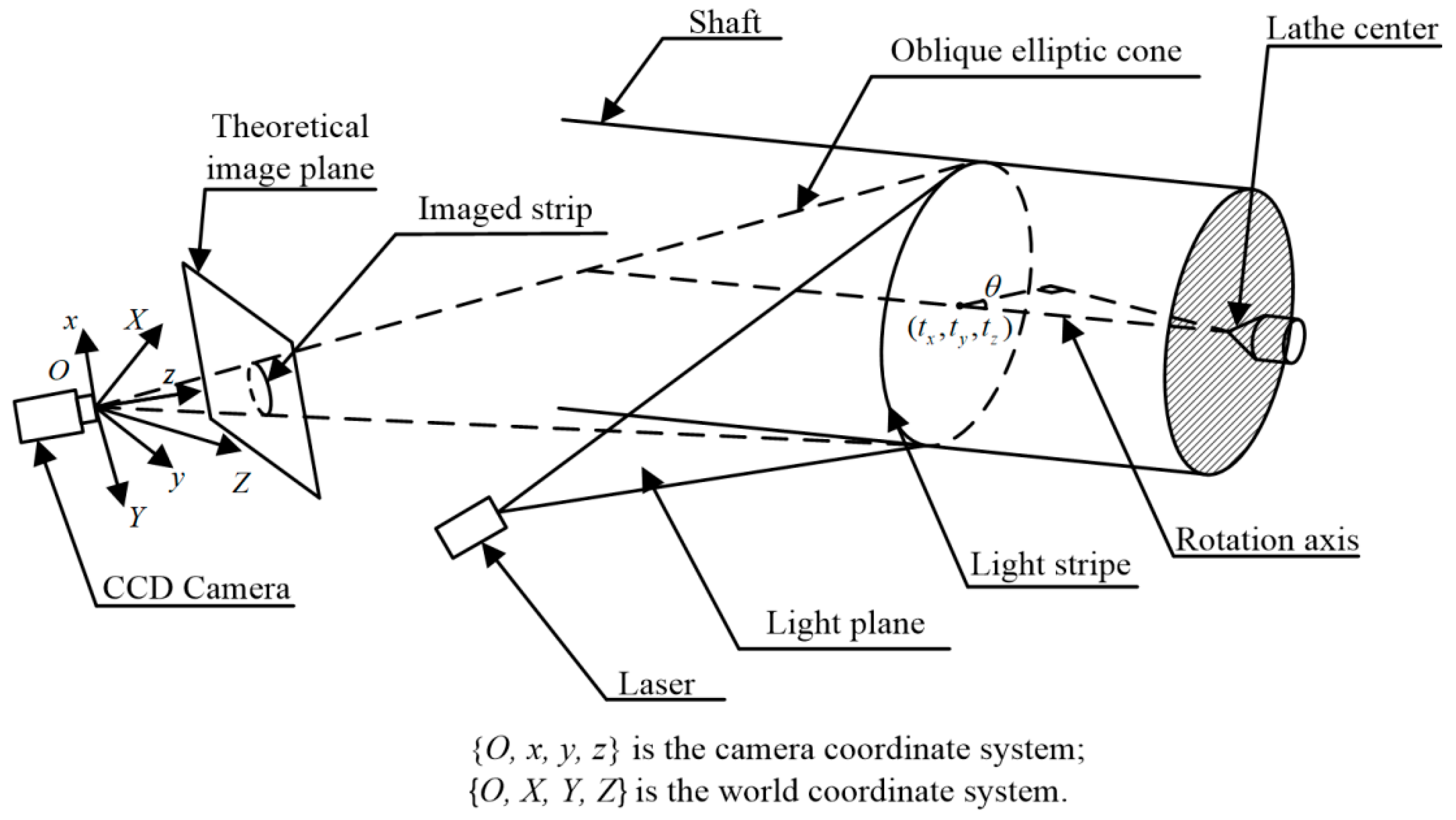
2. Establishment of the Model of Shaft Diameter Measurement
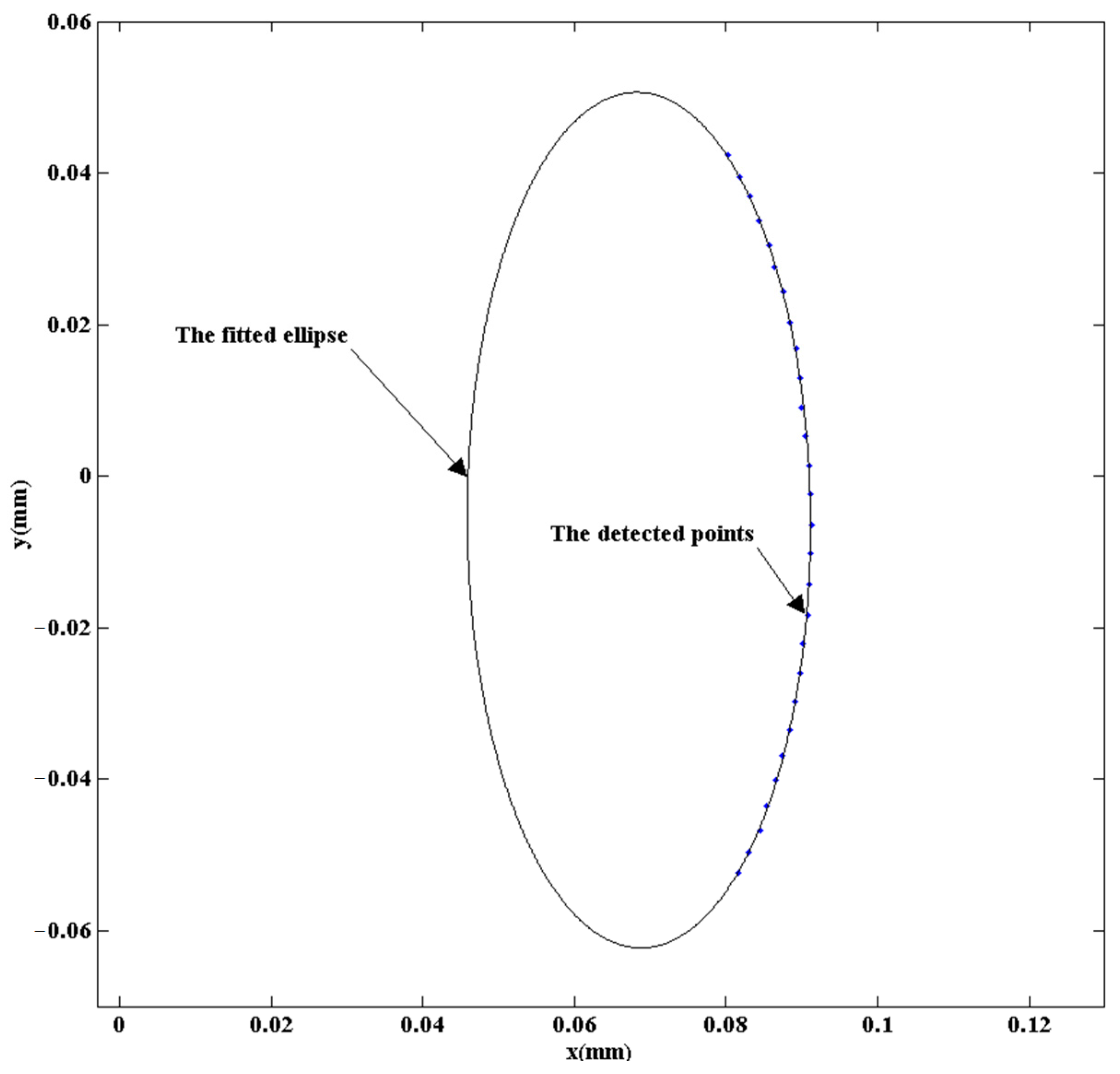
3. Test and Analysis of the Shaft Diameter Measurement Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| 6803.90 | 6803.78 | 2.51 | 640.12 | 480.10 | 0.02 | 19.42 | 0.0004 | −0.0001 |
| The Normal Vector and External Parameter of the Structured Light | ||||||||
| −0.002618 | −0.000139 | −0.001077 | 15.39 | −4.55 | 891.46 | |||
References
- Zhang, Z.; Liu, Y.; Hu, Q.; Zhang, Z.; Wang, L.; Liu, X.; Xia, X. Multi-information online detection of coal quality based on machine vision. Powder Technol. 2020, 374, 250–262. [Google Scholar] [CrossRef]
- Sun, W.; Yeh, S. Using the Machine Vision Method to Develop an On-machine Insert Condition Monitoring System for Computer Numerical Control Turning Machine Tools. Materials 2018, 11, 1977. [Google Scholar] [CrossRef] [PubMed]
- Makela, M.; Rissanen, M.; Sixta, H. Machine vision estimates the polyester content in recyclable waste textiles. Resour. Conserv. Recycl. 2020, 161. [Google Scholar] [CrossRef]
- Jones, J.; Foster, W.; Twomey, C.; Burdge, J.; Ahmed, O.; Pereira, T.; Wojick, J.; Corder, G.; Plotkin, J.; Abdus-Saboor, I. A machine-vision approach for automated pain measurement at millisecond timescales. eLife 2020, 9. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Xu, S.; Lu, H. Non-Destructive Identification and Estimation of Granulation in Honey Pomelo Using Visible and Near-Infrared Transmittance Spectroscopy Combined with Machine Vision Technology. Appl. Sci. 2020, 10, 5399. [Google Scholar] [CrossRef]
- Viejo, C.; Fuentes, S.; Howell, K.; Torrico, D.; Dunshea, F. Robotics and computer vision techniques combined with non-invasive consumer biometrics to assess quality traits from beer foamability using machine learning: A potential for artificial intelligence applications. Food Control 2018, 92, 72–79. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Zhao, H.; Ren, T.; Xu, Z.; Luo, Y. The Machine Vision Measurement Module of the Modularized Flexible Precision Assembly Station for Assembly of Micro- and Meso-Sized Parts. Micromachines 2020, 11, 918. [Google Scholar] [CrossRef]
- Li, W.; Jin, J.; Li, X.; Li, B. Method of rotation angle measurement in machine vision based on calibration pattern with spot array. Appl. Opt. 2010, 49, 1001–1006. [Google Scholar] [CrossRef]
- Lian, F.; Tan, Q.; Liu, S. Block Thickness Measurement of Using the Structured Light Vision. Int. J. Pattern Recognit. Artif. Intell. 2019, 33. [Google Scholar] [CrossRef]
- Chen, J.; Jing, L.; Hong, T.; Liu, H.; Glowacz, A. Research on a Sliding Detection Method for an Elevator Traction Wheel Based on Machine Vision. Symmetry 2020, 12, 1158. [Google Scholar] [CrossRef]
- Shen, H.; Li, S.; Gu, D.; Chang, H. Bearing defect inspection based on machine vision. Measurement 2012, 45, 719–733. [Google Scholar] [CrossRef]
- Moru, D.; Borro, D. A machine vision algorithm for quality control inspection of gears. Int. J. Adv. Manuf. Technol. 2019, 106, 105–123. [Google Scholar] [CrossRef]
- Wu, F.; Mao, J.; Zhou, Y.; Qing, L. Three-line structured light measurement system and its application in ball diameter measurement. Optik 2018, 157, 222–229. [Google Scholar] [CrossRef]
- Bao, H.; Tan, Q.; Liu, S.; Miao, J. Computer Vision Measurement of Pointer Meter Readings Based on Inverse Perspective Mapping. Appl. Sci. 2019, 9, 3729. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, J.; Jiang, X.; Peng, Y.; Wang, L. Mini milling cutter measurement based on machine vision. Procedia Eng. 2011, 15, 1807–1811. [Google Scholar]
- Gao, L.; Wang, Z.; Liu, Y.; Guo, J.; Liu, C. Vision measurement technique of axle based on double beam. Optik 2018, 174, 757–765. [Google Scholar] [CrossRef]
- Wei, G.; Tan, Q. Measurement of shaft diameters by machine vision. Appl. Opt. 2011, 50, 3246–3253. [Google Scholar] [CrossRef]
- Sun, Q.; Hou, Y.; Tan, Q.; Li, C. Shaft diameter measurement using a digital image. Opt. Laser Eng. 2014, 55, 183–188. [Google Scholar] [CrossRef]
- Li, B. Research on geometric dimension measurement system of shaft parts based on machine vision. EURASIP J. Image Video Process. 2018, 10. [Google Scholar] [CrossRef]
- Che, J.; Ratnam, M. Real-time monitoring of workpiece diameter during turning by vision method. Measurement 2018, 126, 369–377. [Google Scholar] [CrossRef]
- Liu, S.; Tan, Q.; Zhang, Y. Shaft Diameter Measurement Using Structured Light Vision. Sensors 2015, 15, 19750–19767. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Jia, Z.; Wang, F.; Ma, X.; Wang, W.; Jia, X.; Song, D. An improved online dimensional measurement method of large hot cylindrical forging. Measurement 2012, 45, 2041–2205. [Google Scholar] [CrossRef]
- Wu, B.; Xue, T.; Zhang, T.; Ye, S. A novel method for round steel measurement with a multi-line structured light vision sensor. Meas. Sci. Technol. 2010, 21, 025204. [Google Scholar] [CrossRef]
- Liu, B.; Wang, P.; Zeng, Y.; Sun, C. Measuring method for micro-diameter based on structured-light vision technology. Chin. Opt. Lett. 2010, 8, 666–669. [Google Scholar]
- Gong, Z.; Sun, J.; Zhang, G. Dynamic Measurement for the Diameter of a Train Wheel Based on Structured-Light Vision. Sensors 2016, 16, 564. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, W.; Lu, Y.; Cheng, X.; Luo, W.; Di, H.; Wang, F. Accurate profile measurement method for industrial stereo-vision systems. Sens. Rev. 2020, 40, 445–453. [Google Scholar] [CrossRef]
- Malyarchuk, V.; Jung, I.; Rogers, J.; Shin, G.; Ha, J. Experimental and modeling studies of imaging with curvilinear electronic eye cameras. Opt. Express 2010, 18, 27346–27358. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, Z. A position-distortion model of ellipse centre for perspective projection. Meas. Sci. Technol. 2003, 14, 1420–1426. [Google Scholar] [CrossRef]
- Li, Z.; Zgadzaj, R.; Wang, X.; Reed, S.; Dong, P.; Downer, M. Frequency-domain streak camera for ultrafast imaging of evolving light-velocity objects. Opt. Lett. 2010, 35, 4087–4089. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, R.; Liu, E.; Yan, K.; Ma, Y. A single-image linear calibration method for camera. Measurement 2018, 130, 298–305. [Google Scholar] [CrossRef]
- Lv, B.; Li, L.; Yan, C. Three-dimensional laser scanning under the pinhole camera with lens distortion. In Proceedings of the 4th IEEE International Conference on Cloud Computing and Intelligence Systems (IEEE CCIS), Beijing, China, 17–19 August 2016; Volume 28, pp. 737–742. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Bouguet, J.Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the Algorithm; Technical Report; OpenCV Document. Intel Microprocessor Research Labs: Santa Clara, CA, USA, 2000. [Google Scholar]
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab. Available online: https://www.vision.caltech.edu/bouguetj/calib_doc/index.html (accessed on 5 June 2020).
- Markovsky, I.; Kukush, A.; Van Huffel, S. Consistent least squares fitting of ellipsoids. Numer. Math. 2004, 98, 177–194. [Google Scholar] [CrossRef]
- Mortari, D. Least-Squares Solution of Linear Differential Equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- Mirzaei, D. Direct approximation on spheres using generalized moving least squares. BIT Numer. Math. 2017, 57, 1041–1063. [Google Scholar] [CrossRef]
- Bos, L.; Sommariva, A.; Vianello, M. Least-squares polynomial approximation on weakly admissible meshes: Disk and triangls. J. Comput. Appl. Math. 2010, 235, 660–668. [Google Scholar] [CrossRef]
- Liang, W.; Chapman, C.; Frisch, M.; Li, X. Geometry Optimization with Multilayer Methods Using Least-Squares Minimization. J. Chem. Theory Comput. 2010, 6, 3352–3357. [Google Scholar] [CrossRef]
- Ahn, S.; Rauh, W.; Warnecke, H. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola. Pattern Recognit. 2001, 34, 2283–2303. [Google Scholar] [CrossRef]
- Fitzgibbon, A.; Pilu, M.; Fisher, R. Direct least square fitting of ellipses. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 476–480. [Google Scholar] [CrossRef]
- Ahn, S.; Rauh, W. Geometric least squares fitting of circle and ellipse. Int. J. Pattern Recognit. Artif. Intell. 1999, 13, 987–996. [Google Scholar] [CrossRef]
- Steger, C. An unbiased detector of curvilinear structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef]
- Qi, L.; Zhang, Y.; Zhang, X.; Wang, S.; Xie, F. Statistical behavior analysis and precision optimization for the laser stripe center detector based on Steger’s algorithm. Opt. Express 2013, 21, 13442–13449. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Liang, Y. Rock Fracture Centerline Extraction based on Hessian Matrix and Steger algorithm. KSII Trans. Internet Inf. Syst. 2015, 9, 5073–5086. [Google Scholar]
- Stainvas, I.; Lowe, D. A generative model for separating illumination and reflectance from images. J. Mach. Learn. Res. 2004, 4, 1499–1519. [Google Scholar]
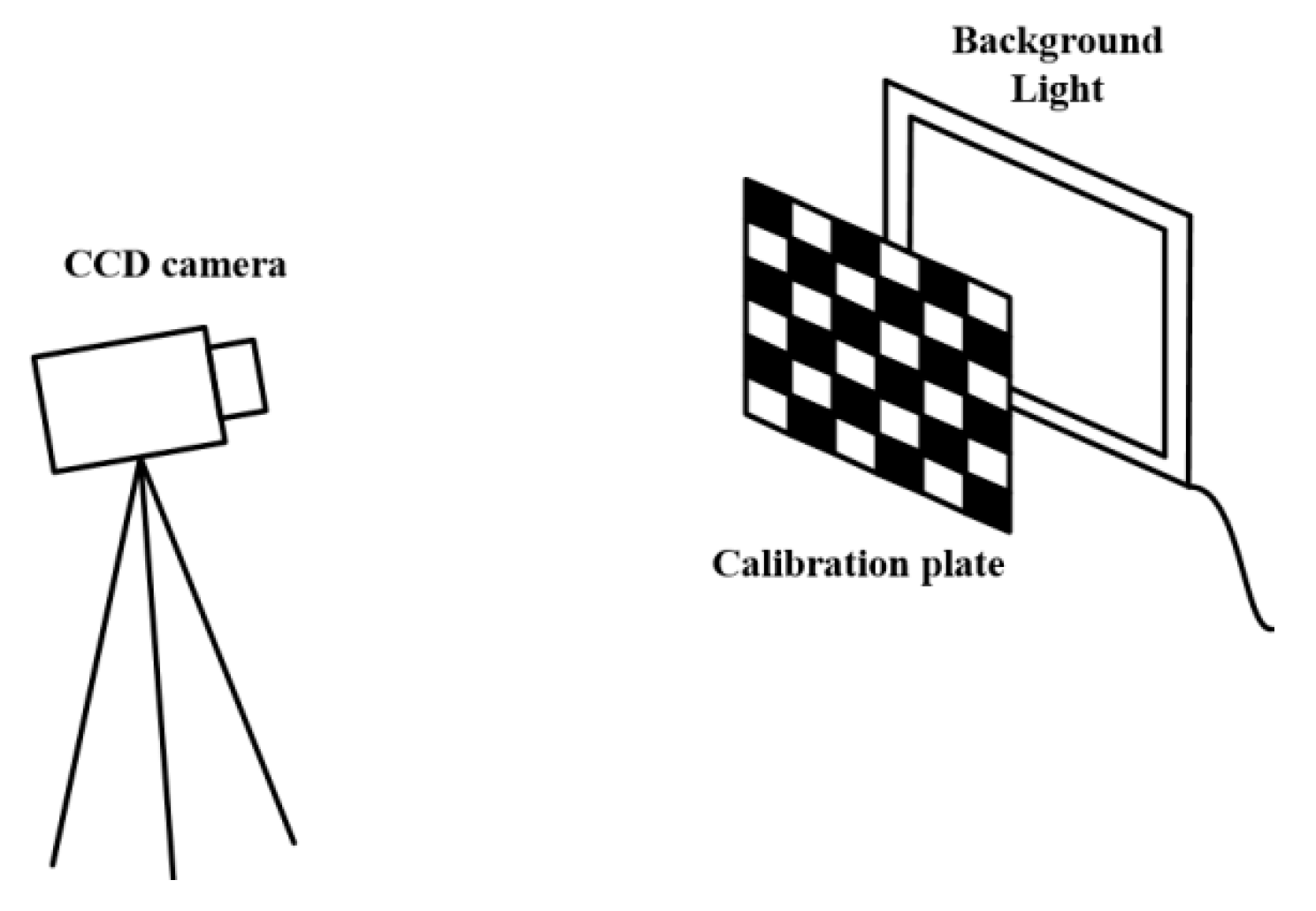


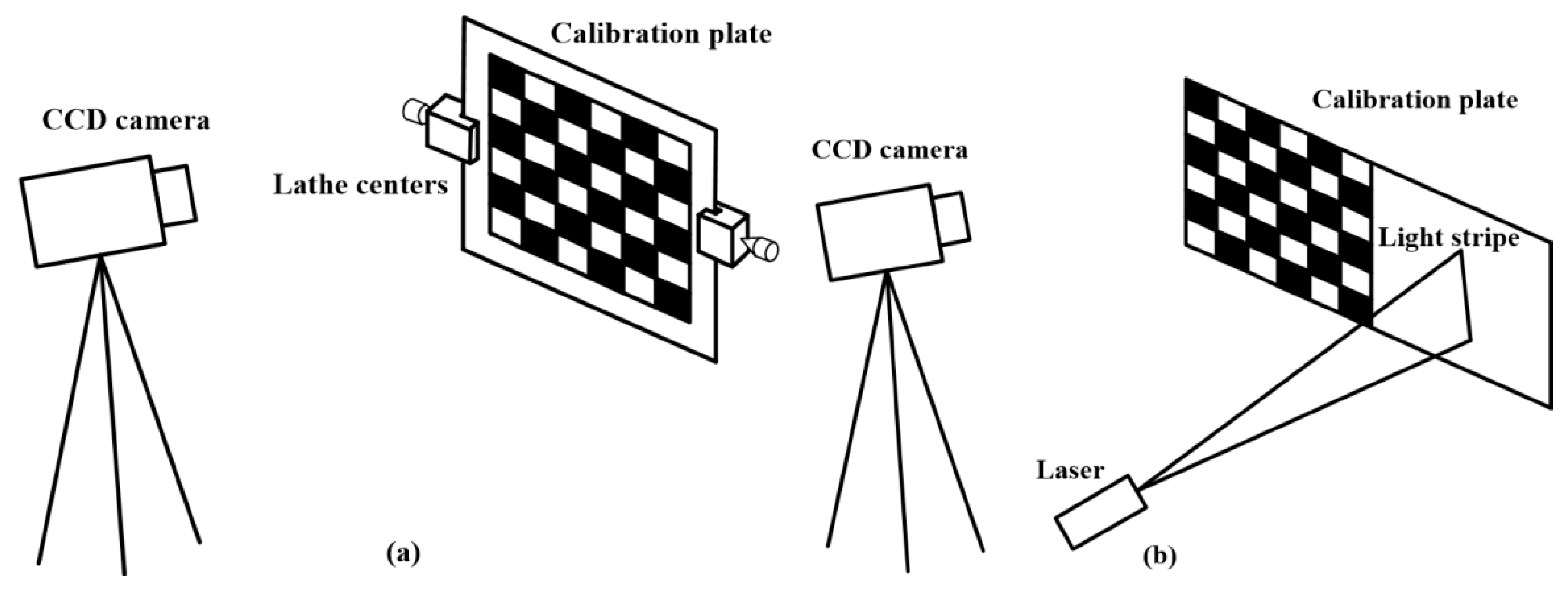

| No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Equipment | CCD camera | Lens | Background light | Calibration plate |
| Model No. | JAI CCD camera | M0814-MP | CCSLFL-200 | CBC 75 mm-2.0 |
| Main Parameters | Resolution: 1376 × 1024 | Focal length: 25 mm | Electric source:12 V/10 W | Precision of the grid: 1 µm |
| 6858.35 | 6859.04 | 1.03 | 622.81 | 467.25 | 0.11 | 7.17 | 0.0007 | 0.0004 | ||
| No. | Pixel Coordinates of Detecting the Both Ellipse Center and 4 Measuring Points | |||||||||
| 1 | 406.29 | 273.09 | 406.31 | 119.53 | 551.76 | 273.51 | 406.44 | 426.59 | 258.69 | 272.67 |
| 2 | 468.67 | 338.08 | 468.81 | 120.25 | 674.89 | 338.79 | 469.14 | 557.35 | 258.74 | 338.93 |
| The Normal Vector and External Parameter of the Calibration Plate | The Transformation Matrix Q | |||||||||
| See (A10) in Appendix A | ||||||||||
| 0.000549 | 0.000030 | −0.001581 | −597.63 mm | |||||||
| No. | Times | Exact Values | Measurement Values | Errors |
|---|---|---|---|---|
| I | 1 | 28 | 28.00146 | 0.00146 |
| 2 | 28 | 28.00151 | 0.00151 | |
| 3 | 28 | 28.00147 | 0.00147 | |
| 4 | 28 | 28.00149 | 0.00149 | |
| 5 | 28 | 28.00152 | 0.00152 | |
| 6 | 28 | 28.00139 | 0.00139 | |
| 7 | 28 | 28.00143 | 0.00143 | |
| 8 | 28 | 28.00154 | 0.00154 | |
| 9 | 28 | 28.00137 | 0.00137 | |
| 10 | 28 | 28.00130 | 0.00130 | |
| Average value | 28 | 28.00145 | 0.00145 | |
| Standard deviation | 0 | 0.00008 | 0.00008 | |
| II | 1 | 40 | 40.00149 | 0.00149 |
| 2 | 40 | 40.00156 | 0.00156 | |
| 3 | 40 | 40.00162 | 0.00162 | |
| 4 | 40 | 40.00147 | 0.00147 | |
| 5 | 40 | 40.00145 | 0.00145 | |
| 6 | 40 | 40.00158 | 0.00158 | |
| 7 | 40 | 40.00143 | 0.00143 | |
| 8 | 40 | 40.00162 | 0.00162 | |
| 9 | 40 | 40.00159 | 0.00159 | |
| 10 | 40 | 40.00156 | 0.00156 | |
| Average value | 40 | 40.00154 | 0.00154 | |
| Standard deviation | 0 | 0.00007 | 0.00007 |
| No. | Times | Exact Values | Measurement Values | Errors |
|---|---|---|---|---|
| I | 1 | 28 | 28.00166 | 0.00166 |
| 2 | 28 | 28.00155 | 0.00155 | |
| 3 | 28 | 28.00156 | 0.00156 | |
| 4 | 28 | 28.00146 | 0.00146 | |
| 5 | 28 | 28.00154 | 0.00154 | |
| 6 | 28 | 28.00149 | 0.00149 | |
| 7 | 28 | 28.00138 | 0.00138 | |
| 8 | 28 | 28.00149 | 0.00149 | |
| 9 | 28 | 28.00155 | 0.00155 | |
| 10 | 28 | 28.00147 | 0.00147 | |
| Average value | 28 | 28.00152 | 0.00152 | |
| Standard deviation | 0 | 0.00008 | 0.00008 | |
| II | 1 | 40 | 40.00157 | 0.00157 |
| 2 | 40 | 40.00168 | 0.00168 | |
| 3 | 40 | 40.00149 | 0.00149 | |
| 4 | 40 | 40.00161 | 0.00161 | |
| 5 | 40 | 40.00171 | 0.00171 | |
| 6 | 40 | 40.00169 | 0.00169 | |
| 7 | 40 | 40.00159 | 0.00159 | |
| 8 | 40 | 40.00166 | 0.00166 | |
| 9 | 40 | 40.00159 | 0.00159 | |
| 10 | 40 | 40.00158 | 0.00158 | |
| Average value | 40 | 40.00161 | 0.00161 | |
| Standard deviation | 0 | 0.00007 | 0.00007 |
| Shaft No. | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| The Roughness (μm) | Ra 5.26 | Ra 5.85 | Ra 5.93 | ||||
| The Shaft Speed (r/min) | 0 | 500 | 0 | 1250 | 0 | 1000 | |
| Known Values | 34.686 | 34.686 | 36.162 | 36.162 | 34.012 | 34.012 | |
| Measurement Values | 34.699 | 34.701 | 36.173 | 36.181 | 34.027 | 34.030 | |
| Errors | Average Values | 0.013 | 0.015 | 0.011 | 0.019 | 0.015 | 0.018 |
| Standard Deviations | 0.005 | 0.006 | 0.006 | 0.008 | 0.005 | 0.007 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Q.; Kou, Y.; Miao, J.; Liu, S.; Chai, B. A Model of Diameter Measurement Based on the Machine Vision. Symmetry 2021, 13, 187. https://doi.org/10.3390/sym13020187
Tan Q, Kou Y, Miao J, Liu S, Chai B. A Model of Diameter Measurement Based on the Machine Vision. Symmetry. 2021; 13(2):187. https://doi.org/10.3390/sym13020187
Chicago/Turabian StyleTan, Qingchang, Ying Kou, Jianwei Miao, Siyuan Liu, and Bosen Chai. 2021. "A Model of Diameter Measurement Based on the Machine Vision" Symmetry 13, no. 2: 187. https://doi.org/10.3390/sym13020187
APA StyleTan, Q., Kou, Y., Miao, J., Liu, S., & Chai, B. (2021). A Model of Diameter Measurement Based on the Machine Vision. Symmetry, 13(2), 187. https://doi.org/10.3390/sym13020187






