Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process
Abstract
1. Introduction
2. Material and Method
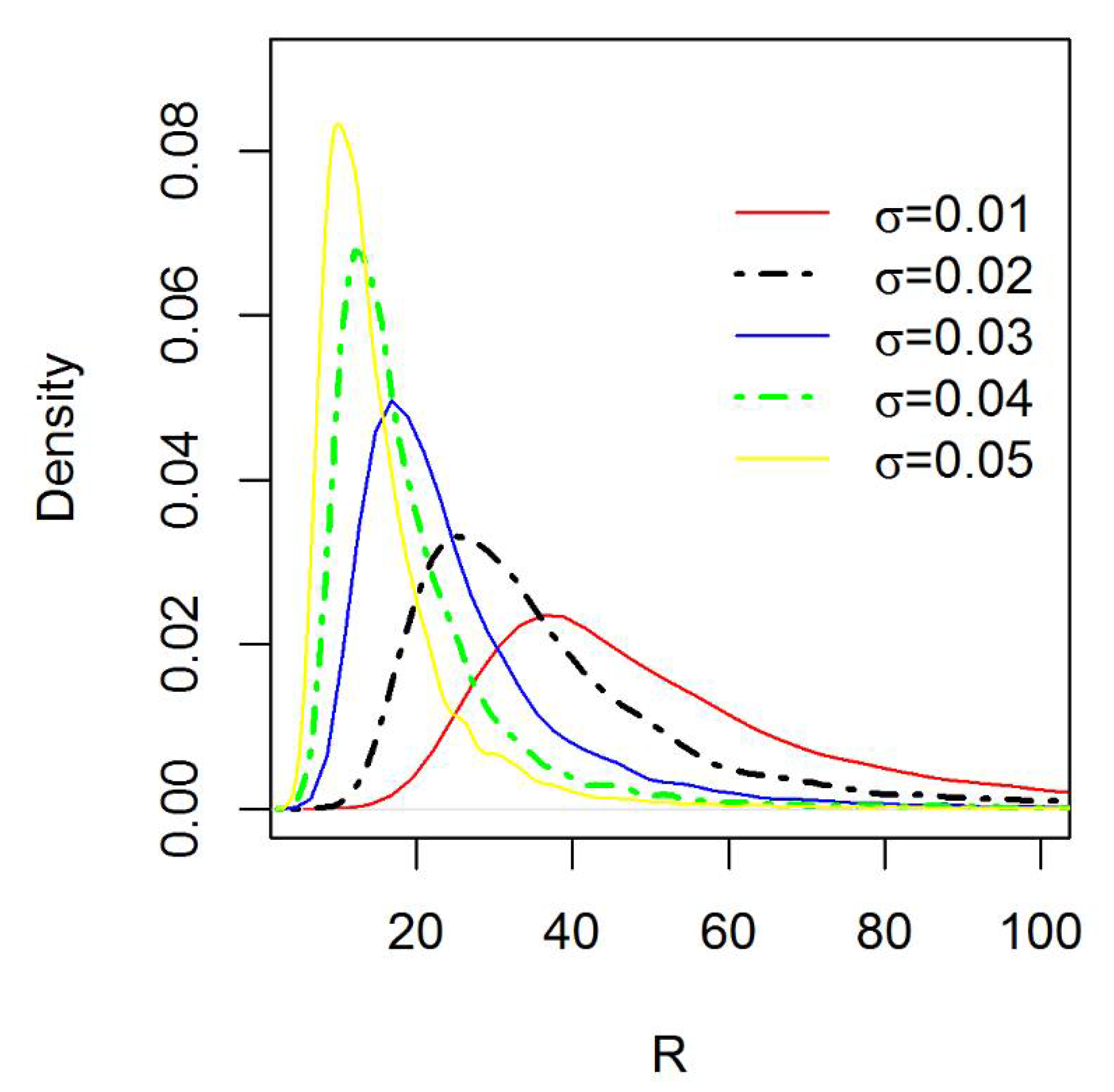
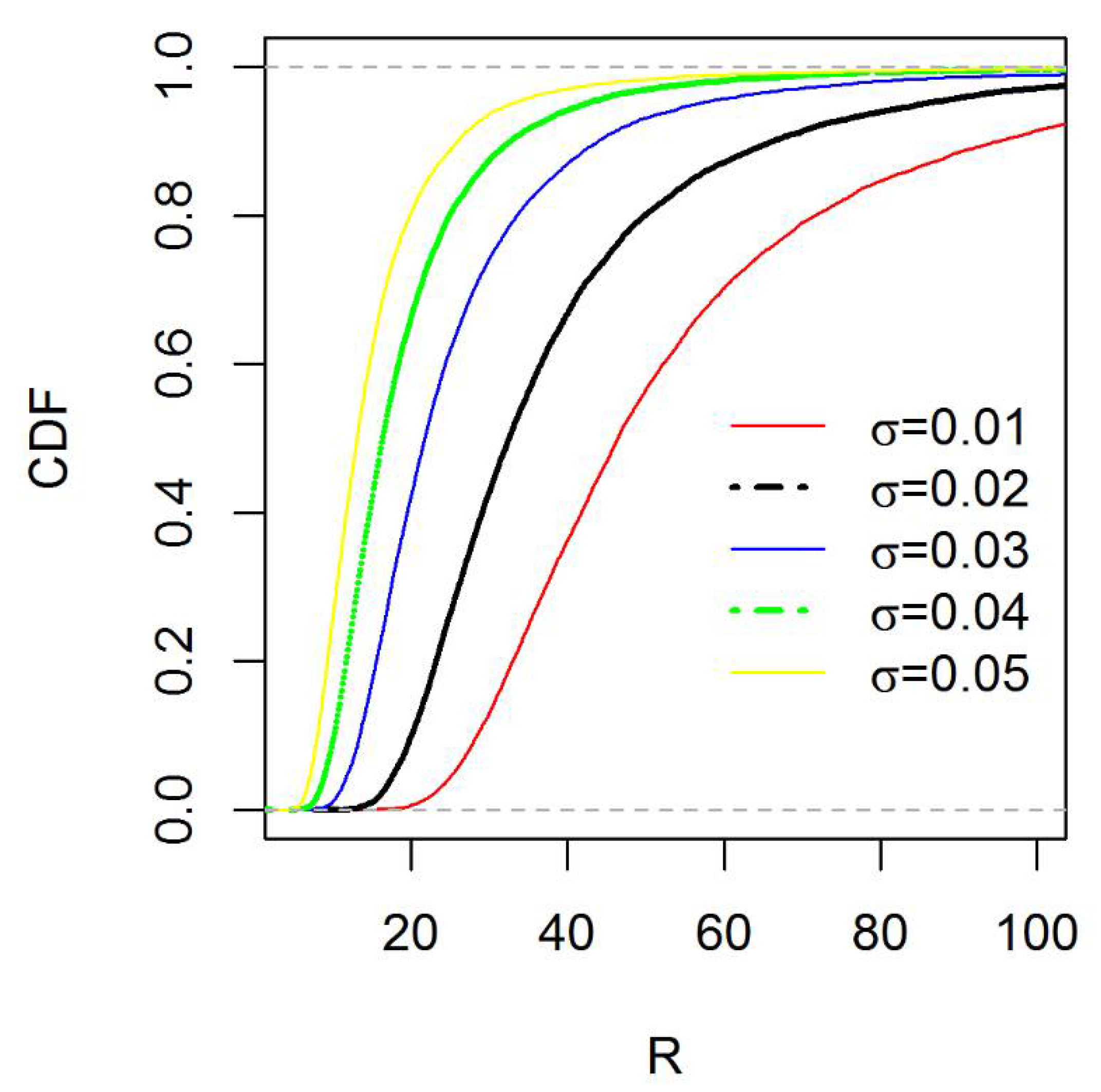
2.1. Inverse Maxwell Distribution and Its Properties
2.2. Derivation of the Control Chart
3. Results
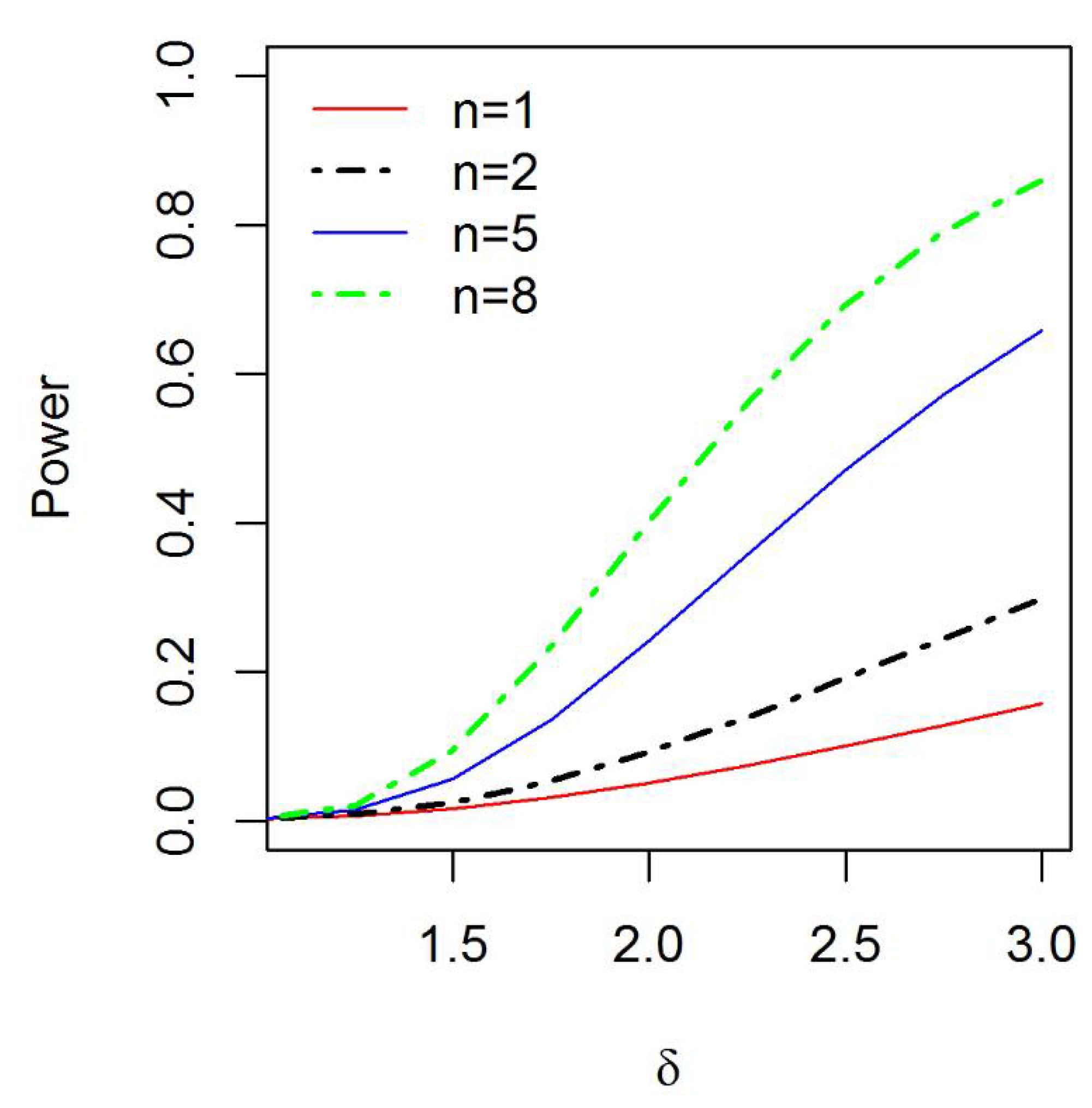
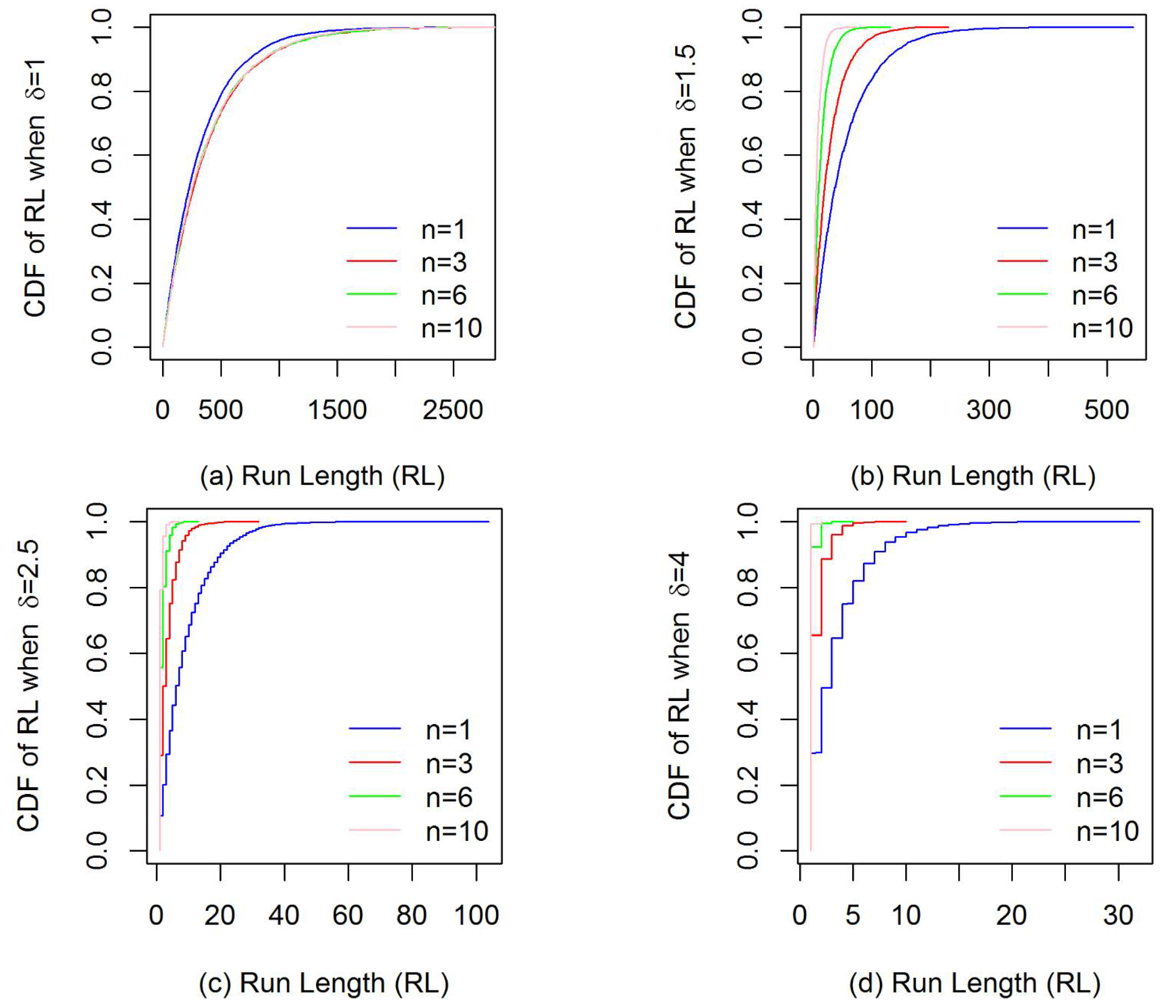
3.1. Performance Evaluation
- The average run length (ARL) is always approximately 370 when the process is in control, (i.e., ) for all considered sample sizes.
- For an in-control process, there is no significant difference between the SDRL values and the corresponding ARL values for any sample size, . For example: The ARL and SDRL values are 370.55 and 369.10, respectively, at . Similarly, when , the ARL and SDRL values are 369.85 and 369.25 respectively.
- The ARL and SDRL values rapidly decrease as the shift increases in the process scale parameter. For example: At 50% increment of shift and for the ARL and SDRL are 28.76 and 28.25, respectively. Under the same condition and at 150% increment of shift, the ARL and SDRL respectively become 3.47 and 2.94. From these values, we can also conclude that the ARL and SDRL are directly proportional to each other.
- In both the in-control and out-of-control situations and for any sample size, the ARL values are greater than the MDRL values. This indicates that the run length distribution of the chart is positively skewed. For example: When and , the ARL and MDRL values are 12.73 and 9, respectively. Additionally, for and , the ARL and MDRL values are 3.36 and 2, correspondingly.
3.2. Simulation Study
- Step 1: Fix the sample size for each random sample.
- Step 2: Generate a random sample of size from.
- Step 3: By taking the square root of , we will get a sample from Maxwell random variable of size .
- Step 4: Obtain a sample from the inverse Maxwell random variable of size by setting .
- Step 5: Estimate the plotting statistics .
- Step 6: Repeat the first five steps until the expected amount of sample subgroups are obtained.
- Step 7: Develop the control limits as proposed in the previous section.
- Step 8: Plot all the values of statistics in contrast to the control limits.
3.3. Comparisons
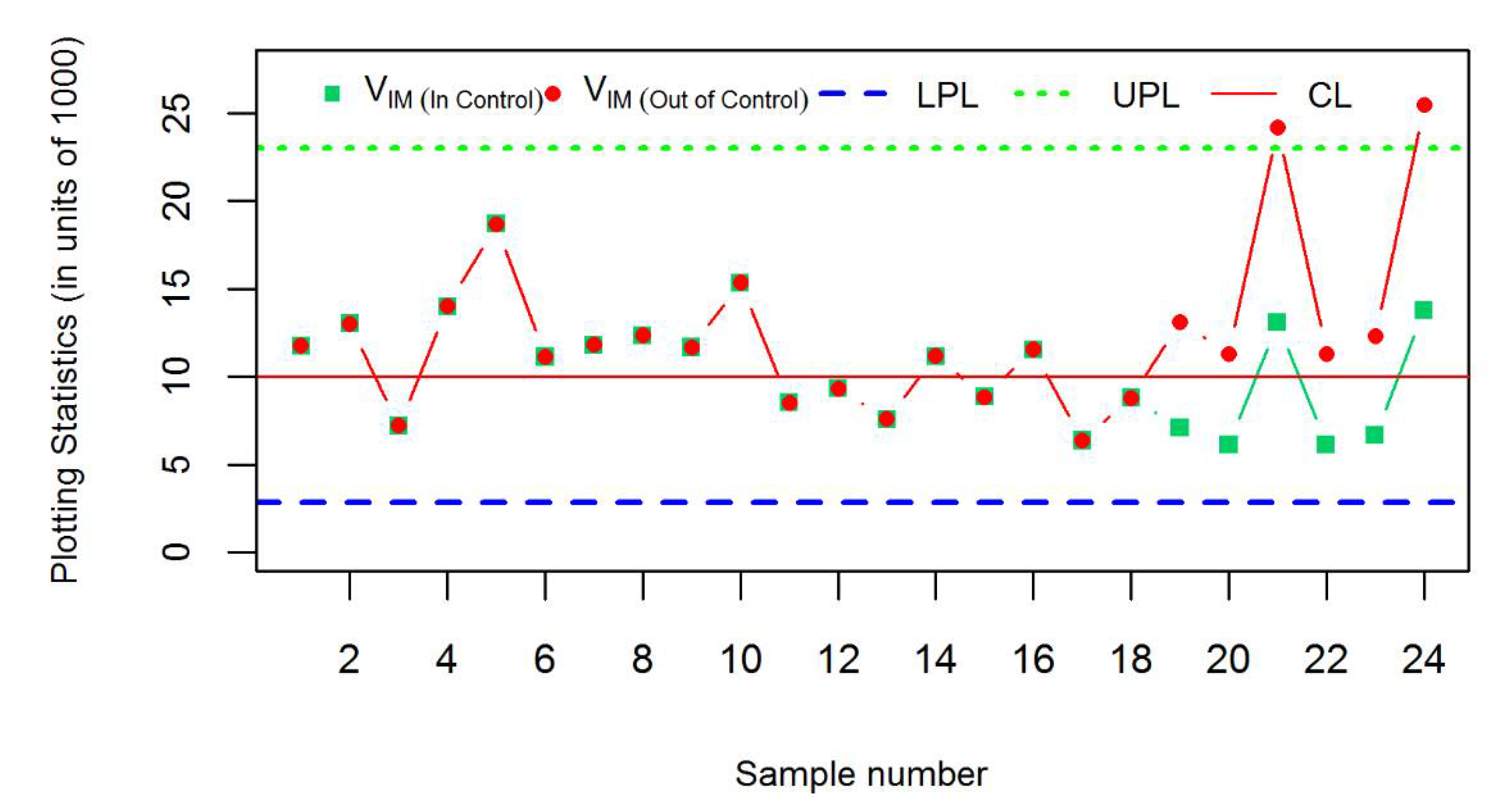
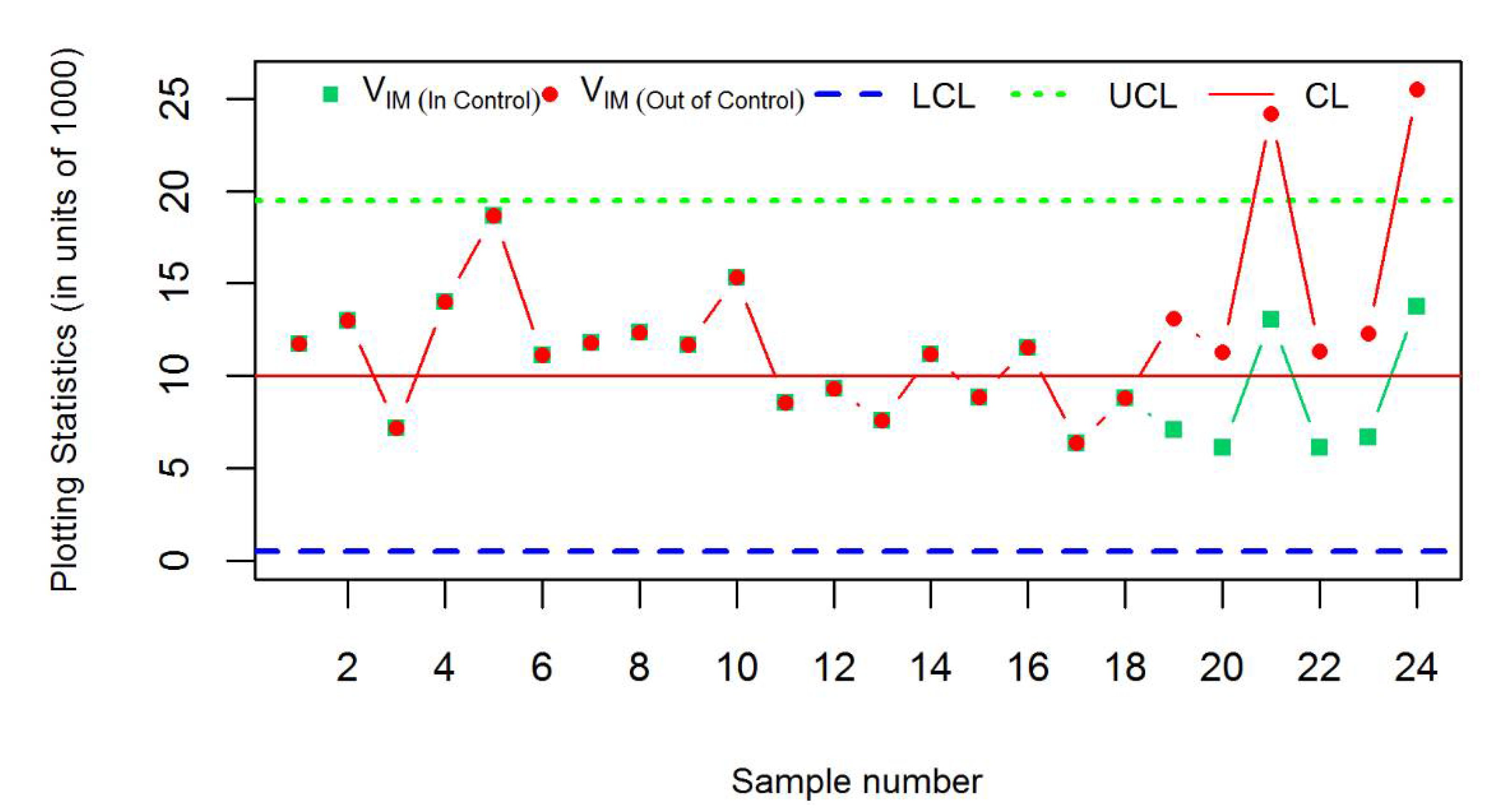
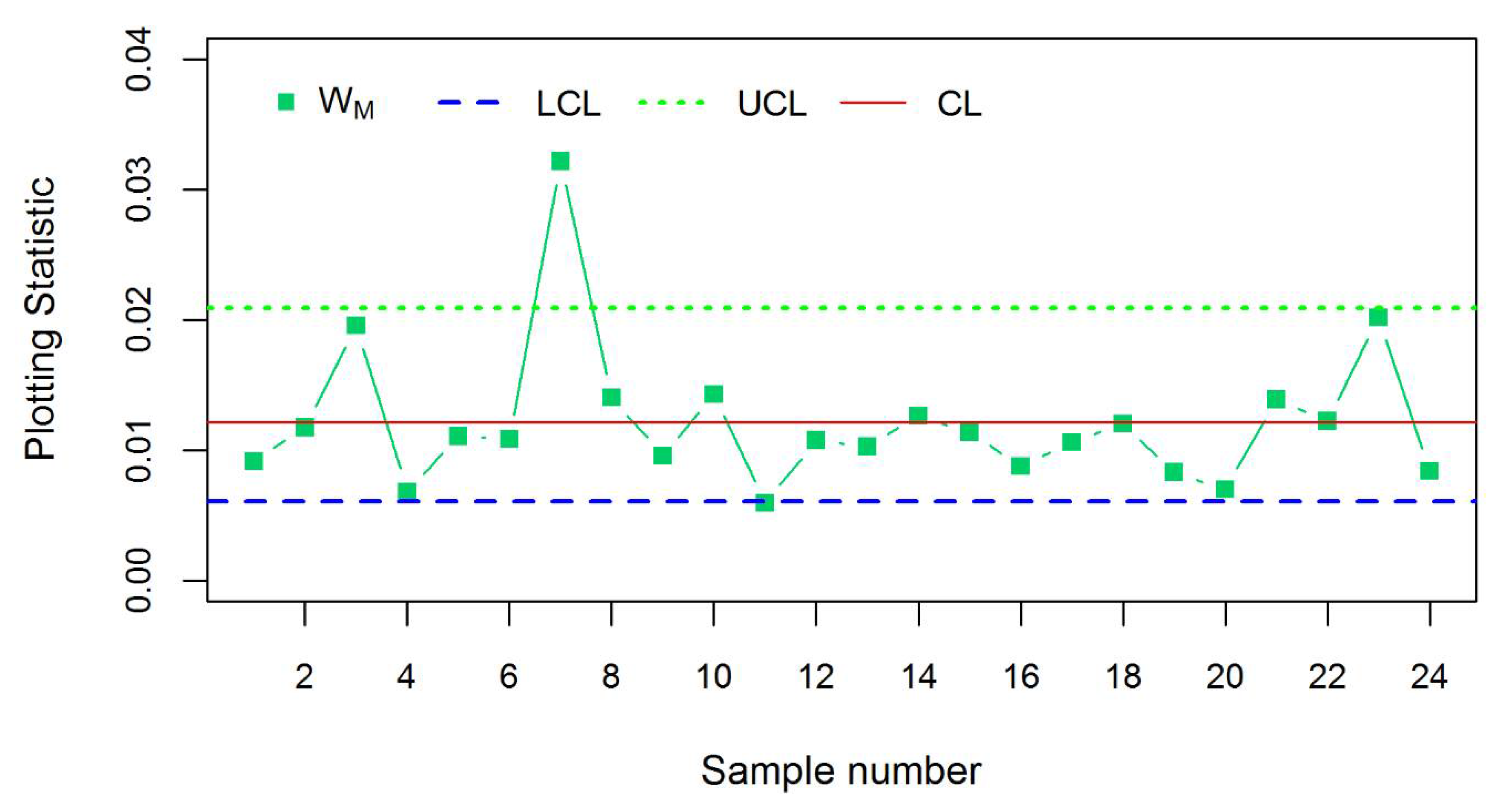
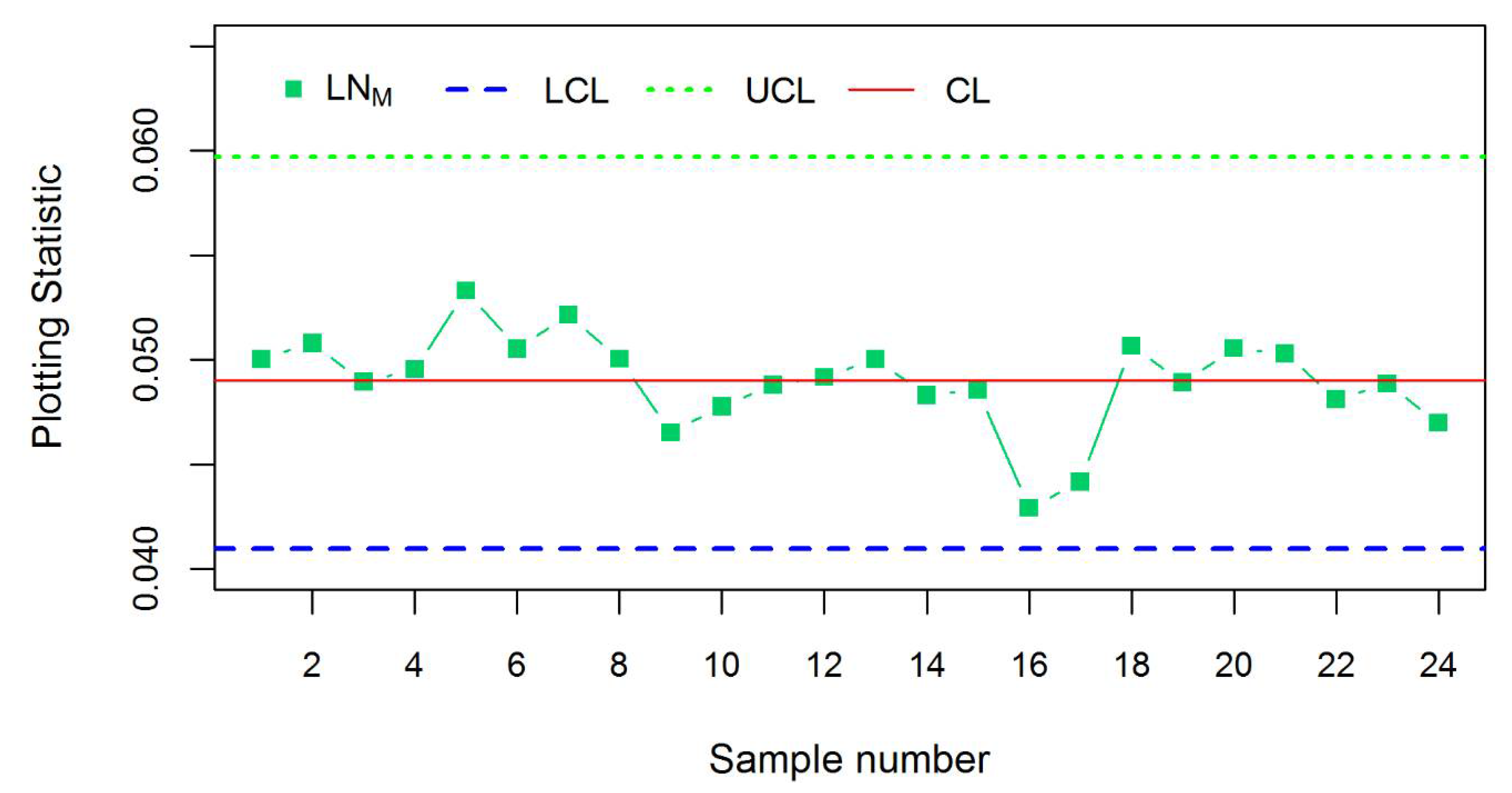
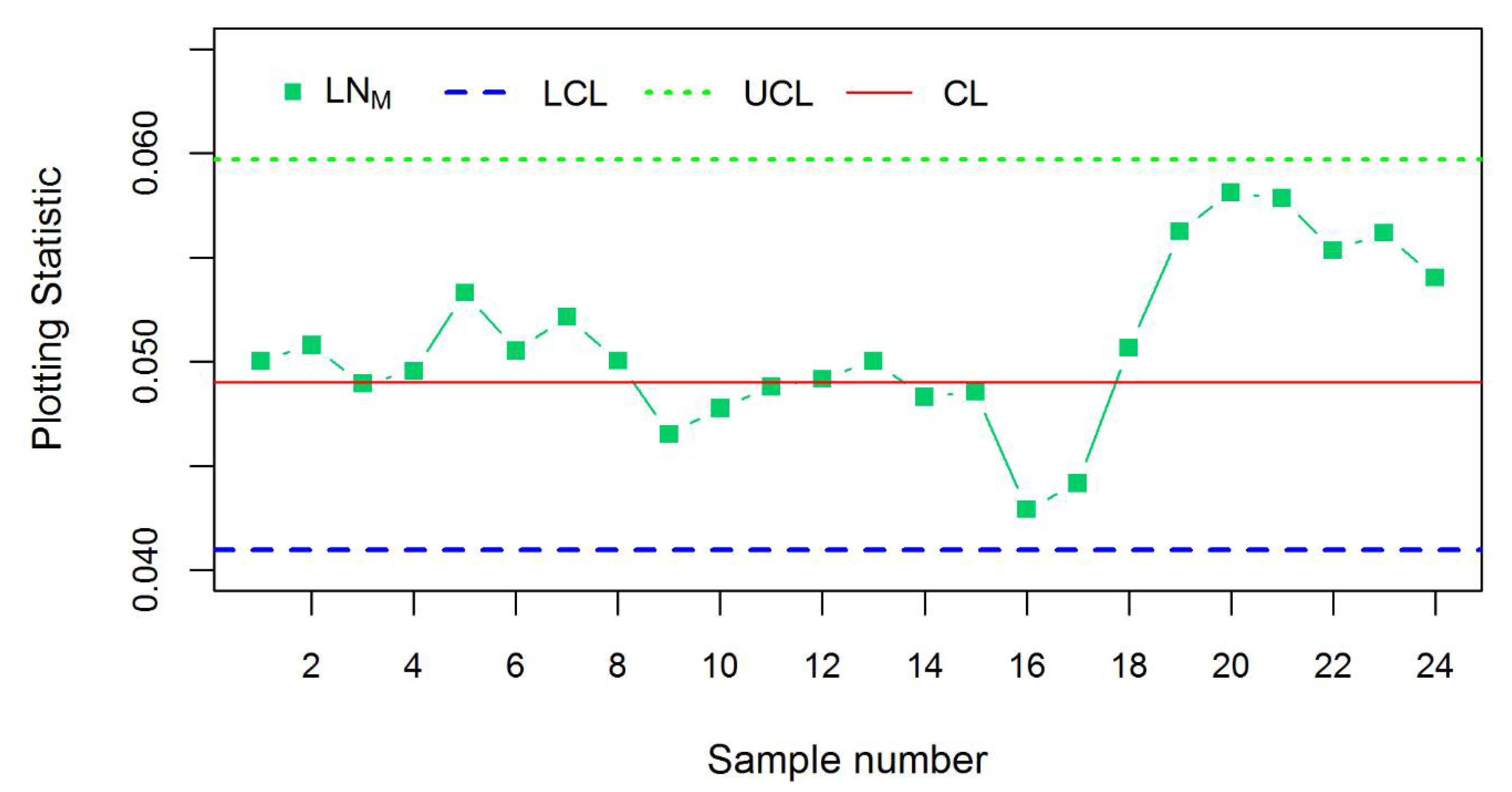
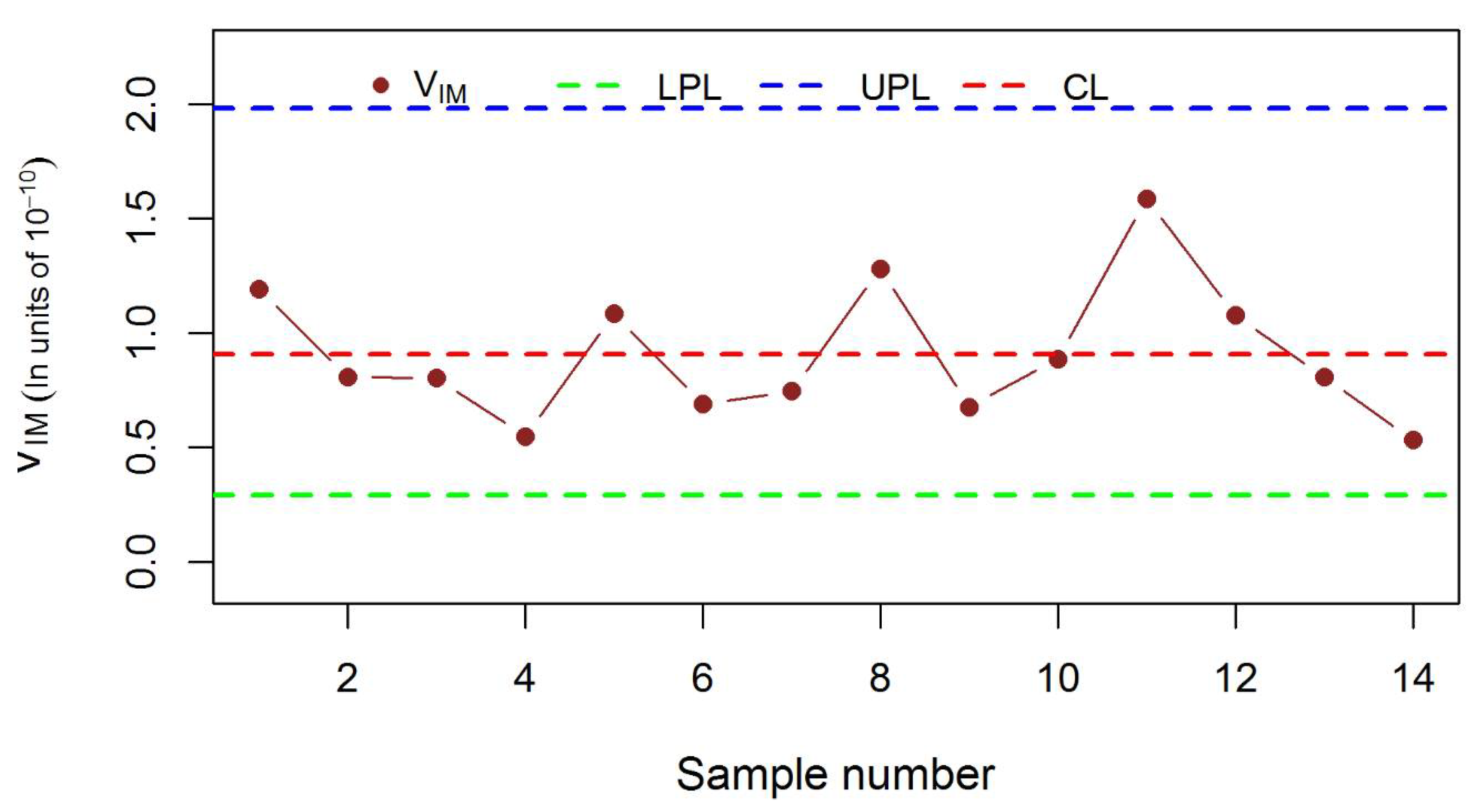
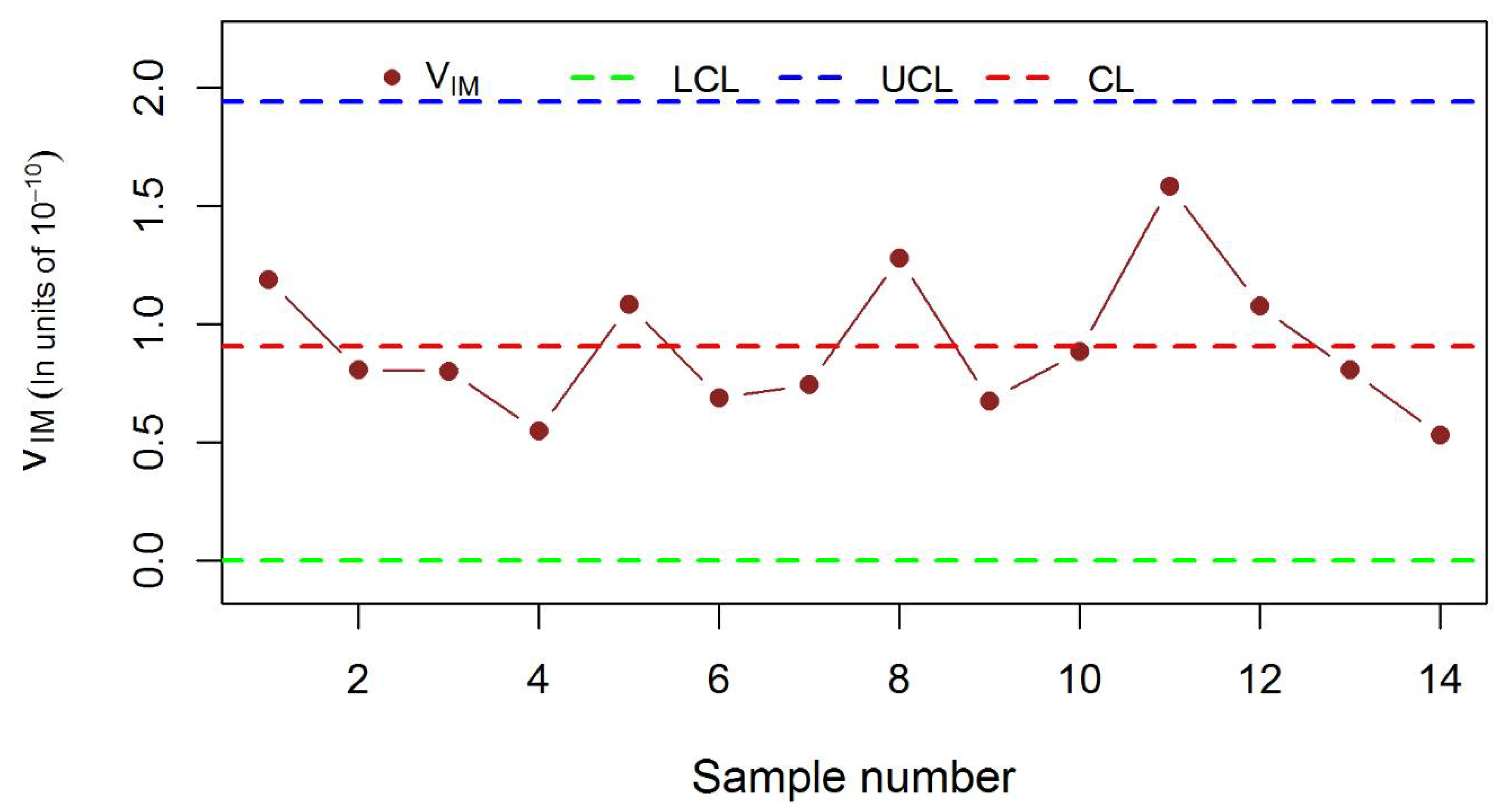
3.4. Real Life Example
4. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| rl.VIM<-function(L1,L2,n,sg,del){ |
| sg2 = del*sg^2; lcl = L1*sg^2; ucl = L2*sg^2; |
| vim = rl =c() |
| for (j in 1:10000) { |
| for (i in 1:10000) { |
| r = 1/sqrt(rgamma(n, 1.5, scale = 2*sg2)) |
| vim[i] = sum(r^-2)/(3*n) |
| if (lcl > vim[i] | ucl < vim[i]) |
| { |
| rl[j] = i |
| break |
| } |
| else |
| { |
| rl[j] = 100000 |
| } |
| } |
| } |
| ARL=mean(rl);SDRL=sd(rl);MDRL=median(rl);Q10=quantile(rl,.10);Q25=quantile(rl,.25);Q50=quantile(rl,.50);Q75=quantile(rl,.75);Q90=quantile(rl,.90) |
| print(cbind(ARL,SDRL,MDRL,Q10,Q25,Q50,Q75,Q90)) |
| } |
References
- Sato, S.; Inoue, J. Inverse gaussian distribution and its application. Electron. Commun. Jpn. (Part III Fundam. Electron. Sci.) 1994, 77, 32–42. [Google Scholar] [CrossRef]
- Krishna, H.; Malik, M. Reliability estimation in Maxwell distribution with progressively Type-II censored data. J. Stat. Comput. Simul. 2012, 82, 623–641. [Google Scholar] [CrossRef]
- Tomer, S.K.; Panwar, M.S. Estimation procedures for Maxwell distribution under type-I progressive hybrid censoring scheme. J. Stat. Comput. Simul. 2015, 85, 339–356. [Google Scholar] [CrossRef]
- Brilliantov, N.V.; Pöschel, T. Deviation from Maxwell distribution in granular gases with constant restitution coefficient. Phys. Rev. E 2000, 61, 2809–2812. [Google Scholar] [CrossRef]
- Mohsin, S.; Kazmi, A.; Aslam, M.; Ali, S. On the Bayesian Estimation for two Component Mixture of Maxwell Distribution, Assuming Type I Censored Data. Int. J. Appl. Sci. Technol. 2012, 2, 197–218. Available online: http://www.ijastnet.com/journals/Vol_2_No_1_January_2012/23.pdf (accessed on 11 March 2020).
- Krishna, H.; Pundir, P. Discrete maxwell distribution. InterStat. J. 2007, 2007, 1–15. Available online: http://interstat.statjournals.net/YEAR/2007/articles/0711003.pdf (accessed on 2 January 2020).
- Mohsin, S.; Kazmi, A.; Aslam, M.; Ali, S. A Note on the Maximum Likelihood Estimators for the Mixture of Maxwell Distributions Using Type-I Censored Scheme. Open Stat. Probab. J. 2011, 3, 31–35. Available online: https://benthamopen.com/contents/pdf/TOSPJ/TOSPJ-3-31.pdf (accessed on 4 February 2020). [CrossRef]
- Hossain, M.P.; Omar, M.H.; Riaz, M. Estimation of mixture Maxwell parameters and its possible industrial application. Comput. Ind. Eng. 2017, 107, 264–275. [Google Scholar] [CrossRef]
- Karlis, D.; Santourian, A. Model-based clustering with non-elliptically contoured distributions. Stat. Comput. 2008, 19, 73–83. [Google Scholar] [CrossRef]
- Singh, K.L.; Srivastava, R.S. Inverse Maxwell Distribution as a Survival Model, Genesis and Parameter Estimation. Res. J. Math. Stat. Sci. 2014, 2, 23–28. [Google Scholar]
- Singh, K.L.; Srivastava, R.S. Estimation of the Parameter in the Size-Biased Inverse Maxwell Distribution. Int. J. Stat. Math. 2014, 10, 52–55. [Google Scholar]
- Singh, K.L.; Srivastava, R.S. Bayesian Estimation of Parameter of Inverse Maxwell Distribution via Size-Biased Sampling. Int. J. Sci. Res. 2014, 3, 1835–1839. [Google Scholar]
- Loganathan, A.; Chelvi, S.M.; Uma, M. Bayes Estimation of Parameter in Inverse Maxwell Distribution under Weighted Quadratic Loss Function. Int. J. Sci. Res. Math. Stat. Sci. 2017, 4, 13–16. [Google Scholar] [CrossRef]
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: https://www.itl.nist.gov/div898/handbook/ (accessed on 4 April 2020).
- Montgomery, D.C. Introduction to Statistical Quality Control, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Woodall, W.H. Controversies and Contradictions in Statistical Process Control. J. Qual. Technol. 2000, 32, 341–350. [Google Scholar] [CrossRef]
- Roberts, S.W. Control Chart Tests Based on Geometric Moving Averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Hossain, M.P.; Omar, M.H.; Riaz, M. New V control chart for the Maxwell distribution. J. Stat. Comput. Simul. 2017, 87, 594–606. [Google Scholar] [CrossRef]
- Hossain, M.P.; Sanusi, R.A.; Omar, M.H.; Riaz, M. On designing Maxwell CUSUM control chart: An efficient way to monitor failure rates in boring processes. Int. J. Adv. Manuf. Technol. 2018, 100, 1923–1930. [Google Scholar] [CrossRef]
- Zhang, C.W.; Xie, M.; Liu, J.Y.; Goh, T.N. A control chart for the Gamma distribution as a model of time between events. Int. J. Prod. Res. 2007, 45, 5649–5666. [Google Scholar] [CrossRef]
- Raza, M.; Raza, S.M.M.; Butt, M.M.; Siddiqi, A.F. Shewhart Control Charts for Rayleigh Distribution in the Presence of Type I Censored Data. J. ISOSS 2016, 2, 210–217. [Google Scholar]
- Raza, S.M.M.; Ali, S.; Butt, M.M. DEWMA control charts for censored data using Rayleigh lifetimes. Qual. Reliab. Eng. Int. 2018, 34, 1675–1684. [Google Scholar] [CrossRef]
- Huang, W.-H.; Yeh, A.B.; Wang, H. A control chart for the lognormal standard deviation. Qual. Technol. Quant. Manag. 2017, 15, 1–36. [Google Scholar] [CrossRef]
- Arafat, S.Y.; Hossain, M.P.; Ajadi, J.O.; Riaz, M. On the Development of EWMA Control Chart for Inverse Maxwell Distribution. J. Test. Eval. 2019, 49. [Google Scholar] [CrossRef]
- Tomer, S.K.; Panwar, M.S. A Review on Inverse Maxwell Distribution with Its Statistical Properties and Applications. J. Stat. Theory Pr. 2020, 14, 1–25. [Google Scholar] [CrossRef]
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models from Data to Decisions, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Derya, K.O.; Canan, H. Control charts for skewed distributions: Weibull, gamma, and lognormal. Metod. Zv. 2012, 9, 95–106. [Google Scholar]
- Chami, P.; Antoine, R.; Sahai, A. On Efficient Confidence Intervals for the Log-Normal Mean. J. Appl. Sci. 2007, 7, 1790–1794. [Google Scholar] [CrossRef][Green Version]
- Huang, W.-H.; Wang, H.; Yeh, A.B. Control Charts for the Lognormal Mean. Qual. Reliab. Eng. Int. 2015, 32, 1407–1416. [Google Scholar] [CrossRef]
- Joffe, A.D.; Sichel, H.S. A Chart for Sequentially Testing Observed Arithmetic Means from Lognormal Populations against a Given Standard. Technometrics 1968, 1, 605–612. [Google Scholar] [CrossRef]
- Abbasi, S.A.; Riaz, M.; Miller, A.; Ahmad, S.; Nazir, H.Z. EWMA Dispersion Control Charts for Normal and Non-normal Processes. Qual. Reliab. Eng. Int. 2015, 31, 1691–1704. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; Wiley-Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Modi, K.; Gill, V. Length-biased Weighted Maxwell Distribution. Pak. J. Stat. Oper. Res. 2015, 11, 465. [Google Scholar] [CrossRef][Green Version]
- Mathew, J.; Chesneau, C. Marshall–Olkin Length-Biased Maxwell Distribution and Its Applications. Math. Comput. Appl. 2020, 25, 65. [Google Scholar] [CrossRef]
| Sample Size (n) | ||||||
|---|---|---|---|---|---|---|
| 0.005 | 0.0027 | 0.002 | ||||
| 1 | 0.0150 | 4.7734 | 0.0099 | 5.0294 | 0.0081 | 5.4221 |
| 2 | 0.0878 | 3.3749 | 0.0706 | 3.6228 | 0.0635 | 3.7430 |
| 3 | 0.1611 | 2.8292 | 0.1380 | 3.0101 | 0.1280 | 3.0975 |
| 4 | 0.2218 | 2.5265 | 0.1959 | 2.6722 | 0.1845 | 2.7425 |
| 5 | 0.2713 | 2.3300 | 0.2442 | 2.4536 | 0.2322 | 2.5132 |
| 6 | 0.3124 | 2.1901 | 0.2848 | 2.2987 | 0.2725 | 2.3507 |
| 7 | 0.3471 | 2.0845 | 0.3194 | 2.1819 | 0.3070 | 2.2284 |
| 8 | 0.3768 | 2.0014 | 0.3493 | 2.0901 | 0.3369 | 2.1324 |
| 9 | 0.4027 | 1.9338 | 0.3753 | 2.0156 | 0.3630 | 2.0546 |
| 10 | 0.4254 | 1.8777 | 0.3984 | 1.9538 | 0.3862 | 1.9901 |
| Sample Size | |||
|---|---|---|---|
| 0.005 | 0.0027 | 0.002 | |
| 2 | 0.3379 | 0.2706 | 0.2432 |
| 3 | 0.8675 | 0.7394 | 0.6851 |
| 4 | 1.5369 | 1.3517 | 1.2715 |
| 5 | 2.3004 | 2.0623 | 1.9579 |
| 6 | 3.1324 | 2.8450 | 2.7180 |
| 7 | 4.0168 | 3.6833 | 3.5351 |
| 8 | 4.9431 | 4.5661 | 4.3979 |
| 9 | 5.9038 | 5.4856 | 5.2984 |
| 10 | 6.8934 | 6.4360 | 6.2307 |
| Sample Size (n) | False Alarm Rate (α) | |||||
|---|---|---|---|---|---|---|
| 0.005 | 0.0027 | 0.002 | ||||
| W1 | W2 | W1 | W2 | W1 | W2 | |
| 2 | 0.8049 | 1.1951 | 0.8438 | 1.1562 | 0.8596 | 1.1404 |
| 3 | 0.5911 | 1.4089 | 0.6514 | 1.3486 | 0.6770 | 1.3229 |
| 4 | 0.3726 | 1.6274 | 0.4482 | 1.5518 | 0.4809 | 1.5191 |
| 5 | 0.1600 | 1.8400 | 0.2470 | 1.7531 | 0.2851 | 1.7149 |
| 6 | 0.0000 | 2.0441 | 0.0518 | 1.9483 | 0.0939 | 1.9060 |
| 7 | 0.0000 | 2.2396 | 0.0000 | 2.1367 | 0.0000 | 2.0909 |
| 8 | 0.0000 | 2.4270 | 0.0000 | 2.3181 | 0.0000 | 2.2696 |
| 9 | 0.0000 | 2.6068 | 0.0000 | 2.4930 | 0.0000 | 2.4420 |
| 10 | 0.0000 | 2.7799 | 0.0000 | 2.6618 | 0.0000 | 2.6087 |
| 1 | 3 | 6 | 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | ||||||||||||
| 1.00 | 370.14 | 371.53 | 258 | 370.55 | 369.10 | 258 | 369.29 | 368.13 | 257 | 369.85 | 369.25 | 254 |
| 1.25 | 146.15 | 145.07 | 101 | 96.07 | 93.96 | 67 | 60.40 | 60.34 | 42 | 39.37 | 39.16 | 27 |
| 1.50 | 62.37 | 61.33 | 44 | 28.76 | 28.25 | 20 | 14.47 | 14.01 | 10 | 8.16 | 7.70 | 6 |
| 1.75 | 32.32 | 31.69 | 23 | 12.73 | 12.13 | 9 | 6.04 | 5.52 | 4 | 3.31 | 2.69 | 2 |
| 2.00 | 19.95 | 19.29 | 14 | 7.37 | 6.79 | 5 | 3.36 | 2.83 | 2 | 2.02 | 1.45 | 1 |
| 2.25 | 13.44 | 13.01 | 9 | 4.71 | 4.12 | 3 | 2.33 | 1.77 | 2 | 1.48 | 0.84 | 1 |
| 2.50 | 9.96 | 9.41 | 7 | 3.47 | 2.94 | 3 | 1.82 | 1.23 | 1 | 1.26 | 0.58 | 1 |
| 2.75 | 7.80 | 7.23 | 6 | 2.77 | 2.17 | 2 | 1.52 | 0.90 | 1 | 1.14 | 0.39 | 1 |
| 3 | 6.39 | 5.99 | 5 | 2.31 | 1.72 | 2 | 1.35 | 0.68 | 1 | 1.08 | 0.29 | 1 |
| 5 | 2.70 | 2.15 | 2 | 1.26 | 0.57 | 1 | 1.03 | 0.17 | 1 | 1.00 | 0.02 | 1 |
| 1 | 3 | 6 | 10 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 41 | 106 | 258 | 514 | 1089 | 41 | 107 | 258 | 513 | 855 | 39 | 105 | 257 | 517 | 841 | 39 | 106 | 254 | 514 | 853 |
| 1.25 | 17 | 42 | 101 | 202 | 433 | 11 | 28 | 67 | 134 | 221 | 7 | 18 | 42 | 84 | 138 | 4 | 12 | 27 | 54 | 91 |
| 1.50 | 7 | 19 | 44 | 86 | 184 | 4 | 9 | 20 | 39 | 65 | 2 | 4 | 10 | 20 | 33 | 1 | 3 | 6 | 11 | 18 |
| 1.75 | 4 | 10 | 23 | 44 | 95 | 2 | 4 | 9 | 17 | 28 | 1 | 2 | 4 | 8 | 13 | 1 | 1 | 2 | 4 | 7 |
| 2.00 | 2 | 6 | 14 | 28 | 58 | 1 | 2 | 5 | 10 | 16 | 1 | 1 | 2 | 4 | 7 | 1 | 1 | 1 | 3 | 4 |
| 2.25 | 2 | 4 | 9 | 18 | 39 | 1 | 2 | 3 | 6 | 10 | 1 | 1 | 2 | 3 | 5 | 1 | 1 | 1 | 2 | 3 |
| 2.50 | 2 | 3 | 7 | 14 | 29 | 1 | 1 | 3 | 5 | 7 | 1 | 1 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | 2 |
| 2.75 | 1 | 3 | 6 | 11 | 23 | 1 | 1 | 2 | 4 | 6 | 1 | 1 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | 2 |
| 3.00 | 1 | 2 | 5 | 8 | 18 | 1 | 1 | 2 | 3 | 5 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
| 5 | 1 | 1 | 2 | 3 | 7 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Average Run Length | ||
|---|---|---|
| Lognormal S-Chart | ||
| 1 | 368.39 | 370.34 |
| 1.50 | 17.72 | 53.92 |
| 2.00 | 4.12 | 24.34 |
| 2.50 | 2.11 | 14.15 |
| 3.00 | 1.52 | 10.71 |
| 3.50 | 1.28 | 8.79 |
| 4.00 | 1.16 | 7.99 |
| Sample Number | Observations | ||||||
|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | |
| 1 | 22.2 | 23.0 | 24.0 | 28.6 | 21.8 | 17.0 | 26.0 |
| 2 | 23.2 | 18.9 | 21.9 | 27.3 | 13.8 | 24.0 | 20.1 |
| 3 | 15.7 | 26.8 | 27.9 | 15.3 | 28.8 | 16.0 | 23.6 |
| 4 | 53.8 | 21.7 | 28.8 | 17.0 | 16.5 | 15.7 | 28.0 |
| 5 | 13.3 | 16.5 | 24.2 | 17.6 | 27.8 | 18.3 | 17.7 |
| 6 | 20.0 | 13.2 | 16.9 | 14.9 | 15.5 | 7.0 | 15.8 |
| 7 | 15.0 | 38.3 | 11.2 | 38.2 | 26.7 | 17.1 | 29.0 |
| 8 | 18.3 | 18.4 | 18.2 | 15.9 | 16.4 | 23.6 | 19.2 |
| 9 | 23.3 | 20.4 | 20.9 | 28.5 | 23.2 | 17.9 | 46.1 |
| 10 | 39.3 | 11.8 | 17.7 | 30.9 | 22.4 | 45.0 | 18.2 |
| 11 | 30.2 | 21.8 | 18.2 | 23.0 | 27.2 | 10.9 | 25.5 |
| 12 | 12.4 | 39.9 | 17.7 | 26.3 | 14.1 | 21.0 | 11.2 |
| 13 | 10.8 | 25.7 | 32.4 | 13.6 | 19.1 | 16.1 | 53.3 |
| 14 | 57.3 | 36.5 | 19.7 | 20.8 | 30.8 | 20.0 | 39.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omar, M.H.; Arafat, S.Y.; Hossain, M.P.; Riaz, M. Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process. Symmetry 2021, 13, 189. https://doi.org/10.3390/sym13020189
Omar MH, Arafat SY, Hossain MP, Riaz M. Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process. Symmetry. 2021; 13(2):189. https://doi.org/10.3390/sym13020189
Chicago/Turabian StyleOmar, M. Hafidz, Sheikh Y. Arafat, M. Pear Hossain, and Muhammad Riaz. 2021. "Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process" Symmetry 13, no. 2: 189. https://doi.org/10.3390/sym13020189
APA StyleOmar, M. H., Arafat, S. Y., Hossain, M. P., & Riaz, M. (2021). Inverse Maxwell Distribution and Statistical Process Control: An Efficient Approach for Monitoring Positively Skewed Process. Symmetry, 13(2), 189. https://doi.org/10.3390/sym13020189






