Applying GMEI-GAN to Generate Meaningful Encrypted Images in Reversible Data Hiding Techniques

Abstract

With the rapid development of information technology, the transmission of information has become convenient. In order to prevent the leakage of information, information security should be valued. Therefore, the data hiding technique has become a popular solution. The reversible data hiding technique (RDH) in particular uses symmetric encoding and decoding algorithms to embed the data into the cover carrier. Not only can the secret data be transmitted without being detected and retrieved completely, but the cover carrier also can be recovered without distortion. Moreover, the encryption technique can protect the carrier and the hidden data. However, the encrypted carrier is a form of ciphertext, which has a strong probability to attract the attention of potential attackers. Thus, this paper uses the generative adversarial networks (GAN) to generate meaningful encrypted images for RDH. A four-stage network architecture is designed for the experiment, including the hiding network, the encryption/decryption network, the extractor, and the recovery network. In the hiding network, the secret data are embedded into the cover image through residual learning. In the encryption/decryption network, the cover image is encrypted into a meaningful image, called the marked image, through GMEI-GAN, and then the marked image is restored to the decrypted image via the same architecture. In the extractor, 100% of the secret data are extracted through the residual learning framework, same as the hiding network. Lastly, in the recovery network, the cover image is reconstructed with the decrypted image and the retrieved secret data through the convolutional neural network. The experimental results show that using the PSNR/SSIM as the criteria, the stego image reaches 45.09 dB/0.9936 and the marked image achieves 38.57 dB/0.9654. The proposed method not only increases the embedding capacity but also maintains high image quality in the stego images and marked images.

1. Introduction

With the booming development of information technology, people can easily transmit and receive information on the Internet. Although the transmission of information over the Internet has brought about a fast and convenient life for us, it has also given rise to concern about information security. Therefore, the issue of information security has been under the spotlight recently. The data hiding technique (DH) is the solution to the above problems. DH [1] uses multimedia as a cover carrier to hide secret data directly in the cover carrier for transmission to implement secure information transmission. The data hiding techniques can be divided into irreversible (IRD) and reversible (RDH) [2]. Reversible data hiding (RDH) techniques [3,4,5,6,7,8,9] not only ensure the secure transmission of information but also restore the hidden secret data and use the multimedia as a cover carrier. The framework of reversible data hiding is shown in Figure 1.

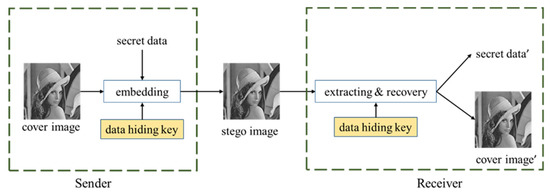
Figure 1. Reversible data hiding framework.

In the traditional RDH methods, the most common hiding techniques fall within three categories: lossless compression [3,4], difference expansion (DE) [5,6], and histogram shifting [7,8]. The lossless compression technique obtains partial space through compressing the image and uses partial space to embed the data. The performance of this method depends on the lossless compression algorithm and the selection of images. Tian (2003) [5] proposed the DE method, which calculates the difference between pixel values, expands the difference value by two times, and then embeds the secret data into the difference value. Thodi et al. (2004) [6] proposed the prediction error expansion (PEE) method, which calculates the different values between pixel and predicted values and then embeds the secret data into the different values. Ni et al. (2006) [7] proposed histogram shifting, using a statistical method to generate a histogram of the pixel values. In the histogram, the place with the highest number of the pixel values is called peak point, whereas the place with the lowest number of the pixel values is called zero point. The shift direction is determined by the relative positions of the peak point and zero point. After shifting, the secret data are embedded in the pixel values.

In RDH, images are encrypted to enhance confidentiality [10,11,12,13,14]. There are two categories of encryption: VRAE (Vacating Room After Encryption) [10,11] and RRBE (Reserving Room Before Encryption) [12,13], as shown in Figure 2. Zhang et al. (2011) [10] proposed the VRAE framework, which uses the partial spatial correlation of the original image to embed data; however, the low spatial correlation of the original image leads to the limited embedding capacity, and some algorithms are irreversible and inseparable. Ma et al. (2013) [13] proposed the RRBE method, which reserves the room based on the pixel correlation of the original image, encrypts the image, and then embeds the secret data into the reserving room. RRBE uses the complete pixel correlation of the original image, which improves the embedding capacity of VRAE and makes it achieve RDH easier. Zhang et al. [14] (2016) proposed a framework, Reversible Image Transformation (RIT), different from the previous two frameworks. One image is encrypted into another plaintext image by block pairing and block transformation, and then the encrypted image is embedded with secret data through algorithms. This method solves the problem that most of the encrypted images are in the form of ciphertext and implements reversible data hiding techniques.

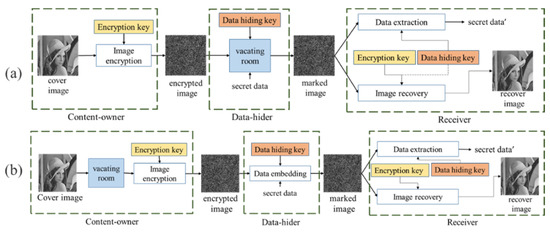
Figure 2. (a) VRAE and (b) RRBE framework.

Reversible data hiding in encrypted images (RDH-EI) improves the confidentiality of secret information and the security of transmission, which achieves an effect of double protection. It can be used in the fields which consider security necessary, such as medical and military information transmission. However, the encrypted carrier is a form of ciphertext, which has a strong probability to attract the attention of potential attackers. The attacker’s method is mainly to use the symmetry of encoder and decoder to find pixels with hidden data. Thus, to deal with the issue of symmetry of encoder and decoder in RDH-EI, an asymmetric scheme is desired. In other words, the principle of the encoder should be different from that of the decoder. Besides, as shown in Figure 2, we can find that both marked images produced by VRAE and RRBE frameworks are meaningless, i.e., the images look like a noise image. This kind of image will inevitably make the attackers realize that there may be information hidden in it.

In recent years, with the rapid development of artificial intelligence (AI) and machine learning, computers can not only solve complex computational problems through algorithms but also learn image features through a large amount of data. Since the convolutional neural network (CNN) is designed for feature extraction from image, a huge number of works [15,16,17,18,19,20] utilize the CNN for dealing with the problem of image processing. Besides, the generative adversarial network (GAN) [21] is designed for generating meaningful data and inherently can produce encoder and decoder by different principles. Therefore, the proposed method implements RDH based on CNN and to generate the meaningful encrypted image using the GAN, which makes the secret data have double protection. To summarize, the contributions of the proposed method are as follows:

(1)

Hiding the secret message into the cover image by using residual block [22], so that the secret information is distributed in the cover image and cannot be discovered.

(2)

Using GMEI-GAN to encrypt the stego image into another meaningful image, so that secret messages have double protection.

(3)

In extractor, the network of last layer uses the Sigmoid activation function to extract the secret message completely.

(4)

In the recovery network, using fully extracted secret message and decrypted image as input, the network does not use pooling and dropout, so that the marked image can be recovered to the cover image.

2. Related Works

As mentioned earlier, most digital image steganography [23,24] utilizes conventional image processing techniques so that the principle of the encoder is the same as that of the decoder. For example, Sahu et al. [23] proposed a multi-directional pixel value differencing and modulus function (MDPVDMF), in which the original image is partitioned into various blocks having 2 × 2 pixels. Meanwhile, three directions of a 2 × 2 pixel block are exploited to identify the optimal direction in terms of embedding capacity and imperceptibility. The pixel value differencing strategy is used to identify the embedding capacity of each block. Then, pixel readjustment strategy based on modulus function is applied to achieve better imperceptibility. Such a pixel-wise strategy makes it hard to produce a meaningful stego image. As a result, we focus on the deep-learning-based method which can produce a meaningful stego image.

2.1. Generative Reversible Data Hiding by Image to Image Translation via GANs

Zhang et al. [25] proposed a generative reversible data hiding technique (GRDH) based on multiple GAN models, which differs from the previous RDH model. The cover image in this paper was generated by noise vector through the deep convolutional generative adversarial network (DCGAN) [26], in which the noise vector was mapped from secret data. Therefore, the cover image would directly contain the secret data. Then, the cover image was transformed into the marked image through CycleGAN [27]. During the recovery, a new extractor was trained to extract the secret data, which means the data hiding framework is reversible. The proposed GRDH was demonstrated to be feasible through the experiment. Figure 3 shows the flowchart of GRDH, divided into three stages for training in the following paragraphs.

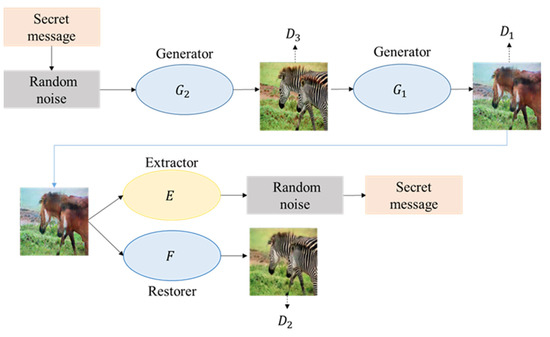
Figure 3. GRDH flowchart.

The first stage is the training of CycleGAN, which consists of two symmetric GAN models. The two GAN models share two generators, and each GAN model contains a discriminator, so there are two generators and discriminators in a CycleGAN model. In this phase, CycleGAN is used to train a generator that generates marked images and a restorer F that generates recovered images. As displayed in Figure 4, the cover images and marked images are regarded as two different collections. Images in each collection must be the same type, such as zebra and horse, and the transformation of the two images is achieved by two generators.

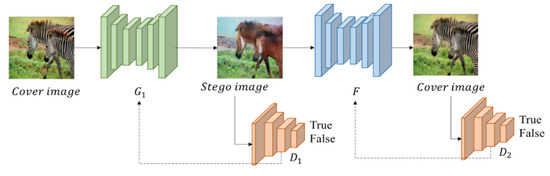
Figure 4. First phase: CycleGAN training.

The second stage is the training of DCGAN. The purpose is to train the generator to generate the cover image from the noise vector, and the secret data will be mapped to the noise vector in advance, so that the secret data will be hidden in the cover image in this stage. DCGAN uses the convolutional neural network to design the generator and the discriminator, and the powerful feature extraction ability of the convolutional neural network enhances the learning ability of the GAN for images. Therefore, in this stage, the generator and the discriminator are trained against each other, so that the cover image generated by the noise is more like the real image in the dataset. Figure 5 shows the training framework of DCGAN.

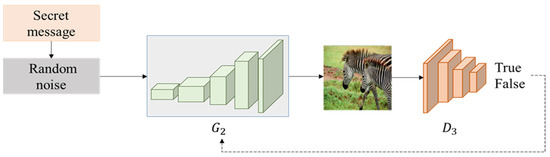
Figure 5. Second phase: DCGAN training.

The third stage is the training of the extractor, based on CNN, and a new extractor, E, is trained. The goal is to extract the noise vector from the marked image before it is considered to achieve reversible data hiding with integrity. The extractor architecture is composed of four convolutional layers and one fully connected layer, and each layer applies activation function Leaky ReLU and batch normalization (BN) [28]; the architecture is illustrated in Figure 6.

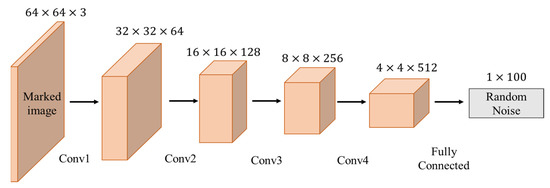
Figure 6. Third phase: extractor architecture.

After training, the output is the same size as the noise vector, and the extractor training loss function is defined as follows:

$$\mathrm{L}\left(\mathrm{E}\right)={\displaystyle \sum }_{i=1}^n{\left(z_i-E\left(G_1\left(G_2\left(z_i\right)\right)\right)\right)}^2$$

(1)

The extractor is trained to be close to the input noise using the loss function. Then, the secret data are converted back to the secret data by the same mapping method, which divides the secret data into several groups, and each group contains $\mathrm{k}$ bits. For instance, when $\mathrm{k}=3$, $\left\{001100010\right\}$ is divided into $\left\{001\right\}, \left\{100\right\}, \left\{010\right\}$, then each group is mapped to a given interval of noise vector $\mathrm{r}$ according to the following equation.

$$r=random\left(\frac{m}{2^{k-1}}-1+\delta ,\frac{m+1}{2^{k-1}}-1-\delta \right)$$

(2)

where $m$ denotes the decimal value of the mapping group, and $\delta$ indicates the interval between delimitations, e.g., $\mathrm{k}=3, \mathrm{and} \mathsf{\delta }=0.001$, mapping every 3 secret bits into a noise vector with values between $\left[-1, 1\right]$. By this method of transformation, each group of secret data can be mapped to a certain interval of noise vector values, so there is a deviation tolerance to ensure the correct rate of secret data retrieval.

Zhang et al. [25] trained different GAN models for image transformation in CycleGAN, similar to image encryption and decryption in RDH. The secret data were mapped to the noise vector to generate the image by DCGAN so that the secret data were embedded into the image. Finally, the extractor was trained to extract the secret data and recover the cover image. The authors used deep learning to implement reversible data hiding.

2.2. Hiding Images in Plain Sight: Deep Steganography

Baluja [29] proposed the image steganography based on CNN to hide the color image as secret data and started the technique of hiding RGB image with an image. The author implemented the steganography in three networks, respectively: the Prep Network, the Hiding Network, and the Reveal Network, as shown in Figure 7. In each network, the image is processed by different sizes of the kernel to obtain the feature map with different features.

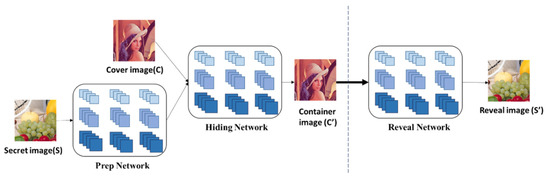
Figure 7. The flowchart of [29].

In the Prep Network, there are two important purposes. The first is that if the secret image is smaller than the cover image, the Prep Network will gradually increase the size of the secret image to the same size as the cover image and distribute the secret image over the pixels of the entire cover image. The second purpose is to transform the color-based pixels into more useful features, such as edges. In the Prep Network, 50 feature maps are generated by using various sizes of kernels, 3 × 3, 4 × 4, and 5 × 5, and then 150 feature maps are combined as the output of the secret image.

In the Hiding Network, 150 secret image feature maps and the cover image are channel-wise, 153 feature maps are combined as input, and an image with a secret image inside is generated by using various size of kernels, 3 × 3, 4 × 4, and 5 × 5. The generated image is called a container image, which must be as close to the cover image as possible. The container image with a secret image inside is generated through the Hiding Network.

In the Reveal Network, as a decoder, the network architecture is to generate a reveal image using various sizes of kernels, 3 × 3, 4 × 4, 5 × 5, through this network. The cover image will be removed from the container image, and the generated image is called reveal image. The main purpose of this network is to make the reveal image similar to the secret image.

In these three networks, a loss function is designed to reduce the error with the following equation:

$$\mathrm{L}\left(\mathrm{c}, \mathrm{c}{}^{\prime },\mathrm{s},\mathrm{s}{}^{\prime }\right)=\left|\left|\mathrm{c}- \mathrm{c}{}^{\prime }\left|\left|+\mathsf{\beta }\right|\right|\mathrm{s}- \mathrm{s}{}^{\prime }\right|\right|$$

(3)

where $\mathrm{c}$ is the cover image, $s$ is the secret image, $\mathrm{c}{}^{\prime }$ is the container image, $\mathrm{s}{}^{\prime }$ is the reveal image, and β is the hyper-parameter for reconstruction error. The author designed these three networks with loss functions to take advantage of the deep network and used CNN to hide the image into the image for the first time, creating the first image steganography with the concept of image hiding image.

2.3. Reversible Image Steganography Scheme Based on a U-Net Structure

Duan et al. [30] proposed image steganography based on the U-Net structure derived from deep steganography [29], which implements image steganography through CNN instead of the traditional way of modifying LSB. The proposed network [30] is divided into two parts, which are hiding network (encoder) and extraction network (decoder), and its network architecture is shown in Figure 8.

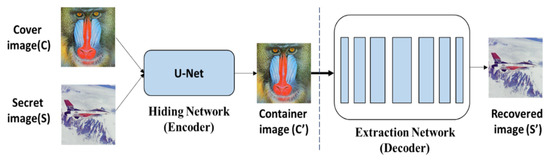
Figure 8. The flowchart of [30].

In the hiding network, the U-Net architecture is used to encode the secret image as the cover image, and then the cover image and the secret image are combined into a six-channel tensor as the input for the hiding network, and the network architecture is shown in Figure 9.

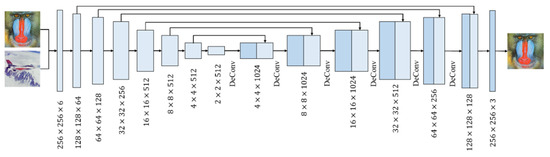
Figure 9. Hiding network of [30].

The hiding network is divided into a compression phase and an extension phase. The compression phase is a typical CNN, which aims to compress the secret image so that it is distributed over all available bits on the cover image. In the compression phase, seven convolutional operations are performed with a kernel size of 4 × 4, and Leaky-ReLU activation and BN are used after each convolution to speed up the network training. Finally, a feature map with a size of 2 × 2 and a number of 512 feature channels is received. In the expansion phase, the deconvolutional layer is employed to upscale the feature map, and the feature map from the compression phase is cascaded with the feature map from the deconvolution layer, aiming to learn the feature maps of different layers. After seven times of deconvolutional operations are processed with a kernel size of 4 × 4, and ReLU activation and BN are used after each deconvolution, the final output, a stego image, containing secret data, is generated.

In the extraction network, the architecture is shown in Figure 10. The authors adopted CNN with the purpose of recovering the secret image from the stego image. To make the secret image recover the data accurately from the hiding network, the authors designed six convolutional layers and each kernel size as 3 × 3. Each convolutional layer is followed by ReLU activation function and BN without using the pooling layer and dropout. In the last layer, the reconstructed secret image is the output using activation function sigmoid.

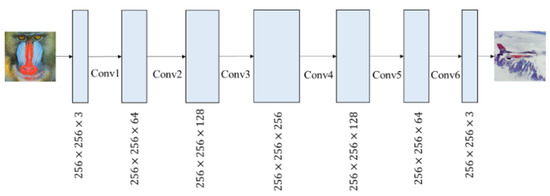
Figure 10. Extraction network of [30].

In order to minimize the loss of container images, cover images, secret images, and recovered images, the mean squared error (MSE) was used as the loss function below:

$$L\left(\mathsf{\theta }\right)=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{i=1}^n{\left|\left|F^j\left(Y;\theta \right)-X_j\right|\right|}^2 ,$$

(4)

where $\theta =\left\{w_i,b_i\right\}$ is the parameter for continuous adjustment of the back propagation,$F^j\left(Y;\theta \right)$ is the generated image, $X_j$ is the real image, and $\mathrm{n}$ is the number of training samples. The network training is performed by Equation (5).

$$L\left(\mathrm{c}, \mathrm{c}{}^{\prime },\mathrm{s},\mathrm{s}{}^{\prime }\right)=\left|\left|\mathrm{c}- \mathrm{c}{}^{\prime }\left|\left|+\mathsf{\alpha }\right|\right|\mathrm{s}- \mathrm{s}{}^{\prime }\right|\right| ,$$

(5)

where $\mathrm{c} \mathrm{and} \mathrm{s}$ are the cover and secret images, respectively; $\mathrm{c}{}^{\prime }$ is the container image; s′ is the recovered image; and α is the weight hyper-parameters. $\left|\left|\mathrm{c}- \mathrm{c}{}^{\prime }\right|\right|$ and $\left|\left|\mathrm{s}- \mathrm{s}{}^{\prime }\right|\right|$ are the losses of the hiding network and the extraction network, respectively. The authors based on the U-net network architecture proposed the method of image steganography and deduced the loss function enabling the method to have obvious advantages in visual effect and steganography ability.

Based on the above important related works, we can observe that existing works focus on either embedding a secret image into a cover image or hiding an encrypted secret message in a cover image. Therefore, we can realize that existing works only address the problem of reversible data hiding in cover images instead of encrypted images. As a result, the secret is at risk of being leaked while the extractor is intercepted by attackers. Accordingly, our proposal highlights the applications of CNN, residual networks, and GAN for secret data hiding, image encryption and decryption, secret data extraction, and image recovery. We hope to achieve the goal of reversible data hiding by hiding a large amount of secret data, generating the encrypted image with good image quality, extracting the secret data, and recovering the image completely.

3. Proposed Method

The purpose of the proposed method is to generate meaningful encrypted images and implement reversible data hiding techniques. Therefore, this study proposes an RDH scheme based on deep learning. The scheme consists of four networks, namely, the hiding network, the encryption/decryption network, the extractor, and the recovery network. The hiding network is responsible for hiding the secret message into the cover image to generate the stego image. The encryption/decryption network is responsible for transforming the cover image into the marked image (encryption) and from the marked image back to the cover image (decryption). The extractor is responsible for extracting the secret message from the marked image, and the recovery network is responsible for recovering the cover image from the decrypted image and the extracted secret message. The flowchart of the proposed method is shown in Figure 11. In this section, the structure and the method for each network are introduced in Section 3.1, Section 3.2, Section 3.3, Section 3.4, respectively.

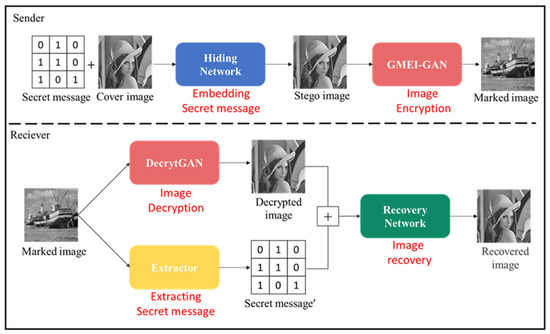
Figure 11. Flowchart of the proposed method.

3.1. Hiding Network

In the hiding network, the input is the secret message and the cover image, and the secret message needs to be preprocessed. The amount of secret message in this paper is based on the length and width of the cover image (e.g., if the size of the cover image is $512\times 512$, then the amount of secret message hiding is $n\times 512\times 512$, where n is the number of channels) and then the secret message is transformed from vector to matrix and combined with the cover image in a channel-wise way. The size of $\left(n+1\right)\times 512\times 512$ is used as the input for the network. The purpose of the hiding network is to hide secret message in the cover image, to find a suitable location in the cover image for hiding, and to minimize the difference between the generated cover image and the marked image. The hiding network architecture is shown in Figure 12, and the number of layers of the network structure is shown in Table 1.

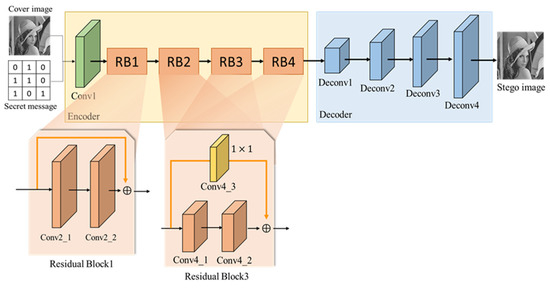
Figure 12. Hiding network architecture.

Table 1. Hiding network structure.

Layers	Filter Size/Stride, Padding	Output Size	Activation Function
Conv1	3 × 3/2,1	32 × 256 × 256	Relu
Conv2_1	3 × 3/1,1	32 × 256 × 256	Relu
Conv2_2	3 × 3/1,1	32 × 256 × 256	Relu
Conv3_1	3 × 3/2,1	64 × 128 × 128	Relu
Conv3_2	3 × 3/1,1	64 × 128 × 128	Relu
Conv3_3	1 × 1/2,0	64 × 128 × 128	-
Conv4_1	3 × 3/2,1	128 × 64 × 64	Relu
Conv4_2	3 × 3/1,1	128 × 64 × 64	Relu
Conv4_3	1 × 1/2,0	128 × 64 × 64	-
Conv5_1	3 × 3/2,1	256 × 32 × 32	Relu
Conv5_2	3 × 3/1,1	256 × 32 × 32	Relu
Conv5_3	1 × 1/2,0	256 × 32 × 32	-
Deconv1	4 × 4/2,1	128 × 64 × 64	Relu
Deconv2	4 × 4/2,1	64 × 128 × 128	Relu
Deconv3	4 × 4/2,1	32 × 256 × 256	Relu
Deconv4	4 × 4/2,1	1 × 512 × 512	Relu

The network architecture can be divided into two parts, encoder and decoder. In the encoder, the concept of residual learning is mainly used to learn more complex features. Since a single-layer residual block cannot enhance the learning effect, the residual block usually needs to be designed with more than two layers of convolution layers. Therefore, this study designed one residual block for every two convolutional layers and each residual block for skip connection, so that the output of each residual block contained the output of the previous residual block. It is worth noting that because the output feature maps of residual blocks had different sizes, a convolution layer was added before each skip connection to make the feature maps have the same size, and the residual block calculation is shown in Figure 13.

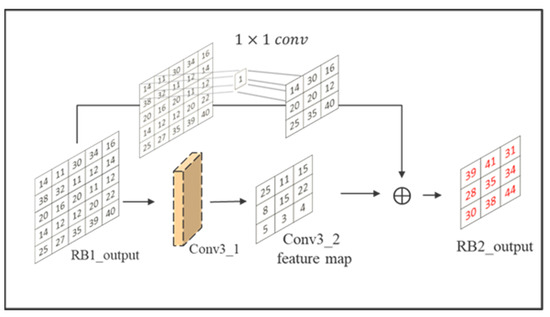
Figure 13. Calculation of residual block.

In the encoder, there is one convolutional layer with a kernel size of $3\times 3$, three convolutional layers with a kernel size of $1\times 1$, four residual blocks, and two convolutional layers with a kernel size of $3\times 3$ in each residual block. The purpose of the first convolutional layer is to extract the features from the input to obtain the features that combine the secret message and the cover image. The purpose of the $1\times 1$ convolutional layers is to allow the residual blocks to output the same feature maps to skip connections. The purpose of the residual blocks is to obtain the features and the original input.

These feature maps are used as input into the residual block. BN and activation function ReLU are added after each convolutional layer in the residual block. BN rescales the data distribution in the batch after each convolution according to the set batch size, so that the output of each layer is normalized to a distribution with $\mathrm{mean}=0$ and $\mathrm{variance}=1$, which can increase the generalization ability and accelerate the training speed to make the model have a better learning rate. The ReLU function outputs 0 for input values smaller than zero and outputs the input values for input values larger than zero. By enhancing the nonlinear simulation capability of the model through activation functions, it can better integrate the secret message with the details of the cover image.

In the decoder, there are four deconvolutional layers. BN and ReLU function are added after each deconvolution layer because the image size is reduced by the convolutional operation in the encoder. Therefore, in the decoder, deconvolution is used for up-sampling so as to restore the image to the original image size, and finally the stego image is output. The process of deconvolution is shown in Figure 14, where the input feature map is scaled up according to the stride size, then the padding is complemented, and finally the convolution is performed to output the feature map of the deconvolutional layer.

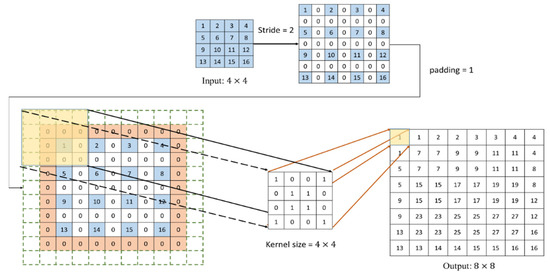
Figure 14. Deconvolutional operation.

During the training process, the secret message and the cover image are combined as input. After the encoder training, the compressed feature map is obtained. For the decoder training, the compressed feature map is used as the input, and the output image is the same size as the cover image, called stego image.

In order to minimize the difference between the stego image and the cover image, the loss function, Mean Absolute Error (MAE), is used, which can better reflect the real situation of the predicted value and the error. Its formula is expressed in Equation (6).

$$\mathrm{MAE}=\frac{1}{M\times N}{\displaystyle \sum }_i^M{\displaystyle \sum }_j^N\left|\left|C_{i,j}-S_{i,j}\right|\right|$$

(6)

where $C$ is a cover image and $S$ is a stego image; $M$ is the weight of image and N is the length of image.

3.2. Encryption and Decryption Networks

After hiding network, the stego image is obtained. In order to prevent the stego image from being easily detected in the process of data transmission, GMEI-GAN (generate meaningful encrypted images by GAN) is proposed in the encryption network, so that the stego image can generate a meaningful image, called marked image. Moreover, in the decryption network, the marked image can be restored by DecryptGAN. The architecture is displayed in Figure 15. These two GANs have the same architecture. The structure of GMEI-GAN is presented in Table 2 and Table 3.

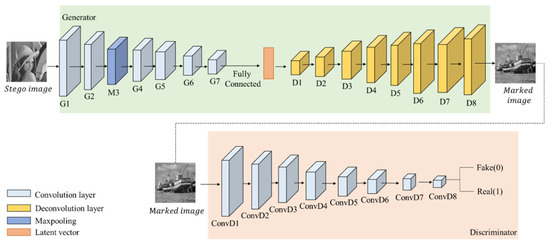
Figure 15. GMEI-GAN architecture.

Table 2. GMEI-GAN-Generator structure.

Layers	Filter Size/Stride, Padding	Output Size	Activation Function
G1	4 × 4/2,1	16 × 256 × 256	Leaky ReLU
G2	4 × 4/2,1	32 × 128 × 128	Leaky ReLU
M3	4 × 4/2,0	32 × 64 × 64	-
G4	4 × 4/2,1	64 × 32 × 32	Leaky ReLU
G5	4 × 4/2,1	128 × 16 × 16	Leaky ReLU
G6	4 × 4/2,1	256 × 8 × 8	Leaky ReLU
G7	4 × 4/2,1	512 × 4 × 4	Leaky ReLU
Fully Connected	-	128	-
D1	4 × 4/1,0	512 × 4 × 4	Leaky ReLU
D2	4 × 4/2,1	256 × 8 × 8	Leaky ReLU
D3	4 × 4/2,1	128 × 16 × 16	Leaky ReLU
D4	4 × 4/2,1	64 × 32 × 32	Leaky ReLU
D5	4 × 4/2,1	32 × 64 × 64	Leaky ReLU
D6	4 × 4/2,1	16 × 128 × 128	Leaky ReLU
D7	4 × 4/2,1	8 × 256 × 256	Leaky ReLU
D8	4 × 4/2,1	1 × 512 × 512	Leaky ReLU

Table 3. GMEI-GAN-Discriminator structure.

Layers	Filter Size/Stride, Padding	Output Size	Activation Function
ConvD1	4 × 4/2,1	16 × 256 × 256	Leaky ReLU
ConvD2	4 × 4/2,1	32 × 128 × 128	Leaky ReLU
ConvD3	4 × 4/2,1	64 × 64 × 64	Leaky ReLU
ConvD4	4 × 4/2,1	128 × 32 × 32	Leaky ReLU
ConvD5	4 × 4/2,1	256 × 16 × 16	Leaky ReLU
ConvD6	4 × 4/2,1	512 × 8 × 8	Leaky ReLU
ConvD7	4 × 4/2,1	512 × 4 × 4	Leaky ReLU
ConvD8	4 × 4/1,0	1 × 1 × 1	Sigmoid

In GMEI-GAN, the generator built is based on the encoder and decoder, using six convolutional layers, eight deconvolutional layers, one max pooling layer, and one fully connected layer. In the encoder, the feature maps are extracted through the convolutional layer, and the dimensions are compressed to reduce the model computation. The final output of the encoder is $4\times 4\times 512$, which is compressed into a $1\times 128$ latent vector by the fully connected layer. In the decoder, the latent vector is used as the input, and the feature vector of the low-dimensional space is converted to the high-dimensional space by deconvolution. The image returns to its initial size, and the output image is called the marked image.

The discriminator uses eight convolutional layers and adds BN and activation function LeakyReLU after each convolutional layer. The difference from ReLU is that LeakyReLU gives a non-zero gradient to negative values. Therefore, the gradient to negative values can be calculated and increases the nonlinear capability.

The sigmoid function is used in the last level of the activation function. Since the sigmoid outputs a value between 0 and 1, it can be used as a discriminator to evaluate whether the image is real (close to 1) or fake (close to 0). The calculation of the discriminator uses the sigmoid function as last layer is shown in Figure 16.

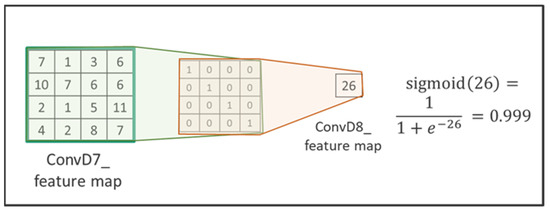
Figure 16. The calculation of Sigmoid function used in the discriminator.

In the training process, the stego image is the input of the generator, the encrypted image is considered as the training target of the generator, and the output is the marked image. MAE is used as the loss function for the purpose of minimizing the difference between the marked image and the encrypted image.

In addition, the aim of the generator is that the generated image can deceive the discriminator to be considered a real image. As for the discriminator, it aims to discriminate the real image from the generated image. The weights for the generator and discriminator models can be adjusted. During the training process, the generator and the discriminator back-propagate the loss function to implement weight updates repeatedly. The loss function of GAN is defined as:

$$\underset{G}{\min } \underset{D}{\max }V\left(G,D\right)={\mathrm{E}}_{x~P_{data}\left(x\right)}\log \left(D\left(x\right)\right)+{\mathrm{E}}_{z~p_z\left(z\right)}\log \left(1-D\left(G\left(z\right)\right)\right)$$

(7)

where G is the generator and D is the discriminator. When the real image is the input of the discriminator, the discriminator needs to maximize the value of the item and determine its closeness to 1. When the image is trained by the generator and the generated image is a fake image, it is the item that the discriminator wants to minimize and determine its closeness to 0. In addition, the generator wants to deceive the discriminator to make its output value as close to 1 as possible. Therefore, the best way is to find a balanced state by updating the parameters of the discriminator and the generator through the loss function.

Although the architecture of DecryptGAN is the same as GMEI-GAN, its input is the marked image and its output is the decrypted image, which is different from GMEI-GAN. In an ideal state, the decrypted image is the same as the cover image. However, in reality, the decrypted image contains a secret message which has not been extracted yet. If the receiver does not know the extraction key, then the secret message cannot be taken out. As a result, the marked image can only be decrypted. In this way, the purpose of protecting the secret message is achieved.

Through GMEI-GAN and DecryptGAN, the images are transformed. The image transformation adopts the encryption and decryption techniques in the RDH, so that the secret message and the cover image have better protection, and the encrypted image is a meaningful image instead of a ciphertext.

3.3. Extractor

To extract the secret message from the marked image, the extractor is having specific architecture, as shown in Figure 17. The network structure is illustrated in Table 4. The extractor consists of an encoder, a decoder, one convolution layer with a kernel size of $3\times 3$, three convolutional layers with a kernel size of $1\times 1$, four residual blocks, and two convolutional layers with a kernel size of $3\times 3$ in each residual block. ReLU and BN are added after each convolutional layer. The purpose of the encoder is to obtain the features of the secret message and compress them into a vector as the output of the encoder. As for the decoder, it is composed of five deconvolutional layers, and ReLU and BN are added after each convolutional layer to increase the non-linear emulation capability.

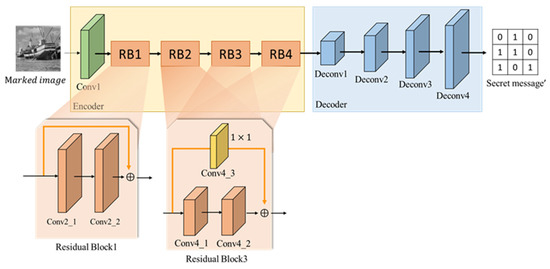
Figure 17. Extractor architecture.

Table 4. Extractor structure.

Layers	Filter Size/Stride, Padding	Output Size	Activation Function
Conv1	3 × 3/2,1	32 × 256 × 256	ReLU
Conv2_1	3 × 3/1,1	32 × 256 × 256	ReLU
Conv2_2	3 × 3/1,1	32 × 256 × 256	ReLU
Conv3_1	3 × 3/2,1	64 × 128 × 128	ReLU
Conv3_2	3 × 3/1,1	64 × 128 × 128	ReLU
Conv3_3	1 × 1/2,0	64 × 128 × 128	-
Conv4_1	3 × 3/2,1	128 × 64 × 64	ReLU
Conv4_2	3 × 3/1,1	128 × 64 × 64	ReLU
Conv4_3	1 × 1/2,0	128 × 64 × 64	-
Conv5_1	3 × 3/2,1	256 × 32 × 32	ReLU
Conv5_2	3 × 3/1,1	256 × 32 × 32	ReLU
Conv5_3	1 × 1/2,0	256 × 32 × 32	-
DeConv1	4 × 4/2,1	128 × 64 × 64	ReLU
DeConv2	4 × 4/2,1	64 × 128 × 128	ReLU
DeConv3	4 × 4/2,1	32 × 256 × 256	ReLU
DeConv4	4 × 4/2,1	16 × 512 × 512	ReLU
DeConv5	3 × 3/1,1	1 × 512 × 512	Sigmoid

Here, the secret message can be any kinds of digital data including text, image, or voice. Before we embed the secret message into the cover image, we transform the message as a binary code, i.e., the secret message consists of 0 and 1. Since the secret message consists of all 0 or 1, the output value of sigmoid is between 0 and 1. Sigmoid is used for the last layer of the activation function, and a threshold value less than 0.5 is set as 0 and greater than 0.5 as 1, as shown in Figure 18. In the training process, the decrypted image is used as the input into the extractor. A vector of the same size as the secret message is obtained from the extractor training. MAE is used as the loss function. The extractor can extract the secret message completely through the proposed network and loss function.

Figure 18. The calculation of Sigmoid function in secret message’.

3.4. Recovery Network

In the recovery network, the recovered image is restored by extracting secret message and decrypted image. Its architecture is shown in Figure 19, and its structure is listed in Table 5.

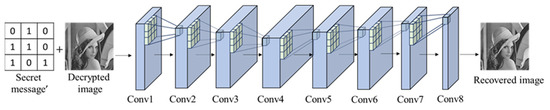
Figure 19. Recovery network architecture.

Table 5. Recovery network structure.

Layers	Filter Size/Stride, Padding	Output Size	Activation Function
Conv1	3 × 3/1,1	32 × 512 × 512	ReLU
Conv2	3 × 3/1,1	64 × 512 × 512	ReLU
Conv3	3 × 3/1,1	128 × 512 × 512	ReLU
Conv4	3 × 3/1,1	256 × 512 × 512	ReLU
Conv5	3 × 3/1,1	128 × 512 × 512	ReLU
Conv6	3 × 3/1,1	64 × 512 × 512	ReLU
Conv7	3 × 3/1,1	32 × 512 × 512	ReLU
Conv8	3 × 3/1,1	1 × 512 × 512	Sigmoid

To prevent the image from being compressed and distorted, there are no pooling layers and dropout operations in the recovery network. In the recovery network, there are eight convolutional layers with a kernel size of $3\times 3$, the padding is set to 1 for each layer, and the stride is set to 1. Furthermore, the feature map obtained from each convolution is the same size as the original image. ReLU and BN are added after each convolutional layer to increase the non-linear emulation capability, and the sigmoid function is added in the last layer. In the recovery network, MAE is used as a loss function to minimize the loss between recovered image and cover image.

4. Experimental Results

This section presents the experimental results. For training the hiding network, we produce all possible secret messages as the training message as training for the secret message set. Please note that the secret message can be any kinds of digital data including text, image, or voice. Before we embed the secret message into the cover image, we transform the message into a binary code, i.e., the secret message consists of 0 and 1. Since the size of secret message is the same as that of cover image, the number of all possible secret messages is 2^k, where k indicates the size of cover image. The training set is 12,000 normalized images from the VOC2012 dataset [31].

The training details of the encryption/decryption networks are listed as follows: batch size equals to 2, learning rate equals to 0.001, and the optimizer is “Adam.” The training set is 12,000 normalized images from VOC2012 dataset with size $256\times 256$ in grayscale and trained with the noised images with random noises. Here, the benchmark dataset VOC2012 is utilized for evaluation of image authentication and recovery. Although the images in the VOC2012 dataset are color images, our proposal can be performed on both color and grayscale images. Since processing color pictures is much harder than processing grayscale images, we transform VOC2012 images into grayscale for convenience. As a result, we can use an insufficient number of images with 0.1 noised ratio for training our model.

In this study, the common evaluation metrics Peak Signal-to-Noise Ratio (PSNR) [32] and structural similarity (SSIM) [33] were used to measure the difference between the stego images and the original images as well as the image quality of the marked images. BPP is adopted as a standard for embedding capacity. BCR is used as a criterion for extracting secret message integrity.

PSNR evaluates image quality by calculating the error between corresponding pixels in dB. A greater PSNR value represents lower image distortion, which can be calculated by Equation (8).

$$\begin{gathered} \mathrm{PSNR}=10\log \left(\frac{MA{X}^2}{MSE}\right) \\ MSE=\frac{1}{M\times N}{\displaystyle \sum }_{i=0}^M{\displaystyle \sum }_{j=0}^N{\left(y_{i,j}-{\widehat{y}}_{i,j}\right)}^2, \end{gathered}$$

(8)

where MAX is the maximum value of the image pixel. Since it is an 8-bit grayscale image, MAX = 255. $\mathrm{y} \mathrm{and} \hat{\mathrm{y}}$ represent the pixel values of two images. M and N represent the length and width of the images.

SSIM measures image similarity through brightness, contrast, and structure. The SSIM value ranges from 0 to 1, whose closeness to 1 means less distortion, which can be calculated by Equation (9).

$$\begin{gathered} \mathrm{L}\left(X,Y\right)=\frac{2u_X{u}_Y+C_1}{u_X^2+u_Y^2+C_1} \\ C\left(X,Y\right)=\frac{2{\sigma }_X{\sigma }_Y+C_2}{{\sigma }_X^2+{\sigma }_Y^2+C_2} \\ S\left(X,Y\right)=\frac{{\mathsf{\sigma }}_{XY}+C_3}{{\mathsf{\sigma }}_X{\mathsf{\sigma }}_Y+C_3} \\ \mathrm{SSIM}\left(X,Y\right)=\mathrm{L}\left(X,Y\right)\times \mathrm{C}\left(X,Y\right)\times \mathrm{S}\left(X,Y\right), \end{gathered}$$

(9)

where $x$ and $y$ are the two images to be compared,$u_X$ and $u_Y$ are the mean of x and y, ${\mathsf{\sigma }}_X{ \mathrm{and} \mathsf{\sigma }}_Y$ are the standard deviations of x and y, ${\mathsf{\sigma }}_{XY}$ is the covariance of x and y, and $C_1$, $C_2$, and $C_3$ are constants which are to keep the denominator from being zero. Usually,$C_1={\left(K_1\times \mathrm{L}\right)}^2$, $C_2={\left(K_2\times \mathrm{L}\right)}^2, \mathrm{and} C_3=C_2/2$ generally set $K_1=0.01,K_2=0.03, \mathrm{and} L=255$. The structural similarity metric defines structural information from the corner of image composition as a combination of three different independent factors, including luminance, contrast, and structure. The mean value is used as an estimate of luminance, the standard deviation as an estimate of contrast, and the covariance as a measure of structural similarity.

BPP is an evaluation of embedding capacity, as shown in Equation (10).

$$\mathrm{BPP}=\frac{number of secret message bits}{image size}$$

(10)

BCR is an evaluation of secret message integrity, as defined in Equation (11), where $\mathrm{C}$ is the number of correct secret message bits, and T is the number of secret messages. $\mathrm{BCR}=100\%$ means that the secret message is extracted completely and correctly.

$$\mathrm{BCR} =\frac{\mathrm{C}}{T}\times 100\%$$

(11)

This section shows the experimental results of the proposed method which used six grayscale images, including Airplane (F-16), Boat, Baboon, Barbara, Lena, and Peppers, as exhibited in Figure 20.

Figure 20. Experimental images.

In Section 4.1, the results of the four-network training experiment are presented, including stego images, marked images, decrypted images, and the comparison of PSNR and SSIM. In Section 4.2, the results of this paper are compared with the above related works.

4.1. Experimental Results of the Proposed Method

We set the initial learning rate as 0.001, the optimizer as Adam, and the number of epochs as 10,000 in these four networks.

4.1.1. Stego Image Quality and Embedding Capacity in Hiding Network

In the hiding network, the length of the secret message is set as $n\times 512\times 512$, where n is the number of embedded BPP and $512\times 512$ is the image size. Figure 21 shows the cover images, the stego images, and their histograms. It can be found that it is hard to find the difference between the cover image and the stego image through eyes. According to the histograms, the overall trend of the high- and low-frequency information of the image remains almost unchanged, and there is no big pixel error.

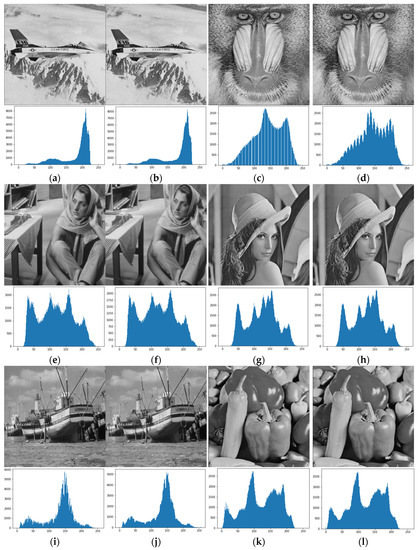
Figure 21. (a,c,e,g,i,k) are cover images and their histograms. (b,d,f,h,j,l) are stego images and their histograms.

Table 6 shows that the embedding capacity of the proposed method can reach 3 BPP, and the image quality is above 40 dB. Generally speaking, the higher the embedding capacity is, the worse the image quality is. Nevertheless, the experimental results prove that in some images, their high embedding capacity does not necessarily affect their image quality directly. In addition, SSIM has the best performance in 1 BPP. It is noted that the image quality is higher in smooth images (e.g., airplane) and is lower in images with more complex textures (e.g., baboon).

Table 6. PSNR (dB)/SSIM and embedding capacity (BPP) of the proposed scheme.

Image	1 BPP	2 BPP	3 BPP
Airplane	46.42/0.9952	45.82/0.9906	44.47/0.9889
Baboon	44.02/0.9929	44.25/0.9909	41.73/0.9836
Barbara	46.36/0.9951	45.21/0.9915	45.57/0.9920
Lena	46.78/0.9920	44.26/0.9841	44.48/0.9838
boat	45.85/0.9931	44.14/0.9883	44.94/0.9835
peppers	47.78/0.9937	46.78/0.9939	46.13/0.9880
Average	46.20/0.9936	44.80/0.9892	44.55/0.9865

4.1.2. Marked and Decrypted Image Quality in Encryption and Decryption Network

In the GMEI-GAN model, the input is the stego image, and the output is the marked image. In contrast, in the DecryptGAN model, the input is the marked image, and the output is the decrypted image. Figure 22 shows the stego image, marked image, and decrypted image. In Figure 22, (a) PSNR/SSIM of the marked image is 38.57/0.9654, and that of the decrypted image is 35.24/0.9625; (b) PSNR/SSIM of the marked image is 34.19/0.8730, and that of the decrypted image is 30.90/0.7750; (c) PSNR/SSIM of the marked image is 36.63/0.9202, and that of the decrypted image is 36.71/0.9187. Different from the traditional encrypted image, the encrypted image of this study is meaningful, which has the PSNR performance of 34 dB and above, while the decrypted image also has the image quality of 30 dB.

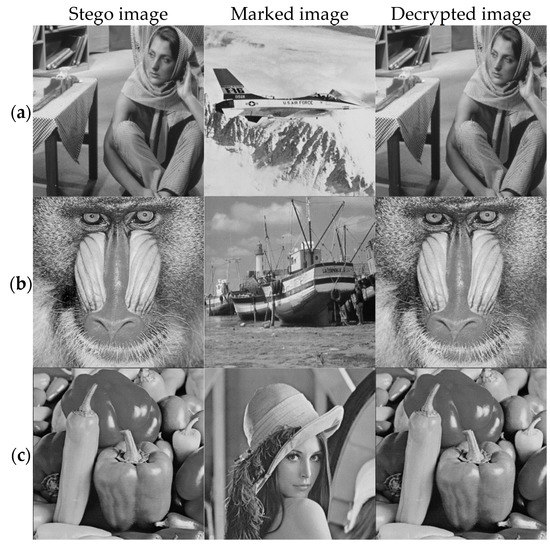
Figure 22. Results of GMEI-GAN and DecryptGAN. (a) shows the results that uses the Barbara image as cover image and the Airplane image as a marked image. (b) shows the results that uses the Baboon image as cover image and the Boat image as a marked image. (c) shows the results that uses the Peppers image as cover image and the Lena image as a marked image.

4.2. Performance Comparison of Experimental Results between the Proposed Method and Other Related Works

In this section, the proposed method is compared with the previously mentioned schemes. The comparison of stego image quality is shown in Table 7. Table 8 displays the comparison for the integrity of extracting the secret message. Six images were used to compare the related works with the proposed method separately.

Table 7. Comparison of PSNR (dB)/SSIM between the proposed method and the methods of Sahu et al. [23], Baluja [29], and Duan et al. [30] for capacity 1 BPP (image size).

Image	Sahu et al. [23]	Baluja [29]	Duan et al. [30]	Proposed Method
Airplane	40.05/0.9225	45.45/0.9974	38.95/0.9665	46.86/0.9970
Baboon	38.12/0.9835	52.62/0.9997	39.45/0.9815	45.57/0.9957
Peppers	39.94/0.9775	55.27/0.9992	41.28/0.9760	46.30/0.9925
Boat	39.56/0.9815	50.45/0.9986	40.33/0.9749	46.62/0.9942
Lena	40.57/0.9443	51.47/0.9981	39.52/0.9663	47.64/0.9963
Barbara	38.54/0.9415	45.34/0.9974	37.46/0.9513	47.20/0.9967
Average	39.46/0.9585	50.1/0.9984	39.50/0.9694	46.70/0.9954

Table 8. Comparison of the integrity of extracting secret message (BCR) between the proposed method and the methods of Sahu et al. [23], Baluja [29], and Duan et al. [30].

Image	Sahu et al. [23]	Baluja [29]	Duan et al. [30]	Proposed Method
Airplane	30.71%	3.57%	27.49%	100%
Baboon	29.47%	1.93%	26.06%	100%
Peppers	32.06%	2.01%	27.95%	100%
Boat	30.69%	2.83%	25.93%	100%
Lena	32.22%	2.74%	30.46%	100%
Barbara	31.78%	1.92%	29.43%	100%
Average	31.16%	2.5%	27.88%	100%

According to Table 7, the average PSNR/SSIM values of the stego images presented in the proposed method and the previous schemes of Sahu et al. [23], Baluja [29], and Duan et al. [30] are 46.7 dB/0.9954, 39.46 dB/0.9585, 50.1 dB/0.9984, and 39.50 dB/0.9694, respectively.

We can observe that Sahu et al.’s work [23] has the best image quality performance of the stego image, but its secret message extraction accuracy is only 31.16% in Table 8, which is useless in real-world application; Baluja’s work [29] has the second best image quality of the stego image, but the secret message extraction accuracy is only 2.55% in Table 8, which is almost irretrievable; the stego image quality of Duan et al. [30] is not satisfactory, while the secret message extraction accuracy is 27.88%. Compared to the above schemes of Baluja [29] and Duan et al. [30], the stego image quality of the proposed method maintains above 45 dB, and the secret message extraction accuracy is 100%.

For the encryption techniques, this study compared the traditional RDH-EI [14] and Sahu et al.’s work [23] with the proposed method. The comparison for PSNR/SSIM of the marked images is shown in Table 9, and the marked images are shown in Figure 23.

Table 9. Comparison of the PSNR/SSIM between the methods of Zhang [14], Sahu et al. [23], and the proposed method.

Marked Image	Zhang et al. [14]	Sahu et al. [23]	Proposed Method
Airplane	31.74/0.6564	40.05/0.9225	38.46/0.9641
Baboon	29.09/0.4191	38.12/0.9835	30.99/0.7853
Peppers	31.52/0.6106	39.94/0.9775	36.58/0.9152
Boat	30.78/0.5617	39.56/0.9815	34.58/0.8830
Lena	31.58/0.6073	40.57/0.9443	36.97/0.9275
Barbara	30.42/0.5520	38.54/0.9415	34.96/0.9181
Average	30.85/0.5678	39.46/0.9585	35.42/0.8988

Figure 23. The marked image of Zhang et al. [14], Sahu et al. [23], the proposed method, and the target image.

Table 9 indicates that the average PSNR/SSIM values of the marked images in the previous scheme of Zhang et al. [14] and the proposed method are 30.85 dB/0.5678 and 35.42 dB/0.8988, respectively. There is a significant difference between the two methods in PSNR/SSIM. Moreover, in Figure 23, the results show that Zhang et al. [14] have some blurred blocks in the images while the images of the proposed method are closer to the target images. Though Zhang et al. [14] distributed the blocks into the original image and the target image, performed block exchange by algorithm calculation, and transformed the blocks in the original image into the blocks in the target image, the SSIM of the output encrypted image was still less similar. In contrast, the proposed method adopted GMEI-GAN to help the original image learn the target image automatically through the weight update, so the SSIM/PSNR of the output encrypted image was higher.

5. Conclusions

The proposed method based on deep neural networks has had an excellent performance in the aspects of embedding rate, stego image quality, encrypted image quality, and secret message extraction rate compared to other related works. Because the traditional encrypted images are usually exhibited in the ciphertext form, GMEI-GAN was employed to encrypt the encrypted images into meaningful images. In addition, RDH requires zero distortion, so the sigmoid function was used to extract the output value between 0 and 1. The experiment has proved that the extracted secret message has zero error with the original secret message. In the recovery network, the completely extracted secret message was adopted as input to enhance the cover image recovery capability. Thus, the recovered image could be recovered with zero distortion after several iterations of training. Therefore, the proposed method not only implemented the RDH but also had great image quality in the encrypted images. Through the design of four networks, the sender could embed and transmit the secret message securely, and the receiver could extract the secret message and recover the image completely as well.

According to the experimental results, there is still improvement in the image quality of both the marked image generated by GMEI-GAN and the decrypted image decrypted by DecryptGAN. Since we are studying the effectiveness of GAN for encryption techniques in reversible data hiding techniques, the model architecture of the proposed method is relatively simple. In the recovery network, this paper uses the classical convolutional neural network without any pooling or dropout operation, which makes the network training time longer. Therefore, in future works, we can try to add new techniques to GAN, such as SA-GAN, which introduces self-attention to enhance the ability of GAN image generation and increase image quality. For the recovery network, a different network architecture is used to reduce the training time of the network.