SimBetaReg Web-Tool: The Easiest Way to Implement the Beta and Simplex Regression Models
Abstract
:1. Introduction
2. Regression Models
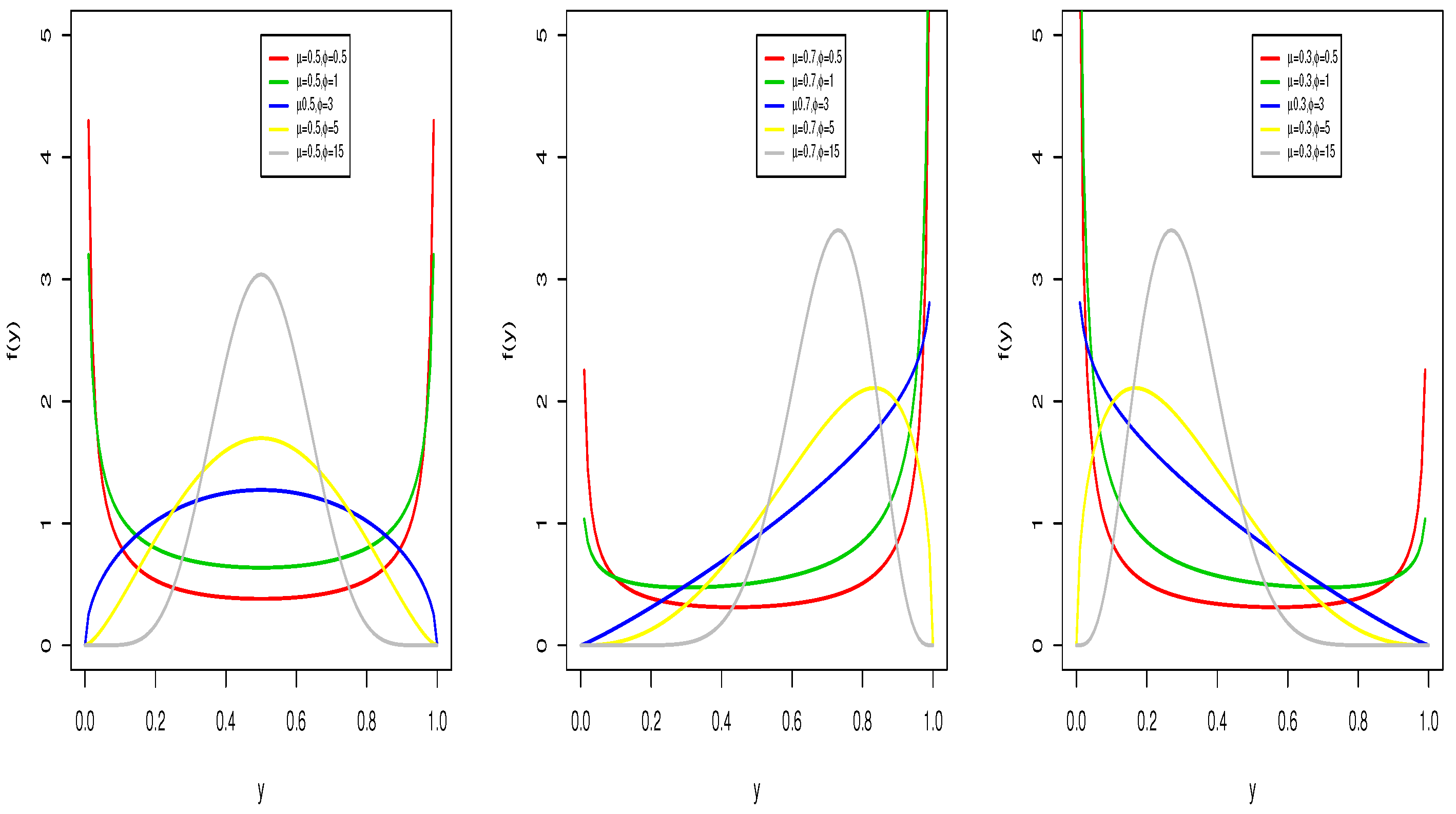
2.1. Beta Regression
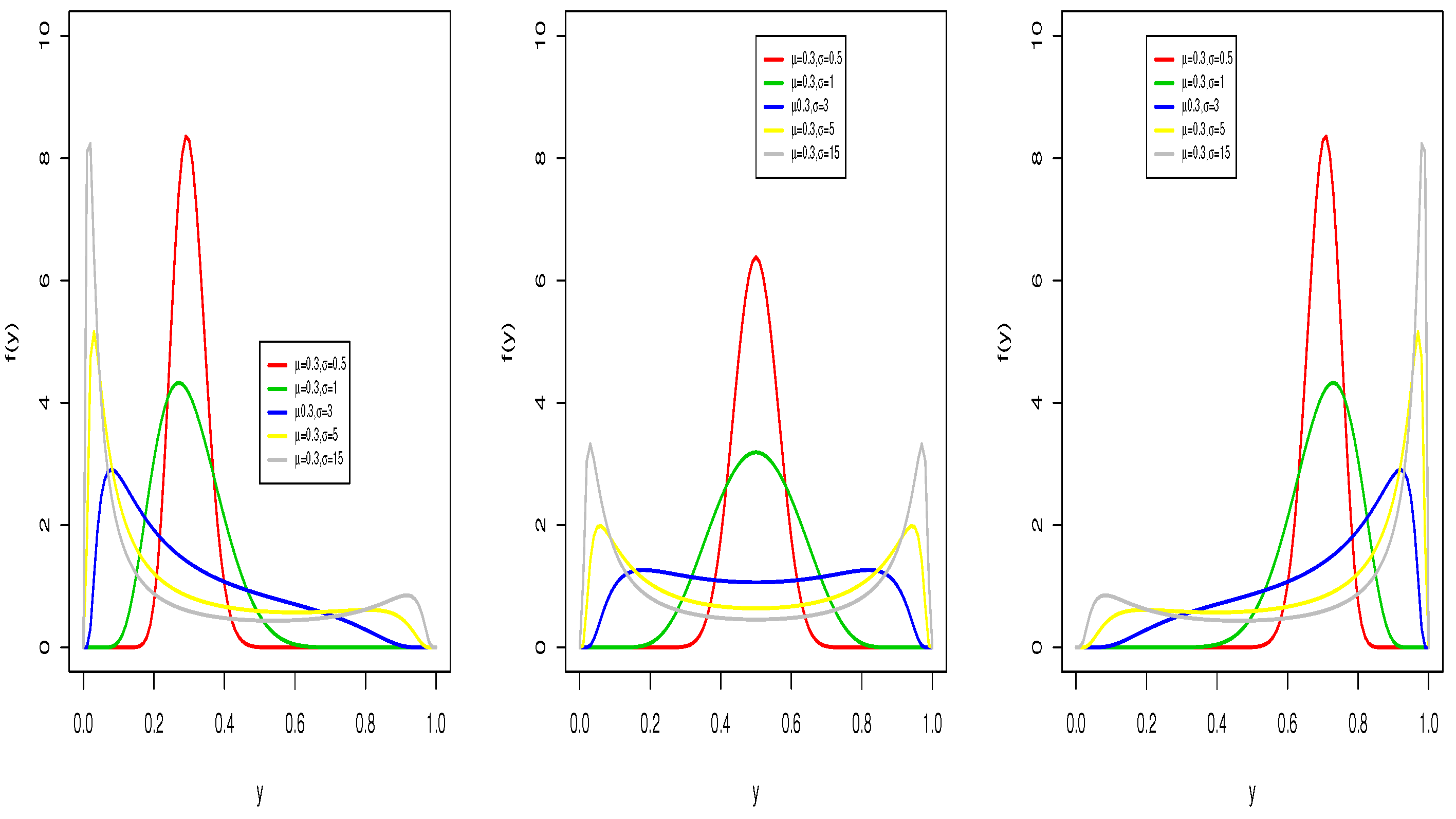
2.2. Simplex Regression
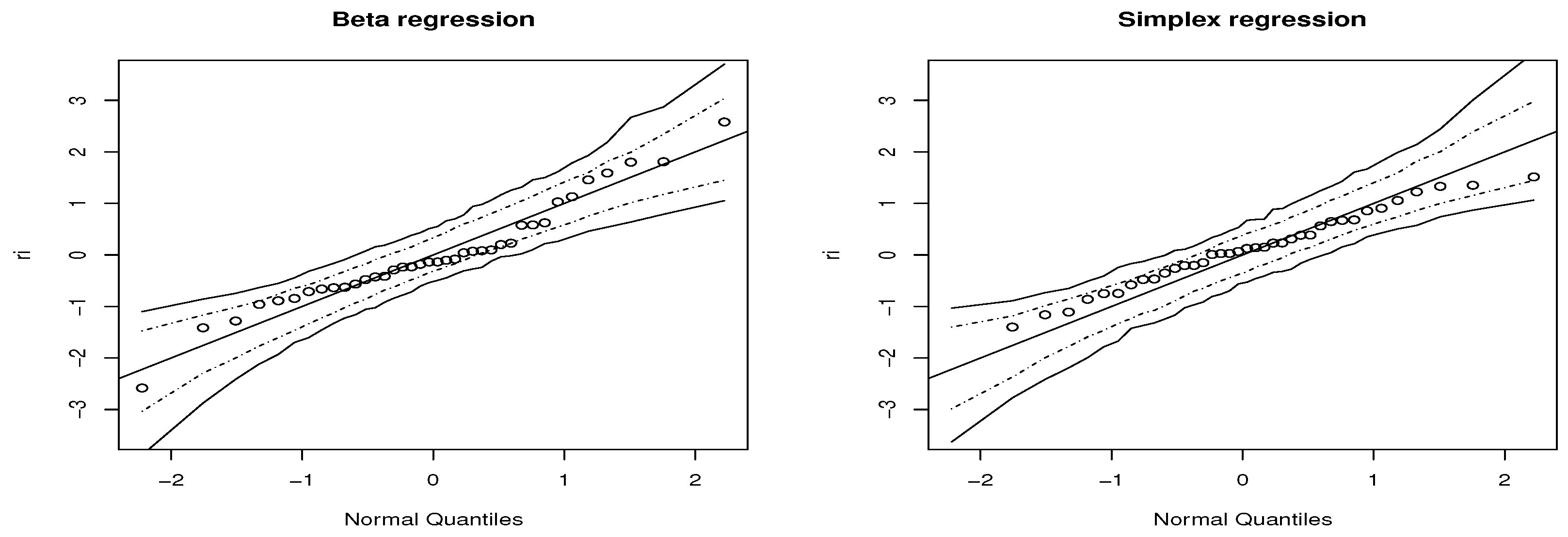
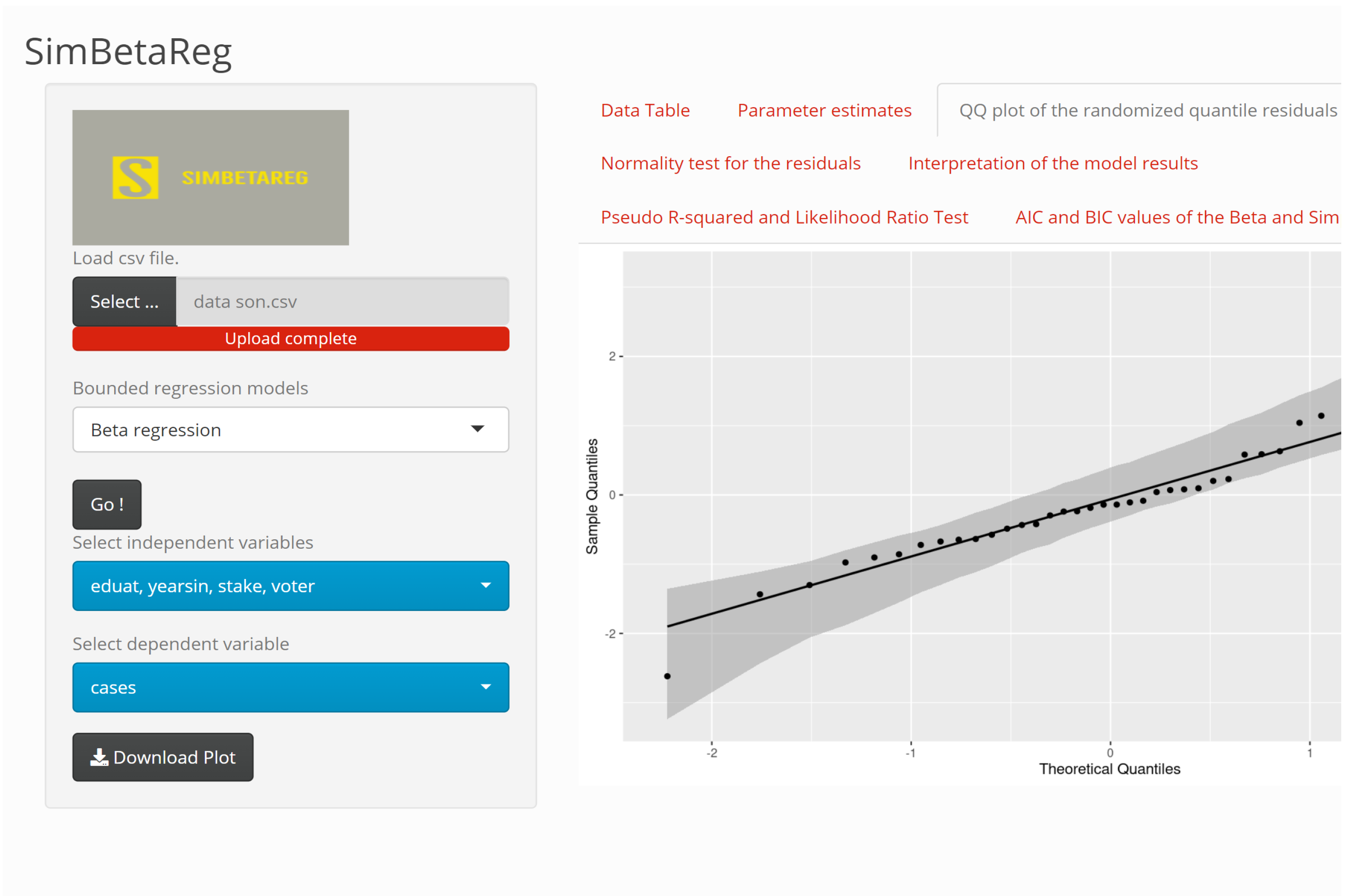
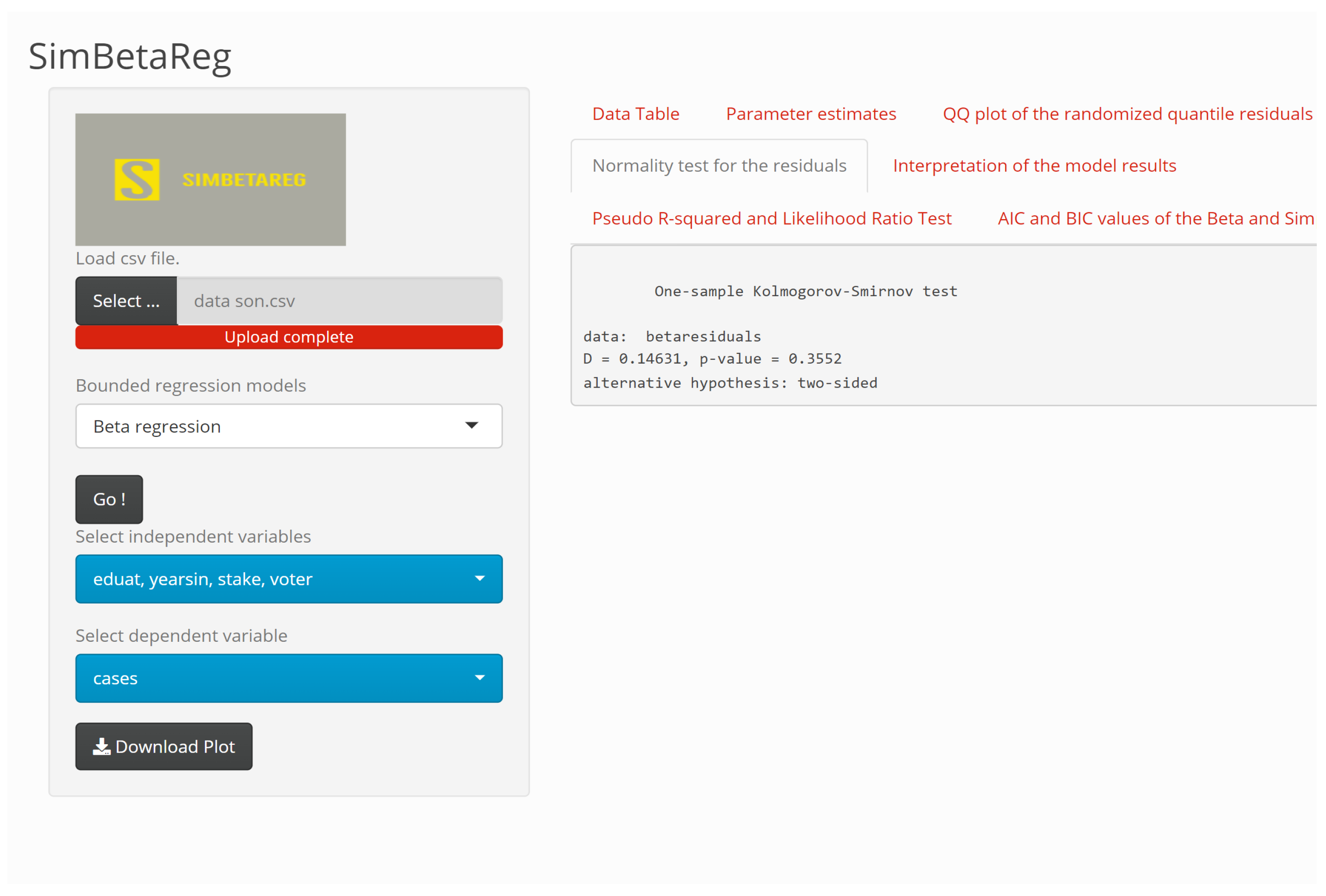
2.3. Randomized Quantile Residuals
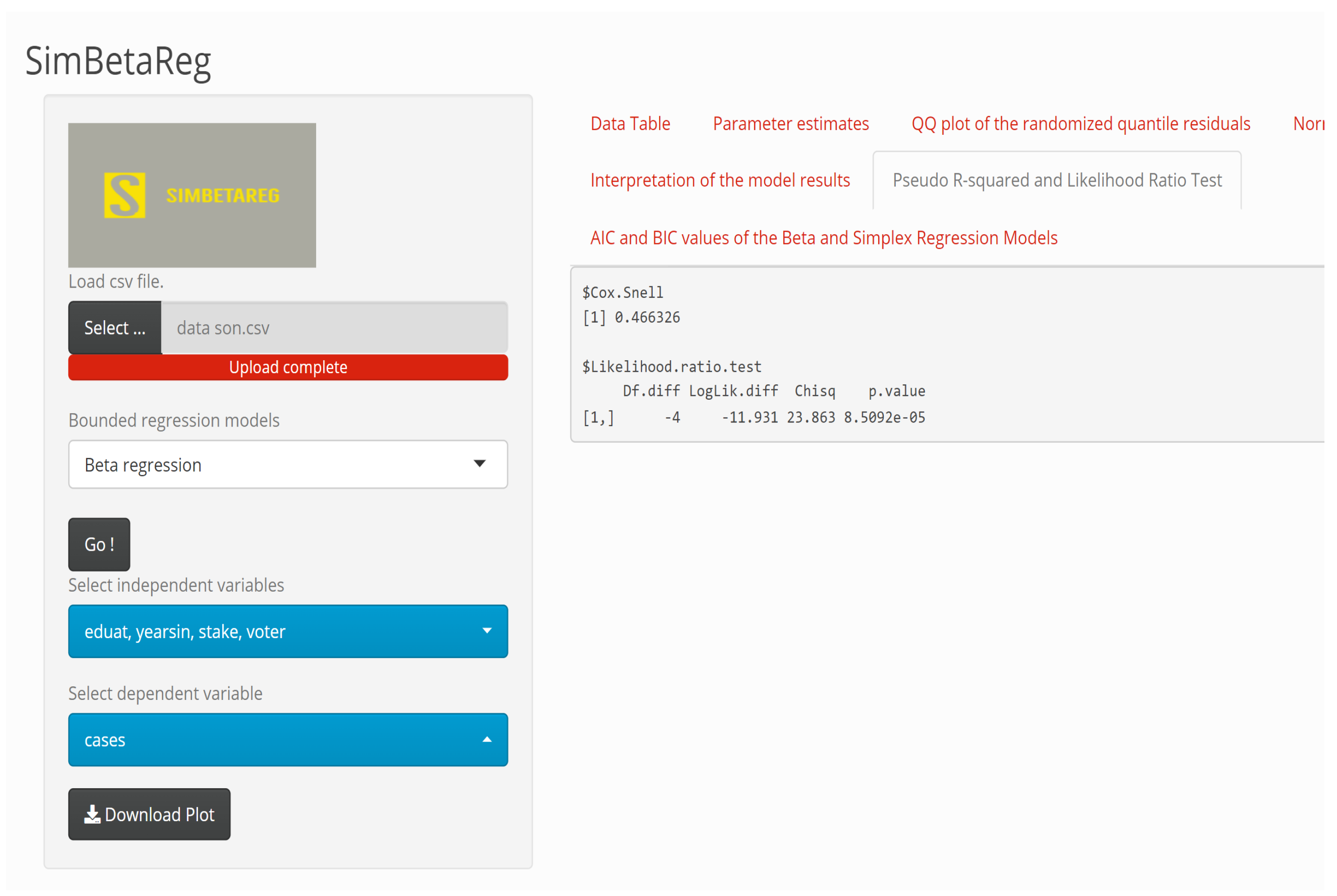
2.4. Model Comparison
3. Empirical Results
3.1. Data Set
3.2. Regression Results
- Educational attainment: .
- Years in education: .
- Stakeholder engagement: .
- Voter turnout: .
3.2.1. Comparison
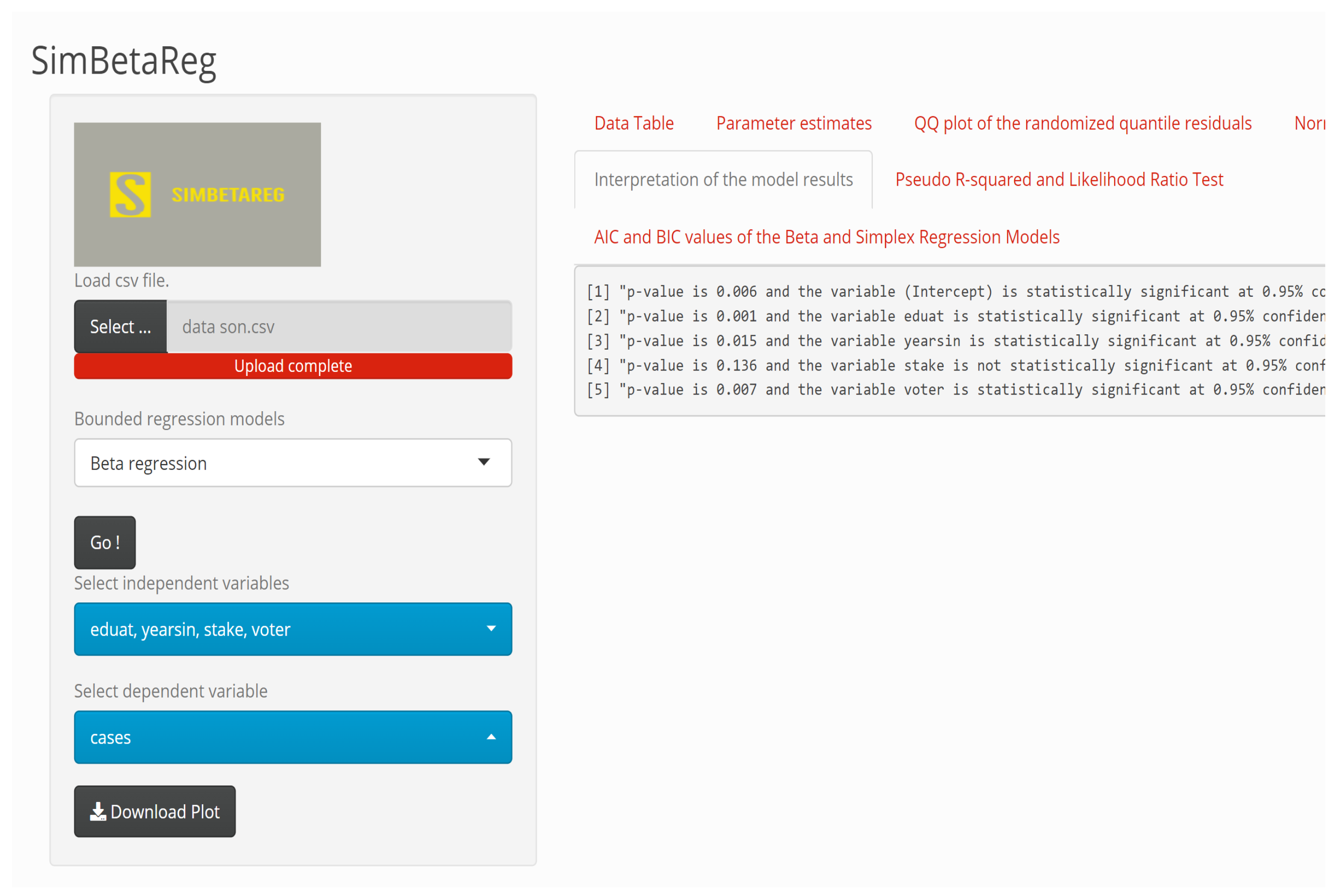
3.2.2. Interpretation
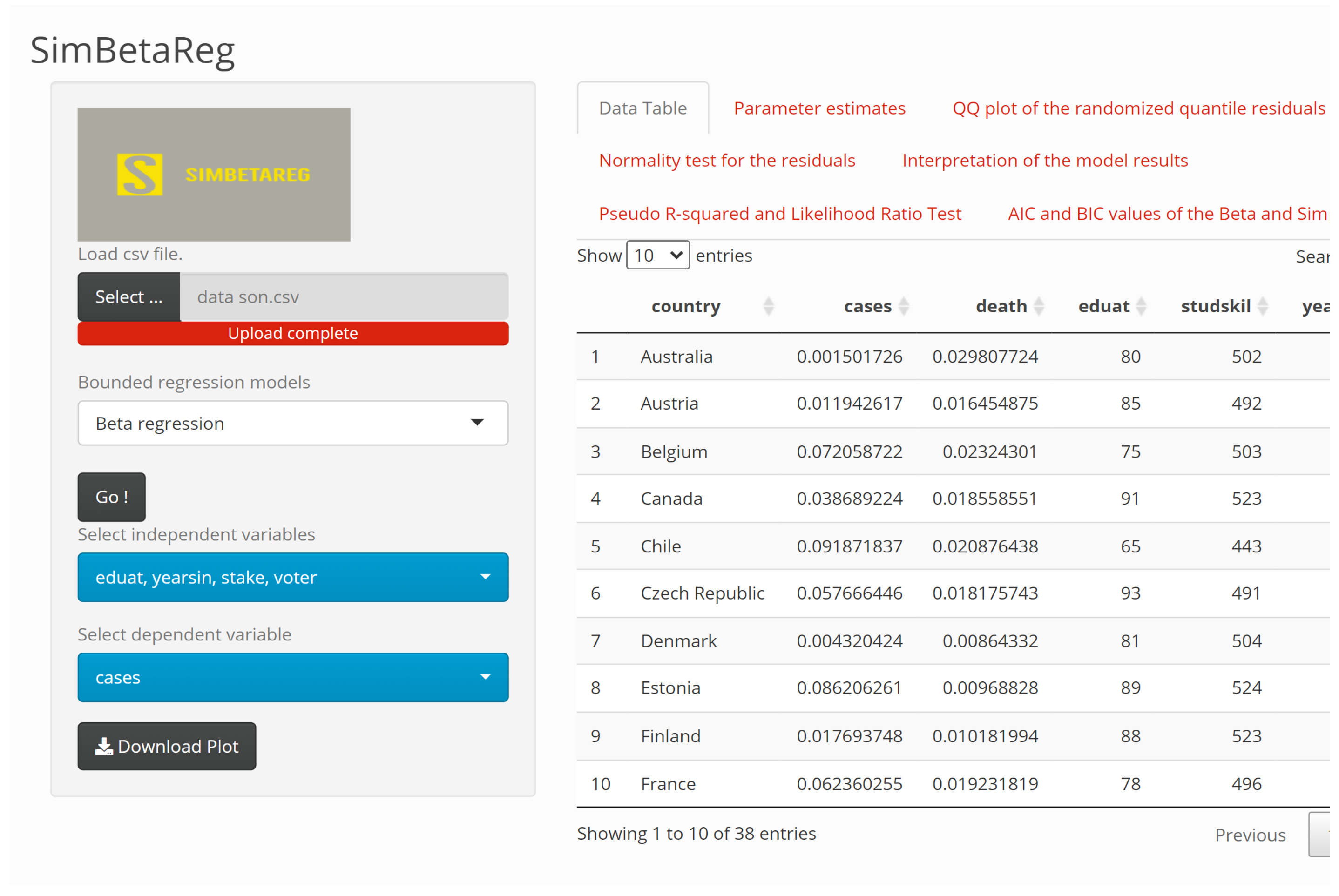
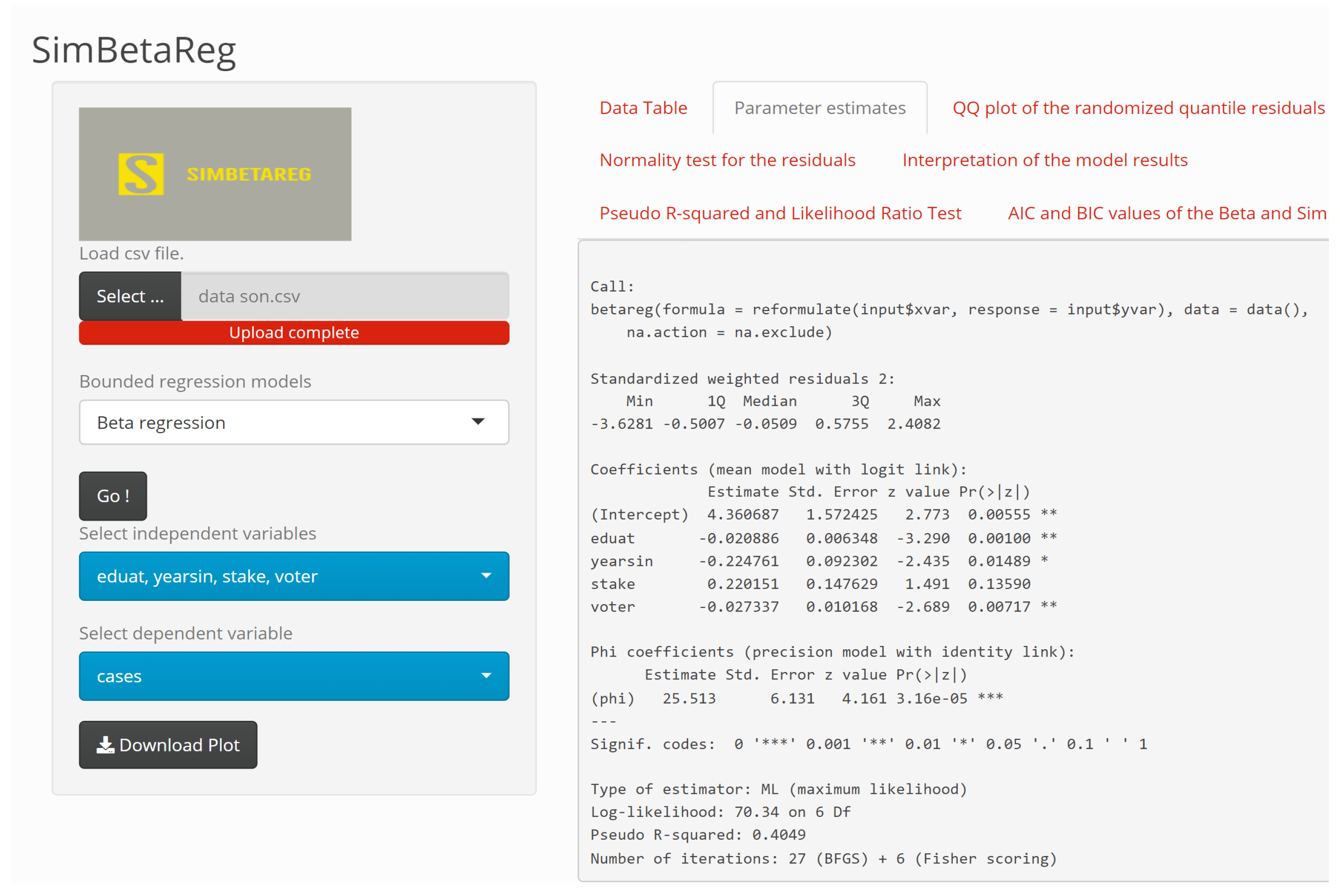
4. SimBetaReg Web-Tool
Used R Packages
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COVID-19 | Coronavirus disease 2019 |
| probability distribution function | |
| CDF | cumulative distribution function |
| MLE | maximum likelihood estimation |
| unit-ISDL | unit-improved second degree Lindley |
| log-WE | log-weighted exponential |
| BLI | Better Life Index |
| KS | Kolmogorov–Smirnov |
References
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Topp, C.W.; Leone, F.C. A family of J-shaped frequency functions. J. Am. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Jørgensen, B. Some parametric models on the simplex. J. Multivar. Anal. 1991, 39, 106–116. [Google Scholar] [CrossRef] [Green Version]
- Altun, E.; Hamedani, G.G. The log-xgamma distribution with inference and application. J. Soc. Française Stat. 2018, 159, 40–55. [Google Scholar]
- Altun, E. The log-weighted exponential regression model: Alternative to the beta regression model. Commun. Stat.-Theory Methods 2021, 50, 2306–2321. [Google Scholar] [CrossRef]
- Altun, E.; Cordeiro, G.M. The unit-improved second-degree Lindley distribution: Inference and regression modeling. Comput. Stat. 2019, 35, 259–279. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. J. Appl. Stat. 2019, 46, 700–714. [Google Scholar] [CrossRef] [Green Version]
- Altun, E.; El-Morshedy, M.; Eliwa, M.S. A new regression model for bounded response variable: An alternative to the beta and unit-Lindley regression models. PLoS ONE 2021, 16, e0245627. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat.-Theory Methods 2018, 48, 3423–3438. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R.; Hudson, I.L. Transmuted kumaraswamy distribution. Stat. Transit. New Ser. 2016, 17, 183–210. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. The unit-Birnbaum–Saunders distribution with applications. Chil. J. Stat. (ChJS) 2018, 9, 47–57. [Google Scholar]
- Pourdarvish, A.; Mirmostafaee, S.M.T.K.; Naderi, K. The exponentiated Topp–Leone distribution: Properties and application. J. Appl. Environ. Biol. Sci. 2015, 5, 251–256. [Google Scholar]
- Ferrari, S.; Cribari-Neto, F. Beta Regression for Modelling Rates and Proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Kieschnick, R.; McCullough, B.D. Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions. Stat. Model. Int. J. 2003, 3, 193–213. [Google Scholar] [CrossRef] [Green Version]
- Song, P.X.-K.; Tan, M. Marginal models for longitudinal continuous proportional data. Biometrics 2000, 56, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Song, P.X.K.; Qiu, Z.; Tan, M. Modeling Heterogeneous Dispersion in Marginal Simplex Models for Continuous Longitudinal Proportional Data. Biom. J. 2004, 46, 540–553. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Z.; Song, P.X.-K.; Tan, M. Simplex Mixed-Effects Models for Longitudinal Proportional Data. Scand. J. Stat. 2008, 35, 577–596. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C. On the unit Burr-XII distribution with the quantile regression modeling and applications. Comput. Appl. Math. 2021, 40, 1–26. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications. Symmetry 2021, 13, 117. [Google Scholar] [CrossRef]
- Mollalo, A.; Rivera, K.M.; Vahedi, B. Artificial Neural Network Modeling of Novel Coronavirus (COVID-19) Incidence Rates across the Continental United States. Int. J. Environ. Res. Public Health 2020, 17, 4204. [Google Scholar] [CrossRef]
- Karmakar, M.; Lantz, P.M.; Tipirneni, R. Association of Social and Demographic Factors with COVID-19 Incidence and Death Rates in the US. JAMA Netw. Open 2021, 4, e2036462. [Google Scholar] [CrossRef] [PubMed]
- Duhon, J.; Bragazzi, N.; Kong, J.D. The impact of non-pharmaceutical interventions, demographic, social, and climatic factors on the initial growth rate of COVID-19: A cross-country study. Sci. Total Environ. 2021, 760, 144325. [Google Scholar] [CrossRef] [PubMed]
- El-Morshedy, M.; Altun, E.; Eliwa, M.S. A new statistical approach to model the counts of novel coronavirus cases. Math. Sci. 2021, 1–14. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Cox, D.R.; Snell, E.J. Analysis of Binary Data, 2nd ed.; Chapman Hall: London, UK, 1989. [Google Scholar]
- Mak, H.W.L. From COVID-19 Pandemic of Five Selected East Asian Cities to Assessment of Data Openness and Integration for Future City Development. 2021. Available online: https://www.researchgate.net/profile/Hugo-Mak-2/publication/354293725_From_COVID-19_Pandemic_of_Five_Selected_East_Asian_Cities_to_Assessment_of_Data_Openness_and_Integration_for_Future_City_Development/links/612fbc430360302a00734baa/From-COVID-19-Pandemic-of-Five-Selected-East-Asian-Cities-to-Assessment-of-Data-Openness-and-Integration-for-Future-City-Development.pdf (accessed on 1 July 2021).
- Cribari-Neto, F.; Zeileis, A. Beta Regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Yee, T.W. Vector Generalized Linear and Additive Models: With An Implementation in R; Springer: New York, NY, USA, 2015. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Stasinopoulos, M.; Rigby, R. gamlss.dist: Distributions for Generalized Additive Models for Location Scale and Shape. R Package Version 5.3-2. 2021. Available online: https://CRAN.R-project.org/package=gamlss.dist (accessed on 1 July 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 1 July 2021).
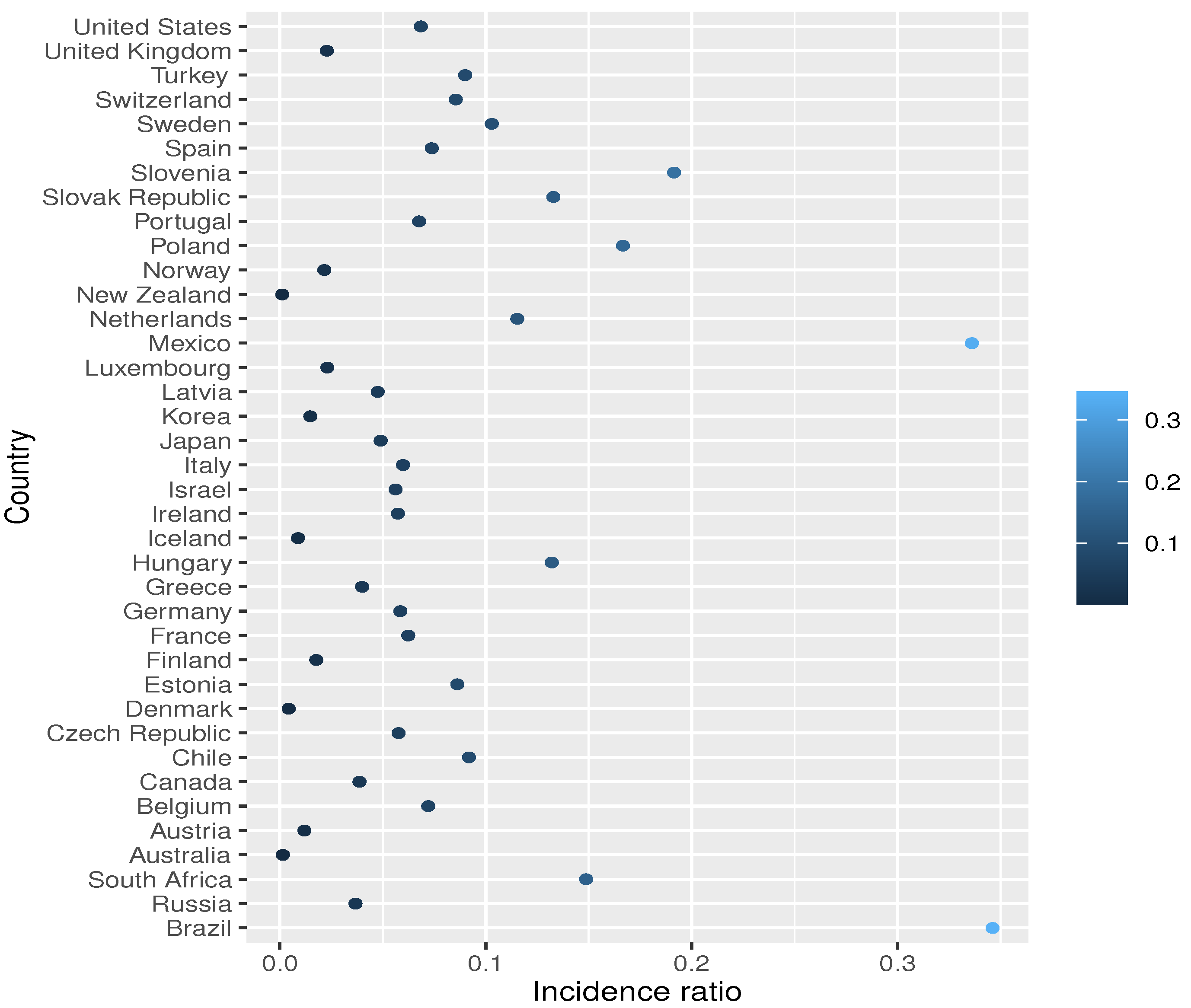
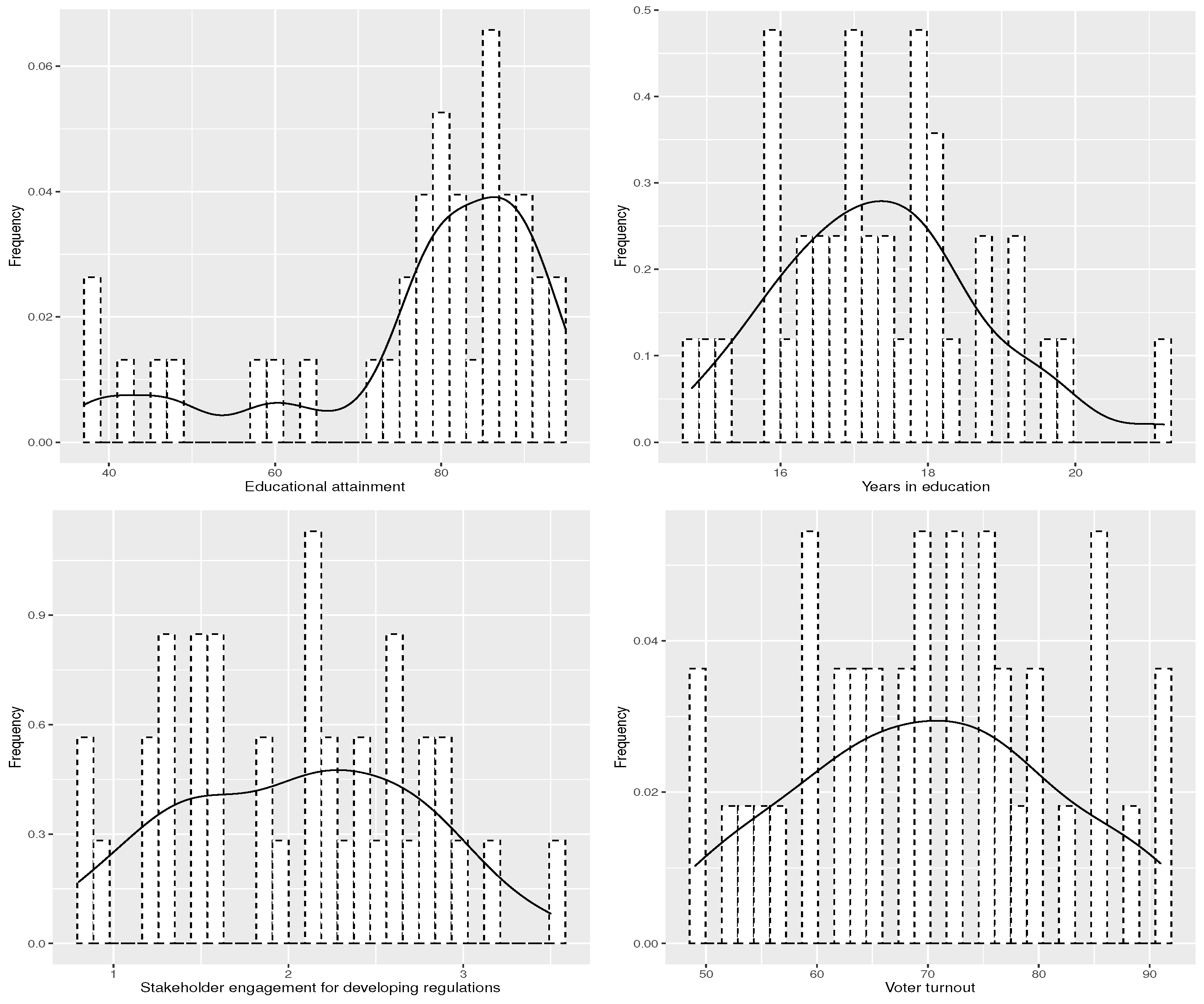
| Variables | n | Mean | SD | Median | Minimum | Maximum | Range | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| Incidence ratio | 38 | 0.08 | 0.08 | 0.06 | 0 | 0.35 | 0.34 | 1.98 | 4.10 |
| Educational attainment | 38 | 77.24 | 16 | 81.50 | 37 | 95 | 58 | −1.23 | 0.35 |
| Years in education | 38 | 17.38 | 1.39 | 17.30 | 14.80 | 21.20 | 6.40 | 0.44 | −0.01 |
| Stakeholder engagement | 38 | 2.05 | 0.70 | 2.10 | 0.80 | 3.50 | 2.70 | −0.02 | −0.96 |
| Voter turnout | 38 | 70.03 | 11.67 | 69.50 | 49 | 91 | 42 | 0.01 | −0.93 |
| Dependent Variable: Incidence Ratio | Beta | Simplex | ||||
|---|---|---|---|---|---|---|
| Parameters | Estimates | SEs | p-Value | Estimates | SEs | p-Value |
| 4.361 | 1.572 | 0.006 | 12.883 | 1.780 | <0.001 | |
| −0.021 | 0.006 | 0.001 | −0.005 | 0.014 | 0.714 | |
| −0.225 | 0.092 | 0.015 | −0.660 | 0.131 | <0.001 | |
| 0.220 | 0.148 | 0.136 | −0.678 | 0.296 | 0.022 | |
| −0.027 | 0.010 | 0.007 | −0.028 | 0.019 | 0.129 | |
| 25.513 | 6.131 | <0.001 | − | − | − | |
| − | − | − | 1.978 | 0.115 | <0.001 | |
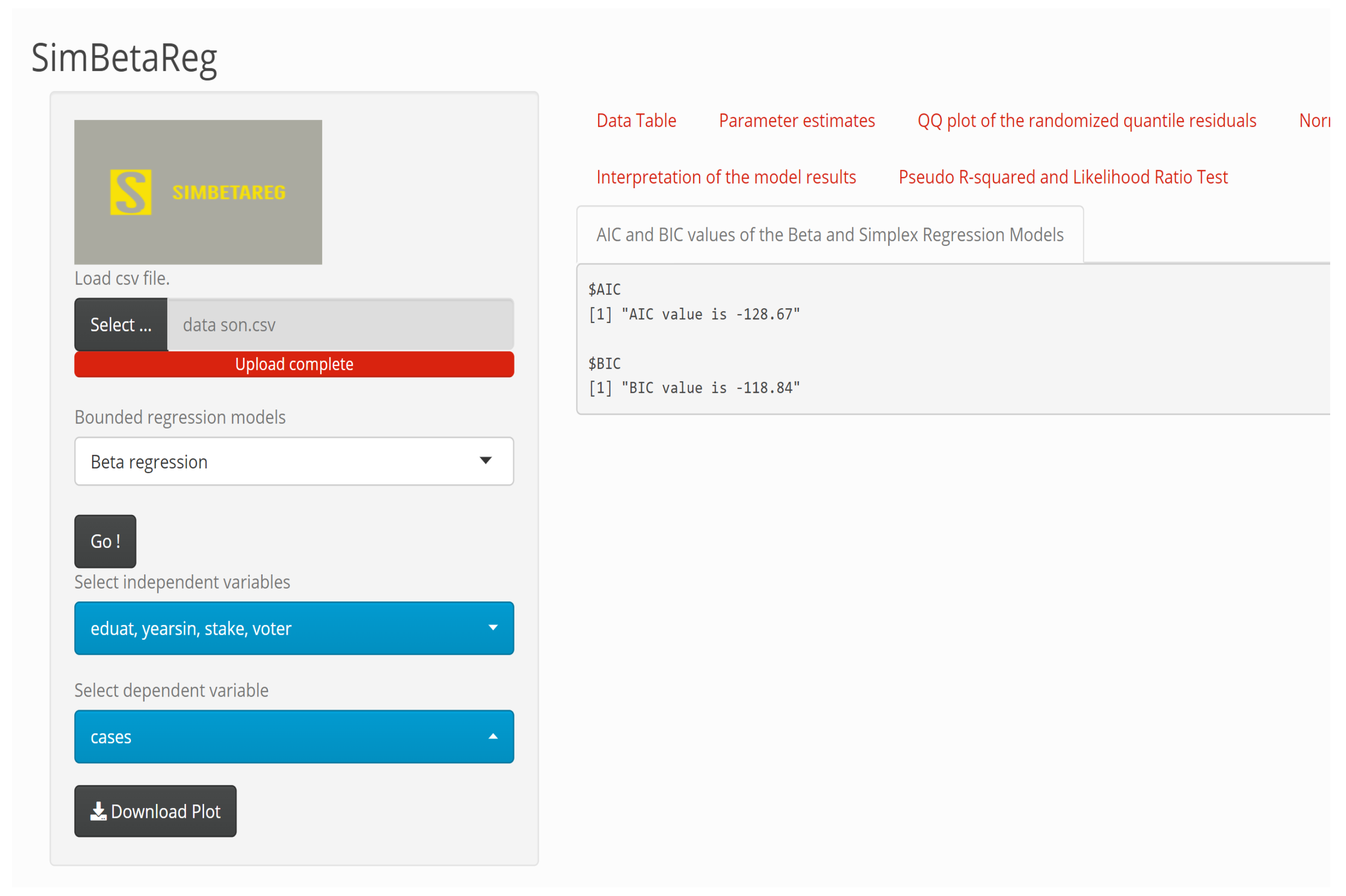
| −70.340 | −50.723 | |||||
| AIC | −128.67 | −89.4449 | ||||
| BIC | −118.845 | −79.6194 | ||||
| Models | KS Test Statistic | p-Value |
|---|---|---|
| Beta regression | 0.1463 | 0.355 |
| Simplex regression | 0.3525 | <0.001 |
| Models | Cox and Snell Pseudo | LR Test Statistic | p-Value |
|---|---|---|---|
| Beta regression | 0.466 | 23.863 | <0.001 |
| Simplex regression | 0.202 | 8.556 | 0.073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altun, E.; El-Morshedy, M. SimBetaReg Web-Tool: The Easiest Way to Implement the Beta and Simplex Regression Models. Symmetry 2021, 13, 2437. https://doi.org/10.3390/sym13122437
Altun E, El-Morshedy M. SimBetaReg Web-Tool: The Easiest Way to Implement the Beta and Simplex Regression Models. Symmetry. 2021; 13(12):2437. https://doi.org/10.3390/sym13122437
Chicago/Turabian StyleAltun, Emrah, and Mahmoud El-Morshedy. 2021. "SimBetaReg Web-Tool: The Easiest Way to Implement the Beta and Simplex Regression Models" Symmetry 13, no. 12: 2437. https://doi.org/10.3390/sym13122437
APA StyleAltun, E., & El-Morshedy, M. (2021). SimBetaReg Web-Tool: The Easiest Way to Implement the Beta and Simplex Regression Models. Symmetry, 13(12), 2437. https://doi.org/10.3390/sym13122437







