Abstract
Multi-Criteria Decision Making (MCDM) methods have rapidly developed and have been applied to many areas for decision making in engineering. Apart from that, the process to select fault-diagnosis sensor for Fuel Cell Stack system in various options is a multi-criteria decision-making (MCDM) issue. However, in light of the choosing of fault diagnosis sensors, there is no MCDM analysis, and Fuel Cell Stack companies also urgently need a solution. Therefore, in this paper, we will use MCDM methods to analysis the fault-diagnosis sensor selection problem for the first time. The main contribution of this paper is to proposed a fault-diagnosis sensor selection methodology, which combines the rank reversal resisted AHP and TOPSIS and supports Fuel Cell Stack companies to select the optimal fault-diagnosis sensors. Apart from that, through the analysis, among all sensor alternatives, the acquisition of the optimal solution can be regarded as solving the symmetric or asymmetric problem of the optimal solution, which just maps to the TOPSIS method. Therefore, after apply the proposed fault-diagnosis sensor selection methodology, the Fuel Cell Stack system fault-diagnosis process will be more efficient, economical, and safe.
1. Introduction
A Fuel Cell Stack system (FCS) refers to a power generation system with fuel cell as the core, fuel supply and circulation system, oxidizer supply system, water/heat management system, control system, etc., and able to continuously output electronic power [1]. The main research interests for FCS include using lightweight materials, optimizing design, and improving the specific power of the fuel cell system, improving the fast cold start capability and dynamic response performance of the FCS system, researching fuel processors with load following capabilities, optimizing supercapacitors and hydrogen storage for system design to improve system efficiency and peak shaving capabilities, recover braking energy, etc. [1].
Apart from that, a fault is a state in which the system cannot perform a prescribed function. Generally speaking, a fault refers to an event in which the function of some components in the system fails and the function of the entire system deteriorates [2]. The FCS is mainly composed of a stack, a fuel processor, a power regulator, and an air compressor. There will be many potential faults which can directly influence the FCS system and FCS cause the system to no work properly [3]. Therefore, the effective use of fault-diagnosis sensors to detect FCS systems becomes very important. The fault diagnosis is the process of using various detection and testing methods to find out whether there is a fault in the system and equipment [4].
A proper fault-diagnosis sensor selection is a deeply significant problem for FCS because of the reason that choosing an unsuitable fault-diagnosis sensor can directly influence the main function testing progress of the FCS fault-diagnosis system. Therefore, selecting a suitable fault-diagnosis sensor can be a very important part to obtain the most optimal consequence for FCS.
Therefore, FCS companies urgently need to choose more efficient, safer, and more affordable fault diagnosis sensors. The fault-diagnosis sensor selection problem is a Multi-Criteria Decision-Analysis (MCDM) problem.
Therefore, in this paper, we use the rank aversion resisted AHP and TOPSIS method to approach the FCS fault-diagnosis sensor selection problem. The main objective of this study is to put forward a fault-diagnosis sensor selection methodology which considers difference criteria and sub-criteria, and helps FCS companies to select the optimal fault-diagnosis sensors, and ensure that the FCS fault-diagnosis process becomes more efficient, economical, and safe.
The rest of this article is structured as follows. The “Literature review” section introduces the background and related research. The “Methods” section describes the methods that we used in this research. The “Case study” section characterizes an example to derive experimental information from and to analyze the consequence of imitation. A detailed discussion and ideas for future work are summarized in the “Discussion” section.
2. Literature Review
A fuel cell is a chemical device that directly converts the chemical energy of the fuel into electrical energy, also known as an electrochemical generator, and it is the fourth power generation technology after hydropower, thermal power, and atomic power [1]. Meanwhile, in addition to the fuel cell’s main body (power generation system), the FCS also has some peripheral devices, including fuel reforming supply system, gasoline supply system, water management system, thermal management system, dangerous communication system, control system, safety system, etc. [5].
To obtain the optimal FCS fault-diagnosis sensor in all alternatives, we can use the asymmetry of the evaluation result. Symmetry and asymmetry are frequent patterns that are widely studied in a variety of fields. In most cases, symmetries can exist in an arithmetic equation, which has been an important part for approving issues or conduct a more in-depth study. In this research, selecting the fault-diagnosis sensor problem can be regarded as the process of solving the symmetric and asymmetric problem in mathematical formulation. To obtain the optimal fault-diagnosis sensor, we have to evaluate different sensor alternatives depending on various evaluation criteria. The criteria usually include positive criteria and negative criteria. Therefore, in the evaluation formula, we need to consider both positive and negative criteria, and get positive and negative evaluation solutions, which can be seen as the symmetry of formula. Meanwhile, to distinguish and sort all the alternatives and get the final optimal sensors, the positive and negative results should be asymmetrical. In fact, in most cases, the evaluation results are asymmetrical.
Selecting the new fault-diagnosis sensor wastes energy and is a complex process, requiring multi-disciplinary cognition and expert experience. Apart from that, with the rapid development of information and communication technology, a large amount of engineering system information data are being produced. Therefore, to select an economical, efficient, and logically well-performed fault-diagnosis sensor, the decision-maker should consider various sources of information [6,7].
The fault-diagnosis sensor selection problem can be seen as a Multi-Criteria Decision-Making (MCDM) [8,9] issue. Multi-Criteria Decision-Making has always been a well-known part of decision making [10]. It concerns establishing or approving determination and planning issues under multi-standards [11]. MCDM supports managers to make a decision, which quantifies a special standard depending on its significance in relation to other targets [12,13]. MCDM methods provide an opportunity to take into account the multidimensional nature of the considered problem [14]. The MCDM technique can also take into account the economic, community, civilization, and circumstance affairs that can enhance the project [15]. MCDM is considered to be a special decision-making process, and the issue can be emphasized as follows: selection is required, the level needs to be defined, all the alternatives need to be prioritized, and different options behaviors need to be illustrated [16]. MCDM methods are very different depending on the various dimensions, for instance a fuzzy environment, for which interests and assessment standards are represented by different methods, including different methods of value aggregation; whether there is a chance it has certain information can also define the different kinds of MCDM methods [17,18,19,20].
There are many MCDM techniques. The traditional classic mainstream MCDM techniques are Analytic Hierarchy Process (AHP) [21,22], Analytic network process (ANP) [23], Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) [24], Classic MAUT [25], ELECTRE [26], PROMETHEE [27], UTA [28], UTADIS [29], etc., while modern classic mainstream MCDM techniques are COMET [30], COPRAS [31], SPOTIS [32], SIMUS [33], and so on.
The AHP technique includes determining the total corresponding standards and compares every two values with each other to estimate the effect of every standard [34]. The AHP can be seen as a measurement based on the comparison between two alternatives, depending on the decision of specialists to obtain the precedence of all the alternatives [35]. AHP is widely applied to MCDM problems in different fields, for instance financial and scheduling, and managers can use this method to establish an MCDM issue under a hierarchy property type [36].
TOPSIS is a generic approach to deal with multi-standard determination issues [37]. Moreover, TOPSIS is also a symmetrical technique used for the ranking of the alternates, and it is the best-known approach for alternative ranking of MCMD problems [38]. The symmetrical TOPSIS technique can estimate critical criteria [39]. The main idea of TOPSIS is that the best alternative among all competitive alternatives should be at the minimum distance from the Positive-Ideal (P-I) solution and have maximum distance from the Negative-Ideal (N-I) solution [38,40], which can be regarded as the process of solving the symmetric problem in mathematical formulation. Furthermore, for determining the best alternative among several others, TOPSIS proves to be a good MCDM method [39]. Apart from that, TOPSIS also has other advantages: (1) The structure of TOPSIS is reasonable; (2) The calculation steps are very easy; (3) It allows to find the optimal options for every standard chosen through an understandable arithmetic from; (4) The significance weights are included in the process of comparison [41].
The COPRAS (Complex Proportional Assessment) technique usually evaluates the maximized/minimized index data, and the influence of these values on the properties in consequence evaluation is taken into account [42]. Moreover, the COPRAS technique supposes a straightforward and different scale, relying on the importance and rank of the effectiveness of the usable alternatives in the appearance of conflicting standards [43,44]. The target of COMET is to approach the issues of MCDM in a fuzzy condition, and this can be seen as a novel way of thinking to approach the issues of MCDM with regards to inconstancy [30]. The method is based on L-R-type GFN, which can obtain the hesitant rank for an option in a definitive standard. SPOTIS is a novel rank reversal-free MCDM method, and it has very low complexity [32]. Moreover, compared with the COMET approach, it requires much less information. SIMUS (Sequential Interactive Model for Urban Systems) is a hybrid model, not only based on Linear Programming but also on traditional approaches, such as ‘Weighted sum’ and ‘Outranking’ procedures, and can handle any number of objectives, albeit not reaching an optimal result as in the case of Linear Programming [33].
Faizi et al. proposed the MCGDM (Multi-Criteria Group Decision Making) methodology, which was based on the B-W technique with Hamacher polymerization operations of intuitive binary combination language sets [45]. This method was proposed for modifying efficiency with operations of determining steps. Božanić et al. proposed methodologies for MCDM depending on the D values, the FUCOM technique and RAFSI technique, and it can approach the industrial mechanical equipment choosing problem [46].
COMET (the Characteristic Objects Method) has an attractive function that can avoid rank reversal; however, compared with AHP and TOPSIS, it requires much more information under the situation of the very common value matrix definition in MCDM issues [32]. Moreover, when we consider the stability between the COPRAS and TOPSIS techniques with a value variable, we find that TOPSIS is better and more insensitive when the value does not change much, and compared with other technologies, the priority result is different [47]. Moreover, compared with TOPSIS and AHP, the COMET method also needs much more information when we confront it with traditional MCDM issues [32]. Furthermore, it is very hard to apply the SPOTIS approach as compared with TOPSIS, due to the fact that there exists uncertainty in the option of minimum and maximum bounds of the standard [32]. SIMUS, because it is based on Linear Programming, and LP works with a very different approach in a decision-making scenario when compared with other methods, can be considered a geometric tactic.
Here, to select the most suitable MCDM technique for fault-diagnosis sensor selection, we have to consider some judgment methods. Marco Cinelli et al. proposed a taxonomy depending on the features of MCDM steps [48], which included three important steps: phase 1—issue statement phase, phase 2—determination recommendation establishment phase, and phase 3—characteristics and method assistance phase. Wątróbski et al. also proposed a taxonomy of MCDA methods, and the proposed taxonomy can be selected as a universal scheme to choose a suitable MCDA technique under a certain decision problem domain [17]. Therefore, we can apply these taxonomies with MCDM techniques and choose a similar MCDM technique(s) for fault-diagnosis sensor selection studies.
- After all the considerations above, we have found that the AHP and TOPSIS method is the most adaptable for the fault-diagnosis sensor selection. We summarized the following reasons: the fault-diagnosis sensor selection problem is a deterministic MCDM problem and, as compared with other methods, AHP and TOPSIS are optimal for deterministic conditions.
- The weight definition in the fault-diagnosis sensor choosing means subjective judgement steps, and it just maps to the AHP method.
- Compared with other complex process methods, it is easy to apply and use the AHP and TOPSIS methods.
- Among all MCDM techniques, the AHP and TOPSIS techniques require less information.
- Among all MCDM techniques, the TOPSIS technique has good stability in a data variable case.
The main consideration in this study is to select the most suitable fault-diagnosis sensor and also consider the various standards when making a decision. These are multi-disciplinary criteria, and there are many intangible or immeasurable factors. Moreover, when choosing engineering methods or equipment, there are many criteria classification methods. Yazdani-Chamzini et al. considered the technical parameters, operational parameters and economical parameters when selecting the most appropriate mining methods [49]. Štirbanović et al. applied the MCDM method for flotation machine selection, which considered the constructional parameters, economical parameters, and technical parameters [50]. Sarrate et al. proposed a methodology depending on fault diagnosis capability optimization for finding a suitable sensors’ location for FCS systems, and considered different fault-diagnosis criteria, such as compressor parameters, inlet manifold parameters, air conditioner parameters, humidifier parameters, FCS anode parameters, and so on [51]. When we define the importance weights of the criteria, there are also intangible or immeasurable factors that should be approached.
The AHP is a targeted and practical decision-making method for analyzing qualitative problems, and the characteristic is to structure the various factors in complex issues through inter-connection to make them organized [35]. Moreover, the AHP is the most commonly used technique due to its simplicity, ease of use, and great flexibility [52]. However, there is a rank versal phenomenon in the AHP method. The rank reversal problem means that when ranking the pros and cons of alternatives to an MCDM problem, adding or reducing an alternative and applying the same decision model will cause inconsistent ranking results. Wang and Elhag proposed methodology to avoid rank reversal in AHP [53]; we can use this method to approach the problem of the rank reversal problem in the AHP method.
Therefore, we can use the AHP method to define the weights of fault-diagnosis sensor importance criteria. Additionally, we can use TOPSIS to obtain the result of the feasible fault-diagnosis sensor alternatives. The most important reason why we use TOPSIS is that it can analyze the length to the P-I result and the N-I result, which just conforms to the symmetry of the formula. Additionally, we can get the asymmetry of all the candidate sensor evaluation result through TOPSIS.
Our main objective is to help FCS companies select more efficient, safer, and more affordable fault-diagnosis sensors. The fault-diagnosis sensor selection problem is an MCDM problem. Therefore, this research utilizes the AHP method (the MCDM method) to determine the importance weights of the fault-diagnosis sensor estimation standard, and TOPSIS is to find suitable solutions. It is then possible for FCS companies to apply this methodology and choose the optimal fault-diagnosis sensor, making the FCS fault-detection process more efficient, economical, and safe.
3. Methods
3.1. The AHP Technique
The whole AHP steps are shown as follows [35]:
- Depending on how thorough the knowledge about the system is, determine the main target and establish the measures and policies involved in the planning and decision-making.
- Establish a hierarchical framwork, and define the location of all the factors that we use in this framwork according to different goals and different functions.
- Determine the degree of correlation between neighboring layer factors. Establish pairwise comparison matrices, determine the relative weight of a factor on the previous layer and the significance of the corresponding factors on this layer.
- Obtain the composite weight of every level factor to the target. Moreover, the sorting needs to be done, and the importance of the main target of the bottom element at the framwork needs to be defined.
- Establish the weight of each layer element of the system goal, perform the total sorting, and determine the importance of the overall goal of the lowest element in the hierarchical structure.
First of all, we have to decide the main issue and the different intellectual ideas. After that, targets, standards, and options will be sorted depending on the hierarchical composition. In this hierarchical structure, the objectives are in the upper layer, usually related to the determined options in the middle layer and all the options located in lower layer. In the third step, we have to make a comparison between the alternatives. Here, we have to define the importance scale. The importance scale refers to how many more times one element is important than another. The AHP Fundamental Scale is shown in Table 1.

Table 1.
The AHP Fundamental Scale [53,54].
After that, the rank of the importance is obtained through a paired comparison matrix among alternative m and alternative n of the form (Equation (1)) [55]:
In Equation (1), amn refers to the value appearance of the determination of pairwise comparison values (alternative m, alternative n) for all alternatives (m, n = 1, 2, …, n). Here, m refers to a row of A and n refers to a column of A. In Equation (1), amn cannot be equal to 0.
In the next process, we have to calculate the normalized value for every matrix and define the corresponding weights for them. The corresponding weights can be obtained from u and λmax (Equation (2)):
where u refers to the right eigenvector and λmax refers to the largest eigenvector.
To avoid the Rank Reversal problem for the AHP technique, it is possible to calculate the rescaled right eigenvector weights (Equation (3)):
where , , and .
In Equation (3), can be seen as the normalization with respect to the original N alternatives. We can calculate the rescaled weight to resist the rank reversal phenomenon for the AHP technique when an option is inserted or dropped.
3.2. TOPSIS Technique
The basic process of the TOPSIS technique can be seen as follows:
- First, establish a decision matrix for alternatives (Equation (4)):where D is the decision matrix, yij is the jth criterion value related to the ith alternative, I is total number of alternatives, and J is total number of criteria.
- Second, obtain the normalized decision matrix Z(=zij) (Equation (5)):where zij is the normalized value for the jth criterion value related to the ith alternative and I is the total number of alternatives. The reason why we use the vector normalization technique is that many researchers have analyzed the effects of different normalizations for TOPSIS, and they have found that the vector normalization method is most suitable for TOPSIS [56,57]. Moreover, in this process, they have computed the consistency of the results of all the alternatives, and analyzed the sensitivity of the weight for different normalization methods applied on TOPSIS.
- Third, obtain the weighted normalized decision matrix X(=xij) (Equation (6)):Here, the normalized value is obtained from the multiplication of the original value and the corresponding weights. In this research, the weight can be defined by the AHP method.
- Fourth, calculate the P-I and N-I results (Equations (7) and (8)):where l′ is the value set associate with benefit criteria and l″ is the value set associate with the cost criteria.where l′ is the value set associated with the benefit criteria and l″ is the value set associate with loss standards.
- Fifth, obtain a symmetric n-dimensional Euclidean distance from every result to the P-I result and the N-I result (Equations (9) and (10)):
- Sixth, obtain the closeness to the ideal result (Equation (11)):
- Seventh, determine the order of the Ci* value to define the performance of the alternatives. The larger the Ci* value is, the better the performance of the alternatives is.
4. Results
4.1. The Whole Process of Fault-Diagnosis Sensors for FCS
The whole process of fault-diagnosis sensor selection method for FCS is provided in Figure 1.
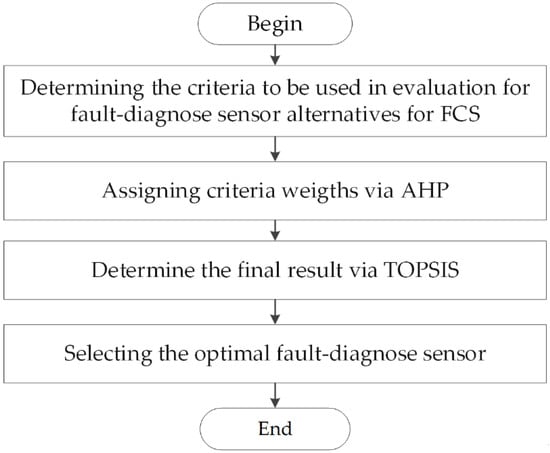
Figure 1.
The whole process of the fault-diagnosis sensor selection method for FCS.
First of all, we should determine the criteria to be used in the evaluation of fault-diagnosis sensor alternatives. Here, the criteria should be defined by multidisciplinary knowledge (cost, efficiency, impact on the environment, safety, and so on). After that, we can assign criteria weights to the AHP method. Next, we can determine the final alternative evaluation result through the TOPSIS method.
4.2. Criteria for Fault-Diagnosis Sensors Selection for FCS
The standard that is used in the chosen fault-diagnosis sensors are decided by the company experts. Here, experts consist of experienced employees from different fault-diagnosis fields and FCS companies. They are very familiar with the size and shape, installation, performance, and expansion of fault-diagnosis sensors. At the same time, they are also very aware of the various safety hazards of sensors, and what a reasonable budget should be for each sensor component.
The proposed criteria and sub-criteria are obtained through related reference research works and from interviews with experts. After that, depending on the initial screening result, four important criteria (Constructional Parameters, Efficient Parameters, Economic Parameters, and Safety Parameters) to be used for fault-diagnosis sensors selection are established. Apart from that, each criterion has several sub-criteria. There are three sub-criteria for Constructional Parameters, six sub-criteria for Economical Parameters, six sub-criteria for Efficient Parameters, and two sub-criteria for Safety Parameters. These criteria are mainly considered to be widely acceptable by the experts. All these criteria are meant to make the fault-diagnosis process for FCS more efficient, more economical, more environmentally friendly, and safer. The four criteria and their descriptions are as follows (see also Table 2).

Table 2.
Criteria and sub-criteria of fault-diagnosis sensors for the Fuel Cell Stack system.
- Constructional Parameters: Constructional parameters are related to the size and shape of the fault-diagnosis sensors, the installation ease, and expansion ability.
- Efficient Parameters: Efficient parameters are related to the efficiency and performance of fault-diagnosis sensors.
- Economical Parameters: Economic parameters include the cost of all parts of the fault-diagnosis sensor.
- Safety Parameters: Safety parameters include the incidence of sensor breakage or electrical leakage and the safety of the sensor system in an emergency.
- Resilience and tolerance: Resilience and tolerance parameters related to the ability of a fault-diagnosis sensor system to provide the required capability in the face of adversity and the fault-tolerant design of the sensor. In an FCS system, there are different kinds of adversities, such as electromagnetic and light interference, sudden power cuts, and the best detection distance range, and we have to evaluate the capacity, which is related to the ability to deal with all these interferences, and ensure that the error diagnosis process of the fault-diagnosis sensor system continues. Tolerance is related to the capability of the fault-diagnosis system to continue error-free work in the situation of an unexpected failure (complete unworking, fixed deviation, drift deviation, and accuracy degradation).
4.3. Assigning the Weights of the Criteria via AHP
In this approach, experts use the AHP method to distribute or decide the standard and sub-standard weights, depending on the professional competence of them. A scheme for FCS, which is deeply recognized by the experts in the field of control science, can describe the FCS working process very well [58,59,60], and the corresponding fault-diagnose sensor system can be seen as Figure 2.
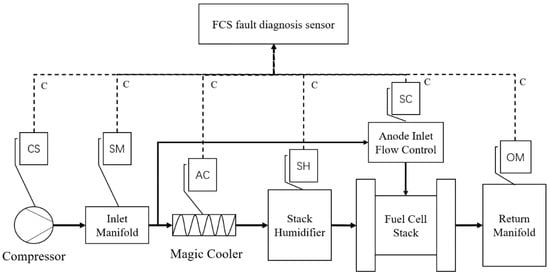
Figure 2.
The FCS scheme and the corresponding fault-diagnosis sensor system. Note. C = Collecting data. CS = Compressor motor checking part. SM = Supply Manifold checking part AC = Air Cooler checking part. SH = Static humidifier checking part. OM = Outlet manifold checking part. SC = Stack cathode checking part.
In Figure 2, we can find that the model FCS mainly includes seven elements. Moreover, the FCS can be seen as the machine which can transform fuel energy into electronic energy [3]. Therefore, in order to allow the chemical energy of the fuel to be converted into electrical energy more smoothly, safely, more effectively, and more economical in the FCS system, there is a need to select and set appropriate FCS fault-diagnosis sensor to check different elements in the FCS system. In Figure 2, we can also find that the FCS fault-diagnosis sensor can be divided in six parts (Compressor motor checking, Supply Manifold checking, Air Cooler checking, Static humidifier checking, Outlet manifold checking, and Stack cathode checking), and the detailed functions of these parts can be described as follows:
- Compressor motor checking: the main function of this part is to check the angular speed and motor torque of the compressor, and record the size of the compressor current.
- Supply Manifold checking: the main function of this part it to check the exist air mass flow rate and temperature of the of the inlet manifold.
- Air Cooler checking: the main function of this part is to check the air mass flow rate and temperature of the magic cooler. Moreover, it can also check the humidity of the magic cooler.
- Static humidifier checking: the main function of this part is to check the exit air mass humidity, temperature, and pressure of the stack humidifier, and also check the injected vapor mass flow rate.
- Outlet manifold checking: the main function of this part if to check the outlet manifold exit air mass flow rate, pressure, and humidity.
- Stack cathode checking: this main function of this part is to check the cathode and anode exit hydrogen mass flow rate, hydrogen pressure, relative hydrogen humidity, and exit vapor mass flow rate.
These checking parts can detect all components of FCS in real time, and return the checking data to the fault diagnosis sensor system. Therefore, depending on the information above and the criteria and sub-criteria in Table 2, we can establish a multi-level hierarchical structure as in Figure 3.
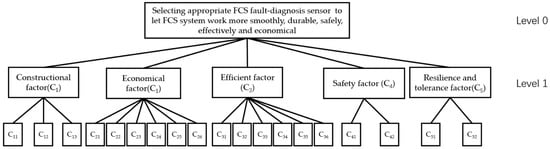
Figure 3.
Multi-level hierarchical structure for the FCS fault-diagnosis sensor criteria weight definition.
In Figure 3, we can find that there are two levels of hierarchical structure. Level 0 is the main target of our research, while level 1 shows the multi-standards, and consists of five main factors to select the FCS fault-diagnosis sensor. Moreover, every main factor also consists of several sub-criteria. The reason why there are only two levels of hierarchical structure is that we only need to use the AHP method to define the weight of all the criteria, and the selection of the FCS fault-diagnosis sensor will be defined in the TOPSIS method.
Therefore, depending on Figure 3, experts can give the paired comparison result depending on the comparison rank information in Table 1. The pairwise comparison result of the criteria and sub-criteria for the fault-diagnosis sensor is shown in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8.

Table 3.
Consequence of comparison of four fault-diagnosis criteria and the rescaled weight of the significance of them.

Table 4.
Pairwise comparison result and weight of the Constructional Parameter (C1) sub-criteria.

Table 5.
Pairwise comparison result and weight of the Economical Parameter (C2) sub-criteria.

Table 6.
Pairwise comparison result and the weight of the Efficient Parameter (C3) sub-criteria.

Table 7.
Consequence of the comparison of Safety Parameter (C4) sub-criteria.

Table 8.
Consequence of the comparison of Resilience and tolerance parameter (C5) sub-criteria.
The weight results (ûi and rvk) in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 are released depending on the Equations (2) and (3) (the rescaled weights for the main right eigenvector for the pairwise comparison are shown in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8). Here, the calculated weight for the fault-diagnosis sensor sub-criteria (wk) is obtained by multiplying the criteria of the rescaled weight ûi and the sub-criteria of the rescaled weight rvk.
4.4. Determining the Final Result via TOPSIS
To determine the final fault-diagnosis sensor selection result for FCS, five fault-diagnosis sensors were evaluated using the TOPSIS method. For evaluation, a 1–5 scale, shown in Table 9, was used.

Table 9.
Evaluation value used for ranking fault-diagnosis sensors for FCS.
Experts can use ranking in Table 9. to evaluate the five fault-diagnosis sensors. The ranking of the five options, corresponding to the fault-diagnosis sensor evaluation sub-standard, can be seen in Table 10.

Table 10.
The ratings of evaluated alternatives with respect to each criterion.
The weighted normalized values determined by using Equation (5), Equation (6), and Table 4, Table 5, Table 6, Table 7 and Table 8, are shown in Table 11.

Table 11.
The weighted normalized value of the alternatives with respect to each criterion.
In Table 11, the MI refers to the loss standard (a smaller value means better results). Moreover, MA refers to the gain standard (larger value means better results). The weighted normalized value for alternative Sensor 1 (SE1) relative to sub-criteria CT11 is 0.102. The value is obtained by multiplying the calculated weight of sub-criteria C11 (wk (0.296 in Table 4)) and the normalized decision matrix value for C11 (). After that, depending on Table 11 and Equations (7) and (8), the P-I and N-I results can be decided. The P-I and N-I results can be seen in Table 12.

Table 12.
The P-I and N-I solutions of the considered fault-diagnosis sensor alternatives.
Depending on the data from Table 11 and Table 12 and Equations (9) and (10), the relative distances of all options from the P-I result and N-I result can be obtained. Finally, we can compute the distance between each option and the P-I result depending on Equation (11). The relative distances between each option and the P-I and N-I solution, and the result of relative closeness to the N-I, can be seen in Table 13.

Table 13.
TOPSIS results.
Table 13 shows the evaluation result of the candidate options depending on the calculation of the TOPSIS methodology. From the Ci* value in Table 13, we can find that the fault-diagnosis sensor SE2 has the highest value (0.747). In contrast, sensor SE4 has the smallest value (0.151). Moreover, we also find that companies pay more attention to the Constructional Parameters (C1) and Economical parameters (C2) (the rescaled weights (ûi) for these two parts in Table 3 are 0.36 and 0.367, respectively). Moreover, in the Constructional Parameters (C1), companies pay more attention to the criteria C11 (the rescaled weight (ûi) for C11 is 0.296; the lower the criteria data, the better), and in the Economical parameters (C2), companies pay more attention to the criteria C21 (the rescaled weight (ûi) for C21 is 0.156; the smaller the criteria value, the better). Therefore, when we use these two criteria (C11, C21) to compare all the sensors, we can find that SE2 has the smallest value (1 for C11 and 2 for C21, see Table 10). Therefore, compared with other sensors, SE2 has the smallest size and shape, while the compressor motor inspection has the lowest cost, and these two parts are also the most important reason why SE2 is optimal. Additionally, companies should pay more attention to these two parts when considering other new sensors. Therefore, given the result above, companies can select fault-diagnosis sensor SE2 to ensure that the FCS fault-diagnosis process is more efficient, economical, and safer compared with other alternatives.
5. Discussion
The fault-detection process is one of the most important steps in the effective operation of Fuel Cell Stack Systems, and Fuel Cell Stack Systems are generally complex and need to be systematically organized in order to achieve high levels of efficiency. A fault-detection sensor can ensure the effective operation of Fuel Cell Stack Systems, and companies need to consider several criteria and restrictions for the sensors’ selection process. Meanwhile, with the rapid development of manufacturing techniques and manufacturing economy problems [61,62,63], safety problems and efficiency problems [64] frequently emerge. Therefore, to ensure a safe and efficient fault-diagnosis process, it is very important for companies to select an adaptable fault-diagnosis sensor that meets these conditions.
Therefore, considering the problems above, this article proposed a fault-diagnosis selection method for Fuel Cell Stack Systems, considering the symmetric and asymmetric problem in a mathematical formulation and also considering the different multi-disciplinary criteria (Construction Parameters, Economical Parameters, Efficient Parameters, and Safety Parameters). To define the weight of the fault-diagnosis evaluation criteria for Fuel Cell Stack Systems, we introduced the AHP (Analytic Hierarchy Process) method. We used the AHP technique to define the importance of the fault-diagnosis evaluation standard or sub-standard. Additionally, we used a method [53] to avoid rank reversal in AHP. From Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, we can get the weight information for all the four main criteria and the calculated weight information for 17 sub-criteria. The calculated weight information value multiplies the weight of the criteria by the associated weight of the sub-criteria. Next, we used TOPSIS to select and obtain the fault-diagnosis sensor in all the alternatives. Here, we considered both the positive and negative criteria, and obtained positive and negative evaluation solutions (Table 11 and Table 12) through the computation of the P-I solution (Equation (7)), NN-I solution (Equation (8)), The symmetric distance from the P-I result (Equation (9)), and the symmetric distance from the N-I result (Equation (10)). From the TOPSIS results in Table 13, companies can obtain and select the most suitable fault-diagnosis sensor (the higher the Ci* value, the better). The main contribution of this paper is to help Fuel Cell Stack Systems companies to select the appropriate fault-diagnosis sensor to ensure that the Fuel Cell Stack Systems fault-diagnosis process is more economical, efficient, and safer.
Although the methodology was developed for the fault-diagnosis sensor selection problem, it is also adaptable for the selection of other manufacturing process facilities, with slight modifications, such as the cutting or welding facility selection problem in car manufacturing companies. Therefore, further studies will need to focus on other directions. In a future study, we will continue to study the comparison of the Technique for Order Performance by Similarity to Ideal Solution, Višekriterijumsko Kompromisno Rangiranje, Complex Proportional Assessment, and PROMETHEE II (complete ranking) techniques based on the results of using different normalization methods. Additionally, a sensitivity analysis should be performed for the ranking result (Table 13), such as the use of coefficients to measure the similarity of two rankings in decision-making problems [65]. Therefore, this will also be a direction for future research. Additionally, engineering information is sometimes incomplete or in a fuzzy environment, which also needs to be addressed in future research.
Our research started with the illustration of the significance of fault-diagnosis sensor selection for a Fuel Cell Stack system. Next, we introduced the main target and the issues regarding the chosen fault-diagnosis sensor. Then, we used this method (a combination of AHP and TOPSIS) to approach fault-diagnosis sensor selection considering different fault-diagnosis sensor evaluation criteria. Ultimately, depending on the proposed methodology, companies will be able choose the most suitable adaptable fault-diagnosis sensor for their Fuel Cell Stack system. This method can be used to ensure that the Fuel Cell Stack system fault-diagnosis process is more efficient, economical, and safer.
Author Contributions
Ideas, G.J. (Guangying Jin) and G.J. (Guangzhe Jin); Method, G.J. (Guangying Jin); Writing—Original Draft Preparation, G.J. (Guangying Jin); Writing—Review and Editing, G.J. (Guangying Jin); Supervision, G.J. (Guangzhe Jin); Funding Acquisition, G.J. (Guangying Jin). All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Talent Research Start-up Founding of Dalian Maritime University, authorization code: 02502329.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aitouche, A.; Olteanu, S.C.; Bouamama, B.O. A survey of diagnostic of fuel cell stack systems. IFAC Proc. Vol. 2012, 45, 84–89. [Google Scholar] [CrossRef]
- Blanke, M.; Frei, W.C.; Kraus, F. What is fault-tolerant control? IFAC Proc. 2000, 33, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Sarrate, R.; Nejjari, F.; Rosich, A. Sensor placement for fault diagnosis performance maximization in distribution networks. In Proceedings of the 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012; IEEE: Barcelona, Spain, 2012; pp. 110–115. [Google Scholar]
- Gao, C.; Duan, G. Fault diagnosis and fault tolerant control for nonlinear satellite attitude control systems. Aerosp. Sci. Technol. 2014, 33, 9–15. [Google Scholar] [CrossRef]
- Rosli, R.E.; Sulong, A.B.; Daud, W.R.W.; Zulkifley, M.A.; Husaini, T.; Rosli, M.I.; Majlan, E.H.; Haque, M.A. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrogen Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Ayağ, Z.; Özdemir, R.G. A fuzzy AHP approach to evaluating machine tool alternatives. J. Intell. Manuf. 2006, 17, 179–190. [Google Scholar] [CrossRef]
- Dağdeviren, M.; Yavuz, S.; Kılınç, N. Weapon selection using the AHP and TOPSIS methods under fuzzy environment. Expert Syst. Appl. 2009, 36, 8143–8151. [Google Scholar] [CrossRef]
- Wang, C.N.; Thanh, N.V.; Su, C.C. The Study of a Multicriteria Decision Making Model for Wave Power Plant Location Selection in Vietnam. Processes 2019, 7, 650. [Google Scholar] [CrossRef] [Green Version]
- Yimen, N.; Dagbasi, M. Multi-Attribute Decision-Making: Applying a Modified Brown–Gibson Model and RETScreen Software to the Optimal Location Process of Utility-Scale Photovoltaic Plants. Processes 2019, 7, 505. [Google Scholar] [CrossRef] [Green Version]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Majumder, M. Impact of Urbanization on Uater Shortage in Face of Climatic Aberrations; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Jin, G.; Sperandio, S.; Girard, P. Selection of design project with the consideration of designers’ satisfaction factors and collaboration ability. Comput. Ind. Eng. 2019, 131, 66–81. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Kizielewicz, B.; Shekhovtsov, A.; Yelmikheiev, M.; Kozlov, V.; Sałabun, W. Comparative Analysis of Solar Panels with Determination of Local Significance Levels of Criteria Using the MCDM Methods Resistant to the Rank Reversal Phenomenon. Energies 2021, 14, 5727. [Google Scholar] [CrossRef]
- Nesticò, A.; Somma, P. Comparative analysis of multi-criteria methods for the enhancement of historical buildings. Sustainability 2019, 11, 4526. [Google Scholar] [CrossRef] [Green Version]
- Nesticò, A.; Elia, C.; Naddeo, V. Sustainability of urban regeneration projects: Novel selection model based on analytic network process and zero-one goal programming. Land Use Policy 2020, 99, 104831. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Vansnick, J.C. On the problem of weights in multiple criteria decision making (the noncompensatory approach). Eur. J. Oper. Res. 1986, 24, 288–294. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ergu, D. When is a decision-making method trustworthy? Criteria for evaluating multi-criteria decision-making methods. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1171–1187. [Google Scholar] [CrossRef]
- Roy, B.; Słowiński, R. Questions guiding the choice of a multicriteria decision aiding method. EURO J. Decis. Process. 2013, 1, 69–97. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. Relative measurement and its generalization in decision making why pairwise comparisons are central in mathematics for the measurement of intangible factors the analytic hierarchy/network process. RACSAM-Rev. Real Acad. Cienc. Exactas Fis. Naturales. Ser. A Mat. 2008, 102, 251–318. [Google Scholar] [CrossRef]
- Jin, G.; Sperandio, S.; Girard, P. Management of the design process: Human resource evaluation in factories of the future. Concurr. Eng. 2018, 26, 313–327. [Google Scholar] [CrossRef]
- Saaty, T.L. Analytic Network Process; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ginting, G.; Fadlina, M.; Siahaan, A.P.U.; Rahim, R. Technical approach of TOPSIS in decision making. Int. J. Recent Trends Eng. Res. 2017, 3, 58–64. [Google Scholar]
- Dyer, J.S. Multiattribute utility theory (MAUT). In Multiple Criteria Decision Analysis; Springer: New York, NY, USA, 2016; pp. 285–314. [Google Scholar]
- Figueira, J.R.; Mousseau, V.; Roy, B. ELECTRE methods. In Multiple Criteria Decision Analysis; Springer: New York, NY, USA, 2016; pp. 155–185. [Google Scholar]
- Brans, J.P.; de Smet, Y. PROMETHEE methods. In Multiple Criteria Decision Analysis; Springer: New York, NY, USA, 2016; pp. 187–219. [Google Scholar]
- Işık, A.T.; Adalı, E.A. UTA Method for the Consulting Firm Selection Problem. J. Eng. Sci. Technol. Rev. 2016, 9, 56–60. [Google Scholar] [CrossRef]
- Manshadi, E.D.; Mehregan MR Safari, H. Supplier classification using UTADIS method based on performance criteria. Int. J. Acad. Res. Bus. Soc. Sci. 2015, 5, 31. [Google Scholar] [CrossRef] [Green Version]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Goswami, S.S.S.; Behera, D.K.K.; Afzal, A.; Razak Kaladgi, A.; Khan, S.A.A.; Rajendran, P.; Subbiah, R.; Asif, M. Analysis of a Robot Selection Problem Using Two Newly Developed Hybrid MCDM Models of TOPSIS-ARAS and COPRAS-ARAS. Symmetry 2021, 13, 1331. [Google Scholar] [CrossRef]
- Dezert, J.; Tchamova, A.; Han, D.; Tacnet, J.M. The spotis rank reversal free method for multi-criteria decision-making support. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; IEEE: Rustenburg, South Africa, 2020; pp. 1–8. [Google Scholar]
- Munier, N. A new approach to the rank reversal phenomenon in MCDM with the SIMUS method. Mult. Criteria Decis. Mak. 2016, 11, 137–152. [Google Scholar] [CrossRef]
- Boudreau-Trudel, B.; Zaras, K. Comparison of analytic hierarchy process and dominance-based rough set approach as multi-criteria decision aid methods for the selection of investment Comparison of analytic hierarchy process and dominance-based rough set approach as multi-criteria decision aid methods for the selection of investment projects. Am. J. of Ind. Bus. Manag. 2012, 2, 7–12. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. Indersci. 2008, 1, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Expert. The Analytic Hierarchy Process (AHP).DTU Transport Compendium Series Part 2, Technical University of Denmark 2014. Available online: http://www.systemicplanning.dk/AHP.pdf (accessed on 21 November 2021).
- Liu, D.; Huang, A.; Liu, Y.; Liu, Z. An Extension TOPSIS Method Based on the Decision Maker’s Risk Attitude and the Adjusted Probabilistic Fuzzy Set. Symmetry 2021, 13, 891. [Google Scholar] [CrossRef]
- Agrawal, A.; Seh, A.H.; Baz, A.; Alhakami, H.; Alhakami, W.; Baz, M.; Kumar, R.; Khan, R.A. Software security estimation using the hybrid fuzzy ANP-TOPSIS approach: Design tactics perspective. Symmetry 2020, 12, 598. [Google Scholar] [CrossRef] [Green Version]
- Sahu, K.; Alzahrani, F.A.; Srivastava, R.K.; Kumar, R. Hesitant fuzzy sets based symmetrical model of decision-making for estimating the durability of Web application. Symmetry 2020, 12, 1770. [Google Scholar] [CrossRef]
- Lai, Y.J.; Liu, T.Y.; Hwang, C.L. Topsis for MODM. Eur. J. Oper. Res. 1994, 76, 486–500. [Google Scholar] [CrossRef]
- Wang, T.C.; Chang, T.H. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst. Appl. 2007, 33, 870–880. [Google Scholar] [CrossRef]
- Alinezhad, A.; Khalili, J. COPRAS Method. In New Methods and Applications in Multiple Attribute Decision Making (MADM); Springer: Cham, Switzerland, 2019; pp. 87–91. [Google Scholar]
- Liou, J.J.; Tamošaitienė, J.; Zavadskas, E.K.; Tzeng, G.H. New hybrid COPRAS-G MADM Model for improving and selecting suppliers in green supply chain management. Int. J. Prod. Res. 2016, 54, 114–134. [Google Scholar] [CrossRef]
- Roy, J.; Kumar Sharma, H.; Kar, S.; Kazimieras Zavadskas, E.; Saparauskas, J. An extended COPRAS model for multi-criteria decision-making problems and its application in web-based hotel evaluation and selection. Econ. Res.-Ekon. Istraživanja 2019, 32, 219–253. [Google Scholar] [CrossRef] [Green Version]
- Faizi, S.; Sałabun, W.; Nawaz, S.; ur Rehman, A.; Wątróbski, J. Best-Worst method and Hamacher aggregation operations for intuitionistic 2-tuple linguistic sets. Expert Syst. Appl. 2021, 181, 115088. [Google Scholar] [CrossRef]
- Božanić, D.; Milić, A.; Tešić, D.; Salabun, W.; Pamučar, D. D numbers–fucom–fuzzy rafsi model for selecting the group of construction machines for enabling mobility. Facta Univ. Ser. Mech. Eng. 2021, 19, 447–471. [Google Scholar] [CrossRef]
- Kraujalienė, L. Comparative analysis of multicriteria decision-making methods evaluating the efficiency of technology transfer. Bus. Manag. Educ. 2019, 17, 72–93. [Google Scholar]
- Cinelli, M.; Kadziński, M.; Gonzalez, M.; Słowiński, R. How to support the application of multiple criteria decision analysis? Let us start with a comprehensive taxonomy. Omega 2020, 96, 102261. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Haji Yakchali, S.; Kazimieras Zavadskas, E. Using a integrated MCDM model for mining method selection in presence of uncertainty. Econ. Res.-Ekon. Istraživanja 2012, 25, 869–904. [Google Scholar] [CrossRef] [Green Version]
- Štirbanović, Z.; Stanujkić, D.; Miljanović, I.; Milanović, D. Application of MCDM methods for flotation machine selection. Miner. Eng. 2019, 137, 140–146. [Google Scholar] [CrossRef]
- Sarrate, R.; Nejjari, F.; Rosich, A. Sensor Placement for Fault Diagnosis Performance Maximization under Budget Constraints. Available online: http://digital.csic.es/bitstream/10261/97613/4/Sensor%20placement.pdf (accessed on 21 November 2021).
- Guerrero-Baena, M.D.; Gómez-Limón, J.A.; Fruet Cardozo, J.V. Are multi-criteria decision making techniques useful for solving corporate finance problems? A bibliometric analysis. Rev. Metodos Cuantitativos Para La Econ. La Empresa 2014, 17, 60–79. [Google Scholar]
- Wang, Y.M.; Elhag, T.M.S. An approach to avoiding rank reversal in AHP. Decis. Support Syst. 2006, 42, 1474–1480. [Google Scholar] [CrossRef]
- Omar, F.; Bushby, S.T.; Williams, R.D. Assessing the performance of residential energy management control Algorithms: Multi-criteria decision making using the analytical hierarchy process. Energy Build. 2019, 199, 537–546. [Google Scholar] [CrossRef]
- Saaty, T.L. What is the analytic hierarchy process? In Mathematical Models for Decision Support; Springer: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Normalization Techniques for Multi-Criteria Decision Making: Analytical Hierarchy Process Case Study. In Proceedings of the Doctoral Conference on Computing, Electrical and Industrial Systems, Costa de Caparica, Portugal, 11–13 April 2016; Springer: Cham, Switzerland, 2016; pp. 261–269. [Google Scholar]
- Chakraborty, S.; Yeh, C.H. A simulation comparison of normalization procedures for TOPSIS. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; IEEE: Troyes, France, 2009; pp. 1815–1820. [Google Scholar]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-oriented modeling and analysis for automotive fuel cell systems. J. Dyn. Syst. Meas. Control 2004, 126, 14–25. [Google Scholar] [CrossRef]
- Pukrushpan, J.T. Modeling and Control of Fuel Cell Systems and Fuel Processors; University of Michigan: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Rosich Oliva, A. Sensor placement for fault diagnosis based on structural models: Application to a fuel cell stak system. Tesi doctoral, UPC, Institut d’Organització i Control de Sistemes Industrials. 2011. Available online: http://hdl.handle.net/2117/94510. (accessed on 21 November 2021).
- Díaz, J.; Fernández, F.J. The impact of hot metal temperature on CO2 emissions from basic oxygen converter. Environ. Sci. Pollut. Res. 2019, 27, 33–42. [Google Scholar] [CrossRef]
- Fernández, F.J.; Folgueras, M.B.; Suárez, I. Energy study in water loop heat pump systems for office buildings in the Iberian Peninsula. Energy Procedia 2017, 136, 91–96. [Google Scholar] [CrossRef]
- Enguita, J.M.; Alvarez, I.; Bobis, C.F.; Marina, J.; Fernández, Y.; Sirat, G.Y. Conoscopic holography-based long-standoff profilemeter for surface inspection in adverse environment. Opt. Eng. 2006, 45, 073602. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, Q.; Shi, H.; Zhang, J. An improved compact genetic algorithm for scheduling problems in a flexible flow shop with a multi-queue buffer. Processes 2019, 7, 302. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Cham, Switzerland, 2020; pp. 632–645. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).