Abstract
In this paper, we define D-magic labelings for oriented graphs where D is a distance set. In particular, we label the vertices of the graph with distinct integers in such a way that the sum of all the vertex labels that are a distance in D away from a given vertex is the same across all vertices. We give some results related to the magic constant, construct a few infinite families of D-magic graphs, and examine trees, cycles, and multipartite graphs. This definition grew out of the definition of D-magic (undirected) graphs. This paper explores some of the symmetries we see between the undirected and directed version of D-magic labelings.
1. Introduction
A labeling of a graph or digraph is simply defined as an assignment of numbers (usually integers) to the vertices, edges, or both, such that certain conditions hold. There are many different types of labelings as can be seen in Gallian’s survey [1]. However, most of these labelings are defined on undirected graphs. In 1985, Bloom and Hsu introduced graceful labelings on directed graphs [2]. In 2008, magic labelings of directed graphs were introduced in [3]. Other magic-type labelings on directed graphs have been studied in [4,5,6,7,8,9].
In Vilfred’s 1994 Ph.D. thesis, distance magic labelings were introduced [10]. A distance magic labeling, or Σ labeling, of a graph G on n vertices is a bijection such that at any vertex x, the weight of x, is constant, where is the open neighbourhood of x, i.e., the set of vertices adjacent to x. Five years later, Jinah [11] defined a variation of the distance magic labeling, called the closed distance magic labeling, where the weight of a vertex x is summed over the closed neighbourhood of x, i.e., the set containing x and all vertices adjacent to x. D-magic labelings were first introduced by O’Neal and Slater as a generalization of these two previously mentioned labelings [12].
Definition 1.
Let G be a graph with n vertices and diameter . Let be a set of distances in G. G is said to be D-magic if there exists a bijection and a magic constant k such that for any vertex x, , where is the D-neighbourhood set of x.
One of the most important results for D-magic labelings is in [13,14] where it is shown that for a particular graph, the magic constant is unique and is determined by its fractional domination number. For more results, refer to survey articles [15,16].
In this paper, we explore the directed version of D-magic labelings.
2. Definitions and Notation
2.1. Oriented Graphs
An oriented graph G can be described as a collection of vertices together with a collection of ordered pairs of vertices called directed edges. If there is an edge , we may write . By definition, oriented graphs do not contain any repeated directed edges, contain no loops (i.e., edges of the form ) and they do not contain bidirectional edges, i.e., if , then . The underlying graph of an oriented graph G is the graph that is obtained by removing the orientations of the directed edges in G. We shall write and .
2.2. Partitions
The ability to partition the integers into sets with equal sums is a critical component of creating magic-type labelings of graphs. Hence, we include a definition and useful result related to integer partitions here.
Definition 2
([17]). An -partition of is a partition of into s subsets, each with sum t.
Theorem 1
([17]). If , , then there exists an -partition of .
2.3. D-Magic Oriented Graphs
Motivated by the previously mentioned definitions, we now introduce a definition for D-magic oriented graphs.
Definition 3.
Let G be an oriented graph with n vertices and diameter . Let be a set of distances in G. An oriented graph G has a D-magic labeling if there is a bijection and a magic constant k such that at any vertex
where
If G admits a D-magic labeling, then G is D-magic. The sum, , at each vertex is the weight.
The smallest example of a D-magic oriented graph is , which is -magic. This is the only oriented graph that is -magic as any graph with two or more vertices would produce distinct weights at each vertex. As we will see in Section 4, there are no D-magic oriented graphs of order 2. For graphs of order 3, there is a -magic labeling of . The smallest non-trivial example is , which is , and -magic.
3. Properties of -Magic Oriented Graphs
In this section, we prove some general properties of D-magic oriented graphs. We start with an observation that is a direct consequence of Definition 3.
Remark 1.
Let and be two disjoint sets of distances. If a labeling is both -magic and -magic then it is also -magic.
In the next lemma we show that a D-magic oriented graph consists of at most one sink, i.e., a vertex of outdegree zero.
Lemma 1.
If G is D-magic, then G contains at most one vertex of outdegree zero. If there is such a vertex, and the magic constant is n.
Proof.
If a vertex has outdegree zero, then it has no vertices of distance away from it. Hence, the only label that could contribute to the sink’s weight would be the label on the vertex itself. Thus, . In addition, if two or more vertices were of outdegree zero, then their weights would not be equal as the only contributing values would be the label on that vertex and vertex labels are not repeated. Finally, if any vertex other than the sink had label n, then the weight at that vertex would be at least n, while the sink’s weight would be no larger than . This is a contradiction as all the weights must be equal. Hence, the sink must have label n and thus, the magic constant of any graph with a sink is n. □
There is an infinite family of graphs with a single vertex of outdegree zero that permit an orientation that is D-magic. Consider the graph G with vertices with . G consists of two distinct cycles of length with vertex sets and , a vertex v that is connected to exactly one vertex in each cycle and a vertex w that is only connected to vertex v. The oriented edges are as follows: for . Then, we can create the bijection such that
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = |
Then, f is a -magic labeling of G with magic constant and vertex w has outdegree zero. Figure 1 provides an example of this construction when .
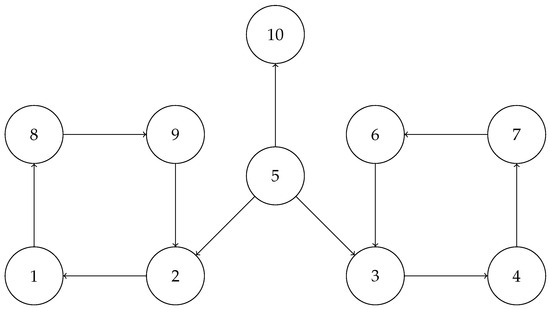
Figure 1.
A -magic graph with magic constant 10 and a vertex of outdegree zero.
In the remainder of this section, we discuss properties of the magic constants. Contrary to the fact that the magic constant for an undirected graph is unique, the D-magic constant does not have to be the same for any given oriented graph. The proof of the uniqueness in [15] relies on the fact that the graph’s adjacency matrix is the same as its transpose which does not occur for oriented graphs. The example in Figure 2 shows two different magic constants for the same oriented graph.
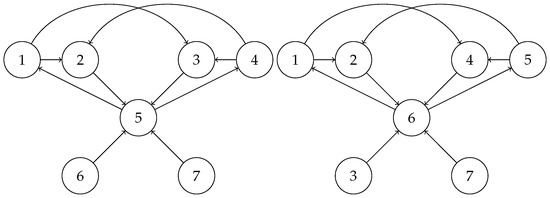
Figure 2.
{1}-magic oriented graphs with different magic constants.
In the next theorem, we provide tight lower and upper bounds for the magic constants of an oriented graph.
Theorem 2.
If G is a D-magic oriented graph with magic constant k and , then . Furthermore, iff and .
Proof.
First, we will show the magic constant cannot be less than 5. Suppose . Let be the vertex with label i.
- If and then and thus would not have the magic constant as its weight. Thus, , but then there is no way for .
- If and , . Thus, , but then as there are no sums of the remaining vertex labels that would total to two.
- If and , then in order for we would need both and , creating a bidirectional edge. Since , we would have that would need to be some distance away from . However, would also have to be distance away from (as this is the only way for ). Suppose without loss of generality that . If , then and we would have a vertex x on the path from to that would be distance away from something larger than three, and thus . If , then would also be distance away from something other than , giving . Thus, in all cases, we arrive at a contradiction.
- A similar argument holds if using and (instead of and ).
Thus, k must be at least 5 and the construction in Theorem 3 shows that is possible. If , then every label is counted at each vertex giving . Conversely, we know that if , the sum at every vertex is equal to the sum of the first n positive integers which would only happen if every vertex label was included. Hence, and . □
OpenQuestion 1.
Characterize all oriented graphs with .
OpenQuestion 2.
Find a better upper bound for k if .
In the following theorem, we construct a -magic oriented graph of order n for each value of k from 5 up to n.
Theorem 3.
For , there exists an oriented graph G of order n which is -magic with magic constant k.
Proof.
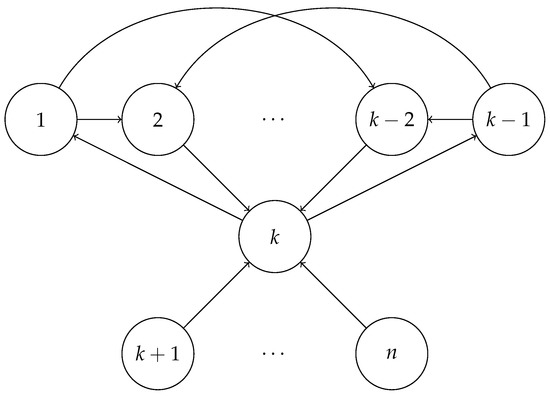
Figure 3 gives the construction technique for any n. All vertices with labels between 2 and are directed towards the vertex labeled k. All vertices with labels between and n are also directed towards the vertex labeled k. The vertex with label k can be directed towards the vertices labeled 1 and . Finally, the vertices 1 and are directed towards the vertices labeled 2 and . □

Figure 3.
Construction technique for magic constant k.
OpenQuestion 3.
For , construct an oriented graph of order n which is -magic with magic constant k.
OpenQuestion 4.
For and , construct an oriented graph G of order n which is D-magic with magic constant k.
4. Classes of -Magic Oriented Graphs
4.1. Trees
Lemma 2.
Any tree with only one sink (vertex of outdegree zero) must have all edges directed towards the sink.
Proof.
Suppose a tree has a least one edge directed away from the sink. Suppose this edge goes from vertex v to vertex u. Then, vertex u must have at least one edge that is directed outward (otherwise u would also be a sink) and away from the sink, to some new vertex w. This new vertex, w, would also have an edge directed outward and away from the sink. This would continue at each new vertex in this outward directed path until we reach a leaf. However, then this leaf would have outdegree zero, a contradiction. Thus, all edges must be directed toward the sink. □
Theorem 4.
Trees with are not D-magic for any distance set D.
Proof.
Suppose there is an oriented tree that is D-magic. By Lemma 1, any D-magic tree can have at most one vertex of outdegree zero, and since any oriented tree has at least one vertex of outdegree zero, we know the tree will have exactly one vertex of outdegree zero, say vertex v. If the tree contains only one vertex of outdegree zero, than all edges must be directed towards that vertex by Lemma 2. This oriented tree will have a path of longest length, say length d. We know , but we also know as this would cause the weight of some vertex to be greater than n. In addition, no value less than d can be in D as this would allow a vertex on that longest path to have a weight greater than n. Finally, there are no paths of length greater than d, so no other values can be added to D. Hence, the only possible element in D is 0, but that does not create a D-magic graph. Thus, no orientation of trees are D-magic for any set D. □
4.2. Cycles
Lemma 3.
If an oriented cycle is D-magic, then the orientation must be unidirectional.
Proof.
By Lemma 1, any oriented cycle can have at most one vertex of outdegree zero. Hence, the only orientations which would satisfy this would be the unidirectional cycle (with no vertices of outdegree zero) or the cycle where there is a source and a sink with two unidirectional paths leaving the source and leading to the sink. However, this second orientation is not possible. The vertex of outdegree zero must have label n. Furthermore, at least one of the two vertices coming into that vertex must have outdegree one (otherwise we would have two vertices of outdegree zero); let that vertex be v. Then, v is at distance one from the vertex with label n and that is its only out-neighbor. Hence, any contributions to the weight of that vertex will come from values that are at distance zero or one away. However, this is a problem as the magic constant must be n, , and we know at least one other number must be in D in order for vertex v to have a sum equal to n, but the only other possibility to add to D to increase the weight of v is to add one to D, but this makes the weight of v greater than n. Hence a D-magic labeling of this orientation is not possible and thus the only orientations of a cycle that are D-magic are unidirectional. □
Theorem 5.
There exist D such that is D-magic for all . In particular, let be the divisors of n. If such that and , then is D-magic with and .
Proof.
For any cycle, , will give a D-magic graph with magic constant as at any vertex, all labels will be counted in the sum.
Let be a divisor of n. Let . Then, if is the vertex set of , we can partition this set into sets, , each of size , where and is formed by adding (modulo n) to each of the subscripts of the entries of . Since this partitions the set n into sets and for some , by Theorem 1, we know there is a way to label the vertices with values from so that the sum of the labels of each of these vertex sets is the same. □
By construction of these D-magic labelings, if is D-magic, it is also -magic where consists of the elements of D that have each been increased by c (mod n) and . So, for example, is -magic and thus also -magic and -magic. Combining this with Remark 1, we also know is -magic, -magic, -magic, and of course -magic.
OpenQuestion 5.
Find all Ds s.t. is D-magic.
4.3. Multipartite Graphs
Theorem 6.
For (mod 4), there is an orientation of that is D-magic for or any D that is a union of these sets.
Proof.
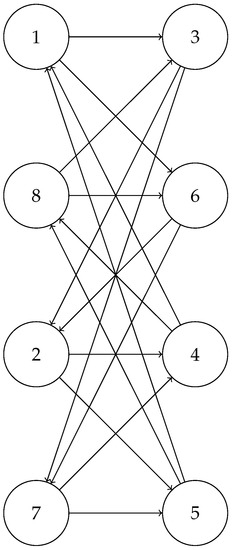
Let be the complete bipartite graph with partite sets and . Note that has vertices. First, we group the vertices within each partite set into pairs. In A, this would give sets and . Within each set of two, label one vertex s and the other vertex for . This would give a sum of for each set of pairs. Then, orient the edges in the following way: vertices in will be oriented to vertices in the sets and vertices in will be oriented to vertices in the sets where all additions are done modulo . Thus, each vertex is oriented towards pairs of vertices and hence each vertex is oriented towards vertices. This gives a total of edges and thus each edge is accounted for and has only one orientation. This gives a magic constant of for any . The magic constant would be for any union of two sets, for any union of three sets, and for the union of all four sets. Figure 4 gives an example of this labeling when . □

Figure 4.
An orientation of that is D-magic.
OpenQuestion 6.
Is D-magic for (mod 4)?
Theorem 7.
(a) Let be odd and . If and , then there exists a partition of n into s parts such that and has an orientation that is -magic with magic constant , -magic with magic constant , and -magic with magic constant .
(b) Let be even and . If and , then there is a partition of n into s parts with and (where I is a 1-factor) has an orientation that is -magic with magic constant , -magic with magic constant , and -magic with magic constant .
Proof.
Let be the vertices of . We decompose into Hamiltonian cycles using Walecki’s construction where each cycle starts at [18]. Then, orient each cycle in a clockwise direction starting at the vertex . This will give each vertex edges directed outward and edges directed inward. Then, we replace each vertex of with vertices for and maintain all the original connections. For example, in , would be connected to and so in our newly constructed graph, all the vertices now at would be connected to all the vertices now at . Using Theorem 1, we label the vertices of each new set of replaced vertices with values so that each new set of vertices has the same sum, t.
Thus, every vertex will be at distance one away from sets of vertices and each set sums to t, giving a -magic constant of . Similarly, since every vertex in a oriented complete graph is at distance one or two away from any other vertex, we also have that every vertex will be at distance two away from sets of vertices and each set sums to t, giving a -magic constant of . Finally, since all vertices are at distance one or two away from each other, the -magic constant is .
In a similar way, we can decompose into Hamiltonian cycles using Walecki’s construction where each cycle starts at [18]. Then, orient each cycle in a clockwise direction starting at the vertex . This gives each vertex edges directed outward. Then, we replace each vertex of with vertices for and maintain all the original connections. In this case, every vertex will be at distance one away from sets of vertices and each set sums to t, giving a -magic constant of . Similarly, since every vertex in this orientation of is at distance one or two away from any other vertex, we also have that every vertex is at distance two away from sets of vertices and each set sums to t, giving a -magic constant of . Finally, since all vertices are distance one or two away from each other, the -magic constant is . □
OpenQuestion 7.
Let , s even, and . Is D-magic for some nontrivial D-set?
5. Conclusions
As can be seen by the questions posed, the study of D-magic oriented graphs is rich with future directions. One possible avenue of additional research is to determine for a given arbitrary oriented graph which D sets make the graph D-magic. Conversely, one could start with a given D set and ask which oriented graphs are D-magic.
Exploring the symmetries between oriented D-magic graphs and D-magic graphs, we see that both have trivial D sets that produce a D-magic labeling (when and ). While trees, cycles, and multipartite graphs have been studied in both cases, the results are quite different. For example, a complete multipartite graph is not -magic, but we have shown there is an orientation of various complete multipartite graphs with a -magic labeling. We also know that is -magic, but there is no orientation that makes it a -magic oriented graph. Hence, it would be worth knowing under what conditions a D-magic graph has an orientation that is also D-magic.
Similarly, while the magic constant is unique in the unoriented case, the magic constant does not have to be unique in the oriented case. While we did not allow for bidirectional edges, if bidirectional edges were allowed, any D-magic graph could be oriented to be D-magic by replacing each edge with a bidirectional edge. Exploring these symmetries further is also an interesting line of future work.
Author Contributions
Conceptualization, A.M. and R.S.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and R.S.; funding acquisition, A.M. and R.S. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
R.S. was partially funded by World Class Research 2019–2021 (Indonesian National Research and Innovation Agency), Grant Number 1220/1T1.C02/TA.OO/2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gallian, J.A. A Dynamic Survey of Graph Labeling. Electron. J. Comb. 2020, 1, #DS6. [Google Scholar]
- Bloom, G.S.; Hsu, D.F. On graceful directed graphs. SIAM J. Algebraic Discret. Methods 1985, 6, 519–536. [Google Scholar] [CrossRef]
- Bloom, G.S.; Marr, A.; Wallis, W.D. Magic digraphs. J. Comb. Math. Comb. Comput. 2008, 65, 205–212. [Google Scholar]
- Balakrishnan, M.; Marimuthu, G.; Arumugam, S. Vertex in-magic arc labelings of digraphs. Electron. Notes Discret. Math. 2015, 48, 33–39. [Google Scholar] [CrossRef]
- Guruvaiah, D.D.; Morekondan, S.R.D.; Marimuthu, G.T. V-super vertex out-magic total labelings of digraphs. Commun. Korean Math. Soc. 2017, 32, 435–445. [Google Scholar]
- Marr, A. Magic vertex labelings of digraphs. Int. J. Math. Comput. Sci. 2009, 4, 91–96. [Google Scholar]
- Arumugam, S.; Balakrishnan, M.; Marimuthu, G. E-super vertex in-magic total labelings of digraphs. Electron. Notes Discret. Math. 2015, 48, 111–118. [Google Scholar] [CrossRef]
- Marr, A. Sparse semi-magic squares and magic labelings of directed graphs. Electron. Notes Discret. Math. 2015, 48, 3–10. [Google Scholar] [CrossRef]
- Marr, A.; Ochel, S.; Perez, B. In-magic total labelings of digraphs. J. Graph Label. 2015, 1, 81–93. [Google Scholar]
- Vilfred, V. Sigma Labelled Graphs and Circulant Graphs. Ph.D. Thesis, University of Kerala, Thiruvananthapuram, India, 1994. [Google Scholar]
- Jinnah, M.I. On Σ-labelled graphs. In Proceedings of Group Discussion on Graph Labeling Problems; KREC: Surathkal, India, 1999; pp. 71–77. [Google Scholar]
- O’Neal, A.; Slater, P. An introduction to distance D-magic graphs. J. Indones. Math. Soc. 2011, 89–107. [Google Scholar] [CrossRef] [Green Version]
- Arumugam, S.; Kamatchi, N.; Vijayakumar, G.R. On The Uniqueness of D-Vertex Magic Constant. Discuss. Math. Graph Theory 2014, 34, 1–8. [Google Scholar] [CrossRef]
- O’Neal, A.; Slater, P. Uniqueness Of Vertex Magic Constants. SIAM J. Disc. Math. 2013, 27, 708–716. [Google Scholar] [CrossRef]
- Arumugam, S.; Froncek, D.; Kamatchi, N. Distance Magic Graphs—A Survey. J. Indones. Math. Soc. 2011, 11–26. [Google Scholar] [CrossRef] [Green Version]
- Rupnow, R. A Survey of Distance Magic Graphs. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2014. [Google Scholar]
- Straight, H.J.; Schillo, P. On the problem of partitioning {1,2,…,n} into subsets having equal sums. Proc. Am. Math. Soc. 1979, 74, 229–231. [Google Scholar] [CrossRef] [Green Version]
- Alspach, B. The Wonderful Walecki construction. Bull. Inst. Comb. Appl. 2008, 52, 7–20. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).