Nuclear Structure Evolution Reflected from Local Relations

Abstract

The structure evolution of nuclei which are in connection with symmetry breaking is one of the important problems not only for nuclear structures, but also for astrophysics and the spectroscopy of exotic nuclei. Many physical quantities can provide useful information of a shell structure, such as nuclear masses and nuclear charge radii. This paper introduces three kinds of local relations, i.e., the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme respectively for the quadrupole deformation parameter and the excitation energy of the first $2^{+}$, $4^{+}$, $6^{+}$ states, the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation for nuclear charge radii and $\alpha$ decay energies, and the so-called “nonpairing” relation for binding energies and nuclear charge radii. All these relations reflect the evolution of nuclear structures, involving shells, subshells, shape coexistence, phase transition and the Wigner effect. Some results from different models can be verified with each other.

1. Introduction

The shell structure is found in many physical systems, such as atoms and nuclei. In the early 1930s, Bartlett discovered certain regularities in the composition of atomic nuclei and speculated that nucleons within nuclei might have their own shell structure [1,2,3]. Subsequently, more systematic studies were conducted by Elsasser, and it was found experimentally that some properties of the nucleus present obvious periodic changes as the number of protons or neutrons increase, and nuclei with several special proton or neutron numbers are particularly stable [4,5,6]. These special numbers are called “magic numbers”, and were explained successfully by Mayer [7,8,9] and Jensen et al. [10,11,12,13,14] through introducing spin-orbit coupling in the mean field. The nuclear shell model, which represents magic numbers as well as experimental phenomena, such as spin, parity, magnetic moment and beta decay, was successfully developed through this line [15], and was proved to be very useful in studying the low-lying states of nuclei [16,17,18].

Nuclear mass (or binding energy) is a fundamental quantity of an atomic nucleus, and its measurement played an important role in the building of the nuclear shell model [7,8,9,10,11,12,13,14,15]. The shell structure of a neutron (proton) can be determined effectively by the double-neutron (-proton) separation energies, for their sudden decrease at magic numbers. For the nuclei away from the stability line, the binding energy decreases, and they become weak-bounded open systems near the drip line. These unstable nuclei may have different magic numbers and systematic evolution of their structures, which is in connection with the symmetry breaking that may arise [19]. In the early years, research was focused on nuclei with a small mass number, due to the limited experimental conditions. Nowadays, more than 3000 nuclei are synthesized experimentally [20,21,22] and more information of the nuclear structure can be obtained.

The structure evolution of nuclei, which is directly reflected in the ground and low-lying states, is one of the advanced topics of nuclear structure, and is also involved in astrophysics and the spectroscopy of exotic nuclei. Recently, many efforts were made toward describing and predicting physical quantities, which provide useful information of shell structure, such as nuclear masses, $\alpha$-decay energies, nuclear charge radii and so on. Some of these works that give relations connecting physical quantities of several neighbor nuclei or reveal certain phenomenon in local regions are called “local” relations, for example, the Garvey–Kelson mass relations [23,24], relations connected with neutron–proton interactions [25,26,27,28,29,30], and the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme [31,32,33,34,35]. In this paper, three kinds of local relations and corresponding information reflecting nuclear structure evolutions are introduced and discussed.

2. Local Relations

In this section, three kinds of local relations that can reflect nuclear structure evolutions are introduced, and the corresponding discussions are made.

2.1. The $N_{\mathrm{p}}{N}_{\mathrm{n}}$ Scheme of the Quadrupole Deformation Parameter $e_2$ or the Excitation Energy $E_{2_1^{+}}$, $E_{4_1^{+}}$ and $E_{6_1^{+}}$

The $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme was described by Casten, where $E_{2_1^{+}}$, $E_{4_1^{+}}/E_{2_1^{+}}$ and $B(E2,0_1^{+}\to 2_1^{+})$ for even–even nuclei exhibit smooth systematics against the product of valence proton number $N_{\mathrm{p}}$ and valence neutron number $N_{\mathrm{n}}$ [31,36,37]. It works equally well for the quadrupole deformation parameter $e_2$ (correlated with the intrinsic quadrupole moment) of all parity types of medium-heavy nuclei in Ref. [34].

In Figure 1, the absolute value of $e_2$ in the Nilsson perturbed–spheroid parameterization taken from Ref. [38] is presented versus $N_{\mathrm{p}}{N}_{\mathrm{n}}$ for nuclei in three different regions [34]. Here only $e_2$ of nuclei with known experimental binding energies [22] are plotted. As discussed in Ref. [34], the correlation between $e_2$ and $N_{\mathrm{p}}{N}_{\mathrm{n}}$ shown in Figure 1 is very compact, except for several anomalies which are labeled by the red circles in Figure 1a and marked by a red circle in Figure 1b,c.

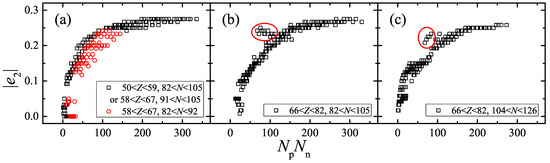
Figure 1. $|e_2|$ in the Nilsson perturbed–spheroid parametrization [38] versus $N_{\mathrm{p}}{N}_{\mathrm{n}}$. (a) For nuclei with $50<Z<67$ and $82<N<105$. (b) For nuclei with $66<Z<82$ and $82<N<105$. (c) For nuclei with $66<Z<82$ and $104<N<126$. The anomalies are labeled by the red circles in panel (a) and marked by a red circle in panels (b,c).

Affected by the $Z=64$ subshell, the red circles in Figure 1a, which correspond to $e_2$ of nuclei with $58<Z<67$ and $82<N<92$, deviate from the other black squares [34]. In addition, $e_2$ of $N=84$ isotones equals 0 as shown in Figure 1a, which is because these nuclei are soft and the difference between the equilibrium deformation and the expected value of the deformation is large [34].

Those anomalies in Figure 1b,c correspond to nuclei with $Z=77$ or 78 and $N=99\sim 109$, which belong to a complex region where there exists large $\gamma$ softness, deformation and transition [34]. In Ref. [35], similar anomalies are pointed out in the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme for the excitation energy of the first $2^{+}$ state $E_{2_1^{+}}$ of even–even nuclei with $Z=78$ or 80 and $83<N<105$, based on the experimental data taken from Ref. [39] (see Figure 2a with the anomalies labeled by the red circles). However, it is no longer obvious with the updated experimental data taken from Ref. [40], as shown in Figure 2b.

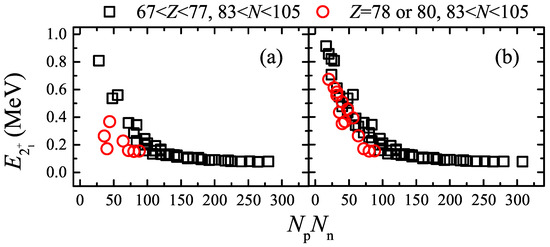
Figure 2. $E_{2_1^{+}}$ versus $N_{\mathrm{p}}{N}_{\mathrm{n}}$ for even-even nuclei with $67<Z<81$ and $83<N<105$. The experimental data are taken from Ref. [39] for panel (a) [35] and Ref. [40] for panel (b), respectively. The red circles correspond to the $E_{2_1^{+}}$ of nuclei with $Z=78$ or 80 and $83<N<105$.

In Ref. [41], $e_2$ is further discussed with the P factor, i.e., $N_{\mathrm{p}}{N}_{\mathrm{n}}/(N_{\mathrm{p}}+N_{\mathrm{n}})$, in the same region of Figure 1b,c. $|e_2|$ in the Nilsson perturbed–spheroid parametrization [38] is plotted versus the P factor in Figure 3, where nuclei with $66<Z<76$ are labeled by black squares, and isotopes with $Z=76\sim 81$ are labeled by colored dots. With the increase in factor P, $|e_2|$ grows smoothly and becomes flat around $P\sim 6$ [41].

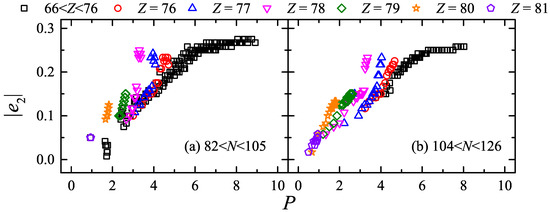
Figure 3. $|e_2|$ in the Nilsson perturbed–spheroid parametrization [38] versus the P factor. Panel (a,b) corresponds to $82<N<105$ and $104<N<126$, respectively. Nuclei with $66<Z<76$ are labeled by black squares, and isotopes with $Z=76\sim 81$ are labeled by red circles, blue up triangles, pink down triangles, green diamonds, orange stars and violet pentagons, respectively.

It is seen that some colored dots depart from black squares obviously. Most of these anomalies correspond to nuclei with $N=97\sim 104$ in Figure 3a and with $N=105\sim 109$ in Figure 3b, which near the midshell $N=104$. This is explained by Ref. [41] that coexisting deformed states may descend into the low-lying spectrum for nuclei with $Z>82$.

Similarly in Ref. [41], the relationship between $E_{2_1^{+}}$ [40] and the P factor is presented in Figure 4a for even–even nuclei with $67<Z<81$ and $83<N<105$. The black squares correspond to nuclei with $67<Z<75$, and isotopes with $Z=76$, 78 and 80 are labeled by colored dots. It is obvious that the deviation between those colored dots and the black squares becomes larger with the increase in Z. This phenomenon also appears in the relation between $E_{4_1^{+}}$, $E_{6_1^{+}}$ [40] and the P factor, as shown in Figure 5a,c.

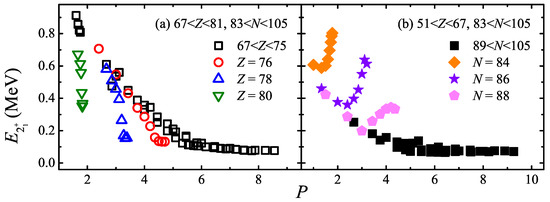
Figure 4. $E_{2_1^{+}}$ [40] versus the P factor for even–even nuclei with $83<N<105$. Panels (a,b) correspond to nuclei with $67<Z<81$ and $51<Z<67$, respectively. The colored hollow dots in panel (a) are isotopes and the colored solid dots in panel (b) are isotones.

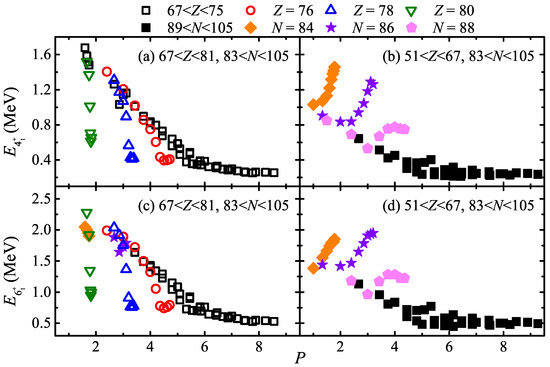
Figure 5. $E_{4_1^{+}}$ and $E_{6_1^{+}}$ [40] versus the P factor for even–even nuclei with $83<N<105$. Panels (a,c) correspond to nuclei with $67<Z<81$, while panels (b,d) correspond to nuclei with $51<Z<67$. The colored hollow dots are isotopes and the colored solid dots are isotones.

In addition, by comparing Figure 3 with Figure 1b,c, and Figure 4a with Figure 2b, it is easy to see that the anomalies for nuclei with $Z=76\sim 80$ are more conspicuous in the P factor plot than in the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme for both $|e_2|$ and $E_{2_1^{+}}$, and behave in a pattern with the proton number Z in the P factor plot [41].

For even–even nuclei with $83<N<105$ and $51<Z<67$, $E_{2_1^{+}}$, $E_{4_1^{+}}$ and $E_{6_1^{+}}$ [40] are also plotted with the P factor in Figure 4b and Figure 5b,d, respectively. It is seen that these excitation energies [40] of nuclei with $N=84$, 86 and 88 (colored solid dots) are also deviated from the others (black solid dots) obviously, as well as those $N=84$ and 86 isotones with $68\le Z\le 74$ as shown in Figure 5c.

2.2. $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ Relation for Nuclear Charge Radii R and $\alpha$ Decay Energies $Q_{\alpha }$

It is shown in Ref. [42] that nuclear charge radii R have a good linear relationship with $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ in a local region. Here, $\alpha$ is a fitting parameter, $N^{\prime }{}_{\mathrm{p}}=Z-Z_0$ and $N^{\prime }{}_{\mathrm{n}}=N-N_0$, where $Z_0$ and $N_0$ are the beginning proton number and neutron number of a local region, respectively. However, some anomalies exist in several local regions [42].

Suppose that $R(N,Z)=k(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})+C$ nuclear charge radii are plotted versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ in Figure 6 and Figure 7 for several different local regions which are pointed to have anomalies in Ref. [42]. Here, the experimental value of R is taken from the CR2013 database [43,44], and k, $\alpha$, C are obtained by ${\chi }^2$-fitting.

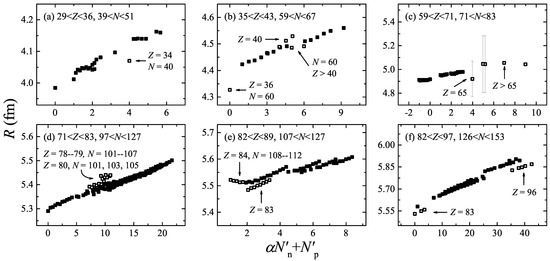
Figure 6. Nuclear charge radii R [43,44] versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ in different regions. The anomalies are labeled by the open squares, and large experimental uncertainties (>0.15 fm) of R are shown in panel (c). The parameter $\alpha$ respectively equals 0.111, 0.534, $-0.102$, 0.417, 0.187 and 1.180 for panels (a–f).

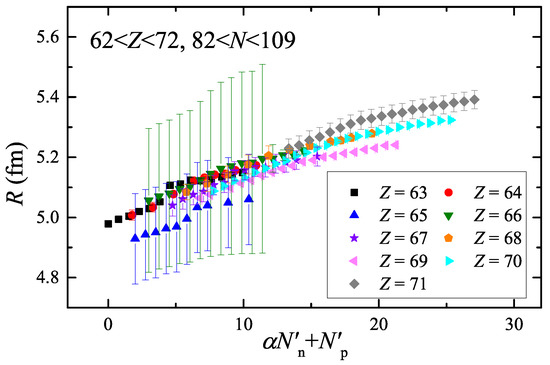
Figure 7. Nuclear charge radii R [43,44] versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$. Different symbols are used to label the chains of isotopes, and the experimental uncertainties of R are given. The parameter $\alpha$ is 0.763.

It is seen that nuclear charge radii of nuclei with $78\le Z\le 80$ and $101\le N\le 107$ in Figure 6d and of nuclei in Figure 7 also show abnormalities [42], which are generally consistent with the anomalies of $|e_2|$ and $E_{2_1^{+}}$, $E_{4_1^{+}}$, $E_{6_1^{+}}$ in the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme and the P factor plot, as discussed in Section 2.1.

The anomalies given in Figure 6b may correspond to the phase transition at $N=60$ and $Z\sim 40$ [45], where it is also explained by Ref. [46] that the sudden deformation here is contrasted with the deformation from a sphere to an ellipsoid.

As shown in Figure 6c and Figure 7, R of nuclei with $Z=65$ have very large experimental uncertainties (about 0.15 fm), which may lead to much lower positions in panels relative to the others [42]. For the other anomalies presented in Figure 6a,e,f and Figure 7, the structure of them should be further studied in the future.

The linear relationship between $\alpha$ decay energies $Q_{\alpha }$ and $(\alpha N_{\mathrm{n}}+N_{\mathrm{p}})$ is also pointed out in Ref. [47]. In Figure 8, $Q_{\alpha }$ taken from Ref. [22] is plotted versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ in four different regions, and those anomalies which deviate from the others (black dots) obviously are labeled by colored dots.

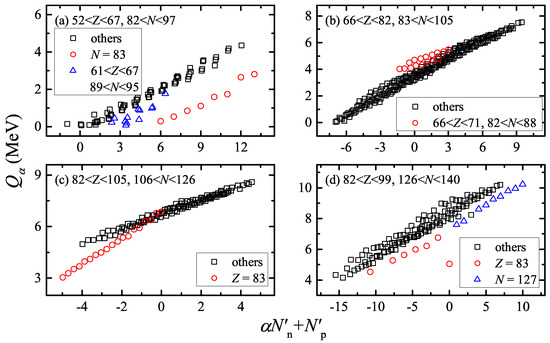
Figure 8. $\alpha$ decay energies $Q_{\alpha }$ [22] versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ in different regions. The anomalies are labeled by colored dots. The parameter $\alpha$ respectively equals $-0.947$, $-0.442$, $-0.277$ and $-1.539$ for panels (a–d).

Blue triangles in Figure 8a correspond to nuclei with $Z\sim 64$ and $N\sim 90$, which may be influenced by the $Z=64$ subshell [31,36,48,49,50]. The red circles in Figure 8b denote nuclei with $66<Z<71$ and $83<N<88$, which also exhibit an anomaly as shown in Figure 5b,d ($E_{4_1^{+}}$, $E_{6_1^{+}}$ versus the P factor) and Figure 7 (R versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$). The deviations of $Q_{\alpha }$ between $Z=83$ isotopes and the others in Figure 8c,d are also reflected in Figure 6e,f.

2.3. The So-Called “Nonpairing” Relation of Binding Energies B and Nuclear Charge Radii R

The so-called “nonpairing” interaction between the last two protons $\delta V_{\mathrm{pp}}$ or the last two neutrons $\delta V_{\mathrm{nn}}$ are defined as follows:

$$\begin{array}{ccc}\hfill -\delta V_{\mathrm{pp}}(Z-1,Z;N)& =& \frac{1}{2}[B(N,Z)-B(N,Z-1)-B(N,Z-2)+B(N,Z-3)],\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill -\delta V_{\mathrm{nn}}(N-1,N;Z)& =& \frac{1}{2}[B(N,Z)-B(N-1,Z)-B(N-2,Z)+B(N-3,Z)],\hfill \end{array}$$

(2)

respectively [45]. $B(N,Z)$ is the binding energy of nuclei with neutron number N and proton number Z.

Based on the AME2020 database [22], $\delta V_{\mathrm{pp}}$ and $\delta V_{\mathrm{nn}}$ are calculated by using Equations (1) and (2), and are plotted versus Z and N, respectively, in Figure 9 [45]. Those blue circles or green tringles, which correspond to nuclei with $Z-N=1$ or 2 for $\delta V_{\mathrm{pp}}$ and $N-Z=1$ or 2 for $\delta V_{\mathrm{nn}}$, are quite large, as shown in Figure 9a,b. This is mainly caused by the Wigner effect [45], which results from the neutron–proton correlation and is dependent on the isospin.

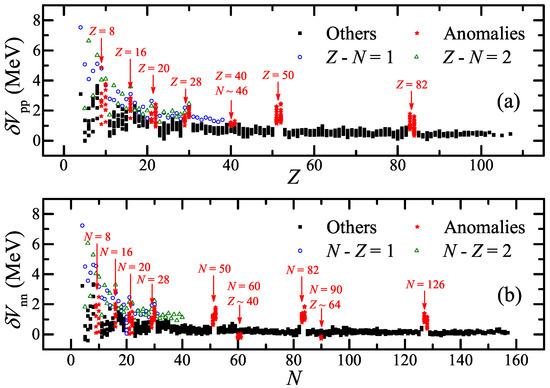
Figure 9. (a): $\delta V_{\mathrm{pp}}$ versus Z. (b): $\delta V_{\mathrm{nn}}$ versus N. The anomalies are labeled by the red stars. The blue circles and green triangles correspond to nuclei with $Z-N=1$ and $Z-N=2$ in panel (a), and those with $N-Z=1$ and $N-Z=2$ in panel (b).

The other anomalies that are irrelevant to the Wigner effect are labeled by the red circles in Figure 9. As pointed in Refs. [45,51,52], these anomalies are “fingerprints” of nuclear structure involving (sub-)shells and phase transitions.

New magic numbers $N,Z=16$ discovered in Refs. [53,54] are represented in Figure 9a,b, respectively [45]. The $Z=40$ subshell (for $N<60$) [31,36,48,55,56] and $Z=64$ subshell (for $N<90$) [31,36,48,49,50] correspond to anomalies with $Z=40$, $N\sim 56$ of $\delta V_{\mathrm{pp}}$ and $Z\sim 64$, $N=90$ of $\delta V_{\mathrm{nn}}$, respectively [45]. In addition, the phase transition at $N=60$ and $Z\sim 40$ also behaves abnormally as shown in Figure 9b [45].

Similar to $\delta V_{\mathrm{nn}}$ discussed above, $\delta R_{\mathrm{nn}}$ is defined in Ref. [42], i.e.,

$$\begin{array}{ccc}\hfill \delta R_{\mathrm{nn}}(N,Z)& =& R(N,Z)-R(N-1,Z)-R(N-2,Z)+R(N-3,Z).\hfill \end{array}$$

(3)

Here, $R(N,Z)$ is the nuclear charge radii of nuclei with neutron number N and proton number Z. Based on the CR2013 database [43,44], $\delta R_{\mathrm{nn}}$ is calculated and plotted versus the neutron number N in Figure 10 [42]. The red dash lines of $\delta R_{\mathrm{nn}}=\pm 0.03$ fm are plotted to guide the eyes.

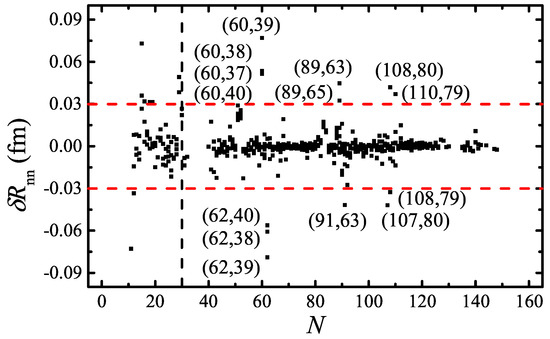
Figure 10. $\delta R_{\mathrm{nn}}$ versus N for $N>10$. The red dash lines correspond to $\delta R_{\mathrm{nn}}=\pm 0.03$ fm. For $N,Z>30$, nuclei $(N,Z)$ with absolute values of $\delta R_{\mathrm{nn}}>0.03$ fm are labeled.

The nuclei $(N,Z)$ with $|\delta R_{\mathrm{nn}}|>0.03$ fm are labeled in Figure 10, and these anomalies can be divided into three regions: (1) $Z=37\sim 40$ and $N=60$ or 62; (2) $Z=63$ or 65 and $N=89$ or 91; (3) $Z=79$, $N=108$ or 110, and $Z=80$, $N=107$ or 108 [42]. These large deviations of $\delta R_{\mathrm{nn}}$ are also consistent with the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation for R, as discussed in Section 2.2 [42].

The anomalies in region 3 of Figure 10 are the same as those in Figure 6d. For the other two regions, Figure 11 is plotted to explain those anomalies. Obvious gaps shown in Figure 11a,b lead to those anomalies of regions 1 and 2 of Figure 10, respectively [42].

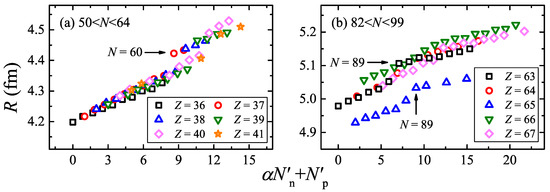
Figure 11. Nuclear charge radii R [43,44] versus $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$. Different symbols are used to label the chains of isotopes. The parameter $\alpha$ is 0.844 for panel (a) and 1.178 for panel (b).

The sudden increase in R at $N=60$ shown in Figure 11a corresponds to the phase transition at $N=60$, $Z\sim 40$ (as discussed above in Figure 6b in Section 2.2). The gap in Figure 11b is influenced by the $Z=64$ subshell [45].

3. Conclusions

In this paper, three kinds of local relations that can reflect many nuclear structure evolutions are introduced, and some results of these models can be verified with each other.

The new magic numbers and Wigner effect can be reflected from $\delta V_{\mathrm{nn}}$ and $\delta V_{\mathrm{pp}}$. The phase transition at $Z\sim 40$ and $N=60$ is shown in the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation, and $\delta R_{\mathrm{nn}}$, $\delta V_{\mathrm{nn}}$ relation. The subshell at $Z=40$ and $N<60$ causes a part of the anomalies in $\delta V_{\mathrm{pp}}$. The $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme of $e_2$, $\delta V_{\mathrm{nn}}$, $\delta R_{\mathrm{nn}}$ and the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation of R and $Q_{\alpha }$ show abnormalities at the $Z=64$ subshell.

The shape coexistence in the region of nuclei with $Z=76\sim 81$ and $N\sim 104$ can be given by the $e_2$ in both the $N_{\mathrm{p}}{N}_{\mathrm{n}}$ scheme and the P factor plot, the $E_{2_1^{+}}$, $E_{4_1^{+}}$, $E_{6_1^{+}}$ in the P factor plot, and the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation and the $\delta R_{\mathrm{nn}}$ relation for nuclear charge radii R.

In addition, anomalies of nuclei with $66<Z<71$ and $82<N<88$ arise in the P factor plot of $E_{2_1^{+}}$, $E_{4_1^{+}}$, $E_{6_1^{+}}$, as well as the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relation of R and $Q_{\alpha }$, and anomalies of $Z=83$ isotopes arise in both the $(\alpha N^{\prime }{}_{\mathrm{n}}+N^{\prime }{}_{\mathrm{p}})$ relations of R and $Q_{\alpha }$. The reason for these anomalies is still unknown and should be studied further.