Abstract
Process tomography, the experimental characterization of physical processes, is a central task in science and engineering. Here, we investigate the axiomatic requirements that guarantee the in-principle feasibility of process tomography in general physical theories. Specifically, we explore the requirement that process tomography should be achievable with a finite number of auxiliary systems and with a finite number of input states. We show that this requirement is satisfied in every theory equipped with universal extensions, that is, correlated states from which all other correlations can be generated locally with non-zero probability. We show that universal extensions are guaranteed to exist in two cases: (1) theories permitting conclusive state teleportation, and (2) theories satisfying three properties of Causality, Pure Product States, and Purification. In case (2), the existence of universal extensions follows from a symmetry property of Purification, whereby all pure bipartite states with the same marginal on one system are locally interconvertible. Crucially, our results hold even in theories that do not satisfy Local Tomography, the property that the state of any composite system can be identified from the correlations of local measurements. Summarizing, the existence of universal extensions, without any additional requirement of Local Tomography, is a sufficient guarantee for the characterizability of physical processes using a finite number of auxiliary systems and with a finite number of input systems.
1. Introduction
The experimental characterization of physical processes is an important component of the scientific method. Such a characterization, known as process tomography, is widely adopted in classical [1] and quantum technologies [2,3,4,5,6,7,8,9,10,11,12,13,14]. In general, one can regard the in-principle feasibility of process tomography as a requirement for the construction of new physical theories: arguably, a sensible physical theory should describe processes that—at least in principle—can be characterized experimentally.
Operational axioms inspired by process tomography were first proposed by D’Ariano in a sequence of works [15,16,17,18], where they featured as potential candidates for an axiomatization of quantum theory. In this paper, we will explore the conditions that guarantee the feasibility of process tomography in general physical theories, independently of the quantum axiomatization problem. Specifically, our goal will be to identify physical conditions that guarantee the achievability of process tomography using a finite number of auxiliary systems and a finite number of input states.
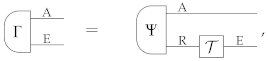
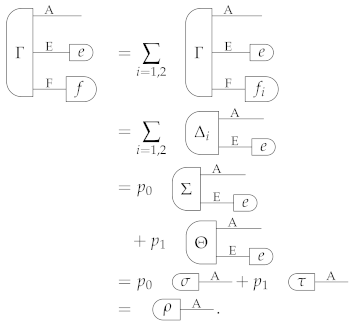
To understand the role of auxiliary systems in process tomography, it is useful to consider first a popular approach known as standard process tomography [2,3], where no auxiliary system is used. Standard process tomography aims at characterizing processes by letting them act on a set of input states and by analyzing the output with a set of measurements, as in the following schematic:
 Here, an unknown process (with input system A and output system B) is tested on a set of fiducial states with a set of fiducial measurements . We use the boldface notation to indicate that the j-th measurement has multiple outcomes, labelled by some index that is not written down explicitly. By choosing a complete set of fiducial states and measurements, one can then identify the action of the process on its input system—that is, one can uniquely determine the function that maps a generic input state of system A into the corresponding output state of system B.
Here, an unknown process (with input system A and output system B) is tested on a set of fiducial states with a set of fiducial measurements . We use the boldface notation to indicate that the j-th measurement has multiple outcomes, labelled by some index that is not written down explicitly. By choosing a complete set of fiducial states and measurements, one can then identify the action of the process on its input system—that is, one can uniquely determine the function that maps a generic input state of system A into the corresponding output state of system B.

In classical and quantum physics, standard process tomography is sufficient to completely characterize physical processes: by determining the function , one can identify the action of the process in every possible experiment, even including experiments where the process acts locally on a part of a composite system. For example, this includes experiments of the form
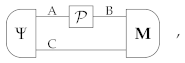 where is applied locally on a joint state Ψ of systems A and system C, and a joint measurement M is performed on systems B and C.
where is applied locally on a joint state Ψ of systems A and system C, and a joint measurement M is performed on systems B and C.

In classical and quantum theory, the outcome probabilities of all experiments of Type (2) are uniquely determined by the outcome probabilities of experiments of Type (1). The origin of this favourable situation is a property, known as Local Tomography, whereby the states of every composite system can be uniquely identified by performing local measurements on the components [16,17,19,20,21,22,23,24,25,26,27]. In quantum foundations, Local Tomography has often been taken as an axiom for the characterization of standard quantum theory (on complex Hilbert spaces) [21,25,28,29,30,31,32,33,34] and as a principle for the construction of new physical theories [22,23,24]. In locally tomographic theories, the action of a process on its input system uniquely determines the action of the process on every composite system [24]. As a result, standard process tomography provides a complete characterization of physical processes.
The situation is radically different when Local Tomography does not hold. A simple counterexample arises in real-vector-space quantum theory [35], a variant of standard quantum theory that violates Local Tomography [19,20] and deviates from standard quantum theory in a number of operational tasks [20,24,36,37,38,39,40,41]. In real-vector-space quantum theory, one can find explicit examples of processes that have the same input-output function, and yet act in completely different ways on composite systems [42].
When Local Tomography fails, the only way to unambiguously identify a process is to test its action on composite systems, using an approach known as ancilla-assisted process tomography [4,5,6,7,8]. This approach consists in performing experiments of the type of Equation (2). Now, the crucial question is: which auxiliary systems C have to be taken into account? In the worst case, the answer could be “all possible systems”: the characterization of an unknown physical process may require experiments performed, as it were, on the whole universe. It seems natural to demand, as a basic principle, that physical theories should be free from this pathology. In a sensible physical theory, it should be in principle possible to identify any given process up to any desired level of accuracy using a finite number of experimental settings. This means: testing the process with a finite number of auxiliary systems, preparing a finite number of states, and performing a finite number of measurements, each with a finite number of outcomes.
In this paper, we will focus on the requirements of a finite number of auxiliary systems/finite number of inputs states, and we will consider the case of process tomography with ideally perfect accuracy. We will require that, at least in principle, physical processes can be completely characterized by probing their action with a finite number of auxiliary systems. Note that, in turn, every finite set of auxiliary systems can be replaced without loss of generality by a single auxiliary system R, for example by merging all the systems of the finite set into a composite system. Indeed, most of the frameworks for general probabilistic theories include a notion of system composition, denoted by ⊗ and corresponding to a generalization of the tensor product in quantum theory [21,22,23,24,27,28,34,42,43,44,45,46,47,48]. As long as the number of components is finite, the composite system is well defined in all these frameworks. At the mathematical level, the composition ⊗ is defined as the tensor product in a monoidal category describing physical systems and processes between them [49,50,51,52]. When monoidal categories are used as a framework for general physical theories, they are often called process theories [53].
These observations motivate the following requirement:
Principle 1
(Dynamically Faithful Systems). For every pair of systems A and B, there exists an auxiliary system R such that all processes with input A and output B can be completely characterized by their action on the states of the composite system A ⊗ R.
We will also consider a slightly stronger requirement, inspired by D’Ariano’s early axiomatization works [15,16,17,18]. The requirement stipulates the achievability of process tomography with a single state of a suitable composite system.
Principle 2
(Dynamically Faithful States). For every pair of systems A and B, there exists an auxiliary system R such that all processes with input A and output B can be completely characterized by their action on a single state of the composite system A ⊗ R.
Dynamically Faithful Systems/Dynamically Faithful States are strictly weaker requirements than Local Tomography. For example, real-vector-space quantum theory violates Local Tomography but satisfies Dynamically Faithful States (and therefore Dynamically Faithful Systems): every real-vector-space process with input A can be uniquely characterized by its action on an entangled state of the composite system A ⊗ A [24]. It is also worth noting that Dynamically Faithful Systems/Dynamically Faithful States do not imply finite dimensionality: for example, all the processes on a quantum system with separable Hilbert space can be characterized by preparing a single bipartite state [6]. Nevertheless, in this paper we will be mostly concerned with finite dimensional systems for simplicity of presentation. Note that we do not make any assumption on the size (however defined) of the system R. A further strengthening of our requirements would by to demand that the size of system R be bounded in terms of the sizes of systems A and B. For example, one could demand that R be embeddable into A ⊗ B, or that R be operationally equivalent to system A, as it happens in quantum theory and in classical probability theory.
The core result of the paper is a mathematical characterization of the theories satisfying Dynamically Faithful States. The characterization is valid for a broad class of physical theories—so broad that, in fact, it even includes non-causal theories where the choices of experiments performed in the future can affect the outcome probabilities of experiments performed in the past. After providing the mathematical characterization, we identify physical conditions that guarantee Dynamically Faithful States. Specifically, we show that Dynamically Faithful States holds in all theories where all correlations of a given physical system with its environment can be probabilistically generated by local operations on a single “universally correlated state”. We call this property Universal Extension. Two important classes of theories satisfying Universal Extension are (1) the theories allowing for conclusive teleportation [49,54], and (2) the theories satisfying three requirements of Causality, Pure Product States, and Purification. Informally, Causality is the requirement that the outcome probabilities of present experiments are independent on the choice of future experiments [24,26,27,28,42,46,53,55,56]. Pure Product States is the requirement that if the parts of a composite system are in pure states, then the whole composite system is in a pure state. Purification is the requirement that every mixed state can be extended to a pure state, and that such extension is unique up to local symmetry transformations [24,26,27,28,42,46,57,58]. Remarkably, the symmetry property of purifications guarantees that every purification is a universal extension, and therefore every theory with purification has Dynamically Faithful States. Our main results can be summarized by the following logical implications:
- Conclusive Teleportation ⟹ Universal Extension;
- Causality, Pure Product States, and Purification ⟹ Universal Extension;
- Universal Extension ⟹ Dynamically Faithful States ⟹ Dynamically Faithful Systems.
The overall conclusion of our results is that Universal Extension guarantees the in-principle characterizability of physical processes, without invoking any assumption of Local Tomography.
2. Materials and Methods
In this section, we briefly introduce the framework and the notation used in the paper.
2.1. Operational-Probabilistic Theories
A major trend in quantum foundations is the study of information-processing tasks in a broad class of general probabilistic theories, which include quantum theory as a special case [21,22,23,24,27,28,42,43,44,45,46,47]. A convenient approach to general probabilistic theories is provided by the framework of operational-probabilistic theories (OPTs) [24,27,28,42,44,45,46,47,48,59]. The framework consists of two distinct conceptual ingredients: an operational structure, describing circuits that produce outcomes, and a probabilistic structure, which assigns probabilities to the outcomes. The operational structure is inspired by the approach of categorical quantum mechanics [49,50,51,52] (see also [53] for a recent presentation), and follows it rather closely, although there are a few relevant differences in the way classical outcomes are treated [48,59].
The OPT framework describes a set of experiments that can be performed on a given set of systems with a given set of physical processes. The framework is based on a primitive notion of composition, whereby every pair of physical systems A and B can be combined into a composite system A ⊗ B. The set of all physical systems is closed under composition, and will be denoted by . Physical processes can be combined in sequence or in parallel to build circuits, such as
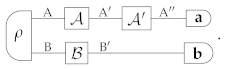

In this example, A, , and are systems, is a state of the composite system A ⊗B, , and are transformations (a.k.a. processes), a and b are measurements. We use boldface fonts a and b for measurements in order to indicate that they generally have multiple outcomes. When necessary, we will explicitly write and , where x and y are measurement outcomes, and and are the sets of possible outcomes of the two measurements, respectively. Here and play the same role as the linear operators associated to the outcomes of quantum measurements. Following a traditional terminology dating back to Ludwig [60], we will call them effects.
Among the physical systems, every OPT includes a trivial system, denoted by I and corresponding to the degrees of freedom ignored by theory. States (resp. effects) are transformations with the trivial system as input (resp. output).
Transformations from the trivial system to itself are called scalars. Physically, they are associated to circuits with no external wires, like the circuit in Equation (3). In the OPT framework, scalars are typically identified with numerical probabilities, valued in the interval . More generally, other identifications are also possible, including signed probabilities or possibilities, as shown in the work of Gogioso and Scandolo [48]. In the following, we will not make any assumption on the nature of the scalars, although we will often call them “probabilities” to facilitate the connection to the existing literature in quantum foundations.
For generic systems A and B, we denote by:
- the set of transformations from A to B, also called transformations of type A → B;
- the set of states of system A;
- the set of effects on system A;
- (or , for short) the sequential composition of two transformations and , with the input of matching the output of ;
- the parallel composition of the transformations and ;
- the identity transformation on system A;
- the identity transformation on the trivial system.
Definition 1.
We say that two transformations and are operationally indistinguishable [24] if they give rise to the same probabilities in all possible experiments, namely


In this paper, we will focus our attention on quotient theories [42,46], where physical transformations that are operationally indistinguishable are identified: in other words, we will assume that Condition (4) implies the equality
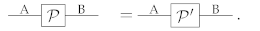
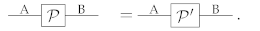
When the scalars are positive real numbers, the set of transformations in the quotient theory can be regarded as elements of an ordered vector space [24,42,46,61].
Every transformation takes place in a test, that is, a non-deterministic process that generates an outcome out of a set of possible outcomes. Mathematically, a test of type A → B, with outcomes in , is a list of transformations of type A → B indexed by elements of the outcome set . We denote such a list by , with for every .
Tests of type I → A are called preparation tests, or sources. A preparation test describes the non-deterministic preparation of the state , heralded by an outcome . In quantum theory, the states in a preparation test are subnormalized density matrices, and the trace of each subnormalized density matrix is interpreted as the probability of the corresponding preparation.
Tests of type A → I are called measurements. A measurement is a collection of effects labelled by measurement outcomes.
A transformation is deterministic if it is part of a test with a single outcome. By definition, deterministic transformations can be performed deterministically by setting up the corresponding test. We use the notations:
- for the set of deterministic transformations of type A → B;
- for the set of deterministic states of system A;
- for the deterministic effects of system A.
For the trivial system I, we assume that there exists only one deterministic transformation of type I → I, namely the identity transformation 1. This assumption was introduced by Coecke in Ref. [62], motivated by the interpretation of the scalars as “probabilities”, which suggests that there should be only one deterministic scalar, corresponding to the notion of certainty.
We assume that the set of tests is closed under coarse-graining, the operation of joining together two or more outcomes. Given a test and a partition of the outcome set into disjoint subsets , we define the coarse-grained test as the test with transformations
At this level, the symbol of sum is just a notation for the operation of coarse-graining: the only mathematical requirements on the coarse-graining operation is that it distributes over parallel and sequential composition, namely
for every transformation ,
for every transformation with input matching the output of , and
for every transformation with output matching the input of . Closely related notions of coarse-graining were proposed in the works of Tull [59], Gogioso and Scandolo [48], where Equations (7)–(9) were assumed together with a few additional requirements.
Since there is only one deterministic transformation of type I → I (the scalar 1), every test of type I → I satisfies the normalization condition
This condition is the analogue of the normalization of a probability distribution. For this reason, in the following we will call the tests of type I → I “probability distributions”, even though in general the scalars may not be real numbers in the interval .
When the scalars are real numbers, the sum notation used above is consistent with the notion of sum in the ordered vector space containing the physical transformations in the quotient theory [24,42,46,61] (cf. Definition 1 and comments below it).
2.2. Framework Assumptions
In this paper, we will make four basic assumptions that are shared by most probabilistic theories in the literature. We spell out the assumptions explicitly because they will play a significant role in our results, and it is convenient to keep track of which assumption is used in which result. For example, we will write “Lemma 1 (A1, A2, A3)” to state that that Lemma 1 follows from Assumptions 1, 2, and 3.
Our first assumption is that all non-deterministic tests arise from deterministic processes followed by measurements. This assumption is compatible with the idea that the outcomes can be read-out from some physical system, like the display of a device, and that such system is also described by the theory. The readout process is then realized as a deterministic transformation, followed by a measurement on the display:
Assumption 1
(Displays [46]). Every test arises from a deterministic transformation followed by a measurement on one of the output systems.
Formally, Assumption 1 is that every test of type A → B can be realized as:
 for some system C, some deterministic transformation , and some measurement .
for some system C, some deterministic transformation , and some measurement .

Our second assumption is that the set of systems described by the theory includes some “coin”, that is, some physical system that generates random outcomes. In the familiar setting where probabilities are numbers in the interval , the assumption is that there exists some two-outcome experiment whose outcome probabilities are both non-zero. In the general case, an analogue of non-zero probability is a cancellative scalar: a scalar s is cancellative if the condition implies for every pair of scalars p and .
Assumption 2
(Coins). There exist two-outcome experiments whose outcome probabilities are both cancellative.
We stress that we do not assume the existence of coins with arbitrary biases: even if the scalars are real numbers, we do not assume that they are the whole interval .
An important property of cancellative scalars is that they cancel out in equations involving arbitrary transformations:
Lemma 1.
For a cancellative scalar s, the condition implies , for every pair of processes and of the same type.
Proof.
Given two processes and of type A → B, the condition implies
 which in turn implies
which in turn implies
 because s is cancellative. Hence, the processes and are operationally indistinguishable, in the sense of Definition 1. Since we are dealing with a quotient theory, this condition implies . □
because s is cancellative. Hence, the processes and are operationally indistinguishable, in the sense of Definition 1. Since we are dealing with a quotient theory, this condition implies . □


Our third assumption is that it is possible to perform randomized tests. Informally, a randomized test is a test where one tosses a coin and performs a test depending on the outcome of the coin toss. Here we give the formal definition for the randomization of two tests (the extension to more than two tests is straightforward):
Definition 2.
Let and be two tests of type A → B, with outcomes in and , respectively, and let be a probability distribution allowed by the theory (i.e., a test of type I → I). The randomization of and with probabilities is a test of type A → B, with outcomes in the disjoint union , in which all elements of are regarded as distinct from all elements of . The test is defined as
Our third assumption is that all randomizations are valid tests:
Assumption 3
(Randomizations). The set of tests is closed under randomizations.
The Randomizations Assumption, together with the possibility of coarse graining, guarantees the existence of random mixtures, defined as follows:
Definition 3.
Let σ and τ be two deterministic states of system A and let be a probability distribution allowed by the theory. The mixture of σ and τ with probabilities is the deterministic state ρ defined by
The fact that ρ is a deterministic state follows from the fact that ρ is the coarse-graining of the randomized test with and.
The notion of mixture introduces a pre-order relation on the set of deterministic states:
Definition 4.
Let ρ and σ be two deterministic states of system A. We say that ρ contains σ, denoted as , if , where is a probability distribution allowed by the theory, is a cancellative scalar, and τ is a deterministic state.
Note that the relation ⊒ is transitive: if and , then .
Our final assumption is about the existence of complete states, defined as follows:
Definition 5.
A deterministic state is complete if for every deterministic state.
The assumption is:
Assumption 4
(Complete States). For every system, there exists at least one complete state.
While Assumptions 1, 2, and 3 are satisfied by most probabilistic theories, including infinite dimensional ones, Assumption 4 is more specific to the finite dimensional setting. It is satisfied in the standard scenario where the set of deterministic states is a finite-dimensional convex set. In this scenario, the complete states are exactly the points in the interior of the convex set. Assumption 4 is also satisfied in some theories where the set of deterministic states is not convex. For example, it is satisfied in Spekkens’ toy theory [63,64], where some convex combinations are forbidden but nevertheless the set of deterministic states contains a complete state. However, Assumption 4 is generally not satisfied by classical and quantum theory infinite dimensions. An infinite-dimensional generalization of the notion of complete state will be discussed in Section 3.2.
2.3. Local Tomography
In this section, we review the property of Local Tomography. The scope of this review is to clarify, by contrast, what it means to characterize physical processes in theories where Local Tomography does not hold.
The Local Tomography has been formulated in several forms and under different names [16,19,20,21,22,23,24,25]. A simple formulation is the following [26].
Definition 6
(Local Tomography). A physical theory satisfies Local Tomography if the state of every composite system is uniquely determined by the joint statistics of local measurements on the components.
Mathematically, Local Tomography states that, for every pair of systems A and B, and for every pair of states of the composite system A ⊗ B, say and , the condition
 implies the equality
implies the equality
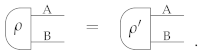

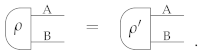
2.4. Standard Process Tomography
Local Tomography has an important implication for the task of characterizing physical processes: in every locally tomographic theory, the action of a process on its input system determines the action of the process on all possible composite systems. Explicitly, one has the following
Proposition 1
(Lemma 14 of [24]). Suppose that the theory satisfies Local Tomography. Then, for every pair of systems A and B and for every pair of processes and of type A → B, the condition
 implies the equality
implies the equality
 or equivalently, the equality
or equivalently, the equality




When system A is finite dimensional, Proposition 1 guarantees that one can characterize an arbitrary process of type A → B by applying it to a fiducial set of input states of system A, and by characterizing the output states of system B with a fiducial set of measurements. This result is the conceptual foundation underpinning standard process tomography [2,3].
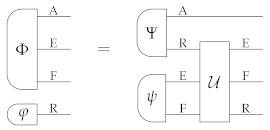
Interestingly, a converse of Proposition 1 also holds, under the assumption that the all states of all composite systems can be probabilistically generated by acting locally on one part of a fixed bipartite state. This point is discussed in Appendix A.
2.5. The Counterexample of Real-Vector-Space Quantum Theory
When Local Tomography does not hold, standard process tomography may not work. A simple example can be found in real-vector-space quantum theory [35], a variant of standard quantum theory that violates Local Tomography [19,20] and deviates from standard quantum theory in a number of operational tasks [20,24,36,37,38,39,40,41]. The example, introduced in [42], involves two processes, and , acting on a “rebit”, that is, a two-dimensional quantum system associated to the vector space . Mathematically, the two processes are defined by the linear maps:
where M is a generic 2 × 2 matrix and are the three Pauli matrices. Now, consider the action of the two processes on a single-rebit, whose possible states are described by density matrices with real entries. Writing a generic real-valued density matrix in the Bloch form
we can easily obtain the relation
meaning that the two processes and act in the same way on every single-rebit input state.
On the other hand, the processes and are clearly different. The difference can be detected by applying the processes on a maximally entangled state of two rebits: for example, using the notation
one has
Note that the output states are not only different, but also orthogonal, meaning that a joint measurement on the two rebits can tell the two states apart without any error. The two states in the r.h.s. of Equation (25) were first studied by Wootters [20] as an example of bipartite states that perfectly distinguishable by global measurements, and yet completely indistinguishable by local measurements in real-vector-space quantum theory.
Summarizing, standard process tomography does not work in real-vector-space quantum theory: in order to unambiguously characterize an unknown process on real-vector space quantum states, it is mandatory to test it on composite systems.
2.6. Process Tomography without the Assumption of Local Tomography
In the lack of Local Tomography, process tomography requires experiments on composite systems. Now, the key question is: which composites have to be tested? In principle, the answer could be “all”: a process with input system A may have to be tested on every composite system A ⊗ C for every possible auxiliary system C. Loosely speaking, the only way to completely characterize a process would be to make experiments on “the whole universe”.
This situation does not arise in real-vector-space quantum theory: there, a complete process tomography can be achieved by preparing a single input state of a single composite system. Specifically, process tomography can be achieved by preparing two identical copies of the input system in a maximally entangled state and by letting the process act on one copy. We do not provide a proof here because later in the paper we will give a general proof valid for all theories obeying the Purification Principle (see Section 3.5.3 for the formal definition). Since real-vector-space quantum theory satisfies the Purification Principle, the general proof applies.).
Summarizing, real-vector-space quantum theory satisfies the principle of Dynamically Faithful States (Principle 2 in the introduction). In the rest of the paper we will investigate the conditions that guarantee the validity of Dynamically Faithful States in general physical theories.
3. Results
3.1. Four Levels of Process Tomography
The goal of tomography is to characterize the action of an unknown process on all possible inputs. Nevertheless, it is also useful to first consider intermediate tasks where the goal is to characterize the process on a subset of inputs. In this section we define three such tasks, listed in order of increasing strength. All together, these three tasks and the task of full process tomography define four levels of characterization of physical processes.
3.1.1. Equality on a Source
Consider the situation where a source prepares system A in a non-deterministic fashion. Such a source can be described by a preparation test , where the preparation of the state is heralded by the outcome x. The states in the source are then used as inputs:
Definition 7.
We say that two processes and , of type A → B, are equal on the source if one has:
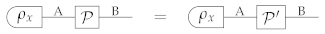
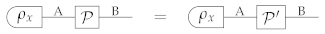
When this is the case, we write.
It is easy to see that is an equivalence relation. The equivalence relation defines a weak notion of process tomography, where the goal is just to identify the action of processes on the fixed set of states .
3.1.2. Equality upon Input of a State
We now consider a stronger notion of process tomography. Instead of characterizing a process on a single source, one can try to characterize the process on all sources with the same average state. The average state of a source is the deterministic state
obtained by coarse-graining over all possible outcomes.
Definition 8.
We say that two processes and , of type A → B, are equal upon input of ρ if they are equal on every source with average state equal to ρ. When this is the case, we write .
The condition is equivalent to the condition
 where the notation means that is contained in , that is, that there exists a source such that and for some cancellative scalar (Note that this definition is slightly more general than Definition 4: here do not require the state to be deterministic).
where the notation means that is contained in , that is, that there exists a source such that and for some cancellative scalar (Note that this definition is slightly more general than Definition 4: here do not require the state to be deterministic).

In quantum information, the notion of equality upon input of was introduced in [65]. Its extension to general probabilistic theories was discussed in [24,27,28].
It is easy to check that equality upon input of is an equivalence relation. Note that, by definition, identifying a process upon input of is more demanding than just identifying it on a specific source with average state .
3.1.3. Equality on the Extensions of a State
All notions of process tomography considered so far focussed on the action of a process on its input system alone. To identify the process, however, one also needs to characterize its local action on composite systems.
Definition 9.
Let be a deterministic state of system, A. An extension of ρ on system E is a deterministic state satisfying the relation:
 for some deterministic effect . We denote by the set of all extensions of ρ on system E.
for some deterministic effect . We denote by the set of all extensions of ρ on system E.

Our third level of process tomography is to identify the action of a process on all the extensions of a given state.
Definition 10.
We say that two processes and are equal on the extensions of if one has
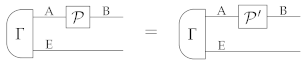 for every possible system E and for every possible extension . In this case, we write .
for every possible system E and for every possible extension . In this case, we write .
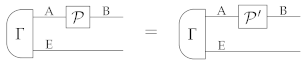
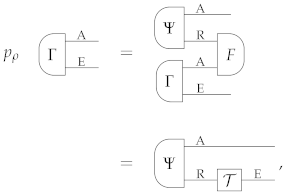
In general, equality of all the extensions of implies equality upon input of . This is because all sources with average state can be viewed as extensions of involving an environment serving as a “display”. Explicitly, we have the following:
Lemma 2
(A1). Let be a deterministic state of system A, and let be an arbitrary source with average state ρ. Then, there exists an extension , for suitable system E, such that, for every pair of processes and of type A → B, with arbitrary system B, the condition
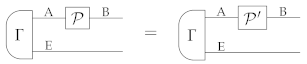 implies the condition
implies the condition
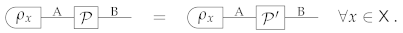
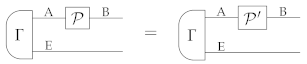
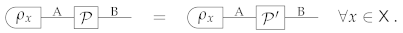
The proof is provided in Appendix B. An immediate consequence is that equality on all the extensions of implies equality upon input of :
Corollary 1
(A1). Let be a deterministic state of system A. Then, for every pair of processes and of type A → B, with arbitrary system B, one has the implication
In Appendix B we also show that the relations and coincide in the special case of theories satisfying Local Tomography and Causality, the principle that the outcome probabilities of present experiments are independent on the choice of future experiments [24,26,27,28,42,46,53,55,56].
3.1.4. Equality on All States
The ultimate goal of process tomography is to identify the action of an unknown process on all possible states. Using the results collected so far, the condition for perfect identification can be expressed as follows:
Lemma 3
(A1). Let and be two processes of type A → B. Then, one has the condition
The proof is provided in Appendix C. Summarizing, two processes of type A → B are equal if and only if they coincide on all the extensions of all deterministic states of system A. In Section 3.4 we will show that, in fact, the extensions of a single state are enough.
3.2. Tomographic Ordering and Dynamically Faithful States
A natural notion in the context of process tomography is the notion of tomographic ordering:
Definition 11.
Let and be two (possibly non-deterministic) states. We say that Φ is tomographically more powerful than Ψ for processes of type A →B, if, for every pair of processes and of type A → B, the condition
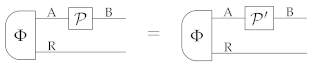 implies the condition
implies the condition
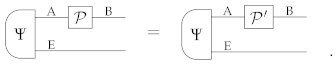 .
.
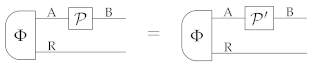
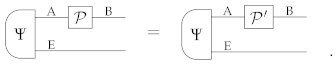
When this is the case, we write .
In general, the relation of tomographic ordering (for a fixed systems A and B) may or may not have a maximum. When it does, this maximum is called a dynamically faithful state:
Definition 12
(Dynamically faithful state [15,16,17,18,24,27,28,42]). A (possibly non-deterministic) state is dynamically faithful for processes of type A→ B if, for every pair of processes and of type A → B, the condition
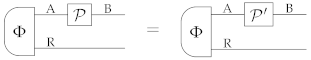 implies
implies
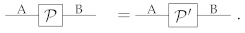
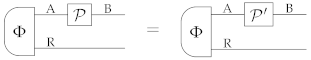
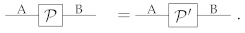
Originally [15,16,17,18], the term “dynamically faithful” was used to refer to states that determine the action of an unknown process on its input system, up to probabilistic rescalings, that is, states for which the condition (35) implies for every state . Later [24,27,28,42], the term was used to denote states that identify the action of the process on arbitrary composite systems, as per Definition 12.
In every theory satisfying the Displays Assumption 1, dynamically faithful states can be taken to be deterministic without loss of generality:
Lemma 4
(A1). For a generic pair of systems A and B, if there exists a dynamically faithful state for processes of type A → B, then there exists a deterministic dynamically faithful state for processes of type A →B.
Proof.
Let be a (possibly non-deterministic) dynamically faithful state for processes of type A → B, and let be a source that produces the state , say for some outcome . Since is dynamically faithful, equality of two processes on the source implies equality of the processes themselves: for every pair of processes and of type A → B, the condition implies the condition . Then, Lemma 2 shows that there exists a deterministic state , for suitable system E, such that the condition implies (and therefore , in the present case). Hence, the deterministic state is dynamically faithful for processes of type A →B. □
3.3. Relation between Tomographic Ordering and Containment
There is an important connection between the tomographic ordering and the containment relation defined earlier in the paper. Recall the definition: a deterministic state contains another deterministic state , denoted as , if is a non-trivial mixture of and some other state , namely where are probabilities and is cancellative. Here we show that the containment relation orders the deterministic states according to the tomographic power of their extensions.
Lemma 5
(A1, A3). Let ρ and σ be two deterministic states of system A. If ρ contains σ, then for every extension of σ, say there exists an extension of ρ, say , such that
for every system B.
The proof is provided in Appendix D.
A simple consequence of Lemma 5 is the following:
Corollary 2
(A1, A3). Let ρ and σ be two deterministic states of system A. If ρ contains σ, then, for every system B and for every pair of processes and of type A → B, the condition implies the condition .
The case of complete states is especially important here. In this case, we have the following:
Corollary 3
(A1, A3). If is a complete state, then, for every system B and every pair of processes and of type A → B, the condition implies the equality .
Proof.
Immediate from Corollary 2, Lemma 3, and the definition of complete state. □
This result plays a crucial role in the rest of the paper. In passing, we note that it also suggests an infinite-dimensional generalization of the notion of complete state. The generalization is as follows: we say that a state is tomographically complete if the relation implies the equality for every pair of processes of type A → B with arbitrary output system B. Corollary 3 shows that every complete state is tomographically complete. In infinite dimensional settings, complete states in the sense of Definition 5 may not exist, and one could regard tomographically complete states as the appropriate notion. Notably, all the results in this paper hold if the notion of complete state is replaced by the more general notion of tomographically complete state.
3.4. Necessary and Sufficient Condition for Dynamically Faithful States
We are now ready to provide the core technical result of the paper:
Theorem 1
(A1, A2, A3, A4). For a generic pair of systems A and B, the following are equivalent:
- there exists a dynamically faithful state for processes of type A → B
- there exists a complete state such that the set of all the extensions of ω has a maximum with respect to the tomographic ordering ⪰A→B.
The proof is provided in Appendix E. The important point of the above theorem is that one can focus the attention on the complete states. In summary, the existence of dynamically faithful states boils down to the existence of a maximally powerful extension of a complete state.
3.5. Physical Conditions for Dynamically Faithful States
We have seen that Dynamically Faithful States holds if and only if every complete state has a maximally powerful extension. Still, this is just a mathematical requirement. Can we find physical reasons for this requirement to be satisfied? Here we give three physically motivated sufficient conditions.
3.5.1. Universal Extension
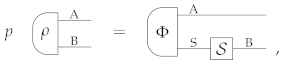
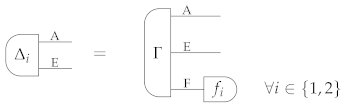
Heuristically, it is natural to imagine that the “maximally powerful extension” in Theorem 1 determines all the other ways in which the system can be correlated to an environment. Going further, we can imagine that all the other correlations can be physically generated from the “maximally powerful extension” using some (possibly non-deterministic) process. The idea motivates the notion of universal extension, from which all the extensions of a given state can be generated:
Definition 13
(Universal extension). A state has a universal extension if there exists a reference system R and a state with the property that every other extension of ρ can be probabilistically generated from Ψ by applying a transformation on R. Explicitly: for every system E, every extension can be obtained as
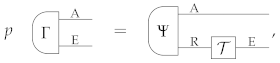 where is a cancellative scalar and is a transformation of type R →E.
where is a cancellative scalar and is a transformation of type R →E.
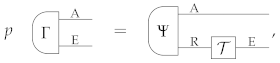
Using this definition, we can formulate a requirement for general physical theories:
Principle 3
(Universal Extension). Every physical system has a complete state with a universal extension.
Note that one could also consider the stronger requirement that every state have a universal extension. The reasons why we did not phrase Principle 3 in this way are (1) universal extensions of complete states are already sufficient for process tomography, and (2) as we will see later in the paper, the possibility of conclusive teleportation guarantees the existence of a universal extension of a a complete state, while in general it may not guarantee the existence of universal extensions of arbitrary states.
We now show that Universal Extension guarantees Dynamically Faithful States. The first step is the following lemma:
Lemma 6.
Suppose that a deterministic state has a universal extension . Then, for every system B and for every pair of processes of type A → B, say and , the condition
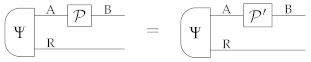 implies the condition
implies the condition
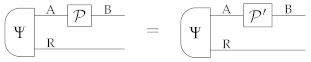
Proof.
Let be an arbitrary extension of , and let be the transformation in Equation (40). By applying the transformation on both sides of Equation (41), we obtain the relation
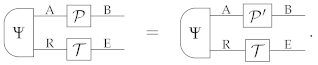
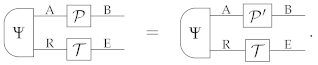
Inserting Equation (40) into both sides of the equality, we then obtain:
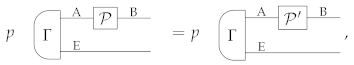 and, since p is cancellative,
and, since p is cancellative,
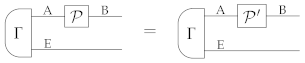 (cf. Lemma 1). Since is an arbitrary extension of , we conclude that the equivalence holds. □
(cf. Lemma 1). Since is an arbitrary extension of , we conclude that the equivalence holds. □
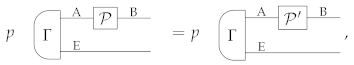
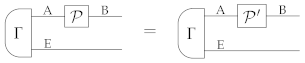
Applying the above lemma to a complete state, we obtain the following
Theorem 2
(A1, A3). Universal Extension implies Dynamically Faithful States.
Proof.
Universal Extension guarantees that there exists a complete state with a universal extension , for some auxiliary system R. Since is a universal extension, for every system B and every pair of processes and of type A → B, the equality
implies the condition
(cf. Lemma 6). Now, since is complete, the equality on the extensions of implies (Corollary 3). To summarize, we obtained that the condition implies . Hence, the state is dynamically faithful for processes of type A → B. Since this construction works for arbitrary A and B, we conclude that the theory satisfies Dynamically Faithful States. □
Notably, Universal Extension implies the existence of a state which is dynamically faithful for processes of type A → B, with arbitrary output system B. In other words, the choice dynamically faithful state depends only on the input of the tested process and not on its output.
3.5.2. Conclusive Teleportation
Quantum teleportation [66] is a protocol for transferring the state of a quantum system from a sender to a receiver using only classical communication and previously established quantum correlations. The most basic version of quantum teleportation is probabilistic: the sender performs a joint measurement on the system to be teleported and on part of a bipartite state, shared with the receiver. If the measurement yields a specific outcome, then the state of the system is transferred to the receiver without any alteration. Probabilistic teleportation is often called conclusive. The analogue of conclusive teleportation in general theories was studied by Abramsky and Coecke in [49] in the context of categorical quantum mechanics, by Barnum, Barrett, Leifer, and Wilce [23] in the context of general probabilistic theories, and by Chiribella, D’Ariano, and Perinotti [24,27] in the context of theories satisfying Purification.
In a general physical theory, conclusive teleportation means that, for every system A there exists a system R, a deterministic state , an effect , and a cancellative scalar such that:
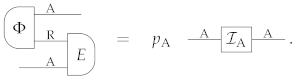
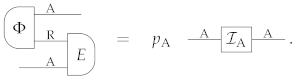
The existence of conclusive teleportation is a valuable operational feature, and may be put forward as a desideratum for general physical theories:
Principle 4
(Conclusive Teleportation). For every physical system A, there exists a conclusive teleportation protocol as in Equation (48).
Modulo a few technical differences, Conclusive Teleportation coincides with the main axiom for compact closed categories in categorical quantum mechanics [49,50,51,52,53]. In this context, it is known that the teleportation state induces a one-to-one correspondence between processes and bipartite states. In other words, is dynamically faithful for processes of type A → B, with arbitrary B. Here we show a stronger result, namely that the state is the universal extension of a complete state:
Proposition 2
(A4). Let be a teleportation state for system A. Then, Φ is the universal extension of a complete state.
The proof is provided in Appendix F, where we also observe that, in general, a theory with conclusive teleportation may not have universal extensions for arbitrary states.
A simple consequence of Proposition 2 is the following:
Corollary 4
(A4). Conclusive Teleportation implies Universal Extension.
Summarizing, we proved the chain of implications:
In short, the possibility of conclusive teleportation guarantees the feasibility of process tomography, even in theories that violate Local Tomography.
3.5.3. Purification
A purification of a given state is an extension of that state to a pure state of a composite system [24,27,42,46,58]. In the standard scenario where the state space of physical systems is a convex set, pure states are defined as the extreme points of the convex set. A diagrammatic definition of pure state, valid also for theories where the scalars are not real numbers, was provided in Ref. [67]. The second definition is equivalent to the first in every theory satisfying Causality [24,26,27,28,42,46,53,55,56], the requirement that it should be impossible to “send signals from the future to the past” (see below for a more precise mathematical statement) and Local Tomography, or Local Tomography on Pure States, a weakening of Local Tomography satisfied by quantum theory on real vector spaces. Specifically, Local Tomography on Pure States is the requirement that Equation (16) implies Equation (17) when at least one of the two states and is an extreme point of the state space.
In the following, we will not commit to a specific definition of pure state. Instead, we will simply assume that for every system A there exists a set of states , called pure, satisfying the condition
We call the above condition Pure Product States. Pure Product States is automatically satisfied by the diagrammatic definition of pure state in [67]. It is also satisfied by the usual definition of pure states as extreme points, when it coincides with the diagrammatic definition.
Let us now review the notion of purification. In its basic form, purification is formulated in theories satisfying Causality. An equivalent condition for Causality is the existence of a unique deterministic effect:
Proposition 3
([24]). A theory satisfies Causality if and only if for every system A there exists a unique deterministic effect .
Theories satisfying Causality are often called causal theories. In a causal theory, a state is an extension of another state if the condition
 is satisfied.
is satisfied.

We are now ready to state the Purification principle in its basic form:
Principle 5
(Purification). For a theory satisfying Causality and Pure Product States, we require that
- every state has a purification: for every system and every deterministic state there exists a system R and a deterministic pure state such that

- every two purifications with the same purifying system are interconvertible via a local symmetry transformation: for every system R, and every pair of deterministic pure states Ψ and in , the condition:implies that there exists a reversible transformation such that
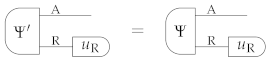
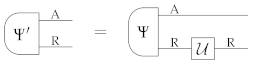
Remarkably, the symmetry property of purifications implies that every purification is a universal extension:
Proposition 4.
Let be an arbitrary state of an arbitrary system A, and let be an arbitrary extension of ρ. If the theory satisfies Causality, Pure Product States, and Purification, then the state Γ can be generated as
 where is an arbitrary purification of ρ and is a deterministic transformation.
where is an arbitrary purification of ρ and is a deterministic transformation.

The proof is provided in Appendix G. The obvious consequence of Proposition 4 is the following
Corollary 5
(A1, A3, A4). If a theory satisfies Causality, Pure Product States, and Purification, then it satisfies Universal Extension, and, in particular, Dynamically Faithful States.
Proof.
Proposition 4 shows that every purification of a given state is a universal extension, in the sense of Definition 13. In particular, every complete state has a universal extension (complete states exist by Assumption 4). Hence, Universal Extension holds. Then, Theorem 2 guarantees that Dynamically Faithful States holds. □
Summarizing, we proved the chain of implications:
Note that this is the same chain of implications as in the previous subsection, except that “Conclusive Teleportation” is now replaced by “Causality + Pure Product States + Purification.” A natural question is whether there are relations between Purification and Conclusive Teleportation. When the scalars are real numbers in the interval , it is known that Purification implies Conclusive Teleportation [24,27,28,42]. More generally, it is also possible to show that Purification implies Conclusive Teleportation in every theory that satisfies two additional axioms of Pure Sharpness and Purity Preservation [58,68,69].
4. Conclusions
In this paper, we analyzed the task of process tomography in general physical theories, exploring the requirement that physical processes should be identifiable by their action on a finite set of auxiliary systems/a finite set of input states. Most of the paper focussed on the requirement that physical processes can be identified by their action on a single state, called dynamically faithful. The existence of dynamically faithful states is a broader condition than the usual principle of Local Tomography, and is satisfied in a number of variants of quantum theory, including quantum theory on real Hilbert spaces and a Fermionic version of quantum theory [70,71]. It is natural to conjecture that dynamically faithful states also exist in a recent extension of standard quantum theory that includes complex, real, and quaternionic Hilbert spaces in a single theory [72]. A formal proof of this statement, however, is currently missing and remains an interesting direction for future research.
One of our main results is that the existence of dynamically faithful states can be guaranteed by a simple physical condition, namely that complete states have a universal extension from which all the other extensions can be generated with non-zero probability. Example of physical theories with this property are the set of theories where conclusive teleportation is possible, and the set of theories satisfying the Causality, Pure Product States, and Purification. For every theory satisfying Causality, Pure Product States, and Purification, process tomography can be achieved using a single bipartite state: specifically, the purification of any complete state of a given system A can be used to characterize all the processes with input system A and arbitrary output system B.
An important observation is that the existence of dynamically faithful states is independent of the Causality axiom, that is, the requirement that the outcome probabilities of present experiments are independent of the choice of future experiments. This observation suggests that the possibility of characterizing physical processes may have a more primitive role than considerations of causality, and that one could adopt Dynamically Faithful States as a foundational principle for general physical theories where causality is emergent.
Funding
This work is supported by the Hong Kong Research Grant Council through grant 17300918 and though the Senior Research Fellowship Scheme SRFS2021-7S02, by the Croucher Foundation, by the John Templeton Foundation through grant 61466, and The Quantum Information Structure of Spacetime (qiss.fr). Research at the Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development Canada and by the Province of Ontario through the Ministry of Research, Innovation and Science. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I wish to thank Mauro D’Ariano for introducing me to quantum tomography and to the problem of deriving quantum theory from physical principles. The discussions we had during my PhD and early postdoc years have planted the seeds for much of the ideas developed in this paper. I also wish to acknowledge discussions with Paolo Perinotti and Carlo Maria Scandolo on the relations between purification and the existence of dynamically faithful states.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. A Converse of Proposition 1
Bipartite states from which other states can be probabilistically generated were introduced in the early work by D’Ariano [15,16,17,18], where they were called preparationally faithful. Originally [15,16], the term referred to states of a bipartite system A ⊗ B with the property that every state of A can be probabilistically generated by a physical transformation on B. In later works [17,18], the term was used for states with the property that every joint state of A ⊗ B can be probabilistically generated by a physical transformation on B. Here we adopt the second definition and extend it to (1) transformations with different inputs and outputs, and (2) theories where the scalars are not necessarily real numbers:
Definition A1.
A state is preparationally faithful from to B if every state can be probabilistically obtained as
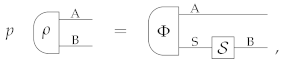 where is a cancellative scalar and is a transformation of type S → B.
where is a cancellative scalar and is a transformation of type S → B.
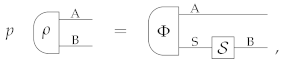
Using the above definition, we introduce a notion of doubly preparationally faithful theories:
Definition A2.
A theory is doubly preparationally faithful if for every pair of systems A and B there exists a system S and a state that is preparationally faithful from A to A and from S to B.
Concrete examples of doubly preparationally faithful theories are finite-dimensional classical probability theory and quantum theory, both on complex and on real vector spaces. In quantum theory, the maximally entangled state of system A ⊗ S, with S ≃ A, is preparationally faithful from S to B with arbitrary B. Indeed, every pure state of the composite system A ⊗ B can be probabilistically obtained from the maximally entangled state as , where is a suitable Kraus operator, c is the matrix with matrix elements , and is the maximum eigenvalue of . Since every pure state can be generated probabilistically from , the same holds for mixed states (in finite dimensions). This shows that is preparationally faithful from S to B, with arbitrary B. A similar argument shows that is preparationally faithful from A to A.
More generally, every process theory where the processes form a compact closed category [49,50,51,52] is doubly preparationally faithful. Physically, these are the theories where every system A comes with a dual system S, such that there exists a state of A ⊗ S that allows for conclusive teleportation of states of A, as well as conclusive teleportation of states of S.
With the above definitions, we have the following proposition:
Proposition A1
(A3). For a doubly preparationally faithful theory, the following are equivalent:
- Local Tomography holds
- standard process tomography completely identifies physical processes, that is, Equation (18) implies Equation (20).
Proof.
Since the implication 1 ⟹ 2 was already proved by Proposition 1, we only need to prove the implication 2 ⟹ 1.
Let A and B be two generic systems, and let and be two generic states of the composite system A ⊗ B. Our goal is to show that then the condition
 implies .
implies .

Let us assume that Equation (A2) holds. Since the theory is doubly preparationally faithful, there exists a system S and a state that is preparationally faithful from A to A and from S to B. Since is preparationally faithful from S to B, there exist two cancellative scalars p and , and two transformations and , of type S → B, such that
 and
and
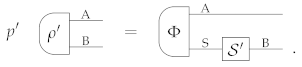

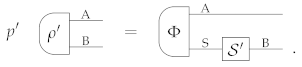
Since the state is preparationally faithful from A to A, for every state there exists a cancellative scalar q and transformation of type A → A such that
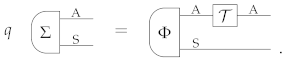
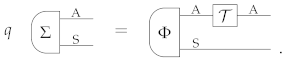
Inserting this relation into Equations (A3) and (A4), we obtain
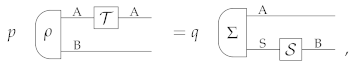 and
and
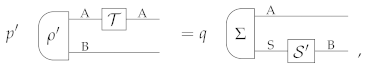
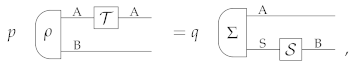
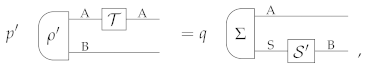
Now, note that and are physical transformations, due to the Randomizations Assumption 3. For these two transformations, we have the relation
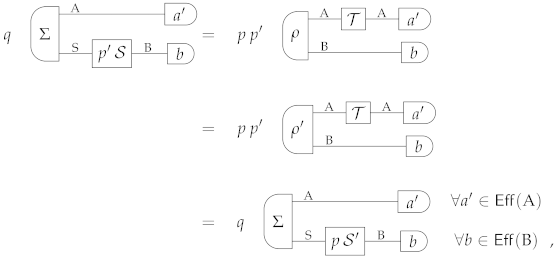 where the second equality follows from Equation (A2), applied to
where the second equality follows from Equation (A2), applied to

Recall that Σ is a generic state of system A ⊗ S. In particular, we can choose Σ to be of the product form . With this choice, Equation (A8) becomes


Choosing to be a deterministic state and to be a deterministic effect, we then obtain


Since q is cancellative for every and , we then obtain


To conclude, recall that is an arbitrary state, and therefore the above equation implies that the processes and give rise to the same outcome probability in every setup of standard process tomography. Since by hypothesis standard process tomography successfully identifies physical processes, we conclude that the equality must hold. Using this fact and Equations (A3) and (A4),we obtain

Since p and are both cancellative, we conclude that the equality must hold. □
Appendix B. Properties of the Relations ≡ ρ and = ρ
We start by showing that the relation is stronger than the relation .
Proof of Lemma 2.
Let be a source with average state . The Display Assumption 1 guarantees that the states in can be prepared as
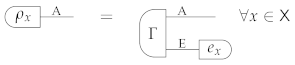 for some system E, some deterministic state , and some measurement . Now, the state is an extension of : indeed, one has
for some system E, some deterministic state , and some measurement . Now, the state is an extension of : indeed, one has
 where e is the deterministic effect (the last equality follows from Equation (9)).
where e is the deterministic effect (the last equality follows from Equation (9)).


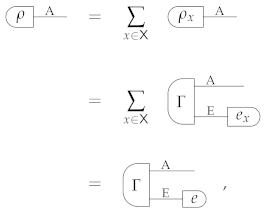
Now, suppose that the condition
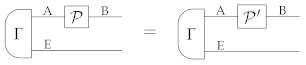 holds. Applying the effect on both sides, one then obtains
holds. Applying the effect on both sides, one then obtains
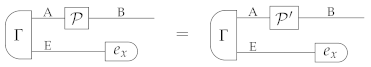 and, using Equation (A13),
and, using Equation (A13),
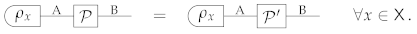 □
□
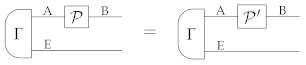
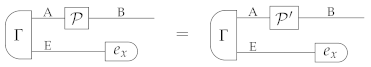
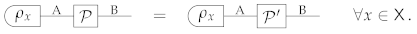
We now show that the two relations and are equivalent in theories satisfying Causality and Local Tomography. We recall that Causality is equivalent to the existence of a unique deterministic effect uA for every system A [24,42,46,55,56].
We can then prove the following proposition:
Proposition A2
(A1). Suppose that a theory satisfies Causality and Local Tomography. Then, for every system A, every deterministic state , and every pair of processes and , of type A → B, one has the condition
Proof.
We know from Corollary 1 that the condition implies the condition . To prove the equivalence, we only need to show the converse implication. Suppose that the condition holds. Then, let be a generic extension of on system E, namely
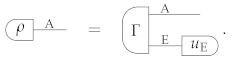
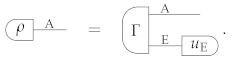
Here we used the Causality Axiom, which guarantees that there exists only one deterministic effect for system E.
At this point, we need to prove the relation
To this purpose, pick an arbitrary measurement and define the preparation test as
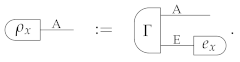
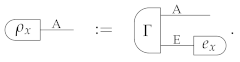
Note that the preparation test has average state : indeed, one has
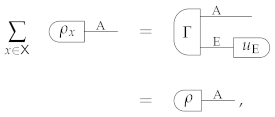 having used Equation (A19) and the fact that is the only deterministic effect on system A.
having used Equation (A19) and the fact that is the only deterministic effect on system A.
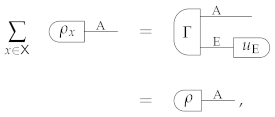
Since the preparation test averages to , the condition implies
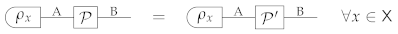 and, using the definition of in Equation (A21),
and, using the definition of in Equation (A21),

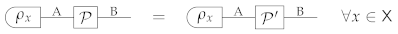

To conclude, note that for a generic measurement one has
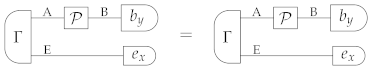 for every and for every . Since the two measurements b and e are generic, Local Tomography implies Equation (A20). Since is a generic extension of , we conclude that . □
for every and for every . Since the two measurements b and e are generic, Local Tomography implies Equation (A20). Since is a generic extension of , we conclude that . □
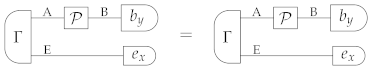
Appendix C. Proof of Lemma 3
The direction ⇒ is immediate. To prove the direction ⇐, let us assume the condition for every deterministic state . Recall that two processes and are equal if and only if
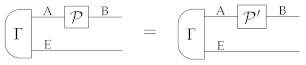 for every system E and for every (possibly non-deterministic) state .
for every system E and for every (possibly non-deterministic) state .
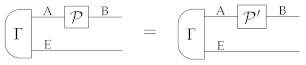
Let us pick a generic E and a generic . Since every state can be prepared in some test (by the Displays Assumption 1), there must exist a test and an outcome such that
Now, let us define the deterministic states
and
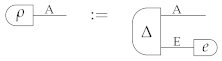 where e is a fixed, but otherwise arbitrary, deterministic effect on system E. By construction, is an extension of . Hence, every extension of is also an extension of . As a consequence, one has the implication
where e is a fixed, but otherwise arbitrary, deterministic effect on system E. By construction, is an extension of . Hence, every extension of is also an extension of . As a consequence, one has the implication
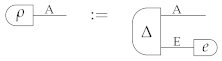
Moreover, one has the implications
(by Corollary 1) and
for every outcome x (by definition of equality upon input of ). Choosing and using Equation (A27), we finally obtain Equation (A26). Since the system E and the state are generic, the equality follows. □
Appendix D. Proof of Lemma 5
Suppose that is a mixture of and with probabilities , namely
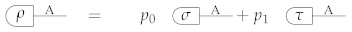 where is a cancellative scalar.
where is a cancellative scalar.
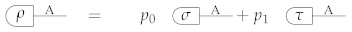
Let be an extension of on system E, so that
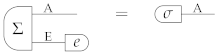 for some deterministic effect e. Let be a deterministic state of system E and let be the extension of defined by , so that
for some deterministic effect e. Let be a deterministic state of system E and let be the extension of defined by , so that

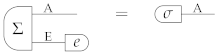

Then, define the randomized preparation test , with and (the randomized preparation is a valid test due to the Randomization Assumption 3). The Displays Assumption 1 guarantees that the states and can be generated as
 for some system F, some deterministic state , and some measurement . By construction, is an extension of : indeed, defining the deterministic effect , one has
for some system F, some deterministic state , and some measurement . By construction, is an extension of : indeed, defining the deterministic effect , one has


Now, suppose that and are two processes of type A → B and suppose that the relation
 holds. Applying the effect on both sides, we then obtain
holds. Applying the effect on both sides, we then obtain
 and therefore
and therefore
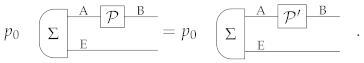
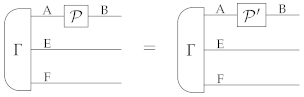

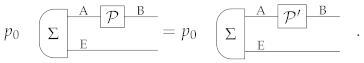
Since is cancellative, the two processes and must coincide on (cf. Lemma 1). Hence, one has . □
Appendix E. Proof of Theorem 1
Proof of 2 ⟹ 1.
Suppose that there exists a complete state, call it , such that the set of all extensions of has a maximum with respect to the tomographic ordering . Let be such maximum, for some auxiliary system R, and let and be two arbitrary processes of type A → B. By definition, the condition implies the equivalence . In turn, the condition implies (Corollary 3). Hence, we obtained that the condition implies , meaning that is dynamically faithful for processes of type A → B.
Proof of 1 ⟹ 2.
Let be a dynamically faithful state for processes of type A → B. Without loss of generality, the state can be taken to be deterministic (Lemma 4). Then, let us pick a deterministic effect on system R, say , and define the state
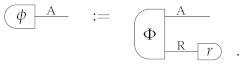
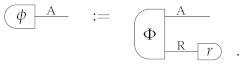
By construction, is an extension of . If is a complete state, this concludes the proof: the complete state has an extension that is a (global) maximum with respect to the tomographic ordering .
If is not complete, we can pick a complete state , an arbitrary deterministic state , and, using the Randomizations Assumption 3, we can define the source with and , where is a probability distribution such that and are both cancellative (the existence of such probability distribution is guaranteed by the Coins Assumption 2). Note that the condition implies , which in turn implies (because is cancellative) and (because is dynamically faithful). Now, let us denote the average state of the source by . Note that one has
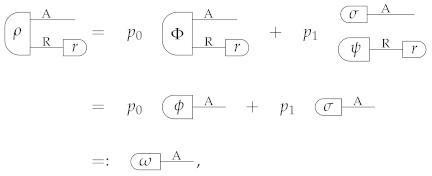 where the state is complete (because contains , and is complete). Then, Lemma 2 guarantees that there exists a deterministic state such that the condition implies , and therefore . Hence, the deterministic state is dynamically faithful. Note that is an extension of , which in turn is an extension of the complete state (by Equation (A42)). Summarizing, is an extension of a complete state and is a (global) maximum with respect to the tomographic ordering . □
where the state is complete (because contains , and is complete). Then, Lemma 2 guarantees that there exists a deterministic state such that the condition implies , and therefore . Hence, the deterministic state is dynamically faithful. Note that is an extension of , which in turn is an extension of the complete state (by Equation (A42)). Summarizing, is an extension of a complete state and is a (global) maximum with respect to the tomographic ordering . □

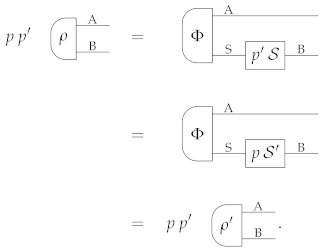
Appendix F. Relations between Conclusive Teleportation and Universal Extension
Let us start by proving Proposition 2, which states that every teleportation state is the universal extension of a complete state.
Proof of Proposition 2.
Let be a binary measurement satisfying the teleportation Equation (48). Let be a complete state of system A (the existence of such state is guaranteed by Assumption 4). Let us define the state
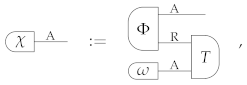 where is the deterministic effect obtained by coarse-graning over the binary measurement . By construction, is an extension of . Moreover, is complete. To prove it, we pick an arbitrary deterministic state and write as for some state and for some binary probability distribution such that is cancellative. Inserting this expression in Equation (A43), we obtain
where is the deterministic effect obtained by coarse-graning over the binary measurement . By construction, is an extension of . Moreover, is complete. To prove it, we pick an arbitrary deterministic state and write as for some state and for some binary probability distribution such that is cancellative. Inserting this expression in Equation (A43), we obtain
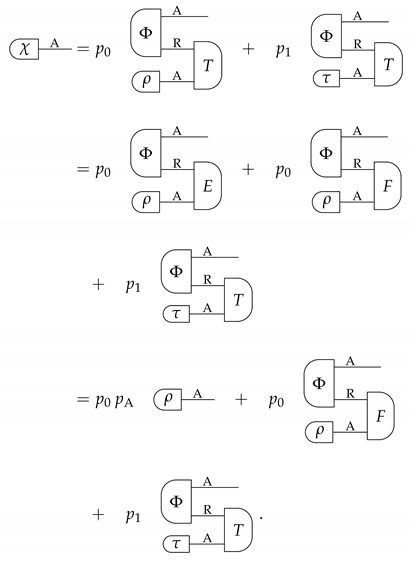


Since and are both cancellative, is cancellative, and therefore contains . Since is arbitrary, we conclude that is complete.
It remains to prove that is a universal extension of . This is easily done using the teleportation Equation (48). Suppose that is another extension of . Then, one has
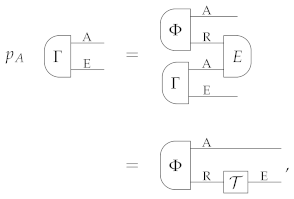 with
with
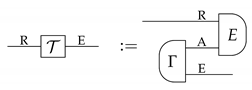

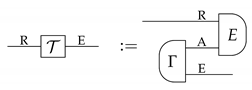
In summary, the extension is probabilistically obtained from the teleportation state . Since is arbitrary, is a universal extension. □
It is worth observing that the proof of Proposition 2 also implies a stronger result: in fact, every bipartite state of the composite A ⊗ B, with arbitrary E, can be probabilistically generated from the teleportation state by means of a physical transformation. In other words, the state is preparationally faithful from system R to system E, in the sense of Definition 14.
It is also worth noting that Conclusive Teleportation does not imply, in general, that every state has a universal extension. A condition that would imply the existence of universal extensions for a generic state is the existence of conclusive teleportation protocols of the form
 where is an extension of , F is a suitable effect, and is a cancellative scalar.
where is an extension of , F is a suitable effect, and is a cancellative scalar.
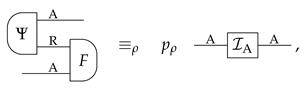
Proposition A3.
If Equation (A47) is satisfied, then the state Ψ is a universal extension of ρ.
Proof.
Suppose that is another extension of . Then, Equation (A47) implies the relation
 with
with
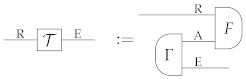

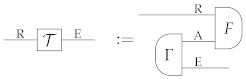
In summary, the extension is probabilistically obtained from the teleportation state . Since is arbitrary, is a universal extension. □
However, Equation (A47) does not appear as a particularly compelling requirement for general physical theories, and therefore we did not include it in our formulation of Conclusive Teleportation.
Appendix G. Proof of Proposition 4
Let be a purification of the state , with purifying system E. Since is an extension of , is also a purification of , with purifying system E ⊗ F. Now, pick an arbitrary deterministic pure state of R, say , and an arbitrary deterministic pure state of E ⊗ F, say . Then, Pure Product States guarantees that the two states and are both pure. By construction, both states are purifications of . Hence, the symmetry property of purifications implies that there exists a reversible process such that

Applying the deterministic effect to system F ⊗ R we then obtain the condition
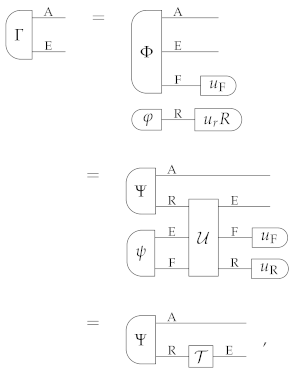 having defined
having defined
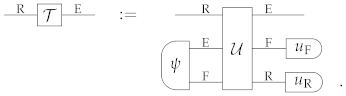 □
□


References
- Williams, R.A.; Beck, M.S. Process Tomography: Principles, Techniques and Applications; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Chuang, I.L.; Nielsen, M.A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 1997, 44, 2455–2467. [Google Scholar] [CrossRef]
- Poyatos, J.; Cirac, J.I.; Zoller, P. Complete characterization of a quantum process: The two-bit quantum gate. Phys. Rev. Lett. 1997, 78, 390. [Google Scholar] [CrossRef]
- Leung, D.W. Towards robust quantum computation. arXiv 2000, arXiv:Cs/0012017. [Google Scholar]
- Leung, D.W. Choi’s proof as a recipe for quantum process tomography. J. Math. Phys. 2003, 44, 528–533. [Google Scholar] [CrossRef]
- D’Ariano, G.; Lo Presti, P. Quantum tomography for measuring experimentally the matrix elements of an arbitrary quantum operation. Phys. Rev. Lett. 2001, 86, 4195. [Google Scholar] [CrossRef]
- Dür, W.; Cirac, J. Nonlocal operations: Purification, storage, compression, tomography, and probabilistic implementation. Phys. Rev. A 2001, 64, 012317. [Google Scholar] [CrossRef]
- Altepeter, J.B.; Branning, D.; Jeffrey, E.; Wei, T.; Kwiat, P.G.; Thew, R.T.; O’Brien, J.L.; Nielsen, M.A.; White, A.G. Ancilla-assisted quantum process tomography. Phys. Rev. Lett. 2003, 90, 193601. [Google Scholar] [CrossRef] [PubMed]
- Mohseni, M.; Rezakhani, A.; Lidar, D. Quantum-process tomography: Resource analysis of different strategies. Phys. Rev. A 2008, 77, 032322. [Google Scholar] [CrossRef]
- Lobino, M.; Korystov, D.; Kupchak, C.; Figueroa, E.; Sanders, B.C.; Lvovsky, A. Complete characterization of quantum-optical processes. Science 2008, 322, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.J. Optimizing quantum process tomography with unitary 2-designs. J. Phys. A Math. Theor. 2008, 41, 055308. [Google Scholar] [CrossRef]
- Bisio, A.; Chiribella, G.; D’Ariano, G.; Facchini, S.; Perinotti, P. Optimal quantum tomography of states, measurements, and transformations. Phys. Rev. Lett. 2009, 102, 010404. [Google Scholar] [CrossRef]
- Shabani, A.; Kosut, R.; Mohseni, M.; Rabitz, H.; Broome, M.; Almeida, M.; Fedrizzi, A.; White, A. Efficient measurement of quantum dynamics via compressive sensing. Phys. Rev. Lett. 2011, 106, 100401. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, C.H.; Kalev, A.; Deutsch, I.H. Quantum process tomography of unitary and near-unitary maps. Phys. Rev. A 2014, 90, 012110. [Google Scholar] [CrossRef]
- D’Ariano, G.M. On the missing axiom of quantum mechanics. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2006; Volume 810, pp. 114–130. [Google Scholar]
- D’Ariano, G.M. How to derive the Hilbert-space formulation of quantum mechanics from purely operational axioms. In AIP Conference Proceedings; AIP: College Park, MD, USA, 2006; Volume 844, pp. 101–128. [Google Scholar]
- D’Ariano, G.M. Operational axioms for quantum mechanics. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2007; Volume 889, pp. 79–105. [Google Scholar]
- D’Ariano, G.M. Probabilistic theories: What is special about quantum mechanics? In Philosophy of Quantum Information and Entanglement; Cambridge University Press: Cambridge, UK, 2010; Volume 85. [Google Scholar]
- Araki, H. On a characterization of the state space of quantum mechanics. Commun. Math. Phys. 1980, 75, 1–24. [Google Scholar] [CrossRef]
- Wootters, W.K. Local accessibility of quantum states. Complex. Entropy Phys. Inf. 1990, 8, 39–46. [Google Scholar]
- Hardy, L. Quantum theory from five reasonable axioms. arXiv 2001, arXiv:quant-ph/0101012. [Google Scholar]
- Barrett, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75, 032304. [Google Scholar] [CrossRef]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Generalized no-broadcasting theorem. Phys. Rev. Lett. 2007, 99, 240501. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.; Perinotti, P. Probabilistic theories with purification. Phys. Rev. A 2010, 81, 062348. [Google Scholar] [CrossRef]
- Hardy, L. Reformulating and reconstructing quantum theory. arXiv 2011, arXiv:1104.2066. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Quantum theory, namely the pure and reversible theory of information. Entropy 2012, 14, 1877–1893. [Google Scholar] [CrossRef]
- Mauro D’Ariano, G.; Chiribella, G.; Perinotti, P. Quantum Theory from First Principles. An Informational Approach; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Chiribella, G.; D’Ariano, G.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Dakic, B.; Brukner, C. Quantum theory and beyond: Is entanglement special? In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: Cambridge, UK, 2011; pp. 365–392. [Google Scholar]
- Masanes, L.; Müller, M.P. A derivation of quantum theory from physical requirements. New J. Phys. 2011, 13, 063001. [Google Scholar] [CrossRef]
- Masanes, L.; Müller, M.P.; Augusiak, R.; Perez-Garcia, D. Existence of an information unit as a postulate of quantum theory. Proc. Natl. Acad. Sci. USA 2013, 110, 16373–16377. [Google Scholar] [CrossRef] [PubMed]
- Barnum, H.; Müller, M.P.; Ududec, C. Higher-order interference and single-system postulates characterizing quantum theory. New J. Phys. 2014, 16, 123029. [Google Scholar] [CrossRef]
- Wilce, A. Conjugates, filters and quantum mechanics. Quantum 2019, 3, 158. [Google Scholar] [CrossRef]
- Selby, J.H.; Scandolo, C.M.; Coecke, B. Reconstructing quantum theory from diagrammatic postulates. Quantum 2021, 5, 445. [Google Scholar] [CrossRef]
- Stueckelberg, E.C. Quantum theory in real Hilbert space. Helv. Phys. Acta 1960, 33, 458. [Google Scholar]
- Wootters, W.K. Entanglement sharing in real-vector-space quantum theory. Found. Phys. 2012, 42, 19–28. [Google Scholar] [CrossRef]
- Hardy, L.; Wootters, W.K. Limited holism and real-vector-space quantum theory. Found. Phys. 2012, 42, 454–473. [Google Scholar] [CrossRef]
- Aleksandrova, A.; Borish, V.; Wootters, W.K. Real-vector-space quantum theory with a universal quantum bit. Phys. Rev. A 2013, 87, 052106. [Google Scholar] [CrossRef]
- Chiribella, G.; Yang, Y.; Yao, A.C.C. Quantum replication at the Heisenberg limit. Nat. Commun. 2013, 4, 2915. [Google Scholar] [CrossRef]
- Wootters, W.K. The rebit three-tangle and its relation to two-qubit entanglement. J. Phys. A Math. Theor. 2014, 47, 424037. [Google Scholar] [CrossRef]
- Wootters, W.K. Optimal information transfer and real-vector-space quantum theory. In Quantum Theory: Informational Foundations and Foils; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–43. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Quantum from principles. In Quantum Theory: Informational Foundations and Foils; Springer: Berlin/Heidelberg, Germany, 2016; pp. 171–221. [Google Scholar]
- Barnum, H.; Wilce, A. Information processing in convex operational theories. Electron. Notes Theor. Comput. Sci. 2011, 270, 3–15. [Google Scholar] [CrossRef]
- Hardy, L. Foliable operational structures for general probabilistic theories. In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: Cambridge, UK, 2011; p. 409. [Google Scholar]
- Hardy, L. A formalism-local framework for general probabilistic theories, including quantum theory. Math. Struct. Comput. Sci. 2013, 23, 399–440. [Google Scholar] [CrossRef]
- Chiribella, G. Dilation of States and Processes in Operational-Probabilistic Theories. In Proceedings of the 11th Workshop on Quantum Physics and Logic, Kyoto, Japan, 4–6 June 2014; Coecke, B., Hasuo, I., Panangaden, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 172, pp. 1–14. [Google Scholar] [CrossRef]
- Hardy, L. Reconstructing quantum theory. In Quantum Theory: Informational Foundations and Foils; Springer: Berlin/Heidelberg, Germany, 2016; pp. 223–248. [Google Scholar]
- Gogioso, S.; Scandolo, C.M. Categorical Probabilistic Theories. In Proceedings of the 14th International Conference on Quantum Physics and Logic, Nijmegen, The Netherlands, 3–7 July 2017; Coecke, B., Kissinger, A., Eds.; Open Publishing Association: The Hague, The Netherlands, 2018; Volume 266, pp. 367–385. [Google Scholar]
- Abramsky, S.; Coecke, B. A Categorical Semantics of Quantum Protocols. In Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science, Turku, Finland, 17 July 2004; pp. 415–425. [Google Scholar] [CrossRef]
- Coecke, B. Kindergarten quantum mechanics—lecture notes. Quantum theory: Reconsideration of foundations-3. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2006; Volume 810, pp. 81–98. [Google Scholar]
- Abramsky, S.; Coecke, B. Categorical quantum mechanics. In Handbook of Quantum Logic And Quantum Structures: Quantum Logic; Engesser, K., Gabbay, D.M., Lehmann, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 261–324. [Google Scholar] [CrossRef]
- Coecke, B. Quantum picturalism. Contemp. Phys. 2010, 51, 59–83. [Google Scholar] [CrossRef]
- Coecke, B.; Kissinger, A. Picturing Quantum Processes; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Teleportation in general probabilistic theories. In Proceedings of the Symposia in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 2012; Volume 71, pp. 25–48. [Google Scholar]
- Coecke, B.; Lal, R. Causal Categories: A Backbone for a Quantum-Relativistic Universe of Interacting Processes. In Proceedings of the QPL VII, Oxford, UK, 29–30 May 2010. [Google Scholar]
- Coecke, B.; Lal, R. Causal categories: Relativistically interacting processes. Found. Phys. 2013, 43, 458–501. [Google Scholar] [CrossRef][Green Version]
- Chiribella, G.; Yuan, X. Quantum theory from quantum information: The purification route. Can. J. Phys. 2013, 91, 475–478. [Google Scholar] [CrossRef]
- Chiribella, G.; Scandolo, C.M. Conservation of information and the foundations of quantum mechanics. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2015; Volume 95, p. 03003. [Google Scholar]
- Tull, S. Operational theories of physics as categories. arXiv 2016, arXiv:1602.06284. [Google Scholar]
- Ludwig, G. Foundations of Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Schmid, D.; Selby, J.H.; Spekkens, R.W. Unscrambling the omelette of causation and inference: The framework of causal-inferential theories. arXiv 2020, arXiv:2009.03297. [Google Scholar]
- Coecke, B. Terminality implies no-signalling... and much more than that. New Gener. Comput. 2016, 34, 69–85. [Google Scholar] [CrossRef]
- Spekkens, R.W. Evidence for the epistemic view of quantum states: A toy theory. Phys. Rev. A 2007, 75, 032110. [Google Scholar] [CrossRef]
- Spekkens, R.W. Quasi-quantization: Classical statistical theories with an epistemic restriction. In Quantum Theory: Informational Foundations and Foils; Springer: Berlin/Heidelberg, Germany, 2016; pp. 83–135. [Google Scholar]
- Nielsen, M.; Chuang, I. Quantum Information and Computation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Chiribella, G. Distinguishability and copiability of programs in general process theories. Int. J. Softw. Inform. 2014, 8, 209–223. [Google Scholar]
- Chiribella, G.; Scandolo, C.M. Microcanonical thermodynamics in general physical theories. New J. Phys. 2017, 19, 123043. [Google Scholar] [CrossRef]
- Chiribella, G.; Scandolo, C.M. Operational axioms for diagonalizing states. arXiv 2015, arXiv:1506.00380. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Manessi, F.; Perinotti, P.; Tosini, A. Fermionic computation is non-local tomographic and violates monogamy of entanglement. EPL Europhys. Lett. 2014, 107, 20009. [Google Scholar] [CrossRef]
- Lugli, M.; Perinotti, P.; Tosini, A. Fermionic state discrimination by local operations and classical communication. Phys. Rev. Lett. 2020, 125, 110403. [Google Scholar] [CrossRef]
- Barnum, H.; Graydon, M.A.; Wilce, A. Composites and categories of Euclidean Jordan algebras. Quantum 2020, 4, 359. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).