Abstract
The precision of current research on fault recognition of marine bearing remains to be improved. Therefore, a recognition method of crack-rubbing coupling fault of bearing under high water pressure based on polar symmetry mode decomposition is proposed in this article. The structure of marine bearing was analyzed, and the system was divided into several subsystems. Then, the nonlinearity relationship among the subsystems was confirmed. One subsystem was used to represent other subsystems, which was imported into the kinetic equation to obtain the equation after dimensionality reduction. According to the results of dimensionality reduction, the features of signal were measured from time domain, energy, and entropy. Meanwhile, the interior features of signal were extracted. Based on the feature extraction, the classifier of probabilistic neural network was introduced. The signal was recognized, and the recognition results were output via the training of signal sample data. Experimental results show that the method has better dimensionality reduction effect and high recognition precision. The method is practical.
1. Introduction
Bearings are an important part of contemporary machinery and equipment, which mainly include four main elements: inner ring, outer ring, rolling element, and cage. In addition, bearings are also important components used in marine systems, which contribute to safe and stable operation of the entire ship. It plays a vital role, but in the process of sailing, the bearing is prone to failure due to the influence of air or water to varying degrees. The most common failure causes of bearings are as follows: fatigue pitting refers to the phenomenon that the surface material is prone to partly falling off under the action of stress when the bearing is running; plastic deformation refers to the fact that the raceway is indicated by a large load. Uneven pits appear; abrasive wear refers to the phenomenon that the bearing is working in a dusty environment, causing the rolling elements and the surface of the ball to wear. It can be seen that, in the course of ship operation, once a bearing failure occurs, it will cause serious harm to other parts and systems of the ship. Therefore, it is of great practical significance to discover the fault point of the bearing in time and repair and replace it in time after it fails. At present, there are two main types of fault identification methods for marine bearings. The first type of fault identification method is to establish a simplified dynamic model of the fault and study the mechanism, the nature, and the influencing factors of the crack [1]. Since the dynamic characteristics of the bearing at low speeds are very complex, this is still impossible. A complete dynamic model of low-speed bearing crack failure is established. The second category is to identify the fault by extracting the fault characteristics of the vibration signal [2]. However, the random signal received by the sensor is always in a non-stationary state and changes with time and space, which brings difficulties to the processing of vibration signals. Many scholars use methods such as spectrum analysis, wavelet transform, and cycle statistics to detect bearing cracks, but these methods are not ideal for early crack fault identification, let alone revealing the essence of the crack propagation process. The fault processing methods of marine bearings mainly include Fourier transform, wavelet transform, and so on. Fourier transform and wavelet transform are time–frequency signal analysis methods, which are developed from the principle of linear superposition and are not suitable for nonlinear and non-stationary vibration signals. Moreover, most bearings in actual operation are in a multi-component failure state. Crack failure and other failures influence and interfere with each other, making it more difficult to extract crack fault characteristics. The adaptive signal processing method is called mask empirical mode decomposition (MEMD), which has good application performance. However, MEMD adds a masking signal to the signal processing, and the selection and the processing of the masking signal are uncertain. In the signal processing process, the added signal cannot be fully integrated, which leads to the performance defects of MEMD [3].
At present, there are many research results on bearing fault identification and diagnosis. For example, in the literature [4], aiming at the diagnosis problem of misalignment-rubbing coupling fault caused by the misalignment fault in a rotor system under sliding bearing support, based on the non-linear finite element method, a dynamics model of a rotor system of a double-disk misalignment-rubbing coupling fault was established via short bearing oil film force, equivalent misalignment torque, and Hertz contact theory. The contact constraint condition was conducted via augmented Lagrange method to ensure that the depth of boundary penetration wasz within the specified tolerance when the turntable and the casing were in contact. Meanwhile, integrated with the experiment, relevant dynamic characteristics of the coupling fault rotor system under support of a sliding bearing were analyzed in conditions of different rotational speeds. It was shown that the rubbing faults play a dominant role in coupling faults, while misalignment faults were in a subordinate position mainly stimulating the high frequency spectrum [5]. Meanwhile, with the increase of rotational speed, a high frequency multiplier dominated the frequency component of the system and gradually entered the chaotic motion state from the quasi-periodic motion [6]. Due to the effect of the misalignment torque and the friction force, the instability of the oil film was partially suppressed, and the oil film oscillation with first and second order was hysteretic. In literature [7], considering the time-varying stiffness, the friction force, and the nonlinear film force of the crack axis, the nonlinear dynamic model of the crack-rubbing double fault rotor-bearing system was established. The numerical integration method was used to solve the problem. Integrated with the bifurcation diagram, the axis trajectory diagram, and the maximum Lyapunov index (LLE) curve, the effects of dimensionless crack depth and rotational speed on system response, stability, and friction force were analyzed qualitatively and quantitatively. The literature [8] considered that the intrinsic characteristic functions of IMF were coupled with each other, and it was difficult to clearly extract the fault characteristics of wheel set bearings of high-speed trains. Aiming at that problem, a new fault detection method for wheel set bearings was proposed. The core of this method was the adaptive decomposition of bearing vibration signal via EMD, the multi-scale IMF was obtained, and a Hankel matrix was constructed with a single-scale IMF signal. The singular value decomposition was carried out for the matrix. The key singular value was selected via differential spectrum of the singular value. The key singular value was reconstructed, and the fault of wheel set bearing was detected via envelope spectrum analysis of the reconstructed signal.
Aiming at the current research results of bearing fault identification under high water pressure to be optimized, a method based on pole symmetry modal decomposition (ESMD) for crack-friction coupling fault identification of high water pressure bearings was proposed. In this paper, the traditional algorithm was improved; the crack fault signal of the main bearing was separated from the observation signal, the background noise interference was eliminated, and the system dimensionality reduction was effectively realized so as to obtain accurate, useful, and true crack fault characteristic information and extract the internal characteristics of the signal. According to the extraction results of characteristic parameters, a probabilistic neural network was introduced to realize the final identification of bearing crack-rubbing coupling faults under high water pressure.
2. Materials and Methods
Ship bearings are an important part of the ship’s propulsion system, which can directly affect the ship’s performance and navigation safety. However, due to the complexity of the working environment of ship bearings, there are many types of data collected using condition monitoring technology, and the structure is complicated. At the same time, under high water pressure, the bearing will produce crack-friction coupling failure. Therefore, the pole symmetry modal decomposition method is used to identify ship bearing faults. This is because the method has unique advantages in trend separation of observation data, abnormal diagnosis, and time–frequency analysis, and its adaptive baseless decomposition mode is more suitable for adaptive fault identification. The structure of the marine bearing used in this study and the detailed drawings of the marine bearing are shown in Figure 1 and Figure 2.

Figure 1.
Structure of marine bearing.

Figure 2.
Detail of marine bearing.
In Figure 1, 1 is a temperature sensor; 2 is a test bearing; 3 is a balance belt; 4 is an axial force hydraulic cylinder; 5 is a gear drive shaft; 6 is a bending moment hydraulic cylinder.
Based on the marine bearing shown in the figure above, the bearing fault identification was carried out, and the identification process is shown in Figure 3.
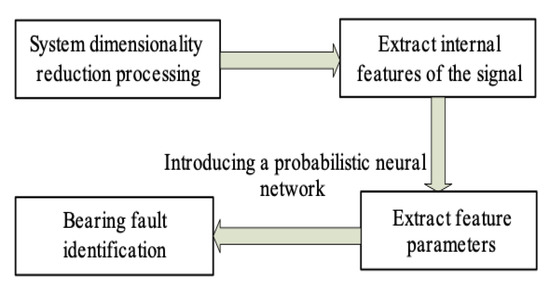
Figure 3.
Fault identification process of bearing crack and rubbing crankshaft.
The detailed process is shown as follows:
- (1)
- Dimensionality reduction was carried out for the system to improve the efficiency and the accuracy of the fault recognition and support the fault detection.
- (2)
- The internal characteristics of the signal were extracted.
- (3)
- According to the extraction results of characteristic parameters, the probability neural network was introduced to achieve the final recognition of bearing crack-rub coupling fault under high water pressure.
- (4)
- The validity of the fault recognition method was verified via experiment and discussion.
- (5)
- Summary was proposed, and prospects were put forward.
2.1. Dimensionality Reduction of System
In order to obtain accurate, useful, and true crack fault characteristic information, the crack fault signal of the main bearing was separated from the observation signal, and the background noise interference needed to be reduced.
Generally, the vibration equation of the system is:
In Formula (1), , F is the nonlinear function, M and K represent the symmetrical positive definite mass matrix and the stiffness matrix, respectively. C is the damping matrix.
The core concept of the nonlinear dimensionality reduction of system is shown as follows. Firstly, the system is divided into several subsystems. Then, the nonlinear relationship among the subsystems is confirmed. One subsystem is used to represent the other subsystems. Finally, the subsystem is imported into the dynamic equation to obtain the equation after dimensionality reduction. Among that the most important step is how to search the nonlinear relationship among the subsystems, which is the distinction of different dimensionality reduction methods. Common methods use invariant manifold theory to confirm the relationship.
Manifold: In a manifold with m dimensions (), each element () has a neighborhood (). In the neighborhood, there is a smooth and reversible mapping, namely .
Locally invariant manifold: Assuming a set , the solutions passed the are all on the set in the time interval. Thus, the is a locally invariant manifold of the original equation.
Invariant manifold: If T can be taken to infinity, namely , the is called the invariant manifold.
In order to better understand inertial manifolds and nonlinear Galerkin method, the concept of central manifolds is first introduced [9].
The eigenvalues corresponding to linear operators are divided into two parts, namely, eigenvalues with zero real part and eigenvalues with negative real part. Assuming that the is the central subspace extended by the eigenvector corresponding to the , and is the stable subspace extended by the eigenvector corresponding to the λn, represents the rectangular projection of . is the projection operator. The Equation (1) can be broken down as follows via linear variation:
Center manifold: For the system described by the Equation (2), if the is the invariant manifold, the is smooth, and the , the is its center manifold. If it is the locally invariant manifold, it is the locally center manifold.
According to the center manifold theorem, for the Equation (2) having the center manifold , the center manifold is substituted into the first equation in Equation (2) to obtain the equation on the center manifold, namely, the original dynamical system with dimensions is reduced to the one with dimensions. Then, the dimensional dynamical system Equation (3) can be obtained.
when the zero solution of the system is stable, the solution of the system on the center manifold can be used to approach the local solution of the original system in the zero attachment infinitely. Normally, the method of undermined coefficients is used to obtain the solution with asymptotic series.
In the dimensionality reduction of dynamical system with infinite dimension or high dimension, the standard Galerkin method is widely used because of its simplicity and efficiency. The standard Galerkin method is a modal truncation method, which usually takes the former low-order mode having a great effect on the system and rejects the effect of the higher-order mode [10]. However, for the specific selection of low order mode number , there is no certain criterion, which is often selected according to experience. In such a dimension reduction method, if the modal order is not chosen properly, sometimes the wrong result will be obtained. Therefore, it has become a problem concerning scholars regarding how to consider the influence of higher-order modes based on the standard Galerkin method to make the reduced dimension system more close to the original system. The nonlinear Galerkin method developed from inertial manifolds and approximate inertial manifolds is a good interpretation [11].
Aiming at Equation (1), let linear operator , thus Equation (4) is obtained.
where the is the modal matrix consisting of former m order eigenvector of matrix corresponding to the master subsystem, while the is the modal matrix consisting of former n order eigenvector of matrix corresponding to the slave subsystems. According to the division rule of and , the eigenvectors corresponding to are divided into the and the . The Equation (4) is substituted into the Equation (1). Premultiplications and are carried out at both sides of the equation. The following differential equation can be obtained [12].
The Equations (5) and (6) are coupled via nonlinear term. The standard Galerkin method rejects the effect of the higher-order mode, namely . Thus, the equation after dimensionality reduction is obtained:
Based on the approximate inertial manifold theory, the approximate relation between and is obtained via nonlinear Galerkin method. Suppose the equation is a nonlinear transcendental equation, and Picard iterative mapping is used to find its solution. If the iteration initial value , the approximate inertial manifold can be obtained [13]. If , it is substituted into the Equation (5) [14]. The equation after the dimensionality reduction is obtained:
In summary, the dimensionality reduction process of the system is shown in Figure 4.
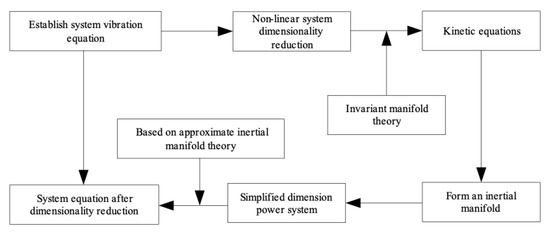
Figure 4.
System dimensionality reduction processing process diagram.
Finally, the system dimension reduction results can effectively reduce the complexity of bearing crack friction coupling fault characteristics under high water pressure and improve the precision of feature extraction.
2.2. Feature Parameters Extraction Based on Polar Symmetry Mode Decomposition
Based on the above dimensionality reduction system, the feature parameters are extracted via the polar symmetry modal decomposition. The polar symmetry modal decomposition is similar to the EMD. A finite number of IMF and one Res are generated after the bearing crack characteristics are processed through time series. However, the definition of IMF is different from the one of EMD.
The ESMD algorithm is shown as follows [15]:
- (1)
- All the extreme points of time series X’ are marked and expressed via .
- (2)
- The midpoint of the line among the extreme points is marked as .
- (3)
- Boundary points and are added via linear interpolation method.
- (4)
- According to , curves are obtained via direct interpolation algorithm. The is calculated.
- (5)
- . The above four steps are repeated until is set up, where the represents the allowable error.In another situation, when the number iterations achieves the set value , the modal function is obtained.
- (6)
- As shown in Equation (10), for , the is solved repeatedly to obtain , respectively, until the end condition is achieved.
- (7)
- The value of maximum screen number is changed in section . The decomposition method is repeated to obtain a series of results.
- (8)
- The making the minimum value in the section . Then, the is substituted. The IMF is obtained via ESMD decomposition. The obtained R’ is the optimal AGM curve.
The extraction of state feature parameters of mechanical equipment is related to the accuracy of recognition of the mechanical fault diagnosis pattern. The state feature of a signal can be characterized from time domain, energy, and entropy. The sample entropy can be used to characterize the complexity of the time series. The Kurtosis is sensitive to the weak impact on pulse variables in the signal, and it is easier to capture fault characteristics of impact pulse. However, it is insensitive to the feature type of bearing, which is very suitable for the detection of faults corresponding to the impact component in rolling bearing.
2.3. Fault Recognition
The typical probabilistic neural network (PNN) is shown in Figure 5. It can be seen that the PNN consists of four parts, namely input layer, mode layer, overlay layer, and output layer. The input layer is the first layer of the neuron. Each input neuron represents an individual attribute in the training/testing dataset. The number of inputs is equal to the number of attributes in the dataset. The value of the input data is multiplied with appropriate weights and transformed to the schema layer. The output layer usually contains only the last layer of a class, because only one output is usually required. During the training, the objective is to determine the most accurate weight assigned to the connecting line. At this stage, the outputs are computed repeatedly and compared with the optimization outputs produced by the training/testing dataset.
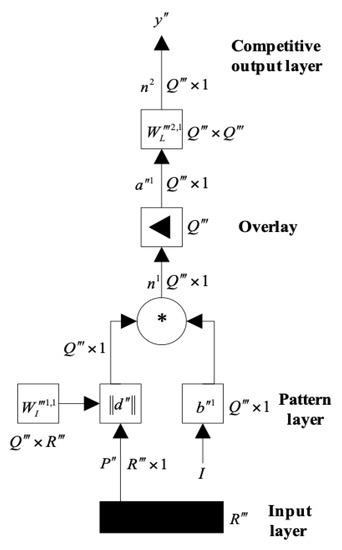
Figure 5.
Structure of probabilistic neural network (PNN).
As shown in Figure 5, represents the quantity of output element. represents the weight vector. represents the Euclidean distance between the input element and the weight vector. The computational formula is shown as follows.
where represents the ith element of vector , represents radial basis transfer function, represents the input vector with the input layer containing elements, represents a new vector consisting of row i element in vector , represents the ith element of vector , function represents competitive transfer function, represents the weight.
The probabilistic neural network has the following excellent properties. The process of network learning and training is simple. The training standard can be quickly achieved. Data classification of a PNN is accurate. As long as the training sample is large enough, a very accurate classification effect can be achieved. The influence of noise on the classification effect is small. Nonlinear data can be computed via a linear method in the PNN with arbitrary accuracy approximation.
The process of bearing fault diagnosis using ESMD and PNN is shown in Figure 6.
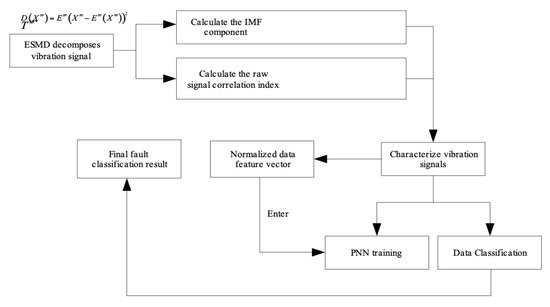
Figure 6.
Bearing fault diagnosis process.
In Figure 6, represents the standard deviation of signal , represents the mean value of signal , represents the covariance of signal and , represents the correlation coefficient of and , represents the energy eigenvector after the normalization.
The detailed process was:
- (1)
- ESMD decomposition was carried out for the vibration signal.
- (2)
- The correlation index of the obtained IMF components and the original signal were calculated and ranked respectively. The former n IMF components were taken to characterize the vibration signal (the value of n depended on the specific vibration signal decomposition).
- (3)
- In order to facilitate PNN training and classification of the data, the obtained IMF component with high correlation was calculated in terms of energy. We created a vector and normalize the obtained vector as a whole.
- (4)
- was input into the PNN as the eigenvector to train until the optimal solution was output. The final classification results of the fault were obtained.
According to the extraction results of the above characteristic parameters, a probabilistic neural network was introduced to realize the final fault recognition.
3. Results
A correlation test was conducted to verify the validity of the method. The experimental platform was the Matlab. The test device mainly included motor, torque sensor, and power meter. The bearing specifications are shown in Table 1.

Table 1.
Bearing specifications (mm).
In this experiment, 50 groups of data were randomly selected from each fault data group of the extracted three feature vectors as the test data input for the above method for training. The residual ten groups of data were used as test data for verification tests. There were 150 training sets and 30 test sets.
In the experiment, the dimensionality reduction effect of the fault recognition method was verified. Figure 7 shows the dimensionality reduction effect diagram.
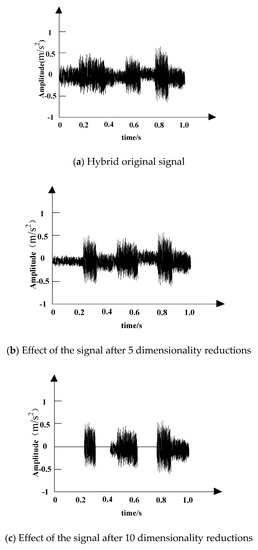
Figure 7.
Dimensionality reductions effect of the recognition method of crack-rubbing coupling fault of bearing under high water pressure based on polar symmetry mode decomposition.
It can be seen from Figure 7 that the method in this paper had a good dimensionality reduction effect. In Figure 7a, the characteristic signal of the mixed original signal had large output fluctuations. After reducing the five dimensions by the method in this paper (Figure 7), considering the signal effect in (b), the characteristic signal was initially suppressed. The characteristic signal after the 10 dimensional reduction is shown in Figure 7c. It can be clearly seen that the characteristic signal was well suppressed, which meant that, in this article, the characteristic signal changed obviously after dimensionality reduction of the method, and other noises in the mixed noise were effectively suppressed. This was because the dimensionality reduction processing in this method could effectively find the nonlinear relationship between the subsystems and used the invariant manifold theory to determine this relationship. The dimensionality reduction results effectively reduced the bearing crack friction under high water pressure. Coupled with the complexity of the fault feature, it helped to extract the feature vector of the fault signal, thereby improving the accuracy of bearing crack fault identification.
In order to further verify the application performance of the research method in this paper, the fault recognition accuracy of different research methods is discussed. We used “Result one” to represent the recognition result of the research method of literature [4], “Result two” to represent the recognition result of the research method of literature [5], and “Result three” to represent the recognition result of the research method of literature [6]. The three methods were compared with this article method in this paper to identify the crack friction coupling fault of high water pressure bearing. The comparison results of the fault identification accuracy of different research methods are shown in Figure 8.
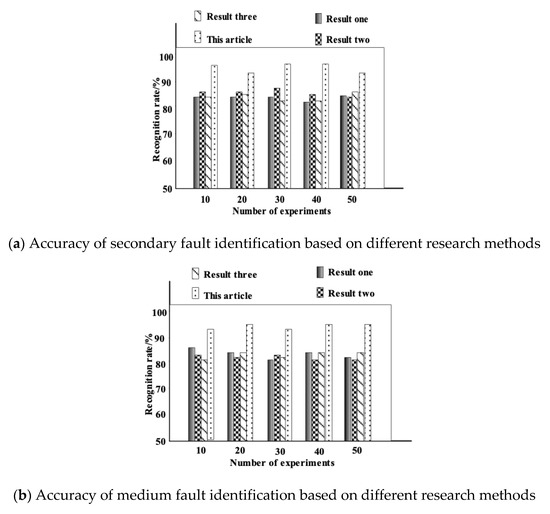
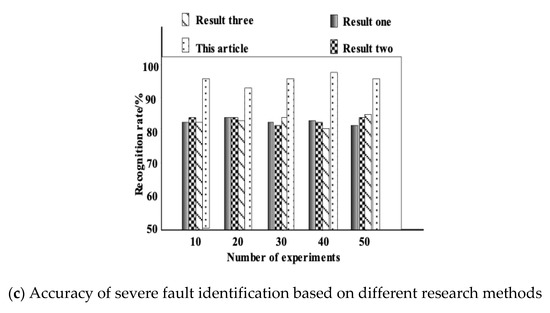
Figure 8.
Comparison of fault recognition accuracy of different research methods.
Analyzing Figure 8a, it can be seen that, when the number of experiments was 10, the accuracy of the method in literature [4] for identifying minor faults was 85%, and the method of literature [5] was 87% for identifying minor faults. The method in literature [6] had an accuracy of 86% for minor faults, while the method in this paper had an accuracy of 96% for minor faults. When the number of experiments was 40, the accuracy of the method in literature [4] was 83% for the secondary faults, the method in literature [5] was 86.8%, and the accuracy of the methods in literature [6] was 85%, while the accuracy of this method for identifying minor faults was 98%. It can be seen that the accuracy of this method in identifying minor faults was significantly higher than other methods.
Analyzing Figure 8b, it can be seen that, when the number of experiments was 20, the method in literature [4] had a recognition accuracy of 86% for moderate faults, the method in literature [5] had a recognition accuracy of 83% for moderate faults, and the method in literature [6] had a recognition accuracy of 85% for moderate faults. The accuracy of the method for identifying moderate faults was as high as 95%. When the number of experiments was 50, the method in literature [4] had an accuracy of 82% for the identification of moderate faults, the method of literature [5] had an accuracy of 81% for the identification of moderate faults, and the method of literature [6] had an accuracy of 87% for the identification of moderate faults. The accuracy of the method for identifying moderate faults was as high as 96%. The recognition rate of moderate faults in this method was significantly higher than other methods.
Analyzing Figure 8c, it can be seen that, when the number of experiments was 10, the method in literature [4] had an accuracy of 82% for serious faults, the method in literature [5] hasdan accuracy of 85% for serious faults, and the method in literature [6] had an accuracy of 82% for serious faults. The fault recognition accuracy was as high as 97%. When the number of experiments was 50, the method in literature [4] had an accuracy of 81% for serious faults, the method in literature [5] had an accuracy of 86% for serious faults, and the method in literature [6] had an accuracy of 88% for serious faults. The fault recognition accuracy was as high as 95%. The severe fault recognition rate of this method was significantly higher than other methods.
It can be seen from Figure 8 that the fault recognition accuracy of this method was higher than other research methods. This was because, in order to improve the accuracy of fault recognition, the method in this paper was based on system dimensionality reduction processing, and the false IMF caused by the interference in the polar symmetry mode decomposition was considered. The feature parameters characterizing the original signal, such as sample entropy, kurtosis, and energy, were extracted and constituted into a pattern recognition model. Integrated with the probabilistic neural network, the final recognition results were output so as to effectively improve the recognition accuracy of this method.
4. Discussion
The pole symmetry modal decomposition method can effectively alleviate the problems of multiple data types and complex structures caused by the use of condition monitoring technology for data collection. It has certain advantages in the trend separation of observation data, abnormal diagnosis, and time–frequency analysis. It also has a strong adaptive baseless decomposition mode. Therefore, under high water pressure, the identification of crack friction coupling faults caused by marine bearings has certain validity. Therefore, this paper studied the design of a bearing crack-rubbing coupling fault identification system under high water pressure based on the pole symmetry modal decomposition method. Through system dimensionality reduction processing, the nonlinear relationship between subsystems was found, and the invariant manifold theory was used to determine its non-linear relationship. Based on the results of system dimensionality reduction, the characteristic parameters were extracted using pole symmetry modal decomposition. The state characteristics of the fault signal were characterized from the entropy parameters and the time domain parameters, respectively, and the signal was characterized from different dimensions so as to obtain the bearing crack friction coupling fault characteristic parameter extraction results. Finally, a probabilistic neural network was introduced to finally realize bearing crack-rubbing coupling fault identification under high water pressure. The article integrated a variety of technologies to improve the traditional methods of identifying ship bearing crack faults and to improve the accuracy of fault identification. The results show that the system dimensionality reduction process can effectively reduce the complexity of the bearing crack friction coupling fault characteristics under high water pressure. At the same time, considering the false IMF caused by interference in the polar symmetry mode decomposition, the final output fault identification result was obtained and had high accuracy.
5. Conclusions
Faults often appear in the rotating machine, such as aero-engine, gas turbine, and so on, and most of them are caused by the fault of the rotor system. Therefore, it is of great significance for rotating machines to analyze fault mechanism and to understand fault characteristics and diagnose fault. A recognition method of crack-rubbing coupling fault of bearing based on polar symmetry mode decomposition was proposed in this article. Integrated with the system dimensionality reduction and the extraction of the signal feature, the support was provided for the fault recognition. The probabilistic neural network was introduced to output fault recognition results. Experimental results show that the method has better fault recognition effect and excellent reliability. Fault diagnosis technology is constantly combined with advanced concepts and technologies such as big data, constantly working towards intelligent development. In the future, the development of fault diagnosis technology will not only be to diagnose the bearing that has already failed but will also rely on big data, artificial intelligence, wireless network, and other technologies. The service life of the bearing can be estimated roughly since its online, thus the bearing can be maintained and changed timely. Thus, the target of non-fault can be achieved.
In the future, the online estimation of bearing life will be studied to effectively reduce the impact of sudden failures on related work.
Author Contributions
In this paper, a method of bearing crack rub impact coupling fault identification under high water pressure based on pole symmetric mode decomposition is proposed. J.H. developed the numerical method and wrote the manuscript. S.D. provided the research ideas and helped draft the manuscript. W.H. checked the manu-script and verified the simulation results. T.X. participated in the design of the study. Y.Y. participated in the numerical model design. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 11872042), Sichuan Science and Technology Program (Nos. 2018JY0024 & 2019YJ0156), China Postdoctoral Science Foundation (2019M653395), Sichuan University Postdoctoral Research Foundation (2019SCU12049).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The Sichuan Science and Technology Program (Project No. 2018JY0024 & 2019YJ0156) and National Natural Science Foundation of China (Project No.11872042).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Esmaeili, K.; Zuercher, M.; Wang, L.; Harvey, T.; White, N.; Holweger, W.; Schlücker, E. A study of white etching crack bearing failure detection using electrostatic sensing in wind turbine gearboxes. Int. J. Cond. Monit. 2018, 12, 12–18. [Google Scholar] [CrossRef]
- Tang, C.; Yao, Q.; Li, Z.; Zhang, Y.; Ju, M. Experimental study of shear failure and crack propagation in water-bearing coal samples. Energy Sci. Eng. 2019, 7, 54–58. [Google Scholar] [CrossRef]
- Shaohu, L.; Yuandeng, W.; Hao, Z. Critical Ultimate Load and Ultimate Bearing Failure of CT110 with Initial Crack Defect. J. Fail. Anal. Prev. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Corne, B.; Vervisch, B.; Derammelaere, S.; Knockaert, J.; Desmet, J. Emulating single point bearing faults with the use of an active magnetic bearing. IET Sci. Meas. Technol. 2018, 12, 39–48. [Google Scholar] [CrossRef]
- Sathujoda, P. Detection of a slant crack in a rotor bearing system during shut-down. J. Struct. Mech. 2020, 48, 266–276. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.Z.; Shi, T.; Ma, H.; Wen, B. Study on misalignment-rubbing coupling fault of rotor system supported by oil film force. J. Mech. Eng. 2016, 52, 79–86. [Google Scholar] [CrossRef]
- Xiang, L.; Gao, X.Y.; Zhang, L.J.; Di, W.W. Dynamic Analysis of a Rotor with Coupling Faults of Crack and Rub-Impact Under Nonlinear Oil-film Force. J. Chin. Soc. Power Eng. 2016, 36, 788–794. [Google Scholar]
- Zhuang, Z.; Chen, X.; Shi, Y.; Liu, Z.C. Research on fault detection of wheel set bearing based on IMF-SVD envelop spectrum method. China Meas. Test 2017, 43, 93–98. [Google Scholar]
- Bruce, T.; Long, H.; Dwyer-Joyce, R.S. Threshold Maps for Inclusion-Initiated Micro-Cracks and White Etching Areas in Bearing Steel: The Role of Impact Loading and Surface Sliding. Springer Open Choice 2018, 66, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Niu, Y.; Wang, E.; Liu, L.; Wang, H.; Wang, M.; Ali, M. Experimental Study on Electric Potential Response Characteristics of Gas-Bearing Coal During Deformation and Fracturing Process. Processes 2019, 7, 72. [Google Scholar] [CrossRef]
- Caesarendra, W.; Pratama, M.; Kosasih, B.; Tjahjowidodo, T.; Glowacz, A. Parsimonious Network Based on a Fuzzy Inference System (PANFIS) for Time Series Feature Prediction of Low Speed Slew Bearing Prognosis. Appl. Sci. 2018, 8, 2656. [Google Scholar] [CrossRef]
- Zhang, T.T.; Jia, M.Y. Common methods of mechanical equipment fault diagnosis technology and application research of new technology. Autom. Instrum. 2017, 10, 38–39. [Google Scholar]
- Glowacz, A. Acoustic fault analysis of three commutator motors. Mech. Syst. Signal Process. 2019, 133, 106226. [Google Scholar] [CrossRef]
- Adam, G.; Witold, G.; Jarosław, K.; Krzysztof, P.; Miroslav, G.; Wahyu, C.; Hui, L.; Frantisek, B.; Muhammad, I.; Faizal, K. Detection of Deterioration of Three-phase Induction Motor using Vibration Signals. Meas. Sci. Rev. 2019, 19, 241–249. [Google Scholar]
- Huang, D.; Yang, J.; Zhou, D.; Litak, G. Novel adaptive search method for bearing fault frequency using stochastic resonance quantified by amplitude-domain index. IEEE Trans. Instrum. Meas. 2019, 99, 1–13. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).