Strategic Integration Decision under Supply Chain Competition in the Presence of Online Channel
Abstract
1. Introduction
- (a)
- competing manufacturers’ and retailers’ strategies in equilibrium;
- (b)
- the equilibrium price in the online and retail channels, and wholesale prices;
- (c)
- the total profits for each SCs?
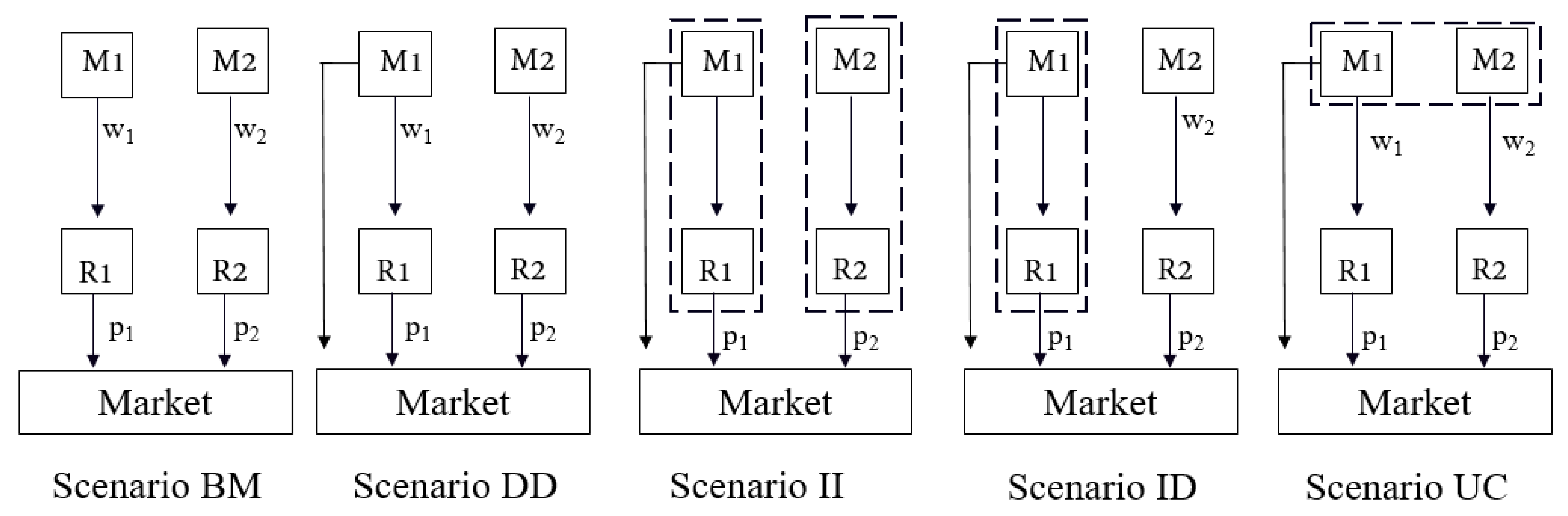
2. Problem Statement
3. Main Analytical Results
3.1. Benchmark Models
3.1.1. Optimal Decisions in Scenario BM
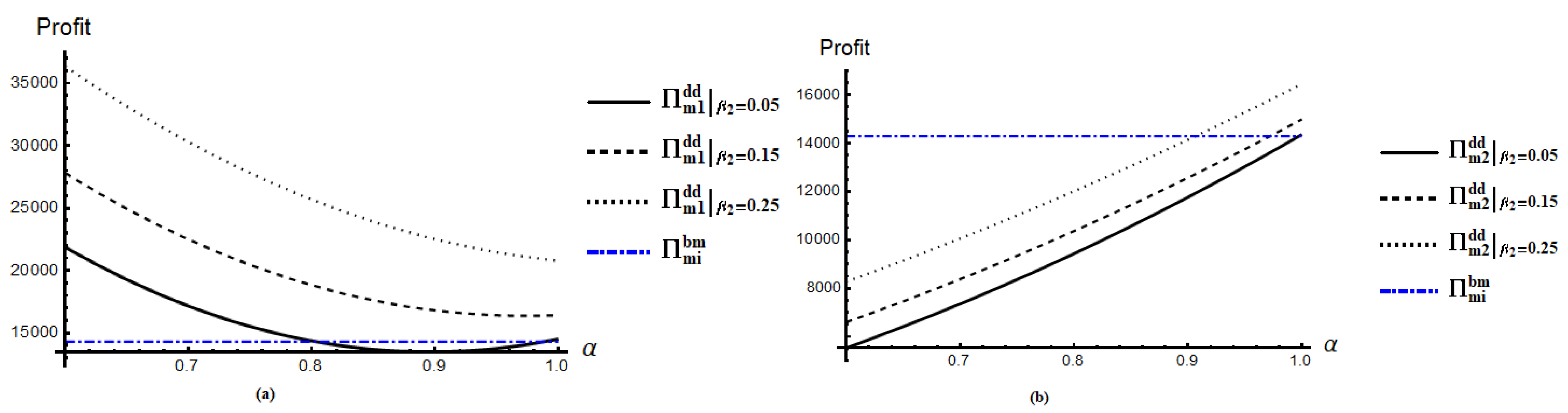
3.1.2. Optimal Decisions in Scenario DD
- 1.
- Market price of product from is always higher compared to , because .
- 2.
- Wholesale price for first product is less compared to product at online channel, i.e., , if .
3.2. Vertical Integration
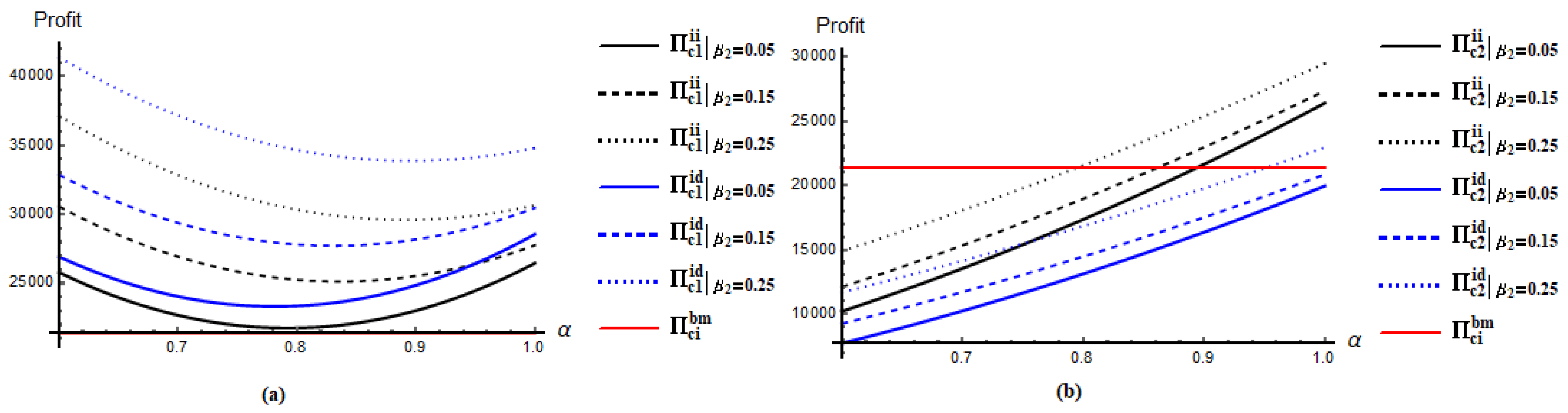
Optimal Decision in Scenario II
- 1.
- Total profit for the first SC is always higher compared to Second SC because .
- 2.
- Market price for the first product in an online channel is higher compared to price of that in the retail channel if , because .
- 3.
- Price of the first product is always higher compared to the second product in retail channel, because .
- 4.
- Profits in the first retail channel is always less compared to the second retail channel because .
3.3. Optimal Decision in Scenario ID
- 1.
- Retail price for the first retail channel remains higher compared to the second retail channel because if . Sales volume for first retail channel is also less compared to second retail channel because
- 2.
- Price of the first product in retail channel will be higher compared to the online channel, if
- (1)
- Total profit for the first SC is higher in Scenario II compared to BM, i.e., if
- (2)
- Total profit for the first SC is higher in Scenario II compared to DD, i.e., if
- (3)
- Total profit for the first SC is higher in Scenario ID compared to Scenario BM, i.e.,
- (4)
- Total profit for the first SC is higher in Scenario ID compared to Scenario DD, i.e.,
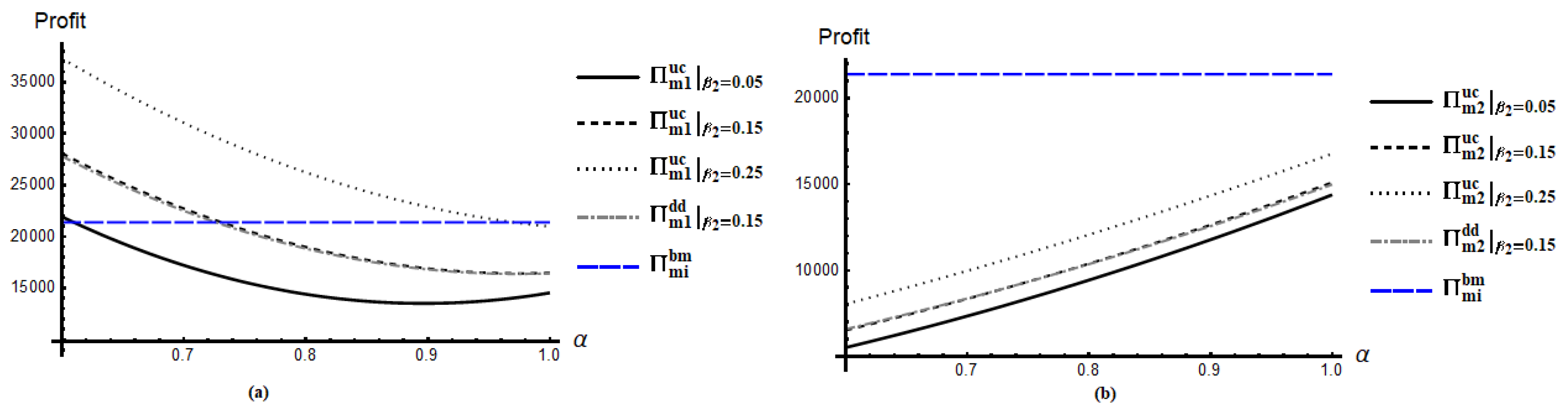
3.4. Optimal Decision in Scenario UC
- 1.
- Unlike all four scenarios in the presence of an online channel, market prices, profits for two retailers, and wholesale prices remain identical for two competing SCs.
- 2.
- Market price of the first product is always higher in an online channel compared to a retail channel, i.e., if
- 3.
- Wholesale price for the first product is less compared to its price at online channel, i.e., , if
- If a competing manufacturer opens an online channel, then consumers can receive the first products at a lower price.
- If an upstream manufacturer opens an online channel, then the retailer in that SC may lose a significant amount of profit, as well as consumers in the future. Due to easy access to the internet, if consumers continuously find the product available online at a cheaper price or similar types of products in other retail outlets at a lower price, they may intend to buy the product online or change their minds in the future.
- All the competing members have the opportunity to receive a higher profit in the presence of an online channel compared to Scenario BM. Due to the additional price option and consumer cross-price elasticity, members are somehow bound to reduce the price for the products. Consequently, demand increases and total profit also increases.
- Both horizontal and vertical integration decisions can improve total profits for each competing SCs.
4. Result Analysis and Discussion
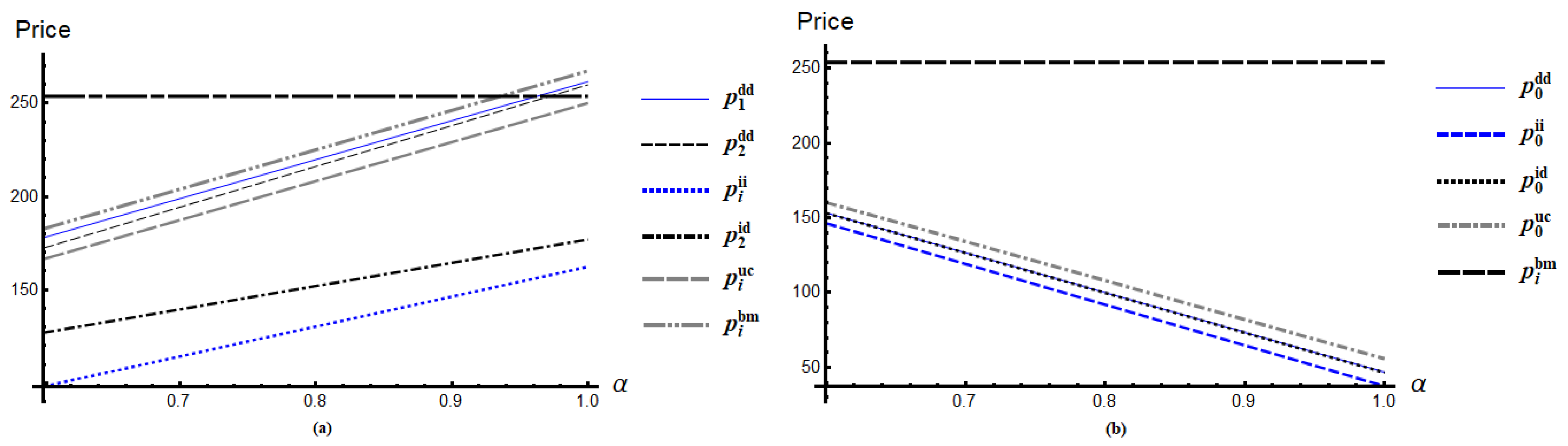
4.1. Nature of Retail Prices in Different Scenarios
4.2. Nature Profits for Two Competing SCs in Five Scenarios
4.3. Managerial Insights
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of the Optimal Decision in Scenario BM
Appendix B. Derivation of the Optimal Decision in Scenario DD
Appendix C. Derivation of the Optimal Decision in Scenario II
Appendix D. Derivation of the Optimal Decision in Scenario ID
Appendix E. Derivation of the Optimal Decision in Scenario UC
Appendix F. Prof of Proposition 3
Appendix G. Optimal Decision in the Absence of Online Channel
| Decision | Scenario BM/DD | Scenario II | Scenario UC | Scenario ID |
|---|---|---|---|---|
| - | - | |||
| - | ||||
| - | - | |||
| - | ||||
| - | - | |||
| - | ||||

Appendix H. List of Symbols
References
- Netessine, S.; Rudi, N. Supply chain choice on the internet. Manag. Sci. 2006, 52, 844–864. [Google Scholar] [CrossRef]
- Ofek, E.; Katona, Z.; Sarvary, M. “Bricks and clicks”: The impact of product returns on the strategies of multichannel retailers. Mark. Sci. 2011, 30, 42–60. [Google Scholar] [CrossRef]
- Yan, R.; Pei, Z.; Myers, C. Do channel members value the multiple-cooperation strategy? J. Retail. Consum. Serv. 2016, 30, 84–95. [Google Scholar] [CrossRef]
- Young, Y. US Ecommerce Sales Grow 14.9% in 2019. 2020. Available online: www.digitalcommerce360.com/article/us-ecommerce-sales/ (accessed on 5 July 2020).
- Chiang, W.Y.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Arya, A.; Mittendorf, B.; Sappington, D.E. The bright side of supplier encroachment. Mark. Sci. 2007, 26, 651–659. [Google Scholar] [CrossRef]
- Yan, R.; Ghose, S. Forecast information and traditional retailer performance in a dual-channel competitive market. J. Bus. Res. 2010, 63, 77–83. [Google Scholar] [CrossRef]
- Huang, T.; Van Mieghem, J.A. Clickstream data and inventory management: Model and empirical analysis. Prod. Oper. Manag. 2014, 23, 333–347. [Google Scholar] [CrossRef]
- Kalnins, A. Pricing variation within dual-distribution chains: The different implications of externalities and signaling for high-and low-quality brands. Manag. Sci. 2017, 63, 139–152. [Google Scholar] [CrossRef]
- Xiao, T.; Shi, J.J. Pricing and supply priority in a dual-channel supply chain. Eur. J. Oper. Res. 2016, 254, 813–823. [Google Scholar] [CrossRef]
- Moon, I.; Sarmah, S.P.; Saha, S. The impact of online sales on centralised and decentralised dual-channel supply chains. Eur. J. Ind. Eng. 2018, 12, 67–92. [Google Scholar] [CrossRef]
- Chen, J.; Liang, L.; Yao, D.Q.; Sun, S. Price and quality decisions in dual-channel supply chains. Eur. J. Oper. Res. 2017, 259, 935–948. [Google Scholar] [CrossRef]
- Dan, B.; Liu, C.; Xu, G.; Zhang, X. Pareto improvement strategy for service-based free-riding in a dual-channel supply chain. Asia Pac. J. Oper. Res. 2014, 31, 1450050. [Google Scholar] [CrossRef]
- Rodriguez, B.; Aydın, G. Pricing and assortment decisions for a manufacturer selling through dual channels. Eur. J. Oper. Res. 2015, 242, 901–909. [Google Scholar] [CrossRef]
- Yan, R.; Pei, Z. Retail services and firm profit in a dual-channel market. J. Retail. Consum. Serv. 2009, 16, 306–314. [Google Scholar] [CrossRef]
- Pei, Z.; Toombs, L.; Yan, R. How does the added new online channel impact the supporting advertising expenditure? J. Retail. Consum. Serv. 2014, 21, 229–238. [Google Scholar] [CrossRef]
- Chen, T.H. Effects of the pricing and cooperative advertising policies in a two-echelon dual-channel supply chain. Comput. Ind. Eng. 2015, 87, 250–259. [Google Scholar] [CrossRef]
- He, Y.; Huang, H.; Li, D. Inventory and pricing decisions for a dual-channel supply chain with deteriorating products. Oper. Res. 2018, 1–43. [Google Scholar] [CrossRef]
- Jamali, M.B.; Rasti-Barzoki, M. A game theoretic approach for green and non-green product pricing in chain-to-chain competitive sustainable and regular dual-channel supply chains. J. Clean. Prod. 2018, 170, 1029–1043. [Google Scholar] [CrossRef]
- Basiri, Z.; Heydari, J. A mathematical model for green supply chain coordination with substitutable products. J. Clean. Prod. 2017, 145, 232–249. [Google Scholar] [CrossRef]
- Fang, D.; Ren, Q. Optimal decision in a dual-channel supply chain under potential information leakage. Symmetry 2019, 11, 308. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, R.; Wang, W. Pricing decision of a manufacturer in a dual-channel supply chain with asymmetric information. Eur. J. Oper. Res. 2019, 278, 809–820. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Yu, M. Pricing decisions in a dual-channel green supply chain with product customization. J. Clean. Prod. 2020, 247, 119101. [Google Scholar] [CrossRef]
- Saha, S.; Sarmah, S.P.; Moon, I. Dual channel closed-loop supply chain coordination with a reward-driven remanufacturing policy. Int. J. Prod. Res. 2016, 54, 1503–1517. [Google Scholar] [CrossRef]
- Choi, S.C. Price competition in a duopoly common retailer channel. J. Retail. 1996, 72, 117–134. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S. Contracting and Information Sharing Under Supply Chain Competition. Manag. Sci. 2008, 54, 701–715. [Google Scholar] [CrossRef]
- Anderson, E.J.; Bao, Y. Price competition with integrated and decentralized supply chains. Eur. J. Oper. Res. 2010, 200, 227–234. [Google Scholar] [CrossRef]
- Xie, G. Modeling decision processes of a green supply chain with regulation on energy saving level. Comput. Oper. Res. 2015, 54, 266–273. [Google Scholar] [CrossRef]
- Zhang, G.; Dai, G.; Sun, H.; Zhang, G.; Yang, Z. Equilibrium in supply chain network with competition and service level between channels considering consumers’ channel preferences. J. Retail. Consum. Serv. 2020, 57, 102199. [Google Scholar] [CrossRef]
- Garrett, B. Why Collaborating with Your Competition Can Be a Great Idea. 2019. Available online: www.forbes.com/sites/briannegarrett/2019/09/19/why-collaborating-with-your-competition-can-be-a-great-idea/?sh=4e77f3dedf86 (accessed on 5 July 2020).
- Wei, J.; Zhao, J.; Hou, X. Integration strategies of two supply chains with complementary products. Int. J. Prod. Res. 2019, 57, 1972–1989. [Google Scholar] [CrossRef]
- Bian, J.; Zhao, X.; Liu, Y. Single vs. cross distribution channels with manufacturers’ dynamic tacit collusion. Int. J. Prod. Econ. 2020, 220, 107456. [Google Scholar] [CrossRef]
- Colombo, S. Mixed oligopolies and collusion. J. Econ. 2016, 118, 167–184. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Cao, Z.H. Equilibrium structures of two supply chains with price and displayed-quantity competition. J. Oper. Res. Soc. 2014, 65, 1544–1554. [Google Scholar] [CrossRef]
- Wang, L.; Song, H.; Wang, Y. Pricing and service decisions of complementary products in a dual-channel supply chain. Comput. Ind. Eng. 2017, 105, 223–233. [Google Scholar] [CrossRef]
- Saha, S. Channel characteristics and coordination in three-echelon dual-channel supply chain. Int. J. Syst. Sci. 2016, 47, 740–754. [Google Scholar] [CrossRef]
- Eriksen, P.S.; Nielsen, P. Order quantity distributions: Estimating an adequate aggregation horizonautomotive industries: A SEM analysis. Manag. Prod. Eng. Rev. 2016, 7, 39–48. [Google Scholar]
- Jafari, H.; Hejazi, S.R.; Rasti-Barzoki, M. Sustainable development by waste recycling under a three-echelon supply chain: A game-theoretic approach. J. Clean. Prod. 2017, 142, 2252–2261. [Google Scholar] [CrossRef]
- Song, Z.; He, S.; An, B. Decision and coordination in a dual-channel three-layered green supply chain. Symmetry 2018, 10, 549. [Google Scholar] [CrossRef]
- Nielsen, I.E.; Majumder, S.; Saha, S. Exploring the intervention of intermediary in a green supply chain. J. Clean. Prod. 2019, 233, 1525–1544. [Google Scholar] [CrossRef]
- Nielsen, I.E.; Majumder, S.; Szwarc, E.; Saha, S. Impact of Strategic Cooperation under Competition on Green Product Manufacturing. Sustainability 2020, 12, 248. [Google Scholar] [CrossRef]
- Saha, S.; Sarmah, S.P. Supply chain coordination under ramp-type price and effort induced demand considering revenue sharing contract. Asia Pac. J. Oper. Res. 2015, 32, 1550004. [Google Scholar] [CrossRef]
- Michna, Z.; Disney, S.M.; Nielsen, P. The impact of stochastic lead times on the bullwhip effect under correlated demand and moving average forecasts. Omega 2020, 93, 102033. [Google Scholar] [CrossRef]

| Notations | Descriptions |
|---|---|
| Indices | |
| i | index for ith SC, |
| j | index for decision scenarios, |
| Parameters | |
| a | market potential for each SC |
| the cross-price sensitivity of consumers between two retail channels, | |
| the cross-price sensitivity of consumers between retail and online channels, | |
| Variables | |
| wholesale price of per unit ith product | |
| retail price of per unit ith product in the traditional retail channel | |
| retail price of per unit first product in the online channel | |
| profit of the ith retailer | |
| profit of the first manufacturer, i.e., sum of profits from the retail channel () and online channel(), and | |
| profit of the second manufacturer | |
| profit of the first SC, i.e., sum of profits form the retail channel() and online channel(), and | |
| total profit of the second SC | |
| sales volume of ith SC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.; Nielsen, I. Strategic Integration Decision under Supply Chain Competition in the Presence of Online Channel. Symmetry 2021, 13, 58. https://doi.org/10.3390/sym13010058
Saha S, Nielsen I. Strategic Integration Decision under Supply Chain Competition in the Presence of Online Channel. Symmetry. 2021; 13(1):58. https://doi.org/10.3390/sym13010058
Chicago/Turabian StyleSaha, Subrata, and Izabela Nielsen. 2021. "Strategic Integration Decision under Supply Chain Competition in the Presence of Online Channel" Symmetry 13, no. 1: 58. https://doi.org/10.3390/sym13010058
APA StyleSaha, S., & Nielsen, I. (2021). Strategic Integration Decision under Supply Chain Competition in the Presence of Online Channel. Symmetry, 13(1), 58. https://doi.org/10.3390/sym13010058






