Fixed Point of Interpolative Rus–Reich–Ćirić Contraction Mapping on Rectangular Quasi-Partial b-Metric Space

Abstract

The purpose of this study is to introduce a new type of extended metric space, i.e., the rectangular quasi-partial b-metric space, which means a relaxation of the symmetry requirement of metric spaces, by including a real number s in the definition of the rectangular metric space defined by Branciari. Here, we obtain a fixed point theorem for interpolative Rus–Reich–Ćirić contraction mappings in the realm of rectangular quasi-partial b-metric spaces. Furthermore, an example is also illustrated to present the applicability of our result.

1. Introduction and Preliminaries

In the year 1968, Kannan [1] extended the well-known Banach contraction:

$$d(G\vartheta ,G\eta )\le \rho \left[d\right(\vartheta ,G\vartheta )+d(\eta ,G\eta \left)\right]\mathrm{for}\mathrm{all}\vartheta ,\eta \in M,$$

where $\rho \in \left[0,\frac{1}{2}\right)$. In 2018, Karapinar [2] established the generalized Kannan-type contraction by using the interpolative approach and proved that such an interpolative Kannan-type contraction mapping owns a fixed point in a complete metric space. Let us recall that given a metric space (M, d), a self-map $G:M$$\to M$ is called an interpolative Kannan-type contraction map, if:

$$d(G\vartheta ,G\eta )\le \rho {\left[d(\vartheta ,G\vartheta )\right]}^{\alpha }·{\left[d(\eta ,G\eta )\right]}^{1-\alpha }\mathrm{for}\mathrm{all}\vartheta ,\eta \in M\setminus \mathit{Fix}\left(G\right)$$

where $\mathit{Fix}\left(G\right)=\{z\in$$M:G$$z=z\}$. Recently, Karapinar/Agarwal/Aydi [3] introduced the following notion of interpolative Rus–Reich–Ćirić contractions in the context of partial metric spaces [4], which keep symmetry as one of their intrinsic properties.

Theorem 1

([3]). In the setting of partial metric space $(M,d)$, if a self-map $G:M$$\to M$ is an interpolative Rus–Reich–Ćirić-type contraction, i.e., there are constants $\rho \in [0,1)$ and $\alpha ,\beta \in (0,1)$ such that:

$$d(G\vartheta ,G\eta )\le \rho {\left[d(\vartheta ,\eta )\right]}^{\beta }{\left[d(\vartheta ,G\vartheta )\right]}^{\alpha }·{\left[d(\eta ,G\eta )\right]}^{1-\alpha -\beta }\mathit{for}\mathit{all}\vartheta ,\eta \in M\setminus \mathit{Fix}\left(G\right),$$

then G owns a fixed point.

In the year 2000, Branciari [5] introduced the notion of the rectangular metric space by replacing the triangle inequality with the quadrilateral inequality in the definition of the metric space. It was noticed by Suzuki [6] that the topological structure of the standard metric space and that the rectangular metric space are not comparable. In 2019, Karapinar [7] defined the interpolative Rus–Reich–Ćirić contraction map on the rectangular metric. Interesting work has been done by several authors [8,9,10,11,12,13,14,15,16,17,18,19] enriching this research field. Firstly, we recall some basic definitions and concepts on the rectangular metric space.

Definition 1

([5]). Let $M\ne \varnothing$. Consider $r:M$$\times M\to {\mathbb{R}}^{+}$ such that for all $\vartheta ,\eta \in M$ and u, v ∈M:

(r1)

$r(\vartheta ,\eta )=0$ iff ϑ = η (identification),

(r2)

$r(\vartheta ,\eta )=r(\eta ,\vartheta )$ (symmetry),

(r3)

$r(\vartheta ,\eta )\le r(\vartheta ,u)+r(u,v)+r(v,\eta )$ (quadrilateral inequality).

$(M,r)$ is called a rectangular metric space.

Example 1.

Let M = [1, ∞). Define r(ϑ, η) = |ln(ϑ/η)|.

Here, r(ϑ/η) = 0 ⇒lnϑ = lnη, which gives ϑ = η.

Again, r(ϑ/η) = r($\eta /\vartheta$).

Furthermore, $r(\vartheta /\eta )$≤ r(ϑ, u) +r(u, v) +r(v, η).

As |ln$(\vartheta /\eta$$\left)\right|$$=|$ln$\vartheta -$$ln\eta |$ $\le |$ln$\vartheta -$ln$u+$ln$u-$ln$v+$ln$v-$ln$\eta |$.

It can be observed that |ln$\left(\frac{\vartheta }{\eta }\right)|\le |$ln$\vartheta -$ln$u|+|$ln$u-$ln$v|+|$ln$v-$ln$\eta |$.

Therefore, $\left(r_3\right)$ holds. Thus, (M, r) is a rectangular metric space.

Definition 2

([7]). Let $(M,r)$ be a rectangular metric. Then:

 (i)

A sequence $\{{\vartheta }_n$}$\subset M$ converges to $\vartheta \in M$ if r$(\vartheta ,\vartheta )=$$\underset{n\to \infty }{lim}$$r(\vartheta ,{\vartheta }_n)$.

 (ii)

A sequence $\{{\vartheta }_n$}$\subset M$ is called a Cauchy sequence if for every ε$>0$, there exists a positive integer $N=N$(ε) such that $r({\vartheta }_n,{\vartheta }_m)<$ε for all $n,m>N$.

 (iii)

(M, r) is said to be complete if each Cauchy sequence in M is convergent.

Definition 3

([7]). Let (M, r) be a rectangular metric space. We say that a mapping G$:M$→ M is continuous at u ∈ M, if we have G${\vartheta }_n$→ Gu (in other words $\underset{n\to \infty }{lim}$$r(G{\vartheta }_n,Gu)=0)$, for any sequence $\{{\vartheta }_n$} in M that is convergent to u ∈ M, that is ${\vartheta }_n$→ u.

Proposition 1

([7]). Suppose that $\{{\vartheta }_n$} is a Cauchy sequence in a rectangular metric space such that $\underset{n\to \infty }{lim}$$r({\vartheta }_n,u)=$$\underset{n\to \infty }{lim}$$r({\vartheta }_n,z)=0$, where u, z ∈ M. Then, u = z.

The following definition gives room for the lack of symmetry in the spaces under study. Let us recall that quasi-metric spaces [20] satisfy the same axioms as metric spaces, but with the requirement of symmetry.

Definition 4

([21]). A quasi-partial b-metric on a non-empty set M is a function $q{p}_b$$:M$$\times M\to {\mathbb{R}}^{+}$ such that for some real number $s\ge 1$ and all $\vartheta ,\eta ,\zeta \in M$:

(QPb₁)

$q{p}_b(\vartheta ,\vartheta )=q{p}_b(\vartheta ,\eta )=q{p}_b(\eta ,\eta )$ implies $\vartheta =\eta$,

(QPb₂)

$q{p}_b(\vartheta ,\vartheta )\le q{p}_b(\vartheta ,\eta )$,

(QPb₃)

$q{p}_b(\vartheta ,\vartheta )\le q{p}_b(\eta ,\vartheta )$,

(QPb₄)

$q{p}_b(\vartheta ,\eta )\le s[q{p}_b(\vartheta ,\zeta )+q{p}_b(\zeta ,\eta )]-q{p}_b(\zeta ,\zeta )$.

$(M,q{p}_b)$ is called a quasi-partial b-metric space. The number s is called the coefficient of $(M,q{p}_b)$.

Lemma 1

([22]). Let $(M,q{p}_b)$ be a quasi-partial b-metric space. Then, the following hold:

 (i)

if $q{p}_b$ (ϑ, $\eta )=$ 0, then $\vartheta =\eta$.

 (ii)

if $\vartheta =\eta$, then $q{p}_b$ (ϑ, η) $>0$ and $q{p}_b$ (η, ϑ) $>0$.

Definition 5

([23]). Let $(M,q{p}_b)$ be a quasi-partial b-metric. Then:

 (i)

a sequence $\{{\vartheta }_n$}$\subset M$ converges to $\vartheta \in M$ if $q{p}_b(\vartheta ,\vartheta )=$$\underset{n\to \infty }{lim}$$q{p}_b(\vartheta ,{\vartheta }_n).$

 (ii)

a sequence $\{{\vartheta }_n$}$\subset M$ is called a Cauchy sequence if $\underset{n,m\to \infty }{lim}q{p}_b({\vartheta }_n,{\vartheta }_m)$ exists.

 (iii)

a quasi-partial b-metric space $(M,q{p}_b$) is said to be complete if every Cauchy sequence $\{{\vartheta }_n$}$\subset M$ converges with respect to ${\tau }_{q{p}_b}$ to a point $\vartheta \in M$ such that:

$$q{p}_b(\vartheta ,\vartheta )=\underset{n,m\to \infty }{lim}q{p}_b({\vartheta }_n,{\vartheta }_m).$$

 (iv)

a mapping $f:M$$\to M$ is said to be continuous at ${\vartheta }_0\in M$ if, for every $\epsilon >0$, there exists:

$$\delta >0\mathrm{such}\mathrm{that}f\left(B({\vartheta }_0,\delta )\right)\subset B(f\left({\vartheta }_0\right),\epsilon ).$$

Lemma 2

([23]). Let (M, $q{p}_b$) be a quasi-partial b-metric space and (M, $dq{p}_b$) be the corresponding b-metric space. Then, (M, $dq{p}_b$) is complete if (M, $q{p}_b$) is complete.

Lemma 3

([24]). Let (M, $q{p}_b$) be a quasi-partial b-metric space and $G:M$→ M be a given mapping. G is said to be sequentially continuous at z ϵ M if for each sequence $\{{\vartheta }_n$} in M converging to z, we have: $G{\vartheta }_n\to$ Gz, that is, $q{p}_b$$(G{\vartheta }_n$, Gz) $=q{p}_b$(Gz, Gz).

2. Main Results

We start this section by introducing the notion of interpolative Rus–Reich–Ćirić-type contractions in the setting of the rectangular quasi-partial b-metric space.

Definition 6.

A rectangular quasi-partial b-metric on a non-empty set M is a function $rq{p}_b$:

M$\times M\to {\mathbb{R}}^{+}$ such that for some real number $s\ge 1$ and all $\vartheta ,\eta ,u,v\in M$:

(RQPb₁)

$rq{p}_b(\vartheta ,\vartheta )=rq{p}_b(\vartheta ,\eta )=rq{p}_b(\eta ,\eta )$⇒$\mu =\eta$,

(RQPb₂)

$rq{p}_b(\vartheta ,\vartheta )\le rq{p}_b(\vartheta ,\eta )$,

(RQPb₃)

$rq{p}_b(\vartheta ,\vartheta )\le rq{p}_b(\eta ,\vartheta )$,

(RQPb₄)

$rq{p}_b(\vartheta ,\eta )\le s[rq{p}_b(\vartheta ,u)+rq{p}_b(u,v)+rq{p}_b(v,\eta )]-rq{p}_b(u,u)-rq{p}_b(v,v)$.

$(M,rq{p}_b)$ is called a rectangular quasi-partial b-metric space. The number s is called the coefficient of $(M,rq{p}_b)$.

Example 2.

Let M $=[0,1]$. Define $rq{p}_b$ (ϑ, η)= |$\vartheta -\eta |+\vartheta$.

Here, $rq{p}_b$ ($\vartheta ,\vartheta )=rq{p}_b(\vartheta ,\eta )=rq{p}_b(\eta ,\eta$) ⇒ϑ = η as ϑ = $|\vartheta -\eta |+\vartheta =\eta$ gives $\vartheta =\eta$.

Again, $rq{p}_b$ (ϑ,ϑ) ≤$rq{p}_b$ (ϑ, η) as $\vartheta \le |$$\vartheta -\eta |+\vartheta$, and similarly, $rq{p}_b$ (ϑ,ϑ) ≤ $rq{p}_b$ ($\eta ,\vartheta$) as $\vartheta \le |\eta -\vartheta |+\eta$ for $0\le \vartheta \le \eta$.

Furthermore, $rq{p}_b$ ($\vartheta ,\eta )+rq{p}_b(u,u)+rq{p}_b(v,v)\le s[rq{p}_b(\vartheta ,u)+rq{p}_b(u,v)+rq{p}_b(v,\eta )]$ as $|\vartheta -\eta |+\vartheta +u+v\le \left[\right|\vartheta -u|+\vartheta +|u-v|+u+|v-\eta |+v]$.

It can be observed that

|ϑ-η|+ϑ+u+v = |ϑ-u+u-v+v-η|+ϑ+u+v ≤|ϑ-u|+|u-v|+|v-η|+ϑ+u+v.

Therefore, ($RQP{b}_4$) holds. Thus, $(M,rq{p}_b)$ is a rectangular quasi-partial b-metric space with s = 1.

Example 3.

Let $M=R$. Define $rq{p}_b(\vartheta ,\eta )={|\vartheta -\eta |+\left|\vartheta \right|+|\vartheta -\eta |}^2$ for any $(\vartheta ,\eta )\in M\times M$ with $s\ge 2$. Here, we can show that $(M,rq{p}_b)$ is a rectangular quasi-partial b-metric space.

If $rq{p}_b(\vartheta ,\vartheta )=rq{p}_b(\vartheta ,\eta )=rq{p}_b(\eta ,\eta )\Rightarrow \vartheta =\eta$.

Furthermore, $rq{p}_b(\vartheta ,\vartheta )\le rq{p}_b(\vartheta ,\eta )$, which satisfies $\left(RQP{b}_2\right)$.

Next, $rq{p}_b(\vartheta ,\vartheta )=\left|\vartheta \right|\le {|\vartheta -\eta |+\left|\vartheta \right|+|\vartheta -\eta |}^2$.

Since,

$$\begin{array}{cc}\hfill \left|\vartheta \right|-\left|\eta \right|& \le \left|\right(\left|\vartheta \right|-\left|\eta \right|\left)\right|\hfill \\ \hfill & \le |\vartheta -\eta |\hfill \\ \hfill & \le {|\vartheta -\eta |+|\vartheta -\eta |}^2\hfill \end{array}$$

which proves $\left(RQP{b}_3\right)$.

Now, $\left(RQP{b}_4\right)$ follows from,

$rq{p}_b(\vartheta ,\eta )+rq{p}_b(u,u)+rq{p}_b(v,v)={|\vartheta -\eta |+\left|\vartheta \right|+|\vartheta -\eta |}^2+\left|u\right|+\left|v\right|$

$$\begin{array}{cc}\hfill & \le 2\left(\right|\vartheta -u|+|u-v|+|v-\eta |+|v-u{|}^2+|u-v{|}^2+|v-\eta {|}^2)\hfill \\ \hfill & \le s[rq{p}_b(\vartheta ,u)+rq{p}_b(u,v)+rq{p}_b(v,\eta )].\hfill \end{array}$$

Definition 7.

Let $(M,rq{p}_b)$ be a rectangular quasi-partial b-metric space. A self-mapping G on M is called an interpolative Rus–Reich–Ćirić-type contraction, if there are $\rho \in [0,1$) and positive reals $\alpha ,\beta$ with $\alpha +\beta <1$ such that:

$$\begin{array}{cc}\hfill rq{p}_b(G\vartheta ,G\eta )& \le \rho {\left[rq{p}_b(\vartheta ,\eta )\right]}^{\beta }.{\left[rq{p}_b(\vartheta ,G\vartheta )\right]}^{\alpha }.{\left[\frac{1}{s}rq{p}_b(\eta ,G\eta )\right]}^{1-\alpha -\beta }\hfill \end{array}$$

(1)

for all $\vartheta ,\eta \in M$$\setminus \mathit{Fix}\left(G\right).$

Theorem 2.

Let $G:M$⟶ M be an interpolative Rus–Reich–Ćirić-type contraction on a complete rectangular quasi-partial b-metric space $(M,rq{p}_b)$, then G has a fixed point in M.

Proof. 

Let ${\vartheta }_0$ be an arbitrary point in M. Consider ${\vartheta }_n$ by ${\vartheta }_n=G^n\left({\vartheta }_0\right)$ for each positive integer n. If there exists $n_0$ such that ${\vartheta }_{n_0}={\vartheta }_{n_0+1}$, then ${\vartheta }_{n_0}$ is a fixed point of G, and we are done. Throughout the proof, we assume that ${\vartheta }_n$$\ne {\vartheta }_{n+1}$ for each $n\ge 0.$

• We shall prove that $\underset{n\to \infty }{lim}$$rq{p}_b({\mu }_n,{\mu }_{n+1})=0$.
• By substituting the values $\vartheta ={\vartheta }_n$ and $\eta ={\mu }_{n-1}$, we find that:

  $$\begin{array}{cc}\hfill & rq{p}_b({\vartheta }_{n+1},{\vartheta }_n)=rq{p}_b(G{\vartheta }_n,G{\vartheta }_{n-1})\hfill \\ \hfill & \le \rho {\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\right]}^{\beta }.{\left[rq{p}_b({\vartheta }_n,G{\vartheta }_n)\right]}^{\alpha }{\left[\frac{1}{s}rq{p}_b({\vartheta }_{n-1},{\vartheta }_{n-1})\right]}^{1-\alpha -\beta }\hfill \\ \hfill & \\ & \le \rho {\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\right]}^{\beta }.{\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})\right]}^{\alpha }{\left[\frac{1}{s}rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\alpha -\beta }\hfill \\ \hfill & \le {\left[rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\alpha }.{\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})\right]}^{\alpha }.\hfill \end{array}$$

  (2)
• We get,

  $$\begin{array}{cc}\hfill {\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})\right]}^{1-\alpha }& \le \rho {\left[rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\alpha }.\hfill \end{array}$$

  (3)
• Therefore, we conclude that,

  $$\begin{array}{cc}\hfill rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})& \le \rho rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\mathrm{for}\mathrm{all}n\ge 1.\hfill \end{array}$$

  (4)
• That is, $\{rq{p}_b({\vartheta }_{n+1},{\vartheta }_n)$} is a non-increasing sequence with non-negative terms.
  Eventually, there is a non-negative constant L such that $\underset{n\to \infty }{lim}$$rq{p}_b({\vartheta }_{n+1},{\vartheta }_n)=L$. Note that $L\ge 0$. Indeed, from (4), we deduce that:

  $$\begin{array}{cc}\hfill rq{p}_b({\vartheta }_n,{\vartheta }_{m+1})& \le \rho rq{p}_b({\vartheta }_{n+1},{\vartheta }_n)\le {\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1).\hfill \end{array}$$

  (5)
• Since $\rho <1$ and by taking $n\to \infty$ in the inequality (5), we deduce that L$=0$.
• Now, we shall show that

  $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}rq{p}_b({\vartheta }_n,{\vartheta }_{n+2})=0\end{array}$$
• Using (4) and (5) and the quadrilateral inequality, we have
  $rq{p}_b({\vartheta }_{n+2},{\vartheta }_n)=rq{p}_b(G{\vartheta }_{n+1},G{\vartheta }_{n-1})$.

  $$\begin{array}{cc}\hfill & \le \rho {\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n-1})\right]}^{\beta }{\left[rq{p}_b({\vartheta }_{n+1},G{\vartheta }_{n+1})\right]}^{\alpha }{\left[\frac{1}{s}rq{p}_b({\vartheta }_{n-1},G{\vartheta }_{n-1})\right]}^{1-\alpha -\beta }\hfill \\ \hfill & \le \rho {\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n-1})\right]}^{\beta }{\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})\right]}^{\alpha }{\left[rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\alpha -\beta }\hfill \\ \hfill & \le \rho {\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n-1})\right]}^{\beta }{\left[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})\right]}^{\alpha }{\left[rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\alpha -\beta }\hfill \\ \hfill & \le \rho {\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n-1})\right]}^{\beta }{\left[rq{p}_b({\vartheta }_{n-1},{\vartheta }_n)\right]}^{1-\beta }\hfill \\ \hfill & \le \rho {\left[srq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})+srq{p}_b({\vartheta }_{n+2},{\vartheta }_n)+srq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\right]}^{\beta }{\left[rq{p}_b({\vartheta }_{n+1},{\vartheta }_n)\right]}^{1-\beta }\hfill \\ \hfill & \le \rho {\left[srq{p}_b({\vartheta }_{n+2},{\vartheta }_n)+2rsq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\right]}^{\beta }{\left[srq{p}_b({\vartheta }_{n+2},{\vartheta }_n)+2rsq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\right]}^{1-\beta }\hfill \\ \hfill & \le \rho \left[s(rq{p}_b({\vartheta }_{n+2},{\vartheta }_n)+2rq{p}_b({\vartheta }_n,{\vartheta }_{n-1}))\right]\hfill \\ \hfill & \le \rho srq{p}_b({\vartheta }_{n+2},{\vartheta }_n)+2\rho srq{p}_b({\vartheta }_n,{\vartheta }_{n-1})\hfill \end{array}$$

  (6)

  Therefore,
  $rq{p}_b({\vartheta }_{n+2},{\vartheta }_n)\le \frac{2\rho s}{1-\rho s}rq{p}_b({\vartheta }_n,{\vartheta }_{n-1}),\mathrm{for}\mathrm{all}n\ge 1.$
• We shall prove that $\{{\vartheta }_n$} is a Cauchy sequence, that is $\underset{n\to \infty }{lim}$$rq{p}_b({\vartheta }_n,{\vartheta }_{n+p})=0$ for all $p\in$$\mathbb{N}$.
• Case 1. Let $p=2m$. By the quadrilateral inequality, we find:

  $$\begin{array}{cc}\hfill & rq{p}_b({\vartheta }_n,{\vartheta }_{n+2m})\le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})+rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+2m})]\hfill \\ \hfill & \le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})]+s^2[rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+3})+rq{p}_b({\vartheta }_{n+3},{\vartheta }_{n+4})+\hfill \\ \hfill & rq{p}_b({\vartheta }_{n+4},{\vartheta }_{n+2m})]\hfill \\ \hfill & \le s[rq{p}_b({\mu }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})]+s^2[rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+3})+rq{p}_b({\vartheta }_{n+3},{\mu }_{n+4})]\hfill \\ \hfill & +s^3[rq{p}_b({\vartheta }_{n+4},{\vartheta }_{n+5})+rq{p}_b({\mu }_{n+5},{\vartheta }_{n+6})+rq{p}_b({\vartheta }_{n+6},{\vartheta }_{n+2m})]\hfill \\ \hfill & \le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})]+\dots +s^{m-1}[rq{p}_b({\vartheta }_{2m-4},{\vartheta }_{2m-3})\hfill \\ \hfill & +rq{p}_b({\vartheta }_{2m-3},{\vartheta }_{2m-2})]+s^{m-1}\left[rq{p}_b({\vartheta }_{n+2m-2},{\vartheta }_{n+2m})\right]\hfill \\ \hfill & \le s[{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+1}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+s^2[{\rho }^{n+2}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+3}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+\dots +\hfill \\ \hfill & s^3[{\rho }^{n+4}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+5}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+\dots +s^{m-1}[{\rho }^{2m-4}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{2m-3}rq{p}_b\hfill \\ \hfill & ({\vartheta }_0,{\vartheta }_1)]+s^{m-1}{\rho }^{n+2m+2}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \\ \hfill & \le s{\rho }^n[1+s{\rho }^2+s^2{\rho }^4+\dots ]rq{p}_b({\vartheta }_0,{\vartheta }_1)+s{\rho }^{n+1}[1+s{\rho }^2+s^2{\rho }^4+\dots ]rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \\ \hfill & +s^{m-1}{\rho }^{n+2m-2}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \\ \hfill & rq{p}_b({\vartheta }_n,{\vartheta }_{n+2m})\le \frac{1+\rho }{1-s{\rho }^2}s{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\left(s\rho \right)}^{2m}{\rho }^{n-2}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \\ \hfill & \le \frac{1+\rho }{1-s{\rho }^2}s{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n-2}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \end{array}$$

  (7)
• Case 2. Let $p=2m+1$.

  $$\begin{array}{cc}\hfill & rq{p}_b({\vartheta }_n,{\vartheta }_{n+2m+1})\le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})+\left(rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+2m+1})\right]\hfill \\ \hfill & \le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})]+s^2[rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+3})+rq{p}_b({\vartheta }_{n+3},{\vartheta }_{n+4})+\hfill \\ & rq{p}_b({\mu }_{n+4},{\vartheta }_{n+2m+1})]\hfill \\ \hfill & \le s[rq{p}_b({\vartheta }_n,{\vartheta }_{n+1})+rq{p}_b({\vartheta }_{n+1},{\vartheta }_{n+2})]+s^2[rq{p}_b({\vartheta }_{n+2},{\vartheta }_{n+3})+rq{p}_b({\vartheta }_{n+3},{\vartheta }_{n+4})]+\dots +\hfill \\ \hfill & s^{m}rq{p}_b({\vartheta }_{n+2m},{\vartheta }_{n+2m+1})]\hfill \\ \hfill & \le s[{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+1}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+s^2[{\rho }^{n+2}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+3}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+\dots \hfill \\ \hfill & +s^3[{\rho }^{n+4}rq{p}_b({\vartheta }_0,{\vartheta }_1)+{\rho }^{n+5}rq{p}_b({\vartheta }_0,{\vartheta }_1)]+\dots +s^m{\rho }^{n+2m}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \\ \hfill & \le s{\rho }^n[1+s\rho +s^2{\rho }^4+\dots ]rq{p}_b({\vartheta }_0,{\vartheta }_1)+s{\rho }^{n+1}[1+s{\rho }^2+s^2{\rho }^4+\dots ]rq{p}_b({\vartheta }_0,{\vartheta }_1)]\hfill \\ \hfill & =\frac{1+\rho }{1-s{\rho }^2}s{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1)\hfill \end{array}$$

  Therefore,

  $$\begin{array}{cc}\hfill rq{p}_b({\vartheta }_n,{\vartheta }_{n+2m+1})& \le \frac{1+\rho }{1-s{\rho }^2}s{\rho }^{n}rq{p}_b({\vartheta }_0,{\vartheta }_1).\hfill \end{array}$$

  (8)

  By (7) and (8), $\underset{n\to \infty }{lim}$$rq{p}_b({\vartheta }_n,{\vartheta }_{n+p})=0$.
  Thus, $\{{\vartheta }_n$} is a Cauchy sequence. Since $(M,rq{p}_b)$ is complete, there exists $z\in$M such that $\underset{n\to \infty }{lim}{\vartheta }_n=z$. Next, we shall prove that z is a fixed point of G.
  Let $\vartheta ={\vartheta }_n$ and $\eta =z$,

  $$\begin{array}{cc}\hfill rq{p}_b({\vartheta }_{n+1},G_z)& =rq{p}_b(G{\vartheta }_n,G_z)\hfill \\ \hfill & \le {\left[rq{p}_b({\vartheta }_n,z)\right]}^{\beta }·{\left[rq{p}_b({\vartheta }_n,G{\vartheta }_n)\right]}^{\alpha }·{\left[\frac{1}{s}rq{p}_b(z,Gz)\right]}^{1-\alpha -\beta }.\hfill \end{array}$$

  (9)

  Letting $n\to \infty$ in (9), we conclude $\underset{n\to \infty }{lim}$$rq{p}_b({\vartheta }_n,G_n)=0$.
  By Proposition 1, we get $Gz=z$. □

Example 4.

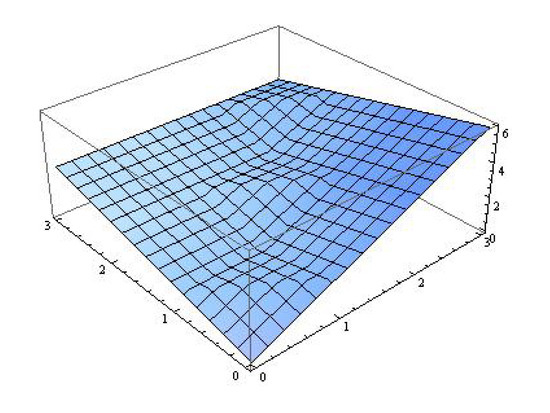
Let $M=\{0,1,2,3\}$. Consider the complete rectangular quasi-partial b-metric as $rq{p}_b(\vartheta ,\eta )=|\vartheta -\eta |+\vartheta$, that is:

${\mathit{rqp}}_{\mathit{b}}(\vartheta ,\eta )$	0	1	2	3
0	0	1	2	3
1	2	1	2	3
2	4	3	2	3
3	6	5	4	3

We define a self-map G on M as $G:$$\left(\begin{array}{cccc}0& 1& 2& 3\\ 0& 0& 1& 0\end{array}\right)$ as shown in Figure 1.

Figure 1. Zero is the fixed point of G.

Choose $\alpha =\frac{1}{2}$, $\beta =\frac{1}{3}$, and $\rho =\frac{6}{10}$.

• Case 1: Let $(\vartheta ,\eta )=(1,1)$. We have:

  $$\begin{array}{cc}\hfill & rq{p}_b(G\vartheta ,G\eta )\le \rho {\left[rq{p}_b(\mu ,\eta )\right]}^{\beta }{\left[rq{p}_b(\vartheta ,G\vartheta )\right]}^{\alpha }{\left[\frac{1}{s}rq{p}_b(\eta ,G\eta )\right]}^{1-\alpha -\beta }\hfill \\ \hfill & rq{p}_b(G1,G1)=0\le \rho {\left[rq{p}_b(1,1)\right]}^{1/3}{\left[rq{p}_b(1,G1)\right]}^{1/2}{\left[\frac{1}{s}rq{p}_b(1,G1)\right]}^{1/6}\hfill \end{array}$$
• Case 2: Let $(\vartheta ,\eta )=(3,3)$:

  $$\begin{array}{c}\hfill rq{p}_b(G3,G3)=0\le \rho {\left[rq{p}_b(3,3)\right]}^{1/3}{\left[rq{p}_b(3,G3)\right]}^{1/2}{\left[\frac{1}{s}rq{p}_b(3,G3)\right]}^{1/6}.\end{array}$$

Thus, zero is the fixed point of G in the setting of the interpolative Rus–Reich–Ćirić-type contraction.

Problem 1.

Let $(M,rq{p}_b)$ be a complete rectangular quasi-partial b-metric space. Consider a family of self-mappings $G_n:M$$\to M$, $n\ge 1$, and $s\ge 1$ such that

$$rq{p}_b(G_i\vartheta ,G_j\eta )\le {\rho }_{i,j}{\left[rq{p}_b(\vartheta ,\eta )\right]}^{{\beta }_j}·{\left[rq{p}_b(\vartheta ,G_i\vartheta )\right]}^{{\alpha }_i}·{\left[{\displaystyle \frac{1}{s}rq{p}_b(\eta ,G_j\eta )}\right]}^{1-{\alpha }_i-{\beta }_j}.$$

What are the conditions on ${\rho }_{i,j},{\alpha }_i,{\beta }_j$ for $G_n$ to have a fixed point?

Definition 8.

Let $(M,rq{p}_b)$ be a rectangular quasi-partial b-metric space. A self-mapping G on M is called an interpolative Kannan contraction, if there are $\rho \in [0,1)$ and positive reals $\alpha \in [0,1)$ such that

$$rq{p}_b(G\vartheta ,G\eta )\le \rho {\left[rq{p}_b(\vartheta ,G\vartheta )\right]}^{\alpha }.{\left[\frac{1}{s}rq{p}_b(\eta ,G\eta )\right]}^{1-\alpha }$$

for all $\vartheta ,\eta \in M$$\setminus \mathit{Fix}\left(G\right)$.

Theorem 3.

Let $G:M\to$ M be an interpolative Kannan contraction on a complete rectangular quasi-partial b-metric space $(M,rq{p}_b)$, then G has a fixed point in M.

We skip this proof as it is similar to Theorem 2.

3. Conclusions

In the present study, the authors investigated the interpolative Rus–Reich–Ćirić contraction mapping and its variants to attain the fixed point on a new metric space known as the rectangular quasi-partial b-metric space. Interpolation in fixed point theory is an advanced and widespread technique, which is acknowledged in several research areas such as metallurgy, earth sciences, and surface physics, etc., due to its application potential in the approximation of signal sensation analysis. The present research will find its place in these applications. Determining the fixed point for a non-self mapping and fractal interpolants will be an interesting work for future study.