Abstract
Objective: The main objective of the tests conducted was to analyze the position variability of the human body’s center of gravity during propelling the wheelchair, and to demonstrate the properties enabling the description of this variability by means of plane figures with a symmetry axis. A secondary objective was to show the impact of the used manual propulsion type and the wheelchair inclination angle in relation to the plane on the dimensions of the position variability areas of the center of gravity. Method and materials: Three patients participated in the research representing 50 centiles of anthropometric dimensions. Each patient carried out fifteen measurement tests on three wheelchairs for three inclination angles of the wheelchair frame in relation to the level. Each measurement test consisted of five propulsion cycles for which the positions of the center of gravity were determined with the sampling frequency of 100 Hz. The measured positions of the center of gravity were approximated with ellipses containing 95.4% of the measurements conducted, assuming their dimension scaling basis in the form of the double value of standard deviation defined based on the registered results. Results: Based on the measurements conducted, the average values of five ellipses parameters were determined for nine cases in which a variable was the type of wheelchair propulsion and its inclination angle in relation to the level. The area of the highest variability of the position of the center of gravity was measured for the wheelchair with a multispeed transmission. The average dimensions of the ellipse semi-axis amounted to 108.53 mm for the semi-axis a and 29.75 for the semi-axis b, the average position of the ellipse center amounted to x = 114.51 mm and y = −10.53 mm, and the average inclination angle of the ellipse α amounted to −6.92°. The area of the lowest variability of the position of the center of gravity was measured for the wheelchair with a hybrid transmission. In this case, the average dimensions of the ellipse semi-axis amounted to 64.07 mm for the semi-axis a and 33.85 for the semi-axis b; whereas, the average position of the ellipse center amounted to x = 245.13 mm and y = −28.24 mm, and the average inclination angle of the ellipse α amounted to −0.56°.
1. Introduction
According to the World Health Organization (WHO) data, 10% of the world’s population is constituted by people with disabilities. A considerable portion of this group includes people with motor disabilities who must use wheelchairs. The main function fulfilled by the wheelchair in the case of such a person is a locomotion function [1]. A wheelchair with a patient constitutes an anthropotechnical system described with a range of interrelated biomechanical parameters, such as speed [2], acceleration [3], muscle activity [4] and the position of the center of gravity [5]. One of the most important biomechanical parameters is the position of the center of gravity. Unfortunately, many biomechanical analyses simplify it to a single fixed point. Such an approach is an excessive simplification because a human body moves continuously during the wheelchair operation.
The human body movement range during propulsion generation depends mainly on the type of wheelchair used. A basic division of wheelchairs results from the type of propulsion system used, and it is as follows: electric wheelchairs, manual wheelchairs and hybrid wheelchairs. Wheelchairs with electric propulsion do not require any physical activity of the user during propulsion generation. Thus, it may be assumed that during the movement of such a wheelchair, the position of the human body center of gravity is constant in relation to any stationary point on the wheelchair. As far as wheelchairs with manual propulsion are concerned, propelling the wheelchair requires human body physical activity, which results in the variability of the position of the center of gravity in relation to any stationary point on the wheelchair. The currently observed trends in the rehabilitation sector indicate the increasing interest of the disabled in hybrid wheelchairs combining manual propulsion with electric propulsion [6]. Such wheelchairs have become more popular because they still require the physical activity of the user, at the same time compensating for its physical limitations by means of the electric propulsion system.
In the event of manual wheelchairs and hybrid wheelchairs, locomotion is the effect of, for instance, pushing the pushrims [7,8]. Pushing the pushrims results in the changes in the position of the human body and its respective segments [9,10], which generates the variability of the position of the human body center of gravity. The changes in the body position may be observed in relation to any point placed on the moving wheelchair. Conditioning the variability of the human body position on the type of manual propulsion used is caused by the specification of a propelling cycle, which consists of a push phase and a return phase [11]. In the push phase (Figure 1A), the upper limbs hold the pushrims, and they push them forwards. At the beginning of the driving phase, the torso rests against the backrest of the wheelchair, the upper limb is bent at the elbow, and the hand is on the pushrims in the extreme rear position. As the driving phase progresses, the upper limb is straightened at the elbow, and the torso is slightly tilted forward. At the end of the driving phase, the hand is still on the pushrims but in the extreme-forward position. At the beginning of the driving phase, the torso rests against the backrest of the wheelchair, the upper limb is bent at the elbow, and the hand is on the pushrims in the extreme rear position. As the driving phase progresses, the upper limb is straightened at the elbow, and the torso is slightly tilted forward. As a result of these activities, there is a dislocation of the human body’s center of gravity towards the front wheels of the wheelchair. During the return phase (Figure 1B), the upper limbs release the pushrims and return freely to their initial position. Free movement of the upper limbs consists of bending them again in the elbow joint without the simultaneous contact of the hand with the pushrims. In addition, in the return phase, the torso is vertically upright so that it rests its entire back against the wheelchair’s backrest. The return phase ends with grasping the pushrims with the hand again in the extreme rear position. The human body kinematics in the return phase translates into a shift of the human body’s center of gravity towards the rear driving wheels. Relating the individual phases of the propulsion movement to the locomotive function, the key phase is the driving one during which the driving force is generated. During its duration, the variability in the position of the center of gravity is more predictable as all gripping members of the human body are in contact with the wheelchair. In the case of the return phase—the influence on the locomotive function is the smallest, but it is characterized by the greatest influence on the randomness and differentiation of the position of the center of gravity of the human body. The familiarity with the variability area of the position of the human body center of gravity in dynamic conditions is crucial in a designing process since it enables defining the application place of a load dependent on the human body weight. Furthermore, defining the position of the center of gravity is significant when determining wheelchair stability [12]. When analyzing the current state of knowledge, it is noticeable that there are no data that describe the variability ranges or occurrence areas of the human body center of gravity in dynamic conditions. Such data would be useful in designing processes or during the computer simulations of the biomechanics of the man-wheelchair anthropotechnic system.

Figure 1.
Time-lapse photos depicting the change of the human body position in the push phase (A) and return phase (B). The dashed green line shows the hand trajectory during its contact with the pushrim; the dashed red line shows the hand trajectory during free return movement.
During the analysis of the position variability of the human body center of gravity, there are a few scenarios, such as maneuvering and driving ahead. In the event of maneuvering, the upper limbs make non-symmetric movements. Whereas, when driving ahead, the upper limbs make a symmetric movement [13,14], which guarantees driving ahead. Such symmetry of the movement of the upper limbs results in the symmetric distribution of the position of the human body center of gravity measured during the propelling cycle.
The main objective of the research carried out was to determine the variability areas of the position of the human body center of gravity. An additional objective of the research was to conduct an analysis parametrizing the indicated area by indicating its symmetric nature. An attempt to demonstrate the constancy of the symmetric nature of the areas indicated required conducting a test for the various configurations of the wheelchair inclination angle and various types of pushrim drives.
2. Materials and Methods
The tests were carried out on three wheelchairs equipped with the various types of manual pushrim drives. The first wheelchair, called hybrid (Figure 2A) (P. 427855), was characteristic of the combination of the manual pushrim drive (1) with electric engines embedded in the hub (2) [15]. This combination resulted in increasing the driving torque generated by the upper limb with the value of the torque generated by the electric engine. In this structure, the manual propulsion system was assisted only when the upper limb made a propelling movement. The second type of wheelchair, also known as the multispeed wheelchair (Figure 2B), had a multispeed hub embedded in the drive wheel (3) (PL 223142). The hub had three speeds with the following transmissions: 0.56, 1.00, 1.96, by means of which the driving force supplied to the pushrims was transformed (1). The third wheelchair type, also referred to as typical (Figure 2C), was a semi-active wheelchair Vermeiren v300. The propulsion system of this wheelchair was characteristic of the direct coupling of pushrims (1) with the drive wheel (4).

Figure 2.
Wheelchairs used during the tests: hybrid manual-electric (A), multispeed with the planetary transmission (B), typical semi-active with the pushrim drive (C); where: 1—pushrims, 2—BLCD (brushless DC motor) electric motor embedded in the hub, 3—planetary transmission embedded in the hub, 4—drive wheel.
The measurement of the position variability of the center of gravity during propelling the above-described wheelchairs was carried out for three patients without any disability (Table 1). The patients were classified according to height, weight, age, the maximum strength of an upper limb generated during pushing and experience in moving on a wheelchair. Each patient was familiarized with the test procedure and completed the voluntary consent form. It was decided to engage people without any motor disabilities to participate in the test on account of the use of the prototype solutions of propulsion systems. The research has been positively evaluated by Bioethical Commission at Karol Marcinkowski Medical University in Poznan, in Poland, Resolution No. 1100/16 of 10 November 2016, under the guidance of Prof. MD Chęciński P. for the research team led by Ph.D. Wieczorek B. The authors obtained the written consent of the examined person for the publication of the research results with its participation. The data are presented in such a way as to ensure its complete anonymity.

Table 1.
Comparison of anthropometric features and the level of experience in wheelchair operation of the test subjects.
The measurement of the position of the human body center of gravity was conducted in the test stand, which was the chassis dynamometer for wheelchairs [16] (P. 424482). The dynamometer was equipped with four strain gauge scales Wi (Figure 3), which enabled the measurement of reaction forces Ri which was the effect of loading the scale with the wheelchair, including a man.

Figure 3.
The used test stand with the indicated strain gauge scales W1–W2 and the force of reactions in the scale supports R1–R2.
The measurement of the position of the human body center of gravity consisted of the measurement of the reaction forces value Ri, based on which, with the defined distances between strain gauge scales (L, H), the position of the human body center of gravity was determined fij (1–4) by the rotational balance on four planes π1–π4 in relation to the coordinate system from originating in the scale W1 (Figure 4 and Figure 5).
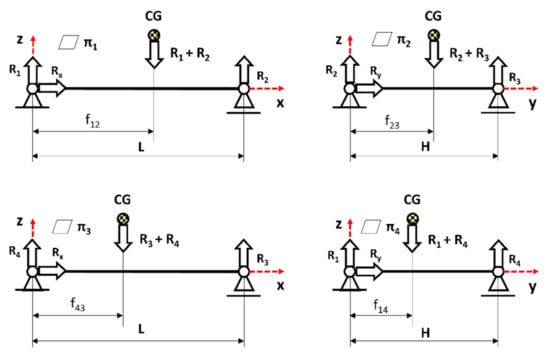
Figure 4.
The outline specifying the data required for determining the position of the center of gravity, where —the center of gravity of the human body, πi—one of four side planes, R1, R2, R3, R4—a reaction in the scale support, fij—the position of the center of gravity on one of the side planes, L—scale length, H—scale width. For the used model Rx = 0 and Ry = 0.

Figure 5.
The scheme of the method for determining the location of the center of gravity on the XY horizontal plane, the description of symbols is given in the text.
Using the determined distances fij (Figure 4), they were marked on the sides of the rectangle drawn on the plan of the locations of the strain gauges Wi, which are also the points of application of the reaction forces Ri. Then two straight lines were drawn through the points Pi marked on the sides of the right angle. These lines intersected at one point on the horizontal XY plane (Figure 5). The x (5) and y (6) coordinates of this point are the searched position of the center of gravity of the human body CG.
The research method required each patient to propel the wheelchair forwards (equal and simultaneous pushes of the left and right pushrim) with the constant speed of pushes amounting to 50 pushes per minute. For each tested wheelchair, the following three inclination angles towards the ground were simulated: 0°, 7°, 14°. One measurement test consisted of five full propulsion cycles [17], during which the position of the center of gravity of the human body was determined with the sampling time of 0.01s. The outcome of each measurement test was the set of points depicting the position variability of the human body center of gravity in dynamic conditions, that is, propelling the wheelchair on the straight-line track. Such a set was replaced with an ellipse defined with such parameters as the position of the ellipse center xCOG and yCOG, semi-axis a, semi-axis b and the ellipse inclination angle α (Figure 6). The position of the ellipse center was determined by calculating the average value of the coordinate x and y of the points measured. The semi-axis length α constituted the double value of the standard deviation (2σ) of the coordinate x of the points measured, whereas, as far as the semi-axis b is concerned, its length corresponding to the double standard deviation (2σ) of the coordinate y of the points measured. Assuming the ellipse dimensions as the double standard deviation ensured the ellipse covering 95.4% of all the points measured. The ellipse inclination α corresponded to the inclination of the trend line determined based on all the measured points [5,18].
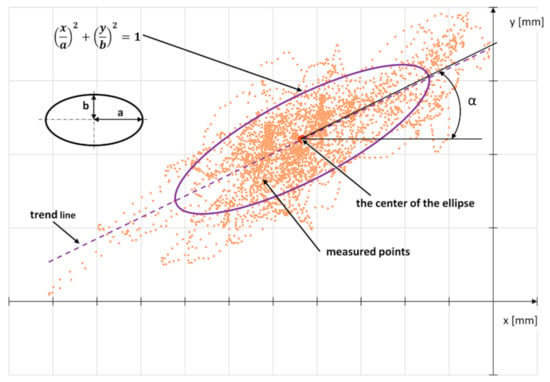
Figure 6.
The outline which illustrates drawing the ellipse determining the position variability of the human body center of gravity based on the measured points of the position of the center of gravity in the exemplary test sample.
For the purpose of analyzing the symmetric nature of the position variability of the human body center of gravity on the horizontal plane, the ellipses were decomposed (Figure 7A). As a result of decomposition, the following ellipse parameters were defined: geometrical dimensions (Figure 7B), inclination angle (Figure 7C) and the position of the ellipse center in relation to the central point of the rear wheels rotation axis (Figure 7D). Specifying such parameters enabled the separate analysis of each ellipse parameter depending on the type of the used propulsion system and the wheelchair inclination angle.
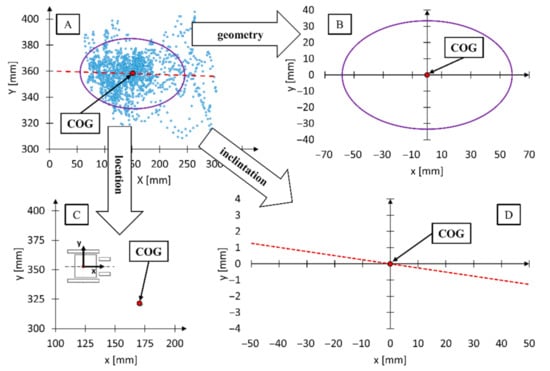
Figure 7.
An example of the ellipse decomposition depicting the variability of the human body center of gravity (A) on the ellipse geometry (B), ellipse center position (C), and the ellipse inclination angle (D).
3. Results
In accordance with the adopted research procedure, the measurement tests were carried out on the typical wheelchair, multispeed wheelchair and hybrid wheelchair. In the event of the multispeed wheelchair and the hybrid wheelchair, the patient carried out the same number of measurement tests for various transmission ratios and the various degrees of electric engine assistance. As far as the multispeed wheelchair is concerned, the patient chose a transmission ratio that was comfortable for such a patient, and it was used during all the measurement tests. Whereas during the tests carried out on the wheelchair with the hybrid propulsion, the control system automatically selected a driving torque amplification coefficient with the torques generated by electric motors. This selection depended on the external conditions; in this case, this was the wheelchair inclination angle. With such limit conditions, the subsequent analysis focused only on the impact of the manual propulsion type and the wheelchair inclination angle on the area and shape of the variability field of the position of the human body center of gravity. The geometrical interpretation of the analyzed ellipse parameters is presented in Figure 8. It specifies the position (a) and center (b) of ellipses in relation to the assumed reference system O, and a directional line (c) defining the trunk inclination direction. In the remainder of this chapter, the averaged results for the three tested patients are presented, while the average test results for individual patients are included in Appendix A.
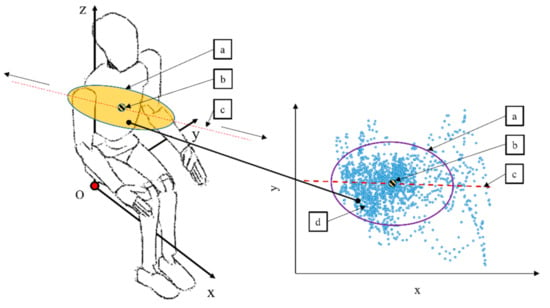
Figure 8.
The outline of the positioning of the analyzed ellipses within the tested patient body, where: a—ellipse which is the variability area of the position of the human body center of gravity, b—ellipse center, c—directional line, d—measured positions of the human body center of gravity during the measurement test.
The decomposition of the measured variability areas of the position of the human body center of gravity consisted of determining such parameters as ellipse dimensions, the position of the ellipse center in relation to the rotation axis center of the wheelchair rear wheels and the ellipse directional line. The directional line defines the ellipse inclination angle in relation to the system axis . Furthermore, it defines the main direction of the trunk movement, and it fulfills the role of the symmetry axis in relation to which the variability area of the position of the human body center of gravity is distributed. The graphs of the directional line course for the tested wheelchairs are presented in Figure 9.
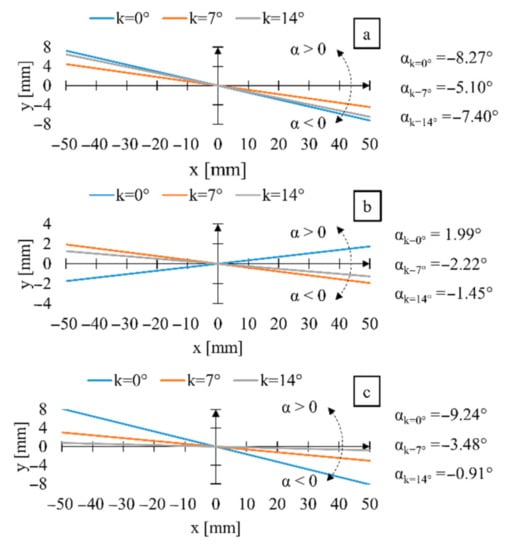
Figure 9.
The graphs of the ellipse directional lines, depending on the wheelchair inclination angle k for (a) wheelchair with the multispeed manual propulsion system, (b) hybrid propulsion system, (c) typical manual propulsion, where αk=0° —directional line inclination angle during propelling the wheelchair inclined at 0°, αk=7° —directional line inclination angle during propelling the wheelchair inclined at 7°, αk=14° directional line inclination angle during propelling the wheelchair inclined at 14°.
The ellipse dimensions analysis allowed the determination of the area size within which, in the horizontal plane XY, the position of the human body center of gravity may be located. The elliptical shape accepted in the method allowed to include 95.5% of all the measured points in the analysis. The diagrams presenting ellipse dimensions, depending on the manual propulsion type, are presented in Figure 10.
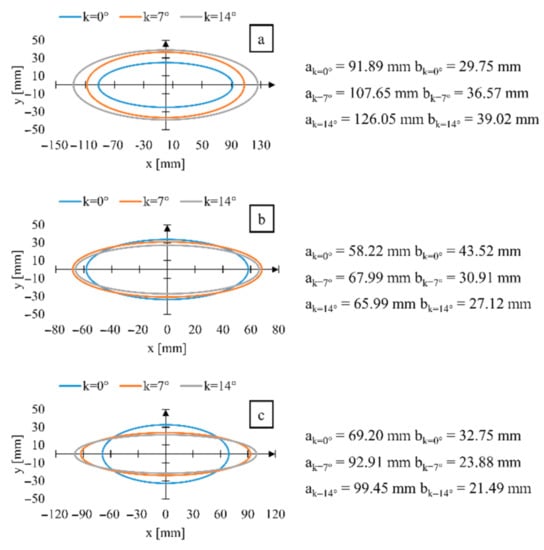
Figure 10.
The ellipse diagrams describing the variability of the position of the human body center of gravity depending on the wheelchair inclination angle k for (a) wheelchair with multispeed manual propulsion system, (b) hybrid propulsion system, (c) typical manual propulsion system, where αk=0°—the length of the semi-axis in the directional axis during propelling the wheelchair inclined at 0°, αk=7°—the length of the semi-axis in the directional axis during propelling the wheelchair inclined at 7°, αk=14°—the length of the semi-axis in the directional axis during propelling the wheelchair inclined at 14°, bk=0°—the length of the semi-axis perpendicular to the directional axis during propelling the wheelchair inclined at 0°, bk=0°—the length of the semi-axis perpendicular to the directional axis during propelling the wheelchair inclined at 7°, bk=0°—the length of the semi-axis perpendicular to the directional axis during propelling the wheelchair inclined at 14°.
The last element enabling the definition of the variability range of the position of the human body center of gravity was the position of the ellipse center (Figure 11). The analysis of this parameter allowed us to determine the position of the ellipses in relation to the rotation axis center of the wheelchair rear wheels. Furthermore, the analysis of this parameter enabled the performance of the observation of the wheelchair inclination angle impact on the shifting of the areas of the variability of the human body center of gravity in relation to the rotation axis of the rear-drive wheels.
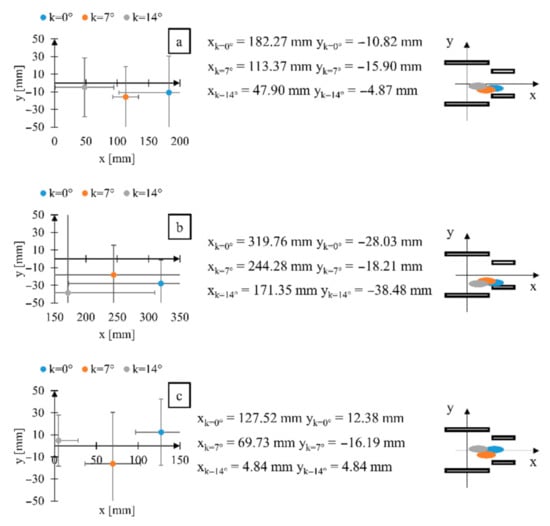
Figure 11.
The diagrams of the position of the ellipse center describing the position variability of the human body center of gravity depending on the wheelchair inclination angle k for (a) wheelchair with multispeed manual propulsion system, (b) hybrid propulsion system, (c) typical manual propulsion system, where xk=0° and yk=0°—the coordinates of the position of the ellipse center during propelling the wheelchair inclined at 0°, where xk=7° and yk=7°—the coordinates of the position of the ellipse center during propelling the wheelchair inclined at 7°, where xk=14° and yk=14°—the coordinates of the position of the ellipse center during propelling the wheelchair inclined at 14°.
The analysis of the measured parameters of the variability area of the position of the human body center of gravity for the tested wheelchairs is presented in Table 2, Table 3 and Table 4. In order to conduct the interpretation of the results obtained, a mean of the respective parameters was appointed M for three tested inclination angles and average increase Δ. The average increase specified the millimeters or degrees with which the parameters changed depending on the change of the wheelchair inclination angle.

Table 2.
The comparison of the ellipse parameters describing the variability area of the position of the human body center of gravity during propelling the wheelchair with the multispeed propulsion system; where: a—the length of the semi-axis parallel to the direction of the trunk movements, b—the length of the semi-axis perpendicular to the direction of the trunk movements, α—the ellipse inclination angle in relation to the human body sagittal plane, x and y—the coordinates of the position of the ellipse center in relation to the rotation axis center of the wheelchair drive wheels.

Table 3.
The comparison of the ellipse parameters describing the variability area of the position of the human body center of gravity during propelling the wheelchair with the hybrid propulsion system; where: a—the length of the semi-axis parallel to the direction of the trunk movements, b—the length of the semi-axis perpendicular to the direction of the trunk movements, α—the ellipse inclination angle in relation to the human body sagittal plane, x and y—the coordinates of the position of the ellipse center in relation to the rotation axis center of the wheelchair drive wheels.

Table 4.
The comparison of the ellipse parameters describing the variability area of the position of the human body center of gravity during propelling the wheelchair with the typical propulsion system; where: a—the length of the semi-axis parallel to the direction of the trunk movements, b—the length of the semi-axis perpendicular to the direction of the trunk movements, α—the ellipse inclination angle in relation to the human body sagittal plane, x and y—the coordinates of the position of the ellipse center in relation to the rotation axis center of the wheelchair drive wheels.
4. Discussion
The analysis of the sets of points of the position of the human body center of gravity measured during propelling the wheelchair in the straight-line track demonstrated the symmetric nature of the points distribution. The symmetry axis, in this case, is the directional line, which at the same time is the trend line of the measured points of the position of the center of gravity. It may be observed that regardless of the case tested, the directional line was always inclined at a certain angle in relation to the axis in the sagittal plane of the human body [19]. The inclination angle of the directional line ranged from −9.24° for the wheelchair with the typical manual propulsion system (Table 4) when climbing the slope of k = 0° to 1.99° for the wheelchair with the hybrid propulsion system when climbing the slope of k = 0° (Figure 9, Table 3). The directional line, through its inclination, depicts the direction in which the trunk bends during propelling the wheelchair [20]. The value of the directional line inclination is strictly connected with the user’s physical capabilities and with the differences between the muscle system of the left limb and the right limb [21,22]. When analyzing the measured values of the directional line inclination angle, it may be noticed that in eight cases, the inclination angle is negative, which should be interpreted that, for such measurement tests, the user’s trunk was bent to the left side. Taking into account the non-symmetry of the maximum force generated by the upper limbs and the dextrality of all the tested persons, it has been stated that the directional line of the trunk movement is directed towards the limb, which generates a higher driving force. In the design application, the value of the ellipse tilt angle informs about the uniformity of the distribution of the points of the center of gravity of the human body between the left and right sides of the wheelchair frame. With a tilt angle of the direction line of 0°, the ideal situation occurs, meaning that the number of loading cycles on the left and right side of the wheelchair frame is the same. In case of an increase in this angle, one of the quarters of the wheelchair frame is loaded more often.
Based on the proved symmetry of the distribution of the points measured, a method was assumed, which replaces the measured points of the position of the center of gravity with the ellipse. The dimensions of this ellipse semi-axis are the double value of the standard deviation of the coordinate of the position of the center of gravity in the event of the semi-axis a and the double value of the standard deviation of the coordinate in the event of the semi-axis b. Such an approximation of the set of the position points of the center of gravity considers 95.4% of all the points measured in the sample. Since in the measurement test, the user performed five full propelling cycles, it was assumed that the rejected 4.6% points included extreme measurements as a result of a measurement error and a human factor causing minor discrepancies between the tracks of the upper limb movement in respective propelling cycles.
The analysis of the dimensions of the position variability field of the center of gravity demonstrated that regardless of the type of propulsion system used; the wheelchair inclination angle affects the geometrical dimensions of the drawn ellipses. In the tested propulsion systems, the following differences in the semi-axis length were observed: 17.08 mm for semi-axis a (Δa) and 4.63 mm for semi-axis b (Δb) with the multispeed propulsion system (Figure 10, Table 2), 15.13 mm for semi-axis a (Δa) and 5.63 mm for semi-axis b (Δb) with the typical propulsion system (Figure 10, Table 2), and 5.89 mm for semi-axis a (Δa) and 8.20 mm for semi-axis b (Δb) with the hybrid propulsion system (Figure 10, Table 3). On the basis of the defined ellipse dimensions, it was stated that the largest variability area of the position of the human body center of gravity was measured for the wheelchair with the multispeed propulsion system (Figure 10, Table 2). In the event of this wheelchair, the average length of the semi-axis a (M a) amounted to 108.53 mm; whereas, the semi-axis b (M b) was 35.11 mm. The smallest variability area of the center of gravity was observed for the wheelchair with the hybrid propulsion system (Figure 10, Table 3), for which the average semi-axis length a (M a) amounted to 64.07 mm, whereas the semi-axis b (M b) was 33.85 mm. This is a significant observation that may indicate that the modification of the typical manual propulsion system results in the change in the distribution of the position of the human body center of gravity in dynamic conditions. The differences in the dimensions of the position variability areas of the center of gravity result from the human body kinematics during propelling the wheelchair [18,19,20]. The presented results of the dimensions of the ellipses show that it is advantageous to use systems supporting the manual traction drive. During their use, the smallest increases in dimensions of the area of the variability of the position of the center of gravity of the human body as a result of changes in the parameters of the wheelchair operation occur. On the basis of the determined ellipses, it was observed that, regardless of the type of the tested drive, the dimensions of the ellipse semi-axis increase with the increase in the inclination angle of the wheelchair frame. The largest increase is observed in the case of the semi-axis .
The functionality and the operating rule of the mechanical propulsion systems, such as the typical pushrim system and the multispeed pushrim system, require the user to apply the increased muscle activity of the upper limbs and the pectoral girdle [21]. As far as the multispeed propulsion system is concerned, the possibility of ratio change results in the various states of the muscle system loading. For reduction ratios, a person propelling the wheelchair did not must generate high levels of propelling force; therefore, the propelling movement was performed with the minimum participation of the trunk muscles. Whereas, while using the multiplication ratios, the wheelchair user had to generate a higher level propelling force, which resulted in the increased muscle activity stimulating larger movement ranges of the body segments, including the trunk inclination angles. An opposite situation was observed in the event of the wheelchair with the hybrid propulsion system. In the case of this propulsion design, the system of electric engines assisted the user in propelling. The assistance took place with varied intensity [14], adapting to the change of the external movement resistances. Thus, the user propelling the wheelchair had to generate a similar propelling force value [22]. The applied electric engine assistance caused the user to feel, in its opinion, a constant and convenient resistance during propelling the wheelchair. This was demonstrated by the low muscle activity in the upper limbs and pectoral girdle, resulting in the small movement ranges of the body segments taking part in propelling the wheelchair. In consequence, the smallest variability area of the position of the human body center of gravity was observed among all the tested propulsion systems.
The analysis of the average measurement results demonstrated that regardless of the propulsion system tested, the increase in the wheelchair inclination angle results in the semi-axis a length increase and a simultaneous decrease in the semi-axis b length. This dependence confirms the impact of the wheelchair inclination angle on the method of propelling the wheelchair [23,24]. The increase in the wheelchair inclination angle results in an increase in the trunk tilt angles and a simultaneous increase in the similarity in the hand movement track during the return phase. The increase in the trunk tilting is reflected in the elongation of the semi-axis a; whereas, the increase in the similarity in the upper limb movement tracks is seen in the decrease of semi-axis b length. It is particularly noticeable in the event of the wheelchair with the multispeed propulsion system.
The wheelchair inclination angle also affects the position of the ellipse center. The tests carried out indicated that the increase in the wheelchair inclination angle causes the entire variability area of the position of the human body center of gravity move towards the rear wheels’ rotation axis. It is possible to notice the linear dependence between the wheelchair inclination angle and the change of the coordinate x of the position of the ellipse center. For the tests performed, the wheelchair inclination with 7° resulted in the movement of the ellipse center with 67.81 mm on average towards the rear wheels rotation axis (Figure 11). Such a dependence was observed for all the tested propulsion systems, notwithstanding the coordinates of the position of the ellipse center for the wheelchair inclination angle of 0° (k = 0°). The uniformity of the variability of the position of the center of the ellipse on the x-axis results from the assumption of the same pitch of the wheelchair tilt angle. The type of drive system used did not affect the change of the x coordinate value. Differences in the position of the center of the ellipse on the y-axis result from the asymmetrical position of the human body in relation to the geometric center of the seat. The type of drive system used did not affect the change of the x coordinate value. Differences in the position of the center of the ellipse on the y-axis result from the asymmetrical position of the human body in relation to the geometric center of the seat. In the case of wheelchairs with an exact adjustment of the seat to the pelvic width of the human body, it would be even smaller. It should be noted that the variability of the position of the center of the ellipse on the y-axis should not be related to the type of drive used or the change in the operating conditions of the wheelchair. First of all, it depends on the individual preferences of the wheelchair user and the degree of matching his anthropometric dimensions to the dimensions of the seat. Furthermore, it may be noticed that in each tested case, the patient did not sit in the geometrical center of the seat, i.e., its sagittal plane did not converge with the wheelchair symmetry plane.
5. Conclusions
The conducted research demonstrated that during propelling the manual wheelchair along a straight section, there is the symmetric distribution of the position points of the center of gravity on the horizontal plane. A symmetry axis, in such a case, is always a directional line depicting the trunk inclination direction. However, the directional line does not converge on the wheelchair symmetry axis, and it is always inclined at a certain angle towards it. A directional line is always directed at the direction of the upper limb characteristic for larger muscle system development. The directional line inclination confirms the non-symmetry of the human body and its physical predispositions in relation to the sagittal plane.
The performed measurements of the position of the human body center of gravity are exposed to extreme measurements divergent from the general trend. This results from the lack of the full repeatability of the performed propelling cycles by the upper limb. This is particularly noticeable in the return phase, when the upper limb has no contact with the pushrims, and it returns freely to its initial position. Notwithstanding the possibility of such measurements, the area of the position variability of the center of gravity may be approximated with an ellipse, which ensures very good mapping of the actual position of the measured points. Each such ellipse is described with five parameters, which may be implemented in various biomechanical calculations requiring information about the position of the center of gravity. Furthermore, unlike the currently existing trends, the data depicting the entire spectrum of the position variability of the center of gravity will be used instead of a single static point.
In the subsequent works, it is planned to extend the research with the measurement of the position of the center of gravity in three axes and the parallel measurement of the motion capture of the human body segments. Such research will enable the connection of the movement track impact of the respective body segments on the parameters depicting the variability area of the position of the human body center of gravity in dynamic conditions. The motion capture analysis would be particularly helpful in depicting the position variability of the center of gravity during the return phase of the upper limb because, in this phase, there are most frequent differences in the movement tracks of the human body segments.
The tests involved three various types of manual pushrim propulsion systems, and they demonstrated that the modification, changing the transformation method of the upper limb muscle strength to the driving torque, significantly affects the distribution variability of the position of the center of gravity. The reason for the above is different methods of propelling each propulsion system. The tests carried out indicated that the best propulsion type was the hybrid propulsion system because it adapted to the variable operating conditions. In this case, regardless of the wheelchair inclination angle and motion resistance, the body segment trajectories were similar. This could be observed in smaller differences in the dimensions of the respective ellipses depicting the variability of the position of the center of gravity. The least advantageous in these terms was the wheelchair with the multispeed propulsion system.
6. Patents
A patent at the Patent Office of the Republic of Poland: PL 223142, Multispeed transmission hub for manual wheelchairs, WIECZOREK Bartosz, ZABŁOCKI Marek, 2012.
Patent application at the Patent Office of the Republic of Poland: P. 427855, Modification Kit for Hybrid Electric-Manual Wheelchair Drive System; (original title in Polish: Zestaw modyfikacyjny układu napędu do hybrydowego elektryczno-ręcznego do wózka inwalidzkiego), WARGUŁA Łukasz, WIECZOREK Bartosz, KUKLA Mateusz, 2018.
Patent application at the Patent Office of the Republic of Poland: P.424482, Simulation device for the wheelchair operating conditions and the measurement of dynamic parameters, GÓRECKI Jan, WIECZOREK Bartosz, KUKLA Mateusz, WILCZYŃSKI Dominik, WOJTKOWIAK Dominik, 2018.
Author Contributions
Conceptualization, B.W.; methodology, B.W.; software, B.W.; validation, B.W., M.K. and Ł.W.; formal analysis, B.W., M.K. and Ł.W.; investigation, B.W., M.K. and Ł.W.; resources, B.W., M.K. and Ł.W.; data curation, B.W., M.K. and Ł.W.; writing—original draft preparation, B.W.; writing—review and editing, B.W. and M.K.; visualization, B.W., M.K. and Ł.W.; supervision, B.W.; project administration, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
Wieczorek Bartosz, Study of the biomechanics of manually propelled wheelchair for innovative manual and hybrid drives (LIDER/7/0025/L-7/15/2016) financed by the National Center for Research and Development, https://www.ncbr.gov.pl/en/.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of Bioethical Commission at the Karol Marcinkowski Medical University in Poznań Poland, Resolution No. 1100/16 of 10 November 2016, under the guidance of Prof. MD Chęciński P. for the research team led by Ph.D. Wieczorek B.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Figure A1, Figure A2 and Figure A3 present a summary of the averaged results of the measurement of the area of variability in the location of the center of gravity for individual patients. In the case of these results, the measurement samples of individual patients were averaged.
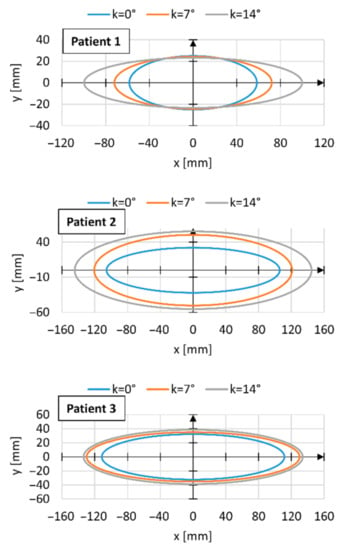
Figure A1.
Dimensions of the areas of variability in the position of the center of gravity of individual patients during the operation of a wheelchair with a multispeed drive for three angles of inclination of the wheelchair k.
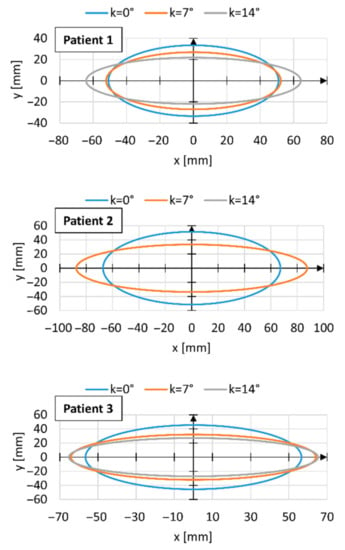
Figure A2.
Dimensions of the areas of variation in the position of the center of gravity of individual patients during the operation of the wheelchair with a hybrid drive for three inclination angles of the wheelchair k. Patient 2 refused to perform the test for the angle of inclination k = 14°.
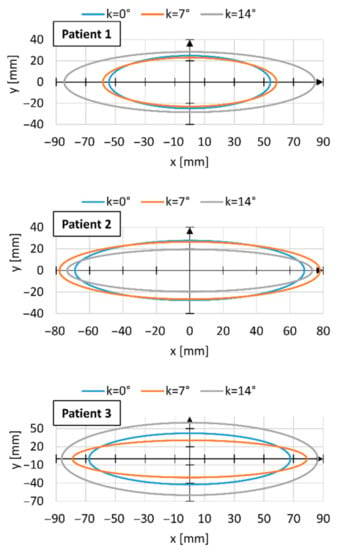
Figure A3.
Dimensions of the areas of variability in the position of the center of gravity of individual patients during the operation of a wheelchair with a classic drive for three angles of inclination of the wheelchair k.
References
- Smith, E.M.; Mortenson, W.B.; Mihailidis, A.; Miller, W.C. Understanding the task demands for powered wheelchair driving: A think-aloud task analysis. Disabil. Rehabil. Assist. Technol. 2020, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Veeger, E.H.; Van Der Woude, L.H.; Rozendal, R.H. Effect of handrim velocity on mechanical efficiency in wheelchair propulsion. Med. Sci. Sports Exerc. 1992, 24, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Coutts, K.D. Kinematics of sport wheelchair propulsion. J. Rehabil. Res. Dev. 1990, 27, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Mulroy, S.J.; Gronley, J.K.; Newsam, C.J.; Perry, J. Electromyographic activity of shoulder muscles during wheelchair propulsion by paraplegic persons. Arch. Phys. Med. Rehabil. 1996, 77, 187–193. [Google Scholar] [CrossRef]
- Wieczorek, B.; Kukla, M.; Warguła, Ł. Methods for measuring the position of the centre of gravity of an anthropotechnic human-wheelchair system in dynamic conditions. Mater. Sci. Eng. Conf. Ser. 2020, 776, 012062. [Google Scholar] [CrossRef]
- Chien, C.-S.; Huang, T.-Y.; Liao, T.-Y.; Kuo, T.-Y.; Lee, T.-M. Design and development of solar power-assisted manual/electric wheelchair. J. Rehabil. Res. Dev. 2014, 51, 1411–1426. [Google Scholar] [CrossRef]
- Boninger, M.L.; Souza, A.L.; Cooper, R.A.; Fitzgerald, S.G.; Koontz, A.M.; Fay, B.T. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Arch. Phys. Med. Rehabil. 2002, 83, 718–723. [Google Scholar] [CrossRef]
- Vanlandewijck, Y.C.; Theisen, D.; Daly, D. Wheelchair Propulsion Biomechanics. Sports Med. 2001, 31, 339–367. [Google Scholar] [CrossRef]
- Mâsse, L.C.; Lamontagne, M.; O’Riain, M.D. Biomechanical analysis of wheelchair propulsion for various seating positions. J. Rehabil. Res. Dev. 1992, 29, 12–28. [Google Scholar] [CrossRef]
- Russell, I.M.; Wagner, E.; Requejo, P.; Mulroy, S.; Flashner, H.; McNitt-Gray, J. Characterization of the shoulder net joint moment during manual wheelchair propulsion using four functional axes. J. Electromyogr. Kinesiol. 2019, 102340. [Google Scholar] [CrossRef]
- Koontz, A.M.; Roche, B.M.; Collinger, J.L.; Cooper, R.A.; Boninger, M.L. Manual Wheelchair Propulsion Patterns on Natural Surfaces During Start-Up Propulsion. Arch. Phys. Med. Rehabil. 2009, 90, 1916–1923. [Google Scholar] [CrossRef] [PubMed]
- Kirby, R.L.; Sampson, M.T.; Thoren, A.F.; Macleod, A.D. Wheelchair stability: Effect of body position. J. Rehabil. Res. Dev. 1995, 32, 367–372. [Google Scholar] [PubMed]
- Soltau, S.L.; Slowik, J.S.; Requejo, P.S.; Mulroy, S.J.; Neptune, R.R. An Investigation of Bilateral Symmetry During Manual Wheelchair Propulsion. Front. Bioeng. Biotechnol. 2015, 3, 86. [Google Scholar] [CrossRef] [PubMed]
- Goosey, V.L. Symmetry of the elbow kinematics during racing wheelchair propulsion. Ergonomics 1998, 41, 1810–1820. [Google Scholar] [CrossRef] [PubMed]
- Wieczorek, B.; Warguła, Ł.; Rybarczyk, D. Impact of a Hybrid Assisted Wheelchair Propulsion System on Motion Kinematics during Climbing up a Slope. Appl. Sci. 2020, 10, 1025. [Google Scholar] [CrossRef]
- Wieczorek, B.; Warguła, Ł. Problems of dynamometer construction for wheelchairs and simulation of push motion. MATEC Web Conf. 2019, 254, 01006. [Google Scholar] [CrossRef]
- Van Der Woude, L.H.V.; Veeger, H.E.J.; Rozendal, R.H.; Sargeant, A.J. Optimum cycle frequencies in hand-rim wheelchair propulsion. Graefe’s Arch. Clin. Exp. Ophthalmol. 1989, 58, 625–632. [Google Scholar] [CrossRef]
- Wieczorek, B.; Kukla, M. Effects of the performance parameters of a wheelchair on the changes in the position of the centre of gravity of the human body in dynamic condition. PLoS ONE 2019, 14, e0226013. [Google Scholar] [CrossRef]
- Zhang, R.; Vogler, C.; Metaxas, D. Human gait recognition at sagittal plane. Image Vis. Comput. 2007, 25, 321–330. [Google Scholar] [CrossRef]
- Finley, M.A.; Rasch, E.K.; Keyser, R.E.; Rodgers, M.M. The biomechanics of wheelchair propulsion in individuals with and without upper-limb impairment. J. Rehabil. Res. Dev. 2004, 41, 385. [Google Scholar] [CrossRef]
- Goosey-Tolfrey, V.L.; Vegter, R.J.K.; Mason, B.S.; Paulson, T.A.W.; Lenton, J.P.; Van Der Scheer, J.W.; Van Der Woude, L.H. Sprint performance and propulsion asymmetries on an ergometer in trained high- and low-point wheelchair rugby players. Scand. J. Med. Sci. Sports 2018, 28, 1586–1593. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez-Farewik, E.M.; Alm, M.; Hultling, C.; Saraste, H. Measuring seating pressure, area, and asymmetry in persons with spinal cord injury. Eur. Spine J. 2003, 13, 374–379. [Google Scholar]
- Cooper, R.A.; Boninger, M.L.; Shimada, S.D.; Lawrence, B.M. Glenohumeral joint kinematics and kinetics for three coordinate system representations during wheelchair propulsion. Am. J. Phys. Med. Rehabil. 1999, 78, 435–446. [Google Scholar] [CrossRef] [PubMed]
- Mulroy, S.J.; Newsam, C.J.; Gutierrez, D.D.; Requejo, P.; Gronley, J.K.; Haubert, L.L.; Perry, J. Effect of Fore-Aft Seat Position on Shoulder Demands During Wheelchair Propulsion: Part 1. A Kinetic Analysis. J. Spinal Cord Med. 2005, 28, 214–221. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).