Abstract
To take advantage of the singular properties of matter, as well as to characterize it, we need to interact with it. The role of optical spectroscopies is to enable us to demonstrate the existence of physical objects by observing their response to light excitation. The ability of spectroscopy to reveal the structure and properties of matter then relies on mathematical functions called optical (or dielectric) response functions. Technically, these are tensor Green’s functions, and not scalar functions. The complexity of this tensor formalism sometimes leads to confusion within some articles and books. Here, we do clarify this formalism by introducing the physical foundations of linear and non-linear spectroscopies as simple and rigorous as possible. We dwell on both the mathematical and experimental aspects, examining extinction, infrared, Raman and sum-frequency generation spectroscopies. In this review, we thus give a personal presentation with the aim of offering the reader a coherent vision of linear and non-linear optics, and to remove the ambiguities that we have encountered in reference books and articles.
1. Introduction
Within the field of chemical physics, optical spectroscopies are mainly used to characterize the structural and chemical composition of materials. Among the most common techniques, we count UV–visible and infrared extinction spectroscopies, fluorescence emission, Raman scattering and sum-frequency generation (SFG). On a theoretical point of view, they all arise from electromagnetism and quantum mechanics, which enable to implement light–matter interactions. As characterized by its dipole moments, a material is able to couple with light at different orders. Extinction spectroscopies are first order phenomena, while SFG is a second order process, and fluorescence emission and Raman scattering are third order processes. The former fall within the scope of linear optics, whereas the latter constitute the core of non-linear optics. Mathematically, an optical process is qualified as an -order process when the material is described by a dipole moment density P, so-called polarization, whose amplitude depends on the power of the light electric field amplitude: . The proportionality coefficient is then characteristic of the inner properties of the material: crystal structure, molecular vibrations, electronic density, chemical composition, internal symmetries and so on. This response factor is denoted . It must be handled with care: the relation between the polarization of the material and the electric field of the light is not as simple as : first, the power of is not necessarily a vector (e.g., is a number), while is a vector; second, each component of may depend on all the components , and of the electric field, so that the response factor is actually a tensor [1]; and third, the frequencies of and of the different spectral contributions to must be explicitly written. In order to properly describe optical spectroscopies, the response functions must be well defined on a mathematical point of view: dimension of the tensor, number of frequency arguments, relation with the polarization and the electric field. Given that it is not the case in many articles, we dwell on that point through this review.
To begin, we must distinguish the response functions, which are temporal functions, from the associated susceptibilities, which are spectral functions. The first ones describe how the polarization of the material evolves along time with respect to the time profile of the light excitation, whereas the second ones give the spectral distribution of all the frequencies which compose the dipolar response of the material. Since then, we often encounter two important ambiguities. First, some authors use complex exponential functions to express the physical quantities instead of Fourier transforms. They assume in this way that the signals are monochromatic and hide all the effects which are related to polychromaticity. For instance, strictly speaking, SFG does not combine a visible and an IR beam, both characterized by their own electric field, but all the couples of frequencies available within the Fourier spectrum of the total electric field. This difference of point of view is schemed in Figure 1. Second, while -order dielectric response functions are always defined as functions of n time variables, the associated susceptibilities are incoherently written as functions of frequency variables: . This confusion derives actually from the previous one, when authors illegitimately assume the fields are monochromatic. Such -argument functions indeed exist mathematically and make sense, but they cannot be assigned to n-argument optical susceptibilities. Section 3.1 of this paper sheds light on these two difficulties. Furthermore, it is not unusual to read misleading interpretations of non-linear processes. For instance, sum-frequency generation is commonly described as a combination of infrared and Raman spectroscopies, but we show that it is not correct (Section 4.5). Another example relates to Raman scattering, which is sometimes considered as a first order phenomenon because the light power of the Raman signal linearly depends on the input light power. There is a difference between the behaviour of the polarization P of a material and that of the emitted/scattered light power . As explained in Section 4.4, this comes from quantum mechanics.
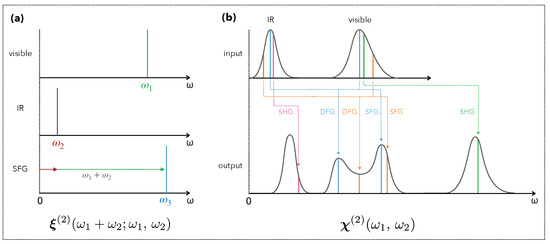
Figure 1.
Mono- and polychromatic picture of second order response functions. (a) Common description of sum-frequency generation (SFG) from a monochromatic point of view, considered to derive from a 3-argument function. (b) Description of second order processes (SFG, DFG, SHG) from a polychromatic point of view, considered to derive from the 2-argument second order susceptibility combining any input frequencies and .
In other words, optical spectroscopies are based on a mathematical formalism which exhibit numerous subtleties. From an experimental point of view, they are extensively used in analytical and physical chemistry to study molecular systems. It is then important to clarify the formalism and to make it accessible to all experimentalists. Hence, this review first recalls the foundations of linear response theory, leading to refraction, absorption, scattering and extinctions processes. Second, we formally introduce the response functions and dielectric susceptibilities as defined to account for second- and third-order processes. We especially dwell on the case of two-dimension SFG spectroscopy, as it is a powerful tool to combine visible (i.e., electronic) and infrared (i.e., vibrational) spectroscopies. Third, we show how it is concretely applied to vibrational spectroscopies. Taking the example of hybrid organic/inorganic systems made of nanostructured interfaces grafted by functional molecules, we evidence the power of two-dimension non-linear spectroscopies for examining vibroelectronic couplings between nanostructures and organic molecules.
2. Linear Response Theory
Most of the experimental studies which aim to probe the physicochemical properties of matter are well described by the theory of linear response. This is indeed the case when samples are probed by low power light excitations. Under the dipolar approximations, atoms, molecules, nanoparticles and solid-state materials are characterized by their electric dipole moments. We recall in this section its definition and develop the consequences on the optical refraction, absorption and extinction processes.
2.1. Polarization of Matter and Optical Response Function
Within neutral matter, the electric polarity of microscopic components is first characterized by their dipole moments . For atoms, as for molecules, which have an electronic cloud of charge , we commonly define , where d denotes the vector connecting the barycentre of the negative charges (of the electronic cloud) to the barycentre of the positive charges (of the nucleus). In this context, reducing the behaviour of matter to that of the dipole moment alone is an approximation. When this is necessary (which will not be our case), we may have to consider quadrupole and octupole moments. It is then possible to define for any macroscopic material system the local polarization as the volume density of dipole moments:
The sum over the integers i describes the set of microscopic components of dipole moment involved in the system. We note V the volume of the total system, N the density of atoms or molecules (considered as uniform) and the mean dipole moment calculated over the entire system.
At equilibrium and in the absence of an external electric field, the microscopic components may, (i), not be polarized () or else, (ii), have a permanent dipole moment (). In the first case, the polarization at equilibrium is clearly zero: . In the second one, it may turn out to be non-zero. However, we often observe an average dipole moment reduced to zero, due to the isotropic orientation distribution of these moments: .
As a matter of fact, materials can most frequently be polarized only thanks to the presence of an external electric field . As far as we are concerned, we will consider this field to be uniform across the system. For instance, in the case of metallic or semiconductor nanoparticles, this approximation remains quite reasonable. Their radius R is indeed much smaller than the wavelength of the light (visible and infrared) which probes them: nm nm. We therefore define the first order optical response function as the 2nd rank tensor (i.e., 2D matrix) which links the induced polarization to the excitation [2,3,4,5]:
In other words, :
This phenomenological relation reflects the fact that the polarization of the system at time t depends on the excitation at any previous time . Moreover, if the material is anisotropic, each component of the polarization can depend on the three components of the electric field. The response function is actually a tensor which consists of a matrix of response functions . In Fourier space, the convolution product of Equation (2) can be simply written as a matrix product:
where the Fourier transforms are here defined for any function f by:
The functions , so called first order dielectric susceptibilities, are the Fourier transforms of the response functions . In the case of an isotropic material, :
A single scalar susceptibility is thus enough to describe the optical response of the system. Generally speaking, polarization can be considered as a secondary source of electric field. As oscillating dipoles, the microscopic components of moments emit their own field, in-phase or out-of-phase with respect to the incident source field, and thereby affect the propagation of the latter. Hence, the response functions govern the propagation of electromagnetic waves in materials and are naturally involved in the description of refraction and absorption phenomena.
2.2. Refraction and Absorption
The propagation of light waves in dielectric materials is commonly described by the D’Alembert Equation [6]:
here given in Fourier space. It involves the dielectric permittivity of the material:
Considering the case of a wave propagating in an isotropic medium along the x direction, we show that [6]:
The complex quantity gives rise to a propagation factor and a damping factor . Actually, can be seen as the wave vector of light within the medium, which defines the refractive index of the material:
while characterizes the ability of the material to absorb light:
The imaginary part of the linear susceptibility is indeed involved in the absorbance of materials. As light intensity is given by , Equation (9) leads to the Beer–Lambert law for single-photon absorption:
relating in this way the absorbance of the system (along an optical path of length x) to the dielectric susceptibility. This relationship will be used in particular to extract the analytical expression of the susceptibility of materials from their absorption spectrum obtained by UV–visible spectrophotometry.
As a matter of fact, if the imaginary part of the susceptibility governs the phenomenon of absorption, its real part governs the phenomena of refraction and dispersion, that is to say all the phenomena of propagation without phase shift:
while the imaginary part introduces a phase shift:
for any component of the electric field. Figure 2 shows the effect of this phase shift on the field transmitted by a dielectric material. This field results from the superposition of two contributions: the field , resulting from optical refraction, and the field , resulting from absorption. Taking into account the phase shift which exists between the field and the polarization , the field is phase-shifted of () compared to the field :
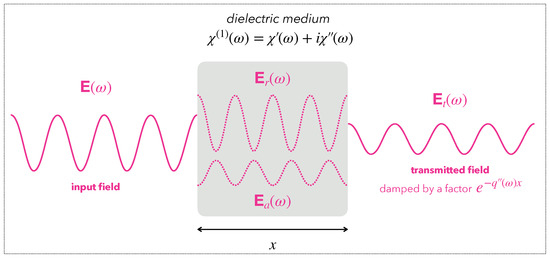
Figure 2.
Wave propagation in a dielectric medium. Illustration of refraction and absorption phenomena within a dielectric system of susceptibility . The incident electric field generates a polarization . The real part of results in the appearance of a field in phase with the incident electric field, while the imaginary part leads to the generation of an electric field in phase opposition. The destructive interference thus occurring gives rise to a transmitted electric field of weaker amplitude (damped by a factor ).
Therefore, these two electric fields add up in a destructive way. From the point of view of wave optics, absorption can thus be described as resulting from destructive interference. In other words, the function measures the coherence of light as it propagates through a dielectric medium.
2.3. Scattering and Extinction
In the case of the propagation of electromagnetic waves through a population of spherical dielectric particles, some part of the light is not only affected by absorption and is deflected in all directions of space. We then speak of scattering [4,7]. From the point of view of geometric optics, this deviation can be explained by multiple reflections and refractions occurring at the particle boundary, as shown in Figure 3a. However, this approach is not realistic. It is indeed necessary to adopt the wave formalism of electromagnetism and to study Mie’s theory to explain this scattering phenomenon [8], as shown schematically in Figure 3b.
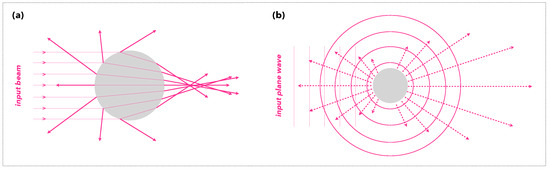
Figure 3.
Geometric and wave description of light scattering. Sketch of the scattering process, (a) from geometric optics and, (b) from wave optics. The dotted arrows represent the intensity of the scattered light according to the scattering angle.
When a light beam of incident intensity propagates through a population of particles of density N, some of the photons are absorbed while others are scattered. These are all lost photons, not indeed transmitted in the beam propagation direction. Since light intensity measures the photon flow within a beam, this results in an extinction cross-section defined so that [7]:
actually measures the probability that a photon is absorbed or scattered by a particle:
It is clear that Equation (16) generalizes the Beer–Lambert law. We can also identify the absorption cross-section:
Mie’s theory tells us that the scattering cross-section of a spherical particle depends on the wavevector and on the polarizability of the particle [7]:
As a reminder, this polarizability is nothing other than the microscopic counterpart of susceptibility:
where denotes the local field applied to the particle of dipole moment .
Like diffraction, scattering significantly manifests itself when the wavelength is about the order of magnitude of the particle radius: . In the case of quantum dots, 1–10 nm. Thus, for the same reasons that it is possible to assume a uniform electric field at the nanoscale, we can reasonably neglect scattering with respect to absorption, provided that particles do not agglomerate to form scattering centres of a few hundred nanometers.
2.4. Extinction Spectroscopies
UV–visible and infrared spectroscopies are generally presented as absorption spectroscopies. To be quite rigorous, these are extinction spectroscopies. When the particles are large enough to scatter light, the Beer–Lambert law of absorbance must be adapted:
While corresponds to absorbance, would be the ‘scatterance’ (term not used in the literature and defined here for the sake of clarity):
This means that UV–visible and infrared spectroscopies, which consist of measuring the quantity as a function of the wavelength or the wavenumber , are sensitive to light scattering. For instance, UV–visible spectroscopy allows highlighting and quantifying the aggregation of metallic or semiconductor nanoparticles when this indeed occurs [9,10].
3. Non-Linear Response of Anisotropic Media
The linear response theory satisfactorily describes the dielectric properties of matter when light does not excite the system into an anharmonic regime. In short, the excitation is not powerful enough to make the electrons and the nuclei explore potential energy surfaces far from their equilibrium (which is precisely characterized by harmonic potential wells). In contrast, when we probe matter with pulsed lasers, it is possible to achieve this new dielectric regime. It is therefore necessary to expand the optical response at higher orders of polarization.
3.1. Second Order Non-Linear Optical Processes
The phenomenological Relation (2) linking the polarization to the electric field can be considered as a first order truncated series expansion. Here, we introduce the second order term involved in the polarization:
where the second order polarization is quadratically dependent on the electric field. This non-linear term is often treated inappropriately, even in reference books [2,3,11]. It is often defined in frequency space (with complex exponential functions) whereas its true definition can only refers to the time evolution of the system, as written in Equation (23). The frequency spectrum of then truly derives from its Fourier transform.
First, the quadratic dependence of on the electric field results in a double convolution product involving a new response function [4,5]:
is a third-rank tensor, i.e., a hyper-matrix of second order response functions . The tensor product ⊗ allows the compact writing of the relation:
As 2-argument functions, the second order response functions are associated to 2-argument susceptibilities deduced from double Fourier transforms [4,5]:
However, the transposition of equation (24) into Fourier space is not as obvious as in the linear case, for which we simply had . Here:
giving:
To simplify this expression, we choose to define the auxiliary function as a (simple) Fourier transform of the response function :
In this case, Equation (28) becomes
where is nothing but the double Fourier transform of , with respect to the temporal variables and . Equation (31) means that the wave generated by the medium at the frequency , via , derives from a coupling governed by the tensor between all the frequencies available in the spectrum of . In other words, the non-linearity of the material makes it possible to couple two different frequencies ( and ) into a third one (). This non-linearity therefore allows the system to generate new frequencies, which is prohibited by the theory of linear response. This property characterizes moreover all the non-linear processes: they are always inelastic (the output frequency is different from the input frequency).
While most of the reference books and articles confuse and [2,3,4,11], here we make explicit the mathematical relation between them and establish the rigorous description of the non-linear second order optical response (Figure 1). By combining Equations (26) and (29), we get:
From the definition of as a double Fourier transform of , we therefore identify:
Therefore, the tensor can be interpreted as the spectral weight associated with the generation of the frequency by the non-linear coupling of frequencies and , so that . It is not equal to the susceptibility , which encodes for its part all the possible ways to couple two frequencies and available in the input light spectrum. As shown in Figure 4, the dielectric medium radiates in this way new fields at the frequencies:
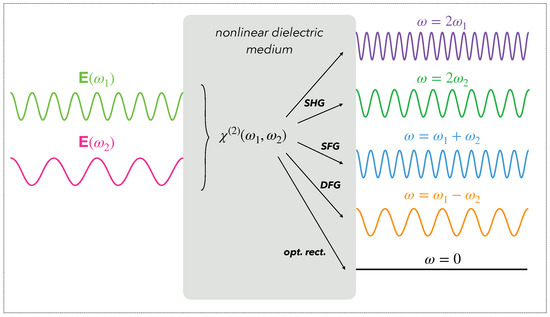
Figure 4.
Second order non-linear optical processes. Sketch of the processes of second harmonic generation (SHG), sum-frequency generation (SFG) and difference-frequency generation (DFG). These are driven by the second order dielectric susceptibility of the material, which couples two input frequencies and to generate new signals.
- , via : for SFG, sum-frequency generation;
- , via : for DFG, difference-frequency generation;
- , via , for SHG, second harmonic generation;
- , via , corresponding to optical rectification.
Finally, Equations (31) and (33) allow us to give a synthetic description of the non-linear second order optical processes. These are governed by:
with:
This last equation constitutes the quadratic counterpart of the linear constitutive relation .
3.2. Symmetry Rules
While all dielectric materials exhibit a linear response to optical excitation, they do not necessarily all respond non-linearly. Within the electric dipole approximation, to have a non-zero susceptibility , the material must not be centrosymmetric [2,3,4,5]. Indeed, let us examine the case of a centrosymmetric system for which . The physical transformation which reverses the orientation of the electric field:
similarly transforms the polarization, by centrosymmetry of causes and effects: . However, at the same time:
We must therefore both satisfy centrosymmetry, which implies , and Equation (38), which implies . In other words, , and : centrosymmetric materials cannot be the site of second order non-linear processes.
Apart from the case of anisotropic crystals and chiral structures which often constitute good non-linear materials, second order non-linearities can arise, first, at the interface between two dielectric media (given the breakdown of symmetry implied by this geometry) or, second, from the quadrupolar response of bulk materials. This is also why sum-frequency generation is very useful for the study of metal [12] and semiconductor [13] nanoparticles. Deposited on a substrate probed by pulsed lasers (Figure 5a), these nanoparticles can be analysed in a fine way given that the SFG signal is specific and characteristic of the interface: the would-be pollutants distributed in volume do not contribute to the signal. In addition, as nanoparticles are chemically functionalized on their surface (Figure 5b), it is also possible to examine the interactions at the interface between them and their surrounding molecules [14].
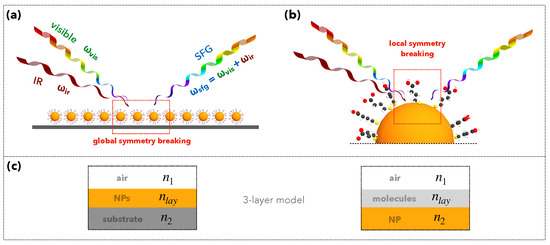
Figure 5.
Sum-frequency generation at nanostructured interfaces. Schematic representation of the SFG process in the case of functionalized nanoparticles grafted on a solid substrate. The two input frequencies belong to the visible () and the infrared () spectral ranges. This configuration is characterized by (a) a breaking of the global centrosymmetry at the macroscopic scale of the substrate and (b) a breaking of the local centrosymmetry at the surface of nanoparticles. (c) These two interfaces can be modelled as a 3-layer surface characterized by three refractive indices , and .
3.3. Sum-Frequency Generation at Interfaces
Since the SFG process is specific to interfaces, we choose to base this Review on the above-mentioned example of recent studies of nanoparticles [12,13] deposited on solid substrates, as represented in Figure 5. The aim of this section is therefore to establish the practical equations which allow us to interpret the SFG measurements carried out on such flat samples.
If we consider the generic situation presented in Figure 6, we notice that the sample geometry is invariant by any translation in the plane and any azimuthal rotation around the z-axis. Therefore, the tensor of the system exhibit only four non-zero and independent coefficients for symmetry reasons [15,16]:
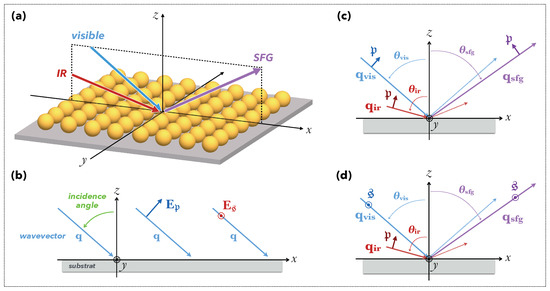
Figure 6.
SFG process at flat interfaces. (a) Schematic representation of SFG at the surface of a nanostructured sample. The visible, IR and SFG beams belong to the same plane of incidence . (b) Definition of the and polarizations, with respect to the plane of incidence . (c) Directions and polarizations of the beams in configuration. (d) Directions and polarizations of the beams in configuration.
Indeed, as the z-axis is the axis along which the centrosymmetry is broken, all the components which do not contain at least one z index are zero: 8 components are first removed. Owing to invariance of translation and isotropy within the plane , all the components containing x and y as indices are zero: 6 more components are removed. Since every plane containing the z-axis is a plane of symmetry and that , all the components with two z indices are zero: we get rid of 6 other components. Thus remains components, among which the permutation is an identity, due to the 2D-isotropy of the planar geometry. As a result, Equation (38) enumerates the 4 interesting terms.
Moreover, this translational invariance implies a phase matching condition on the parallel components (with respect to the surface plane) of the wavevectors of the two visible and infrared beams which probe the surface [17]:
where we write , and , the respective wavevectors of the visible, infrared and SFG beams. In general, we will always denote wavevectors by the letter . They are defined by their norm, by virtue of Equation (10):
and directed according to the direction of propagation of the wave. The momentum is the physical quantity which must be conserved when there is translational invariance, hence the condition of phase agreement (39). This allows us to determine the angle under which the SFG signal is emitted by reflection:
As the beams propagate though air, we consider that .
During SFG spectroscopy measurements, we commonly select two particular polarizations of the incident beams: the polarization , for which the electric field is parallel to the plane of incidence , and the polarization (from the German senkrecht, meaning perpendicular), for which the electric field is normal to the plane of incidence. These polarizations are depicted in the Figure 6 and characterized by the unit vectors:
where the index u refers to the visible or the infrared. The SFG signal can be detected in polarization or :
As far as we are concerned, we are only interested in the two configurations given in Figure 6c,d, namely the configuration , for which all the beams are -polarized, and the configuration , for which the visible is -polarized, the infrared -polarized and SFG detected in polarization. The choice of these polarization triplets actually depends on the nature of the sample substrate: to obtain an optimum SFG signal, it is important to use the configuration which maximizes the substrate reflectivity, as we usually acquire the SFG signal reflected by the surface.
In polarization scheme (SFG, Vis and IR beams, respectively), the laser excitation consists of the superposition of two monochromatic visible and infrared waves polarized according to :
while in configuration:
In the first case, we measure the -component of the SFG field generated by the 2nd order polarization. Therefore, the intensity of the SFG signal in is determined by the scalar quantity:
Taking into account the expression of the electric field (45), with Equations (34) and (35) relating to the electric field via the second order susceptibility, we obtain:
involving the effective second order susceptibility:
This result is consistent with the literature [17], with the difference that we have not taken into account the Local Field correction factors which must strictly multiply . These Local Field correction factors account for the reflectivity and optical dispersion of the sample. They are introduced in the next section. In the case of the configuration, the equations are simplified:
with:
The SFG intensity is then proportional to the square norm of the scalar polarization, which results in [17]:
where or , depending on the polarization configuration, and and designate the intensities of the two incident beams. The measurement of the SFG intensity thus enables to extract the square norm of the effective susceptibility , but not directly the susceptibilities .
3.4. Local Field Correction Factors: Light Intensity Modulation by Interface Symmetry
To be completely rigorous in our interpretations, we must take into account the influence of Local Field correction factors on the SFG response. We have omitted them so far, but their contribution is generally not negligible. In configuration, these factors, noted , modulate the susceptibilities as follows:
They account for the refraction and reflection processes between the different layers of which the interface is made. In the case of typical interfaces, we use the 3-layer model, as shown in Figure 5c. Hence, the Fresnel coefficients can be factorized in the form , with [17]:
and:
The indices u refer to the visible, infrared or SFG. It is worth noting that:
and the transmission angle of each beam is deduced from Snell-Descartes laws:
3.5. Third Order Non-Linear Optical Processes
Beyond second order, the optical processes of the third order are no longer governed by the geometry of the dielectric media and do not require any particular breaking of centrosymmetry: all materials can exhibit a third order contribution. In addition, most of the 3rd order processes are scattering processes since they do not involve phase matching condition, which is quite different from the 2nd order processes.
These processes include Raman scattering and fluorescence [2,3,4], which are concomitant processes. In both cases, a pump beam at frequency excites the system. The spectrum of the light emitted by inelastic process () is measured to obtain electronic (fluorescence) or vibrational (Raman, in the framework of Figure 7 for molecular optical spectroscopy) information. Formally, for a three-state system , and , illustrated in Figure 7, the susceptibility which governs inelastic processes of order 3 actually involves two factors [4]:
where and denote the relaxation rates associated with the transitions () and (). The first factor is resonant for : the measured optical signal corresponds to the transition from the electronic state (excited) to the vibrational state (fundamental), characteristic of a relaxation by fluorescence (Figure 7a). The second factor resonates at : the associated signal corresponds to a vibrational excitation of the system; the pump transfers a part of its energy , in this case the quantity , to stimulate the vibrational state (Figure 7b). This is the Stokes Raman process, from which we distinguish the anti-Stokes Raman process, described by and giving a signal at (Figure 7c). While fluorescence is a process that occurs between real electronic states, Raman scattering involves virtual states. As such, fluorescence can be qualified as a resonant scattering process whereas Raman scattering is a non-electronically resonant process.
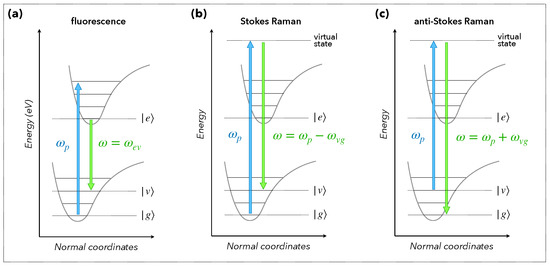
Figure 7.
Fluorescence and Raman scattering. Illustration of third order non-linear processes: (a) fluorescence, (b) Stokes Raman scattering and (c) anti-Stokes Raman scattering. We note the ground state, a vibrational state within the ground state, and an electronic excited state. The definition of normal coordinates is given in Section 4.1 in the case of molecules.
Furthermore, there are other third order non-linear processes, among which we count the optical Kerr effect, two-photon absorption (via ), third harmonic generation (via ) and sum-frequency generation under static field (via ) [2,3,4,18,19].
4. Vibrational Spectroscopies
In physical chemistry, molecular SFG vibrational spectroscopy was established experimentally in 1987 by Y.R. Shen at Berkeley (USA) through its three seminal papers published on pentadecanoic acid [20,21] and coumarin monolayers [22]. SFG spectroscopy is used in many applications such as (but not only) for the study of electrochemical [23,24,25,26] and catalytic [27,28,29] processes at liquid/solid and gas/solid interfaces. In the recent literature, SFG spectroscopy is intensively performed for the study of the water/air interface [30,31,32] or water/solid interface [33,34]. SFG allows in particular to examine the molecular organization of these interfaces, in presence or absence of organic pollutants [35,36], the formation of micellar complexes at the surface during the addition of various surfactants [37], or even the ultra-fast dynamics of water molecules near the free surface [38]. This opens up the SFG to the study of biological systems (among which lipid layers are emblematic [39,40,41]), with the objective to obtain structural information on the biological molecules (for peptides and proteins, see a recent exhaustive review [42]) located at the liquid/air or liquid/solid interfaces (e.g., conformational order, orientation of functional groups and chirality [43,44,45,46]).
SFG spectroscopy is a technique dedicated to the study of vibroelectronic coup-lings [47,48,49,50,51,52,53,54,55]. Indeed, it combines a visible excitation, which stimulates electronic transitions in materials such as metals or semiconductors, and an infrared excitation, which allows to simultaneously perform vibrational spectroscopy of organic species. SFG spectroscopy (2nd order process) therefore comes within the scope of vibrational spectroscopies, alongside infrared absorption (linear or 1st order process) and Raman scattering (3rd order process). We recall here the formalism used to describe the vibration modes of molecules and, in order to contextualize the particular place occupied by SFG spectroscopy, we compare these three spectroscopic probes.
4.1. Molecular Vibrations
Molecules can be mathematically described as a collection of N elastically bonded atoms. We denote by , , the displacement vector of the p-th atom in the reference frame of the centre of mass of the molecule. This vector is defined with respect to the equilibrium position of each atom. To describe the vibrations of the molecule, a first change of coordinates must be done. We use the mass-weighted Cartesian coordinates [56]:
These mass-weighted coordinates make it possible to easily express the kinetic energy:
The elastic bond between the atoms of the molecule results from the limited development of their potential interaction energy in the vicinity of their equilibrium positions [56]:
By setting the zero energy such that 0, and since the potential energy reaches its minimum at equilibrium, i.e., 0:
The Euler–Lagrange dynamic equation thus leads to coupled differential equations:
which admit solutions of the form , where is an eigenvalue of the matrix , i.e., , and a constant depending on the initial conditions. The scalar quantities correspond to the vibration frequencies of the normal modes which diagonalize the matrix of inter-atomic interactions. These are also associated with the normal coordinates defined so that the potential energy explicitly reflects the existence of an elastic interaction between the atoms of the molecule:
It can also be shown that these normal coordinates are linear combinations of the mass-weighted coordinates [56]. By noting the basis change matrix:
This means that each specific vibration mode consists of a collective oscillation of its atoms. When a molecule vibrates, all of its atoms oscillate at the same frequency and pass through their equilibrium position at the same time. We generally distinguish two classes of normal modes, represented in Figure 8: stretching and angular distorsion. In the cases of hydrogen, carbon, nitrogen and oxygen, which are light atoms abundant in organic species, the modes of angular distorsion, whose wavenumbers do not exceed 1500 cm, are much less energetic than the stretching modes, which can be around 4000 cm (Figure 9).
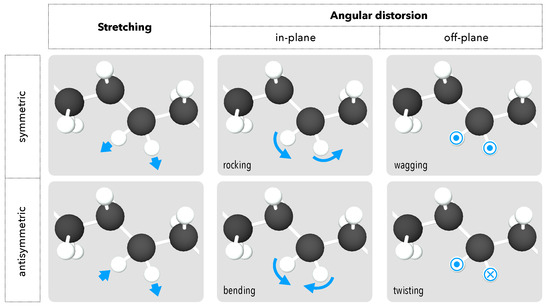
Figure 8.
Normal vibration modes. Schematic representation of the different vibration modes observed within molecules. Here we take the example of CH chemical group.
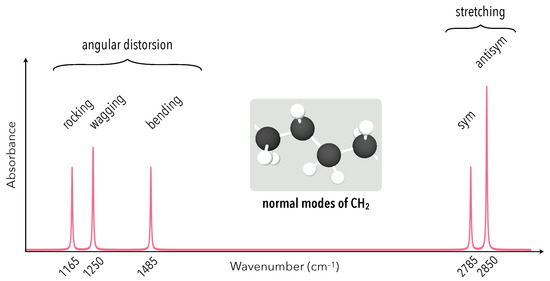
Figure 9.
Infrared spectroscopy of methylene. Typical shape of the IR spectrum associated with C−H vibration modes within CH groups.
4.2. Transition Dipole Moments and Susceptibility
Until now, we have only considered the classical definition of the dipole moment . In quantum mechanics, this physical quantity has a corresponding operator described by the matrix , where n and m label the set of quantum states:
We speak in this case of transition dipole moment, each corresponding to the dipole moment that the system acquires when it is promoted from state to state . The selection rules of the different spectroscopies directly derive from these transition dipole moments, allowing or prohibiting certain optical transitions. In the case of a molecular vibration , the dipole moment can be expanded in the vicinity of the equilibrium position as follows:
Denoting the ground state by , and assuming that the equilibrium is characterized by a zero dipole moment, i.e., , we see that the transition moments only depend on the variation of with respect to the normal coordinates [56]:
For a quantum system, the linear susceptibility depends on the transition moments. Kubo’s theorem (which results from the quantum treatment of the theory of linear response via the density matrix formalism) indeed gives [57]:
where is the Heaviside function. The mean value is defined with respect to the density matrix characterizing the statistic of the system at equilibrium. For any operator A:
This leads to the well-known expression [2,3,4,58]:
which relates the transition dipole moments to the linear susceptibility. Taking into account Equation (67), molecular systems are characterized by the tensor relation:
This is quite logical and substantial. On the one hand, the transition moments are 1st rank tensors (i.e., vectors). The product of two 1st rank tensors does indeed give a new 2nd rank tensor: here [59]. On the other hand, describes the zero order of the dielectric response (We use here the notation of Landau proper to Taylor expansion. For polarization, we typically have: , where E denotes the scalar amplitude of the electric field. Saying that a response function is in means that it describes the response to the order , and dominates all terms of order greater than or equal to n.), behaving like , which means that describes the dielectric response to order 1, behaving like as expected. These remarks will prove to be very enlightening thereafter.
4.3. Infrared Spectroscopy
The first vibrational spectroscopy technique relies on infrared absorption [56,60,61]. It is a linear optical process driven by the susceptibility of the medium. This technique is widely used for the identification of molecular species, each molecule having its own infrared response, according to its modes of vibration. As soon as the energy brought by the excitation matches the frequency of a vibrational eigenmode, we observe an absorption band, as described in Figure 9. The vibration modes of a molecule are not systematically detectable by infrared spectroscopy. In particular, the dipole moment of the molecule must vary when the molecule vibrates [2,3,56,62]:
Indeed, Section 2.2 taught us that absorption was governed by the imaginary part of the linear susceptibility. Equations (67) and (70) lead then to the infrared absorbance [63]:
As announced, the intensity of the infrared signal directly depends on the dipole moment variation with respect to the normal coordinates, which confirms the selection rule (72). Especially, this rule explains that the antisymmetric normal modes absorb more efficiently than the symmetric modes (Figure 9), the former being generally accompanied by a greater increase in the dipole moment. Equation (73) also tells us that each active vibration mode gives rise to a Lorentzian resonance in the absorption spectrum, which justifies the shape of the spectrum presented in Figure 9.
4.4. Raman Spectroscopy
As said in Section 3.5, the Raman process consists of the inelastic scattering of a pump beam by the vibration modes of the medium. By measuring the frequency of the scattered light, it is thus possible to retrieve the value of the eigenfrequencies, given by , and to identify the present molecular species [64], provided that the associated vibration modes are Raman active. While the selection rules for infrared absorption is related to the transition dipole moments, the Raman selection rules are based on the polarizability , which we expand to the first order in [4,65]:
Assuming that the vibration mode v is potentially activated within the molecule (by thermal agitation in particular), is a sinusoidal function of frequency and amplitude : . Using then the relation , although it is not very rigorous, we get:
Thus, we identify the elastic Rayleigh scattering at the frequency (75), the inelastic Stokes Raman scattering at the frequency (76) and the inelastic anti-Stokes Raman scattering at the frequency (77). Although its use is common, this presentation is not satisfactory. Formally, Equations (75)–(77) show Raman scattering as a linear process, which is obviously not the case (since inelastic). This mathematical contradiction actually translates our inability to describe by classical electromagnetism the incoherent processes of Raman scattering and fluorescence [66]. These two processes are indeed spontaneous and random, so that each photon scattered in Raman (or emitted in fluorescence) has a random phase. Consequently, they give rise to incoherent fields, whose value is zero in average. Moreover, it is because of this inconsistency, characterized by the absence of a phase matching condition, that the scattered and incident powers maintain a linear relation [58] (as described in Equations (75)–(77)), despite the non-linearity of the optical process. The classical approach that we have just presented here predicts formally the Stokes and anti-Stokes Raman processes, and justifies also the selection rule specific to Raman spectroscopy, that is:
As demonstrated elsewhere in quantum mechanics [2,3,58,62,67], a vibration mode is Raman active if the polarizability of the molecule depends on the normal mode coordinate. It is not a coincidence if the polarizability is involved in the Raman process. As a 3rd order non-linear process, Raman spectroscopy is driven by [63,68,69]:
Like the tensor Relation (71), Equation (79) mathematically manifests the non-linearity of the physical phenomenon. First, the polarizability is a 2nd rank tensor. The product of two 2nd rank tensors gives a 4th rank tensor: . Second, describes the 1st order dielectric response, behaving like , which is consistent with the fact that describes the 3rd order response, behaving like . Analogously to infrared spectroscopy, the Raman spectrum of scattered light is then represented by [63]:
As the foundations of infrared and Raman spectroscopies are now established, it is possible to present the specificities of SFG spectroscopy and understand its interest in the study of vibroelectronic couplings within matter.
4.5. SFG Spectroscopy
We commonly read in the literature that SFG spectroscopy is a combination of infrared and Raman spectroscopies. Figure 10 illustrates this point of view by considering the case of a three-state quantum system. For purely molecular systems, this enables to justify the SFG selection rules. In this case, the non-linear susceptibility , behaving like , is proportional to the transition polarizability, behaving like , and the transition dipole moment, behaving like [2,3,63]:
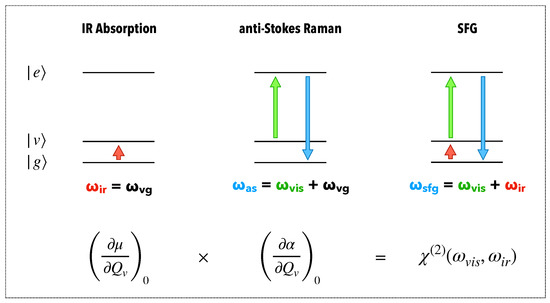
Figure 10.
Vibrational spectroscopies. Comparison between the three techniques of vibrational spectroscopy: infrared absorption, anti-Stokes Raman scattering and sum-frequency generation. We represent three quantum states , and for the system, with the same meaning than Figure 7.
This relation tells us that a vibration mode is active in SFG spectroscopy if it is active in both infrared absorption and Raman scattering. However, we cannot ignore that the infrared and Raman processes are driven by the tensor Relations (71) and (79), which logically means that their combination would give rise to a 5th order optical process: , much different from SFG. Considering sum-frequency generation as a combination of infrared and Raman processes is thus misleading: . The only way to formally link to and is by defining contracted tensors [59], even though it is fundamentally and conceptually improper to describe SFG as a combination of IR and Raman spectroscopies.
To understand the specificity of SFG spectroscopy, we compare it to infrared and Raman spectroscopies in Table 1. Especially, SFG is resonant with respect to the infrared, and consists in a coherent emission (which is hardly the case of Raman). Another advantage of SFG is its surface specificity and that it can be doubly resonant [70]: in addition to its resonant character in the infrared, inherited from IR absorption, the SFG signal can be resonant in the visible. This situation is shown in Figure 10, where the visible and SFG frequencies match electronic transitions.

Table 1.
Comparison of vibrational spectroscopies. Comparative table of the three vibrational spectroscopies: infrared absorption, Raman scattering and SFG. Raman scattering can be resonant in the visible spectral range when the frequency of the pump beam coincides with an electronic transition (the excited state is therefore not virtual but indeed real, as illustrated in Figure 10). SFG can be doubly resonant, with respect to the infrared and visible beams, as shown in Figure 10.
Therefore, three spectroscopic approaches can be employed. The first one is conventional: it consists in measuring the intensity of the SFG signal for a given visible excitation (i.e., at a fixed frequency ) by varying the frequency of the infrared excitation [9,71]. The corresponding spectra carry the vibrational information of the probed system (Figure 11a). In a less conventional way, it is possible to compare several vibrational SFG spectra obtained for different visible excitations (Figure 11b) and thereby deduce the influence of the electronic properties of the system on the expression of its vibrational fingerprint [13,72]. Eventually, in a last unconventional manner, a third approach consists of measuring the SFG intensity for a given infrared excitation, preferably matching a vibration mode (i.e., ), by varying the frequency of the visible excitation (Figure 11c) [14,73].
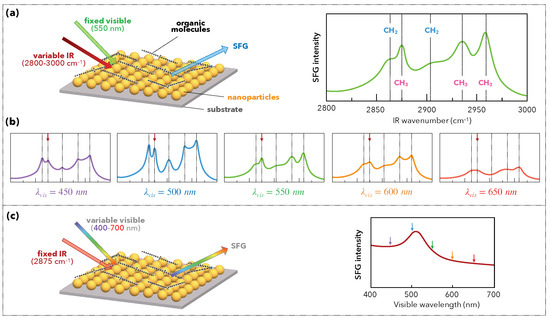
Figure 11.
Principle of 2-dimension sum-frequency generation. (a) Conventional use of SFG spectroscopy on a nanostructured sample functionalized by organic molecules. The SFG spectrum consists in measuring the SFG intensity as a function of the IR wavenumber for a fixed visible wavelength ( nm). (b) Comparison of five vibrational SFG spectra obtained for five different visible wavelengths. For each vibration mode, the variation of the intensity from a visible wavelength to another is characteristic of electronic structure of the system (nanoparticles). (c) Unconventional use of SFG spectroscopy at variable visible wavelength. The spectrum is acquired at a fixed IR wavenumber that coincides with the vibration mode indicated on the spectra of Figure 11b.
When we exploit SFG spectroscopy in its vibrational dimension, by fixing and by varying , the spectrum is described by [3,63]:
This equation reflects the vibrational response of the molecular system, obviously resonant in the infrared range when the excitation frequency coincides with the eigenfrequency . In the typical case of functionalized nanoparticles grafted on a solid substrate, it is also necessary to take into account the SFG response of the substrate and the nanoparticles. Generally, these components do not exhibit vibration modes over the probed infrared spectral range. The SFG spectra are then modelled by an effective susceptibility of the form [72,74]:
The first term corresponds to the non-resonant response (with respect to the infrared) of the inorganic components (i.e., substrate and nanoparticles). The amplitude A and the phase can possibly depend on the electronic response of these objects, hence:
The sum over v describes the vibrational resonances associated with each of the molecular vibration modes of eigenfrequencies . These are complex Lorentzian functions, as suggested by Equation (82). In the general case of hybrid organic/inorganic interfaces, the amplitudes of vibration can be conditioned by the electronic activity of the inorganic components. As such, they potentially admit a dependence on the visible frequency:
As the terms of Equation (83) are complex numbers, this experimentally results in interference patterns on the SFG spectra. Figure 12 illustrates this point. According to Equation (50), the SFG intensity is proportional to the square norm of the effective second order susceptibility. Considering the case of a single mode of vibration:
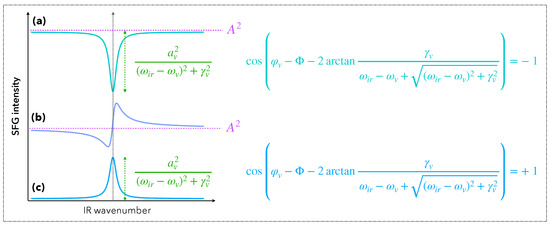
Figure 12.
Interference profiles of SFG spectra. Typical profiles of the vibrational SFG spectra: (a) in the destructive case, (b) in an intermediate case, (c) in the constructive case. The quantity corresponds to the non-resonant background. It is not specific to the molecular species but to the inorganic components of the system.
The first term defines what is called the non-resonant background of the SFG signal. The second term is the vibrational resonance, and the third is an interference term between the substrate and the adsorbate. In the constructive case, the vibration appears as a peak on the SFG spectrum (Figure 12c); in the destructive case, it appears as a dip (Figure 12a). The above-mentioned description of the SFG response of an interface is phenomenological and easy to use for data fitting. In addition, it is worth noting that recent theoretical and analytical models developed for doubly resonant SFG and DFG spectroscopies give a quantified description of complex phenomena related to vibronic couplings inside molecules [75,76].
4.6. Prospects in SFG Spectroscopy and Microscopy
Beyond the mathematical formalism introduced here and applied to surface-specific Two-colour SFG spectroscopy, we emphasize that the intrinsic symmetry properties of SFG spectroscopy allow to relate its susceptibility chiral components to the broader concept of vibrational optical activity (VOA) already developed for infrared and Raman spectroscopy, widening the field of investigation not only for any type of surface or (buried) interface but also for bulk materials (in volume). Nowadays, chiral SFG spectroscopy is a potential powerful local probe aimed at playing specifically with (bio)molecular symmetry rules in primary, secondary and ternary biological structures. In fact, it is the object of numerous experimental developments and studies [77], constituting the utmost probe of VOA [78,79] for both interfacial and bulk samples, which is counter-intuitive at first glance for non-linear 2nd order optical probes in the latter case. Moreover, chiral SFG allows to distinguish between non-zero susceptibility components as a function of the sample symmetry at the molecular, nanometer and microscopic scale: it allows therefore to discriminate chiral interface, chiral bulk, achiral interface and achiral bulk properties, respectively. In these conditions, it is clear that SFG sensitivity is greatly enhanced as a function of the selected polarization combination triplet for in the 3-dimensional space. It can therefore be applied to distinguish different enantiomers in racemic mixtures, analyse the geometry inside polymer thin films or a the air/proteins interfaces. More exciting for the future, it could be also applied to selectively detect complementary DNA strands in the development of biosensors for medical purposes. A dedicated theoretical formalism for VOA SFG has to be developed in the future and our contribution could constitute a solid foundation for such a demanding task.
Finally, promising developments show that it is possible to use SFG in microscopy imaging [80,81,82,83], thus offering the possibility of probing interfaces at least with 100 nm spatial resolution.
5. Conclusions
In this review, by revisiting past and current literature on the fundamentals of linear (first order) and non-linear optics (second and third orders), we have established a coherent and unified mathematical description for the major optical vibrational and electronic spectroscopies thanks to a progressive description of their own characteristics and interest field: absorption, scattering, fluorescence, infrared, Raman and sum-frequency generation (SFG) processes, compatible with the current and past experimental observations. This made it possible to remove the ambiguities observed in literature for the description of the susceptibilities of materials. The emblematic case of SFG spectroscopy has been addressed in details because it relies on the selection and exclusion rules of infrared and Raman spectroscopies, strictly correlated to (centro)symmetry properties of interface and bulk materials. While nowadays SFG spectroscopy is mainly aimed at probing surfaces and interfaces at multiscale, from the atomic to the biological scale, the presence of chiral parameters in the design of complex hybrid organic/inorganic systems opens the door to a bright and exciting future in the analysis of their physico-chemical properties: a new age of non-linear spectroscopy is on the edge!
Author Contributions
C.H. and T.N. prepared, wrote, edited and reviewed the paper. T.N. draw all the figures of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not relevant to this Review.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SFG | Sum-frequency generation |
| DFG | Difference-frequency generation |
| SHG | Second harmonic generation |
| VOA | Vibrational optical activity |
References
- Battaglia, F.; George, T.F. Tensors: A guide for undergraduate students. Am. J. Phys. 2013, 81, 498–511. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 2nd ed.; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Hache, F. Optique Non Linéaire; EDP Sciences: Les Ulis, France, 2016. [Google Scholar]
- He, G.S. Nonlinear Optics and Photonics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Haug, H.; Koch, S. Quantum Theory of the Optical and Electronic Properties of Semiconductors, 5th ed.; World Scientific: Singapore, 2009. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Dalstein, L.; Haddada, M.B.; Barbillon, G.; Humbert, C.; Tadjeddine, A.; Boujday, S.; Busson, B. Revealing the Interplay between Adsorbed Molecular Layers and Gold Nanoparticles by Linear and Nonlinear Optical Properties. J. Phys. Chem. C 2015, 119, 17146–17155. [Google Scholar] [CrossRef]
- Hottechamps, J.; Noblet, T.; Brans, A.; Humbert, C.; Dreesen, L. How quantum dots aggregation enhances Förster Resonant Energy Transfer. ChemPhysChem 2020, 21, 853–862. [Google Scholar] [CrossRef] [PubMed]
- Bloembergen, N. Nonlinear Optics, 4th ed.; World Scientific: Singapore, 1965. [Google Scholar]
- Dalstein, L.; Humbert, C.; Haddada, M.B.; Boujday, S.; Barbillon, G.; Busson, B. The Prevailing Role of Hotspots in Plasmon-Enhanced Sum-Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2019, 10, 7706–7711. [Google Scholar] [CrossRef]
- Noblet, T.; Dreesen, L.; Boujday, S.; Méthivier, C.; Busson, B.; Tadjeddine, A.; Humbert, C. Semiconductor quantum dots reveal dipolar coupling from exciton to ligand vibration. Commun. Chem. 2018, 1, 76. [Google Scholar] [CrossRef]
- Noblet, T.; Boujday, S.; Méthivier, C.; Erard, M.; Hottechamps, J.; Busson, B.; Humbert, C. Two-Dimensional Layers of Colloidal CdTe Quantum Dots: Assembly, Optical Properties, and Vibroelectronic Coupling. J. Phys. Chem. C 2020, 124, 25873–25883. [Google Scholar] [CrossRef]
- Fumi, F.G. The direct-inspection method in systems with a principal axis of symmetry. Acta. Cryst. 1952, 5, 691–694. [Google Scholar] [CrossRef]
- Sioncke, S.; Verbiest, T.; Persoons, A. Second-order nonlinear optical properties of chiral materials. Mater. Sci. Eng. Rep. 2003, 42, 115–155. [Google Scholar] [CrossRef]
- Zhuang, X.; Miranda, P.B.; Kim, D.; Shen, Y.R. Mapping molecular orientation and conformation interfaces by surface nonlinear optics. Phys. Rev. B 1999, 59, 12632–12640. [Google Scholar] [CrossRef]
- Vidal, F.; Busson, B.; Tadjeddine, A. Probing electronic and vibrational properties at the electrochemical interface using SFG spectroscopy: Methanol electro-oxidation on Pt(110). Chem. Phys. Lett. 2005, 403, 324–328. [Google Scholar] [CrossRef]
- Joutsuka, T.; Hirano, T.; Sprikb, M.; Morita, A. Effects of third-order susceptibility in sum frequency generation spectra: A molecular dynamics study in liquid water. Phys. Chem. Chem. Phys. 2018, 20, 3040. [Google Scholar] [CrossRef] [PubMed]
- Hunt, J.; Guyot-Sionnest, P.; Shen, Y. Observation of C-H stretch vibrations of monolayers of molecules optical sum-frequency generation. Chem. Phys. Lett. 1987, 133, 189–192. [Google Scholar] [CrossRef]
- Guyot-Sionnest, P.; Hunt, J.; Shen, Y. Sum-frequency vibrational spectroscopy of a Langmuir film: Study of molecular orientation of a two-dimensional system. Phys. Rev. Lett. 1987, 59, 1597–1600. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Suhr, H.; Shen, Y. Surface vibrational spectroscopy by infrared-visible sum frequency generation. Phys. Rev. B 1987, 35, 3047–3050. [Google Scholar] [CrossRef] [PubMed]
- Nicolau, B.G.; Garcia-Rey, N.; Dryzhakov, B.; Dlott, D.D. Interfacial Processes of a Model Lithium Ion Battery Anode Observed, in Situ, with Vibrational Sum-Frequency Generation Spectroscopy. J. Phys. Chem. C 2015, 119, 10227–10233. [Google Scholar] [CrossRef]
- Yang, S.; Noguchi, H.; Uosaki, K. Electronic Structure of the CO/Pt(111) Electrode Interface Probed by Potential-Dependent IR/Visible Double Resonance Sum Frequency Generation Spectroscopy. J. Phys. Chem. C 2015, 119, 26056–26063. [Google Scholar] [CrossRef]
- Braunschweig, B.; Mukherjee, P.; Haan, J.L.; Dlott, D.D. Vibrational sum-frequency generation study of the CO2 electrochemical reduction at Pt/EMIM-BF4 solid/liquid interfaces. J. Electroanal. Chem. 2017, 800, 144–150. [Google Scholar] [CrossRef]
- Garcia-Rey, N.; Dlott, D.D. Studies of electrochemical interfaces by broadband sum frequency generation. J. Electroanal. Chem. 2017, 800, 114–125. [Google Scholar]
- Feng, R.; Liu, A.; Liu, S.; Shi, J.; Zhang, R.; Ren, Z. In Situ Studies on the Dissociation and Photocatalytic Reactions of CH3OH on TiO2 Thin Film by Sum Frequency Generation Vibrational Spectroscopy. J. Phys. Chem. C 2015, 119, 9798–9804. [Google Scholar] [CrossRef]
- Vanselous, H.; Stingel, A.M.; Petersen, P.B. Interferometric 2D Sum Frequency Generation Spectroscopy Reveals Structural Heterogeneity of Catalytic Monolayers on Transparent Materials. J. Phys. Chem. Lett. 2017, 8, 825–830. [Google Scholar] [CrossRef] [PubMed]
- Ouvrard, A.; Wang, J.; Ghalgaoui, A.; Nave, S.; Carrez, S.; Zheng, W.; Dubost, H.; Bourguignon, B. CO Adsorption on Pd(100) Revisited by Sum Frequency Generation: Evidence for Two Adsorption Sites in the Compression Stage. J. Phys. Chem. C 2014, 118, 19688–19700. [Google Scholar] [CrossRef]
- Morita, A.; Hynes, J.T. A Theoretical Analysis of the Sum Frequency Generation Spectrum of the Water Surface. II. Time-Dependent Approach. J. Phys. Chem. B 2002, 106, 673–685. [Google Scholar] [CrossRef]
- Medders, G.R.; Paesani, F. Dissecting the Molecular Structure of the Air/Water Interface from Quantum Simulations of the Sum-Frequency Generation Spectrum. J. Am. Chem. Soc. 2016, 138, 3912–3919. [Google Scholar] [CrossRef] [PubMed]
- Chiang, K.Y.; Dalstein, L.; Wen, Y.C. Affinity of Hydrated Protons at Intrinsic Water/Vapor Interface Revealed by Ion-Induced Water Alignment. J. Phys. Chem. Lett. 2020, 11, 679–701. [Google Scholar] [CrossRef] [PubMed]
- Khatib, R.; Backus, E.H.G.; Bonn, M.; Perez-Haro, M.J.; Gaigeot, M.P.; Sulpizi, M. Water orientation and hydrogen-bond structure at the fluorite/water interface. Sci. Rep. 2016, 6, 24287. [Google Scholar] [CrossRef] [PubMed]
- Urashima, S.; Myalitsin, A.; Nihonyanagi, S.; Tahara, T. The Topmost Water Structure at a Charged Silica/Aqueous Interface Revealed by Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 4109–4114. [Google Scholar] [CrossRef]
- Tuladhar, A.; Piontek, S.M.; Borguet, E. Insights on Interfacial Structure, Dynamics, and Proton Transfer from Ultrafast Vibrational Sum Frequency Generation Spectroscopy of the Alumina(0001)/Water Interface. J. Phys. Chem. C 2017, 121, 5168–5177. [Google Scholar] [CrossRef]
- Kusaka, R.; Ishiyama, T.; Nihonyanagi, S.; Morita, A.; Tahara, T. Structure at the air/water interface in the presence of phenol: A study using heterodyne-detected vibrational sum frequency generation and molecular dynamics simulation. Phys. Chem. Chem. Phys. 2018, 20, 3002. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Nguyen, A.V.; Evans, G.M. Interfacial Water Structure at Surfactant Concentrations below and above the Critical Micelle Concentration as Revealed by Sum Frequency Generation Vibrational Spectroscopy. J. Phys. Chem. C 2015, 119, 15477–15481. [Google Scholar] [CrossRef]
- Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Ultrafast Dynamics at Water Interfaces Studied by Vibrational Sum Frequency Generation Spectroscopy. Chem. Rev. 2017, 117, 10665–10693. [Google Scholar] [CrossRef] [PubMed]
- Toledo-Fuentes, X.; Lis, D.; Cecchet, F. Structural Changes to Lipid Bilayers and Their Surrounding Water upon Interaction with Functionalized Gold Nanoparticles. J. Phys. Chem. C 2016, 120, 21399–21409. [Google Scholar] [CrossRef]
- Saha, A.; SenGupta, S.; Kumar, A.; Naik, P.D. Interaction of L-Phenylalanine with Lipid Monolayers at Air-Water Interface at Different pHs: Sum-Frequency Generation Spectroscopy and Surface Pressure Studies. J. Phys. Chem. C 2018, 122, 3875–3884. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Tanab, J.; Ye, S. In situ examination of a charged amino acid-induced structural change in lipid bilayers by sum frequency generation vibrational spectroscopy. Phys. Chem. Chem. Phys. 2018, 20, 5657. [Google Scholar] [CrossRef] [PubMed]
- Hosseinpour, S.; Roeters, S.; Bonn, M.; Peukert, W.; Woutersen, S.; Weidner, T. Structure and Dynamics of Interfacial Peptides and Proteins from Vibrational Sum-Frequency Generation Spectroscopy. Chem. Rev. 2020, 120, 3420–3465. [Google Scholar] [CrossRef]
- Laaser, J.E.; Skoff, D.R.; Ho, J.J.; Joo, Y.; Serrano, A.L.; Steinkruger, J.D.; Gopalan, P.; Gellman, S.H.; Zanni, M.T. Two-Dimensional Sum-Frequency Generation Reveals Structure and Dynamics of a Surface-Bound Peptide. J. Am. Chem. Soc. 2014, 136, 956–962. [Google Scholar] [CrossRef]
- Yan, E.C.Y.; Fu, L.; Wang, Z.; Liu, W. Biological Macromolecules at Interfaces Probed by Chiral Vibrational Sum Frequency Generation Spectroscopy. Chem. Rev. 2014, 114, 8471–8498. [Google Scholar] [CrossRef]
- Schmüser, L.; Roeters, S.; Lutz, H.; Woutersen, S.; Bonn, M.; Weidner, T. Determination of Absolute Orientation of Protein α-Helices at Interfaces Using Phase-Resolved Sum Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2017, 8, 3101–3105. [Google Scholar] [CrossRef]
- Xiao, M.; Wei, S.; Li, Y.; Jasensky, J.; Chen, J.; Brooks, C.L.; Chen, Z. Molecular interactions between single layered MoS2 and biological molecules. Chem. Sci. 2018, 9, 1769. [Google Scholar] [CrossRef]
- Raab, M.; Becca, J.C.; Heo, J.; Lim, C.K.; Baev, A.; Jensen, L.; Prasad, P.N.; Velarde, L. Doubly resonant sum frequency spectroscopy of mixed photochromic isomers on surfaces reveals conformation-specific vibronic effects. J. Chem. Phys. 2019, 150, 114704. [Google Scholar] [CrossRef]
- Peremans, A.; Caudano, Y.; Thiry, P.A.; Dumas, P.; Zhang, W.Q.; Rille, A.L.; Tadjeddine, A. Electronic Tuning of Dynamical Charge Transfer at an Interface: K Doping of C60/Ag(111). Phys. Rev. Lett. 1997, 78, 2999–3002. [Google Scholar] [CrossRef]
- Caudano, Y.; Silien, C.; Humbert, C.; Dreesen, L.; Mani, A.A.; Peremans, A.; Thiry, P.A. Electron-phonon couplings at C60 interfaces: A case study by two-color, infrared-visible sum-frequency generation spectroscopy. J. Electron Spectroscop. Relat. Phenom. 2003, 129, 139–147. [Google Scholar] [CrossRef]
- Elsenbeck, D.; Das, S.K.; Velarde, L. Substrate influence on the interlayer electron-phonon couplings in fullerene films probed with doubly-resonant SFG spectroscopy. Phys. Chem. Chem. Phys. 2017, 19, 18519. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Westerberg, S.; Shen, Y.R.; Ross, P.N.; Somorjai, G.A. Probing the charge-transfer state of CO on Pt(111) by two-dimensional infrared-visible sum frequency generation spectroscopy. Phys. Rev. B 2004, 69, 153413. [Google Scholar] [CrossRef]
- Bozzini, B.; D’Urzo, L.; Mele, C.; Busson, B.; Humbert, C.; Tadjeddine, A. Doubly Resonant Sum Frequency Generation Spectroscopy of Adsorbates at an Electrochemical Interface. J. Phys. Chem. C 2008, 112, 11791–11795. [Google Scholar] [CrossRef]
- Dreesen, L.; Humbert, C.; Celebi, M.; Lemaire, J.J.; Mani, A.A.; Thiry, P.A.; Peremans, A. Influence of the metal electronic properties on the sum-frequency generation spectra of dodecanethiol self-assembled monolayers on Pt(111), Ag(111) and Au(111) single crystals. Appl. Phys. B 2002, 74, 621–625. [Google Scholar] [CrossRef]
- Lis, D.; Caudano, Y.; Henry, M.; Demoustier-Champagne, S.; Ferain, E.; Cecchet, F. Selective Plasmonic Platforms Based on Nanopillars to Enhance Vibrational Sum-Frequency Generation Spectroscopy. Adv. Opt. Mater. 2013, 1, 244–255. [Google Scholar] [CrossRef]
- Hayashi, M.; Lin, S.H.; Raschke, M.B.; Shen, Y.R. A Molecular Theory for Doubly Resonant IR-UV-vis Sum-Frequency Generation. J. Phys. Chem. A 2002, 106, 2271–2282. [Google Scholar] [CrossRef]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover Publications: New York, NY, USA, 1955. [Google Scholar]
- Mahan, G.D. Many-Particle Physics, 2nd ed.; Plenum Press: New York, NY, USA, 1990. [Google Scholar]
- Albrecht, A.C. On the Theory of Raman Intensities. J. Chem. Phys. 1961, 34, 1476. [Google Scholar] [CrossRef]
- Chen, F.; Gozdzialski, L.; Hung, K.K.; Stege, U.; Hore, D.K. Assessing the Molecular Specificity and Orientation Sensitivity of Infrared, Raman, and Vibrational Sum-Frequency Spectra. Symmetry 2021, 13, 42. [Google Scholar] [CrossRef]
- Atkins, P.W. Physical Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Lin-Vien, D.; Colthup, N.B.; Fateley, W.G.; Grasselli, J.G. The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Porezag, D.; Pederson, M.R. Infrared intensities and Raman-scattering activities within density-functional theory. Phys. Rev. B 1996, 54, 7830–7836. [Google Scholar] [CrossRef] [PubMed]
- Hung, K.K.; Stege, U.; Hore, D.K. IR Absorption, Raman Scattering, and IR-Vis Sum-Frequency Generation Spectroscopy as Quantitative Probes of Surface Structure. Appl. Spec. Rev. 2015, 50, 351–376. [Google Scholar] [CrossRef]
- Veilly, E.; Roques, J.; Jodin-Caumon, M.C.; Humbert, B.; Drot, R.; Simoni, E. Uranyl interaction with the hydrated (001) basal face of gibbsite: A combined theoretical and spectroscopic study. J. Chem. Phys. 2008, 129, 244704. [Google Scholar] [CrossRef] [PubMed]
- Kakkar, R. Atomic and Molecular Spectroscopy: Basic Concepts and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Polavarapu, P.L. Ab Initio Vibrational Raman and Raman Optical Activity Spectra. J. Chem. Phys. 1990, 94, 8106–8112. [Google Scholar] [CrossRef]
- Potma, E.O.; Mukamel, S. Coherent Raman Scattering Microscopy; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Roy, S.; Beutier, C.; Hore, D.K. Combined IR-Raman vs vibrational sum-frequency heterospectral correlation spectroscopy. J. Mol. Struct. 2018, 1161, 403–411. [Google Scholar] [CrossRef]
- Huang, J.H.; Shen, Y.R. Theory of doubly resonant infrared-visible sum-frequency and difference-frequency generation from adsorbed molecules. Phys. Rev. A 1994, 49, 3973–3981. [Google Scholar] [CrossRef]
- Humbert, C.; Noblet, T.; Dalstein, L.; Busson, B.; Barbillon, G. Sum-Frequency Generation Spectroscopy of Plasmonic Nanomaterials: A Review. Materials 2019, 12, 836. [Google Scholar] [CrossRef] [PubMed]
- Humbert, C.; Dahi, A.; Dalstein, L.; Busson, B.; Lismont, M.; Colson, P.; Dreesen, L. Linear and nonlinear optical properties of functionalized CdSe quantum dots prepared by plasma sputtering and wet chemistry. J. Colloid Interface Sci. 2015, 445, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Dreesen, L.; Humbert, C.; Sartenaer, Y.; Caudano, Y.; Volcke, C.; Mani, A.A.; Peremans, A.; Thiry, P.A.; Hanique, S.; Frère, J.M. Electronic and Molecular Properties of an Adsorbed Protein Monolayer Probed by Two-Color Sum-Frequency Generation Spectroscopy. Langmuir 2004, 20, 7201–7207. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.C.; Hore, D.K. Determining the Orientation of Chemical Functional Groups on Metal Surfaces by a Combination of Homodyne and Heterodyne Nonlinear Vibrational Spectroscopy. J. Phys. Chem. C 2017, 121, 28043–28050. [Google Scholar] [CrossRef]
- Busson, B. Doubly resonant SFG and DFG Spectroscopies: An analytic model for data analysis including distorted and rotated vibronic levels. I. Theory. J. Chem. Phys. 2020, 153, 174701. [Google Scholar] [CrossRef] [PubMed]
- Busson, B. Doubly resonant SFG and DFG Spectroscopies: An analytic model for data analysis including distorted and rotated vibronic levels. II. Applications. J. Chem. Phys. 2020, 153, 174702. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, T.A.; Okuno, M. Chapter 9—Heterodyne-detected chiral vibrational sum frequency generation spectroscopy of bulk and interfacial samples. In Molecular and Laser Spectroscopy; Gupta, V., Ozaki, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 315–348. [Google Scholar]
- Nafie, L. Vibrational optical activity: From discovery and development to future challenges. Chirality 2020, 32, 667–692. [Google Scholar] [CrossRef] [PubMed]
- Fujisawa, T.; Unno, M. Chapter 2—Vibrational optical activity spectroscopy. In Molecular and Laser Spectroscopy; Gupta, V., Ozaki, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 41–82. [Google Scholar]
- Lee, C.M.; Kafle, K.; Huang, S.; Kim, S.H. Multimodal Broadband Vibrational Sum Frequency Generation (MM-BB-V-SFG) Spectrometer and Microscope. J. Phys. Chem. B 2016, 120, 102–116. [Google Scholar] [CrossRef] [PubMed]
- Allgeyer, E.S.; Sterling, S.M.; Gunewardene, M.S.; Hess, S.T.; Neivandt, D.J.; Mason, M.D. Combining Total Internal Reflection Sum Frequency Spectroscopy Spectral Imaging and Confocal Fluorescence Microscopy. Langmuir 2015, 31, 987–994. [Google Scholar] [CrossRef] [PubMed]
- Fang, M.; Santos, G.; Chen, X.; Baldelli, S. Roles of oxygen for methanol adsorption on polycrystalline copper surface revealed by sum frequency generation imaging microscopy. Surf. Sci. 2016, 648, 35–41. [Google Scholar] [CrossRef]
- Wang, H.; Gao, T.; Xiong, W. Self-Phase-Stabilized Heterodyne Vibrational Sum Frequency Generation Microscopy. ACS Photonics 2017, 4, 1839–1845. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).