Abstract
In this paper we present a cryptographic primitive based on non-commutative cryptography. This primitive is used for key exchange protocol (KEP) construction. We prove that the security of this primitive relies on a nondeterministic polynomial complete (NP-Complete) decisional problem. Recently there are no known quantum cryptanalysis algorithms effectively solving NP-Complete problems. So far, KEPs are widely used in secure communication channel creation, e.g., in hypertext transfer protocol secure (https://) and are based on traditional cryptographic primitives representing commutative cryptography. However, the security of these protocols does not rely on NP-Complete problems and hence, according to P. W. Shorr, they are vulnerable to quantum cryptanalysis. We use one of seven non-commuting groups of order 16 which is not isomorphic to any other group to define a platform group for a key exchange protocol based on previously considered matrix power function (MPF). By investigating basic properties on the group and their implementation for our goals we fix the order of actions in MPF from left to right. Furthermore, we define a special form of the base matrix and separate templates for left and right power matrices. Using properties of the specified templates and Schaeffer criteria we prove that the security of the proposed key exchange relies on an NP-Complete decisional problem.
1. Introduction
1.1. Early Days of Asymmetric Cryptography
The history of asymmetric cryptography starts in 1976 when W. Diffie and M. Hellman published their groundbreaking work [1]. In that paper authors showed how two protocol parties, Alice and Bob, can agree on a shared key using publicly known data and their private keys. This is what was later called an asymmetric key exchange protocol (KEP). It is based on the discrete exponent function in the cyclic algebraic group.
The security of this protocol relies on the Diffie–Hellman decisional problem, i.e., the problem of distinguishing between a valid shared key algebraically linked to a public keys of both parties and some randomly generated garbage value. To break this protocol, it is sufficient to solve a discrete logarithm problem (DLP), i.e., to invert a discrete exponential function. The other popular and more modern KEP, based on a similar method, called discrete exponent functions, in elliptic curve groups was briefly mentioned in [2] where N. Koblitz discusses analogues based on elliptic curves of then known public key cryptosystems. In analogy with DLP in cyclic groups, to break this protocol it is sufficient to solve a DLP problem in elliptic curve groups.
P. Shor proved that solving DLP in both cyclic and elliptic curve groups is efficient using quantum cryptanalysis algorithms [3], i.e., the solution can be found in polynomial time. Therefore, the traditional KEPs have no perspectives when sufficiently powerful computers appear.
Hence, the construction of post-quantum cryptographic primitives resistant to quantum cryptanalysis is currently an important field in modern cryptography research.
1.2. NP-Complete Problems and Post-Quantum Cryptography
It is known that nondeterministic polynomial complete (NP-Complete) problems, such as the three-satisfiability problem, is an uncrackable nut even for quantum computers since no quantum algorithms solving such problems in polynomial time are known. Therefore, the perspective trend in the construction post-quantum algorithms is cryptographic primitive creation based on NP-Complete problems.
The theory of NP-Complete problems is covered in detail in [4]. The definition of NP-Complete problem is the following [4]:
Definition 1.
A decisional problem is said to be NP-complete if and any problem is polynomially reducible to , i.e., there exists a function computed in polynomial time such that for all instances there exists a solution to if and only if there exists a solution to .
It has been proven that neither the DLP nor RSA problem mentioned above (used in the well-known Rivest–Shamir–Adleman cryptosystem [5]) are not in the NP-Complete complexity class. Moreover, quantum algorithms to solve these problems in polynomial time are known due to P. Shor [3].
For this reason, the scientific community began to search for a cryptographic primitives whose security relies on NP-Complete problems. In this connection the Hidden Field Equations (HFE) cryptosystems were described in [6]. The security of this approach was studied in papers [7,8,9] and several others. Another approach to build cryptographic primitives based on NP-Complete problems is described in [10] where lattice-based cryptography is covered.
As major traditional cryptosystems, these belong to commutative cryptography since their construction relies on commuting algebraic systems. Worth mentioning is the fact that successive attacks (using convenient computers) were described by various authors. In [8], several examples of successful subexponential attacks were presented. Authors of [7] discussed relinearization issue of HFE cryptosystem. Moreover, in [9] a research of Grobner basis application to solve HFE was proposed. Sensitivity of lattice-based signature schemes to fault attacks was considered in [11]. However, despite these facts, the investigation in this trend is continuing.
Together with the commutative approach, non-commutative cryptography is in developing phase. One direction was to use non-commuting algebraic structure, such as Braid groups. The conjectured hard problem with analogy to DLP was assumed to be a conjugacy search problem in non-commuting Braid groups. Some of the more infamous examples of such protocols are presented in [12,13]. However, a conjugacy search problem was not proven to be NP-Complete. Furthermore, V. Shpilrain proved that conjugacy search problem can be replaced by the other easier problem when dealing with Ko-Lee KAP and hence it not guarantee conjectured security [14].
1.3. Our Previous Contributions and Novelty of This Paper
Our research in this field relies on the properties of the so-called matrix power function (MPF). The idea behind the definition of MPF is somewhat similar to regular matrix multiplication. Over the years, several cryptographic protocols based on this function have been proposed. These include [15,16,17,18] and used commutative algebraic structures as a platform. In [15] the authors introduced the first key exchange protocol based on MPF. There, an approach of the authors was similar to W. Diffie and M. Hellman. However, the security of their protocol relied on a completely different problem as compared to [1]. Paper [16] focused on the application of MPF to the construction ofa substitution-box (S-box). This was the first attempt to apply MPF in symmetric cryptography. Later, the research of our team leaned to asymmetric cryptography and we published papers [17,18]. In those articles, we presented the asymmetric encryption algorithm and analysed its performance in embedded systems. Furthermore, we improved the security of our protocol in [19] and evaluated computational cost of protocol execution in elementary operations.
Consequently, protocols described in [15,17] were attacked using linear algebra in [20]. The authors of the latter paper showed that the system of matrix equations used to find the private key of Alice (or Bob) can be transformed to a system of linear equations and hence mentioned protocols can be broken in polynomial time. Eventually, we were able to evade this attack in our paper [21]. We also performed an investigation of public parameter generation issues in [22].
In their paper, [20] authors suggested interesting ideas to escape the linear algebra attack they described. One of these ideas was the application of non-commuting algebraic structures to construct the platform semigroup for MPF. Partly for this reason we turned our attention to exploring the realm of this particular type of algebraic structures which suit our needs. The first attempt to perform a successful key exchange using a non-commuting algebraic structure as a platform semigroup was presented in [23]. Furthermore, in [24] we have an asymmetric encryption scheme and have shown that it relies on an NP-Complete decisional problem. However, it is important to note that MPF defined over the so-called modified medial group is associative.
In this paper we recall one of the possible non-commuting groups to be used as a platform for MPF. Previous investigation of the properties of the MPF defined over the group presented in [25] has shown that we can construct cryptographic primitives using this group as a platform. Due to the properties of presented in that paper, we have to define templates for private session parameters. The novelty of our article is covered by the following facts:
- By applying properties of we construct a executable KEP despite the fact that in general MPF defined over considered group is not associative;
- The constrains of private session parameters come naturally from predefined templates. These constrains are used to limit the choice of private session parameters to non-invertible matrices only, thus preventing any attempts of a linear algebra attack.
- The security of our proposed key exchange protocol is based on NP-Complete decisional problem and satisfies the generalized decisional Diffie–Hellman assumption. The proof of NP-Completeness of the considered problem is the main goal of this article.
1.4. Application of Our Protocol in Real Life
A clear example of application of key exchange protocol in our everyday life is the https:// protocol which uses Secure Socket Layer (SSL) or Transport Layer Secrity (TLS) protocols in the transport layer. Particularly, these protocols are used in e-banking, e-government, e-business and other confidential communication systems. They provide secure channel realization between two parties, Alice and Bob. The main part of such a secure channel creation is KEP allowing to create a common symmetric secret key between the parties. This key is used for communication data encryption between Alice and Bob and is a secure channel itself. For KEP realization we use MPF based on platform semigroup which adds an additional security with respect to the traditional KEPs based on classical Diffie–Hellman approach. We show that this protocol satisfies the decisional Diffie–Helman assumption and the problem analogous to discrete logarithm problem relies on the solution of the NP-Complete problem.
1.5. Organization of the Paper
The rest of this paper is organized as follows: in Section 2 we present the non-commuting group to be used as a platform for our cryptosystem and revise the main function to be used in our construction; in Section 3 we define templates to be used for the construction and present a key exchange protocol together with the proof of its validity; in Section 4 we present the proof that our protocol relies on an NP-Complete problem. As usual, conclusions are presented in the last section.
2. Preliminaries
2.1. Description of the Modular Group of Order 16
Groups of order 16 were studied in detail mainly by H. Grundman, T. Smith and their co-authors. In papers [26,27], authors considered realizability of each of the groups of order 16 as a Galois group over a field of characteristics not 2. As authors pointed out in [26], the realizability of a 2-group over a field of characteristic 2 depends only on the minimal number of generators of . In their paper [27] authors examined, in total, fourteen distinct groups of order 16 and divided them into five commuting groups, two decomposable groups obtained by taking a direct product of two non-commuting groups of order 8 and seven indecomposable groups. One of the latter ones is the modular group of order 16, known by its notation as . Using two generators a and b the group is defined by the following relations:
Worthy of note is the fact that we are not concerned with the nature of generators a and b. As is a multiplicative group, our focus is on the powers of these generators and basic actions with the elements of the considered group.
As pointed out above, the index 16 indicates, there are exactly 16 distinct elements in the defined group. One of these is a neutral element . Note also that generators a and b do not commute. In fact, relying on the definition of , we have that and .
It also follows from the definition of that each element can be represented in two distinct forms: or . Hence we have to define a normal form of the element .
Definition 2.
The representation of element in the form is called a normal form of w.
It is important to note that we defined the form as normal and consider it throughout this paper. Evidently, our results remain valid if we switch to the opposite form of the elements.
Proposition 1.
Every element can be represented in a normal form.
Proof of Proposition 1.
Let us consider an element . If then the element w is in its normal form since obviously . Furthermore, if , then w is in its normal form . Obviously the normal form of element is .
Consider the case and . It follows from the definition of that equivalent elements can be written in the following way:
This ends the proof as any element of the form has an equivalent represented in a normal form regardless of the powers and k. □
We can now formulate as propositions the basic operations of . Since this group is multiplicative, we focus on the multiplication, powering and calculation of an inverse element. Note, that we are going to use powers and . We also keep in mind that powers of generator a are reduced modulo 8 and powers of generator b are reduced modulo 2 and hence omit modules in our expressions.
Proposition 2.
Given two elements and their product is calculated in the following way:
Proof of Proposition 2.
The case of is trivial since we obtain the first case of Formula (3) if is even and the second case of the same formula if is odd.
Let us assume that and is even. Then due to equality (2) we can rewrite the considered product as follows:
i.e., we obtained the first case of Formula (3).
Consider the last case, i.e., let and let be odd. Then similarly as before due to equality (2) we get:
Hence we have a third case of Formula (3). □
Proposition 3.
Given an element its n-th power is calculated in the following way:
where notation stands for integer part of .
Proof of Proposition 3.

The case of is trivial and hence we omit it, since we clearly obtain the first case of (4).
In the case of we can rewrite the power n using its binary representation as follows:
where . Then the n-th power of an element can be calculated in a following way:
It is now clear that for an even value of we can apply the so-called squaring algorithm presented above together with the equality (2). It is easy to check that no extra summands appear in this case. Hence we get second case of (4).
As for the latter case of formula (4), let us assume that and hence is odd. We consider the squaring algorithm together with the equality (2). Second and fourth powers of the element are calculated as follows:
since all the powers of the generator a are reduced modulo 8. Hence we can see, that an extra summand of 4 appears when rising to either second or sixth power. For odd values of n we can now use the squaring algorithm together with the second case of Formula (3) to obtain the extra summand of 4 when rising to third or seventh power.
Let us now consider the function .
We clearly see from Table 1, that the function indicates if the extra summand of 4 appears or not. This proves validity of Formula (4). □

Table 1.
Values of function .
Proposition 4.
Given an element , its inverse is calculated in the following way:
Proof of Proposition 4.
This is a special case of Proposition 3 where due to the following trivial identity:
This ends the proof. □
Further in our paper we use this group to define the structure of the base matrix to be used for key exchange based on the so-called matrix power function (MPF).
2.2. Description of MPF and Its Basic Properties
Over the last decade we presented several cryptographic primitives based on MPF. Formally this function is defined in the following way:
Definition 3.
Let entries of the base matrix W be chosen from a (semi)group and let entries of matrices X and Y be chosen from a ring , where τ is the maximum multiplicative order of the elements of . MPF is a mapping denoted in the following way:
where is a set of matrices defined over the specified set and entries of the value matrix E are calculated as follows:
We also call the multiplicative (semi)group a platform (semi)group and the ring -a power ring. Furthermore, we refer to W as a base matrix and to as power matrices.
Previously in our research, we mainly used commutative algebraic structures to define a platform (semi)group. Cryptographic security of such primitives as key exchange or asymmetric encryption was based on a problem of private data recovery, which we defined as follows:
Definition 4.
The MPF problem is to find matrices X and Y in (6) when given a base matrix W and an MPF value matrix E.
Furthermore, we apply constrains on power matrices X and Y to make this problem applicable to our goals. Usually these constrains were constructed by defining two sets of matrices using linear spans of publicly known matrices. Hence we demand that X and Y must be contained in appropriate linear spans. The simplest form of this linear span is
where is some fixed publicly known matrix. Example with more complicated linear span of matrices was presented in [21]. We also analyzed this linear span in greater detail in [22].
We can see, that this problem is based on the following property of MPF:
i.e., the order of actions in (6) does not matter. This can be easily shown for any commuting platform semigroup, which is used to define entries of matrices W and E. This result is also valid for the so-called modified medial semigroup. We have previously used this semigroup to construct a key exchange protocol. We have also shown, that obtaining a private key from Alice’s (or Bob’s) public key in an NP-complete problem.
However, the identity (7) in general does not hold in case of non-commuting platform semigroup as is in our case. Therefore we define the following functions:
Definition 5.
If the actions in MPF are performed from left to right, then we call this function the left-to-right MPF (LRMPF), i.e.,
Definition 6.
If the actions in MPF are performed from right to left, then we call this function the right-to-left MPF (RLMPF), i.e.,
It is clear that in case of commuting platform semigroup due to the property (7) as was in our previous research.
Furthermore, MPF defined over a commuting platform semigroup has the following properties:
However, these identities do not hold in the general case and hence the key exchange protocol, defined previously in [15] cannot be executed between Alice and Bob if the platform semigroup is non-commuting due to failure of properties (7), (10) and (11).
Nevertheless, we can use some facts from our previous research to establish a working key exchange protocol between Alice and Bob. To achieve this goal, we have previously considered the basic properties of the MPF defined over in [25]. Relying on the obtained conclusions and a specified form of the base matrix W we defined several possible templates for power matrices mainly focusing on the left side of (8). In this paper we focus on LRMPF and consider the matrix W to define a slightly different form of this matrix. We think that the new structure described in this paper makes an important contribution to the complexity of the so-called LRMPF problem. Furthermore we define an extra template for the right side power matrices, which cannot be ignored when executing the proposed protocol.
3. Key Exchange Protocol
3.1. Definition of Publicly Known Data
We start this section by defining the shared public parameter-a base matrix W to be used in the key exchange execution. The structure of this matrix is as follows:
Note that entries of each column of matrix W aside from the c-th one commute, whereas, in general, entries of matrix W do not commute. Note also that we fixed the parity of the powers of generators a and b in the first and last columns of matrix W, whereas the parity of other entries of this matrix is irrelevant. These facts are essential for defining the templates of the power matrices in our protocol.
The idea we shall use for constructing a key exchange protocol is based on the properties of the previously discussed in [25]. Our goal is to remove the non-commuting entries of the matrix W by calculating the public session parameter of the form (6), where are two power matrices defined over .
To achieve the desired result we fist define a template for the left side power matrices [25]:
Template 1.
Choose matrix X in (6) so that .
By applying this template we guarantee that the non-commuting entries are removed in all columns aside from the c-th one in the intermediate value , due to basic operations defined in . Furthermore, to eliminate the non-commuting entries of the only remaining column we define a template for the right side power matrices:
Template 2.
Choose matrix Y in (6) so that and .
The latter template will play an important role when considering the complexity of the so-called LRMPF problem, which is fundamental in the security analysis of our protocol.
3.2. Description of Our KEP
The setup of our protocol consists of random generation of the following publicly known data:
- Base matrix W defined over and having the structure (12);
- Power matrix L defined over and satisfying Template 1;
- Power matrix R defined over and satisfying Template 2.
Alice calculates her session parameters by executing the following steps:
- She chooses at random a vector of entries .
- Alice uses vector of scalars to calculate two matrices as polynomials of L and R respectively:
- She then uses the obtained values of X and Y to calculate matrix as follows:
Alice keeps secret and makes her public session parameter visible online.
Bob calculates his session parameters in a similar way:
- Bob generates a random vector of coefficients .
- He then uses these coefficients to calculate matrices U and V in a following way:
- He calculates matrix as follows:
Bob keeps vector of coefficients a secret and publishes online his public session parameter .
Alice and Bob can obtain a shared session key K by exchanging their public session keys and calculating the following expressions:
- Alice calculates ;
- Bob calculates .
Let us denote the set of matrices defined over by . Similarly we denote the set of matrices defined over by . Hence and . Moreover, let us denote the linear span of the matrices by . Analogously . All these sets can be viewed as public parameters pre-generated in advance. For more clarity we present a diagram of our protocol in Figure 1. We use the blue colour to refer to public parameters and the defined sets of matrices. We reserve the red colour for parameters which are kept secret. Public session keys of both parties are visible to everyone and hence we use green colour to denote this fact.
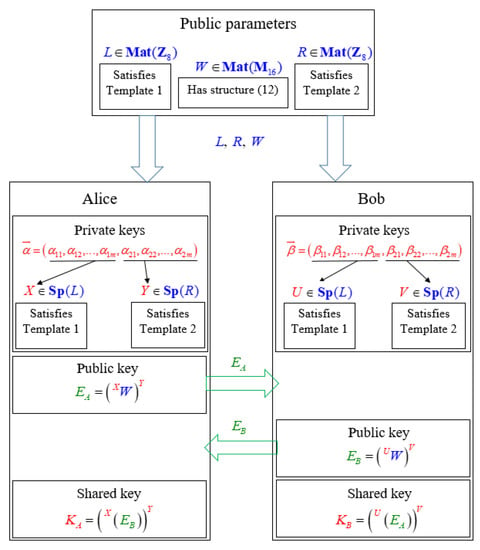
Figure 1.
Diagram of the presented key exchange protocol.
3.3. Proof of Validity of Our KEP
The validity of the proposed key exchange relies on several facts, presented here without proofs to shorten the paper:
Fact 1.
The polynomial structure of private matrices X and U preserves validity of Template 1.
Fact 2.
The polynomial structure of private matrices Y and V preserves validity of Template 2 in the following way:
- If (or ), then no extra terms are needed;
- If (or ), then an extra term needs to be added.
Fact 3.
The entries of matrix H in all the columns aside from the c-th one are various powers of the generator a.
Fact 4.
The entries of matrix , where matrix Y satisfies Template 2 are various powers of the generator a.
Fact 5.
Due to the defined templates and the latter two facts the consequent actions performed during the protocol execution are no different from regular MPF and hence we have:
Fact 6.
If the power matrices Y and V satisfy Template 2, then the following identity holds:
4. Complexity of LRMPF Problem
4.1. Definition of the LRMPF Decisional Problem
Algebraically breaking the presented key exchange is equivalent to solving at least one of the following systems of equations:
with constrains specified by Templates 1 and 2. These templates cannot be ignored, since otherwise the protocol falls apart due to failure of properties (13) and (14).
We can see that any knowledge about X and Y does not leak any information about U and V, since they are generated independently. Hence, systems (15) and (16) are unrelated to each other and can be considered separately. For this reason, we turn our attention to the recovery of Alice’s private matrices in (15), keeping in mind that the all the obtained results in this section are also true for Bob’s private matrices U and V.
In this section, we consider the complexity of solving the following problem, which is equivalent to a system of Equation (15):
Definition 7.
The decisional LRMPF problem is to determine if there is a pair of matrices and such that , where matrices W and are publicly known.
In other words, we wish to determine if the considered decisional problem can be solved in polynomial time by a deterministic Turing machine. Furthermore, we desire to determine if this problem can be reduced to any NP-Complete problem.
Let us define a reduction of this problem to its simplified form for a more convenient analysis. To achieve this goal we define a homomorphism which maps elements of multiplicative non-commuting group to additive commuting group .
4.2. Construction of an Homomorphism
To start with, we define a multiplicative commuting group of order 2 in a following way:
where g is a generator of the group. We can now define the following mapping :
Proposition 5.
Denoting the multiplication operation in by * for two arbitrary elements the following identity holds:
Proof of Proposition 5.
This fact follows directly from the definition of multiplication operation (3) in . More precisely, for any two arbitrary elements and we have:
where for the first two cases of Formula (3) and for the last case of this formula. Hence
However it is also true that
Hence homomorphic property (18) of defined mapping is proven. □
Moreover, we define the following trivial isomorphism which is called a discrete logarithm base g:
Finally, we define a homomorphism for an arbitrary element :
The defined mapping is clearly an homomorphism based on Proposition 5 and basic properties of a logarithm function. Furthermore, homomorphism can be used to represent parity of the generator .
4.3. Reduction of LRMPF Problem to Binary Matrix Multivariate Quadratic Problem
We now apply the defined homomorphism to matrices and in (15) entrywise. Hence we obtain binary matrices and such that:
Here and onward, we use the lower index b to indicate binary matrices.
Keeping in mind, that is an additive group we now have, that multiplication operation in switched to addition operation in . Furthermore, denoting the multiplication operation in by · and due to basic property of the discrete logarithm function for an arbitrary and an arbitrary power we have:
Hence all powering operations in have now been transformed to multiplications in .
Formally, the value of MPF in (15) can be defined as an element in certain non-associative semibimodule () [28]. It represents the left-right action of matrix semiring to the matrix semigroup . The semibimodule properties can be verified directly.
Let be some morphism from our defined to some , i.e., . Then for any and the following property should hold:
where ⊙ is a matrix Hadamard multiplication operation in , ⊕ is certain matrix Hadamard operation in and are right and left action operations of matrices and on the elements and respectively.
We define to be an matrix defined by homomorphisms in (19). Hence we have
Clearly, is acting on every element of W by homomorphism .
It follows from the definition that as we desired, where be a bimodule with action defined by matrices over the field to the product of matrices , , represented in the following way
where matrices , . Entries of matrices are computed using (19)–(21). The multiplication of matrices in (22) is computed in a regular way, reducing all the entries modulo 2.
Relying on the properties of homomorphism , the newly-defined mapping satisfies property (20), as desired. Note that operations are somewhat similar to regular multiplication of matrices with a non-standard addition action based on calculations of powers in expression (3) whereas non-standard multiplication action is based on expression (4). Furthermore, operation ⊕ is a non-standard matrix addition based on the expression (3).
It is also important to note, that due to reduction modulo 2 all the non-standard actions mentioned above become standard, since the non-commuting nature of is lost. Hence the property (20) is transformed as follows:
Hence, we have proven that
The expression (22) corresponds to some binary matrix multivariate quadratic problem (BMMQ) [24]. Consequently, by applying homomorphism defined by (19) we have reduced the initial decisional LRMPF problem to the following form:
Definition 8.
The decisional BMMQ problem is to determine if there exists a pair of matrices and satisfying the following equation defined over :
where binary matrices and are publicly known.
4.4. Proof of NP-Completeness of the LRMPF Decisional Problem
The BMMQ problem is a subproblem of defined above LRMPF problem. Due to homorphism mapping the LRMPF problem to the BMMQ problem, the answer “Yes” to the LRMPF problem implies answer “Yes” to the BMMQ problem. Hence to prove the NP-Completeness of the LRMPF problem it is sufficient to prove the NP-Completeness of the BMMQ problem [29].
Proposition 7.
Decisional BMMQ problem is NP-Complete.
Rather than presenting explicit proof of Proposition 7 we focus only on the sketch of it as the full proof is similar to the one presented in [24].
Sketch of proof of Proposition 7.
Since matrices L and R have to be binary while also satisfying Templates 1 and 2, we reduce these matrices to obtain matrices and respectively. We also reduce the templates modulo 2. Hence Templates 1 and 2 are modified in the following way for the binary case, see Templates 3 and 4.
Hence neither of power matrices are invertible making the following transformations impossible:
Previously, we have considered a problem similar to the one presented in Definition 8 in [24]. However, there we considered a circulant form of the power matrices X and Y. Using Schaeffer’s criteria [30] in their modified form, we have proven that constrained singular BMMQ problem is NP-Complete (see Theorem 2 of [24]). Similar observations can also be made for our case, i.e., decisional BMMQ problem does not satisfy any of the criteria specified in the Schaeffer’s dichotomy theorem [30], which states that then the satisfiability problem GSAT is in P if at least one of the following criteria is satisfied and is NP-Complete otherwise:
- (a)
- Every relation in S is satisfied when all the variables are 0 (0-valid clause);
- (b)
- Every relation in S is satisfied when all the variables are 1 (1-valid clause);
- (c)
- Every relation in S is definable by a CNF formula in which each conjunct has at most one negated variable (dual Horn clause);
- (d)
- Every relation in S is definable by a CNF formula in which each conjunct has at most one unnegated variable (Horn clause);
- (e)
- Every relation in S is definable by a CNF formula having at most two literals in each conjunct (bijunctive clause);
- (f)
- Every relation in S is the set of solutions of a system of linear equation over the two element field (affine clause).
Now all that remains is to check the inconsistency of each criterion explicitly. Note that the vector of unknowns which is considered in decisional BMMQ problem is the polynomial coefficient vector (or in Bob’s case) resulting in a system of multivariate quadratic (MQ) equations with unknowns. □
Template 3.
Choose binary matrix in (6) so that .
Template 4.
Choose binary matrix in (6) so that .
It is now clear that we have obtained a certain NP-Complete problem which is also a subproblem of the initial decisional LRMPF problem. Evidently we claim that:
Proposition 8.
The decisional LRMPF problem is NP-Complete.
Hence, we see that the security of the presented key exchange relies on an NP-Complete problem. Moreover, we think that the computational variant of this problem, i.e., finding at least one pair of matrices satisfying (15) is actually harder than finding a pair satisfying Templates 3 and 4 while also satisfying equation (24). This is due to the non-commuting nature of the platform group . However, intensive analysis of this assumption is needed thus far.
As mentioned previously, during the execution of this protocol, neither Alice nor Bob gain any information about each others’ session secrets, namely Alice cannot recover matrices U and V, whereas Bob is unable to determine matrices X and Y. Moreover, according to the proven result, it is now clear that the compromise of session secrets corresponds to the solution of an NP-Complete problem, so no adversary is able to compromise the agreed secret key if he is unable to solve the LRMPF decisional problem, which was proven to be NP-Complete. It is strong evidence that this cannot be done, since according to the current state-of-the-art, even quantum computers are unable to solve NP-Complete problems in polynomial time. Hence, only information described in Section 3.1 is available to Alice, Bob and adversaries.
5. Conclusions
In this paper, we defined a key exchange protocol using a non-commuting group as a platform group of MPF. However, since MPF in general is not associative if defined over a non-commuting platform group, the proposed cryptographic primitive can be executed only if extra constrains are used for the base and power matrices. The security of the presented key exchange is based on the complexity of the decisional LRMPF problem that is analogue to the well-known decisional Diffie–Hellman assumption.
Relying on the basic properties of the platform group and MPF, we defined a special form of base matrix W and two templates for left and right power matrices which are private session keys. Since, according to the derived templates, all power matrices have to be non-invertible, no transformations of the LRMPF problem to a linear system of equations are possible to perform a linear algebra attack. Hence, Templates 1 and 2 are the key factors to ensuring security of our KEP against such an attack.
We defined decisional LRMPF and BMMQ problems. Using modified Schaeffer criteria [30] we proved that BMMQ it is NP-Complete.
We found a homomorphic mapping of the LRMPF problem to the BMMQ problem, hence proving that BMMQ is a subproblem of the LRMPF problem. Then, according to common principle, if the BMMQ problem is NP-Complete, so is the LRMPF problem [29].
So, the security of our proposed key exchange protocol is based on the NP-Complete LRMPF decisional problem and satisfies the generalized decisional Diffie–Hellman assumption. Therefore, we can make a conjecture that, according to the recent development of quantum cryptanalysis, our protocol is not vulnerable to such kinds of attacks.
Author Contributions
The idea of this paper came from A.M. Accompanied by other coauthors of this paper he developed the methodology used in this paper. E.S. supervised this paper and made great contributions to the overall quality of the paper. K.L. provided the software for investigations together with A.M. Both authors performed investigations to ensure validity of the presented results. All three authors collected resources for this paper and validated the obtained results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Gawiejnowicz, S. -complete problems. In Models and Algorithms of Time-Dependent Scheduling; Springer: Berlin/Heidelberg, Germany, 2020; pp. 35–44. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Patarin, J. Hidden fields equations (HFE) and isomorphisms of polynomials (IP): Two new families of asymmetric algorithms. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1996; pp. 33–48. [Google Scholar]
- Kipnis, A.; Shamir, A. Cryptanalysis of the HFE public key cryptosystem by relinearization. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1999; pp. 19–30. [Google Scholar]
- Courtois, N.T. The security of hidden field equations (HFE). In Cryptographers’ Track at the RSA Conference; Springer: Berlin/Heidelberg, Germany, 2001; pp. 266–281. [Google Scholar]
- Faugere, J.C.; Joux, A. Algebraic cryptanalysis of hidden field equation (HFE) cryptosystems using Gröbner bases. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2003; pp. 44–60. [Google Scholar]
- Micciancio, D.; Regev, O. Lattice-based cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–191. [Google Scholar]
- Bindel, N.; Buchmann, J.; Krämer, J. Lattice-based signature schemes and their sensitivity to fault attacks. In Proceedings of the 2016 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Santa Barbara, CA, USA, 16 August 2016; pp. 63–77. [Google Scholar]
- Ko, K.H.; Lee, S.J.; Cheon, J.H.; Han, J.W.; Kang, J.S.; Park, C. New public-key cryptosystem using braid groups. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2010; pp. 166–183. [Google Scholar]
- Anshel, I.; Anshel, M.; Goldfeld, D. An algebraic method for public-key cryptography. Math. Res. Lett. 1999, 6, 287–292. [Google Scholar] [CrossRef]
- Shpilrain, V.; Ushakov, A. The conjugacy search problem in public key cryptography: Unnecessary and insufficient. Appl. Algebra Eng. Commun. Comput. 2006, 17, 285–289. [Google Scholar] [CrossRef]
- Sakalauskas, E.; Listopadskis, N.; Tvarijonas, P. Key agreement protocol (KAP) based on matrix power function. In Advanced Studies in Software and Knowledge Engineering; Information Science and Computing; Institute of Information Theories and Applications FOI ITHEA: Sofia, Bulgaria, 2008; pp. 92–96. [Google Scholar]
- Sakalauskas, E.; Luksys, K. Matrix power function and its application to block cipher s-box construction. Int. J. Inn. Comp. Inf. Contr. 2012, 8, 2655–2664. [Google Scholar]
- Mihalkovich, A.; Sakalauskas, E. Asymmetric cipher based on MPF and its security parameters evaluation. Proc. Lith. Math. Soc. Ser. A 2012, 53, 72–77. [Google Scholar]
- Mihalkovich, A.; Sakalauskas, E.; Venckauskas, A. New asymmetric cipher based on matrix power function and its implementation in microprocessors efficiency investigation. Elektronika ir Elektrotechnika 2013, 19, 119–122. [Google Scholar] [CrossRef]
- Sakalauskas, E.; Mihalkovich, A. New asymmetric cipher of non-commuting cryptography class based on matrix power function. Informatica 2014, 25, 283–298. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Jia, J. A linear algebra attack on the non-commuting cryptography class based on matrix power function. In International Conference on Information Security and Cryptology; Springer: Cham, Switzerland, 2016; pp. 343–354. [Google Scholar]
- Sakalauskas, E.; Mihalkovich, A. Improved Asymmetric Cipher Based on Matrix Power Function Resistant to Linear Algebra Attack. Informatica 2017, 28, 517–524. [Google Scholar] [CrossRef]
- Mihalkovich, A.; Levinskas, M. Investigation of Matrix Power Asymmetric Cipher Resistant to Linear Algebra Attack. In International Conference on Information and Software Technologies 2019; Springer: Cham, Switzerland, 2019; pp. 197–208. [Google Scholar]
- Sakalauskas, E. Enhanced matrix power function for cryptographic primitive construction. Symmetry 2018, 10, 43. [Google Scholar] [CrossRef]
- Sakalauskas, E.; Mihalkovich, A. MPF Problem over Modified Medial Semigroup Is NP-Complete. Symmetry 2018, 10, 571. [Google Scholar] [CrossRef]
- Mihalkovich, A. On the associativity property of MPF over M16. Proc. Lith. Math. Soc. Ser. A 2018, 59, 7–12. [Google Scholar] [CrossRef]
- Grundman, H.; Smith, T. Automatic realizability of Galois groups of order 16. Proc. Am. Math. Soc. 1996, 124, 2631–2640. [Google Scholar] [CrossRef]
- Grundman, H.G.; Smith, T.L.; Swallow, J.R. Groups of order 16 as Galois groups. Expo. Math 1995, 13, 289–319. [Google Scholar]
- Inassaridze, N.; Kandelaki, T.; Ladra, M. Categorical interpretations of some key agreement protocols. J. Math. Sci. 2013, 195, 439–444. [Google Scholar] [CrossRef][Green Version]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; Freeman: San Francisco, CA, USA, 1979; Volume 74. [Google Scholar]
- Schaefer, T.J. The complexity of satisfiability problems. In Proceedings of the Tenth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 1–3 May 1978; ACM: New York, NY, USA, 1978; pp. 216–226. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).