Chiral Oscillations and Spontaneous Mirror Symmetry Breaking in a Simple Polymerization Model
Abstract
1. Introduction
2. The Expanded APED Model
3. Bifurcation Analysis
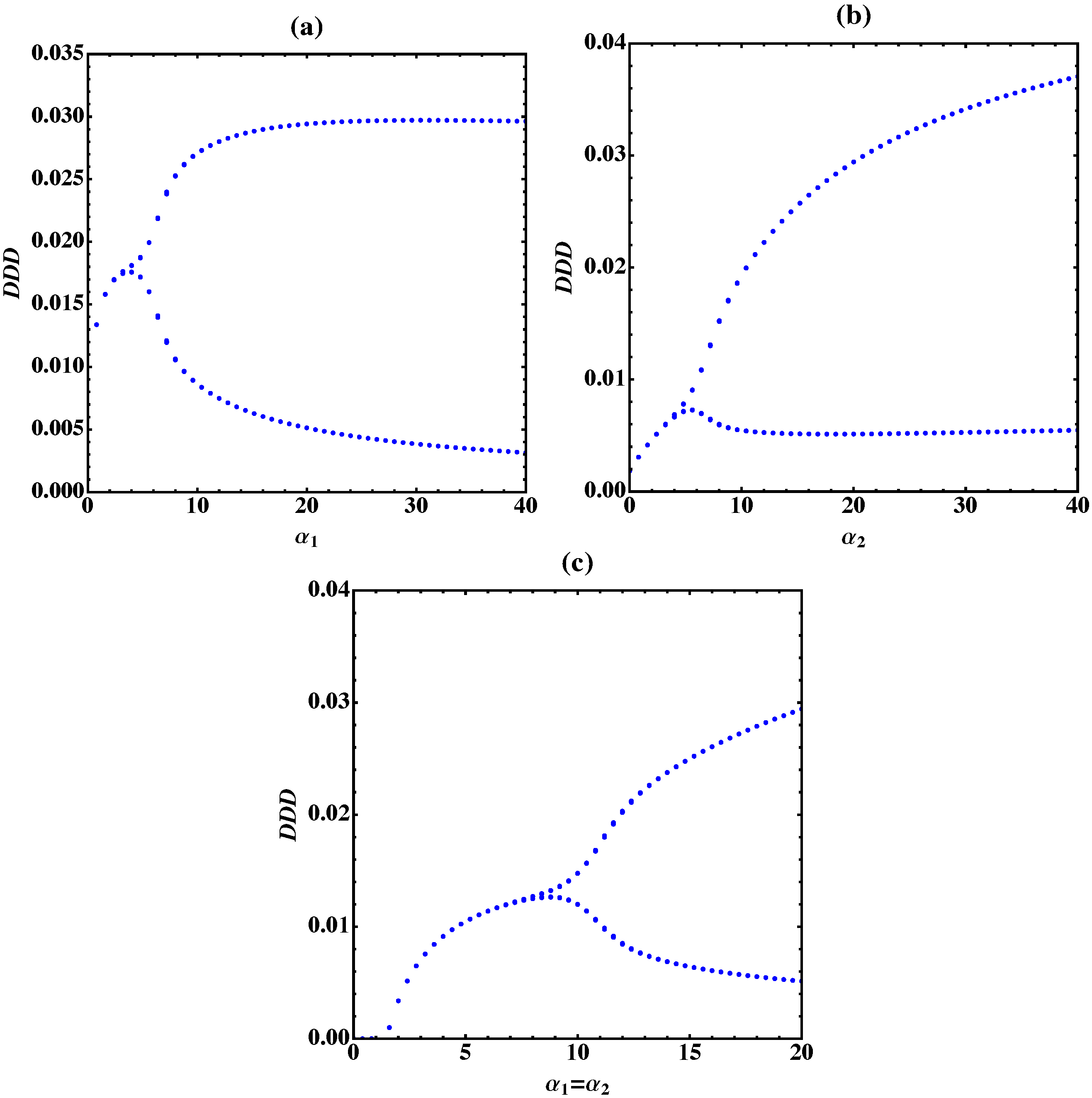
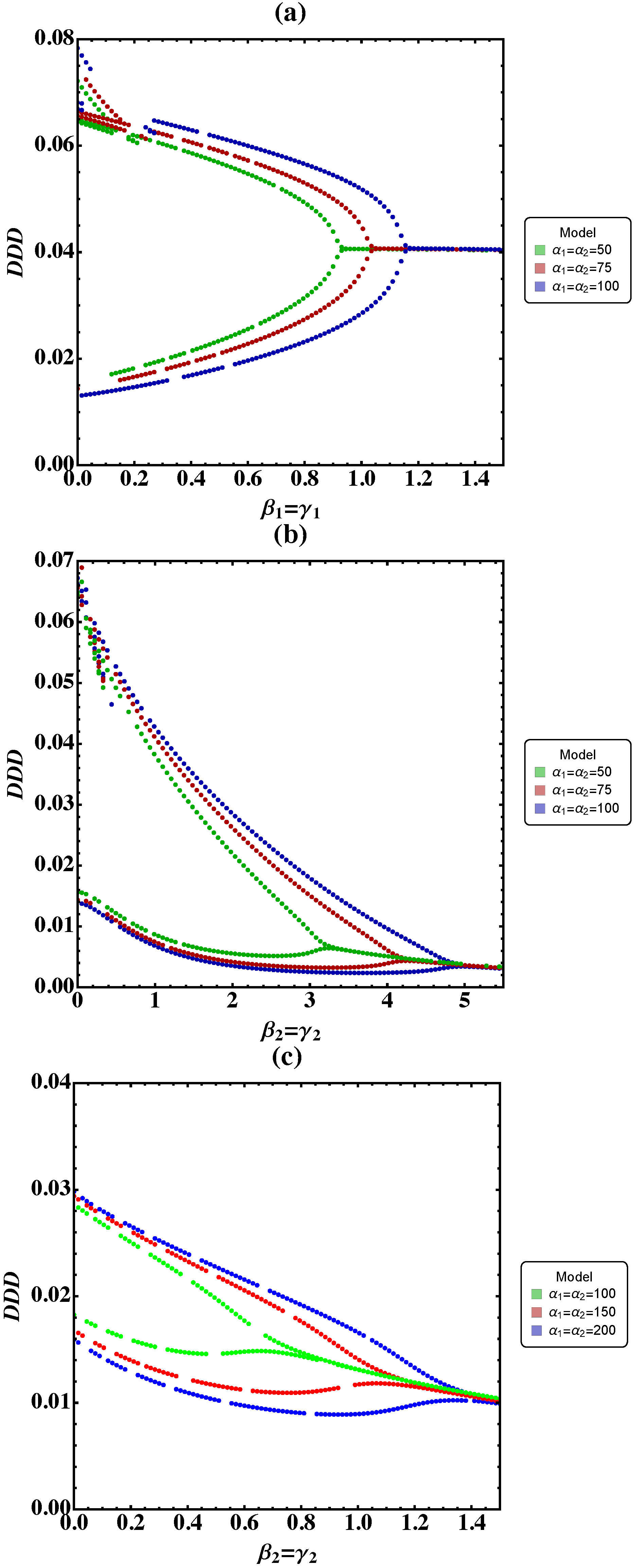
3.1. Trimer Model
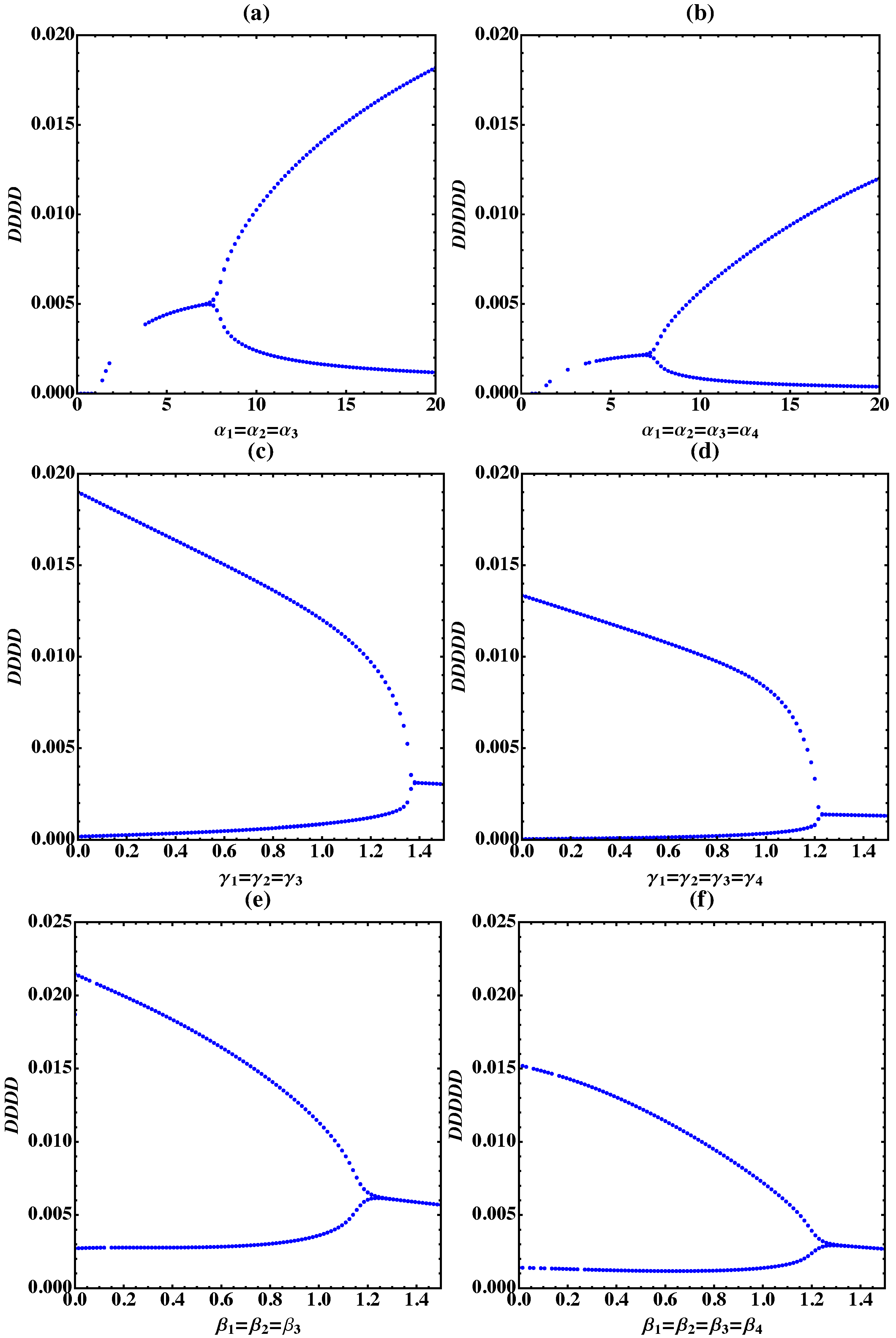
3.2. Tetramer and Pentamer Models
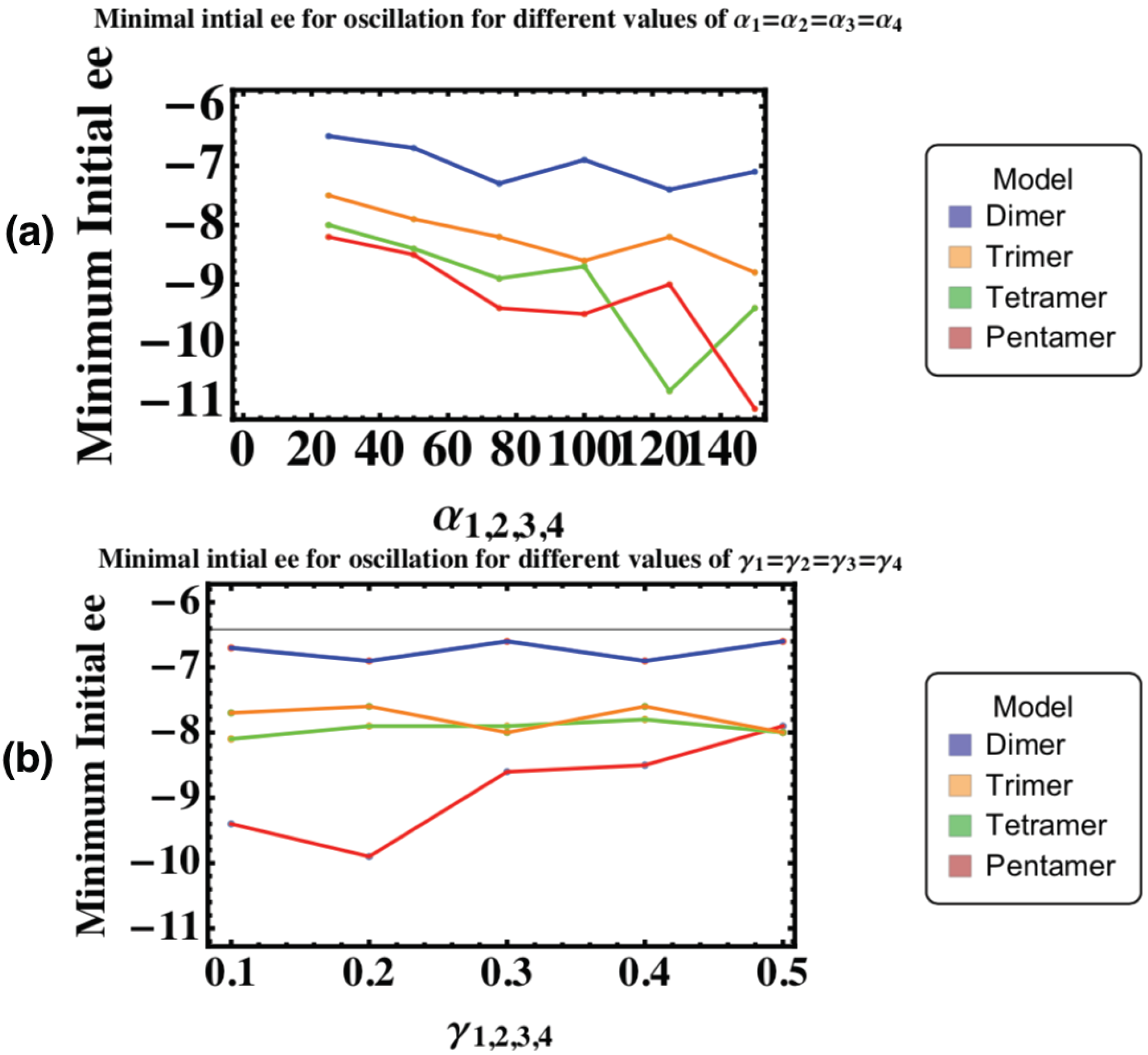
4. Minimum Initial Enantiomeric Excess
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frank, F.C. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta 1953, 11, 459–463. [Google Scholar] [CrossRef]
- Soai, K.; Shibata, T.; Morioka, H.; Choji, K. Asymmetric autocatalysis and amplification of enantiomeric of a chiral molecule. Nature 1995, 378, 767–768. [Google Scholar] [CrossRef]
- Ribo, J.M.; Hochberg, D. Stability of racemic and chiral steady states in open and closed chemical systems. Phys. Lett. A 2008, 373, 111–122. [Google Scholar] [CrossRef]
- Blackmond, D.G. Asymmetric amplification and its implications for the origin of homochirality. Proc. Natl. Acad. Sci. USA 2004, 101, 5732–5736. [Google Scholar] [CrossRef]
- Islas, J.R.; Lavabre, D.; Grevy, J.M.; Lamoneda, R.H.; Cabrera, H.R.; Micheau, J.C.; Buhse, T. Mirror-symmetry breaking in the Soai reaction: A kinetic understanding. Proc. Natl. Acad. Sci. USA 2005, 102, 13743–13748. [Google Scholar] [CrossRef]
- Sandars, P.G.H. A toy model for the generation of homochirality during polymerization. Orig. Life Evol. Biosph. 2003, 33, 575–587. [Google Scholar] [CrossRef]
- Brandenburg, A.; Anderson, A.C.; Höfner, S.; Nilsson, M. Homochiral growth through enantiomeric cross inhibition. Orig. Life. Evol. Biosph. 2005, 35, 225–241. [Google Scholar] [CrossRef]
- Brandenburg, A.; Anderson, A.C.; Höfner, S.; Nilsson, M. Dissociation in a polymerization model of homochirality. Orig. Life. Evol. Biosph. 2005, 35, 507–521. [Google Scholar] [CrossRef]
- Wu, M.; Walker, S.I.; Higgs, P.G. Autocatalytic replication and homochirality in biopolymers: Is homochirality a requirement of life or a result of it? Astro 2012, 12, 818–829. [Google Scholar] [CrossRef]
- Plasson, R.; Bersisni, H.; Commeyras, A. Recycling Frank: Spontaneous emergence of homochirality in noncatalytic systems. Proc. Natl. Acad. Sci. USA 2004, 48, 16733–16738. [Google Scholar] [CrossRef]
- Brandenburg, A.; Lehto, H.J.; Lehto, K.M. Homochirality in an early peptide world. Astro 2007, 7, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Stich, M.; Blanco, C.; Hochberg, D. Chiral and chemical oscillations in a simple dimerization model. Phys. Chem. Chem. Phys. 2013, 15, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Blanco, C.; Hochberg, D. Chiral polymerization: Symmetry breaking and entropy production in closed systems. Phys. Chem. Chem. Phys. 2011, 13, 839–849. [Google Scholar] [CrossRef] [PubMed]
- Sajewicz, M.; Gontarska, M.; Kronenbach, D.; Leda, M.; Kowalska, T.; Epstein, I.R. Condensation oscillations in the peptidization of phenylglycine. J. Syst. Chem. 2010, 1, 651–662. [Google Scholar] [CrossRef][Green Version]
- Danger, G.; Plasson, R.; Pascal, R. An experimental investigation of the evolution of chirality in a potential dynamic peptide system: N-terminal epimerization and degradation into diketopoperazine. Phys. Chem. Chem. Phys. 2010, 6, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, R.D.; Doty, P. Configurational and stereochemical effects in the amine-initiated polymerization of n-carboxy-anhydrides. J. Am. Chem. Soc. 1956, 78, 4810–4812. [Google Scholar]
- Bartlett, P.D.; Jones, R.H. A kinetic study of leuchs anhydrides in aqueous solution. J. Am. Chem. Soc. 1957, 79, 2153–2159. [Google Scholar] [CrossRef]
- Mauksch, M.; Tsogoeva, S.B. Life’s Single Chirality: Origin of Symmetry Breaking in Biomolecules. In Biomimetic Organic Synthesis; Poupon, E., Nay, B., Eds.; WILEY-VCH: Weinheim, Germany, 2011; Volume 2, pp. 823–846. [Google Scholar]
- Joyce, G.F.; Visser, G.M.; van Boeckel, C.A.A.; van Boom, J.H.; Orgel, L.E.; van Westrenen, J. Chiral selection in poly(C)-directed synthesis of oligo(G). Nature 1984, 310, 602–604. [Google Scholar] [CrossRef]
- Micskei, K.; Rabai, G.; Gal, E.; Caglioti, L.; Palyi, G. Oscillatory symmetry breaking in the Soai reaction. J. Phys. Chem. B 2008, 14, 9196–9200. [Google Scholar] [CrossRef]
- Sato, I.; Kadowaki, K.; Ohgo, Y.; Soai, K. Highly enantioselective autocatalysis induced by chiral ionic crystals of sodium chlorate and sodium bromate. J. Mol. Catal. A Chem. 2004, 216, 209–214. [Google Scholar] [CrossRef]
- Bonner, W.A.; Bean, B.D. Asymmetric photolysis with elliptically polarized light. Orig. Life Evol. Biosph. 2000, 30, 513–517. [Google Scholar] [CrossRef] [PubMed]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bock, W.; Peacock-López, E. Chiral Oscillations and Spontaneous Mirror Symmetry Breaking in a Simple Polymerization Model. Symmetry 2020, 12, 1388. https://doi.org/10.3390/sym12091388
Bock W, Peacock-López E. Chiral Oscillations and Spontaneous Mirror Symmetry Breaking in a Simple Polymerization Model. Symmetry. 2020; 12(9):1388. https://doi.org/10.3390/sym12091388
Chicago/Turabian StyleBock, William, and Enrique Peacock-López. 2020. "Chiral Oscillations and Spontaneous Mirror Symmetry Breaking in a Simple Polymerization Model" Symmetry 12, no. 9: 1388. https://doi.org/10.3390/sym12091388
APA StyleBock, W., & Peacock-López, E. (2020). Chiral Oscillations and Spontaneous Mirror Symmetry Breaking in a Simple Polymerization Model. Symmetry, 12(9), 1388. https://doi.org/10.3390/sym12091388





