Economic Segregation Under the Action of Trading Uncertainties
Abstract
1. Introduction
2. A Brief Excursion on Kinetic Modeling of Opinion Formation
3. Kinetic Modeling of Uncertain Trading Activity
4. Statistical Study of the Marginal Wealth Distribution
4.1. Literature Approaches
4.2. Bayesian Approach
5. Numerical Results Based on Markov Chain Monte Carlo
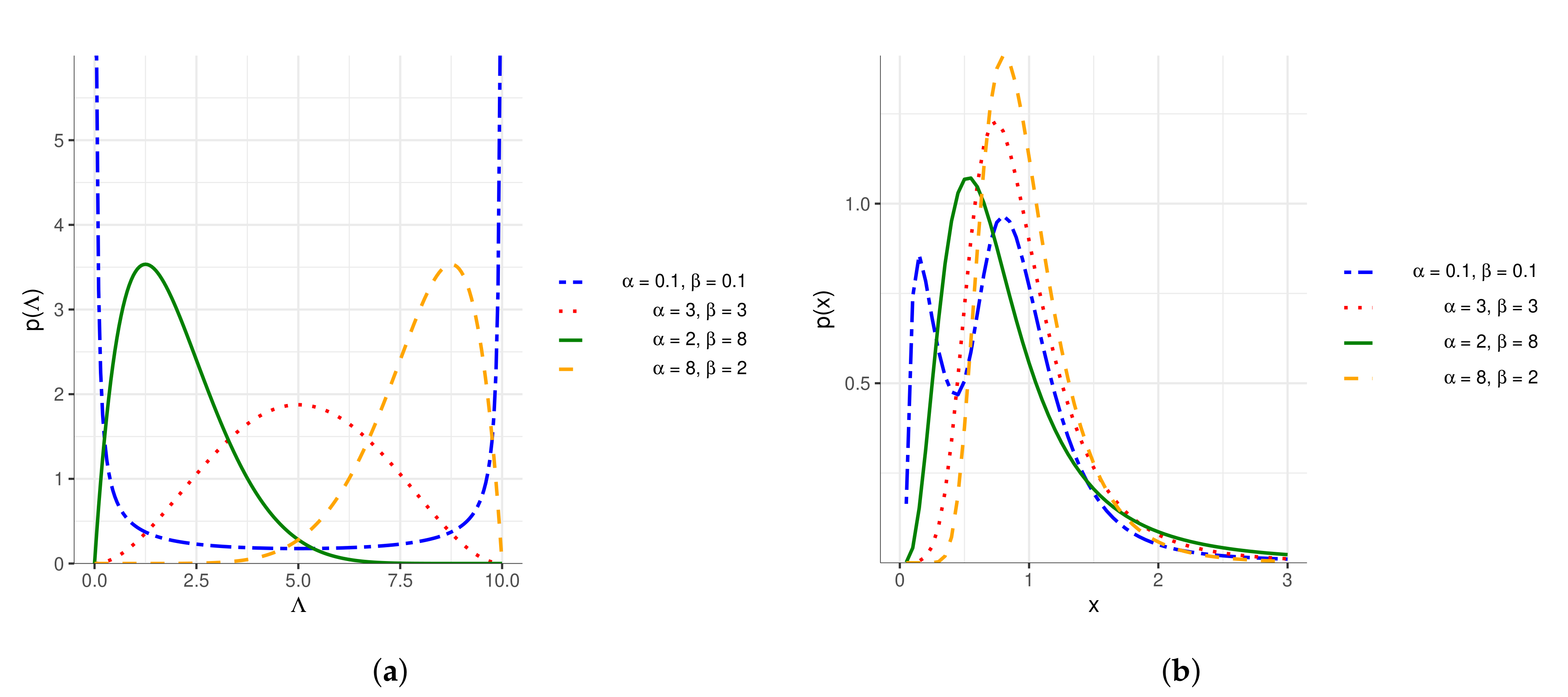
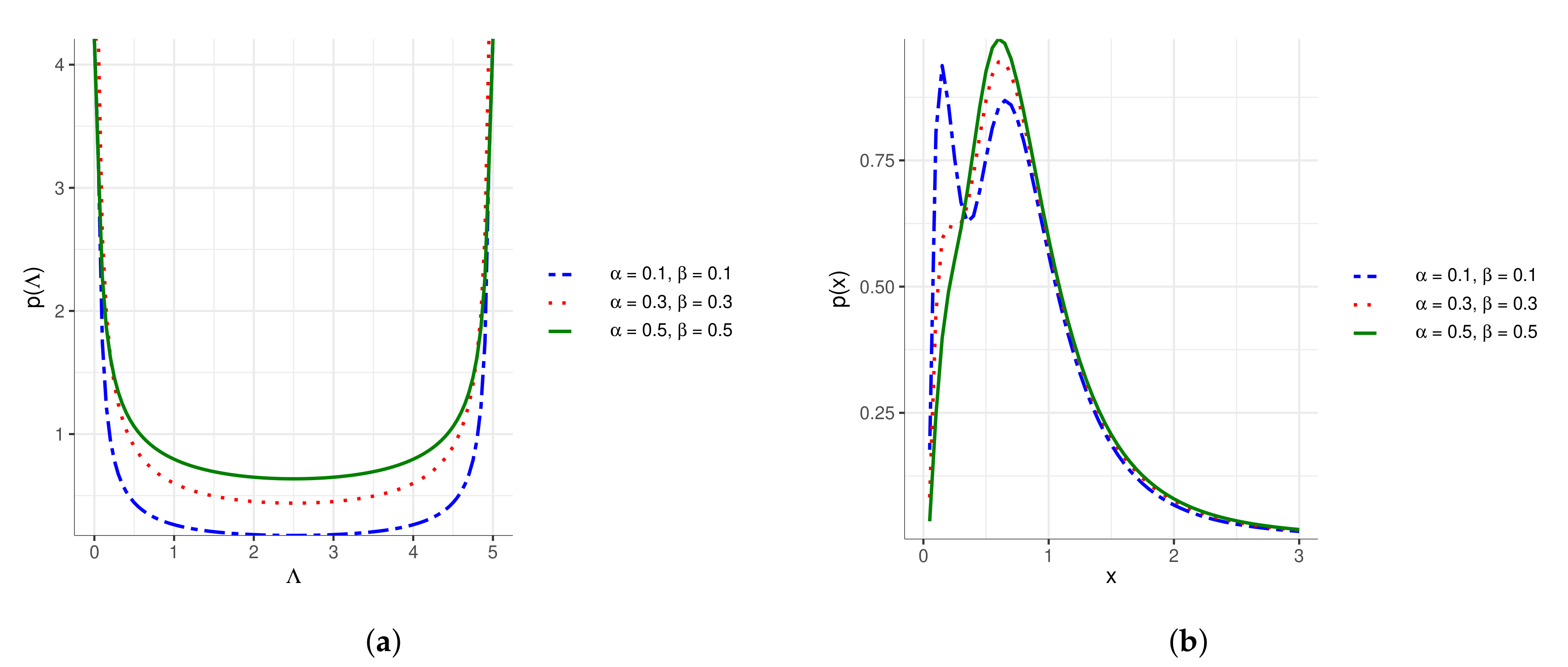
5.1. Estimation of the Marginal Function
- The support was shifted by 0.3 (which in the case of the function (27) is the value of the parameter ).
- The support was multiplied by a factor equal to 10 to highlight the shape of the wealth distribution.
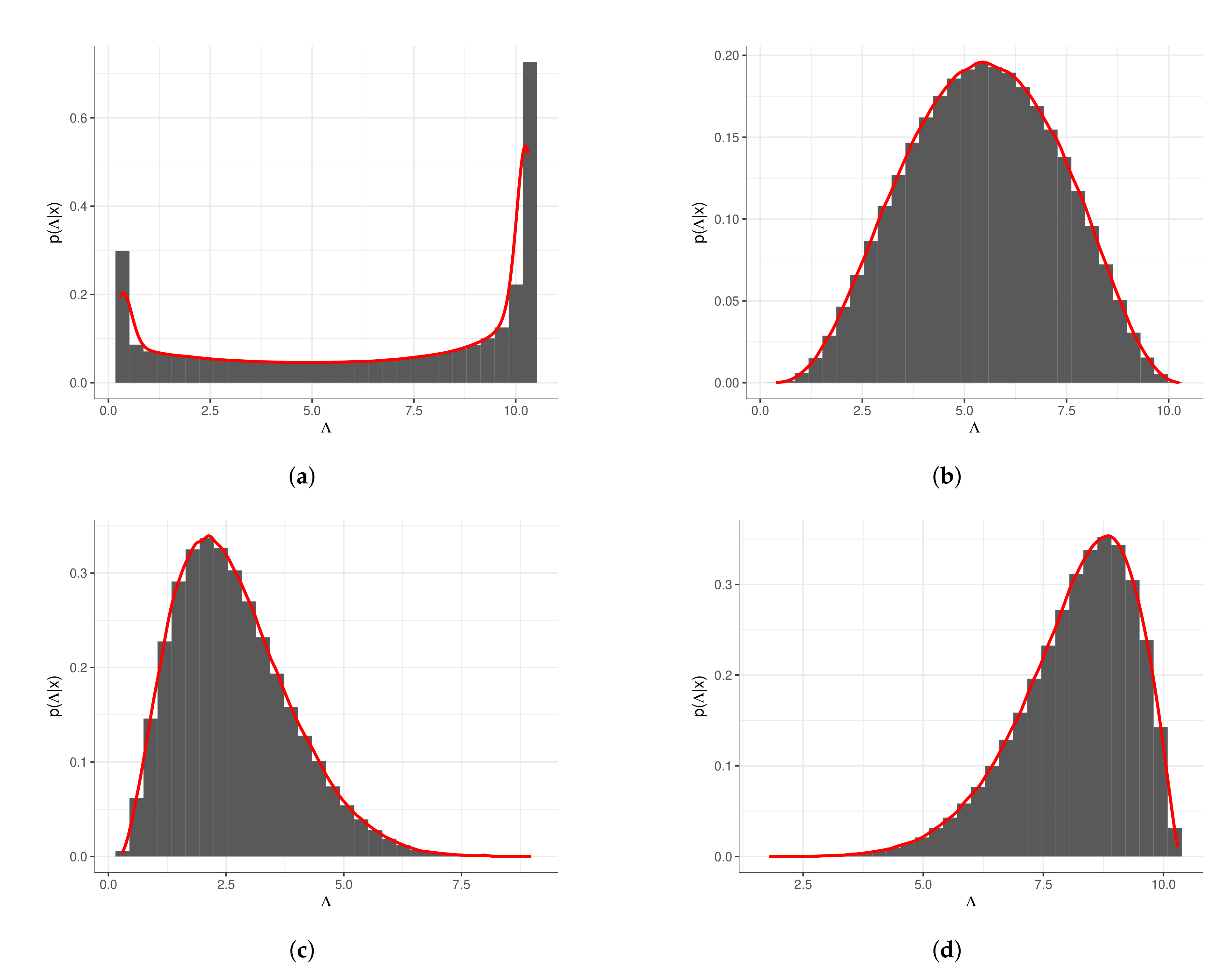
5.2. Estimation of the Posterior Function
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bassetti, F.; Toscani, G. Explicit equilibria in a kinetic model of gambling. Phys. Rev. E 2010, 81, 066115. [Google Scholar] [CrossRef] [PubMed]
- Bassetti, F.; Toscani, G. Explicit equilibria in bilinear kinetic models for socio-economic interactions. ESAIM Proc. Surv. 2014, 47, 1–16. [Google Scholar] [CrossRef]
- Bisi, M.; Spiga, G.; Toscani, G. Kinetic models of conservative economies with wealth redistribution. Commun. Math. Sci. 2009, 7, 901–916. [Google Scholar] [CrossRef]
- Cáceres, M.J.; Toscani, G. Kinetic approach to long time behavior of linearized fast diffusion equations. J. Stat. Phys. 2007, 128, 883–925. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chakrabarti, B.K.; Manna, S.S. Pareto law in a kinetic model of market with random saving propensity. Physica A 2004, 335, 155–163. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chakrabarti, B.K.; Stinchcombe, R.B. Master equation for a kinetic model of trading market and its analytic solution. Phys. Rev. E 2005, 72, 026126. [Google Scholar] [CrossRef]
- Chakraborti, A. Distributions of money in models of market economy. Int. J. Mod. Phys. C 2002, 13, 1315–1321. [Google Scholar] [CrossRef]
- Chakraborti, A.; Chakrabarti, B.K. Statistical mechanics of money: How saving propensity affects its distribution. Eur. Phys. J. B 2000, 17, 167–170. [Google Scholar] [CrossRef]
- Cordier, S.; Pareschi, L.; Piatecki, C. Mesoscopic modelling of financial markets. J. Stat. Phys. 2009, 134, 161–184. [Google Scholar] [CrossRef]
- Dragulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B 2000, 17, 723–729. [Google Scholar] [CrossRef]
- Düring, B.; Matthes, D.; Toscani, G. Kinetic equations modelling wealth redistribution: A comparison of approaches. Phys. Rev. E 2008, 78, 056103. [Google Scholar] [CrossRef] [PubMed]
- Düring, B.; Matthes, D.; Toscani, G. A Boltzmann-type approach to the formation of wealth distribution curves. Riv. Mat. Univ. Parma 2009, 8, 199–261. [Google Scholar] [CrossRef]
- Gupta, A.K. Models of wealth distributions: A perspective. In Econophysics and Sociophysics: Trends and Perspectives; Chakrabarti, A., Chakraborti, B.K., Chatterjee, A., Eds.; Wiley VHC: Weinheim, Germany, 2006; pp. 161–190. [Google Scholar]
- Ispolatov, S.; Krapivsky, P.L.; Redner, S. Wealth distributions in asset exchange models. Eur. Phys. J. B 1998, 2, 267–276. [Google Scholar] [CrossRef]
- Maldarella, D.; Pareschi, L. Kinetic models for socio–economic dynamics of speculative markets. Physica A 2012, 391, 715–730. [Google Scholar] [CrossRef]
- Matthes, D.; Toscani, G. On steady distributions of kinetic models of conservative economies. J. Stat. Phys. 2008, 130, 1087–1117. [Google Scholar] [CrossRef]
- Slanina, F. Inelastically scattering particles and wealth distribution in an open economy. Phys. Rev. E 2004, 69, 046102. [Google Scholar] [CrossRef] [PubMed]
- Toscani, G.; Brugna, C.; Demichelis, S. Kinetic models for the trading of goods. J. Stat. Phys. 2013, 151, 549–566. [Google Scholar] [CrossRef]
- Pareto, V. Cours d’Économie Politique; Librairie Droz: Geneva, Switzerland, 1964. [Google Scholar]
- Bassetti, F.; Toscani, G. Mean field dynamics of collisional processes with duplication, loss and copy. Math. Mod. Meth. Appl. Sci. 2015, 25, 1887–1925. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Fornasier, M.; Rosado, J.; Toscani, G. Asymptotic flocking dynamics for the kinetic Cucker-Smale model. SIAM J. Math. Anal. 2010, 42, 218–236. [Google Scholar] [CrossRef]
- Ha, S.-Y.; Jeong, E.; Kang, J.-H.; Kang, K. Emergence of multi-cluster configurations from attractive and repulsive interactions. Math. Models Methods Appl. Sci. 2012, 22, 1250013. [Google Scholar] [CrossRef]
- Kashdan, E.; Pareschi, L. Mean field mutation dynamics and the continuous Luria-Delbrück distribution. Math. Biosci. 2012, 240, 223–230. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Toscani, G. A kinetic description of mutation processes in bacteria. Kinet. Relat. Models 2013, 6, 1043–1055. [Google Scholar] [CrossRef]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Chakraborti, A.; Chakravarty, S.R.; Chatterjee, A. Econophysics of Income and Wealth Distributions; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Naldi, G.; Pareschi, L.; Toscani, G. Mathematical Modeling of Collective Behavior in Socio-Economic and Life Sciences; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pareschi, L.; Toscani, G. Interacting Multiagent Systems. Kinetic Equations & Monte Carlo Methods; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Sen, P.; Chakrabarti, B.K. Sociophysics: An Introduction; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Herty, M.; Tosin, A.; Visconti, G.; Zanella, M. Reconstruction of traffic speed distributions from kinetic models with uncertainties. In Mathematical Descriptions of Traffic Flow: Micro, Macro and Kinetic Models; Tosin, A., Puppo, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Piccoli, B.; Tosin, A.; Zanella, M. Model-based assessment of the impact of driver-assist vehicles using kinetic theory. arXiv 2019, arXiv:1911.04911. [Google Scholar]
- Tosin, A.; Zanella, M. Uncertainty damping in kinetic traffic models by driver-assist controls. arXiv 2019, arXiv:1904.00257. [Google Scholar]
- Tosin, A.; Zanella, M. Kinetic-controlled hydrodynamics for traffic models with driver-assist vehicles. Multiscale Model Simul. 2019, 17, 716–749. [Google Scholar]
- Furioli, G.; Pulvirenti, A.; Terraneo, E.; Toscani, G. Non-Maxwellian kinetic equations modeling the evolution of wealth distribution. Math. Models Methods Appl. Sci. 2020, 30, 685–725. [Google Scholar] [CrossRef]
- Bouchaud, J.F.; Mézard, M. Wealth condensation in a simple model of economy. Physica A 2000, 282, 536–545. [Google Scholar] [CrossRef]
- Cordier, S.; Pareschi, L.; Toscani, G. On a kinetic model for a simple market economy. J. Stat. Phys. 2005, 120, 253–277. [Google Scholar] [CrossRef]
- Bisi, M. Some kinetic models for a market economy. Boll. Unione Mat. Ital. 2017, 10, 143–158. [Google Scholar] [CrossRef]
- Düring, B.; Pareschi, L.; Toscani, G. Kinetic models for optimal control of wealth inequalities. Eur. Phys. J. B 2018, 91, 265. [Google Scholar] [CrossRef]
- Düring, B.; Toscani, G. Hydrodynamics from kinetic models of conservative economies. Physica A 2007, 384, 493–506. [Google Scholar] [CrossRef]
- Düring, B.; Toscani, G. International and domestic trading and wealth distribution. Commun. Math. Sci. 2008, 6, 1043–1058. [Google Scholar] [CrossRef]
- Torregrossa, M.; Toscani, G. Wealth distribution in presence of debts. A Fokker–Planck description. Commun. Math. Sci. 2018, 16, 537–560. [Google Scholar] [CrossRef]
- Bobylëv, A.V. The method of the Fourier transform in the theory of the Boltzmann equation for Maxwell molecules. Dokl. Akad. Nauk SSSR 1975, 225, 1041–1044. [Google Scholar]
- Cercignani, C. The Boltzmann Equation and Its Applications; Springer Series in Applied Mathematical Sciences; Springer: New York, NY, USA, 1988; Volume 67. [Google Scholar]
- Dolfin, M.; Leonida, L.; Outada, N. Modeling human behavior in economics and social science. Phys. Life Rev. 2017, 22–23, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Furioli, G.; Pulvirenti, A.; Terraneo, E.; Toscani, G. Fokker–Planck equations in the modelling of socio-economic phenomena. Math. Models Methods Appl. Sci. 2017, 27, 115–158. [Google Scholar] [CrossRef]
- Torregrossa, M.; Toscani, G. On a Fokker–Planck equation for wealth distribution. Kinet. Relat. Models 2018, 11, 337–355. [Google Scholar] [CrossRef]
- Toscani, G. Entropy dissipation and the rate of convergence to equilibrium for the Fokker–Planck equation. Quart. Appl. Math. 1999, LVII, 521–541. [Google Scholar] [CrossRef]
- Toscani, G.; Villani, C. Sharp entropy dissipation bounds and explicit rate of trend to equilibrium for the spatially homogeneous Boltzmann equation. Commun. Math. Phys. 1999, 203, 667–706. [Google Scholar] [CrossRef]
- Villani, C. A Review of Mathematical Topics in Collisional Kinetic Theory. In Handbook of Mathematical Fluid Dynamics; Friedlander, S., Serre, D., Eds.; Elsevier: New York, NY, USA, 2002; Volume 1. [Google Scholar]
- Albi, G.; Pareschi, L.; Zanella, M. Uncertainty quantification in control problems for flocking models. Math. Probl. Eng. 2015, 15, 850124. [Google Scholar] [CrossRef]
- Bellomo, N.; Colasuonno, F.; Knopoff, D.; Soler, J. From a systems theory of sociology to modeling the onset and evolution of criminality. Netw. Heterog. Media 2015, 10, 421–441. [Google Scholar] [CrossRef]
- Bellomo, N.; Herrero, M.A.; Tosin, A. On the dynamics of social conflicts looking for the Black Swan. Kinet. Relat. Models 2013, 6, 459–479. [Google Scholar] [CrossRef]
- Bellomo, N.; Soler, J. On the mathematical theory of the dynamics of swarms viewed as complex systems. Math. Models Methods Appl. Sci. 2012, 22, 1140006. [Google Scholar] [CrossRef]
- Gualandi, S.; Toscani, G. Pareto tails in socio-economic phenomena: A kinetic description. Economics 2018, 12, 1–17. [Google Scholar] [CrossRef]
- Gualandi, S.; Toscani, G. Human behavior and lognormal distribution. A kinetic description. Math. Models Methods Appl. Sci. 2019, 29, 717–753. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chakrabarti, B.K.; Manna, S.S. Money in gas-like markets: Gibbs and Pareto laws. Phys. Scr. 2003, 106, 36. [Google Scholar] [CrossRef]
- Lim, G.; Min, S. Analysis of solidarity effect for entropy, Pareto, and Gini indices on two-class society using kinetic wealth exchange model. Entropy 2020, 22, 386. [Google Scholar] [CrossRef]
- Patriarca, M.; Chakraborti, A.; Kaski, K.; Germano, G. Kinetic theory models for the distribution of wealth: Power law from overlap of exponentials. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 93–110. [Google Scholar]
- Patriarca, M.; Chakraborti, A.; Germano, G.O. Influence of saving propensity on the power-law tail of the wealth distribution. Physica A 2006, 369, 723–736. [Google Scholar] [CrossRef][Green Version]
- Ghosh, A.; Chatterjee, A.; Inoue, J.I.; Chakrabarti, B.K. Inequality measures in kinetic exchange models of wealth distributions. Physica A 2016, 451, 465–474. [Google Scholar] [CrossRef][Green Version]
- Ferrero, J.C. The monomodal, polymodal, equilibrium and nonequilibrium distribution of money. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Cernusco, Italy, 2005; pp. 159–167. [Google Scholar]
- Ferrero, J.C. The individual income distribution in Argentina in the period 2000–2009. A unique source of non stationary data. arXiv 2010, arXiv:1006.2057. [Google Scholar]
- Bellomo, N.; Bingham, R.; Chaplain, M.A.; Dosi, G.; Forni, G.; Knopoff, D.A.; Lowengrub, J.; Twarock, R.; Virgillito, M.E. A Multi-Scale Model of Virus Pandemic: Heterogeneous Interactive Entities in a Globally Connected World. Math. Mod. Meth. Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Dimarco, G.; Pareschi, L.; Toscani, G.; Zanella, M. Wealth distribution under the spread of infectious diseases. Phys. Rev. E 2020, 102, 022303. [Google Scholar] [CrossRef]
- Toscani, G. Kinetic models of opinion formation. Commun. Math. Sci. 2006, 4, 481–496. [Google Scholar] [CrossRef]
- Pareschi, L.; Toscani, G.; Tosin, A.; Zanella, M. Hydrodynamics models of preference formation in multi-agent societies. J. Nonlin. Sci. 2019, 29, 2761–2796. [Google Scholar] [CrossRef]
- Toscani, G.; Tosin, A.; Zanella, M. Opinion modeling on social media and marketing aspects. Phys. Rev. E 2018, 98, 022315. [Google Scholar] [CrossRef] [PubMed]
- Albi, G.; Pareschi, L.; Zanella, M. Opinion dynamics over complex networks: Kinetic modelling and numerical methods. Kinet. Relat. Models 2017, 10, 1–32. [Google Scholar] [CrossRef]
- Ben-Naim, E. Opinion dynamics: Rise and fall of political parties. Europhys. Lett. 2005, 69, 671–677. [Google Scholar] [CrossRef]
- Ben-Naim, E.; Krapivsky, P.L.; Redner, S. Bifurcation and patterns in compromise processes. Physica D 2003, 183, 190–204. [Google Scholar] [CrossRef]
- Ben-Naim, E.; Krapivsky, P.L.; Vazquez, F.; Redner, S. Unity and discord in opinion dynamics. Physica A 2003, 330, 99–106. [Google Scholar] [CrossRef]
- Weisbuch, G.; Deffuant, G.; Amblard, F. Persuasion dynamics. Physica A 2005, 353, 555–575. [Google Scholar] [CrossRef]
- Furioli, G.; Pulvirenti, A.; Terraneo, E.; Toscani, G. Wright–Fisher–type equations for opinion formation, large time behavior and weighted Logarithmic–Sobolev inequalities. Ann. IHP Anal. Non Linéaire 2019, 36, 2065–2082. [Google Scholar] [CrossRef]
- Villani, C. Contribution à L’étude Mathématique des Équations de Boltzmann et de Landau en théorie Cinétique des gaz et des Plasmas. Ph.D. Thesis, Univ. Paris-Dauphine, Paris, France, 1998. [Google Scholar]
- Villani, C. On a new class of weak solutions to the spatially homogeneous Boltzmann and Landau equations. Arch. Ration. Mech. Anal. 1998, 143, 273–307. [Google Scholar] [CrossRef]
- Tosin, A.; Zanella, M. Boltzmann-type models with uncertain binary interactions. Commun. Math. Sci. 2018, 16, 962–984. [Google Scholar] [CrossRef]
- Kac, M. Probability and Related Topics in the Physical Sciences; New York Interscience: London, UK, 1959. [Google Scholar]
- Carrillo, J.A.; Pareschi, L.; Zanella, M. Particle based gPC methods for mean-field models of swarming with uncertainty. Commun. Comput. Phys. 2019, 25, 508–531. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Pareschi, L.; Zanella, M. Monte Carlo gPC methods for diffusive kinetic flocking models with uncertainties. Viet. J. Math. 2019, 47, 931–954. [Google Scholar] [CrossRef]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; John Wiley and Sons: Chichester, UK, 2009. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrik 1970, 57, 97–109. [Google Scholar] [CrossRef]

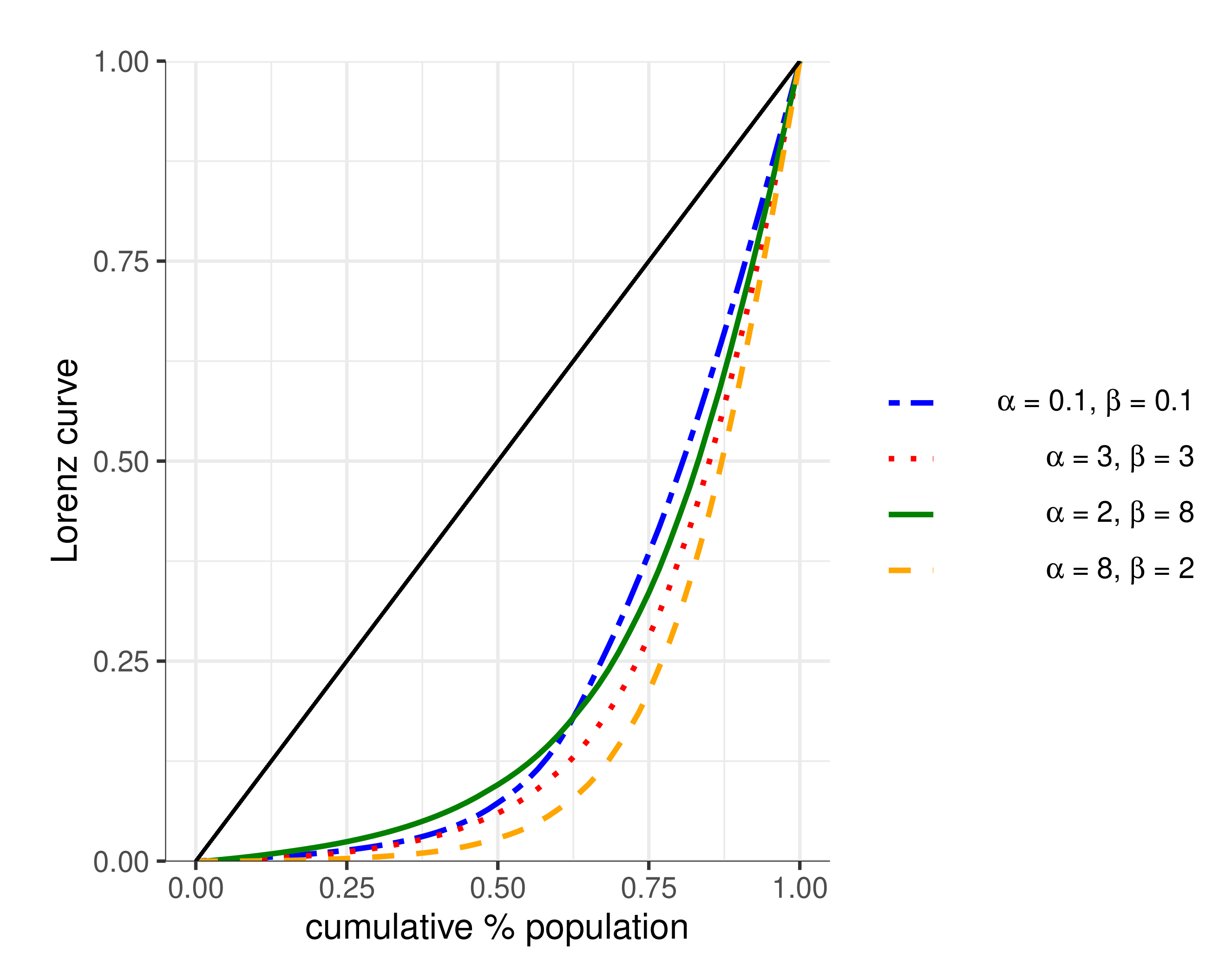
| Prior Parameters | Gini Index |
|---|---|
| , | 0.55 |
| , | 0.61 |
| , | 0.56 |
| , | 0.67 |
| Prior Parameters | Posterior Parameters |
|---|---|
| , | , |
| , | , |
| , | , |
| , | , |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballante, E.; Bardelli, C.; Zanella, M.; Figini, S.; Toscani, G. Economic Segregation Under the Action of Trading Uncertainties. Symmetry 2020, 12, 1390. https://doi.org/10.3390/sym12091390
Ballante E, Bardelli C, Zanella M, Figini S, Toscani G. Economic Segregation Under the Action of Trading Uncertainties. Symmetry. 2020; 12(9):1390. https://doi.org/10.3390/sym12091390
Chicago/Turabian StyleBallante, Elena, Chiara Bardelli, Mattia Zanella, Silvia Figini, and Giuseppe Toscani. 2020. "Economic Segregation Under the Action of Trading Uncertainties" Symmetry 12, no. 9: 1390. https://doi.org/10.3390/sym12091390
APA StyleBallante, E., Bardelli, C., Zanella, M., Figini, S., & Toscani, G. (2020). Economic Segregation Under the Action of Trading Uncertainties. Symmetry, 12(9), 1390. https://doi.org/10.3390/sym12091390






