Abstract
With the increasing automation of mechanical equipment, fault diagnosis becomes more and more important. However, the factors that cause mechanical failures are becoming more and more complex, and the uncertainty and coupling between the factors are getting higher and higher. In order to solve the given problem, this paper proposes a single-valued neutrosophic set ISVNS algorithm for processing of uncertain and inaccurate information in fault diagnosis, which generates neutrosophic set by triangular fuzzy number and introduces the formula of the improved weighted correlation coefficient. Since both the single-valued neutrosophic set data and the ideal neutrosophic set data are considered, the proposed method solves the fault diagnosis problem more effectively. Finally, experiments show that the algorithm can significantly improve the accuracy degree of fault diagnosis, and can better satisfy the diagnostic requirements in practice.
1. Introduction
With the development of automation technology, these mechanical machines gradually came into the stage of fully automated control operation [1,2,3,4,5]. In this way, people’s hands are comparatively free, and machines are more intelligent and comprehensive; however, this kind of full automation greatly increases the probability of mechanical equipment failure as well [6,7,8,9,10,11]. If the mechanical equipment has faults, the quality of the manufactured products will not pass the standard, which will affect the economic benefits of the enterprise [12,13,14,15]; additionally, it will bring potential danger to personal safety [16,17,18,19]. In order to solve this problem, it is necessary to carry out fault diagnosis on mechanical equipment on a regular basis to detect and repair mechanical equipment and ensure its normal operation.
1.1. Research Status
Therefore, the fault diagnosis of mechanical equipment has been widely concerned by many scholars, and has been applied in the military [20,22,23,24], medical [25,26,27,28], economic [29,30,31,32], and other fields. In ref. [33], looking at the problem of low efficiency of fault diagnosis of automobile exhaust system, based on a cold test, a fault diagnosis method is proposed for port vehicle exhaust system based on the principal component analysis. The variance contribution rate of principal component model is analyzed by the change of each variable of measurement data, and the fault diagnosis is achieved; In ref. [34], aiming at the problem of fault diagnosis of the data-driven system, a new diagnosis method based on Bayesian network (BN) combined with fault frequency is proposed to realize fault diagnosis; In ref. [35], based on the particle filter (PF) program, a dual estimation method is applied to fault diagnosis; In ref. [36], for the problem of bearing diagnosis under the condition of variable speed, the method of support vector machine and neural network is used for bearing fault diagnosis; On the basis of machine learning technology, a new depth neural network model with domain self-adaptability is proposed in ref. [37], which realizes fault diagnosis, but the selection of the best parameters of the model is random, and the application of the model is limited.
In the actual operating environment of mechanical equipment, fault information is usually inaccurate, incomplete and uncertain. It is difficult to use the above fault diagnosis method for deterministic analysis and processing of fault information. In order to deal with the uncertain and inaccurate information in the fault information, so as to better handle the fault information and get more accurate fault diagnosis results, Smarandache [38] proposed the theory of neutrosophic set from a philosophical point of view. It describes the uncertainty, imprecision, and inconsistent information in the objective world much better. The literature [39] introduced the theory of interval neutrosophic set and single-valued neutrosophic set; The literature [40] proposed the theory of simplified neutrosophic set; Literature [41] proposed a single-valued neutrosophic set SVNS method with a weighted correlation coefficient to realize fault diagnosis. However, the correlation coefficient does not comprehensively consider the single-valued neutrosophic set and ideal neutrosophic set data under various faults [42,43,44,45,46], only the maximum value between them is considered [47,48,49]. This does not completely deal with the uncertain and inaccurate information in the fault information, and may lead to an incorrect diagnosis.
1.2. Contribution of This Work
Based on the problems above, properly handling the uncertain information in the fault diagnosis process is an important goal to be achieved, however, complicated and changeable environmental information, the mutual influence between the factors causing the failure are difficult to handle. Due to neutrosophic set’s outstanding performance in handling uncertain information issues, this paper proposes a single-valued neutrosophic set ISVNS algorithm, which generates neutrosophic set by triangular fuzzy number and introduces the formula of the improved weighted correlation coefficient. In addition, the ISVNS algorithm comprehensively considers the single-valued neutrosophic set and ideal neutrosophic set data of various faults, so make it possible to analyze the data more comprehensively and make more accurate judgments. Finally, an example was used to diagnose the fault; the degree of accuracy of the fault diagnosis was calculated; the excellent productivity of the improved method, proposed in this paper was obtained by comparison. For the current difficulties in dealing with some uncertain issues, this method may have some enlightenment.
Due to the Overall Equipment Effectiveness (OEE) and the Overall labor effectiveness (OLE) are simple and practical production management tool, which has been widely used in European and American manufacturing and Chinese multinational companies. The global equipment efficiency index has become an important standard for measuring the production efficiency of enterprises, so it is also important to consider the proposed method’s impact on OEE and OLE. During the simulation process in the laboratory, the ratio of the operating hours and the planned working hours is relatively high; therefore, the fault can be repaired in a more timely manner based on the diagnosis result, and the OEE and the OLE can be improved.
The remainder of this paper is organized as follows. Section 2 briefly introduced triangular fuzzy numbers and single-valued neutrosophic sets. Section 3 proposed improved correlation coefficient between single-valued neutrosophic sets. In Section 4, a numerical example is given to fault diagnosis and fault diagnosis accuracy based on the proposed approach. Some conclusions are shown in Section 5.
2. Preliminaries
2.1. Triangular Fuzzy Numbers
About data sets , take its minimum value , average value , maximum value , so named as triangular fuzzy number [9] of this data set D, as shown in Figure 1:
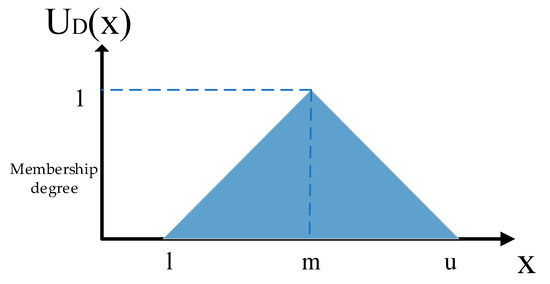
Figure 1.
Geometric Interpretation of Triangular Fuzzy Number.
It can be seen from the geometric interpretation of the triangular fuzzy number in the figure above:
If , so completely belongs to ;
If , so takes a certain degree of data set ;
If or , so completely does not belong to the data set .
And, for two triangle fuzzles and , have the following counting method:
2.2. Single-Valued Neutrosophic Sets
Neutrosophic set introduced by Smarandache [38] is an effective tool for solving the problems under complex environment. The definition of neutrosophic set is as follows.
Definition 1.
denote a space of points or objects, and each element of it is denoted as. A neutrosophic setinis characterized by a truth-membership function, an indeterminacy-membership functionand a falsity-membership function. ,andare real standard or non-standard subsets of,. That is:
For Formula (1), .
To facilitate the application of neutrosophic set in real scientific and engineering problems, the notion of SVNS was defined as follows.
Definition 2.
denote a space of points or objects, and each element of it is denoted as. A neutrosophic setinis characterized by a truth-membership function, a indeterminacy-membership functionand a falsity-membership function. If,andsatisfied:
then an SVNSincan be denoted as:
which is called an SVNS. Especially, ifincludes only one element,is called a single-valued neutrosophic number (SVN).
For any two SVNSs (, operational relations are defined as follows:
These are a series of common laws in operation for SVNSs.
Moreover, the assumption and operation requirements are as follows: Because ISVNS algorithm generates neutral set by triangular fuzzy number, the fault template data of each fault must be greater than or equal to 3.
3. The Proposed Method
3.1. Correlation Coefficient between Single-Valued Neutrosophic Sets
For any two neutrosophic sets and , the improved correlation coefficient is defined as follows:
In addition, the correlation coefficient for any and must satisfy the following three mathematical rules10:
For Formula (5), prove separately as follows:
- (1)
- According to the structural symmetry of the Formula (5), the condition is satisfied.
- (2)
- For each element in the Formula (5), they are satisfied , so obviously ; The proof of inequality as follows:And because of the inequality:Therefore, we can get:Therefore:There is:Finally, contacting the previous types, there are:In summary, the condition is satisfied;
- (3)
- If , so for any , all , , , we can see from the structure of Formula (5), .
In practical application, it is usually necessary to consider the weight of neutrosophic sets, so the weighted correlation coefficient of neutrosophic sets is given:
Among them, represents the weight of the fault template, and . In addition, the formula satisfies the three conditions of the formula and proves to be the same as the Formula (5), which is not repeated here.
3.2. Fault Diagnosis Method
Based on the above analysis, properly handling the uncertain information in the fault diagnosis process is an important goal to be achieved, however, complicated and changeable environmental information, the mutual influence between the factors causing the failure are difficult to handle. Due to neutrosophic set’s outstanding performance in handling uncertain information issues, this paper proposes a single-valued neutrosophic set ISVNS algorithm, which generates neutrosophic set by triangular fuzzy number and introduces the formula of the improved weighted correlation coefficient.
The objectives of the proposed algorithm are to rationally process the uncertain information in the diagnosis process, and obtain correct and reasonable fault diagnosis results from the fault data. Therefore, the laboratory simulation of the algorithm is carried out under the assumption that the actual fault is one of several known fault templates, the collected fault data is reasonable, and there is no major abnormality. The operating requirement is to collect fault data in a stable and equal time interval way. The detailed flow chart of the fault diagnosis method is shown in Figure 2:

Figure 2.
The detailed flow chart of the fault diagnosis method.
Step 1: For fault template set , and test sample set .
Firstly, three fuzzy numbers of fault template data and test sample data are generated, and the calculation method is as follows:
In a group number, the largest value is the right end value of the triangle; the minimum value is the left end-point of the triangle; the average value is the upper-end value of the triangle; the height of the triangle is 1, as shown in Figure 1.
Step 2: By comparing the three fuzzy number of each attribute of the test sample and the three fuzzy number of the same attribute of the fault template, the degree of determinacy-membership , the degree of non-membership , and the degree of indeterminacy-membership are obtained, as shown in Figure 3, and the calculation method is as follows:
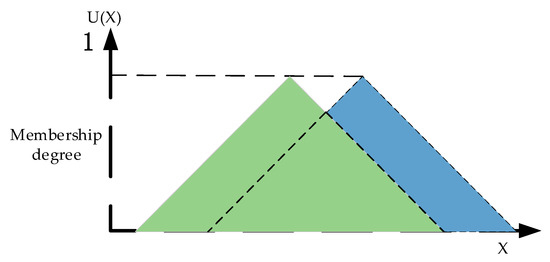
Figure 3.
Each degree of membership and neutrsophic set generate a schematic diagram.
: The ratio of the overlapping area of the analyzed sample triangular fuzzy number and the triangular fuzzy number of the fault template under a certain attribute, and the analyzed sample total area of the triangular fuzzy number;
: The ratio of the area of the part not overlapped with the fault template in the analyzed sample triangular fuzzy number to the total area of the analyzed triangular fuzzy number. Moreover, for each attribute, the sum of the non-membership degree and the determined membership degree is 1;
: The calculation of the indeterminacy-membership degree is as follows:
Among them, , , is the overlapping area of the analyzed sample triangular fuzzy number and the triangular fuzzy number of the fault template under the current attributes, is the area of the k fault triangular fuzzy number of the under the current attribute.
Finally, each degree of membership, the relationship of and is shown below:
Among them respectively denote the degree of determinacy-membership, the degree of non-membership, and the degree of indeterminacy-membership between and , also .
Step 3: can be expressed as single-valued neutrosophic set , at this point, a single-valued neutrsophic set decision matrix can be generated as follows:
Step 4: After obtaining the single-valued neutrosophic set decision matrix , the ideal single-valued neutrudophic number for attribute can be generated by column as follows:
Among them, respectively denote the maximum value of the jth column in , the minimum value of the jth column in , the minimum value of the jth column in .
Step 5: According to Formula (7), generated weighted correlation coefficient based on single-valued neutrsophic set decision matrix and the ideal single-valued neutrudophic number , the calculation formula is as follows:
Among them, represents the weight of the attribute, and ; denote single-valued neutrosophic set for attribute from decision matrix , denote the ideal single-valued neutrudophic number for attribute .
Step 6: Finally, sorting the of each analyzed sample, the largest value indicates that the template data belongs to this kind of fault.
4. Illustrative Example and Discussion
In this section, in order to demonstrate the validity and accuracy rate of the proposed method, an example of a motor rotor is used. The data in this paper is originated from ref. [11], and the data analysis software is the LABVIEW environment12.
4.1. Fault Diagnosis
The specific steps for fault diagnosis using the ISVNS method proposed in this paper are as follows:
- (i).
- According to the fault template data, the triangular fuzzy numbers under various attributes are obtained, in turn, as shown in Table 1:
 Table 1. Triangle fuzzy number of fault template.According to the analyzed sample data, the triangular fuzzy numbers under various attributes are obtained, in turn, as shown in Table 2:
Table 1. Triangle fuzzy number of fault template.According to the analyzed sample data, the triangular fuzzy numbers under various attributes are obtained, in turn, as shown in Table 2: Table 2. Triangular fuzzy numbers data of the analyzed sample.For the analyzed sample Xk ( represents the attribute), Xk and (where represent three kinds of faults) are used for matching, respectively. The neutrosophic numbers statistics generated by the determined-membership degree T, non-membership degree F, and indeterminacy-membership degree I, are calculated, as shown in Table 3:
Table 2. Triangular fuzzy numbers data of the analyzed sample.For the analyzed sample Xk ( represents the attribute), Xk and (where represent three kinds of faults) are used for matching, respectively. The neutrosophic numbers statistics generated by the determined-membership degree T, non-membership degree F, and indeterminacy-membership degree I, are calculated, as shown in Table 3: Table 3. The calculation result of the membership degree of the analyzed sample X.
Table 3. The calculation result of the membership degree of the analyzed sample X. - (ii).
- Next, for the same fault template, neutrosophic sets with different attributes under fuzzy sample X, we can get the single-valued neutrosophic decision matrix, as shown in Table 4:
 Table 4. Single-valued neutrosophic set decision matrix under sample X.
Table 4. Single-valued neutrosophic set decision matrix under sample X. - (iii).
- According to the single-valued neutrosophic set decision matrix and Formula (11) under sample X in Table 4, the ideal neutrosophic set can be obtained as follows:
- (iv).
- The weights of attributes are all the same, that is the weight matrix is as follows:Next, according to Table 4, Formula (7), (13), (14), for the fault template type () and the ideal single-valued neutrosophic set , calculate the improved weight correlation coefficient as follows:
- (v).
- Finally, according to Formula (15), , it can be seen that the analyzed samples X1-X4 belong to the first type of fault, namely, the X fault.
4.2. Fault Diagnosis Accuracy
To verify the accuracy of fault diagnosis, separately extract arbitrary 40 faults data from the three faults template [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]; These 120 faults data are used as a diagnosis template. Diagnose the fault type to which it belongs. Finally, compare each test sample with its original fault template [43,44], Calculate the overall accuracy of fault diagnosis.
The SVNPWA algorithm in ref. [44] is used for verifying these 120 unknown fault samples, and the diagnosis accuracy is 98.33%. Moveover, the ISVNS algorithm proposed in this paper also applied for diagnosing the same 120 unknown fault samples, and the diagnosis accuracy is 99.16%. The diagnosis results are shown in Table 5.

Table 5.
Diagnosis results of applying the SVNPWA and proposed algorithm.
It can be seen from Table 5: Compared with the SVNPWA algorithm, the fault diagnostic accuracy rate of the ISVNS algorithm, proposed in this paper, is improved by 0.83%. That is, the ISVNS algorithm can better satisfy the diagnostic needs than the basic SVNPWA algorithm.
5. Conclusions
This paper proposes an ISVNS algorithm, which introduces the improved weighted correlation coefficient formula, and more comprehensively considers both single-valued neutrosophic set and ideal neutrosophic set under various faults, effectively solved the problem of fault diagnosis. An example of a motor rotor is illustrated that the ISVNS algorithm could improve the diagnostic accuracy rate compared with the SVNPWA algorithm. In conclusion, the ISVNS algorithm can obtain better fault diagnosis accuracy, and satisfy the fault diagnosis needs in practice.
Since the collection and aggregation of data on technical faults is a laborious process. Moreover, the parameters in the diagnosis process are automatically generated in the laboratory simulation, without human intervention—therefore, the proposed method could be automating in practical application. Therefore, the next step of the work will focus on how to automating the proposed method in order to scale the use of the proposed algorithm.
Author Contributions
Conceptualization, W.J. and S.I.; methodology, W.J., S.I. and Y.Z.; validation, S.I.; formal analysis, W.J., S.I., Y.Z., X.D. and J.G.; writing—original draft preparation, S.I.; writing—review and editing, W.J., S.I., Y.Z., X.D. and J.G.; funding acquisition, W.J. All authors have read and agreed to the published version of the manuscript.
Funding
The work is partially supported by National Natural Science Foundation of China (Program No. 61703338), Equipment Pre-Research Fund (Program No. 61400010109), National Science and Technology Major Project (2017-I-0001-0001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Deng, X.; Zhang, Z.; Jiang, W. A new failure mode and effects analysis method based on dempster–shafer theory by integrating evidential network. IEEE Access 2019, 7, 79579–79591. [Google Scholar]
- Ma, Y.; Wang, J.; Wang, J.; Wu, X. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2017, 28, 2745–2765. [Google Scholar]
- Wei, G.; Zhang, Z. Some single-valued neutrosophic bonferroni power aggregation operators in multiple attribute decision making. J. Ambient. Intell. Humaniz. Comput. 2018, 10, 1–20. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar]
- Zhang, Y.; Jiang, W.; Deng, X. Fault diagnosis method based on time domain weighted data aggregation and information fusion. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. A total uncertainty measure for d numbers based on belief intervals. Int. J. Intell. Syst. 2019. [Google Scholar] [CrossRef]
- Han, C.; Shih, R.; Lee, L. Quantifying signed directed graphs with the fuzzy set for fault diagnosis resolution improvement. Ind. Eng. Chem. Res. 2010, 33, 1943–1954. [Google Scholar]
- Li, Y.; Shu, N. Transformer fault diagnosis based on fuzzy clustering and complete binary tree support vector machine. Trans. China Electrotech. Soc. 2016, 31, 64–70. [Google Scholar]
- Jiang, W.; Zhong, Y.; Deng, X. A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data. Symmetry 2018, 10, 346. [Google Scholar]
- Fu, C.; Chang, W.; Liu, W.; Yang, S. Data-driven group decision making for diagnosis of thyroid nodule. Sci. China Inf. Sci. 2019, 62, 212205. [Google Scholar]
- Xu, X.; Wen, C. Theory and Application of Multi-Source and Uncertain Information Fusion; Science Press: Beijing, China, 2012; pp. 98–108. [Google Scholar]
- Geng, J.; Ma, X.; Zhou, X.; Wang, S.; Yang, S.; Jiao, L. Saliency-Guided Deep Neural Networks for SAR Image Change Detection. IEEE Transactions on Geoence and Remote Sensing. Remote. Sens. Lett. 2019, 99, 1–13. [Google Scholar] [CrossRef]
- Sun, C.; Li, S.; Den, Y. Determining Weights in Multi-Criteria Decision Making Based on Negation of Probability Distribution under Uncertain Environment. Mathematics 2020, 8, 191. [Google Scholar] [CrossRef]
- Kandasamy, W.B.V.; Smarandache, I.; Neutrosophic, F. Components Semigroups and Multiset Neutrosophic Components Semigroups. Symmetry 2020, 12, 818. [Google Scholar]
- Yang, W.; Cai, L.; Edalatpanah, S.A.; Smarandache, F. Triangular Single Valued Neutrosophic Data Envelopment Analysis: Application to Hospital Performance Measurement. Symmetry 2020, 12, 588. [Google Scholar]
- Zhou, Q.; Mo, H.; Deng, Y. A New Divergence Measure of Pythagorean Fuzzy Sets Based on Belief Function and Its Application in Medical Diagnosis. Mathematics 2020, 8, 142. [Google Scholar] [CrossRef]
- Zhou, X.; Li, P.; Smarandache, F.; Khalil, A.M. New Results on Neutrosophic Extended Triplet Groups Equipped with a Partial Order. Symmetry 2019, 11, 1514. [Google Scholar] [CrossRef]
- Saber, Y.; Alsharari, F.; Smarandache, F. On Single-Valued Neutrosophic Ideals in Šostak Sense. Symmetry 2020, 12, 193. [Google Scholar] [CrossRef]
- Liu, B.; Deng, Y. Risk Evaluation in Failure Mode and Effects Analysis Based on D Numbers Theory. Int. J. Comput. Commun. Control. 2019, 14, 672–691. [Google Scholar]
- Caliskan, F.; Zhang, Y.; Wu, N.E.; Shin, J.-Y. Actuator Fault Diagnosis in a Boeing 747 Model via Adaptive Modified Two-Stage Kalman Filter. Int. J. Aerosp. Eng. 2014, 2014, 10. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Evaluating Green Supply Chain Management Practices under Fuzzy Environment: A Novel Method Based on D Number Theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. D number theory based game-theoretic framework in adversarial decision making under a fuzzy environment. Int. J. Approx. Reason. 2019, 106, 194–213. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W.; Wang, Z. Zero-sum polymatrix games with link uncertainty: A Dempster-Shafer theory solution. Appl. Math. Comput. 2019, 340, 101–112. [Google Scholar]
- Zieja, M.; Golda, P.; Zokowski, M.; Majewski, P. Vibroacoustic technique for the fault diagnosis in a gear transmission of a military helicopter. J. Vibroengineering 2017, 19, 1039–1049. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Broumi, S.; Kumar, A. Medical Diagnosis Based on Single-Valued Neutrosophic Probabilistic Rough Multisets over Two Universes. Symmetry 2018, 10, 213. [Google Scholar] [CrossRef]
- Jiang, W.; Cao, Y.; Deng, X. A Novel Z-network Model Based on Bayesian Network and Z-number. IEEE Trans. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Jiang, W. A correlation coefficient for belief functions. Int. J. Approx. Reason. 2018, 103, 94–106. [Google Scholar] [CrossRef]
- Oliveira, C.C.; da Silva, J.M. Fault Diagnosis in Highly Dependable Medical Wearable Systems. J. Electron. Test. 2016, 32, 467–479. [Google Scholar] [CrossRef]
- Strydom, J.J.; Miskin, J.J.; Mccoy, J.T.; Auret, L.; Dorfling, C. Fault diagnosis and economic performance evaluation for a simulated base metal leaching operation. Miner. Eng. 2018. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, L.; Jiang, W. Uncertainty measurement with belief entropy on the interference effect in the quantum-like Bayesian Networks. Appl. Math. Comput. 2019, 347, 417–428. [Google Scholar]
- He, Z.; Jiang, W. An evidential Markov decision making model. Inf. Sci. 2018, 467, 357–372. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Bearing Fault Diagnosis for Direct-Drive Wind Turbines via Current-Demodulated Signals. Ind. Electron. IEEE Trans. 2013, 60, 3419–3428. [Google Scholar]
- Ji, W.; Li, B. Fault Diagnosis Method of Exhaust System of Port Vehicle. J. Coast. Res. 2018, 83, 469–473. [Google Scholar]
- Askarian, M.; Zarghami, R.; Jalali-Farahani, F.; Navid, M. Fault Diagnosis of Chemical Processes Considering Fault Frequency via Bayesian Network. Can. J. Chem. Eng. 2016, 94, 2315–2325. [Google Scholar] [CrossRef]
- Daroogheh, N.; Meskin, N.; Khorasani, K. Particle Filter-Based Fault Diagnosis of Nonlinear Systems Using a Dual Particle Filter Scheme. IEEE Trans. Control Syst. Technol. 2016. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Khan, S.A.; KIM, J.-M. Incipient fault diagnosis in bearings under variable speed conditions using multiresolution analysis and a weighted committee machine. J. Acoust. Soc. Am. 2017, 142, EL35. [Google Scholar] [CrossRef]
- Lu, W.; Liang, B.; Cheng, Y.; Meng, D.; Yang, J.; Zhang, T. Deep Model Based Domain Adaptation for Fault Diagnosis. IEEE Trans. Ind. Electron. 2016, 64, 2296–2305. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis and Synthetic Analysis; American Research Press: Rehoboth, MI, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Proceedings of the 8th Joint Conference on Information Sciences. Joint Conference Information Science, Salt Lake City, UT, USA, 21–26 July 2005; pp. 94–97. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar] [CrossRef]
- Ye, J. Another Form of Correlation Coefficient between Single Valued Neutrosophic Sets and Its Multiple Attribute Decision-Making Method. Neutrosophic Sets Syst. 2013. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y. Weighted belief function of sensor data fusion in engine fault diagnosis. Soft Comput. 2020, 24, 2329–2339. [Google Scholar] [CrossRef]
- Xiao, F.; Ding, W. Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl. Soft Comput. 2019, 79, 254–267. [Google Scholar]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
- Gou, L.; Zhong, Y. A New Fault Diagnosis Method Based on Attributes Weighted Neutrosophic Set. IEEE Access 2019, 7, 117740–117748. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, C.; Deng, X. A new probability transformation method based on a correlation coefficient of belief functions. Int. J. Intell. Syst. 2019, 34, 1337–1347. [Google Scholar] [CrossRef]
- Broumi, S.; Nagarajan, D.; Bakali, A.; Talea, M.; Smarandache, F.; Lathamaheswari, M. The shortest path problem in interval valued trapezoidal and triangular neutrosophic environment. Complex Intell. Syst. 2019, 5, 391–402. [Google Scholar] [CrossRef]
- Broumi, S.; Nagarajan, D.; Bakali, A.; Talea, M.; Smarandache, F.; Lathamaheswari, M.; Kavikumar, J. Implementation of neutrosophic function memberships using matlab program. Neutrosophic Sets Syst. 2019, 27, 44–52. [Google Scholar]
- Chakraborty, A. A new score function of pentagonal neutrosophic number and its application in networking problem. Int. J. Neutrosophic Sci. 2020, 1, 40–51. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).