Preliminary Design and Cross-Sectional Form Study of Closed-Type Concrete-Filled Steel Tube Support for Traffic Tunnel
Abstract
:1. Introduction
2. Conceptual Design of Closed-Type CFST Support
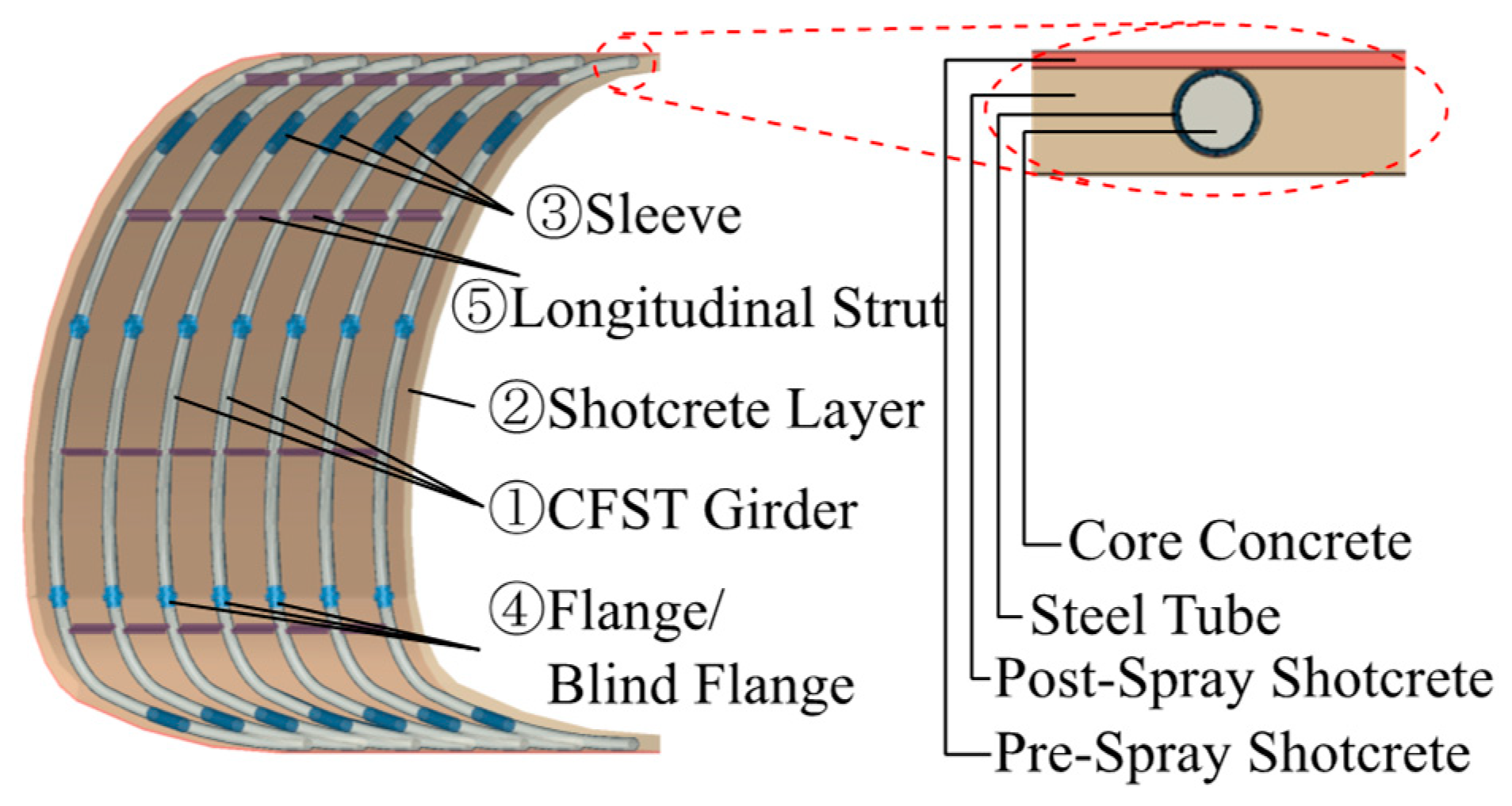
2.1. Basic Component of Closed-Type CFST Support
- CFST girder: The rigid skeleton and one of the main bearing parts of the supporting structure. It is formed by several sections of arc-shaped steel tubes filled with concrete, connected by casings, flanges, and other connecting parts. When the CFST girder is required to be installed section by section, the end of the girder should be connected with a flange and temporarily closed by a blind flange. After the core concrete is initially solidified, it can be connected to the steel tube of the next section after removing the blind flange.
- Shotcrete layer: Another main bearing part of the supporting structure. The shotcrete layer can make the support and the surrounding rock fit closely. The shotcrete layer is generally applied in two steps. The first layer of shotcrete has the function of stabilizing and protecting the surface of the surrounding rock in time, and at the same time acting as a force-transmitting coupling material between the CFST girder and the surrounding rock. The thickness of the first layer is generally not less than 4 cm. The second layer of shotcrete is applied after the initial solidification of the core concrete. The shotcrete should be sprayed in layers and sections, densely fill all of the gaps between the steel tube and the first shotcrete layer. The second layer should cover the entire supporting structure.
- Sleeves: The sleeves are the connecting part of the CFST girder. The length of the sleeve is generally about 1 m, and its wall thickness can be the same as or slightly thinner than the constrained steel tube. The sleeve connection will not block the flow of concrete inside the CFST girder, so it is not suitable for the connection of the construction joint.
- Flange/blind flange: Flange/blind flange is another kind of connection component. Unlike the sleeve, the flange can be temporarily blocked by adding a blind flange, so that the CFST girder can be filled with the core concrete in sections to match various tunnel construction methods.
- Longitudinal strut: The role of the longitudinal strut is to improve the integrity of the structure and the ability to resist out-of-plane loads. If the craftsmanship permits, the longitudinal strut can also be a CFST beam with a smaller diameter.
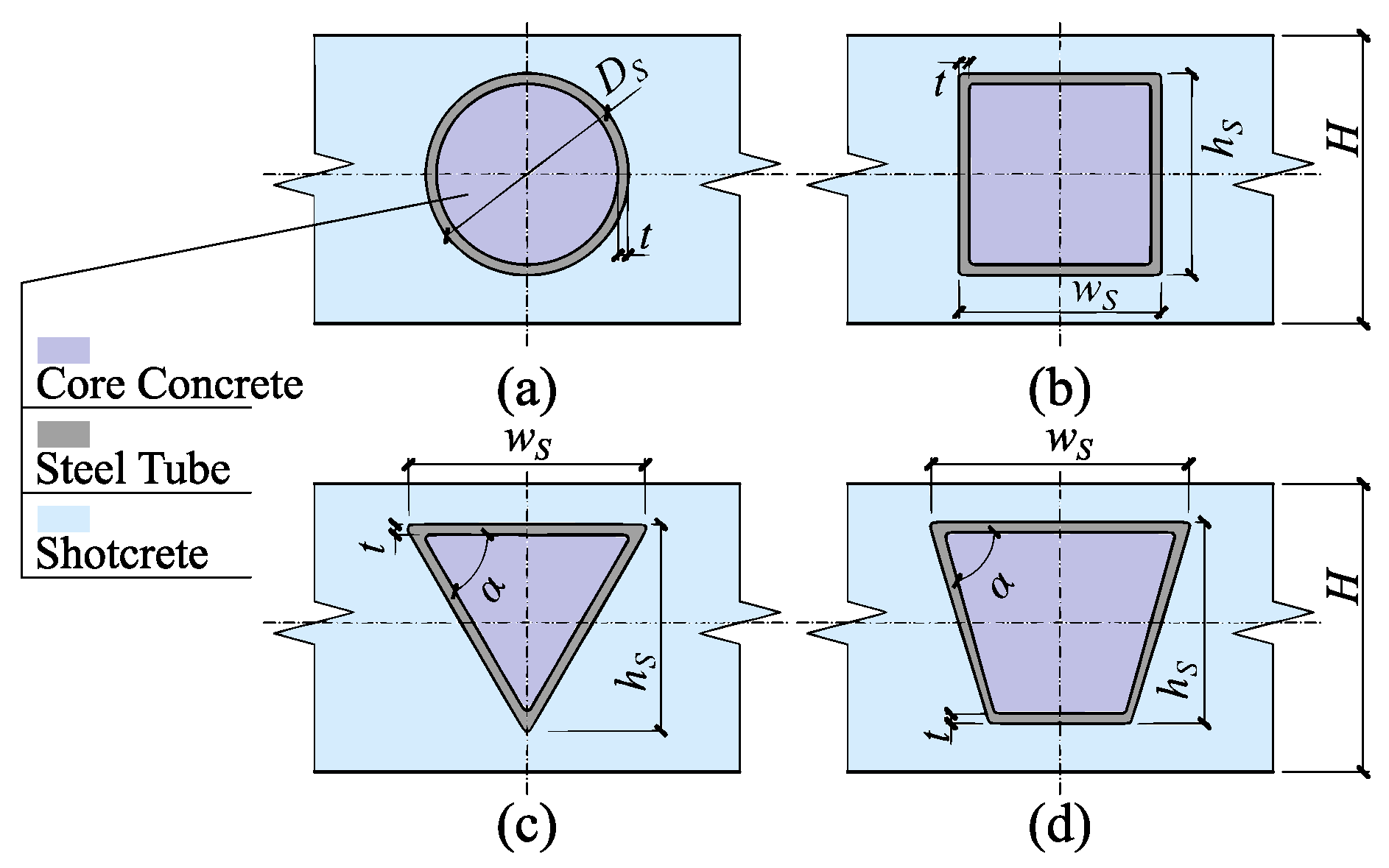
2.2. Cross-Sectional Form and Its Design Principles of Closed-Type CFST Support
- It should have reliable working performance under a compression or compression-bending force, and has the ability to resist bidirectional alternating bending. To fulfill this requirement, the section must have a certain tensile strength on both sides of the neutral axis. Therefore, the steel tube should have sufficient cross-sectional area on both sides of the neutral axis.
- At the initial stage of construction, it should be able to withstand the surrounding rock load through the presprayed shotcrete layer, which means the steel tube should have a sufficiently large contact area with the presprayed shotcrete layer.
- The steel tube and the shotcrete should have good cooperative performance and constructability. So, the shape of the steel tube should not cause excessive dead angles when spraying the shotcrete, in order to ensure the compactness of shotcrete.
- Has a certain ability to resist out-of-plane loads and torsional effects.
- Circular-shaped: The circular-shaped CFST has the best restraining effect on the core concrete, and it has the same bending resistance in all directions. Its ability to resist torsion and resist local buckling is also excellent. In addition, the circular steel tube and its accessories are easy to obtain, so the application of circular-shaped CFST is the most extensive. However, the circular-shaped CFST also have the disadvantages of relatively large dead space for shotcrete spraying.
- Rectangular-shaped: Like the circular-shaped CFST, the rectangular-shaped CFST also has excellent torsional resistance. The biggest advantage of the rectangular-shaped CFST compared to the circular-shaped is that it has a larger contact area with the presprayed shotcrete, so its early bearing performance will be better, theoretically. However, some studies have pointed out that the restraining effect of the square steel tube is less obvious, and the stress is unevenly distributed along the tube wall, which is prone to stress concentration and local buckling instability. Moreover, the manufacturing difficulty of the rectangular-shaped CFST is also higher than that of circular-shaped CFST.
- Triangular-shaped: The triangular-shaped CFST is similar to the three-legged lattice girder commonly used in tunnel support. Its main advantages are that the steel utilization rate is much higher than other forms of steel tube. Theoretically, it is easier to ensure the compactness of shotcrete. However, the bending resistance in different directions of triangular-shaped CFST is different, which is not ideal for the tunnel support that alternately undergoes bidirectional bending. In addition, there are few studies on the application of triangular-shaped CFST, so its mechanical properties are still in doubt. The difficulty of steel tube processing and concrete pouring of the triangular-shaped CFST is also likely to be higher than other cross-sectional forms.
- Trapezoid-shaped: Trapezoid-shaped is a cross-sectional form between rectangular and triangular, and has the advantages of both. The concept of trapezoidal-shaped CFST is similar to U-shaped and D-shaped CFST, so it can actually be regarded as the same type. Theoretically, the well-designed trapezoidal-shaped CFST may get an excellent balance between performance and economy. However, the trapezoidal-shaped CFST also has many problems. First, the trapezoidal-shaped steel tube is more difficult to manufacture. Second, the design of the trapezoidal-shaped CFST lacks experienced guidance.
3. Research Plan of Cross-sectional Form Selection
3.1. Finite Element Model
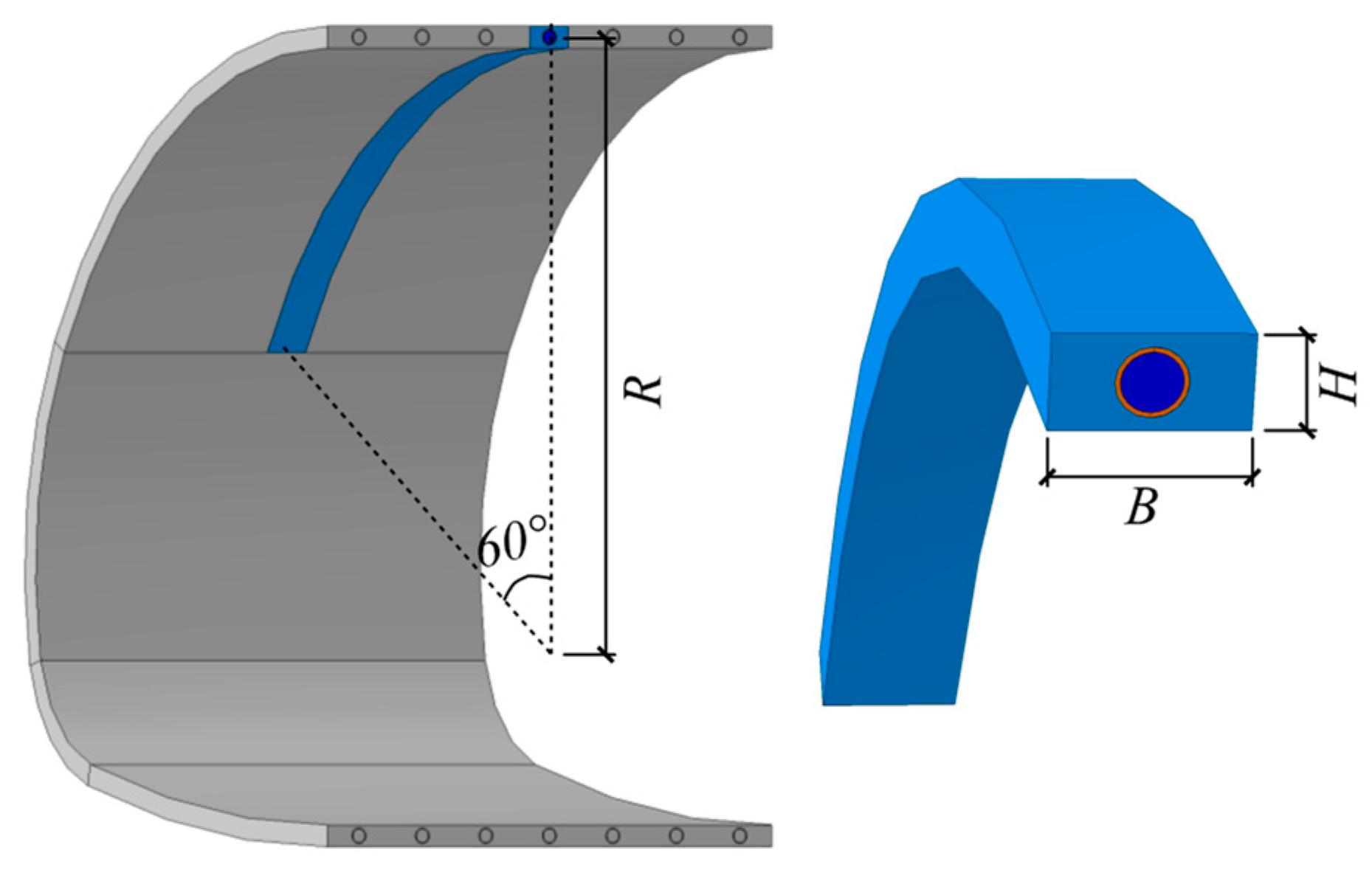
3.1.1. Abstraction of Primary Support
3.1.2. Model and Mesh Discretization
- The 8-node linear solid elements (C3D8R) were used throughout the model.
- The core concrete, steel tube, and shotcrete were meshed respectively.
- The steel tube (or the profile steel girder) had an approximate grid size of 10 mm on its cross-section and 50 mm along its axis.
- The core concrete had an approximate grid size of 8~20 mm on its cross-section and 40 mm along its axis.
- The shotcrete had an approximate grid size of 15 mm on its cross-section and 80 mm along its axis.
3.1.3. Boundary Conditions
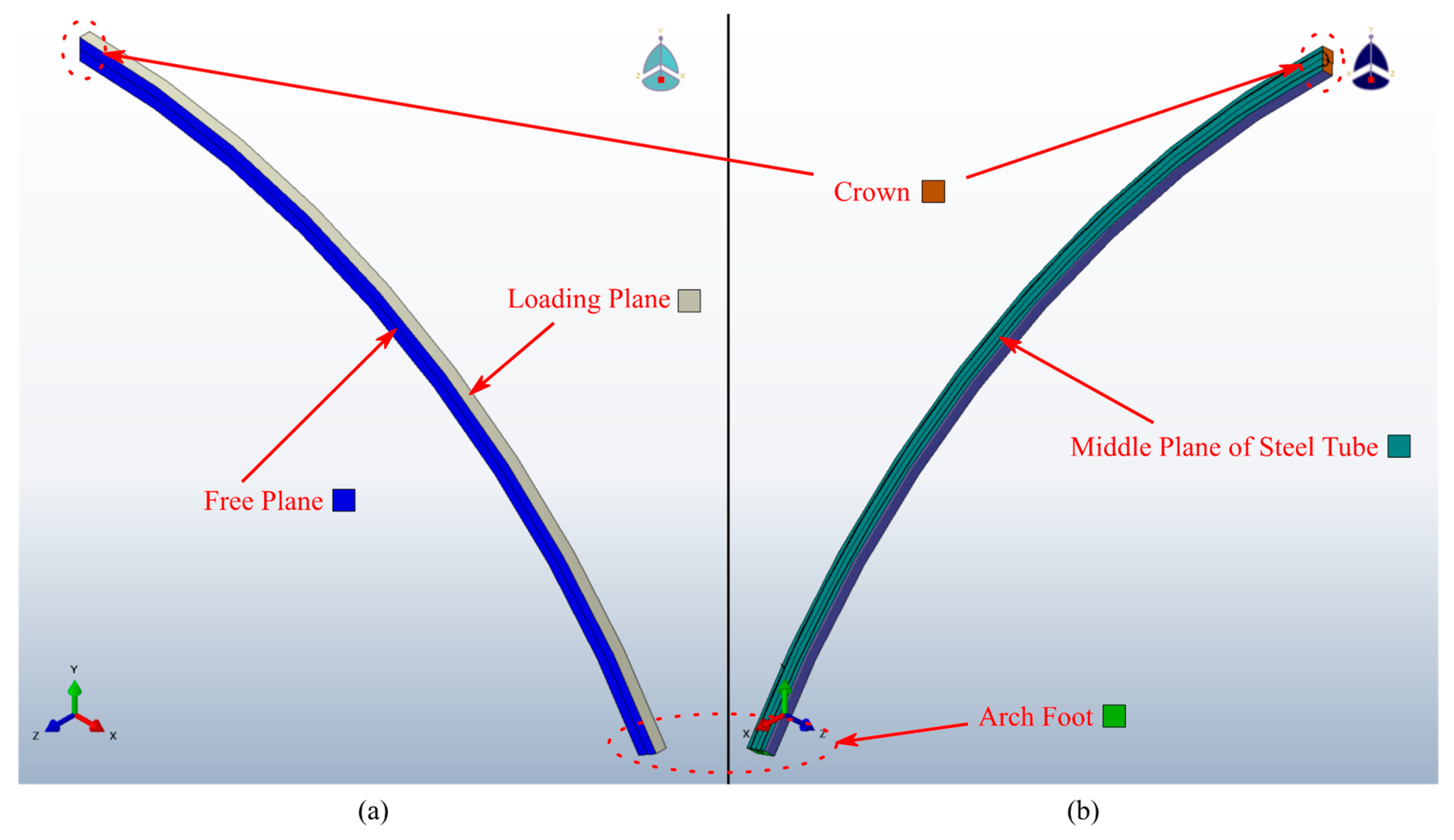
- The top surface of the model (refer to the brown-colored zone in Figure 4) corresponds to the symmetry plane at the crown of the circular arch member. The X-direction symmetry boundary condition for the solid element (constraint X-direction translational freedom) was adopted for the nodes on this surface.
- The bottom surface of the model (refer to the green-colored zone in Figure 4) corresponds to the junction point between the crown and the bench when the tunnel is excavated by the bench method. Before the excavation of the bench, in order to temporarily stabilize the support, foot anchors are usually applied at this point to provide horizontal and vertical restraint. Therefore, the foot of the arch member can be regarded as a fixed point. According to this assumption, rigid constraints (constraint the translational freedom in all spatial directions) were adopted for the nodes on the bottom face of the member.
- The outer surface of the arch (refer to the grey-colored zone in Figure 4) corresponds to the contact surface between the surrounding rock and the support, so it is the surface that the loads acting on. According to the Chinese standard [18], when there are no asymmetry factors such as bias pressure, the distribution of the load near the crown area is very close to the hydrostatic pressure state. Therefore, a uniformly distributed load was adopted for the normal direction of this surface, in order to simulate the load of the tunnel support in the most general case. The value of the load was automatically calculated by the arc length method, which will be mentioned later.
- The boundary surface of the Z-negative direction (refer to the cyan-colored zone in Figure 4) corresponds to the symmetry plane defined by the cross-sectional center line and the member axis. Thus, the Z-direction symmetry boundary condition was adopted for this surface.
- The boundary surface of Z-positive direction (refer to the blue-colored zone in Figure 4) is a free surface.
- When CFST is used as a bending member, studies have proved [17] that the bond-slip has little effect on the overall mechanical response of the member. Thus, tie constraints were established at the interface between the steel tube and the concrete, without considering the bond-slip effect.
3.1.4. Solution Scheme
- Establish the model and impose all boundary conditions except the load.
- Apply gravity and perform a general static analysis to obtain the equilibrium state of the member under its own weight.
- Apply the load mentioned in Section 3.1.3. Then perform the arc length analysis. The termination condition of the analysis is that the crown settlement reaches 2 m.
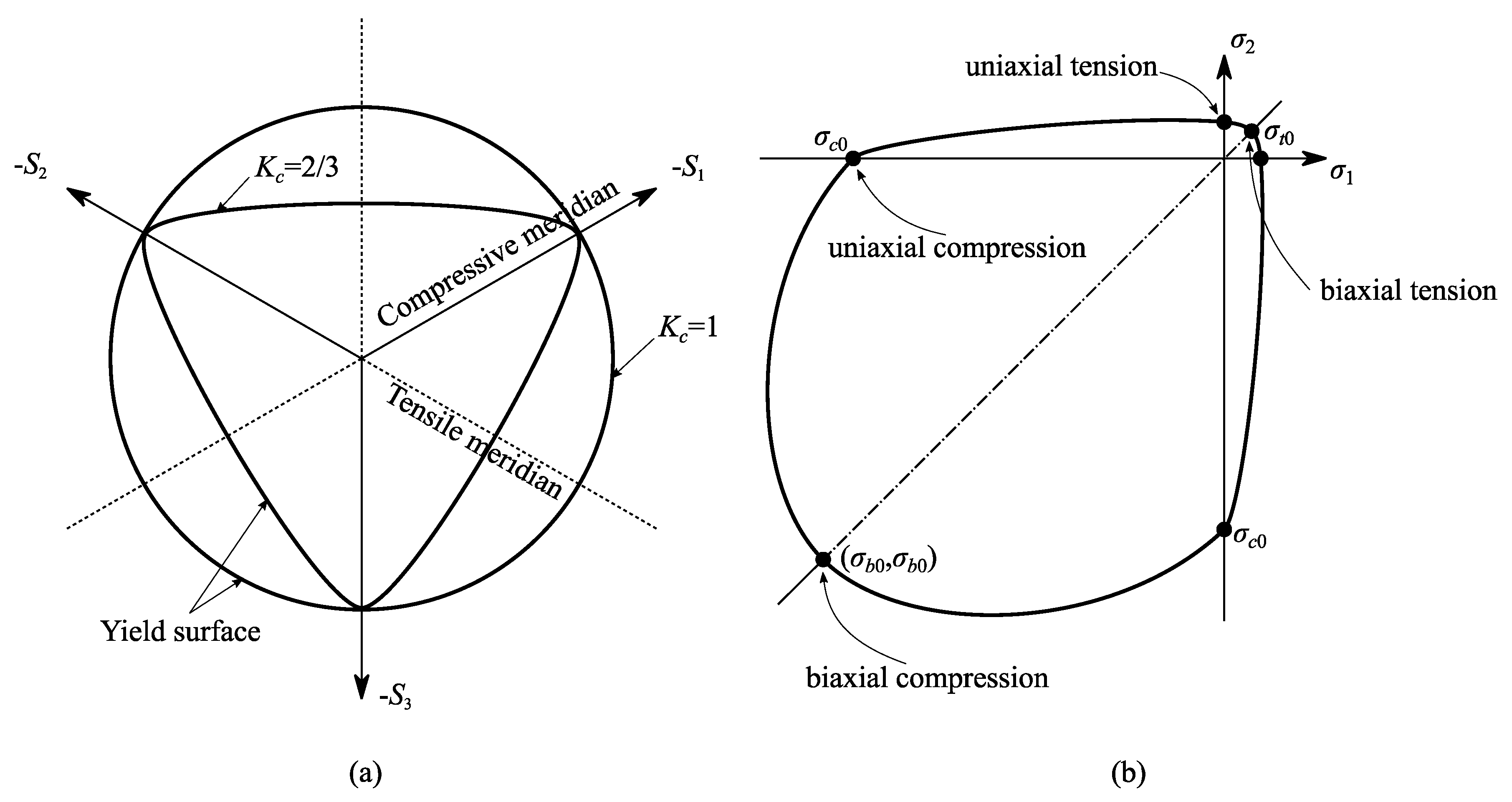
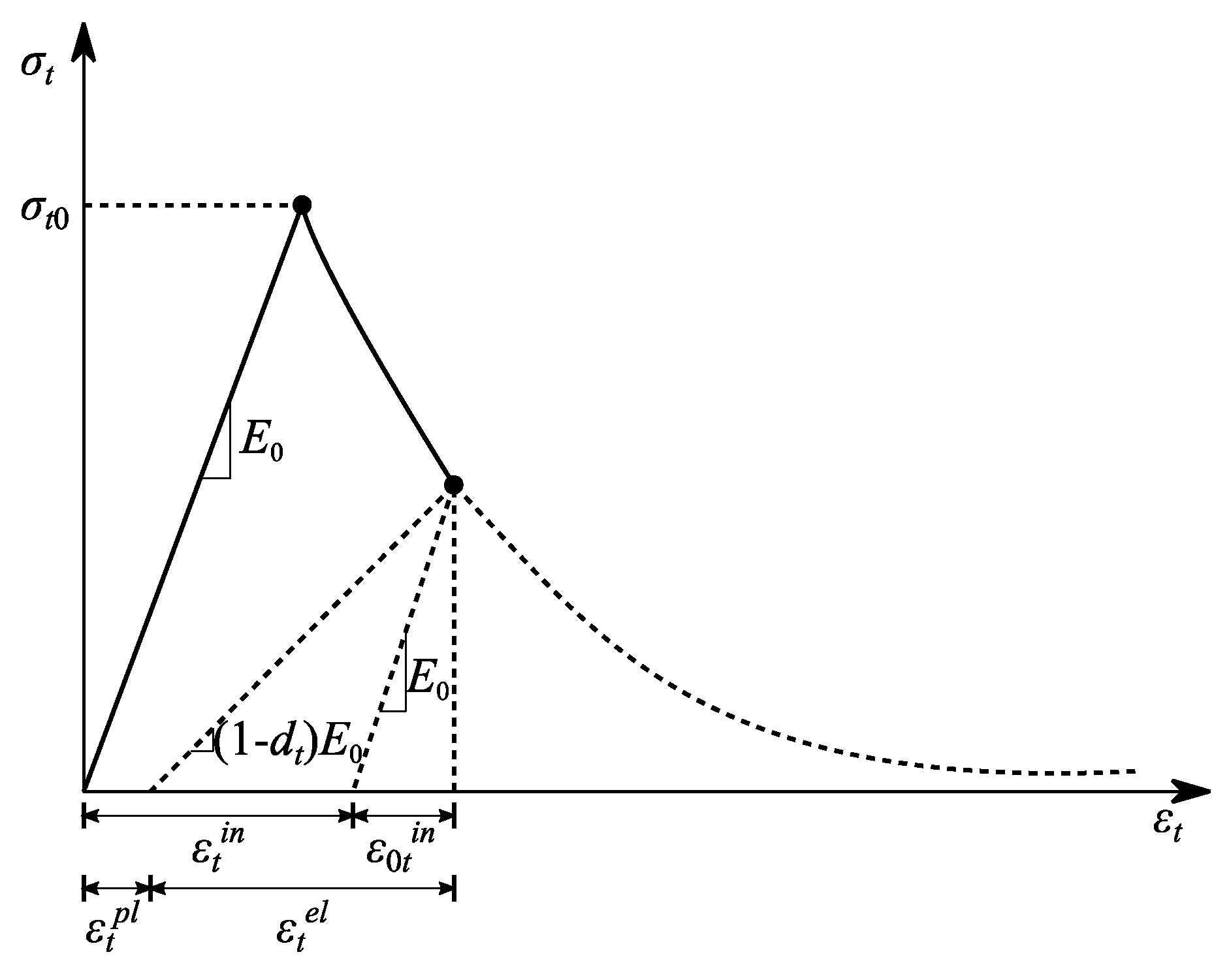
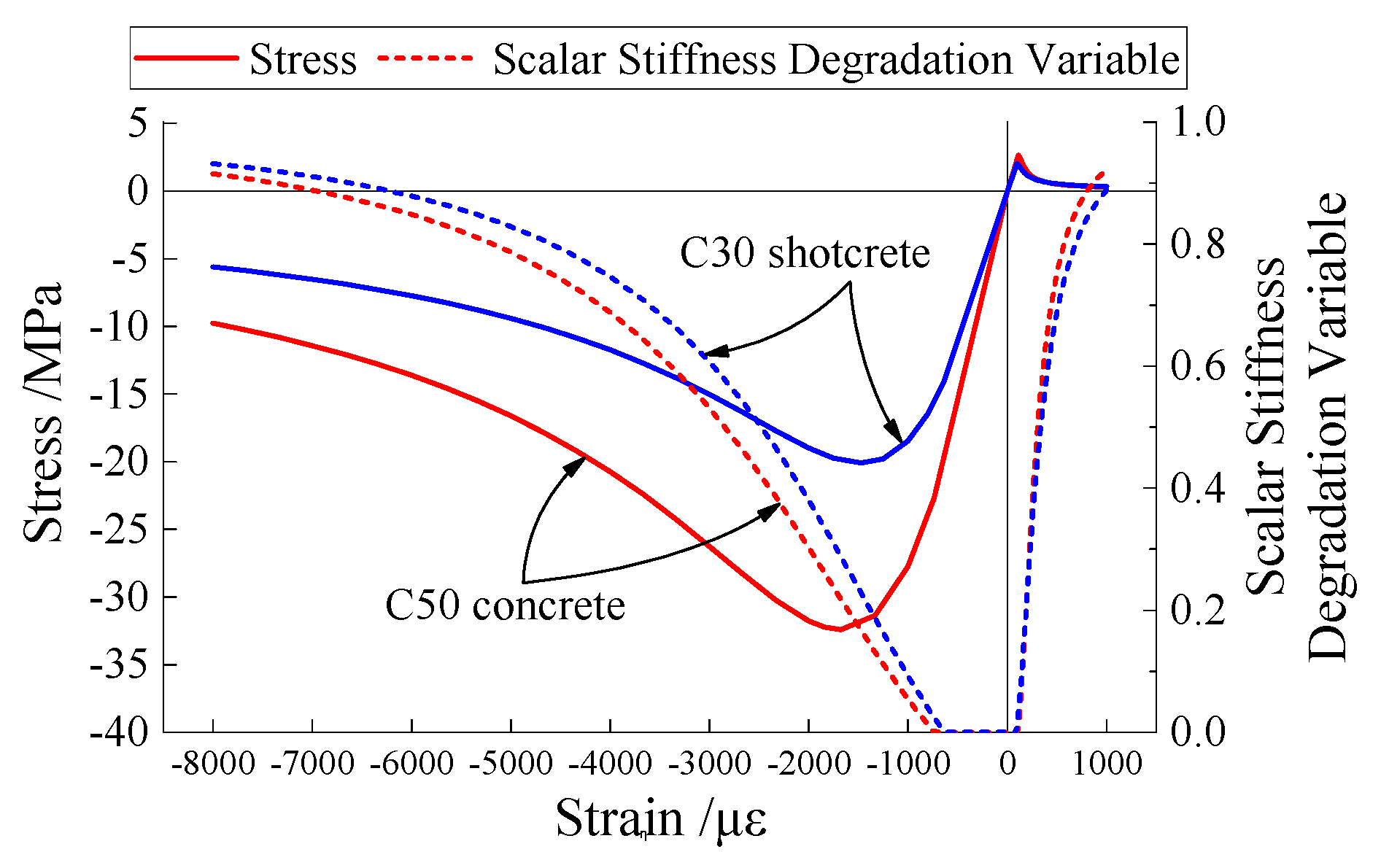
3.2. Constitutive Model and Material Parameter
3.2.1. Concrete
3.2.2. Steel
3.3. Research Cases
- 1.
- Group 1: With the benchmark of steel consumption
- 2.
- Group 2: With the benchmark of steel tube height (or outer diameter)
4. Results and Analysis
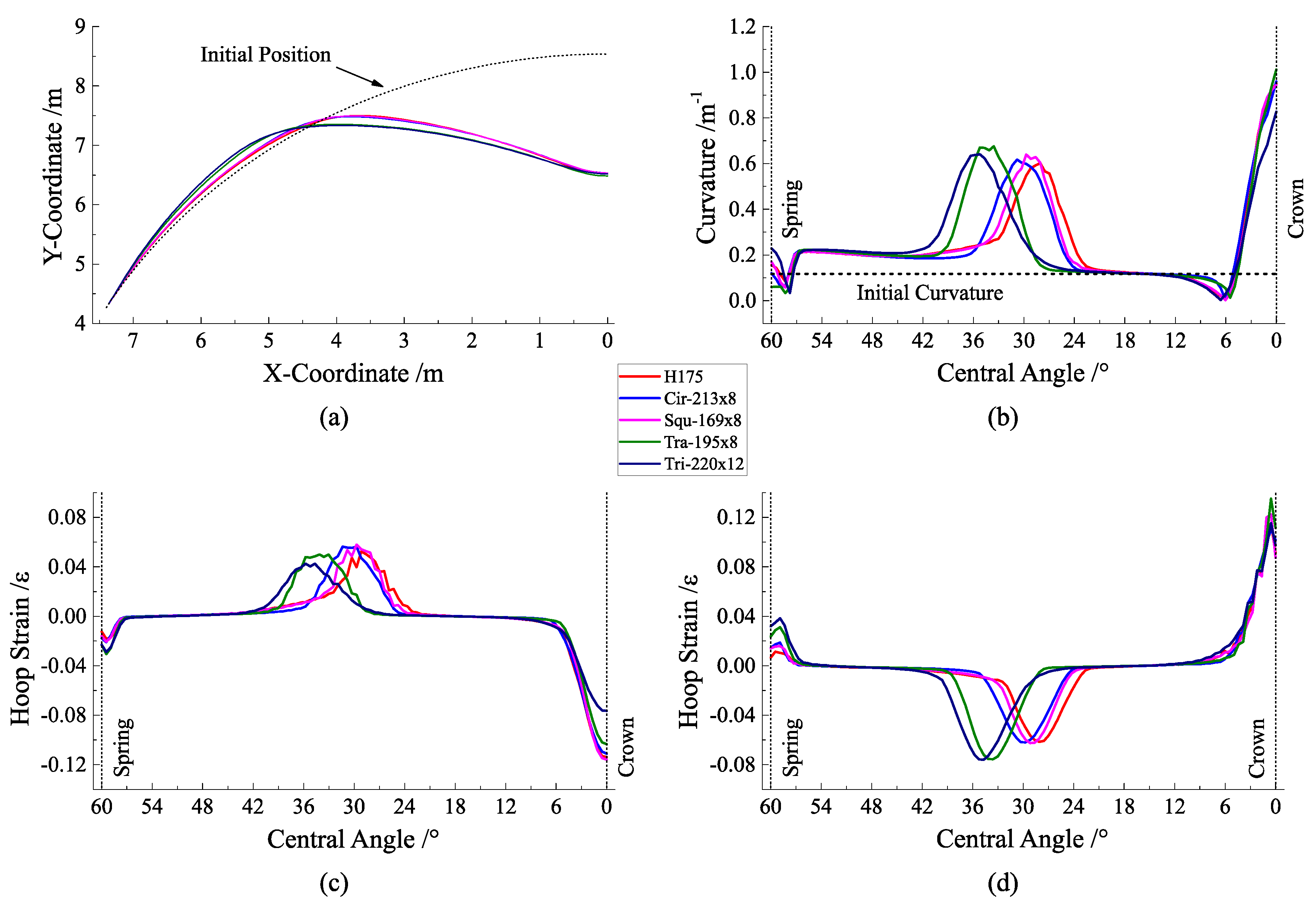
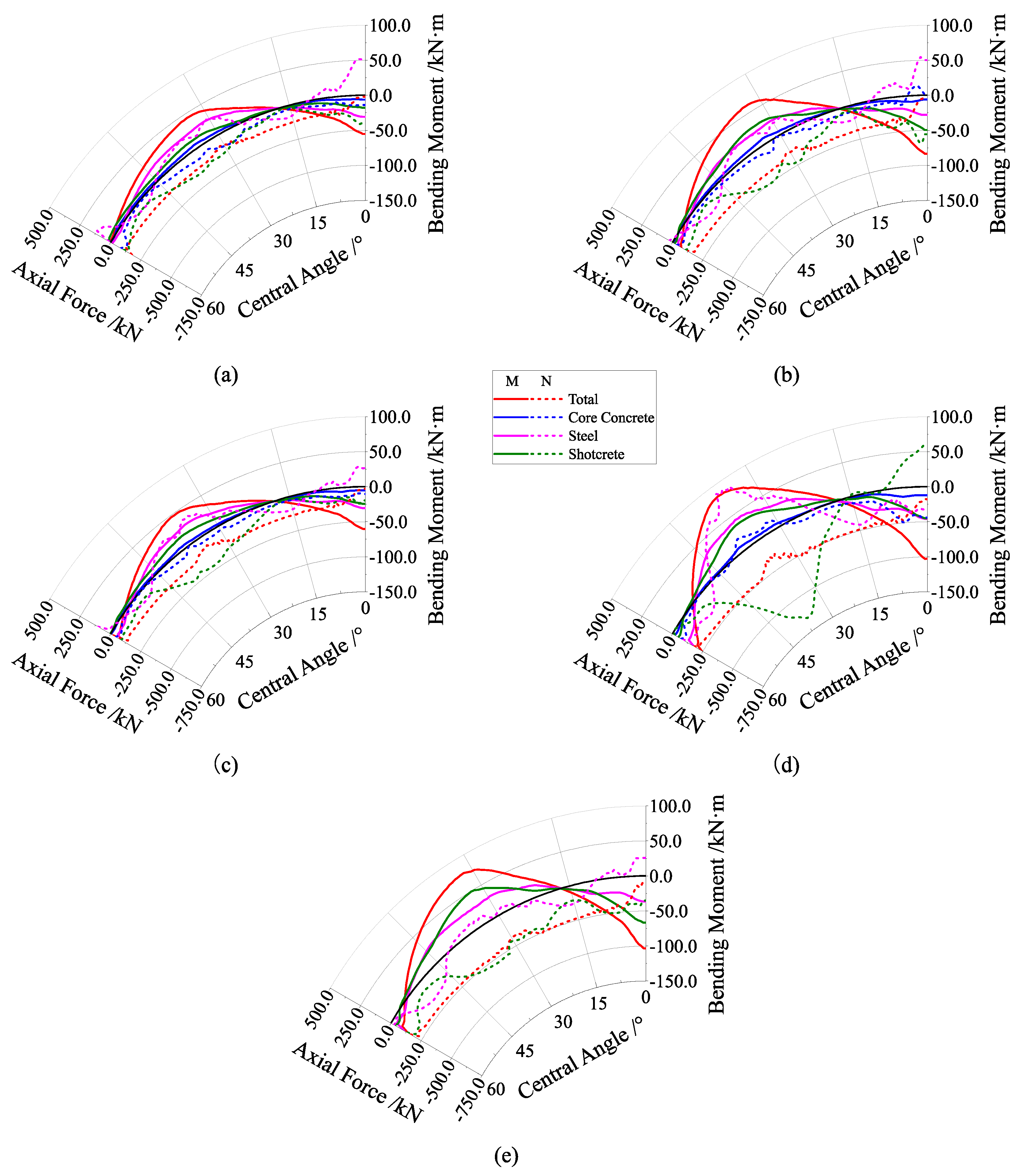
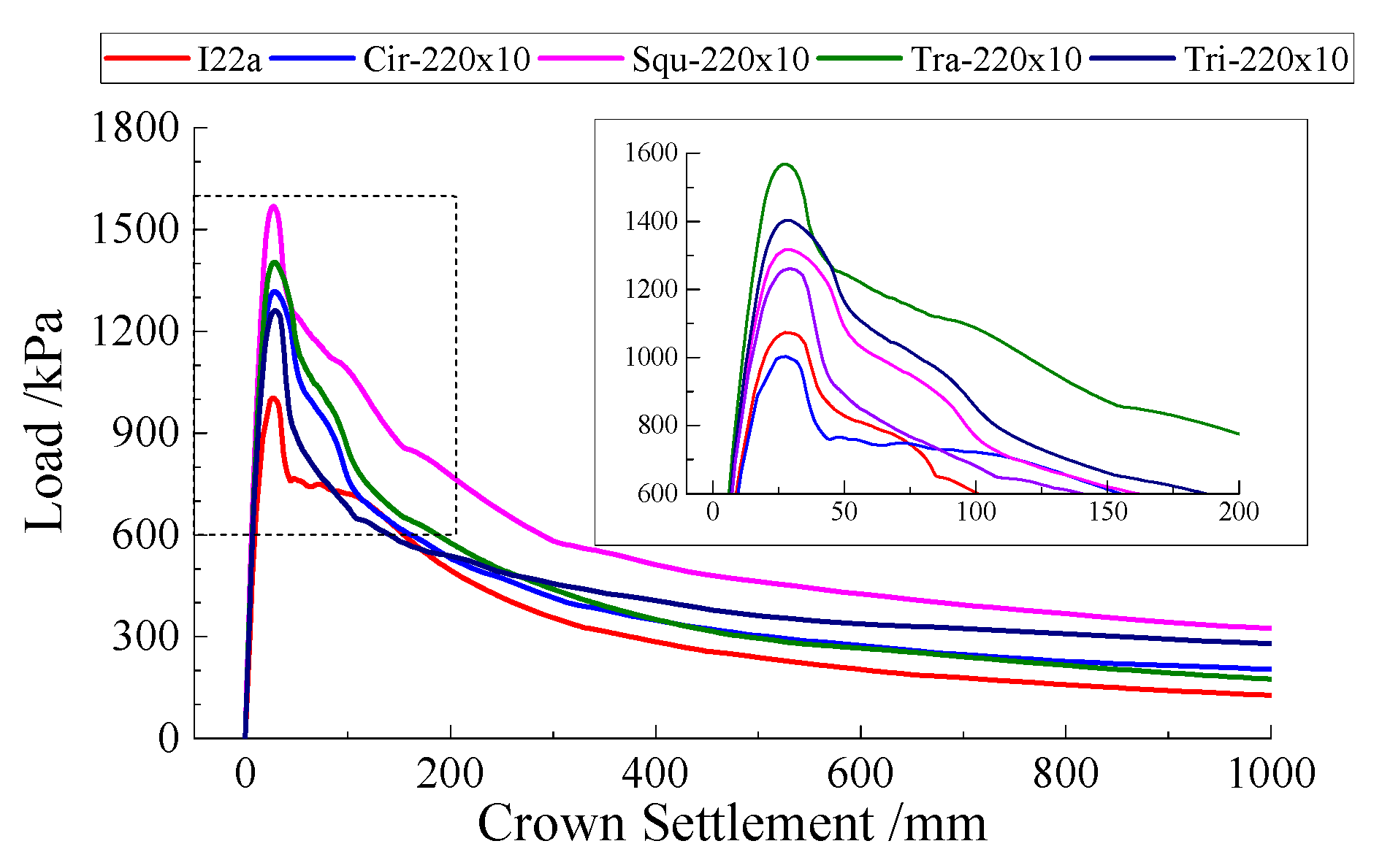
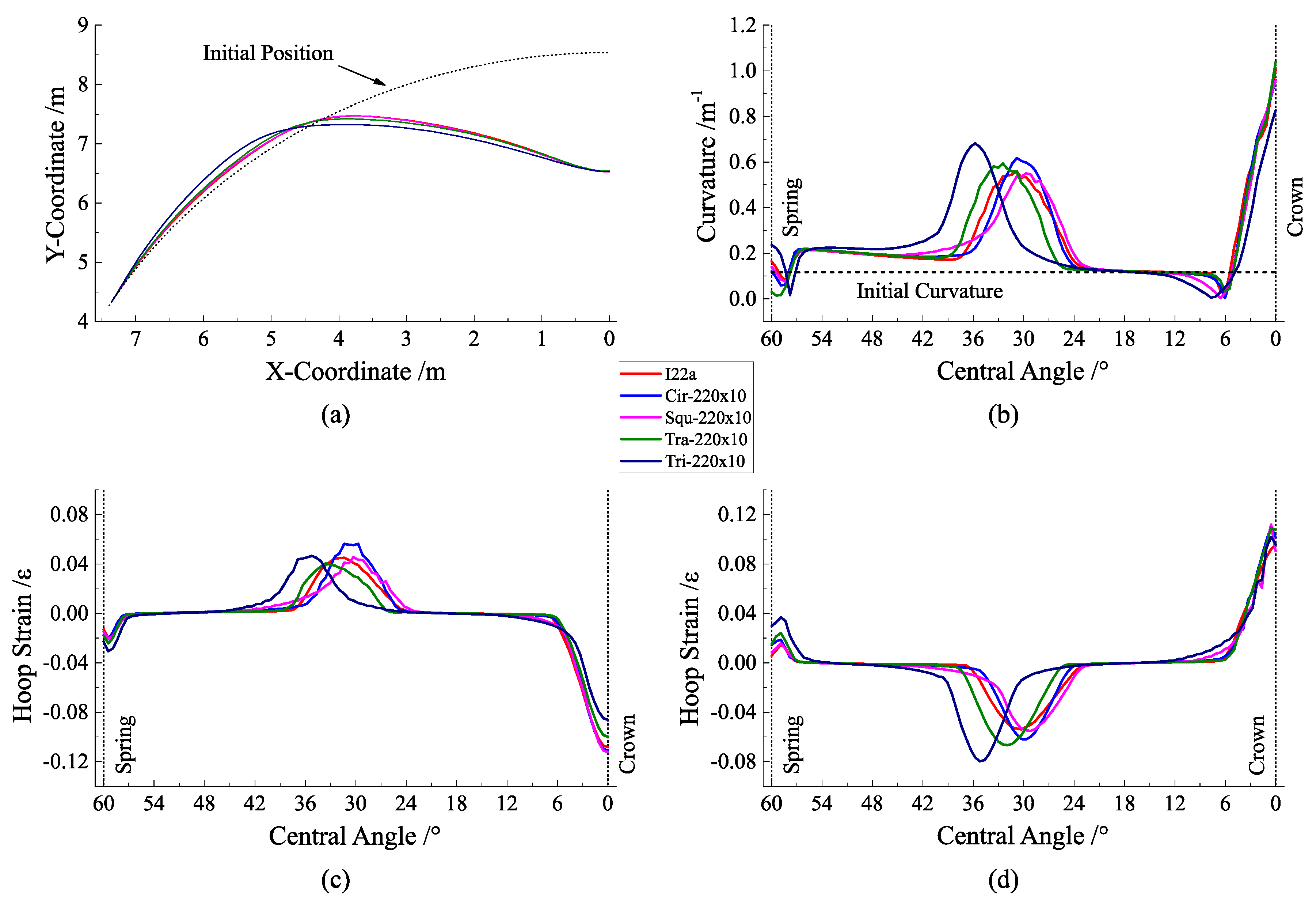
4.1. Analysis of Research Group 1
4.2. Analysis of Research Group 2
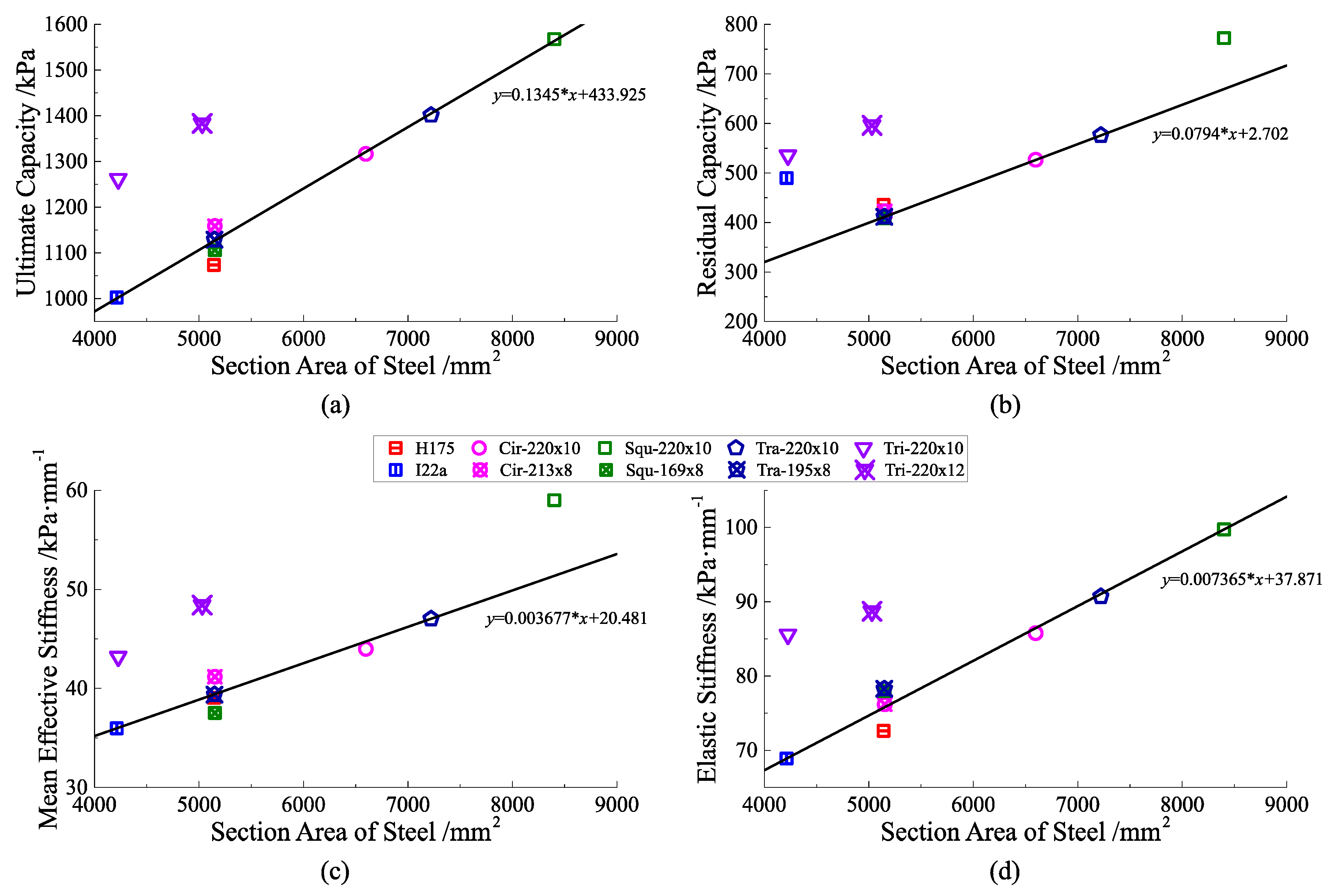
4.3. Comprehensive Analysis and Suggestions on the Cross-Sectional Form
- Ultimate bearing capacity: the load corresponding to the peak point of the load–crown settlement curve.
- Residual bearing capacity: from the load–crown settlement curve, it can be seen that after the crown settlement reached 200 mm, the decrease rate of the curve tended to be stable. Therefore, the corresponding load on the curve when the crown settlement is 200 mm is defined as the residual bearing capacity.
- Mean effective stiffness: the ratio of the ultimate bearing capacity and the crown settlement corresponding to it. The mean effective stiffness can be a measure of the ability to resist the deformation without failure.
- Elastic stiffness: the ratio of the load and crown settlement corresponding to the critical point that the deformation mechanism of the member changes from elastic to elastoplastic. It can be a measure of the ideal resistance to deformation.
5. Conclusions
6. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, B. Control Mechanism and Application of Confined Concrete for Super Large Section Tunnel on Weak Surrounding Rock. Ph.D. Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Cai, S.H. Recent development of steel-confined concrete structures in China. Chin. Civ. Eng. J. 1999, 32, 16–26. [Google Scholar] [CrossRef]
- Ahmed, E.; Atorod, A. Behavior and strength of circular concrete-filled tube columns. J. Constr. Steel Res. 2002, 58, 1567–1591. [Google Scholar] [CrossRef]
- Choi, C.S.; Jung, H.S.; Choi, H.K. Behaviour of concrete filled steel square-tube stub column with steel-fiber reinforced high strength concrete. Adv. Mat. Res. 2013, 663, 125–129. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.S.; Hadidy, A.E. Structural behaviour and design of elliptical high-strength concrete-filled steel tubular short compression members. Eng. Struct. 2018, 173, 495–511. [Google Scholar] [CrossRef]
- Mansouri, A. Shear strength of concrete-filled steel tubes based on experimental results. J. Struct. Eng. 2020, 146, 04020097. [Google Scholar] [CrossRef]
- Ouyang, Y.; Kwan, A.K.H. Use of analytical lateral-axial strain relation in FE analysis of axially loaded rectangular CFST columns. Eng. Struct. 2018, 166, 142–151. [Google Scholar] [CrossRef]
- Cho, J.H.; Moon, J.H.; Ko, H.J. Flexural strength evaluation of concrete-filled steel tube (CFST) composite girder. J. Constr. Steel Res. 2018, 151, 12–24. [Google Scholar] [CrossRef]
- Qu, G.L. Research on Flexural Performance of Concrete-Filled Steel Tubular Support and Its Application. Ph.D. Thesis, China University of Mining & Technology, Beijing, China, 2013. [Google Scholar]
- Liu, K.M. Compressed and Bending Performance Experiment of Concrete Filled Steel Tube Circular Arch and Supporting Application. Ph.D. Thesis, China University of Mining & Technology, Beijing, China, 2016. [Google Scholar]
- Huang, W.P.; Yuan, Q.; Tan, Y.L. An innovative support technology employing a concrete-filled steel tubular structure for a 1000-m-deep roadway in a high in situ stress field. Tunn. Undergr. Space Technol. 2018, 73, 26–36. [Google Scholar] [CrossRef]
- Gao, Y.F.; Liu, K.M.; Feng, S.W. Early strength concrete experiment and applied research of early strength concrete-filled steel tubular supports in extremely soft rock roadways. J. Min. Saf. Eng. 2015, 32, 537–543. [Google Scholar] [CrossRef]
- Li, X.B.; Yang, R.S.; Gao, Y.F. Study on combined support technology of bolt-mesh-shotcrete and concrete filled steel tubular supports for soft rock roadway in Yangzhuang mine. J. Min. Saf. Eng. 2015, 32, 285–290. [Google Scholar] [CrossRef]
- Gao, Y.F.; Liu, K.M.; He, X.S. Steel tube concrete support applied to dynamic pressure roadway in kilometers deep mine. Coal Sci. Technol. 2015, 43, 7–12. [Google Scholar] [CrossRef]
- Li, S.C.; Wang, X.; Wang, Q. Mechanical property research and failure characteristics of U-type confined concrete arch in deep roadway. Eng. Mech. 2016, 33, 178–187. [Google Scholar]
- Li, W.T.; Wang, Q.; Wang, D.C. Experimental study on short columns under axial load of U-type confined concrete arch centering and its application in mine. J. Min. Saf. Eng. 2014, 31, 1–9. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.T.; Li, S.C. Field test study on mechanical properties of U-type confined concrete arch centering and support system in deep roadway. J. Cent. South Univ. Sci. Technol. 2015, 46, 2250–2260. [Google Scholar]
- JTG/T D70-2010. Guidelines for Design of Highway Tunnel; China Communications Press: Beijing, China, 2010. [Google Scholar]
- Crisfield, M.A. An arc-length method including line searches and accelerations. Int. J. Numer. Methods Eng. 1983, 19, 1269–1289. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- GB 50010-2010. Code for Design of Concrete Structures; China Architecture & Building Press: Beijing, China, 2010. [Google Scholar]
- Liu, W.; Xu, M.; Chen, Z.F. Parameters calibration and verification of concrete damage plasticity model of ABAQUS. Ind. Constr. 2014, 44, 167–213. [Google Scholar] [CrossRef]
- Li, X.B. Steel Tube Confined Concrete Strength and the Roadway Compression Ring Enhanced Support Theory. Ph.D. Thesis, China University of Mining & Technology, Beijing, China, 2012. [Google Scholar]
- GB 50017-2017. Standard for Design of Steel Structures; China Architecture & Building Press: Beijing, China, 2017. [Google Scholar]



| Parameter | Description/Unit | Value | |
|---|---|---|---|
| C50 Concrete | C30 Shotcrete | ||
| E0 | Initial elastic modulus/GPa | 34.5 | 25 |
| ν | Poisson’s ratio | 0.2 | 0.2 |
| ρ | Mass density/t·m−3 | 2.3 | 2.2 |
| fc,r | Ultimate uniaxial compressive strength/MPa | 32.4 | 20.1 |
| εc,r | Compression strain corresponding to fc,r/με | 1678 | 1471 |
| αc | Shape coefficient of uniaxial compression σ-ε curve | 1.499 | 0.746 |
| ft,r | uniaxial tensile strength/MPa | 2.64 | 2.01 |
| εt,r | Tension strain corresponding to ft,r/με | 110.1 | 95.24 |
| αt | Shape coefficient of uniaxial tension σ-ε curve | 2.191 | 1.264 |
| ψ | Dilation angle/° | 15 | 15 |
| σb0/σc0 | Biaxial compressive strength ratio | 1.16 | 1.16 |
| Kc | Tensile and compressive yield ratio | 0.67 | 0.67 |
| κ | Eccentricity of plastic flow potential surface | 0.1 | 0.1 |
| ωc | Stiffness recovery coefficients of tension–compression | 1 | 1 |
| ωt | Stiffness recovery coefficients of compression–tension | 0 | 0 |
| Parameter | Description/Unit | Value |
|---|---|---|
| ES | Young’s modulus/GPa | 206 |
| ν | Poisson’s ratio | 0.31 |
| ρ | Mass density/t·m−3 | 7.85 |
| fy | Yield stress/MPa | 279 |
| fu | Ultimate strength/MPa | 450 |
| Cross-Sectional Form | Steel Tube Height/Diameter (mm) | Wall Thickness (mm) | Case Alias | Cross-Sectional Area of Steel (mm2) | Axial Compressive Modulus (GN) | Bending Modulus (MN·m2) |
|---|---|---|---|---|---|---|
| Circular | 213 | 8 | Cir-D213×8 | 5152 | 2.91 | 15.13 |
| Rectangular | 169 | 8 | Squ-H169×8 | 5152 | 2.84 | 13.99 |
| Triangular | 220 | 12 | Tri-H220×12 | 5031 | 2.82 | 16.92 |
| Trapezoidal | 195 | 8 | Tra-H195×8 | 5148 | 2.84 | 15.1 |
| H175 profile steel | 175 | - | H175 | 5142 | 2.62 | 14.77 |
| Cross-Sectional Form | Steel Tube Height/Diameter (mm) | Wall Thickness (mm) | Case Alias | Cross-Sectional Area of Steel (mm2) | Axial Compressive Modulus (GN) | Bending Modulus (MN·m2) |
|---|---|---|---|---|---|---|
| Circular | 220 | 10 | Cir-D220×10 | 6597 | 3.18 | 16.86 |
| Rectangular | 220 | 10 | Squ-H220×10 | 8400 | 3.59 | 21.99 |
| Triangular | 220 | 10 | Tri-H220×10 | 4227 | 2.68 | 16 |
| Trapezoidal | 220 | 10 | Tra-H220×10 | 7221 | 3.27 | 19.26 |
| I22a profile steel | 220 | - | I22a | 4213 | 2.45 | 15.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Lei, K. Preliminary Design and Cross-Sectional Form Study of Closed-Type Concrete-Filled Steel Tube Support for Traffic Tunnel. Symmetry 2020, 12, 1368. https://doi.org/10.3390/sym12081368
Li L, Lei K. Preliminary Design and Cross-Sectional Form Study of Closed-Type Concrete-Filled Steel Tube Support for Traffic Tunnel. Symmetry. 2020; 12(8):1368. https://doi.org/10.3390/sym12081368
Chicago/Turabian StyleLi, Lei, and Ke Lei. 2020. "Preliminary Design and Cross-Sectional Form Study of Closed-Type Concrete-Filled Steel Tube Support for Traffic Tunnel" Symmetry 12, no. 8: 1368. https://doi.org/10.3390/sym12081368
APA StyleLi, L., & Lei, K. (2020). Preliminary Design and Cross-Sectional Form Study of Closed-Type Concrete-Filled Steel Tube Support for Traffic Tunnel. Symmetry, 12(8), 1368. https://doi.org/10.3390/sym12081368




