Abstract
We develop the combinatorics of edge symmetry and edge colorings under the action of the edge group for icosahedral giant fullerenes from C80 to C240. We use computational symmetry techniques that employ Sheehan’s modification of Pόlya’s theorem and the Möbius inversion method together with generalized character cycle indices. These techniques are applied to generate edge group symmetry comprised of induced edge permutations and thus colorings of giant fullerenes under the edge symmetry action for all irreducible representations. We primarily consider high-symmetry icosahedral fullerenes such as C80 with a chamfered dodecahedron structure, icosahedral C180, and C240 with a chamfered truncated icosahedron geometry. These symmetry-based combinatorial techniques enumerate both achiral and chiral edge colorings of such giant fullerenes with or without constraints. Our computed results show that there are several equivalence classes of edge colorings for giant fullerenes, most of which are chiral. The techniques can be applied to superaromaticity, sextet polynomials, the rapid computation of conjugated circuits and resonance energies, chirality measures, etc., through the enumeration of equivalence classes of edge colorings.
1. Introduction
Symmetry, combinatorial enumerations, chirality, symmetry-based reactivity, spectroscopy, and the synthesis of fullerenes have been a subject of study over the years [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Whereas the vertex groups or the automorphism groups of graphs of fullerenes, point group symmetries of molecules, solids, and fullerenes have been quite well studied [1,2,3,4,20,24,26,29,30,31,32,33,34,35,36,37,38,39], this is not the case with the edge symmetry or edge groups, especially concerning giant fullerenes. Although the two symmetry groups are isomorphic to each other, the induced permutations on the edges of the associated molecular graphs by vertex permutations are not always obvious or easily obtained. Such an edge group comprising of edge permutations that preserve the connectivity of the fullerene graph is required for many applications, including edge colorings under the group action. Then, special cases of equivalence classes of edge colorings correspond to equivalence classes of conjugated circuits or resonance structures [43,44,45,46,47,48,49,50,51,52,53] and thus can provide an efficient platform for the rapid computation of resonance energies, conjugated circuits, and other properties that provide insight into aromaticity and superaromaticity [43,44,45,46,47,48,49,50,51,52,53]. Fullerenes are a special class of compounds containing only carbons with 12 pentagons and a varied number of hexagons. Fullerenes are especially interesting candidates for the edge colorings, as they contain a network of alternating arrangements of single and double bonds, which results in a large number of resonance structures or conjugated circuits [43,44,45,46,47,48,49,50,51,52,53], especially for giant fullerenes. Although one can employ high-level ab initio quantum chemical computations on giant fullerenes with supercomputers, techniques such as conjugated circuit theory and the combinatorial enumeration of resonance structures provide a viable and efficient alternating platform for shedding light into the structures and reactivity [43,44,45,46,47,48,49,50,51,52,53] of polycyclic aromatics and thus potentially giant fullerenes. Such combinatorial enumerations have been of interest [54,55,56,57,58,59], and especially Kekulė addition patterns related to edge colorings of smaller fullerenes [60].
Combinatorial enumeration of Kekulė structures, conjugated circuits, and resonance structures of both acyclic and cyclic polyacenes have been the topic of several studies [43,44,45,46,47,48,49,50,51,52,53], as such techniques aid in the computation of topological resonance energies, stabilities, and reactivities of polycyclic, acyclic aromatics, and fullerenes. We note that the various Kekulė structures are special cases of edge colorings of the associated graphs, and thus the enumeration of equivalence classes of edge colorings aid in the simplification of such computations, as all members of a given equivalence class would make the same contribution to the topological resonance energies or the stabilities of fullerenes or polycyclic aromatic compounds.
Experimental studies on fullerenes and giant fullerenes have been focused on the synthesis, structures, chirality, reactivity, and spectroscopy of fullerenes and their derivatives [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Giant fullerene cages and onions of fullerenes are interesting because they can be employed to encapsulate metallic oxides as well as small clusters inside fullerenes such as C180 and C240 [5,6,7,20,21,22,23,28], and such cages find a variety of applications including the environmental remediation of high-level nuclear wastes [61,62,63]. The chirality of substituted fullerenes such as chlorinated fullerenes and their spectroscopy has also received attention [4,21,24,26,30,33]. The edge connectivity of fullerenes can shed light not only on the halogenation reactions but also on chemisorption. The existence of inequivalent edges in fullerenes would provide an opportunity to study reactivity contrast upon the addition of molecules such as H2, N2, and O2, etc., as inequivalent edges can result in different reactivity patterns. Thus, edge colorings under the edge group action of giant fullerenes can provide insights into reactivity patterns especially in chemisorptive reactions and reactions that involve the attachment of molecules to the edges of fullerenes. The icosahedral giant series of fullerenes with the formula C60k for k = m2 of which C60, C240, C540, C960, etc., are members are especially interesting for their high symmetry and chirality of derivatives of these members. The enumeration of the isomers of polysubstituted giant icosahedral fullerenes was considered by the present author in a recent study [4]. Subsequently, stimulated by the pentagonal face dynamics of nanocones and chirality concepts, Balsubramanian et al. [64] recently outlined a combinatorial scheme for the face colorings of icosahedral giant fullerenes. The present study complements the previous two related works [4,64] in that this is the first study on the edge colorings of giant fullerenes, which is a topic of considerable interest in the context of reactivity, stability, enumeration of Kekulė structures, conjugated structures, achirality, and chirality arising from the edge colorings and edge groups etc., of giant fullerenes. The edge colorings considered here are also relevant to heterofullerenes such as C48N12 [37,65].
Stimulated by the intriguing symmetry, chirality, edge substitution, and reactivity of giant fullerenes, in the present study, we undertake edge symmetry and edge colorings under the group action for a series of giant fullerenes, namely C80, C180, and C240. We show that the Möbius inversion technique combined with our generalization of Sheehan’s modification54 of Pόlya’s theorem to all characters yields powerful combinatorial generating functions for the edge colorings of giant fullerenes for all of the irreducible representations of the symmetry group of fullerenes. We focus on the edge colorings of high symmetry icosahedral giant fullerenes that have been of both experimental and theoretical interest.
2. Möbius Inversion Technique with Generalization of Sheehan’s Theorem to All Characters as Tools for the Combinatorics of Edge Groups and Edge Colorings of Giant Fullerenes
The key advantage of the Möbius inversion technique in the context of cycle index polynomials is that when a group acts on two different sets and if the cycle types for the permutations for the action on the smaller sets are known, then the technique can be used to obtain the cycle types of a larger set of objects. The application of the technique results in the inversion of a polynomial generating function from one set to the other through the divisors, which we used extensively in the context of hypercube enumerations for coloring the various hyperplanes for all of the irreducible representations of the hyperoctahedral group [55]. That is, the coefficient of xq in the inverted polynomial generating function Qp(x) shown below obtained from a known polynomial Fd(x) generates the permutational cycle types for a larger set from a smaller set—for example, the edges of a 7D hypercube from the permutational matrix types for the hexeracts of the 7D hypercube [55].
where the sum is over all divisors d of p, and is the Möbius function that yields the cycle types of larger sets, where Fd(x) is the known polynomial in x as constructed from the permutations of objects of a smaller set with the Group G commonly acting on both sets. The Möbius function, which in the above equation is denoted as , takes values 1, −1, −1, 0, −1, 1, −1, 0, 0, 1… for arguments 1 to 10. The Möbius function for any number is 0, +1, or −1 depending on whether it is a perfect square and the number of prime factors in the argument.
Figure 1 shows a regular icosahedron, a vertex–edge combo coloring of the icosahedron with 5 different colors, the C20 dodecahedron, and the C60 buckminsterfullerene—all of which exhibit the icosahedral symmetry. Fullerenes are vertex regular graphs with 3 vertex degrees that contain 12 pentagons. Therefore, for any fullerene, the number of edges is given by 3n/2, where n is the number of vertices. For example, there are 360 edges in the case of the C240 icosahedral fullerene. Each of the proper and improper rotational operations of the icosahedron induces a permutation on the set of 360 edges of C240, a permutation on the 240 vertices, and a permutation on 122 faces of the giant C240 fullerene with the icosahedral point group symmetry. Euler’s formula connects the number of vertices, edges, and edges of the fullerene; thus, we can obtain the number of any one of them when the other two are known. The group action on the edges of the fullerene can be obtained through a number of techniques, including the generation of the edge automorphism group from the vertex automorphism group of the graph. However, we note that the permutational cycle types of group action on the edges can be obtained computationally through the Möbius sum. It can also been seen that certain operations such as the C5 rotational axis for an icosahedral fullerene cage pass through the center of a pentagon (see Figure 2e) and not through any of the vertices with the exception that for the 12-vertex icosahedron (see Figure 1a,b), the C5 axis passes through two opposite vertices of the icosahedron. Hence, this is directly related to the Möbius concept of whether the fold-ness of the rotational axis divides the number of objects in the set or not. For example, for the C5 axis, the number 5 does not divide 12 in the case of the vertices of an icosahedron, thus leaving a remainder of 2 when 5 is divided by 12. This necessitates the C5 axis to pass through two vertices that are across each other for the icosahedron. For giant fullerenes such as C240, the C5 axis passes through the center of a pentagon, and as 5 is a divisor of 240, it is clear that the vertex permutation will be described by 548. As seen from Table 1, the conjugacy class representatives of the icosahedral fullerene group comprises the set {E, C6, C5, C3, C2, Ci, S10, S12, S6, σd}. For all of the icosahedral fullerenes considered here, all the edges are not equivalent or alternatively, the edges are divided into more than one equivalence class for such giant fullerenes. In such a scenario, it is more suitable to consider a generalization of Pόlya’s theorem outlined by Sheehan [54], which we further generalize to all characters and the edge action of the icosahedral group.
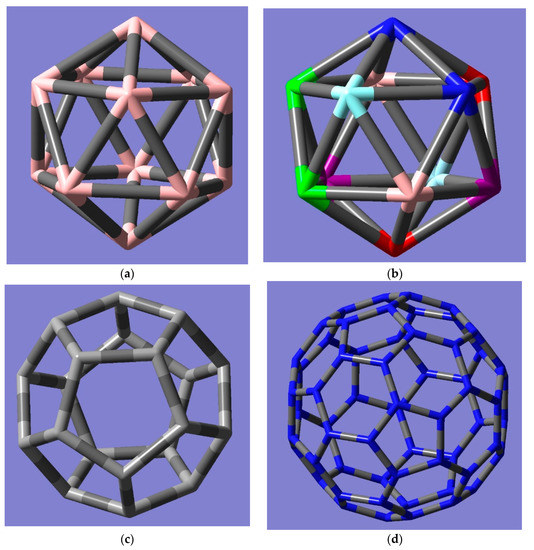
Figure 1.
A regular icosahedron (a), a combo of vertex–edge coloring of the icosahedron with 5 colors (b), where an edge incident on two vertices is defined with the corresponding vertex colors—for example, blue-red edge (b), C20 dodecahedral fullerene (c), and C60 Buckminsterfullerene (d)—all with Ih icosahedral symmetry. The C5 axes pass through each vertex of the icosahedron colored to show the pentagon, and the C3 axes pass through the center of triangular face, while the C2 axes pass through the center of an edge.
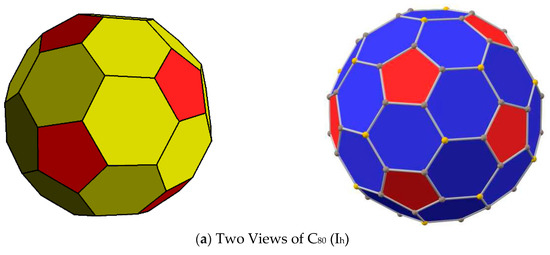
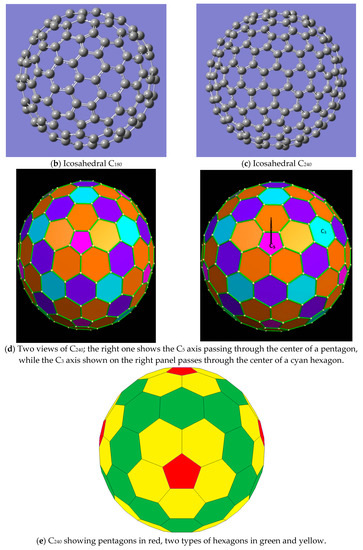
Figure 2.
Strucural representations for C80, C180, and C240 fullerene cages considered here for edge colorings. Panel (d) is reproduced from https://robertlovespi.net/ and it is copyright-free.

Table 1.
Character table of Ih, permutation cycles and their lengths for the 60 pent–hex edges and remaining hex–hex edges of C60 (Ih), Icosahedron, C80 (Ih), C180 (Ih), and C240 (Ih) upon action on edges.a
Consider a set D consisting of the edges of a fullerene, and because for all the fullerenes considered here, there exists more than one equivalence classes of edges, we further partition the edge set D of fullerenes into two sets Y1, Y2, … Ym where Yi is an equivalence class partition of the edges of the fullerene. That is, , where m = number of the edges of the fullerene cage.
The action of a group G, in this case the icosahedral group of 120 operations, on the set D, induces a permutation in various Yi sets such that every cycle is contained within the set Yi. Consequently, an edge coloring of the fullerene can be considered as a map from D to R, where R is the set of colors, but because D is partitioned into various equivalence classes, one may choose an independent set of colors for each set Yi. Sheehan [54] has considered such a generalization of Pόlya’s theorem for the enumeration under group action for the case where the set D is partitioned into multiple sets. We note that Sheehan’s generalization of Pόlya’s theorem reduces even the Redfield–Read superposition theorem to a special case. Sheehan’s technique [54] is further generalized here to all characters of the irreducible representations of the icosahedral group for the edge colorings of fullerenes. These techniques also yield the number of chiral and all achiral colorings of the fullerene cages for a different distribution of colors.
The generalized character cycle index (GCCI) polynomial for any character of the automorphism group G of the fullerene cage under consideration is defined as
where the sum is over all the permutation representations of g ∈ G, and cij(g) is the number of j-cycles of g ∈ G upon its action on the set Yi. That is, the second index j in cij(g) stands for the length of the cycle (that is a j-cycle) generated in the Yi set upon the action of g ∈ G. We also note that unlike the ordinary cycle index of Pólya’s enumeration theorem, the generalization considered here generates a GCCI for each irreducible representation of the Ih group for the icosahedral fullerene. Consequently, we employ an even more powerful generating function than the ordinary Pólya or the Sheehan cycle index [54] to enumerate the edge colorings of giant fullerenes for each irreducible representation (IR).
Define [n] as an ordered partition, or the composition of n into p parts such that n1 ≥ 0, n2 ≥ 0, …, np ≥ 0, . We can obtain a multinomial generating function (GF) in λs with n1 colors of the type λ1, n2 colors of the type λ2 … np colors of the type λp, which are defined as follows:
where are multinomials given by
Let R be a set of colors partitioned into sets R1, R2 … Rm with the same number of partitions as the Y sets such that . Furthermore, let wij be the weight of each color rj in the set Ri. The generating function for each irreducible representation for the edge colorings of giant fullerene cages considered here is given by
where pi = |Ri|. The GFs obtained above for each IR and various color distributions provides the number of edge coloring with varying color distribution for the different equivalence classes of the edges, independent of each other and those that transform according to the irreducible representation whose character is given by χ. Thus, all of the techniques demonstrated including the Möbius function method, GCCIs, and generating functions were all programmed into FORTRAN ’95 codes using the quadruple precision arithmetic as the number of edge colorings explode combinatorially. We note that in order to make the codes efficient, especially for larger fullerenes, we have taken considerable efforts to optimize the codes by designing efficient algorithms for the computations of multinomial and binomial numbers using recursion as opposed to an explicit evaluation of factorials and identifying the equivalence of multinomials, thereby eliminating duplicative computations. Furthermore, although we have obtained the results for all of the irreducible representations in the ensuing section, we show the results only for the chiral and totally symmetric irreducible representations, as these are the most interesting cases for the present study. However, we point out that the results obtained for other irreducible representations are quite important in several other applications such as the enumeration of nuclear spin functions, nuclear spin statistics, Electron Spin Resonance (ESR) spin function enumerations for the assignment of the observed hyperfine structures, and so on [57,58,59]. Thus, there is a wealth of information latent in these generating functions for the various irreducible representations for giant fullerenes.
3. Results and Discussions
Table 1 displays the various conjugacy classes of the icosahedral group, the permutation orbit structures for the edges for C80 (Ih), C180 (Ih), and C240 (Ih), and the character values of the Ih group under each conjugacy class. The three structures considered here are shown in Figure 2 together with other structures of icosahedral symmetry in Figure 1. Among the fullerenes considered here, we illustrate the procedure of constructing the GCCIs with C80 (Ih) (the chamfered dodecahedron shown in Figure 2), the related edges of the icosahedron in Figure 1a,b, and the corresponding generating functions. There are two types of edges in C80 as seen from Figure 2 analogous to buckminsterfullerene C60 (Figure 1d): the edges that are shared by a pentagon and hexagon are distinct from the edges shared by two hexagons. Thus, for the case of C80, there are two equivalent class edges: namely, Y1 and Y2. Let the first set correspond to the edges shared by a pentagon and hexagon. As there are exactly 12 pentagons in any fullerene, it is evident that the cardinality of the set Y1 is 60. This leaves 60 edges that are common to two hexagons in the case of C80; or, the cardinality of the set Y2 is also 60 for the case of C80. However, as can be seen from Table 1, the cardinalities of sets Y1 and Y2 are 60 and 30, respectively for the buckminsterfullerene case. From Table 1, we combine the cycle types that are shown for the pent–hex edges together with the cycle types for C80 (hex–hex) edges to obtain the GCCIs for the Ag and Au irreducible representations of the Ih group shown below:
We note that it is coincidental that the cardinalities of both equivalence classes for the edge sets of C80 became the same and equal to 60, which is not the case in general. For the C60 buckminster fullerene, the cardinalities of the two sets are 60 and 30, respectively, and thus, we obtain different terms for s1j and s2j in each of the terms of the GCCIs for C60 for the Ag and Au IRs, as shown below:
Generating functions for the two cases with 4 different colors to color the edges common to a pentagon and hexagon (denoted as pent–hex edges) and 3 different colors (say red, green, and blue) to color the edges common to two hexagons (denoted as hex–hex) for the Ag of C60 are shown first in Equation (10).
The corresponding GF for the Au IR is obtained in an analogous manner, and it shown as Equation (11):
The above multinomial generating functions can be expanded and simplified for each IR of the Ih group, and these functions offer a greater flexibility for the edge colorings compared to the ordinary Pόlya’s expansion, because the GF has terms partitioned into coloring hex–hex edges and pent–hex edges differently. Thus, the GFs obtained above have the ability to enumerate edge colorings with different specifications:
- (a)
- if all hex–hex edges of C60 are colored with one color (white) and pent–hex edges are colored with multiple colors;
- (b)
- (c)
- if both pent–hex and hex–hex edges are colored with multiple colors from a single set R of colors without making any distinction between the two sets of edges.
- (d)
- if all hex–hex edges are colored with colors from a single set, while all pent–hex edges are colored with colors chosen from a different set of colors, thus making a distinction between the pent–hex and hex–hex edges.
For each of the cases listed above, one can obtain a set of GFs for each IR of the Ih group, thus yielding a powerful set of enumerative combinatorial generating functions. Hence, we consider each such case.
For case (a), the edge colorings of C60 are obtained by setting d and e to 0 in Equation (10), which yields Equation (12):
when the above expressions are expanded and simplified for each IR, the results can be expressed in terms of partitions of integer 60 in 4 parts. For example, the partition [15 15 15 15] of 60 corresponds to the term 115a15b15c15 = a15b15c15, and hence, the coefficient a15b15c15 in the multinomial expansion gives the number of ways 60 pent–hex edges of C60 can be colored with 15 white, 15 green, 15 blue, and 15 red colors keeping all hex–hex edges white. The GF for the Au IR generates the number of chiral pairs for the corresponding chiral partition [15 15 15 15] for the pent–hex colorings. Thus, the sum of the numbers for Ag and Au enumerated for each color partition yields the total number of all possible pent–hex colorings that encompass both achiral colorings and chiral pairs. In general, for each IR of the Ih group the results enumerated represent the number of colorings that transform according to the IR for the given color partition. These general results for any IR find applications to nuclear spin statistics beyond electrons, for example, spin 3/2 fermions and quarks [57,58,59].
The GF is obtained for the case (b) by setting the edge weights a, b, and c to 0 in Equation (10), which results in Equation (13):
Expression (13) thus obtained for the Ag IR yields the number of equivalence classes of coloring hex–hex edges with 3 different colors while keeping all the pent–hex colors white. The above expression when generalized to include two more colors with weights f and g—that is, every term (1 + dk + ek) in Equation (13) is replaced with (1 + dk + ek + fk + gk)—we obtain the results shown in Table 2 for the colorings of the edges of the icosahedron (Figure 1a,b) with up to 5 different colors under the action of the Ih group. Only some of the color partitions are shown in Table 2, as the number of terms in the multinomial GF for coloring 30 edges with 5 different colors is .

Table 2.
Edge colorings of an icosahedron with up to 5 different colors (green, blue, red, cyan, burgundy)—one such coloring is in Figure 1 a.
If all edges are colored with colors chosen from a single set of colors (case (c)), we obtain the GF for each IR by setting wij = wj for all i, which leads to the following GF for Ag for the case with 4 colorings of 120 edges of C80 (Ih) without differentiating the pent–hex and hex–hex edges. Thus, the expression obtained is shown in Equation (14):
The above expression (14) can be expanded; except for the first few terms, there is a combinatorial explosion. Note that the number of terms in the above expansion or the number of ordered partitions of 120 into 4 parts is . Consequently, an exhaustive construction of the combinatorial tables for all such edge colorings will take too much space, although they have all been generated by our computer code. Hence, we restrict to some of the binomial coloring terms shown in Table 3, Table 4 and Table 5.

Table 3.
Edge colorings of C80.

Table 4.
Edge colorings of C180.

Table 5.
Edge Colorings of C240.
However, for any given color partition, the respective coefficient can be directly obtained from the GFs without having to expand the entire multinomial function for the edge colorings. Thus, we have constructed the tables of our enumerations for the Ag and Au IRs of the Ih group for C80, C180, and C240 only for binomial colorings. Owing to a large number of edges for the giant fullerenes, both the number of terms in the expansion and the coefficients of various terms result in a combinatorial explosion for the edge colorings. Table 3, Table 4 and Table 5 show our computed results for the three giant fullerenes for only binomial colorings (black and white colors) for coloring the edges for the Ag and Au IRs. Although as shown above, we can obtain a more itemized distribution for the edge coloring such as pent–hex, hex1–hex1, hex1–hex2… colorings depending on the number of equivalence classes of hex–hex edges, for the sake of simplicity, we show in Table 3, Table 4 and Table 5 only the overall binomial color distributions without making further distinction into the types of edges. Table 3 shows the binomial colorings of 120 edges of C80, where in Table 3, k represents the number of black colors while 120-k is the number of white colors. We have shown the results for both Au and Ag IRs where the numbers for Au yield the numbers of chiral pairs for each edge-coloring partition shown in Table 3. As can be seen from Table 3, one needs a minimum of two black colors with the remaining 118 edges colored in white in order to produce a chiral edge coloring. As the number of black colors increases, the number of chiral colorings also increases, reaching a maximum of 805,124,240,336,360,915,214,413,591,091,584 chiral pairs. The corresponding number for Ag is 805,124,240,336,361,157,749,996,742,071,252, suggesting that as we approach the peak of the binomial distribution, almost every edge coloring is chiral.
Table 4 shows our computed results as for the binomial edge colorings of C180. A striking contrast between C180 and C80 as well as C60 is that the number of Ag colorings for k = 1 is 4 for C180, which means there are 4 kinds of edges for C180, unlike the smaller icosahedral fullerenes. Moreover, there is exactly one chiral pair of edge coloring for the case k = 1 as inferred from Table 4 for the Au IR. There 5 edge colorings for C180 with 269 white colors and 1 black color, among which there exists a chiral pair: a result that was not known until now. For the case of k = 2 or two black colors, it is seen that among 639 edge colorings for C180, there are 294 chiral pairs, and the remaining 51 colorings are totally achiral. Analogous to C80, the number of edge colorings grows combinatorially, resulting in an explosion already for k = 30, and hence, numerical results are not shown beyond k = 30. We see from Table 4 that almost all edge colorings of C180 are chiral. Although we do not consider the case of C140 icosahedral fullerene, the parent cage itself is chiral, as it belongs to the I group. Consequently, every edge coloring of C140 is chiral, which is a direct consequence of the chirality of the parent cage. The results in Table 5 for the edge colorings of C240, the largest of the fullerenes considered here, reveal that there are 6 edge colorings for the one black color and the remaining white colors, among which there is exactly a chiral pair, and the remaining 4 colorings are achiral.
The numbers for k = 2 (two black colors) suggest that there are 1122 edge colorings with 523 chiral pairs and 76 achiral colorings. As seen from Table 5, for k = 26 (26 black colors), there are 23,844,803,619,432,111,008,453,439,294,860,623,872 chiral pairs of edge colorings and 74,228,417,154,323,763,200 achiral colorings for C240.
The total numbers of all edge colorings, the number of chiral pairs, and the number of achiral colorings can be readily derived from the numbers enumerated in the tables for C80 through C240. Let Nk(Ag) and Nk(Au) be the numbers enumerated in the tables for the various values of k. Thus, we obtain:
Nk (Total; Binomial Edge colors) = Nk(Ag) + Nk(Au)
Ck (Chiral; Binomial Edge colors) = 2Nk(Au)
ACk (Achiral; Binomial Edge colors) = Nk(Ag) − Nk(Au).
We also note that as k approaches 3n/4, where n is the number of vertices of the fullerene, we obtain Equation (18):
As can be seen from Table 2, Table 3, Table 4 and Table 5, the numbers of edge colorings rise astronomically even for 2 colorings, and hence, we obtain analytical expressions for any k. Such expressions can be derived from the original GCCI for the Ag and Au IRs for the edge colorings of the giant C240 fullerene cage as shown below:
where , where [ ] is an ordered partition of k into 2 parts such that both parts must be even.
where
We can also obtain the number of inequivalent ways of labeling all the edges of an icosahedral fullerene with n vertices as follows:
We can divide the above expression further into pent–hex and hex–hex edges with expressions (22) and (23), respectively:
4. Conclusions
In the present study, we have outlined powerful combinatorial techniques that synthesized Möbius inversion with the generalized version of Sheehan’s modification of Pόlya’s theorem to all characters of the irreducible representations of the icosahedral group and applied the techniques to enumerate the edge colorings of giant fullerene cages. We developed a computer code that was used to construct the results specifically for the binomial chiral and achiral edge colorings of giant fullerenes. We also showed how the techniques can be divided into combinatorial parts with varied color partitions for the pent–hex and hex–hex edges contained in these giant fullerenes. The existence of chiral colorings even for one black edge coloring was demonstrated for the C180 and C240 fullerenes. It was shown that the ratios of chiral colorings and total number of edge colorings asymptotically reach unity as the number of black colors becomes almost equal to the number of white colors. The present enumeration of edge colorings, especially with restrictions to nearest neighbor exclusion, can be of immense use in the combinatorics of equivalence classes of Kekulė structures and thus in the computations of stabilities of giant fullerenes using the conjugated circuit method or the topological resonance theory method. The present techniques considered in this study could have applications to NMR, multiple quantum NMR, and ESR where one seeks the number of different types of dipolar couplings or edge colorings. The present enumeration techniques can also be extended in the future to nanomaterials such as carbon nanotubes, carbon nanocones, nanotori, and other nanomaterials of ongoing experimental interest.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ghorbani, M.; Dehmer, M.; Emmert-Streib, F. Properties of Entropy-Based Topological Measures of Fullerenes. Mathematics 2020, 8, 740. [Google Scholar] [CrossRef]
- Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Emmert-Streib, F.; Mowshowitz, A. Hosoya entropy of fullerene graphs. Appl. Math. Comput. 2019, 352, 88–98. [Google Scholar] [CrossRef]
- Ghorbani, M.; Matthias, D.; Rajabi-Parsa, M.; Mowshowitz, A.; Emmert-Streib, F. On properties of distance-based entropies on fullerene graphs. Entropy 2019, 21, 482. [Google Scholar] [CrossRef]
- Balasubramanian, K. Enumeration of stereo, position and chiral isomers of polysubstituted giant fullerenes: Applications to C180 and C240. Fuller. Nanotub. Carbon Nanostruct. 2020, 2810, 1–10. [Google Scholar] [CrossRef]
- Feng, L.; Hao, Y.; Liu, A.; Slanina, Z. Trapping Metallic Oxide Clusters inside Fullerene Cages. Acc. Chem. Res. 2019, 52, 1802–1811. [Google Scholar] [CrossRef]
- Yu, P.; Shen, W.; Bao, L.; Pan, C.; Slanina, Z.; Lu, X. Trapping an unprecedented Ti3C3 unit into the icosahedral C80 fullerene: A crystallographic survey. Chem. Sci. 2019, 10, 10925–10930. [Google Scholar] [CrossRef]
- Hu, S.; Liu, T.; Shen, W.; Slanina, Z.; Akasaka, T.; Xie, Y.; Uhlik, F.; Huang, W.; Lu, X. Isolation and Structural Characterization of Er@C2v (9)-C82 and Er@Cs(6)-C82: Regioselective Dimerization of a Pristine Endohedral Metallofullerene Induced by Cage Symmetry. Inorg. Chem. 2019, 58, 2177–2182. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. Long carbon chain molecules in circumstellar shells. Astrophys. J. 1987, 314, 352–355. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.; Irsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, K.; Nakahara, N.; Wakabayashi, T.; Suzuki, S.; Shiromaru, H.; Miyake, Y.; Saito, K.; Ikemoto, I.; Kainosho, M.; Achiba, Y. NMR Characterization of Isomers of C78, C82 and C84 Fullerenes. Nature 1992, 357, 142–145. [Google Scholar] [CrossRef]
- Diederich, F.; Whetten, R.L.; Thilgen, C.; Ettl, R.; Chao, I.T.O.; Alvarez, M.M. Fullerene isomerism: Isolation of C2v,-C78 and D3-C78. Science 1991, 254, 1768–1770. [Google Scholar] [CrossRef] [PubMed]
- Simeonov, K.S.; Amsharov, K.Y.; Jansen, M. Chlorinated Derivatives of C78-Fullerene Isomers with Unusually Short Intermolecular Halogen–Halogen Contacts. Chem. A Eur. J. 2008, 14, 9585–9590. [Google Scholar] [CrossRef]
- Simeonov, K.S.; Amsharov, K.Y.; Krokos, E.; Jansen, M. An epilogue on the C78-fullerene family: The discovery and characterization of an elusive isomer. Angew. Chem. Int. Ed. 2008, 47, 6283–6285. [Google Scholar] [CrossRef]
- Diederich, F.; Ettl, R.; Rubin, Y.; Whetten, R.L.; Beck, R.; Alvarez, M.; Anz, S.; Sensharma, D.; Wudl, F.; Khemani, K.C.; et al. The higher fullerenes: Isolation and characterization of C76, C84, C90, C94, and C70O, an oxide of D5h-C70. Science 1991, 252, 548–551. [Google Scholar] [CrossRef]
- Troyanov, S.I.; Yang, S.; Chen, C.; Kemnitz, E. Six IPR isomers of C90 fullerene captured as chlorides: Carbon cage connectivities and chlorination patterns. Chem. A Eur. J. 2001, 17, 10662–10669. [Google Scholar] [CrossRef]
- Haddon, R.C.; Smalley, R.E. C240—The most chemically inert fullerene? Chem. Phys. Lett. 1997, 272, 38–42. [Google Scholar] [CrossRef]
- Wang, B.C.; Chiu, Y.N. Geometry and orbital symmetry relationships of giant and hyperfullerenes, pp. C240, C540, C960 and C1500. Synth. Met. 1993, 56, 2949–2954. [Google Scholar] [CrossRef]
- Terrones, M.; Terrones, G.; Terrones, H. Structure, Chirality, and Formation of Giant Icosahedral Fullerenes and Spherical Graphitic Onions. In Science of Crystal Structures; Springer: Cham, Switzerland, 2015; pp. 101–112. [Google Scholar]
- Martin, J.W.; McIntosh, G.J.; Arul, R.; Oosterbeek, R.N.; Kraft, M.; Söhnel, T. Giant fullerene formation through thermal treatment of fullerene soot. Carbon 2017, 125, 132–138. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity in Ih symmetrical fullerenes: The 2 (N + 1) 2 rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
- Dodziuk, H.; Ruud, K.; Korona, T.; Demissie, T.B. Chiral recognition by fullerenes: CHFClBr enantiomers in the C82 cage. Phys. Chem. Chem. Phys. 2016, 18, 26057–26068. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.B., III; Strongin, R.M.; Brard, L.; Furst, G.T.; Romanow, W.J.; Owens, K.G.; Goldschmidt, R.J.; King, R.C. Synthesis of prototypical fullerene cyclopropanes and annulenes. Isomer differentiation via NMR and UV spectroscopy. J. Am. Chem. Soc. 1995, 117, 5492–5502. [Google Scholar] [CrossRef]
- Thilgen, C.; Gosse, J.; Diederich, F. Chirality in fullerene chemistry. Top. Stereochem. 2003, 23, 1–124. [Google Scholar] [CrossRef]
- Yang, S.; Wang, S.; Kemnitz, E.; Troyanov, S.I. Chlorination of IPR C100 fullerene affords unconventional C96Cl20 with a nonclassical cage containing three heptagons. Angew. Chem. Int. Ed. 2014, 53, 2460–2463. [Google Scholar] [CrossRef]
- Wang, S.; Yang, S.; Kemnitz, E.; Troyanov, S.I. New giant fullerenes identified as chloro derivatives, pp. isolated-pentagon-rule C108 (1771) Cl12 C106 (1155) Cl24 as well as nonclassical C104Cl24. Inorg. Chem. 2016, 55, 5741–5743. [Google Scholar] [CrossRef]
- Ghorbani, M.; Songhori, M.; Ashrafi, A.R.; Graovac, A.A. Symmetry group of (3, 6)-fullerenes. Fuller. Nanotub. Carbon Nanostruct. 2015, 23, 788–791. [Google Scholar] [CrossRef]
- Balasubramanian, K. Enumeration of chiral and positional isomers of substituted fullerene cages (C20-C70). J. Phys. Chem. 1993, 97, 6990–6998. [Google Scholar] [CrossRef]
- Balasubramanian, K. Enumeration of isomers of substituted fullerene cages C20- C50. Chem. Phys. Lett. 1993, 202, 399–405. [Google Scholar]
- Ghorbani, M.; Jalali, M. Counting numbers of permutational isomers of hetero fullerenes. Dig. J. Nanomater. Biostruct. 2008, 3, 269–275. [Google Scholar]
- Balasubramanian, K. Enumeration of chiral and achiral edge and face substitutions of buckminsterfullerene. Chem. Phys. Lett. 1995, 237, 229–238. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological characterization of five C78 fullerene isomers. Chem. Phys. Lett. 1993, 206, 210–216. [Google Scholar] [CrossRef]
- Balasubramanian, K. Laplacians of Fullerenes (C42-C90). J. Phys. Chem. 1995, 99, 6509–6518. [Google Scholar] [CrossRef]
- Balasubramanian, K. Characteristic polynomials of fullerene cages. Chem. Phys. Lett. 1992, 198, 577–586. [Google Scholar] [CrossRef]
- Balasubramanian, K. Group theoretical analysis of vibrational modes and rovibronic levels of extended aromatic C48N12 azafullerene. Chem. Phys. Lett. 2004, 391, 64–68. [Google Scholar] [CrossRef]
- Balaban, A.T.; Liu, X.; Klein, D.J.; Babić, D.; Schmalz, T.G.; Seitz, W.A.; Randić, M. Graph invariants for fullerenes. J. Chem. Inf. Comput. Sci. 1995, 35, 396–404. [Google Scholar] [CrossRef]
- Fripertinger, H. The cycle index of the symmetry group of the fullerene C60. MATCH Commun. Math. Comput. Chem 1996, 33, 121–138. [Google Scholar]
- Poater, A.; Saliner, A.G.; Carbó-Dorca, R.; Poater, J.; Solà, M.; Cavallo, L.; Worth, A.P. Modeling the structure-property relationships of nanoneedles: A journey toward nanomedicine. J. Comput. Chem. 2009, 30, 275–284. [Google Scholar] [CrossRef]
- Carbo-Dorca, R.; Besalu, E. Construction of coherent nano quantitative structure–properties relationships (nano-QSPR) models and catastrophe theory. SAR QSAR Environ. Res. 2011, 22, 661–665. [Google Scholar] [CrossRef]
- Terrones, M.; Terrones, G.; Terrones, H. Structure, chirality, and formation of giant icosahedral fullerenes and spherical graphitic onions. Struct. Chem. 2002, 13, 373. [Google Scholar] [CrossRef]
- Aihara, J.I.; Makino, M.; Ishida, T.; Dias, J.R. Analytical study of superaromaticity in cycloarenes and related coronoid hydrocarbons. J. Phys. Chem. A 2013, 117, 4688–4697. [Google Scholar] [CrossRef] [PubMed]
- Makino, M.; Dias, J.R.; Aihara, J.I. Bond Resonance Energy Verification of σ-Aromaticity in Cycloalkanes. J. Phys. Chem. A 2020, 124, 4549–4555. [Google Scholar] [CrossRef] [PubMed]
- Aihara, J.I.; Hosoya, H. Aromaticity of multiply charged fullerene ions. Bull. Chem. Soc. Jpn. 1993, 66, 1955–1958. [Google Scholar] [CrossRef]
- Sakamoto, K.; Nishina, N.; Enoki, T.; Aihara, J.I. Aromatic character of nanographene model compounds. J. Phys. Chem. A 2014, 118, 3014–3025. [Google Scholar] [CrossRef]
- Ciesielski, A.; Krygowski, T.M.; Cyrański, M.K.; Dobrowolski, M.A.; Aihara, J.I. Graph–topological approach to magnetic properties of benzenoid hydrocarbons. Phys. Chem. Chem. Phys. 2009, 11, 11447–11455. [Google Scholar] [CrossRef]
- Balasubramanian, K. Combinatorial Enumeration of Isomers of Superaromatic Polysubstituted Cycloarenes and Coronoid Hydrocarbons with Applications to NMR. J. Phys. Chem. A 2018, 122, 8243–8257. [Google Scholar] [CrossRef]
- Dias, J.R. Handbook of Polycyclic Hydrocarbons. Part A: Benzenoid Hydrocarbons; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Dias, J.R. Perimeter Topology of Benzenoid Polycyclic Hydrocarbons. J. Chem. Inf. Model. 2005, 45, 562–571. [Google Scholar] [CrossRef]
- Randić, M. Graph theoretical approach to π-electron currents in polycyclic conjugated hydrocarbons. Chem. Phys. Lett. 2010, 500, 123–127. [Google Scholar] [CrossRef]
- Aihara, J.I. Topological resonance energy, bond resonance energy, and circuit resonance energy. J. Phys. Org. Chem. 2008, 21, 79–85. [Google Scholar] [CrossRef]
- Aihara, J.I.; Hosoya, H. Spherical aromaticity of buckminsterfullerene. Bull. Chem. Soc. Jpn. 1988, 61, 2657–2659. [Google Scholar] [CrossRef]
- Sheehan, J. On Pόlya’s Theorem. Can. J. Math. 1967, 19, 792–799. [Google Scholar] [CrossRef]
- Balasubramanian, K. Computational Enumeration of Colorings of Hyperplanes of Hypercubes for all Irreducible Representations and Applications. J. Math. Sci. Model. 2018, 2, 158–180. [Google Scholar] [CrossRef]
- Balasubramanian, K. Computational Combinatorics of Colorings of hyperplanes of 7D-hypercube for all Irreducible Representation. J. Comput. Chem. 2020, 41, 653–686. [Google Scholar] [CrossRef]
- Balasubramanian, K. Nuclear Spin Statistics of Fullerene Cages C20-C40. J. Phys. Chem. 1993, 97, 4647–4658. [Google Scholar] [CrossRef]
- Balasubramanian, K. Group theory, nuclear spin statistics and tunneling splittings 1,3,5-triamino-2,4,6-trinitrobenzene. Chem. Phys. Lett. 2004, 398, 15–21. [Google Scholar] [CrossRef]
- Balasubramanian, K. Relativity and the Jahn–Teller, Berry pseudorotations of TBP clusters: Group theory, spin–orbit and combinatorial nuclear spin statistics of TBP Desargues–Levi isomerization graph. J. Math. Chem. 2018, 56, 2194–2225. [Google Scholar] [CrossRef]
- Babić, D.; Došlić, T.; Douglas, J.; Klein, D.J.; Misra, A. Kekulenoid addition patterns for fullerenes and some lower homologs. Bull. Chem. Soc. Jpn. 2004, 77, 2003–2010. [Google Scholar]
- Majumdar, D.; Roszak, S.; Balasubramanian, K.; Nitsche, H. Theoretical study of aqueous uranyl carbonate (UO2CO3) and its hydrated complexes: UO2CO3·nH2O (n = 1–3). Chem. Phys. Lett. 2003, 372, 232–241. [Google Scholar] [CrossRef]
- Schwaiger, L.K.; Parsons-Moss, T.; Hubaud, A.; Tueysuez, H.; Balasubramanian, K.; Yang, P.; Nitsche, H. Actinide and lanthanide complexation by organically modified mesoporous silica. Abstr. Pap. ACS 2010, 239, 98. [Google Scholar]
- Parsons-Moss, T.; Schwaiger, L.K.; Hubaud, A.; Hu, Y.J.; Tuysuz, H.; Yang, P.; Balasubramanian, K.; Nitsche, H. Plutonium complexation by phosphonate-functionalized mesoporous silica. Abstr. Pap. ACS 2011, 241, 48. [Google Scholar]
- Balasubramanian, K.; Ori, O.; Cataldo, F.; Ashrafi, A.R.; Putz, M.V. Face Colorings and Chiral Face Colorings of Icosahedral Giant Fullerenes: C80 to C240. Fuller. Nanotub. Carbon Nanostruct. 2020. (In Press)
- Balasubramanian, K. Nuclear spin statistics of extended aromatic C48N12 azafullerene. Chem. Phys. Lett. 2004, 391, 69–74. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).