Abstract
The extension of the Standard model by three right-handed neutrino fields exhibit appealing symmetry between left-handed and right-handed sectors, which is only violated by interactions. It can accommodate three flavor quasi-Dirac neutrino mixing scheme, which allows processes with violation of both lepton flavor and total lepton number symmetries. We propose a unitary matrix for parameterizing the mixing among three flavors of quasi-Dirac neutrino. This mixing matrix is constructed by two unitary matrices that diagonalizes the Dirac mass term in the Lagrangian. By only assuming the Standard Model weak interaction, it is found that probabilities of neutrino oscillations among active flavor states and effective masses measured by single beta decay, by neutrinoless double-beta decay and by cosmology only depend on single unitary matrix relevant to mixing of active neutrino flavors. Further, by considering and uncertainties in the measured oscillation probability of electron antineutrino from reactor, derivation of the constraint on the Majorana neutrino mass component is demonstrated. The consequence for effective Majorana neutrino mass governing the neutrinoless double-beta decay is discussed.
1. Introduction
The discovery of neutrino oscillations in experiments with atmospheric, solar, reactor, and accelerator neutrinos have provided compelling evidence that flavor neutrinos oscillate from one flavor (electron-, muon-, and tau-) to another due to neutrino mixing and that neutrinos possess nonzero masses [1], which offer an insight on new physics beyond the Standard Model (SM) [2].
The data from all neutrino oscillation experiments are well described by the three-neutrino mixing:
where is the field of the neutrino with mass and are the elements of the Pontecorvo-Maki-Nakagawa-Sakata unitary neutrino matrix [3,4].
The observation of neutrino oscillations implies that the flavor lepton numbers , , and are not conserved, which follows from the presence of flavor-mixing neutrino mass term in Lagrangian of the theory. If the total lepton number is conserved, neutrinos with definite masses are Dirac particles (i.e., different from their antiparticle). The theoretical expectation is that L is not conserved and, consequently, neutrinos are Majorana particles (i.e., identical to its own antiparticle). The fundamental problem of nature of neutrinos, which is directly related with the origin of neutrino masses and mixing, can be experimentally solved by the observation of the L violating processes, e.g., neutrinoless double-beta () decay [5,6].
In the case of the most general Dirac-Majorana mass term, fields of neutrinos with definite masses are of Majorana nature and their number depends on number of sterile fields (not entering in the gauge interaction Lagrangian of the SM) and is larger than three [7]. The Dirac-Majorana mass term can accommodate the seesaw scenario [8,9,10,11], which helps to understand the smallness of the neutrino masses constrained by laboratory and cosmological measurements. In the classical realization of the seesaw scenario with three right-handed neutrino fields, the Dirac-Majorana mass term is dominated by the lepton-number-violating right-handed neutrino Majorana masses giving rise to three light and active neutrinos, and three very heavy sterile neutrinos. Out of these, only the three active neutrinos participate in solar, atmospheric, and terrestrial neutrino flavor oscillations.
The goal of this paper is to discuss an opposite scenario, in which the Dirac-Majorana mass term is dominated by the Dirac masses. Such a scenario, in general, leads to six Majorana neutrino states with pairwise quasi-degenerate masses, referred to as quasi-Dirac neutrinos, see, e.g., [12,13,14,15] and references therein. Here, all six states participate in neutrino flavor oscillations providing much richer oscillation phenomenology. The tiny neutrino masses can be ascribed to the smallness of neutrino Yukawa couplings with difficulty to explain why the fermion masses span twelve orders of magnitude. The solution to this problem can be inspired by extra-dimensional models [16] or can be due a radiative mechanism for neutrino mass generation [17]. Once the right-handed neutrino fields are accepted in the theory, it is mandatory to also investigate the quasi-Dirac neutrino regime of the Dirac-Majorana mass term. The quasi-Dirac neutrinos are distinct from, so called, pseudo-Dirac neutrinos [7,18], which also exhibit quasi-degenerate mass spectrum, however they are composed exclusively of active neutrino flavors.
In this paper, a special form of mixing matrix corresponding to this case, which is constructed with two unitary matrices, will be presented and motivated. By assuming single small Majorana component of neutrino masses, the oscillation probabilities and quantities measured in single and -decay experiments and in cosmology will be determined. Further, restriction on this parameter coming from oscillations of electron antineutrinos will be studied and consequences for observation of the -decay will be given.
2. Theory
The quasi-Dirac (QD) neutrino scenario requires a number of right-handed neutrino fields added into the SM Lagrangian, which mix with the SM left-handed neutrino fields via both the Dirac mass matrix and the Majorana mass matrices , as opposed to the older idea of pseudo-Dirac neutrinos [7]. In this work, we limit ourselves to the natural case of . In that case, the neutrino Dirac–Majorana mass term in Lagrangian is given as
where the mass matrix is a symmetric matrix
where is a complex matrix parametrized by 18 real numbers, and are complex symmetric matrices parametrized by 12 real numbers each. Altogether, it makes 42 real parameters, out of which six are mass eigenvalues and six are phases absorbed by three left-handed and three right-handed neutrino fields. One is left with 15 angles and 15 phases of the unitary mixing matrix , which diagonalizes the mass matrix according to
where is a diagonal mass matrix, which, in general, is given by three Dirac masses and 3 mass splittings , so that six neutrino mass eigenvalues are parametrized as
The QD neutrino regime is defined by hierarchy . This can be achieved in two different regimes: (A) , or (B) . In order to get the QD mass spectrum within the regime (B), extreme fine-tuning of elements of and is required, so that large contributions to the mass splitting cancel out. Clearly, some symmetry would be needed to make it natural. In what follows, the subject of our interest is regime (A).
A general parametrization of the unitary diagonalization matrix can be introduced according to Xing [19] as a product of three unitary matrices (Here, we are using just slightly different parametrization from that used in [19], . The difference is in the ordering of matrices in the product).
where and mix exclusively active or sterile neutrino flavors, or , respectively,
each containing three angles and three phases. The remaining nine angles and nine phases are included in the matrix , for which the perturbative expansion up to the linear order in the mixing angles gathered in the general matrix X is
For the purpose of the QD scenario, it is useful to reproduce the pure Dirac case for . This can be done by inserting a constant unitary matrix into the definition of the QD unitary diagonalization matrix
where
The expansion of the matrix up to first order in X is then given as
From that, it can be seen that for the unitary matrix diagonalizing the pure Dirac mass term is reproduced,
provided that the Dirac mass matrix is diagonalized by a bi-unitary transformation
where the tilde denotes that the matrix is diagonalized with the eigenvalues of on its diagonal.
The elements of the matrix X are actually calculable perturbatively from the known entries of the neutrino mass matrix, and , under the assumption that the X is just small perturbation of the Dirac diagonalization matrix at the same level as the Majorana masses are small perturbations of the purely Dirac mass matrix , i.e., under the assumption
The perturbative diagonalization of the Dirac–Majorana mass matrix (3) to the first order gives the relation between X and , dependent on and its bi-unitary diagonalization,
which is obtained by the requirement that the off-diagonal blocks of vanish to the first order in X and . Simultaneously, the perturbative expressions for diagonal blocks of QD mass matrix after the block-diagonalization to the first order in X and is given as
which should be further diagonalized in order to come to the mass eigenvalues (5). Interestingly, the X does not enter the first-order expression for the block-diagonalized masses.
The Equations (11) and (17) are the three-flavor generalization of the toy one-flavor QD neutrino case discussed in [14,15]. It exhibits the same feature that the mass splitting and mixing angles X are two independent sets of beyond-Dirac parameters. In the special case, when
we encounter the analogous situation to the pseudo-Dirac neutrinos that are described in [18]. In that case, the neutrino mass matrix provides three pairs of eigenvalues degenerate in magnitude, which correspond to three Dirac neutrinos. The lepton number violating masses are, however, non-zero, as well as the beyond-Dirac mixing angles X. These new Dirac neutrinos carry a new lepton number , which is, however, explicitly broken by weak interactions. Weak interactions generate tiny mass splitting [18] (One should be careful here, as the condition (18) is derived from the perturbative expressions linear in and . It is expected that higher-order terms also lift the degeneracy).
In the analysis within the present work, we will use just simplified model, which is exclusively focused on studying the effects of neutrino mass splitting. Therefore, we set all beyond-Dirac mixing angles to zero, i.e.,
As a consequence, the first order expression for the block-diagonalized masses (17) becomes exact. On top of that, again for simplicity, we choose and in such way that
leading to the simplified QD neutrino mass spectrum with a universal Majorana mass splitting
As a result of these assumptions, it is the matrix
which plays the role of the QD generalization of the PMNS mixing matrix.
3. Consequences of Our Specific QD Scenario for Processes Measuring Neutrino Masses
The general formula for probabilities of neutrino oscillations from flavor to flavor for our specific scenario that is given by (21) and (22) can be written as
From here, it can be clearly seen that, if and takes value only for active neutrino flavors, i.e., , only the matrix U, and not V, is entering the oscillation probabilities. For the matrix U, we take the standard parmetrization
where
, and are three mixing angles, is the violating Dirac phase and and are two violating Majorana phases. In terms of U, the oscillation probabilities among active neutrinos under our assumptions (19) and (20) are given by,
The matrix V enters the probability for oscillations, in which sterile neutrino flavors, , are involved. With , Equation (26) reproduces the well known expression of oscillation probability for three-neutrino mixing.
The oscillation probabilities are functions of 15 mass-squared differences. Among them, just five are independent and are expressed in terms of 6 parameters, either , or and . Within our constrained neutrino mass spectrum (21), , they are explicitly given as
for , and for
There are just four parameters, and . These can be traded for another set of four parameters, , , and , as we can write
As a result, due to the additional assumption (21), , we can completely fix the neutrino mass spectrum, including its absolute mass scale by fitting all oscillation frequencies given by five independent mass-squared differences. This is, of course, not possible in general case with three independent mass splittings , as fixing of the five independent mass-squared differences is not enough to determine six mass parameters, and .
The amplitude for the decay is given by the effective Majorana neutrino mass defined as
For our constrained case and , it reduces to the expression
It means that the effective neutrino mass for decay is, in our scenario, directly proportional to the mass splitting with the factor of proportionality of the order of ∼ given the best fit values for and , and for marginalized values of the Majorana phases and .
The effective electron neutrino mass for single beta decay is in our case
where is the effective neutrino mass for standard three neutrino mixing case.
The sum of the six QD neutrino mass eigenvalues is the parameter relevant for cosmology. It turns out trivially that the cosmology is insensitive to the universal mass splitting used in our simplified model as long as :
The factor of reflects the QD (or Dirac) nature of neutrinos, in which case, effectively, only two out of their four states are kept in equilibrium with cosmological plasma of the early Universe by the interactions of the SM.
4. The Survival Probabilities of Electron Antineutrino
In this section, we discuss the survival probability () of electron antineutrino produced at the reactor with energy E and detected at the detector after traversing a baseline L. In three-flavor model of neutrino oscillation, the well-known expression of , which can be obtained by putting in Equation (26), is given by
In above equation, and are solar and atmospheric mass-squared differences, respectively. The parameter and are mixing angles that are related to our matrix U [3,4]. One can see that the survival probability is a function of mass-squared differences, and does not depend on the absolute mass scale of neutrino. In case of quasi-Dirac nature of neutrino, , and the mixing among active and sterile neutrinos modifies the neutrino oscillation probabilities. For , we obtain the expression of survival probability from Equation (26), as follows,
with
For very small , with an approximation of , Equation (37) boils down to the following simplified expression of survival probability of ,
where . Using this simple expression, we can explain the following features of survival probability with a small value of .
- We see that is directly proportional to ratio multiplied with . Thus, as we go to higher , the effect of becomes larger.
- Since is very small when compared to , the term in second part of Equation (38) becomes negligible as compared to two other terms containing and , respectively. As a result, the second part of Equation (38) in the case of NO () is always smaller than that in IO scenario (). Therefore, we expect the modification in survival probability due to non-zero to be smaller when the mass pattern is NO than that for IO.
In Figure 1, we show the survival probabilities of electron antineutrino as a function of energy for 1.5 km (top panels), 53 km (middle panels), and 180 km (bottom panels) baselines—relevant for short, medium, and long-baseline reactor neutrino oscillation experiments, respectively. We show the probabilities for three cases: , mixing case, eV, and with black, green, and red lines, respectively. The plots shown in left (right panels) are with normal (inverted) ordering for which () is lightest Dirac mass. Here, for cases and , lightest Dirac mass is assumed to be 0.01 eV. The value of oscillation parameters that we use in this study are given in Table 1. These values are similar as obtained in the global fit to neutrino oscillation data [20,21,22]. Note that, if the neutrino oscillation data are fitted in the current framework with six quasi-Dirac neutrinos, the best-fit value of mixing angles and mass-squared difference may be slightly different than that we use. However, we expect that these values will not be beyond the current allowed range, as obtained in the global fit of neutrino data in three-flavor Dirac neutrino mixing framework [20,21,22].
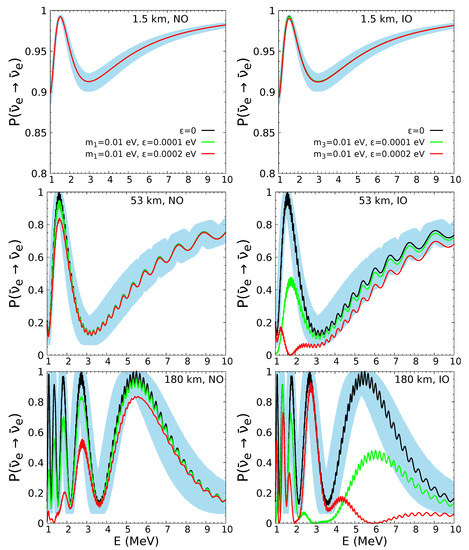
Figure 1.
The survival probabilities of as the functions of energy E for 1.5 km (upper panel), 53 km (middle panel), and 180 km (lower panel) baselines. The plots in left and right panels are with NO and IO as mass orderings, respectively. The probabilities are shown for three cases: , mixing case, eV, and eV, with black, green, and red lines, respectively. In cases (ii) and (iii), the lightest Dirac mass is 0.01 eV. The cyan bands represent survival probabilities in three-flavor neutrino oscillation framework with allowed range of oscillation parameters. The benchmark values of oscillation parameters along and their allowed ranges, as used in this study, are given in Table 1.

Table 1.
The benchmark values of the oscillation parameters and their and allowed ranges that we use in this paper. These values are similar, as obtained in the global fit to neutrino oscillation data [20,21,22].
The common feature that emerges from all of the panels of Figure 1 is the larger effect of non-zero in survival probabilities for IO than NO. The reason behind this is already discussed while using Equation (37). In case of km baseline, the survival probability of shown in red and green lines (cases and ) are exactly same as black line (with ), as can be seen from top panels of Figure 1. This is true for both the mass orderings, NO and IO. From this observation, one can infer that the short-baseline experiments will not be able to see the signal for the quasi-Dirac nature of neutrino if is of the order of eV. For baseline 53 km (see middle panels of Figure 1), survival probabilities with cases (ii) and (iii) are similar to case (i), except a small difference at MeV if mass ordering is NO. However, with IO, survival probabilities get modified by a large amount in the whole range of E (1 MeV to 10 MeV) due to non-zero considered here. This proves that medium baseline neutrino oscillation experiment, like JUNO, will be able to see the signal for quasi-Dirac nature of neutrino with eV only if mass ordering is IO. As we go to higher L, for an example L = 180 km (see bottom panels of Figure 1), survival probabilities with eV (green and red lines) are significantly different than that of the three-flavor. Thus, we expect that long-baseline reactor neutrino experiments are suitable for providing better constraint on .
5. Constraints on Majorana Component of Neutrino Masses
A preliminary idea about the allowed values of lightest Dirac mass and can be achieved from survival probabilities for a fixed neutrino energy and baseline. Keeping the oscillation parameters fixed at the benchmark values, we scan the lightest Dirac mass ( for NO and for IO) and in the range of eV to eV to reproduce the survival probabilities in the range that is allowed by the three-flavor neutrino oscillation framework and the current or uncertainties of oscillation parameters.
Figure 2 presents the allowed region in the plane of lightest Dirac mass and which we obtain following the above mentioned method for 1.5 km baseline and two fixed energies 4 MeV (top panels) and 8 MeV (bottom panels) for demonstration purpose. We present these limits with benchmark values (green line), (pink and red lines) and (cyan and blue lines) allowed range of oscillation parameters. The limits in the case of IO (right panels) is more stringent than that for NO (left panels) for both of the energies due to a larger effect of in survival probabilities for IO, which is explained in Section 4.
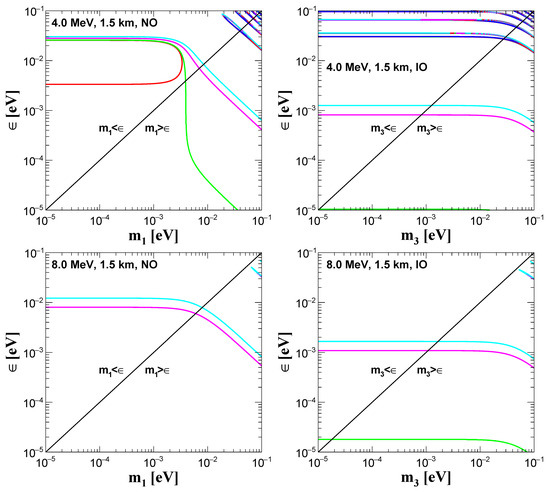
Figure 2.
The top (bottom) panels show the allowed ranges of lightest Dirac mass and that are obtained using 1.5 km baseline and 4 MeV (8 MeV) energy. The left and right panels are obtained with NO and IO, respectively. In all of the panels, pink (cyan) and red (blue) lines correspond to minimum and maximum survival probabilities, respectively, allowed in three-flavor neutrino oscillation picture with () uncertainty of oscillation parameters. The green line corresponds to survival probability in framework with the benchmark value of oscillation parameters. For details, see text. The benchmark values of oscillation parameters along with their and allowed ranges, used in this study, are given in Table 1.
If we ignore the small features above eV, which are expected to have just a small chance to survive after the full oscillation data analysis of the QD scenario, one may say that the region below the cyan line in all of the panels Figure 2 are allowed by uncertainty of oscillation parameters. Here, we do not demand that these limits are final since the detailed statistical analysis with spectral information of events with detector properties would give the concrete results. Our attempt here is to demonstrate the validity of the theory that we propose based on the oscillation probabilities in a simplified manner. The study of quasi-Dirac neutrino with detailed analysis of events at the neutrino oscillation experiments to constraint the lightest Dirac mass and in this framework would be interesting for future study.
Obviously, Figure 2 shows larger region of - parametric space than corresponding to QD scenario defined by . Namely, the additional regions lie around and above the diagonal axis, where the lightest Dirac mass gets comparable and smaller to , respectively. The allowed region, below the cyan line, however still guarantees that at least the heaviest pair of neutrinos is of QD nature.
If the limits that are given by the cyan lines () in the Figure 2 will be approved by the future full analysis, the conservative limits on the effective neutrino Majorana mass within our simplified QD model will be
As seen from Equation (31), the represents linear effect of , in contrast to the correction to the effective electron mass for single-beta decay given in Equation (32), which is quadratic in . Therefore, the effect of on the single-beta decay within our simplified QD model is expected to be, at most, at the level of few percent, as long as in NO or in IO. The cosmology is in this regime even completely insensitive to , see Equation (33).
The above conclusions are valid for the universal Majorana mass contribution to neutrino masses. More comprehensive analysis with non-universal ( to 3) and mixing angles as free parameters could modify this conclusion about and its dependence on Dirac component of lightest neutrino mass via neutrino oscillation analysis. Recall that the oscillation probabilities of neutrinos depend on both Dirac and Majorana masses.
6. Conclusions
The quasi-Dirac neutrino mixing scheme incorporating three pairs of Majorana neutrinos with quasi-degenerate masses was analyzed. The diagonalization of the Dirac-Majorana mass term with unitary neutrino mixing matrix, which is generally parametrized with 15 mixing angles and 15 CP-violating phases, was discussed. By exploiting the limiting case of three Dirac neutrinos and assuming a small Majorana component in neutrino masses, the quasi-Dirac neutrino mixing matrix constructed with two unitary mixing matrices, each of them incorporating three mixing angles and three phases, was proposed. For the sake of simplicity, only left-handed weak interaction of the SM was assumed. It was found that probabilities for oscillations of 3 flavor neutrinos () can be described with eight parameters, namely three angles (, , and ) and one Dirac CP phase having origin in a single unitary matrix, two mass squared differences ( and ), the lightest neutrino mass ( for normal ordering and for inverted ordering of Dirac neutrino masses), and a small Majorana neutrino mass parameter . Recall that, within the commonly considered mixing scheme of three neutrinos, the required number of parameters is only two less (three mixing angles, one phase, and two mass squared differences). Further, it was established that the effective Majorana mass entering the -decay rate is proportional to , the sum of neutrino masses measured by cosmology only contains contributions of Dirac masses , , and , and that the effective neutrino mass measured in tritium -decay is practically not affected by as long as it is a small quantity when compared to the Dirac masses, .
The first simplified analysis of parameters of 3+3 quasi-Dirac neutrino mixing scheme was performed by exploiting the and uncertainty of measured probability of oscillations from a reactor. The mixing angles , , and mass squared differences and were considered to be those that were determined within the PMNS unitary mixing scheme with three neutrinos. The lightest Dirac neutrino mass and were considered to be free parameters. It was manifested that a tiny value of below 1 MeV is not affecting the current phenomenology representing, e.g., by the Daya–Bay experiment, but they can have significant impact on the JUNO experiment registering oscillations of antineutrinos at significantly larger distance. A detailed study on restriction of , which depends on the considered value of lightest neutrino mass and ordering of neutrinos (normal or inverted) was presented. We keep our study simplified to have better insight. For this, in this paper, we study the consequences of quasi-Dirac scenario in neutrino oscillation when only considering the reactor experiments, since the oscillation channel that governs the disappearance of reactor is independent of Dirac CP phase as well as same as vacuum oscillation probabilities. It goes without saying that a more comprehensive analysis covering oscillations of atmospheric, solar, and terrestrial neutrinos in which all involved parameters are assumed to be free are a subject of interest. The three Majorana constituents of the neutrino mass would be considered as a free parameters and a comprehensive study of all parameters of this model would be performed by considering data of all types of neutrino oscillations experiments. It might be that due to a large number of degrees of freedom some unconventional solutions could be found, which will require additional neutrino oscillations experiments with different baselines, energy, and high statistics of data. Of course, this task is beyond the scope of the present article.
Author Contributions
A.K., A.S. and F.Š. contributed equally to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the VEGA Grant Agency of the Slovak Republic under Contract No. 1/0607/20 and by the Ministry of Education, Youth and Sports of the Czech Republic under the INAFYM Grant No. CZ.02.1.01/0.0/0.0/16_019/0000766.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Bilenky, S. Neutrino oscillations: From a historical perspective to the present status. Nucl. Phys. B 2016, 908, 2–13. [Google Scholar] [CrossRef]
- Pontecorvo, B. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. Sov. Phys. JETP 1968, 26, 984–988. [Google Scholar]
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the unified model of elementary particles. Prog. Theor. Phys. 1962, 28, 870–880. [Google Scholar] [CrossRef]
- Vergados, J.D.; Ejiri, H.; Šimkovic, F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod. Phys. E 2016, 25, 1630007. [Google Scholar] [CrossRef]
- Dolinski, M.J.; Poon, A.W.; Rodejohann, W. Neutrinoless Double-Beta Decay: Status and Prospects. Ann. Rev. Nucl. Part. Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Petcov, S. Massive Neutrinos and Neutrino Oscillations. Rev. Mod. Phys. 1987, 59, 671, Erratum in 1989, 61, 169; Erratum in 1988, 60, 575–575. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Ramond, P.; Slansky, R. Complex Spinors and Unified Theories. Conf. Proc. C 1979, 790927, 315–321. [Google Scholar]
- Yanagida, T. Horizontal gauge symmetry and masses of neutrinos. Conf. Proc. C 1979, 7902131, 95–99. [Google Scholar]
- Mohapatra, R.N.; Senjanović, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912–915. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrino masses in SU(2) ⨂ U(1) theories. Phys. Rev. D 1980, 22, 2227–2235. [Google Scholar] [CrossRef]
- Valle, J.W.F. Neutrinoless double-β decay with quasi-Dirac neutrinos. Phys. Rev. D 1983, 27, 1672–1674. [Google Scholar] [CrossRef]
- De Gouvêa, A.; Huang, W.C.; Jenkins, J. Pseudo-Dirac neutrinos in the new standard model. Phys. Rev. D 2009, 80, 073007. [Google Scholar] [CrossRef]
- Anamiati, G.; Fonseca, R.M.; Hirsch, M. Quasi-Dirac neutrino oscillations. Phys. Rev. D 2018, 97, 095008. [Google Scholar] [CrossRef]
- Anamiati, G.; De Romeri, V.; Hirsch, M.; Ternes, C.A.; Tórtola, M. Quasi-Dirac neutrino oscillations at DUNE and JUNO. Phys. Rev. D 2019, 100, 035032. [Google Scholar] [CrossRef]
- Dienes, K.R.; Dudas, E.; Gherghetta, T. Neutrino oscillations without neutrino masses or heavy mass scales: A Higher dimensional seesaw mechanism. Nucl. Phys. B 1999, 557, 25–59. [Google Scholar] [CrossRef]
- Cai, Y.; Herrero-García, J.; Schmidt, M.A.; Vicente, A.; Volkas, R.R. From the trees to the forest: A review of radiative neutrino mass models. Front. Phys. 2017, 5, 63. [Google Scholar] [CrossRef]
- Wolfenstein, L. Different Varieties of Massive Dirac Neutrinos. Nucl. Phys. B 1981, 186, 147–152. [Google Scholar] [CrossRef]
- Xing, Z.Z. A full parametrization of the 6 X 6 flavor mixing matrix in the presence of three light or heavy sterile neutrinos. Phys. Rev. D 2012, 85, 013008. [Google Scholar] [CrossRef]
- Capozzi, F.; Di Valentino, E.; Lisi, E.; Marrone, A.; Melchiorri, A.; Palazzo, A. Addendum to: Global constraints on absolute neutrino masses and their ordering. arXiv 2020, arXiv:2003.08511. [Google Scholar] [CrossRef]
- De Salas, P.; Gariazzo, S.; Mena, O.; Ternes, C.; Tórtola, M. Neutrino Mass Ordering from Oscillations and Beyond: 2018 Status and Future Prospects. Front. Astron. Space Sci. 2018, 5, 36-1–36-50. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Hernandez-Cabezudo, A.; Maltoni, M.; Schwetz, T. Global analysis of three-flavour neutrino oscillations: Synergies and tensions in the determination of θ23, δCP, and the mass ordering. JHEP 2019, 1, 106. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).